Estimating Increased Transient Water Storage with Increases in Beaver Dam Activity
Abstract
1. Introduction
2. Materials and Methods
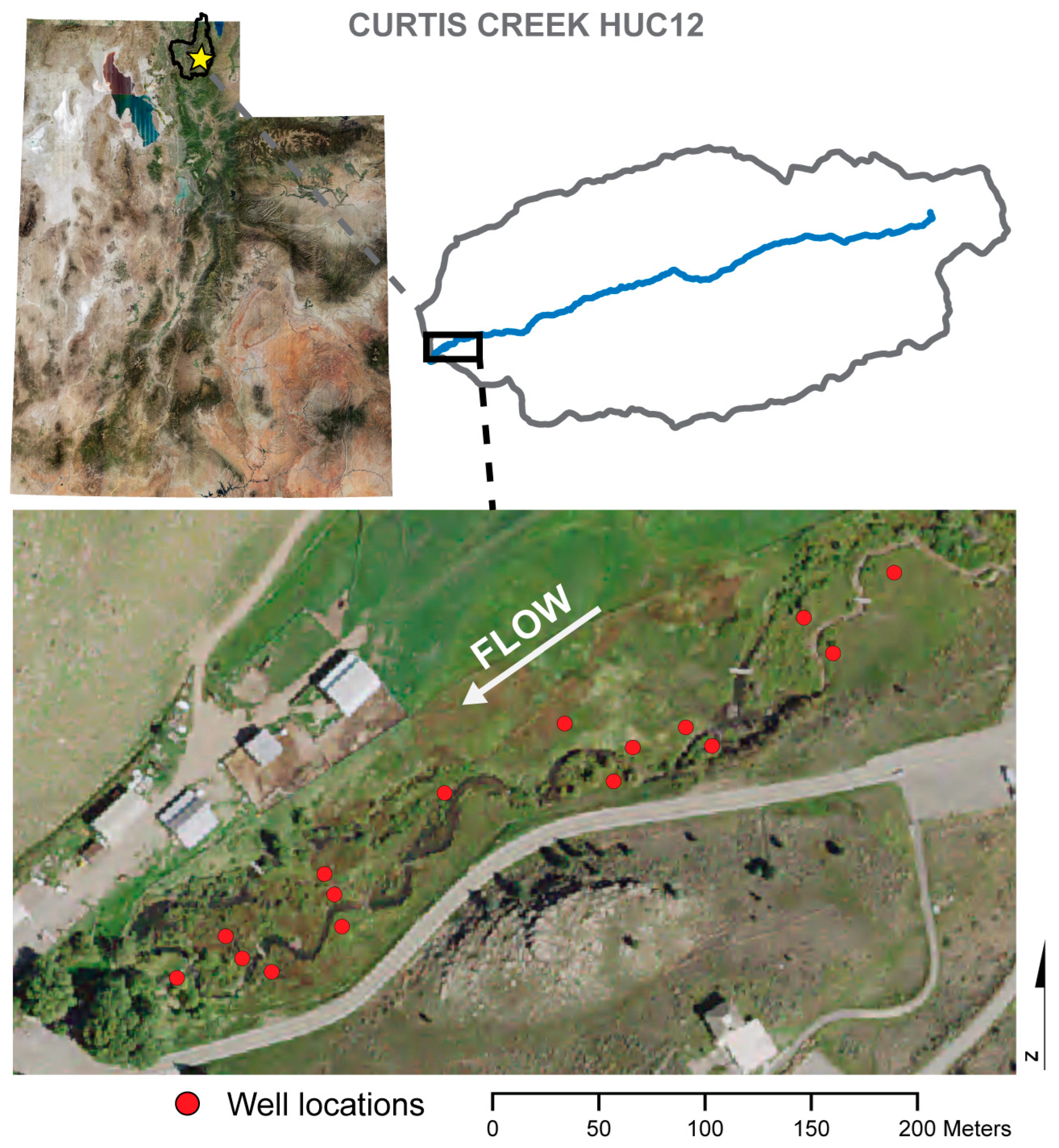
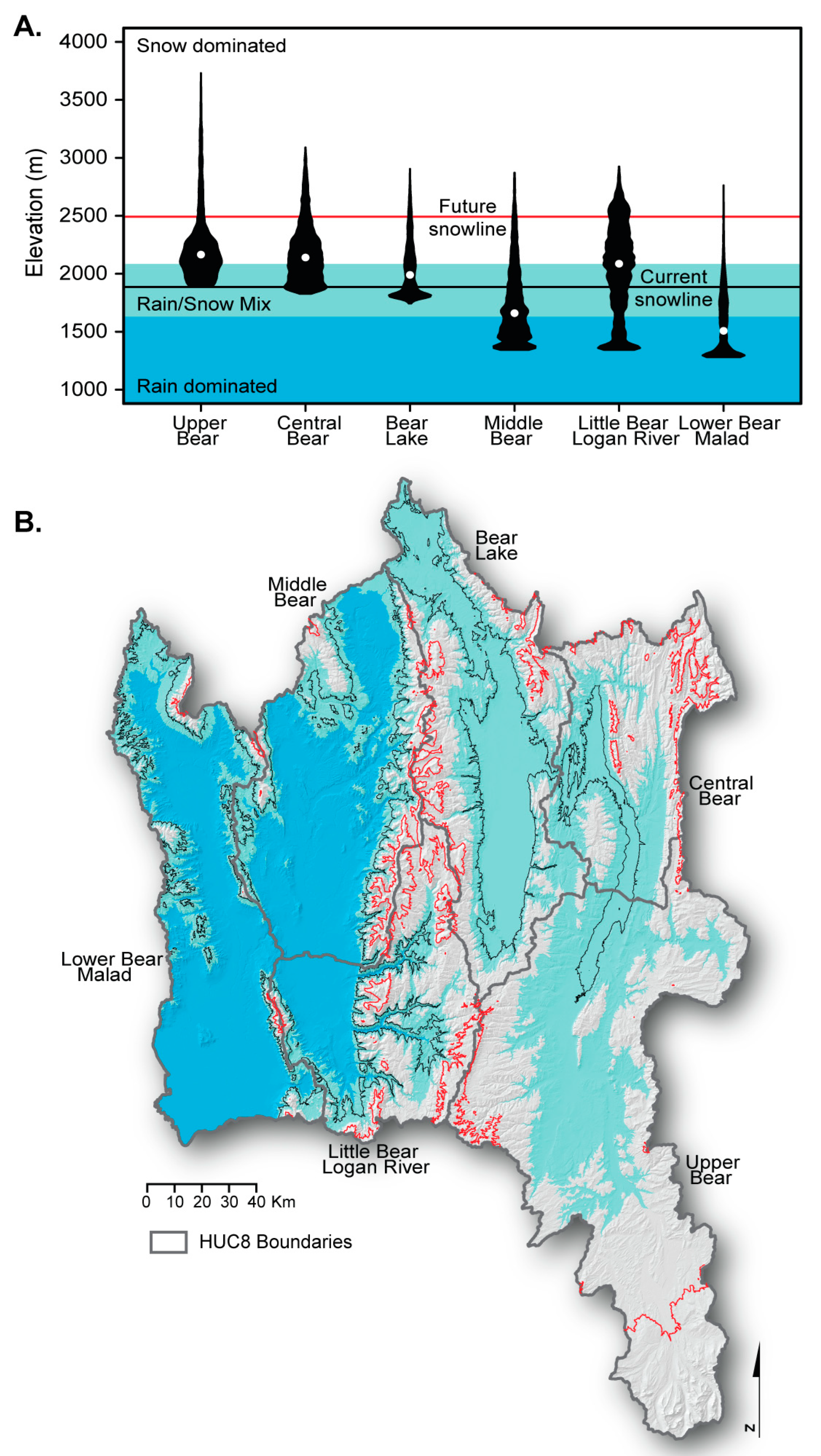
2.1. Study Area
2.2. Modeling Beaver Dam Capacity
Placement of Individual Beaver Dams
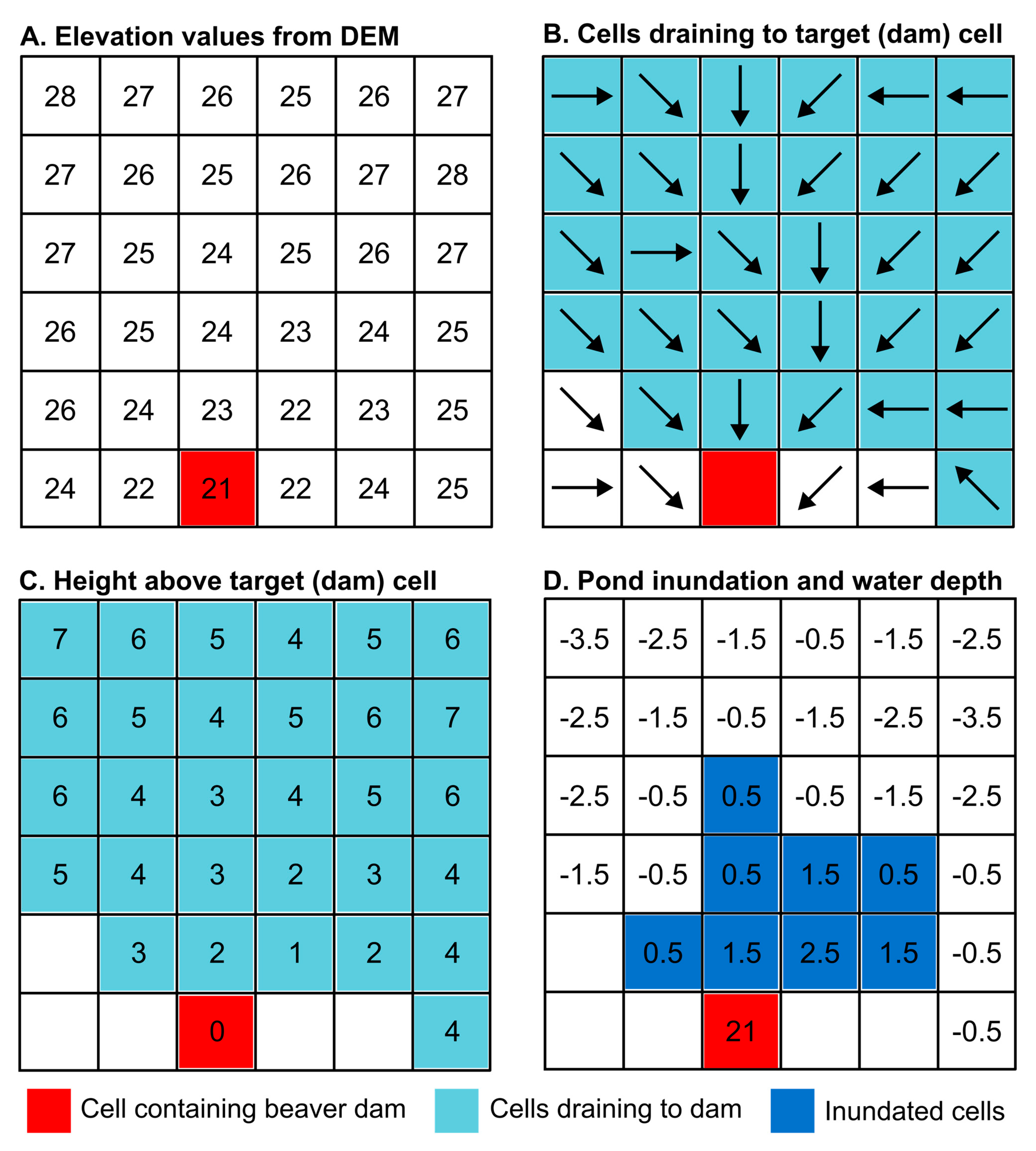
2.3. Modeling Beaver Pond Water Storage
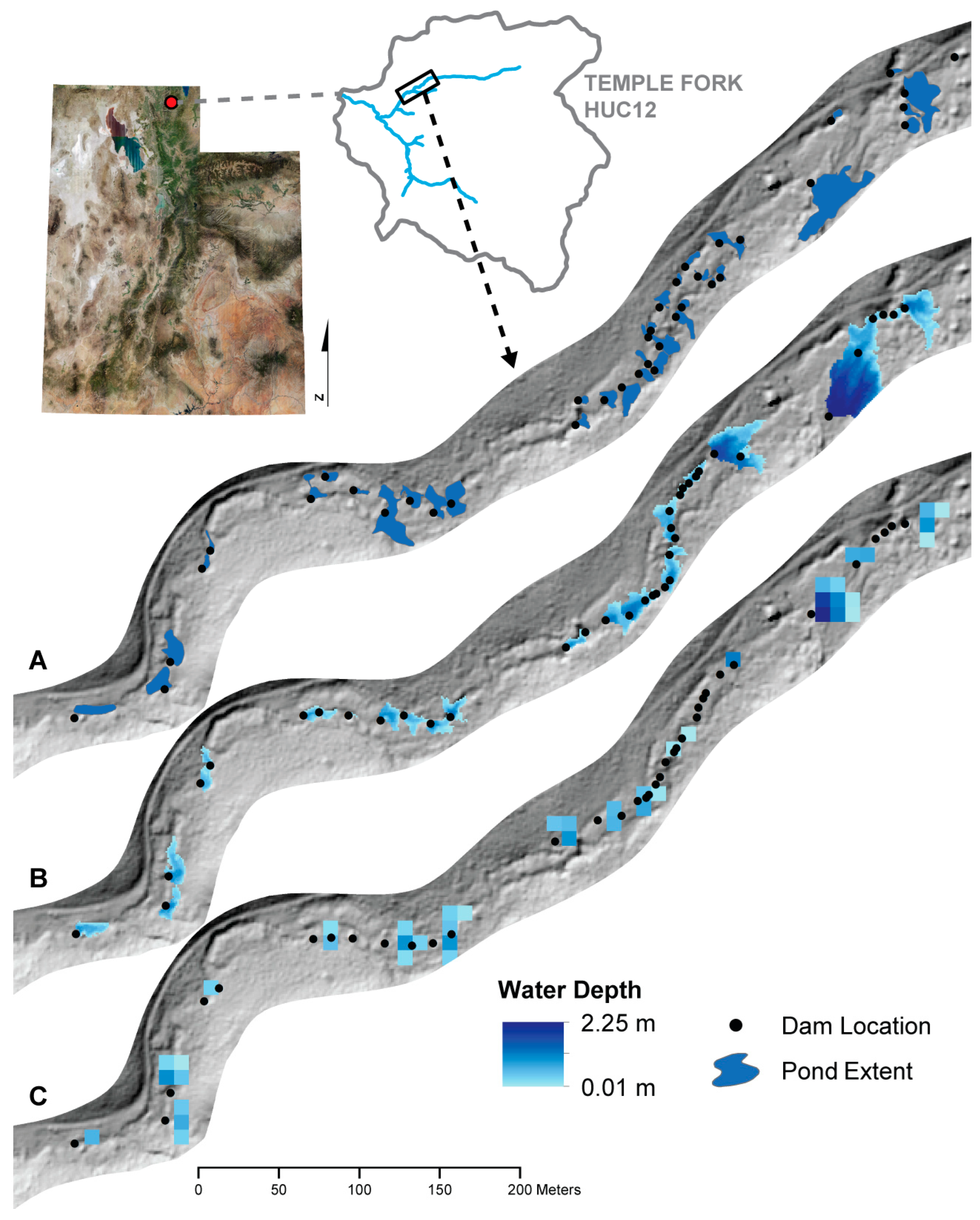
2.3.1. Surface Water Storage Model
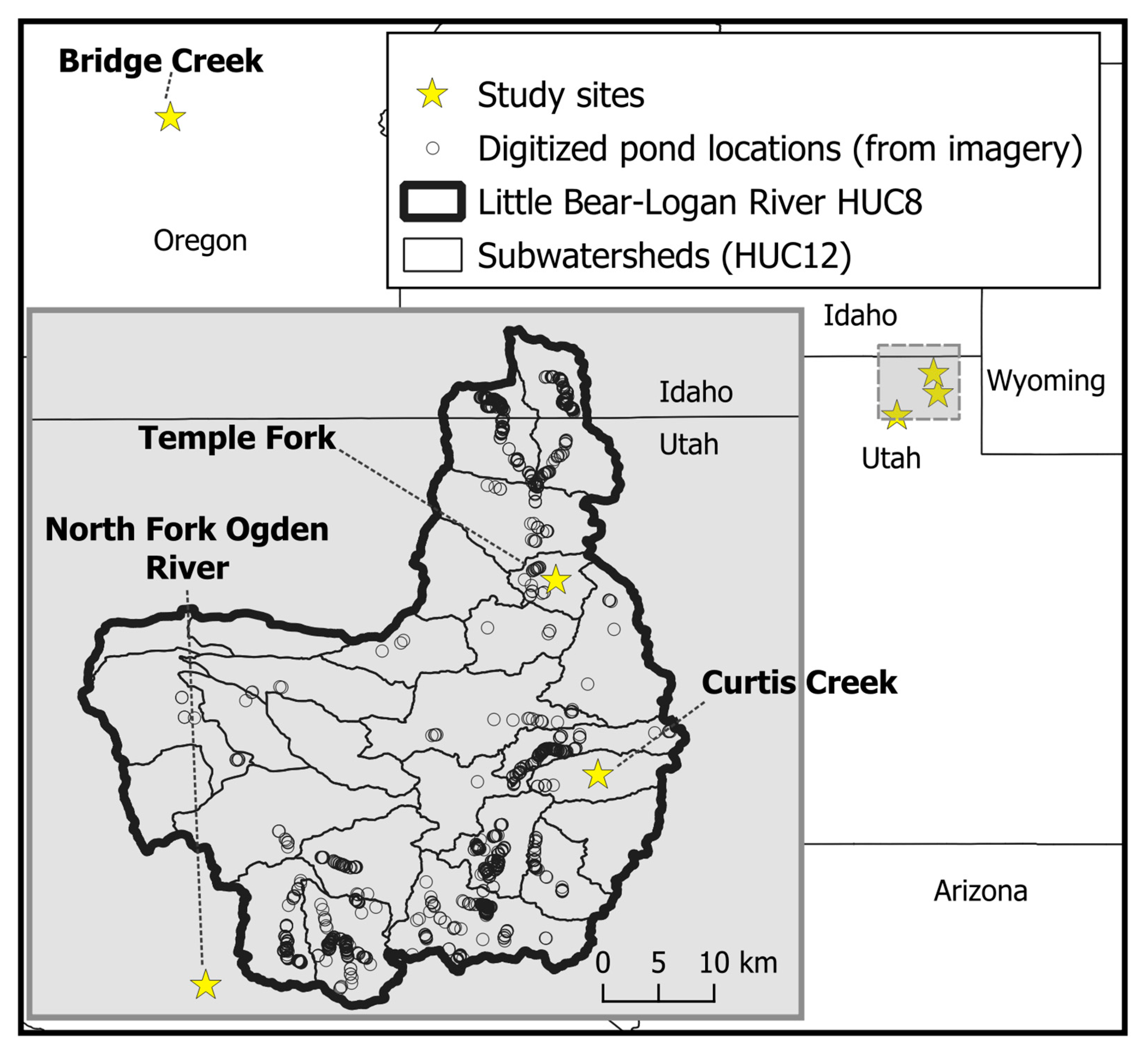
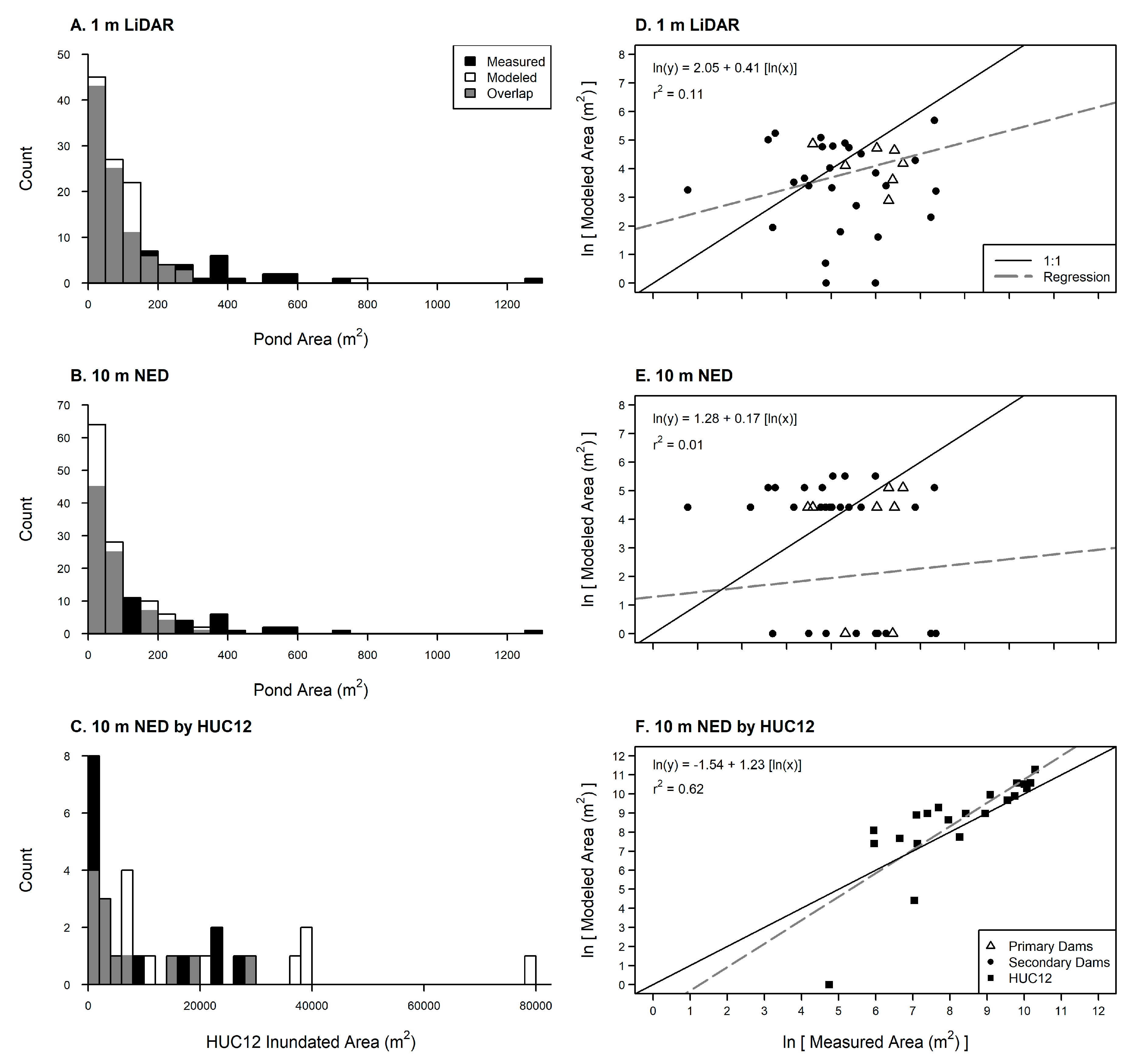
2.3.2. Surface Water Validation Data
2.3.3. Surface Water Storage Validation
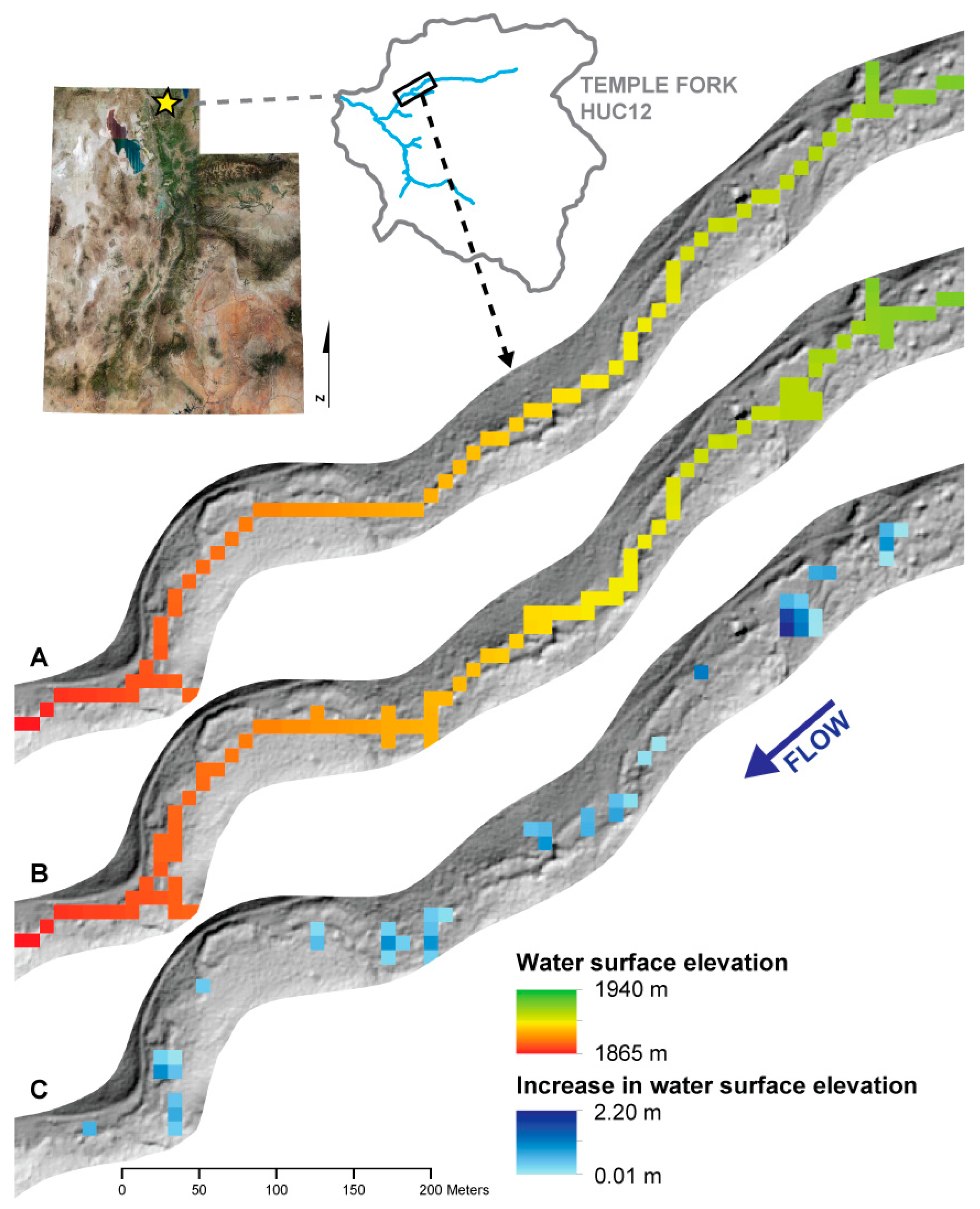
2.3.4. Groundwater Storage Model
2.3.5. Groundwater Storage Validation
2.3.6. Estimating Total Water Storage
2.4. Estimating Snowpack Decline
3. Results
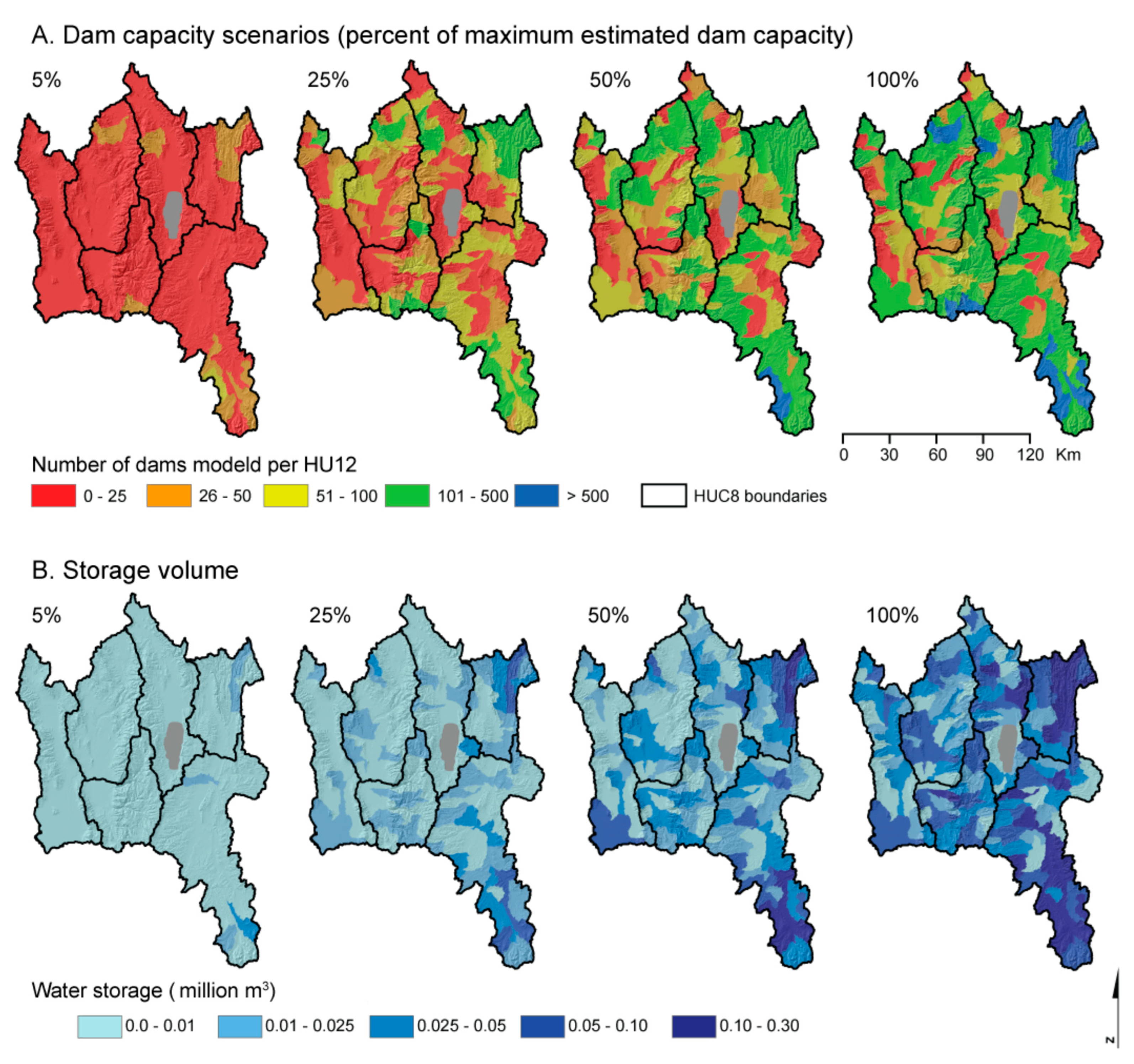
3.1. Beaver Dam Capacity
3.2. Beaver Pond Water Storage
3.2.1. Surface Water Storage
3.2.2. Groundwater Storage
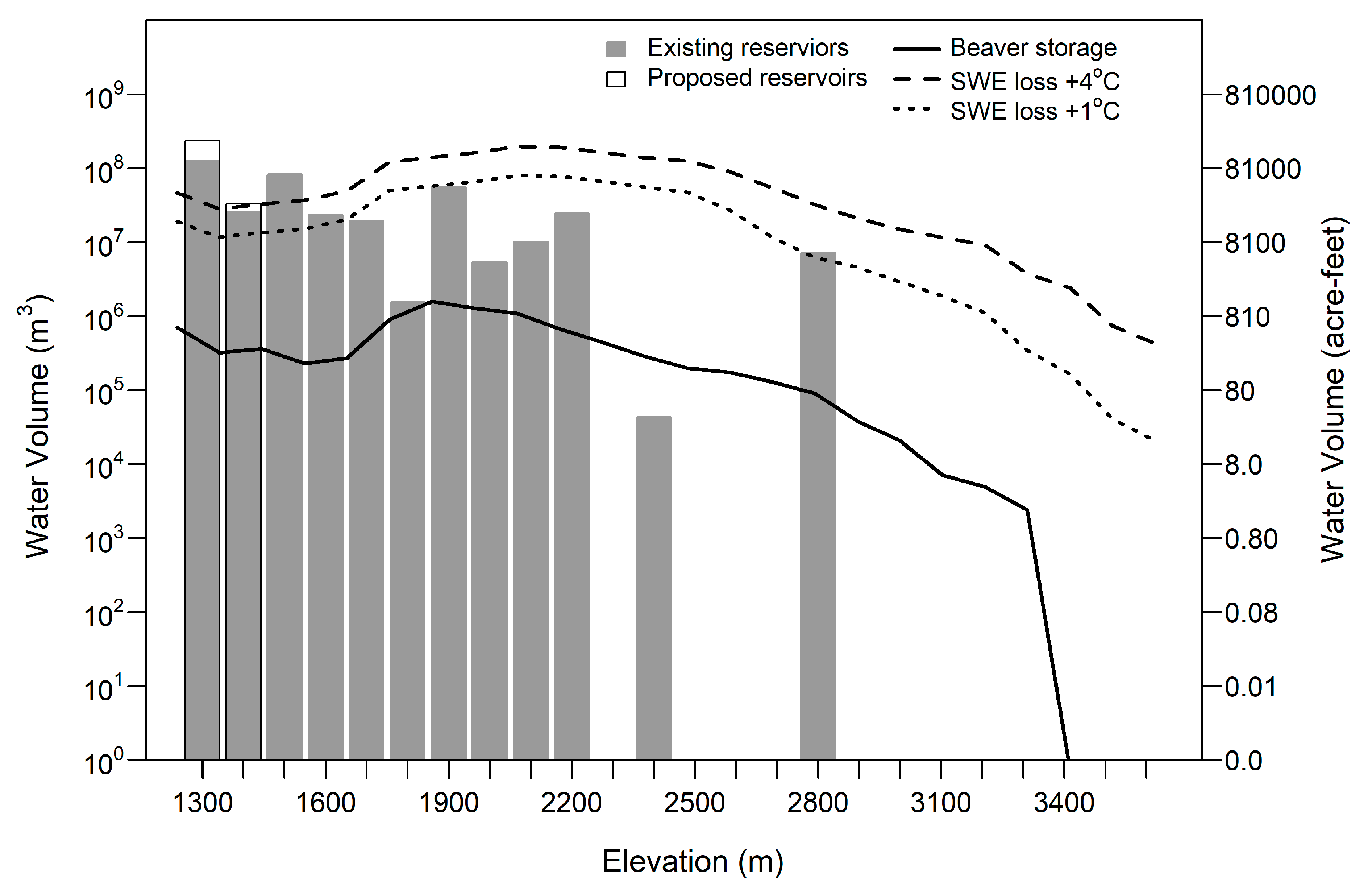
3.2.3. Total Water Storage
3.3. Snowpack Decline
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential Impacts of a Warming Climate on Water Availability in Snow-Dominated Regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Mote, P.W.; Hamlet, A.F.; Clark, M.P.; Lettenmaier, D.P. Declining Mountain Snowpack in Western North America. Bull. Am. Meteorol. Soc. 2005, 86, 39–49. [Google Scholar] [CrossRef]
- Mote, P.W. Climate-Driven Variability and Trends in Mountain Snowpack in Western North America. J. Clim. 2006, 19, 6209–6220. [Google Scholar] [CrossRef]
- Nyssen, J.; Pontzeele, J.; Billi, P. Effect of Beaver Dams on the Hydrology of Small Mountain Streams: Example from the Chevral in the Ourthe Orientale Basin, Ardennes, Belgium. J. Hydrol. 2011, 402, 92–102. [Google Scholar] [CrossRef]
- Karran, D.J.; Westbrook, C.J.; Wheaton, J.M.; Johnston, C.A.; Bedard-Haughn, A. Rapid Surface-Water Volume Estimations in Beaver Ponds. Hydrol. Earth Syst. Sci. 2017, 21, 1039–1050. [Google Scholar] [CrossRef]
- Dittbrenner, B.J.; Schilling, J.W.; Torgersen, C.E.; Lawler, J.J. Relocated Beaver Can Increase Water Storage and Decrease Stream Temperature in Headwater Streams. Ecosphere 2022, 13, e4168. [Google Scholar] [CrossRef]
- Macfarlane, W.W.; Wheaton, J.M.; Bouwes, N.; Jensen, M.L.; Gilbert, J.T.; Hough-Snee, N.; Shivik, J.A. Modeling the Capacity of Riverscapes to Support Beaver Dams. Geomorphology 2017, 277, 72–99. [Google Scholar] [CrossRef]
- Dittbrenner, B.J.; Pollock, M.M.; Schilling, J.W.; Olden, J.D.; Lawler, J.J.; Torgersen, C.E. Modeling Intrinsic Potential for Beaver (Castor Canadensis) Habitat to Inform Restoration and Climate Change Adaptation. PLoS ONE 2018, 13, e0192538. [Google Scholar] [CrossRef] [PubMed]
- Lowry, M.M. Groundwater Elevations and Temperature Adjacent to a Beaver Pond in Central Oregon; Oregon State University: Corvallis, OR, USA, 1993. [Google Scholar]
- Westbrook, C.J.; Cooper, D.J.; Baker, B.W. Beaver Dams and Overbank Floods Influence Groundwater-Surface Water Interactions of a Rocky Mountain Riparian Area. Water Resour. Res. 2006, 42, 1–12. [Google Scholar] [CrossRef]
- Woo, M.; Waddington, J.M. Effects of Beaver Dams on Subarctic Wetland Hydrology. Arctic 1990, 43, 223–230. [Google Scholar] [CrossRef]
- Pilliod, D.S.; Rohde, A.T.; Charnley, S.; Davee, R.R.; Dunham, J.B.; Gosnell, H.; Grant, G.E.; Hausner, M.B.; Huntington, J.L.; Nash, C. Survey of Beaver-Related Restoration Practices in Rangeland Streams of the Western USA. Environ. Manag. 2018, 61, 58–68. [Google Scholar] [CrossRef] [PubMed]
- Correll, D.L.; Jordan, T.E.; Weller, D.E. Beaver Pond Biogeochemical Effects in the Maryland Coastal Plain. Biogeochemistry 2000, 49, 217–239. [Google Scholar] [CrossRef]
- Majerova, M.; Neilson, B.T.; Schmadel, N.M.; Wheaton, J.M.; Snow, C.J. Impacts of Beaver Dams on Hydrologic and Temperature Regimes in a Mountain Stream. Hydrol. Earth Syst. Sci. 2015, 19, 3541–3556. [Google Scholar] [CrossRef]
- Puttock, A.; Graham, H.A.; Cunliffe, A.M.; Elliott, M.; Brazier, R.E. Eurasian Beaver Activity Increases Water Storage, Attenuates Flow and Mitigates Diffuse Pollution from Intensively-Managed Grasslands. Sci. Total Environ. 2017, 576, 430–443. [Google Scholar] [CrossRef] [PubMed]
- Hood, G.A.; Bayley, S.E. Beaver (Castor Canadensis) Mitigate the Effects of Climate on the Area of Open Water in Boreal Wetlands in Western Canada. Biol. Conserv. 2008, 141, 556–567. [Google Scholar] [CrossRef]
- Cross, M.S.; Zavaleta, E.S.; Bachelet, D.; Brooks, M.L.; Enquist, C.A.F.; Fleishman, E.; Graumlich, L.J.; Groves, C.R.; Hannah, L.; Hansen, L. The Adaptation for Conservation Targets (ACT) Framework: A Tool for Incorporating Climate Change into Natural Resource Management. Environ. Manag. 2012, 50, 341–351. [Google Scholar] [CrossRef] [PubMed]
- Gibson, P.P.; Olden, J.D. Ecology, Management, and Conservation Implications of North American Beaver (Castor Canadensis) in Dryland Streams. Aquat. Conserv. Mar. Freshw. Ecosyst. 2014, 24, 391–409. [Google Scholar] [CrossRef]
- Karran, D.J.; Westbrook, C.J.; Bedard-Haughn, A. Beaver-Mediated Water Table Dynamics in a Rocky Mountain Fen. Ecohydrology 2018, 11, e1923. [Google Scholar] [CrossRef]
- Hafen, K.C.; Wheaton, J.M.; Roper, B.B.; Bailey, P.; Bouwes, N. Influence of Topographic, Geomorphic, and Hydrologic Variables on Beaver Dam Height and Persistence in the Intermountain Western United States. Earth Surf. Process. Landf. 2020, 45, 2664–2674. [Google Scholar] [CrossRef]
- Ronnquist, A.L.; Westbrook, C.J. Beaver Dams: How Structure, Flow State, and Landscape Setting Regulate Water Storage and Release. Sci. Total Environ. 2021, 785, 147333. [Google Scholar] [CrossRef]
- Gurnell, A.M. The Hydrogeomorphological Effects of Beaver Dam-Building Activity. Prog. Phys. Geogr. Earth Environ. 1998, 22, 167–189. [Google Scholar] [CrossRef]
- Beedle, D.L. Physical Dimensions and Hydrologic Effects of Beaver Ponds on Kuiu Island in Southeast Alaska; Oregon State University: Corvallis, OR, USA, 1991. [Google Scholar]
- Feiner, K.; Lowry, C.S. Simulating the Effects of a Beaver Dam on Regional Groundwater Flow through a Wetland. J. Hydrol. Reg. Stud. 2015, 4, 675–685. [Google Scholar] [CrossRef]
- Scamardo, J.; Wohl, E. Sediment Storage and Shallow Groundwater Response to Beaver Dam Analogues in the Colorado Front Range, USA. River Res. Appl. 2020, 36, 398–409. [Google Scholar] [CrossRef]
- Scamardo, J.E.; Marshall, S.; Wohl, E. Estimating Widespread Beaver Dam Loss: Habitat Decline and Surface Storage Loss at a Regional Scale. Ecosphere 2022, 13, e3962. [Google Scholar] [CrossRef]
- Barrett, A.P. National Operational Hydrologic Remote Sensing Center Snow Data Assimilation System (SNODAS) Products at NSIDC; National Snow and Ice Data Center, Cooperative Institute for Research in Environmental Sciences: Boulder, CO, USA, 2003. [Google Scholar]
- USACE National Inventory of Dams, Water Control Infrastructure. 2005. Available online: https://nationalmap.gov/small_scale/mld/dams00x.html (accessed on 10 April 2017).
- Bowen Collins & Associates; HDR Engineering. Bear River Pipeline Concept Report; Consultant Job No. 233-09-01; Bowen Collins & Associates: Draper, UT, USA; HDR Engineering: Omaha, NE, USA, 2014; Available online: https://www.cachecounty.gov/assets/department/water/brpipeline/Vol%201_Final_Bear%20River%20Pipeline%20Concept%20Rpt.pdf (accessed on 14 May 2024).
- Lokteff, R.L.; Roper, B.B.; Wheaton, J.M. Do Beaver Dams Impede the Movement of Trout? Trans. Am. Fish. Soc. 2013, 142, 1114–1125. [Google Scholar] [CrossRef]
- Portugal, E.; Wheaton, J.M.; Sorenson, K.; Majerova, M.; Hunt, B.; Bouwes, N. Hardware Ranch Adaptive Beaver Management Plan; Prepared for Utah Division of Wildlife Resources: Logan, UT, USA, 2015; 26p. [Google Scholar]
- Gesch, D.; Oimoen, M.; Greenlee, S.; Nelson, C.; Steuck, M.; Tyler, D. The National Elevation Dataset. Photogramm. Eng. Remote Sens. 2002, 68, 5–32. [Google Scholar]
- Rennó, C.D.; Nobre, A.D.; Cuartas, L.A.; Soares, J.V.; Hodnett, M.G.; Tomasella, J.; Waterloo, M.J. HAND, a New Terrain Descriptor Using SRTM-DEM: Mapping Terra-Firme Rainforest Environments in Amazonia. Remote Sens. Environ. 2008, 112, 3469–3481. [Google Scholar] [CrossRef]
- Zheng, X.; Tarboton, D.G.; Maidment, D.R.; Liu, Y.Y.; Passalacqua, P. River Channel Geometry and Rating Curve Estimation Using Height above the Nearest Drainage. JAWRA J. Am. Water Resour. Assoc. 2018, 54, 785–806. [Google Scholar] [CrossRef]
- Fryirs, K.A.; Wheaton, J.M.; Brierley, G.J. An Approach for Measuring Confinement and Assessing the Influence of Valley Setting on River Forms and Processes. Earth Surf. Process. Landf. 2016, 41, 701–710. [Google Scholar] [CrossRef]
- Gilbert, J.T.; Macfarlane, W.W.; Wheaton, J.M. The Valley Bottom Extraction Tool (V-BET): A GIS Tool for Delineating Valley Bottoms across Entire Drainage Networks. Comput. Geosci. 2016, 97, 1–14. [Google Scholar] [CrossRef]
- Harbaugh, A.W. MODFLOW-2005, the US Geological Survey Modular Ground-Water Model: The Ground-Water Flow Process; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2005. [Google Scholar]
- Niswonger, R.G.; Panday, S.; Ibaraki, M. MODFLOW-NWT, a Newton Formulation for MODFLOW-2005. US Geol. Surv. Tech. Methods 2011, 6, A37. [Google Scholar]
- Glover, K.C. Stream-Aquifer System in the Upper Bear River Valley, Wyoming; Department of the Interior, US Geological Survey: Reston, VA, USA, 1990. [Google Scholar]
- Robinove, C.J.; Berry, D.W. Availability of Ground Water in the Bear River Valley, Wyoming; United States Department of the Interior Geological Survey: Reston, VA, USA, 1963. [Google Scholar]
- Wieczorek, M.E. Area- and Depth-Weighted Averages of Selected SSURGO Variables for the Conterminous United States and District of Columbia; US Geological Survey: Reston, VA, USA, 2014. [Google Scholar]
- Bakker, M.; Post, V.; Langevin, C.D.; Hughes, J.D.; White, J.T.; Starn, J.; Fienen, M.N. Scripting MODFLOW Model Development Using Python and FloPy. Groundwater 2016, 54, 733–739. [Google Scholar] [CrossRef] [PubMed]
- McKay, L.; Bondelid, T.; Dewald, T.; Johnston, J.; Moore, R.; Rea, A. NHDPlus Version 2: User Guide; US Environmental Protection Agency: Washington, DC, USA, 2012. [Google Scholar]
- Tennant, C.J.; Crosby, B.T.; Godsey, S.E.; VanKirk, R.W.; Derryberry, D.R. A Simple Framework for Assessing the Sensitivity of Mountain Watersheds to Warming-driven Snowpack Loss. Geophys. Res. Lett. 2015, 42, 2814–2822. [Google Scholar] [CrossRef]
- Butler, D.R.; Malanson, G.P. Sedimentation Rates and Patterns in Beaver Ponds in a Mountain Environment. Geomorphology 1995, 13, 255–269. [Google Scholar] [CrossRef]
- Butler, D.R. Characteristics of Beaver Ponds on Deltas in a Mountain Environment: Beaver Ponds on Mountain Deltas. Earth Surf. Process. Landf. 2012, 37, 876–882. [Google Scholar] [CrossRef]
- Meentemeyer, R.K.; Butler, D.R. Hydrogeomorphic Effects of Beaver Dams in Glacier National Park, Montana. Phys. Geogr. 1999, 20, 436–446. [Google Scholar] [CrossRef]
- Sturtevant, B.R. A Model of Wetland Vegetation Dynamics in Simulated Beaver Impoundments. Ecol. Model. 1998, 112, 195–225. [Google Scholar] [CrossRef]
- Burchsted, D.; Daniels, M.; Thorson, R.; Vokoun, J. The River Discontinuum: Applying Beaver Modifications to Baseline Conditions for Restoration of Forested Headwaters. BioScience 2010, 60, 908–922. [Google Scholar] [CrossRef]
- Barnes, W.J.; Dibble, E. The Effects of Beaver in Riverbank Forest Succession. Can. J. Bot. 1988, 66, 40–44. [Google Scholar] [CrossRef]



| Study Site | Data Source | Measured Variables | Count |
|---|---|---|---|
| Bridge Creek, OR | 0.1 m bathymetric DEM | Maximum pond volume | 32 |
| Curtis Creek, UT | 0.1 m bathymetric DEM | Maximum pond volume | 8 |
| Temple Fork, UT | 0.1 m bathymetric DEM | Maximum pond volume | 16 |
| North Fork Ogden River, UT | Field survey | Pond area | 34 |
| Temple Fork, UT | Field survey | Pond area | 74 |
| Little Bear–Logan River | Aerial imagery | Pond area | 1211 |
| HUC8 | BRAT Capacity (%) | P. Dams | S. Dams | Stream Length (km) | Dam Density (Dams/ km) | TS (mil. m3) | SWS (mil. m3) | GWS (mil. m3) |
|---|---|---|---|---|---|---|---|---|
| Upper Bear | 5 | 166 | 412 | 1605 | 0.4 | 0.15 | 0.04 | 0.11 |
| 25 | 880 | 2261 | 1605 | 2.0 | 0.76 | 0.24 | 0.53 | |
| 50 | 1923 | 4447 | 1605 | 4.0 | 1.73 | 0.51 | 1.22 | |
| 100 | 4825 | 8013 | 1605 | 8.0 | 4.14 | 1.07 | 3.07 | |
| Central Bear | 5 | 123 | 287 | 1027 | 0.4 | 0.08 | 0.03 | 0.05 |
| 25 | 670 | 1470 | 1027 | 2.1 | 0.43 | 0.15 | 0.28 | |
| 50 | 1356 | 2891 | 1027 | 4.1 | 0.90 | 0.30 | 0.59 | |
| 100 | 3153 | 5326 | 1027 | 8.3 | 2.07 | 0.62 | 1.46 | |
| Bear Lake | 5 | 89 | 195 | 975 | 0.3 | 0.05 | 0.01 | 0.03 |
| 25 | 439 | 984 | 975 | 1.5 | 0.23 | 0.08 | 0.15 | |
| 50 | 936 | 1906 | 975 | 2.9 | 0.55 | 0.18 | 0.37 | |
| 100 | 2128 | 3255 | 975 | 5.5 | 1.31 | 0.37 | 0.94 | |
| Middle Bear | 5 | 100 | 211 | 1208 | 0.3 | 0.03 | 0.01 | 0.02 |
| 25 | 492 | 1055 | 1208 | 1.3 | 0.20 | 0.08 | 0.12 | |
| 50 | 1080 | 2066 | 1208 | 2.6 | 0.47 | 0.17 | 0.29 | |
| 100 | 2928 | 3205 | 1208 | 5.1 | 1.16 | 0.39 | 0.77 | |
| Little Bear– Logan River | 5 | 62 | 153 | 651 | 0.3 | 0.03 | 0.01 | 0.02 |
| 25 | 297 | 744 | 651 | 1.6 | 0.18 | 0.06 | 0.13 | |
| 50 | 692 | 1502 | 651 | 3.4 | 0.46 | 0.14 | 0.32 | |
| 100 | 1868 | 2739 | 651 | 7.1 | 1.05 | 0.30 | 0.76 | |
| Lower Bear- Malad | 5 | 42 | 98 | 1124 | 0.1 | 0.01 | 0.00 | 0.01 |
| 25 | 246 | 469 | 1124 | 0.6 | 0.12 | 0.04 | 0.08 | |
| 50 | 585 | 656 | 1124 | 1.1 | 0.28 | 0.08 | 0.20 | |
| 100 | 1435 | 1264 | 1124 | 2.4 | 0.64 | 0.18 | 0.47 | |
| Entire Basin | 5 | 582 | 1356 | 6591 | 0.3 | 0.36 | 0.11 | 0.25 |
| 25 | 3024 | 6983 | 6591 | 1.5 | 1.93 | 0.64 | 1.29 | |
| 50 | 6572 | 13,468 | 6591 | 3.0 | 4.38 | 1.39 | 3.00 | |
| 100 | 16,337 | 23,802 | 6591 | 6.1 | 10.38 | 2.92 | 7.46 |
| Storage Type | Modeled Dam Height Quantile | 5% | 25% | 50% | 100% |
|---|---|---|---|---|---|
| Surface water | 0.025 0.500 0.975 | 0.04 0.11 0.34 | 0.25 0.64 1.93 | 0.55 1.39 3.99 | 1.21 2.92 8.75 |
| Ground water | 0.025 0.500 0.975 | 0.11 0.24 0.55 | 0.60 1.29 3.17 | 1.43 3.00 6.93 | 3.60 7.46 17.69 |
| Total | 0.025 0.500 0.975 | 0.15 0.36 0.89 | 0.85 1.93 5.10 | 1.98 4.38 10.92 | 4.81 10.38 26.44 |
| BRAT Capacity | Modeled Dam Height Quantile | Mean SW Volume (m3) | SD SW Volume (m3) | * Mean GW Volume (m3) |
|---|---|---|---|---|
| 5 | 0.025 | 22.0 | 29.4 | 81.2 |
| 0.500 | 57.5 | 64.0 | 182.2 | |
| 0.975 | 175.1 | 437.1 | 408.4 | |
| 25 | 0.025 | 25.2 | 32.6 | 86.4 |
| 0.500 | 64.3 | 70.6 | 184.4 | |
| 0.975 | 192.8 | 472.3 | 454.1 | |
| 50 | 0.025 | 27.2 | 33.9 | 105.9 |
| 0.500 | 68.6 | 72.2 | 222.5 | |
| 0.975 | 196.9 | 410.3 | 514.5 | |
| 100 | 0.025 | 30.1 | 37.1 | 151.4 |
| 0.500 | 72.8 | 76.5 | 313.3 | |
| 0.975 | 217.8 | 508.8 | 743.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hafen, K.C.; Wheaton, J.M.; Roper, B.B.; Bailey, P.; Macfarlane, W.W.; Neilson, B.T.; Tennant, C.J. Estimating Increased Transient Water Storage with Increases in Beaver Dam Activity. Water 2024, 16, 1515. https://doi.org/10.3390/w16111515
Hafen KC, Wheaton JM, Roper BB, Bailey P, Macfarlane WW, Neilson BT, Tennant CJ. Estimating Increased Transient Water Storage with Increases in Beaver Dam Activity. Water. 2024; 16(11):1515. https://doi.org/10.3390/w16111515
Chicago/Turabian StyleHafen, Konrad C., Joseph M. Wheaton, Brett B. Roper, Philip Bailey, William W. Macfarlane, Bethany T. Neilson, and Christopher J. Tennant. 2024. "Estimating Increased Transient Water Storage with Increases in Beaver Dam Activity" Water 16, no. 11: 1515. https://doi.org/10.3390/w16111515
APA StyleHafen, K. C., Wheaton, J. M., Roper, B. B., Bailey, P., Macfarlane, W. W., Neilson, B. T., & Tennant, C. J. (2024). Estimating Increased Transient Water Storage with Increases in Beaver Dam Activity. Water, 16(11), 1515. https://doi.org/10.3390/w16111515







