Study on the Annual Runoff Change and Its Relationship with Fractional Vegetation Cover and Climate Change in the Chinese Yellow River Basin
Abstract
1. Introduction
2. Materials and Methods
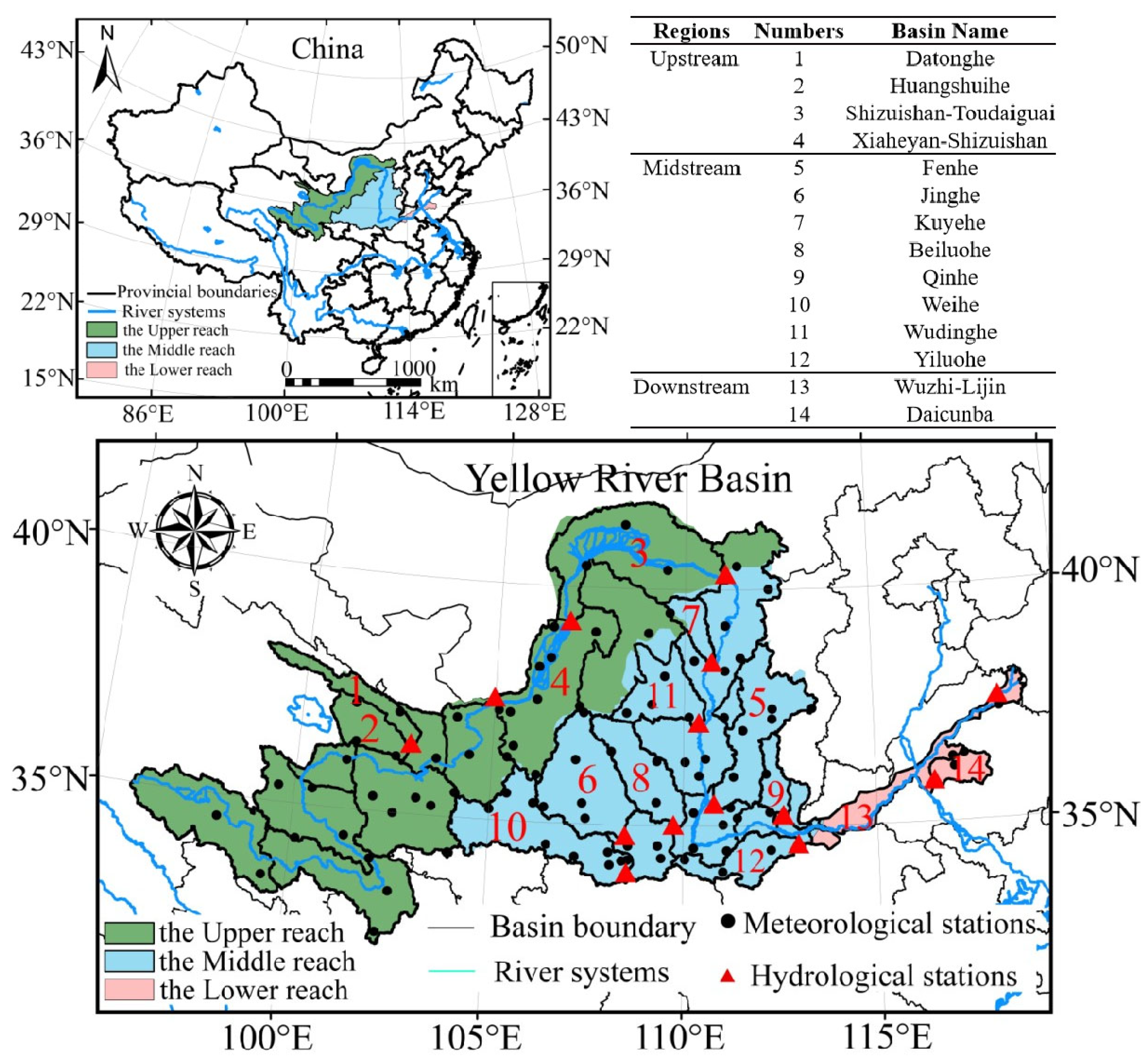
2.1. Study Area
2.2. Data Sources and Processing
- (1)
- Meteorological and Hydrological Data
- (2)
- Soil Data
- (3)
- NDVI Data
- (4)
- CMIP6 Climate Model Data
2.3. Methodology
- (1)
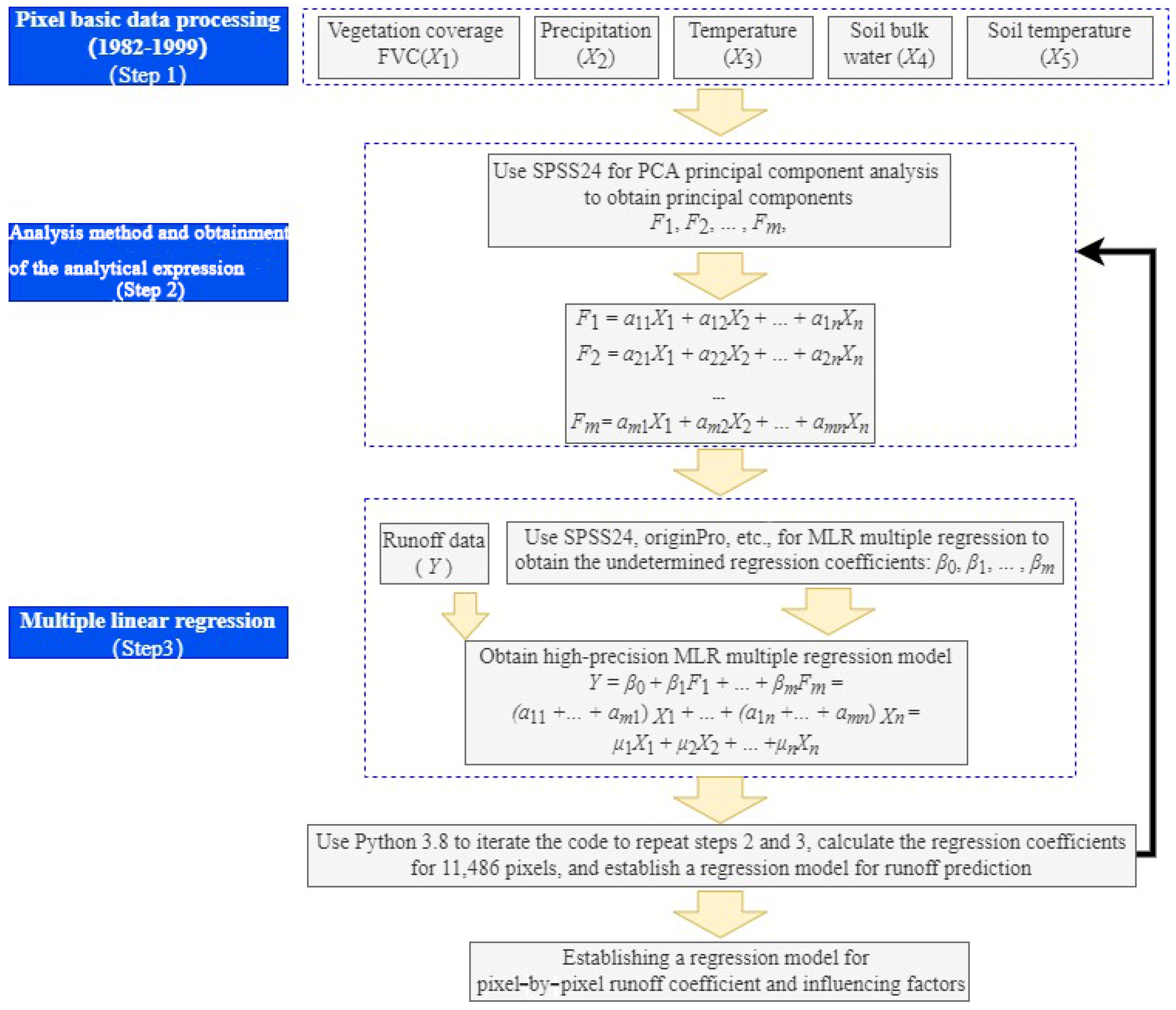
- PCA-MLR Multiple Linear Regression Model
- (2)
- Establishing a runoff coefficient model based on PCA-MLR
2.4. Data Analysis
3. Results
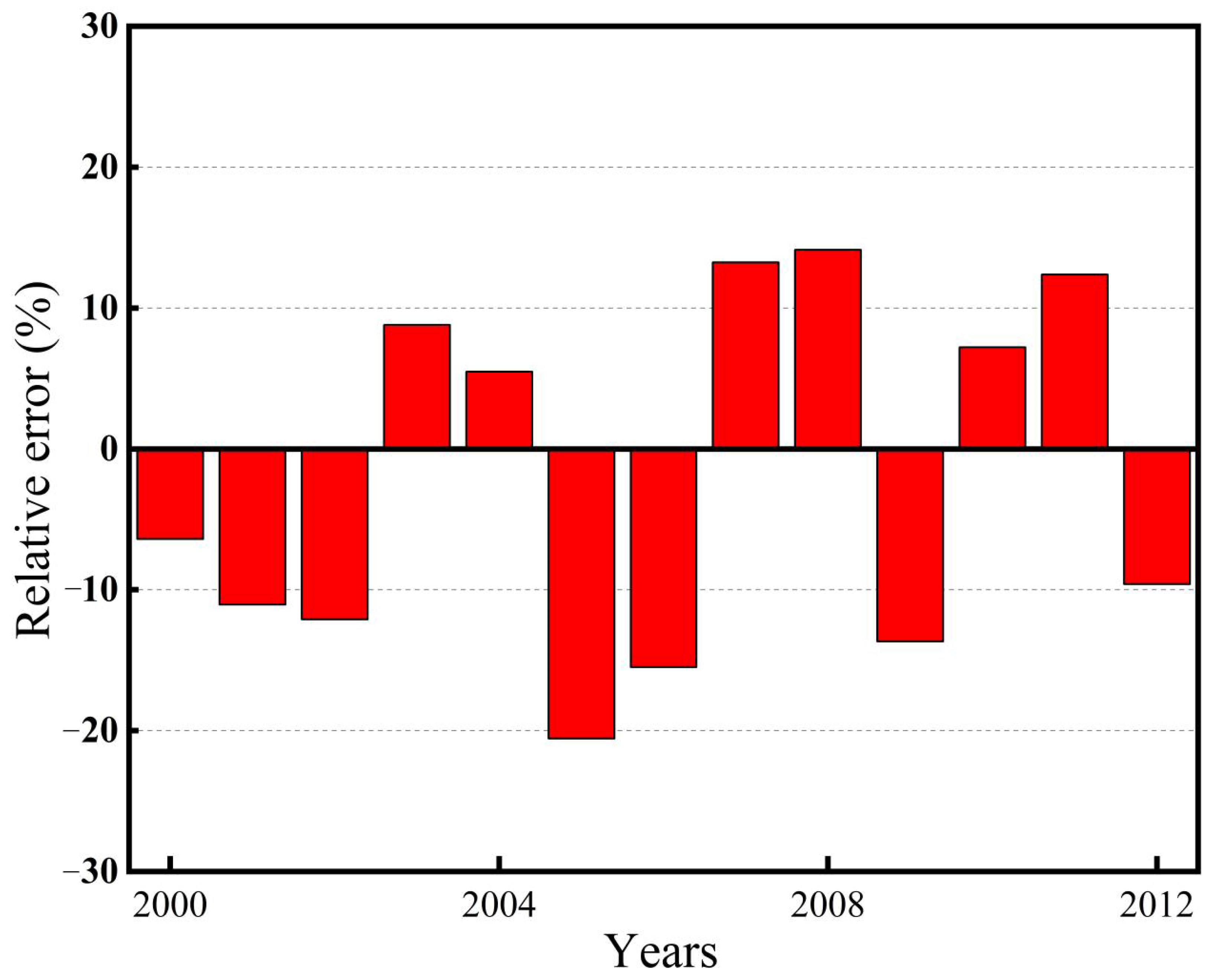
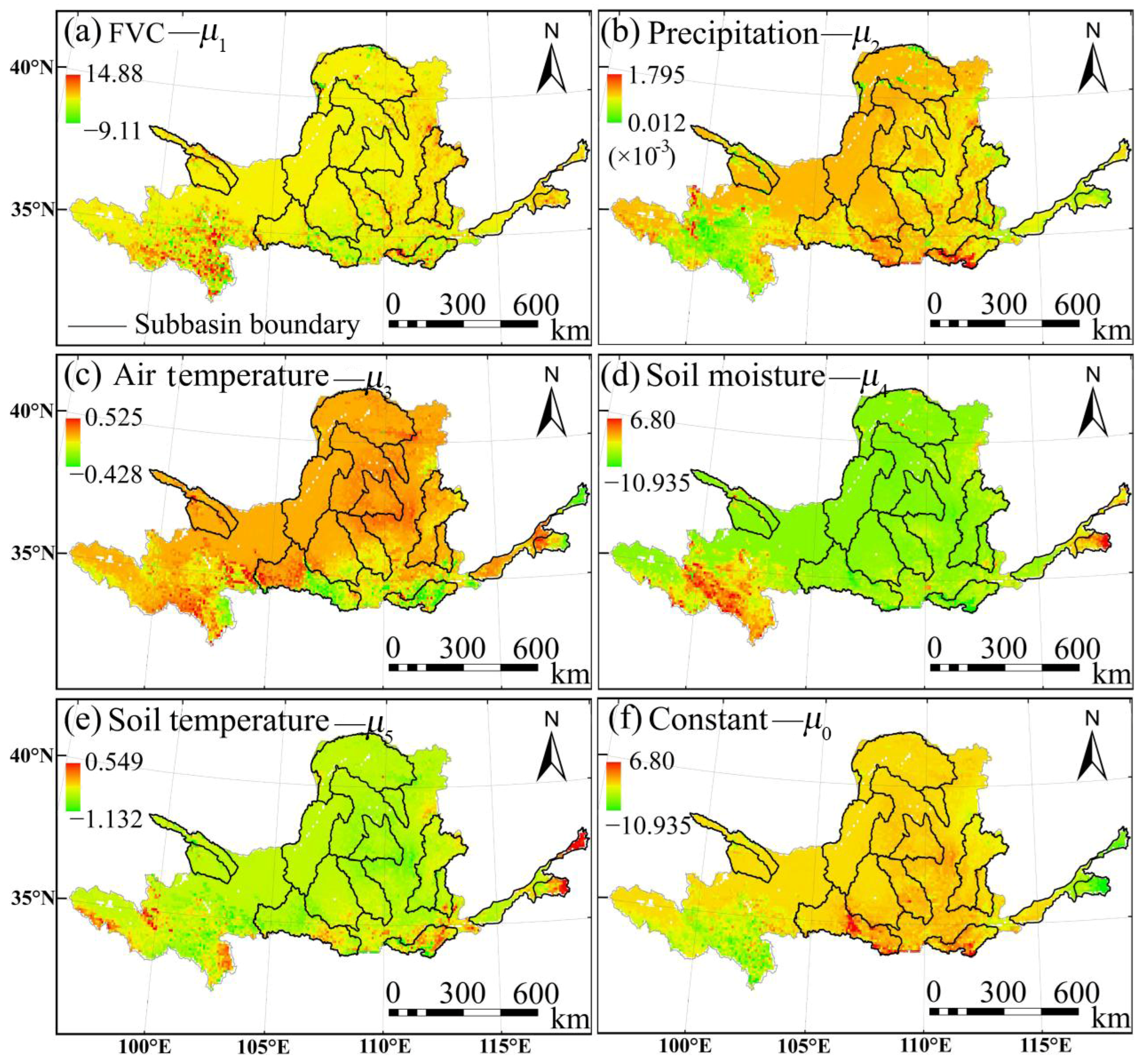
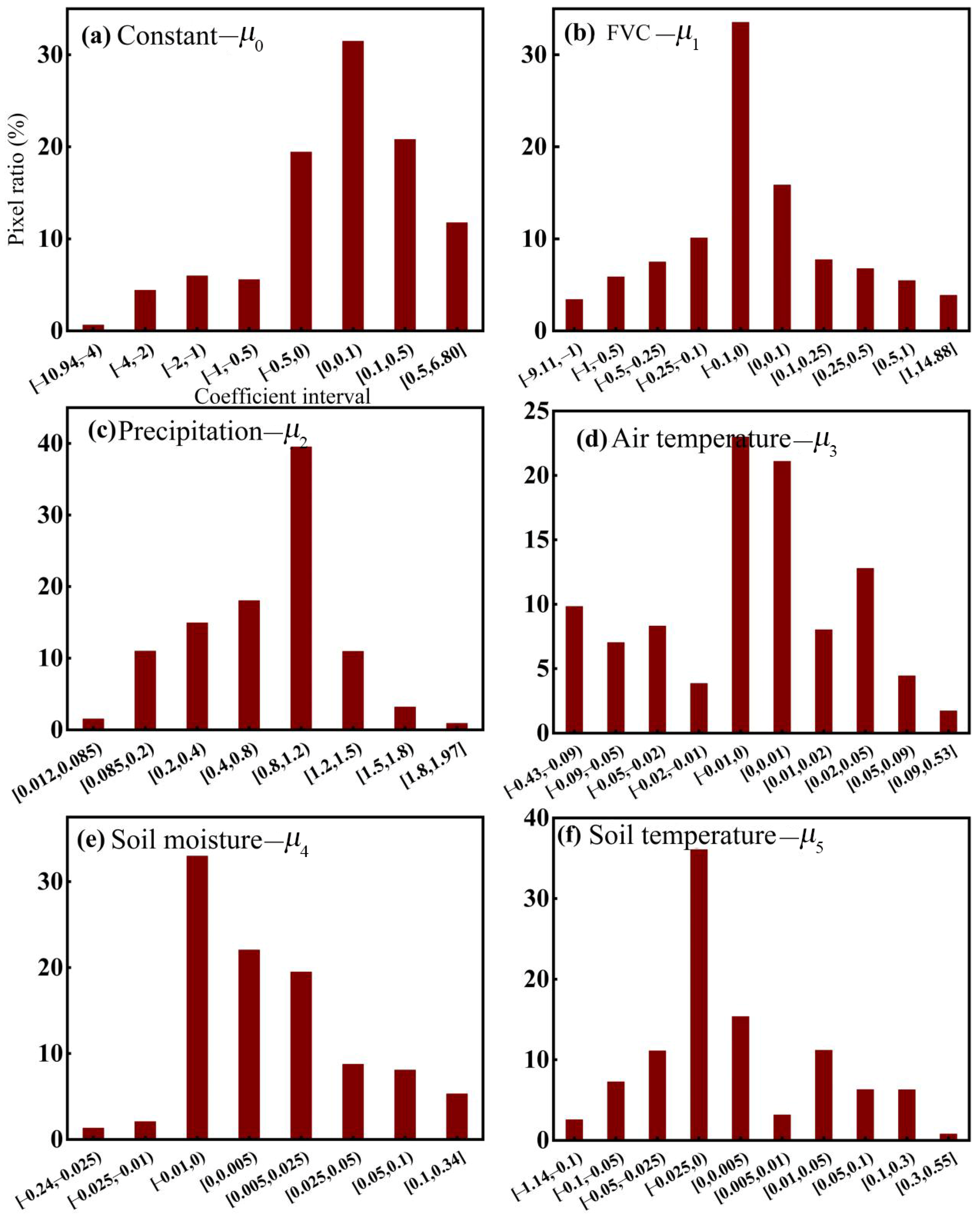
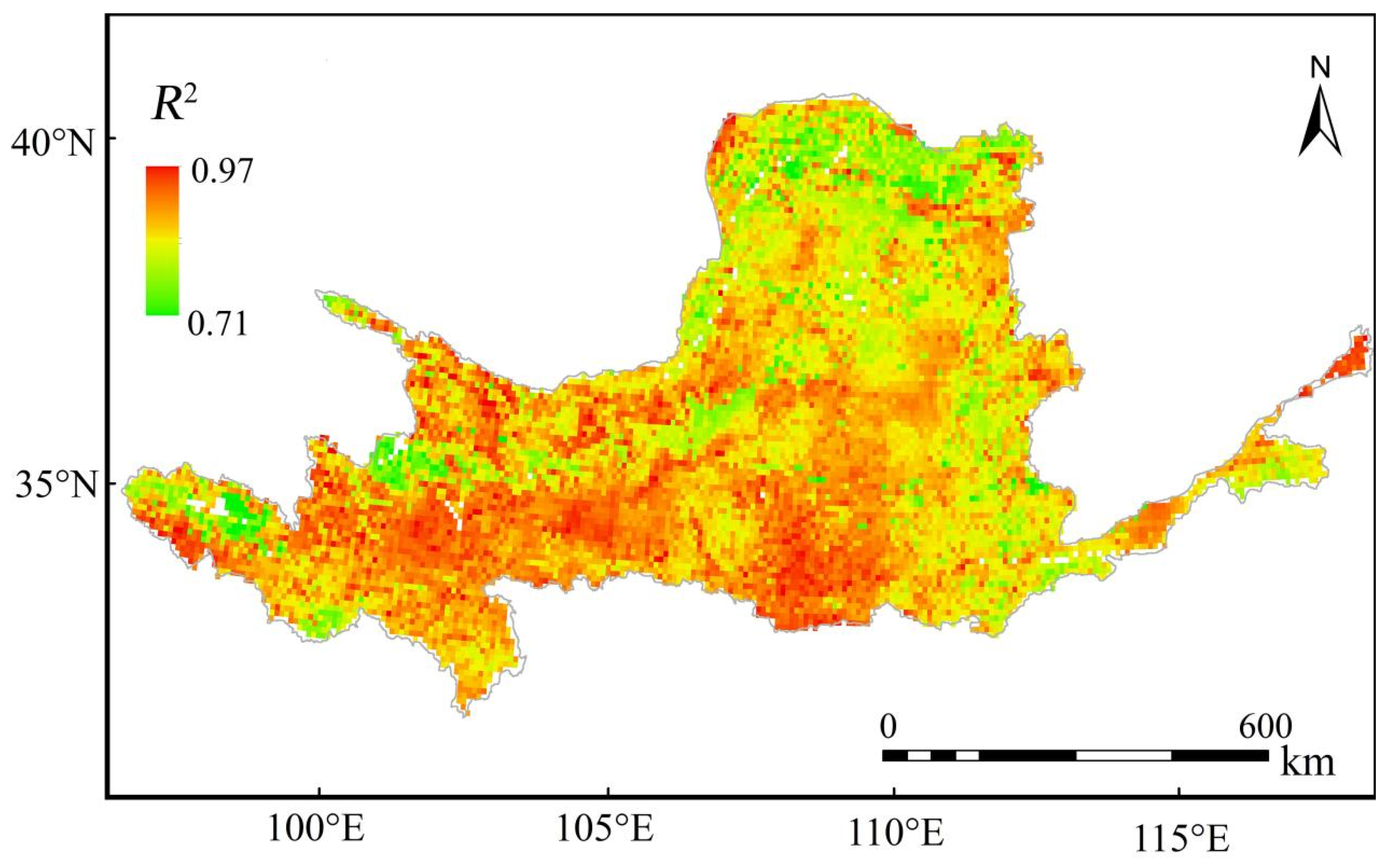
3.1. Runoff Coefficient Model
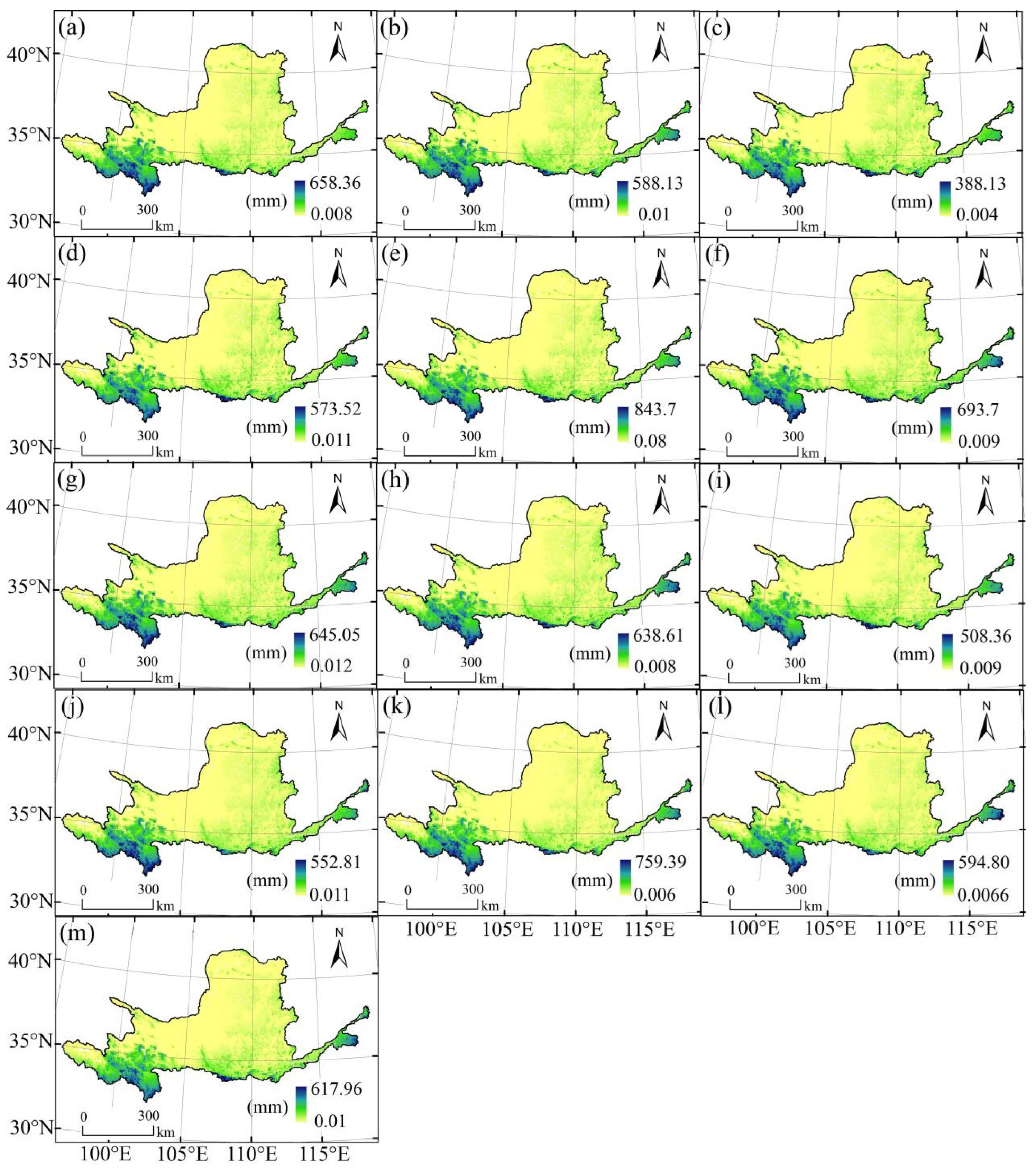
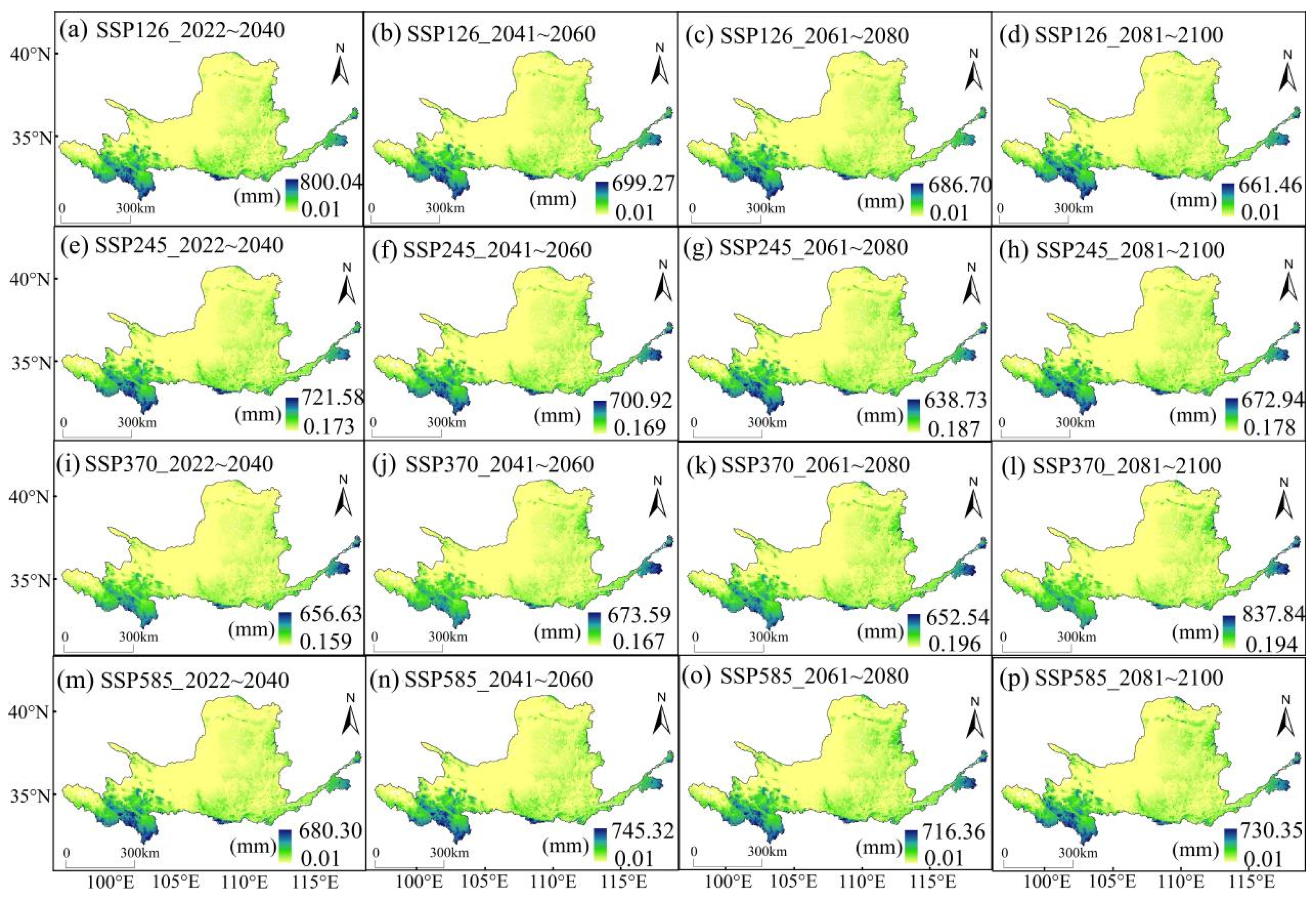
3.2. Future Spatiotemporal Runoff Predictions under Climate Models
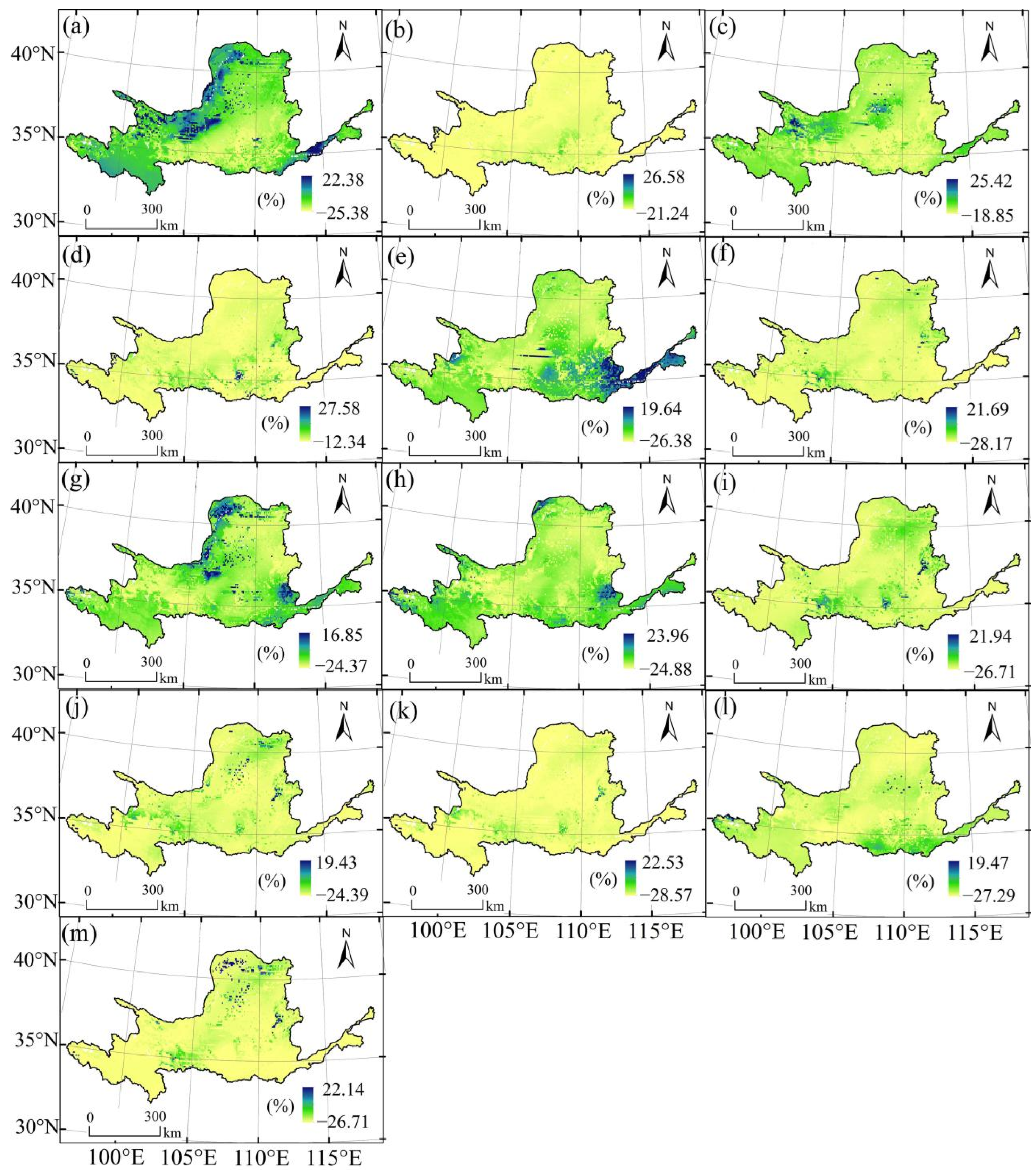
3.3. Spatial Distribution of Runoff Change Rates under Future Climate Models
4. Discussions
4.1. Vegetation Coverage and Runoff
4.2. Runoff Prediction under Future Climate Models
4.3. Limitation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, Y.; Zhou, Y.; Wang, Y.; Lu, F.; Xiao, W.; Hou, B.; Yu, Y.; Liu, J.; Xue, W. Impacts of Precipitation Type Variations on Runoff Changes in the Source Regions of the Yangtze and Yellow River Basins in the Past 40 Years. Water 2022, 14, 4115. [Google Scholar] [CrossRef]
- Chen, L.; Yang, M.; Liu, X.; Lu, X. Attribution and Sensitivity Analysis of Runoff Variation in the Yellow River Basin under Climate Change. Sustainability 2022, 14, 14981. [Google Scholar] [CrossRef]
- Zhuang, X.; Fan, Y.; Li, Y.; Wu, C. Evaluation climate change impacts on Water Resources over the Upper Reach of the Yellow River Basin. Water Resour. Manag. 2023, 37, 2875–2889. [Google Scholar] [CrossRef]
- Wang, S.; Fu, B.J.; Piao, S.L.; Lü, Y.H.; Ciais, P.; Feng, X.M.; Wang, Y.F. Reduced sediment transport in the Yellow River due to anthropogenic changes. Nat. Geosci. 2016, 9, 38–41. [Google Scholar] [CrossRef]
- Li, C.; Zhang, Y.; Shen, Y.; Yu, Q. Decadal water storage decrease driven by vegetation changes in the Yellow River Basin. Sci. Bull. 2020, 65, 1859–1861. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Luo, M.; Liu, T.; Bao, A.M.; Feng, X.W.; Chen, X. Local Climate Change and the Impacts on Hydrological Processes in an Arid Alpine Catchment in Karakoram. Water 2017, 9, 344. [Google Scholar] [CrossRef]
- Zhao, A.; Zhang, A.; Liu, J.; Feng, L.; Zhao, Y. Assessing the effects of drought and “Grain for Green” Program on vegetation dynamics in China’s Loess Plateau from 2000 to 2014. Catena 2019, 175, 446–455. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, Y. Response of Runoff-Sediment System to Vegetation Variation in the Yellow River Basin in the Last 20 Years. Land 2023, 12, 428. [Google Scholar] [CrossRef]
- Guo, X.; Du, M.; Gao, P.; Tian, P.; Zhao, G.; Mu, X.; Geng, R. Response of runoff-sediment processes to vegetation restoration patterns under different rainfall regimes on the Loess Plateau. Catena 2024, 234, 107647. [Google Scholar] [CrossRef]
- Huang, T.; Liu, Y.; Wu, Z.; Xiao, P.; Wang, J.; Sun, P. Quantitative analysis of runoff alteration based on the Budyko model with time-varying underlying surface parameters for the Wuding River Basin, Loess Plateau. Ecol. Indic. 2024, 158, 111377. [Google Scholar] [CrossRef]
- Liu, C.; Melack, J.; Tian, Y.; Huang, H.; Jiang, J.; Fu, X.; Zhang, Z. Detecting Land Degradation in Eastern China Grasslands with Time Series Segmentation and Residual Trend analysis (TSS-RESTREND) and GIMMS NDVI3g Data. Remote Sens. 2019, 11, 1014. [Google Scholar] [CrossRef]
- Muhury, N.; Apan, A.A.; Marasani, T.N.; Ayele, G.T. Modelling Floodplain Vegetation Response to Groundwater Variability Using the ArcSWAT Hydrological Model, MODIS NDVI Data, and Machine Learning. Land 2022, 11, 2154. [Google Scholar] [CrossRef]
- Wang, B.; Wang, H.; Jiao, X.; Huang, L.; Chen, H.; Guo, W. Runoff change in the Yellow River Basin of China from 1960 to 2020 and its driving factors. J. Arid Land 2023, 16, 168–194. [Google Scholar] [CrossRef]
- Li, L.; Peng, Q.; Wang, M.; Cao, Y.; Gu, X.; Cai, H. Quantitative analysis of vegetation drought propagation process and uncertainty in the Yellow River Basin. Agric. Water Manag. 2024, 295, 108775. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, J.; Tan, M.L.; Lu, P.; Xue, Z.; Liu, M.; Wang, X. Impacts of vegetation restoration on soil erosion in the Yellow River Basin, China. Catena 2024, 234, 107547. [Google Scholar] [CrossRef]
- Bai, Y.; Zhu, Y.; Liu, Y.; Wang, S. Vegetation Greening and Its Response to a Warmer and Wetter Climate in the Yellow River Basin from 2000 to 2020. Remote Sens. 2024, 16, 790. [Google Scholar] [CrossRef]
- Bai, T.; Wang, X.S.; Han, P.F. Controls of groundwater-dependent vegetation coverage in the yellow river basin, china: Insights from interpretable machine learning. J. Hydrol. 2024, 631, 130747. [Google Scholar] [CrossRef]
- Jian, S.; Pei, Y.; Zhu, T.; Yu, X. Spatiotemporal change and attribution analysis of future runoff on the Yellow River basin of China. J. Hydrol. Reg. Stud. 2023, 49, 101494. [Google Scholar] [CrossRef]
- Jian, S.; Shi, S.; Cui, J.; Zhu, T.; Hu, C. Study on fractional vegetation cover dynamic in the Yellow River Basin, China from 1901 to 2100. Front. For. Glob. Change 2023, 6, 1157285. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, G.; Tian, P.; Mu, X.; Tian, X.; Feng, J.; Bai, Y. Runoff changes in the major river basins of China and their responses to potential driving forces. J. Hydrol. 2022, 607, 127536. [Google Scholar] [CrossRef]
- Guo, B.; Wei, C.; Yu, Y.; Liu, Y.; Li, J.; Meng, C.; Cai, Y. The dominant influencing factors of desertification changes in the source region of Yellow River: Climate change or human activity? Sci. Total Environ. 2022, 813, 152512. [Google Scholar] [CrossRef]
- Sun, Z.; Chang, N.-B.; Opp, C.; Hennig, T. Evaluation of ecological restoration through vegetation patterns in the lower Tarim River, China with MODIS NDVI data. Ecol. Inform. 2011, 6, 156–163. [Google Scholar] [CrossRef]
- Fu, B.; Burgher, I. Riparian vegetation NDVI dynamics and its relationship with climate, surface water and groundwater. J. Arid Environ. 2015, 113, 59–68. [Google Scholar] [CrossRef]
- Yang, J.; Wang, T.; Yang, D.; Yang, Y. Insights into runoff changes in the source region of Yellow River under frozen ground degradation. J. Hydrol. 2023, 617, 128892. [Google Scholar] [CrossRef]
- Yalcin, E. Quantifying climate change impacts on hydropower production under CMIP6 multi-model ensemble projections using SWAT model. Hydrol. Sci. J. 2023, 68, 1915–1936. [Google Scholar] [CrossRef]
- Zhou, J.; Lu, H.; Yang, K.; Jiang, R.; Yang, Y.; Wang, W.; Zhang, X. Projection of China’s future runoff based on the CMIP6 mid-high warming scenarios. Sci. China Earth Sci. 2023, 66, 528–546. [Google Scholar] [CrossRef]
- Li, L.; Hao, Z.-C.; Wang, J.H.; Wang, Z.H.; Yu, Z.B. Impact of future climate change on runoff in the head region of the Yellow River. J. Hydrol. Eng. 2008, 13, 347–354. [Google Scholar] [CrossRef]
- Li, L.; Shen, H.; Dai, S.; Xiao, J.; Shi, X. Response of runoff to climate change and its future tendency in the source region of Yellow River. J. Geogr. Sci. 2012, 22, 431–440. [Google Scholar] [CrossRef]
- Ji, G.; Lai, Z.; Xia, H.; Liu, H.; Wang, Z. Future runoff variation and flood disaster prediction of the yellow river basin based on CA-Markov and SWAT. Land 2021, 10, 421. [Google Scholar] [CrossRef]
- Jing, L.; Zhi, L.; Zhe, L. Analysis of spatiotemporal variations in land use on the Loess Plateau of China during 1986~2010. Environ. Earth Sci. 2016, 75, 25–32. [Google Scholar]
- Xie, M.; Ren, Z.; Li, Z.; Zhang, X.; Ma, X.; Li, P.; Shen, Z. Evolution of the precipitation–stream runoff relationship in different precipitation scenarios in the Yellow River Basin. Urban Clim. 2023, 51, 101609. [Google Scholar] [CrossRef]


| Factors | Initial | Extract |
|---|---|---|
| FVC (X1) | 1 | 0.939 |
| Precipitation (X2) | 1 | 0.875 |
| Air temperature (X3) | 1 | 0.954 |
| Soil moisture (X4) | 1 | 0.851 |
| Soil temperature (X5) | 1 | 0.955 |
| Years | F1 | F2 | F3 | Years | F1 | F2 | F3 |
|---|---|---|---|---|---|---|---|
| 1982 | −19.40 | 141.78 | −48.99 | 1991 | −11.52 | 103.52 | −34.52 |
| 1983 | −23.66 | 161.63 | −56.70 | 1992 | −34.10 | 217.55 | −77.60 |
| 1984 | −32.56 | 203.58 | −71.95 | 1993 | −12.18 | 103.80 | −34.52 |
| 1985 | −14.49 | 113.17 | −37.95 | 1994 | −19.63 | 147.06 | −50.61 |
| 1986 | −18.66 | 134.99 | −46.65 | 1995 | −22.19 | 158.52 | −54.73 |
| 1987 | −19.02 | 141.69 | −49.01 | 1996 | −15.57 | 107.98 | −40.85 |
| 1988 | −12.39 | 105.79 | −35.03 | 1997 | −12.44 | 111.98 | −37.59 |
| 1989 | −26.06 | 177.04 | −62.44 | 1998 | −10.83 | 108.07 | −36.13 |
| 1990 | −20.50 | 150.41 | −51.97 | 1999 | −16.80 | 136.72 | −47.28 |
| Sub-Basins | Formula | R2 and P |
|---|---|---|
| Datonghe | α = 0.142X1 + 0.22X2 + 0.022X3 + 0.013X4 − 0.036X5 − 0.272 | R2 = 0.88, P < 0.01 |
| Huangshuihe | α = 0.075X1 + 0.265X2 + 0.022X3 + 0.017X4 − 0.031X5 − 0.33 | R2 = 0.82, P < 0.01 |
| Shizuishan–Toudaoguai | α = −0.094X1 + 0.132X2 + 0.006X3 + 0.004X4 − 0.005X5 − 0.01 | R2 = 0.73, P < 0.01 |
| Xiaheyan–Shizuishan | α = −0.035X1 + 0.034X2 + 0.005X3−0.002X4 − 0.008X5 + 0.073 | R2 = 0.72, P < 0.01 |
| Fenhe | α = 0.289X1 + 0.205X2 − 0.009X3 + 0.005X4 − 0.006X5 + 0.011 | R2 = 0.83, P < 0.01 |
| Jinghe | α = −0.196X1 + 0.025X2 − 0.044X3 + 0.0003X4 + 0.005X5 + 0.56 | R2 = 0.85, P < 0.01 |
| Kuyehe | α = 0.062X1 + 0.15X2 + 0.019X3 + 0.001X4 − 0.015X5 − 0.013 | R2 = 0.88, P < 0.01 |
| Beiluohe | α = −0.007X1 + 0.177X2 − 0.02X3 + 0.01X4 − 0.008X5 + 0.287 | R2 = 0.81, P < 0.01 |
| Qinhe | α = 0.146X1 + 0.225X2 − 0.019X3 + 0.006X4 − 0.005X5 − 0.20 | R2 = 0.74, P < 0.05 |
| Weihe | α = −0.147X1 + 0.07X2 − 0.076X3 + 0.004X4 + 0.016X5 + 0.69 | R2 = 0.77, P < 0.05 |
| Wudinghe | α = −0.093X1 + 0.201X2 + 0.035X3−0.002X4 − 0.047X5 − 0.387 | R2 = 0.82, P < 0.01 |
| Yiluohe | α = 0.201X1 + 0.172X2 − 0.083X3−0.01X4 + 0.005X5 + 0.797 | R2 = 0.79, P < 0.01 |
| Wuzhi–Lijin | α = 0.16X1 + 0.55X2 − 0.037X3 + 0.07X4 + 0.095X5 − 1.84 | R2 = 0.80, P < 0.01 |
| Daicuba | α = 0.217X1 + 0.739X2 − 0.033X3 + 0.127X4 + 0.15X5 − 3.537 | R2 = 0.83, P < 0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Mu, H.; Jian, S.; Li, X. Study on the Annual Runoff Change and Its Relationship with Fractional Vegetation Cover and Climate Change in the Chinese Yellow River Basin. Water 2024, 16, 1537. https://doi.org/10.3390/w16111537
Xu L, Mu H, Jian S, Li X. Study on the Annual Runoff Change and Its Relationship with Fractional Vegetation Cover and Climate Change in the Chinese Yellow River Basin. Water. 2024; 16(11):1537. https://doi.org/10.3390/w16111537
Chicago/Turabian StyleXu, Lin, Hongxu Mu, Shengqi Jian, and Xinan Li. 2024. "Study on the Annual Runoff Change and Its Relationship with Fractional Vegetation Cover and Climate Change in the Chinese Yellow River Basin" Water 16, no. 11: 1537. https://doi.org/10.3390/w16111537
APA StyleXu, L., Mu, H., Jian, S., & Li, X. (2024). Study on the Annual Runoff Change and Its Relationship with Fractional Vegetation Cover and Climate Change in the Chinese Yellow River Basin. Water, 16(11), 1537. https://doi.org/10.3390/w16111537





