Water–Energy–Milk Nexus: Empirical Evidence from Saudi Arabia
Abstract
1. Introduction
2. Literature Review
2.1. Milk–Water Nexus
2.2. Milk–Energy Nexus
2.3. Milk–Water–Energy Nexus
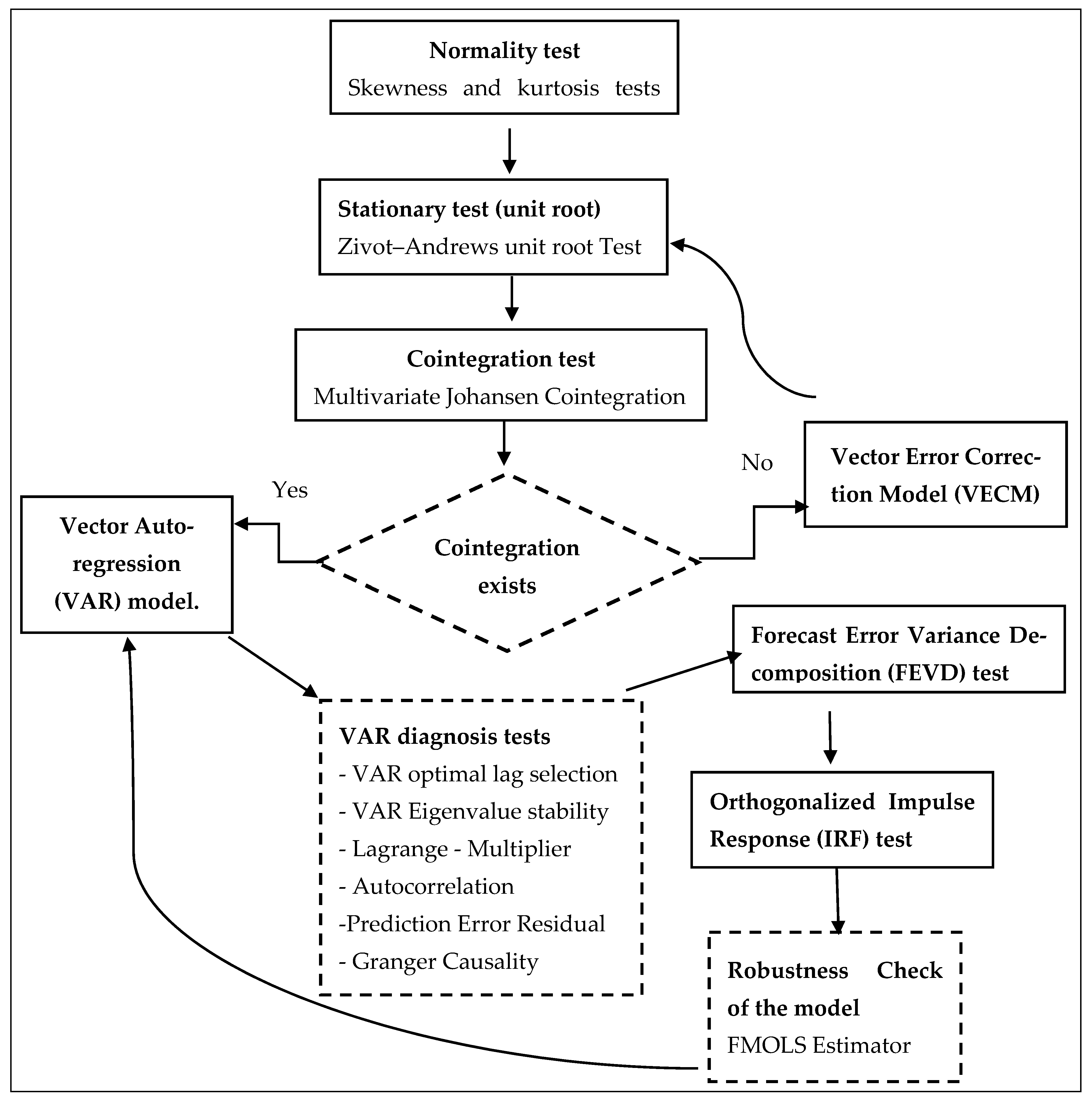
3. Data and Methods
3.1. Data
3.2. Approaches
3.2.1. Unit Root and Cointegration Tests
3.2.2. VAR Model
3.2.3. Granger Causality Test
3.2.4. Impulse Response Functions and Variance Decompositions
4. Results and Discussion
4.1. Unit Root and Cointegration Results
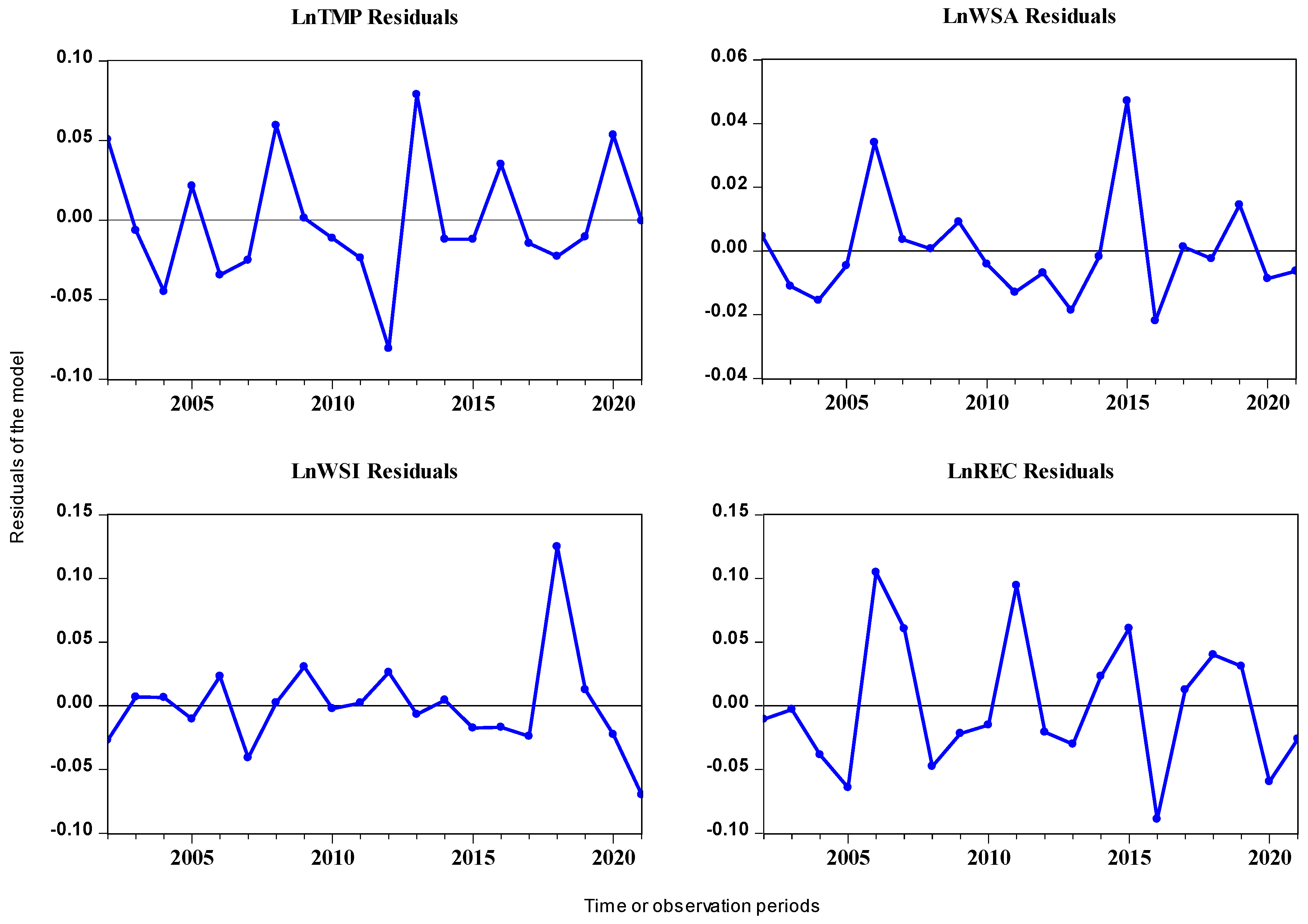
4.2. VAR Results
4.3. Granger Causality Approach Results
4.4. Forecast Error Variance Decomposition Results
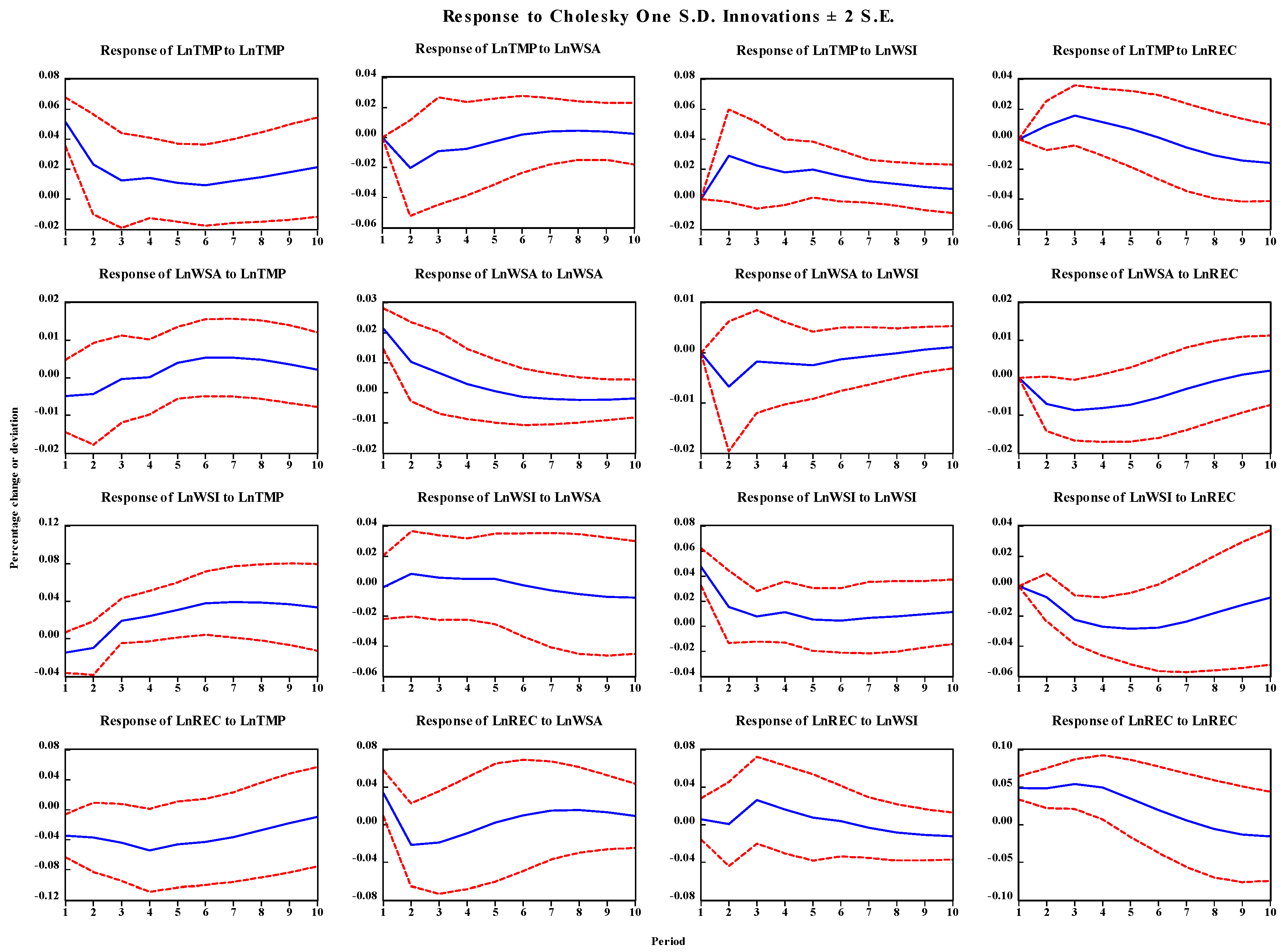
4.5. Impulse Response Function Results
4.6. Robustness Check: FMOLS Estimator Results
5. Conclusions and Policy Implications
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Variable | Model (A) Intercept * | Model (B) Trend ** | Model (C) Trend and Intercept *** | |||
|---|---|---|---|---|---|---|
| t-Stat | SBD | t-Stat | SBD | t-Stat | SBD | |
| LnTMP | −5.599 | 2015 | −5.018 | 2009 | −5.741 | 2015 |
| lnWSA | −6.035 | 2007 | −5.048 | 2011 | −6.034 | 2007 |
| LnWSI | −4.625 | 2015 | 4.282 | 2008 | −5.450 | 2018 |
| LnREC | −5.631 | 2016 | −4.658 | 2017 | −7.947 | 2016 |
Appendix B
| Trace Statistics Test | Conclusion | ||||||
|---|---|---|---|---|---|---|---|
| Hypothesized No. of CE(s) | Params | LL | Eigenvalue | Trace Statistic | Critical Value (1%) | p-Value | |
| r = 0 | 20 | 142.929 | 50.057 | 54.682 | 0.031 | H0 accepted | |
| r ≥ 1 | 27 | 155.791 | 0.7237 | 24.333 | 35.458 | 0.187 | H0 accepted |
| r ≥ 2 | 32 | 164.002 | 0.5601 | 7.909 | 19.937 | 0.475 | H0 accepted |
| r ≥ 3 | 35 | 167.957 | 0.309 | 0.490 | 6.635 | 0.484 | H0 accepted |
| r ≥ 4 | 36 | 167.957 | 0.024217 | ||||
| Maximum Eigenvalue test | |||||||
| Hypothesized No. of CE(s) | Params | LL | Eigenvalue | Max-Eigen statistic | Critical Value (1%) | p-Value | |
| r ≥ 0 | 20 | 142.929 | 25.724 | 32.715 | 0.085 | H0 accepted | |
| r ≥ 1 | 27 | 155.791 | 0.724 | 16.424 | 25.861 | 0.201 | H0 accepted |
| r ≥ 2 | 32 | 164.003 | 0.560 | 7.419 | 18.520 | 0.441 | H0 accepted |
| r ≥ 3 | 35 | 167.957 | 0.310 | 0.490 | 6.635 | 0.484 | H0 accepted |
| r ≥ 4 | 36 | 167.957 | 0.024 | ||||
| Information criteria | |||||||
| Hypothesized No. of CE(s) | Params | LL | Eigenvalue | SBIC | HQIC | AIC | |
| r ≥ 0 | 20 | 142.929 | −11.297 | −12.098 | −12.293 | Not selected | |
| r ≥ 1 | 27 | 155.791 | 0.724 | 11.535 | −12.617 | −12.879 | Not selected |
| r ≥ 2 | 32 | 164.003 | 0.560 | −11.607 * | −12.889 | −13.200 | Selected |
| r ≥ 3 | 35 | 167.957 | 0.310 | −11.529 | −12.931 * | 13.271 | Selected |
| r ≥ 4 | 36 | 167.957 | 0.024 | ||||
References
- Food and Agriculture Organization of the United Nations. The State of the World’s Land and Water Resources for Food and Agriculture 2021—Systems at Breaking Point; FAO: Rome, Italy, 2021. [Google Scholar]
- Koncagül, E.; Connor, R. The United Nations World Water Development Report 2023: Partnerships and Cooperation for Water; Facts, Figures and Action Examples; UNESCO World Water Assessment Programme: Perugia, Italy, 2023. [Google Scholar]
- World Bank. High and Dry: Climate Change, Water, and the Economy; World Bank: Washington, DC, USA, 2016. [Google Scholar]
- Food and Agriculture Organization of the United Nations. Water Scarcity. Available online: https://www.fao.org/land-water/water/water-scarcity/en/ (accessed on 16 February 2024).
- Imasiku, K.; Ntagwirumugara, E. An Impact Analysis of Population Growth on Energy-water-food-land Nexus for Ecological Sustainable Development in Rwanda. Food Energy Secur. 2020, 9, e185. [Google Scholar] [CrossRef]
- Zakariazadeh, A.; Ahshan, R.; Al Abri, R.; Al-Abri, M. Renewable Energy Integration in Sustainable Water Systems: A Review. Clean. Eng. Technol. 2024, 18, 100722. [Google Scholar] [CrossRef]
- Dong, K.; Hochman, G.; Zhang, Y.; Sun, R.; Li, H.; Liao, H. CO2 Emissions, Economic and Population Growth, and Renewable Energy: Empirical Evidence across Regions. Energy Econ. 2018, 75, 180–192. [Google Scholar] [CrossRef]
- Hamzehkolaei, F.T.; Amjady, N. A Techno-Economic Assessment for Replacement of Conventional Fossil Fuel Based Technologies in Animal Farms with Biogas Fueled CHP Units. Renew. Energy 2018, 118, 602–614. [Google Scholar] [CrossRef]
- Barron-Gafford, G.A.; Pavao-Zuckerman, M.A.; Minor, R.L.; Sutter, L.F.; Barnett-Moreno, I.; Blackett, D.T.; Thompson, M.; Dimond, K.; Gerlak, A.K.; Nabhan, G.P.; et al. Agrivoltaics Provide Mutual Benefits across the Food–Energy–Water Nexus in Drylands. Nat. Sustain. 2019, 2, 848–855. [Google Scholar] [CrossRef]
- Amhamed, A.; Genidi, N.; Abotaleb, A.; Sodiq, A.; Abdullatif, Y.; Hushari, M.; Al-Kuwari, M. Food Security Strategy to Enhance Food Self-Sufficiency and Overcome International Food Supply Chain Crisis: The State of Qatar as a Case Study. Green Technol. Resil. Sustain. 2023, 3, 3. [Google Scholar] [CrossRef]
- Al-Wabel, M.I.; Sallam, A.; Ahmad, M.; Elanazi, K.; Usman, A.R.A. Extent of Climate Change in Saudi Arabia and Its Impacts on Agriculture: A Case Study from Qassim Region. In Environment, Climate, Plant and Vegetation Growth; Springer International Publishing: Cham, Switzerland, 2020; pp. 635–657. [Google Scholar]
- Mekonnen, M.M.; Neale, C.M.U.; Ray, C.; Erickson, G.E.; Hoekstra, A.Y. Water Productivity in Meat and Milk Production in the US from 1960 to 2016. Environ. Int. 2019, 132, 105084. [Google Scholar] [CrossRef] [PubMed]
- Noya, I.; González-García, S.; Berzosa, J.; Baucells, F.; Feijoo, G.; Moreira, M.T. Environmental and Water Sustainability of Milk Production in Northeast Spain. Sci. Total Environ. 2018, 616–617, 1317–1329. [Google Scholar] [CrossRef] [PubMed]
- Elzaki, R.M.; Al-Mahish, M. Food Insecurity and Water Management Shocks in Saudi Arabia: Bayesian VAR Analysis. PLoS ONE 2024, 19, e0296721. [Google Scholar] [CrossRef]
- Grossi, G.; Vitali, A.; Lacetera, N. Impact of Summer Cooling Management on Milk Water Footprint in Dairy Cows. J. Clean. Prod. 2022, 367, 133062. [Google Scholar] [CrossRef]
- Malliaroudaki, M.I.; Watson, N.J.; Ferrari, R.; Nchari, L.N.; Gomes, R.L. Energy Management for a Net Zero Dairy Supply Chain under Climate Change. Trends Food Sci. Technol. 2022, 126, 153–167. [Google Scholar] [CrossRef]
- Zlaoui, M.; Dhraief, M.Z.; Hilali, M.E.-D.; Dhehibi, B.; Ben Salem, M.; Jebali, O.; Rekik, M. Can Small-Scale Dairy Farm Profitability Increase with the Use of Solar Energy Technology? An Experimental Study in Central Tunisia. Energies 2023, 16, 4925. [Google Scholar] [CrossRef]
- Vida, E.; Tedesco, D.E.A. The Carbon Footprint of Integrated Milk Production and Renewable Energy Systems—A Case Study. Sci. Total Environ. 2017, 609, 1286–1294. [Google Scholar] [CrossRef]
- Minoofar, A.; Gholami, A.; Eslami, S.; Hajizadeh, A.; Gholami, A.; Zandi, M.; Ameri, M.; Kazem, H.A. Renewable Energy System Opportunities: A Sustainable Solution toward Cleaner Production and Reducing Carbon Footprint of Large-Scale Dairy Farms. Energy Convers. Manag. 2023, 293, 117554. [Google Scholar] [CrossRef]
- Edwin, M.; Joseph Sekhar, S. Techno- Economic Evaluation of Milk Chilling Unit Retrofitted with Hybrid Renewable Energy System in Coastal Province. Energy 2018, 151, 66–78. [Google Scholar] [CrossRef]
- Sultana, M.N.; Uddin, M.M.; Ridoutt, B.G.; Peters, K.J. Comparison of Water Use in Global Milk Production for Different Typical Farms. Agric. Syst. 2014, 129, 9–21. [Google Scholar] [CrossRef]
- Liao, W.-T.; Su, J.-J. Evaluation of Water Scarcity Footprint for Taiwanese Dairy Farming. Animals 2019, 9, 956. [Google Scholar] [CrossRef] [PubMed]
- Murphy, E.; de Boer, I.J.M.; van Middelaar, C.E.; Holden, N.M.; Shalloo, L.; Curran, T.P.; Upton, J. Water Footprinting of Dairy Farming in Ireland. J. Clean. Prod. 2017, 140, 547–555. [Google Scholar] [CrossRef]
- Owusu-Sekyere, E.; Jordaan, H.; Chouchane, H. Evaluation of Water Footprint and Economic Water Productivities of Dairy Products of South Africa. Ecol. Indic. 2017, 83, 32–40. [Google Scholar] [CrossRef]
- Payen, S.; Falconer, S.; Ledgard, S.F. Water Scarcity Footprint of Dairy Milk Production in New Zealand—A Comparison of Methods and Spatio-Temporal Resolution. Sci. Total Environ. 2018, 639, 504–515. [Google Scholar] [CrossRef]
- Usva, K.; Virtanen, E.; Hyvärinen, H.; Nousiainen, J.; Sinkko, T.; Kurppa, S. Applying Water Scarcity Footprint Methodologies to Milk Production in Finland. Int. J. Life Cycle Assess. 2019, 24, 351–361. [Google Scholar] [CrossRef]
- Houari, Y.; Benamar, B.; Abdelkader, H.; Kheloufi, B. Water Footprint of Milk Production Systems in Semi-Arid Plains of North Africa. Biotechnol. Anim. Husb. 2021, 37, 27–43. [Google Scholar] [CrossRef]
- Williams, L.R.; Jackson, E.L.; Bishop-Hurley, G.J.; Swain, D.L. Drinking Frequency Effects on the Performance of Cattle: A Systematic Review. J. Anim. Physiol. Anim. Nutr. 2017, 101, 1076–1092. [Google Scholar] [CrossRef] [PubMed]
- Daros, R.R.; Bran, J.A.; Hötzel, M.J.; von Keyserlingk, M.A.G. Readily Available Water Access Is Associated with Greater Milk Production in Grazing Dairy Herds. Animals 2019, 9, 48. [Google Scholar] [CrossRef]
- Miglierina, M.; Bonadeo, N.; Ornstein, A.; Becú-Villalobos, D.; Lacau-Mengido, I. In Situ Provision of Drinking Water to Grazing Dairy Cows Improves Milk Production. N. Z. Vet. J. 2018, 66, 37–40. [Google Scholar] [CrossRef]
- Grossi, S.; Rossi, L.; Dell’Anno, M.; Biffani, S.; Sgoifo Rossi, C.A. Effects of Heated Drinking Water on the Growth Performance and Rumen Functionality of Fattening Charolaise Beef Cattle in Winter. Animals 2021, 11, 2218. [Google Scholar] [CrossRef]
- Giri, A.; Bharti, V.K.; Kalia, S.; Arora, A.; Balaje, S.S.; Chaurasia, O.P. A Review on Water Quality and Dairy Cattle Health: A Special Emphasis on High-Altitude Region. Appl. Water Sci. 2020, 10, 79. [Google Scholar] [CrossRef]
- Osuji, E.; Igberi, C.; Enyia, C.; Nwachukwu, E.; Nwose, R.; Adeolu, A.; Tim-Ashama, A.; Nkwocha, G.; Eleazar, A.; Gabriel, D. Impact of Climate Change on Milk Production in Nigeria. Online J. Anim. Feed Res. 2023, 13, 246–252. [Google Scholar] [CrossRef]
- Ziolkowska, J. Socio-Economic Implications of Drought in the Agricultural Sector and the State Economy. Economies 2016, 4, 19. [Google Scholar] [CrossRef]
- Abbas, Q.; Han, J.; Adeel, A.; Ullah, R. Dairy Production under Climatic Risks: Perception, Perceived Impacts and Adaptations in Punjab, Pakistan. Int. J. Environ. Res. Public. Health 2019, 16, 4036. [Google Scholar] [CrossRef]
- Alderfasi, A.A.; Nielsen, D.C. Use of Crop Water Stress Index for Monitoring Water Status and Scheduling Irrigation in Wheat. Agric. Water Manag. 2001, 47, 69–75. [Google Scholar] [CrossRef]
- Ahammed, S.J.; Homsi, R.; Khan, N.; Shahid, S.; Shiru, M.S.; Mohsenipour, M.; Ahmed, K.; Nawaz, N.; Alias, N.E.; Yuzir, A. Assessment of Changing Pattern of Crop Water Stress in Bangladesh. Environ. Dev. Sustain. 2020, 22, 4619–4637. [Google Scholar] [CrossRef]
- Iqbal, M.S.; Singh, A.K.; Ansari, M.I. Effect of Drought Stress on Crop Production. In New Frontiers in Stress Management for Durable Agriculture; Springer: Singapore, 2020; pp. 35–47. [Google Scholar]
- Oğuz, C.; Yener, A. The Use of Energy in Milk Production; a Case Study from Konya Province of Turkey. Energy 2019, 183, 142–148. [Google Scholar] [CrossRef]
- Mohsenimanesh, A.; LeRiche, E.L.; Gordon, R.; Clarke, S.; MacDonald, R.D.; MacKinnon, I.; VanderZaag, A.C. Review: Dairy Farm Electricity Use, Conservation, and Renewable Production—A Global Perspective. Appl. Eng. Agric. 2021, 37, 977–990. [Google Scholar] [CrossRef]
- Kimming, M.; Sundberg, C.; Nordberg, Å.; Baky, A.; Bernesson, S.; Hansson, P.-A. Replacing Fossil Energy for Organic Milk Production—Potential Biomass Sources and Greenhouse Gas Emission Reductions. J. Clean. Prod. 2015, 106, 400–407. [Google Scholar] [CrossRef]
- Üçtuğ, F.G. The Environmental Life Cycle Assessment of Dairy Products. Food Eng. Rev. 2019, 11, 104–121. [Google Scholar] [CrossRef]
- Entrena-Barbero, E.; Rebolledo-Leiva, R.; Vásquez-Ibarra, L.; Fernández, M.; Feijoo, G.; González-García, S.; Moreira, M.T. Water-Energy-Food Nexus Index Proposal as a Sustainability Criterion on Dairy Farms. Sci. Total Environ. 2023, 874, 162507. [Google Scholar] [CrossRef] [PubMed]
- Alamri, Y.; Alrwis, K.; Ghanem, A.; Kamara, S.; Alaagib, S.; Aldawdahi, N. The Economic Nexus between Energy, Water Consumption, and Food Production in the Kingdom of Saudi Arabia. Economies 2023, 11, 113. [Google Scholar] [CrossRef]
- Food and Agriculture Organization of the United Nations. SDG Indicators. Available online: https://www.fao.org/faostat/en/%3f#data/SDGB (accessed on 16 February 2024).
- The World Bank Databank: Sustainable Energy for All. Available online: https://databank.worldbank.org/source/sustainable-energy-for-all/Type/TABLE/preview/on (accessed on 16 February 2024).
- Cheng, F.; Fu, Z. Macroeconomic Forecasting Based on Mixed Frequency Vector Autoregression and Neural Network Models. Wirel. Commun. Mob. Comput. 2022, 2022, 2956289. [Google Scholar] [CrossRef]
- Sims, C.A. Macroeconomics and Reality. Econometrica 1980, 48, 1. [Google Scholar] [CrossRef]
- Temiz, D.; Gökmen, A.; Abubakar, M.S. Foreign Direct Investment and Its Impact on Economic Performance: The Case of Turkey and Nigeria. J. Transnatl. Manag. 2015, 20, 207–230. [Google Scholar] [CrossRef]
- Zivot, E.; Andrews, D.W.K. Further Evidence on the Great Crash, the Oil-Price Shock, and the Unit-Root Hypothesis. J. Bus. Econ. Stat. 1992, 10, 251. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root. Econometrica 1981, 49, 1057. [Google Scholar] [CrossRef]
- Usman, O.; Iorember, P.T.; Olanipekun, I.O. Revisiting the Environmental Kuznets Curve (EKC) Hypothesis in India: The Effects of Energy Consumption and Democracy. Environ. Sci. Pollut. Res. 2019, 26, 13390–13400. [Google Scholar] [CrossRef] [PubMed]
- Omoju, O.E.; Li, J.; Zhang, J.; Rauf, A.; Sosoo, V.E. Implications of Shocks in Energy Consumption for Energy Policy in Sub-Saharan Africa. Energy Environ. 2020, 31, 1077–1097. [Google Scholar] [CrossRef]
- Johansen, S.; Juselius, K. Maximum Likelihood Estimation and Inference on Cointegration—With Applications to the Demand for Money. Oxf. Bull. Econ. Stat. 1990, 52, 169–210. [Google Scholar] [CrossRef]
- Cheptiş, A. The Impact of External Shocks on Economic Growth: An Empirical Study Based on the SVAR Models. Proc. Int. Conf. Bus. Excell. 2022, 16, 650–659. [Google Scholar] [CrossRef]
- Kim, H.; Lee, J.-T. On Inferences about Lag Effects Using Lag Models in Air Pollution Time-Series Studies. Environ. Res. 2019, 171, 134–144. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.-L.; Hu, J.-W.; Kong, L.-S.; Zhang, X. Relationship between Energy Production and Water Resource Utilization: A Panel Data Analysis of 31 Provinces in China. J. Clean. Prod. 2017, 167, 88–96. [Google Scholar] [CrossRef]
- Wang, Y.; Xiao, W.; Wang, Y.; Zhao, Y.; Wang, J.; Hou, B.; Song, X.; Zhang, X. Impact of China’s Urbanization on Water Use and Energy Consumption: An Econometric Method and Spatiotemporal Analysis. Water 2018, 10, 1323. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica 1969, 37, 424. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Z.; Qin, Y.; Skare, M. Innovation, the Knowledge Economy, and Green Growth: Is Knowledge-Intensive Growth Really Environmentally Friendly? Energy Econ. 2022, 115, 106331. [Google Scholar] [CrossRef]
- Alsaedi, Y.H.; Tularam, G.A. The Relationship between Electricity Consumption, Peak Load and GDP in Saudi Arabia: A VAR Analysis. Math. Comput. Simul. 2020, 175, 164–178. [Google Scholar] [CrossRef]
- Salahuddin, M.; Alam, K. Internet Usage, Electricity Consumption and Economic Growth in Australia: A Time Series Evidence. Telemat. Inform. 2015, 32, 862–878. [Google Scholar] [CrossRef]
- Johansen, S. Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models. Econometrica 1991, 59, 1551. [Google Scholar] [CrossRef]
- Guzmán-Luna, P.; Mauricio-Iglesias, M.; Flysjö, A.; Hospido, A. Analysing the Interaction between the Dairy Sector and Climate Change from a Life Cycle Perspective: A Review. Trends Food Sci. Technol. 2022, 126, 168–179. [Google Scholar] [CrossRef]
- Elahi, E.; Weijun, C.; Jha, S.K.; Zhang, H. Estimation of Realistic Renewable and Non-Renewable Energy Use Targets for Livestock Production Systems Utilising an Artificial Neural Network Method: A Step towards Livestock Sustainability. Energy 2019, 183, 191–204. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, J.; Wang, X.; Zhang, X. Assessing the Impact of Changing Environment on Coal Mining Water Use in China. Water-Energy Nexus 2023, 6, 177–186. [Google Scholar] [CrossRef]
- Staupe-Delgado, R. The Water–Energy–Food–Environmental Security Nexus: Moving the Debate Forward. Environ. Dev. Sustain. 2020, 22, 6131–6147. [Google Scholar] [CrossRef]
- Čechura, L.; Žáková Kroupová, Z.; Benešová, I. Productivity and Efficiency in European Milk Production: Can We Observe the Effects of Abolishing Milk Quotas? Agriculture 2021, 11, 835. [Google Scholar] [CrossRef]
- Innes, D.J.; Pot, L.J.; Seymour, D.J.; France, J.; Dijkstra, J.; Doelman, J.; Cant, J.P. Fitting Mathematical Functions to Extended Lactation Curves and Forecasting Late-Lactation Milk Yields of Dairy Cows. J. Dairy Sci. 2024, 107, 342–358. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Wu, Q. Evaluation of the Relationship between Energy Consumption, Economic Growth, and CO2 Emissions in China’ Transport Sector: The FMOLS and VECM Approaches. Environ. Dev. Sustain. 2020, 22, 6537–6561. [Google Scholar] [CrossRef]

| 1. Correlation Matrix | ||||
| Variable | TMP | WSA | WSI | REC |
| TMP | 1.00 | |||
| WSA | 0.29 (0.19) | 1.00 | ||
| WSI | 0.93 *** (0.00) | 0.51 *** (0.01) | 1.00 | |
| REC | −0.06 (0.78) | −0.006 (0.98) | −0.15 (0.51) | 1.00 |
| 2. Descriptive Statistics | ||||
| Mean | 1,873,405.00 | 776.70 | 33.51 | 232.94 |
| Std. dev. | 645,574.60 | 27.99 | 12.08 | 35.73 |
| Min | 952,500.00 | 719.17 | 11.35 | 181.71 |
| Max | 2,916,104.00 | 830.15 | 52.49 | 285.33 |
| 3. Normality Tests: | ||||
| A. Skewness and kurtosis tests | ||||
| Statistics test | Pr (skewness) | Pr (kurtosis) | Joint test | |
| chi2(2) | Prob > chi2 | |||
| TMP | 0.864 | 0.017 | 5.71 | 0.058 |
| WSA | 0.648 | 0.788 | 0.28 | 0.869 |
| WSI | 0.890 | 0.695 | 0.17 | 0.917 |
| REC | 0.611 | 0.035 | 4.73 | 0.094 |
| B. Shapiro–Wilk W test | ||||
| Statistics test | W | V | Z | Prob > z |
| TMP | 0.922 | 1.982 | 1.387 | 0.083 |
| WSA | 0.971 | 0.732 | −0.632 | 0.736 |
| WSI | 0.943 | 1.441 | 0.740 | 0.229 |
| REC | 0.908 | 2.340 | 1.724 | 0.042 |
| Predictor Variable | Response Variable: Equations | |||
|---|---|---|---|---|
| LnTMP: Equation (4) | LnWSA: Equation (5) | LnWSI: Equation (6) | LnREC: Equation (7) | |
| LnTMP (-1) | 0.115 [0.142] (0.809) | −0.044 [0.093] (−0.474) | −0.128 [0.108] (−1.185) | −0.062 [0.324] (−0.190) |
| LnTMP (-2) | 0.213 [0.141] (1.509) | 0.037 [0.093] (0.396) | 0.151 [0.107] (1.407) | −0.212 [0.322] (−0.660) |
| LnTMP (-3) | 0.184 [0.128] (1.440) | −0.179 [0.084] (−2.133) ** | 0.363 [0.097] (3.740) *** | −0.344 [0.291] (−1.183) |
| LnWSA (-1) | −0.164 [0.340] (−0.483) | 0.567 [0.222] (2.551) *** | 0.088 [0.257] (0.343) | −3.023 [0.772] (−3.917) *** |
| LnWSA (-2) | −1.610 [0.628] (−2.565) *** | −0.042 [0.411] (−0.103) | 0.282 [0.476] (0.592) | 2.000 [1.427] (1.401) |
| LnWSA (-3) | 1.516 [0.427] (3.549) *** | −0.572 [0.280] (−2.045) ** | 0.472 [0.324] (1.458) | −0.858 [0.971] (−0.884) |
| LnWSI (-1) | 0.389 [0.157] (2.483) ** | 0.021 [0.103] (0.208) | 0.355 [0.119] (2.986) *** | 0.244 [0.356] (0.685) |
| LnWSI (-2) | 0.313 [0.156] (2.012) ** | 0.100 [0.102] (0.978) | 0.048 [0.118] (0.409) | 0.018 [0.354] (0.051) |
| LnWSI (-3) | −0.185 [0.139] (−1.327) | 0.055 [0.091] (0.597) | −0.006 [0.106] (−0.058) | 0.237 [0.317] (0.747) |
| lnREC (-1) | −0.220 [0.122] (−1.812) * | −0.119 [0.080] (−1.498) | 0.006 [0.092] (0.067) | 1.016 [0.276] (3.677) *** |
| lnREC (-2) | 0.790 [0.178] (4.429) *** | −0.026 [0.117] (−0.223) | −0.573 [0.135] (−4.243) *** | −0.511 [0.405] (−1.261) |
| lnREC (-3) | −0.460 [0.097] (−4.739) *** | 0.137 [0.064] (2.148) ** | 0.308 [0.074] (4.187) *** | 0.380 [0.221] (1.718) * |
| Constants | 6.418 [3.231] (1.986) ** | 9.085 [2.115] (4.296) *** | −7.527 [2.449] (−3.074) *** | 20.301 [7.343] (2.765) *** |
| PARMS | 13 | 13 | 13 | 13 |
| RMSE | 0.035 | 0.023 | 0.027 | 0.080 |
| R-sq | 0.996 | 0.790 | 0.997 | 0.913 |
| X2 | 4504.641 *** | 71.424 *** | 5996.207 *** | 200.198 *** |
| Lag | LogL | LR | FPE | AIC | SC | HQ |
|---|---|---|---|---|---|---|
| 0 | 71.393 | NA | 9.76 × 10−9 | −7.094 | −6.895 | −7.060 |
| 1 | 145.885 | 109.778 * | 2.17 × 10−11 | −13.251 | −12.257 | −13.083 |
| 2 | 163.335 | 18.368 | 2.47 × 10−11 | −13.404 | −11.614 | −13.101 |
| 3 | 201.290 | 23.972 | 5.97 × 10−12 * | −15.715 * | −13.130 * | −15.277 * |
| * Root | Modulus |
|---|---|
| 0.987 | 0.987 |
| 0.777 + 0.418 i | 0.882 |
| 0.777 −0.418 i | 0.882 |
| 0.449 +0.759 i | 0.882 |
| 0.449–0.759 i | 0.882 |
| −0.326 + 0.764 i | 0.831 |
| −0.326–0.764 i | 0.831 |
| 0.741 | 0.741 |
| −0.614 | 0.614 |
| −0.516 + 0.139 i | 0.534 |
| −0.516–0.139 i | 0.053 |
| 0.173 | 0.173 |
| Lagrange Multiplier Test | |||
|---|---|---|---|
| Lag | X2 | P > X2 | Decision |
| 1 | 12.583 | 0.703 | H0 accepted |
| 2 | 20.865 | 0.184 | H0 accepted |
| 3 | 16.322 | 0.431 | H0 accepted |
| 4 | 18.978 | 0.270 | H0 accepted |
| Predict error, residual | Mean (Std. dev) | [Min] [Max] | |
| Value | −1.08 × 10−10 (0.039) | [−0.081] [0.079] | Accuracy in the model’s predictions |
| Equation: LnTMP | |||
|---|---|---|---|
| Excluded | Chi2 | p-Value | Causality, Direction |
| LnWSA | 21.876 | 0.000 *** | WSA ←→TMP. bidirectional |
| LnWSI | 23.235 | 0.000 *** | WSI ←→ TMP, bidirectional |
| LnREC | 46.222 | 0.000 *** | REC←→ TMP, bidirectional |
| All | 121.55 | 0.000 *** | Causality |
| Equation: LnWSA | |||
| Excluded | Chi2 | p-value | Causality, direction |
| LnTMP | 9.6907 | 0.021 ** | TMP ←→ WSA, bidirectional |
| LnWSI | 7.6562 | 0.054 * | WSI ←→WSA, bidirectional |
| LnREC | 17.668 | 0.001 *** | REC ←→ WSA, bidirectional |
| All | 24.454 | 0.004 *** | Causality |
| Equation: LnWSI | |||
| Excluded | Chi2 | p-value | Causality, direction |
| LnTMP | 39.863 | 0.000 *** | TMP ←→ WSI, bidirectional |
| LnWSA | 12.841 | 0.005 *** | WSA←→ WSI, bidirectional |
| LnREC | 89.934 | 0.000 *** | REC→ WSI, unidirectional |
| All | 236.05 | 0.000 *** | Causality |
| Equation: LnREC | |||
| Excluded | Chi2 | p-value | Causality, direction |
| LnTMP | 8.0037 | 0.046 * | TMP ←→REC, bidirectional |
| LnWSA | 18.66 | 0.000 *** | WSA←→ REC, bidirectional |
| LnWSI | 4.908 | 0.179 | No causality |
| All | 42.218 | 0.000 *** | Causality |
| Horizons | Variance Decomposition of LnTMP | Variance Decomposition of LnWSA | ||||||
|---|---|---|---|---|---|---|---|---|
| TMP | WSA | WSI | REC | TMP | WSA | WSI | REC | |
| 1 | 100.000 | 0.000 | 0.000 | 0.000 | 0.701 | 99.300 | 0.000 | 0.000 |
| 2 | 85.921 | 1.775 | 1.088 | 11.216 | 2.007 | 89.840 | 0.169 | 7.985 |
| 3 | 46.518 | 2.872 | 7.245 | 43.365 | 8.135 | 69.488 | 0.265 | 22.112 |
| 4 | 40.650 | 11.481 | 7.135 | 40.734 | 7.462 | 63.726 | 0.249 | 28.563 |
| 5 | 43.004 | 11.135 | 6.609 | 39.252 | 7.389 | 63.791 | 0.247 | 28.574 |
| 6 | 38.167 | 23.914 | 5.481 | 32.438 | 7.250 | 63.010 | 0.602 | 29.138 |
| 7 | 38.808 | 28.140 | 4.415 | 28.637 | 7.340 | 62.948 | 0.682 | 29.031 |
| 8 | 38.095 | 25.549 | 3.539 | 32.817 | 7.258 | 62.383 | 0.675 | 29.684 |
| 9 | 37.254 | 25.466 | 3.330 | 33.950 | 7.149 | 62.122 | 0.689 | 30.040 |
| 10 | 37.706 | 24.075 | 3.151 | 35.068 | 7.383 | 61.220 | 0.772 | 30.624 |
| Horizons | Variance Decomposition of LnWSI | Variance Decomposition of LnREC | ||||||
| TMP | WSA | WSI | REC | TMP | WSA | WSI | REC | |
| 1 | 5.542 | 50.771 | 43.687 | 0.000 | 13.002 | 26.082 | 2.276 | 58.641 |
| 2 | 5.323 | 52.801 | 41.859 | 0.017 | 17.072 | 17.862 | 3.397 | 61.670 |
| 3 | 18.127 | 22.781 | 14.635 | 44.457 | 19.546 | 15.388 | 3.797 | 61.269 |
| 4 | 27.541 | 26.568 | 6.786 | 39.104 | 26.255 | 12.006 | 3.490 | 58.249 |
| 5 | 28.739 | 25.045 | 5.011 | 41.205 | 26.042 | 10.279 | 3.158 | 60.522 |
| 6 | 32.806 | 23.162 | 4.090 | 39.942 | 26.191 | 10.519 | 3.127 | 60.163 |
| 7 | 32.211 | 21.956 | 3.781 | 42.051 | 25.271 | 14.262 | 2.972 | 57.495 |
| 8 | 32.386 | 22.284 | 3.820 | 41.509 | 25.393 | 15.165 | 2.943 | 56.499 |
| 9 | 32.569 | 23.126 | 3.693 | 40.612 | 25.721 | 15.094 | 2.934 | 56.252 |
| 10 | 34.268 | 22.343 | 3.590 | 39.799 | 26.334 | 15.090 | 2.904 | 55.672 |
| Predictor Variable | Coefficient (β) | Newey–West Std. Error | t-Statistic |
|---|---|---|---|
| LnWSA | −2.016 | 0.5180 | −3.891 *** |
| LnWSI | 0.032 | 0.002 | 20.564 *** |
| LnREC | 0.002 | 0.000 | 4.994 *** |
| C | 26.194 | 3.437 | 7.621 *** |
| R-squared | 0.927 | ||
| S.E. of regression | 0.102 | ||
| S.D. dependent variance | 0.349 | ||
| Long-run variance | 0.005 | ||
| Sum squared residues | 0.178 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elzaki, R.M.; Al-Mahish, M.; Alzahrani, F. Water–Energy–Milk Nexus: Empirical Evidence from Saudi Arabia. Water 2024, 16, 1538. https://doi.org/10.3390/w16111538
Elzaki RM, Al-Mahish M, Alzahrani F. Water–Energy–Milk Nexus: Empirical Evidence from Saudi Arabia. Water. 2024; 16(11):1538. https://doi.org/10.3390/w16111538
Chicago/Turabian StyleElzaki, Raga M., Mohammed Al-Mahish, and Fahad Alzahrani. 2024. "Water–Energy–Milk Nexus: Empirical Evidence from Saudi Arabia" Water 16, no. 11: 1538. https://doi.org/10.3390/w16111538
APA StyleElzaki, R. M., Al-Mahish, M., & Alzahrani, F. (2024). Water–Energy–Milk Nexus: Empirical Evidence from Saudi Arabia. Water, 16(11), 1538. https://doi.org/10.3390/w16111538







