Optimizing the Numerical Simulation of Debris Flows: A New Exploration of the Hexagonal Cellular Automaton Method
Abstract
1. Introduction
2. Methods
2.1. Model Introduction
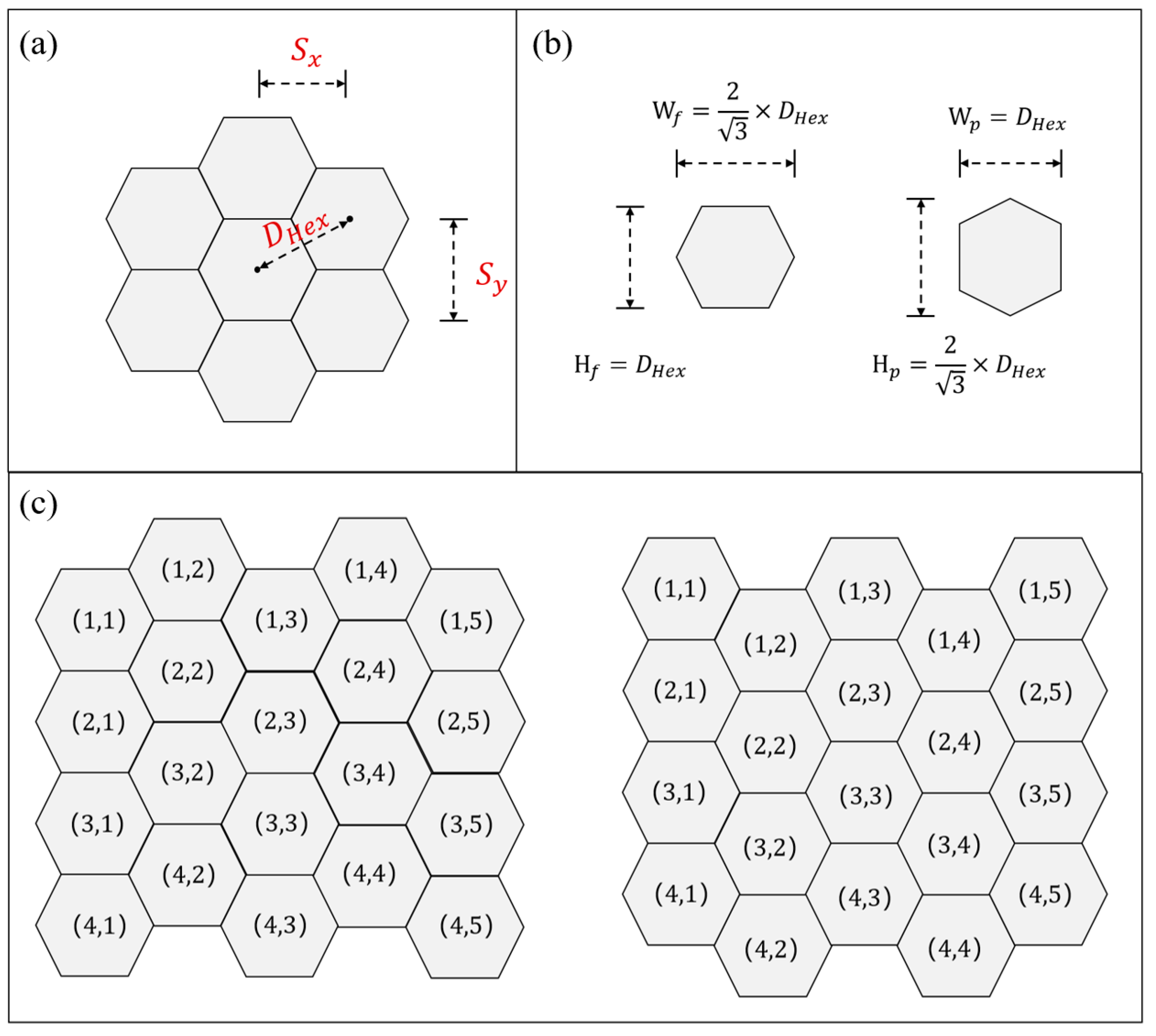
- Cell and Lattice
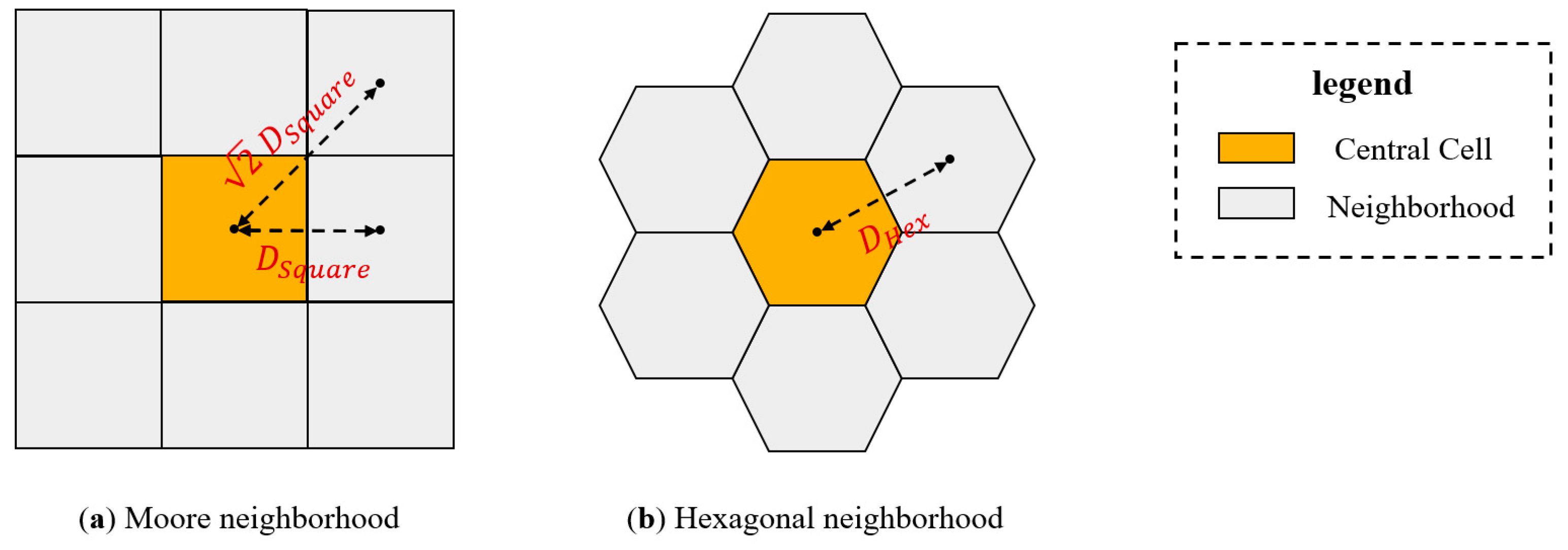
- Neighborhood:
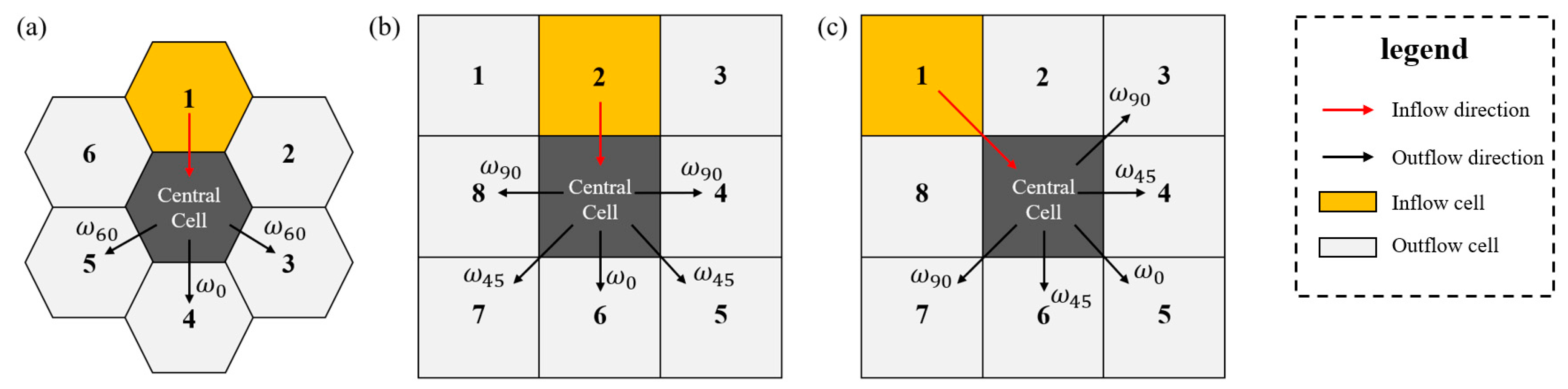
- Transition Functions:
2.2. Flow Direction Function
2.2.1. Terrain Probability
2.2.2. Persistence Probability
2.2.3. Probability Combination
2.3. The Sink-Filling Approach
2.4. Maximum Length Function
2.5. Path Simulation Function Based on Monte Carlo Iterative
3. Case Study
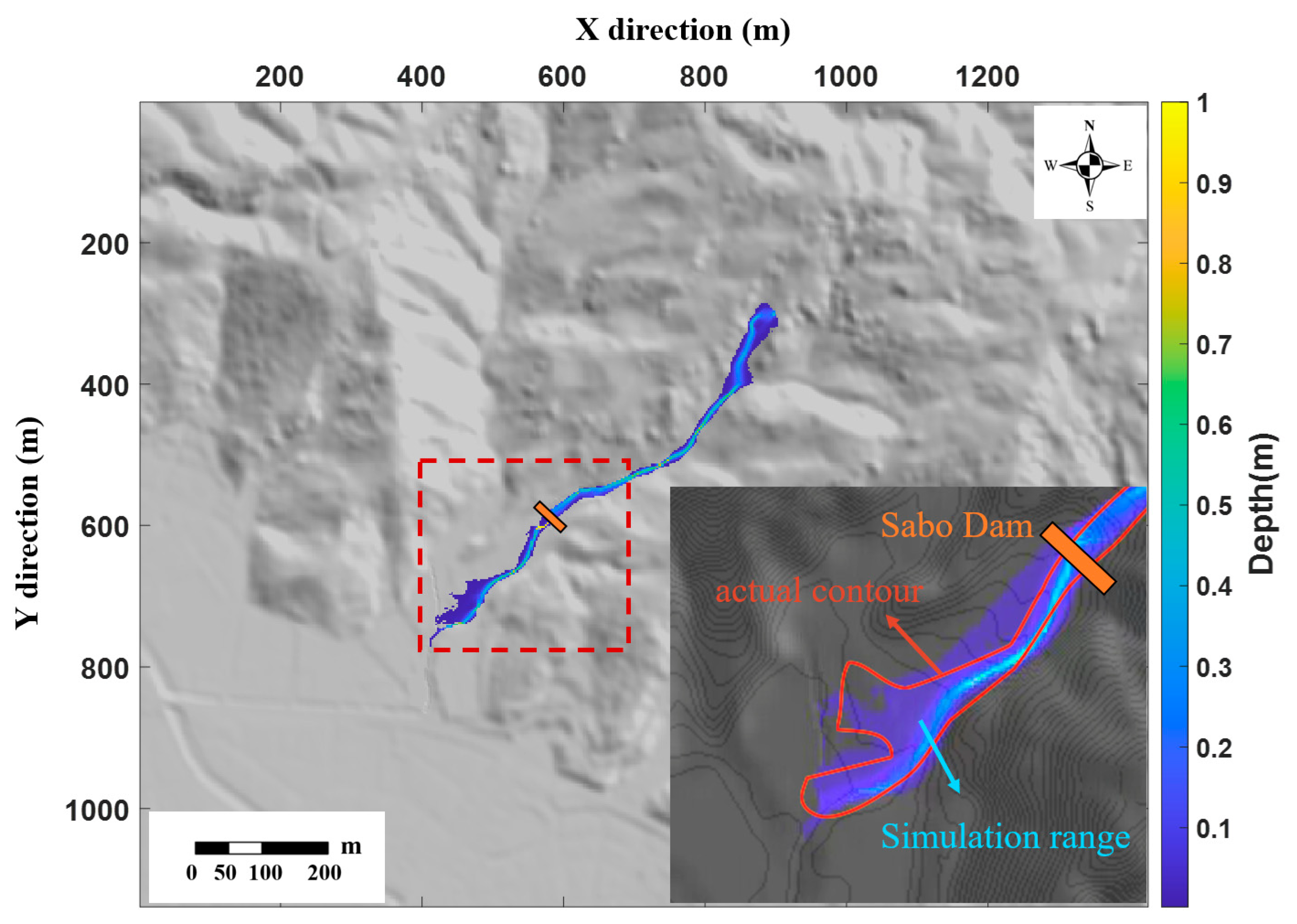
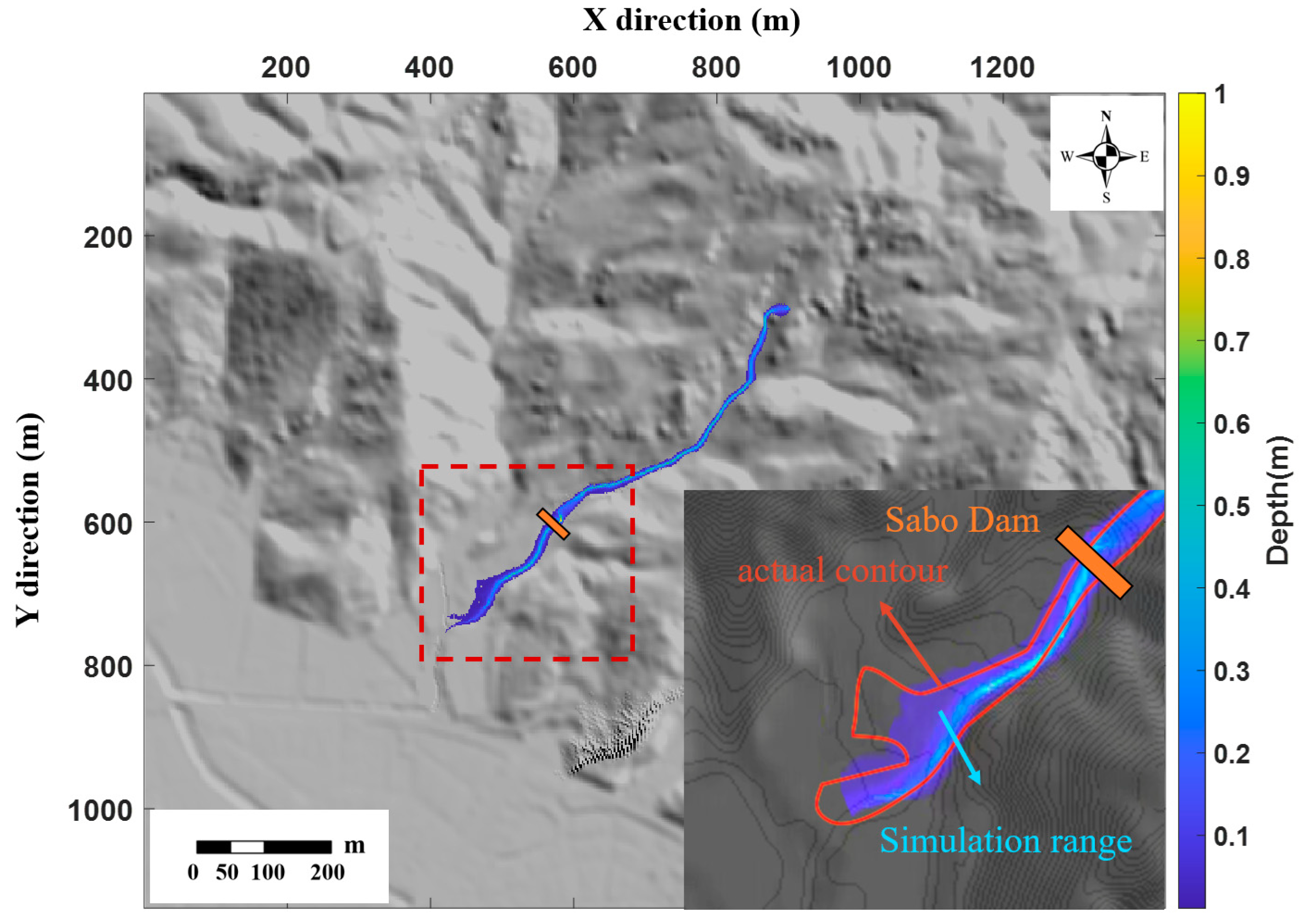
3.1. Yohutagawa Debris Flow
3.2. Flume Test
3.3. Result Analysis
4. Discussion
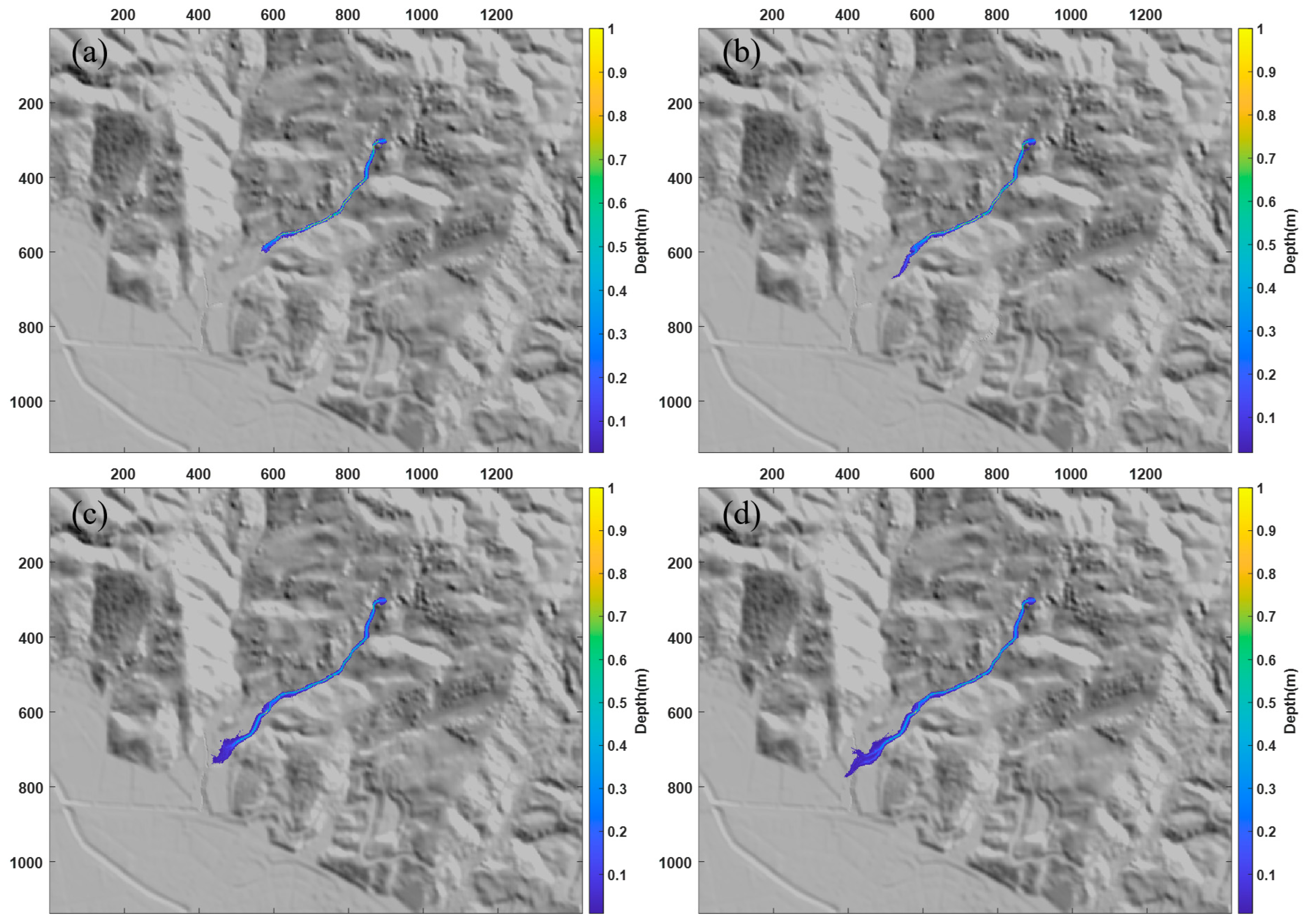
4.1. Interpolation Accuracy
4.2. Interpolation Efficiency
4.3. Dam-Crossing Test
5. Conclusions
- The hexagonal honeycomb network configuration closely resembles a circular shape compared to quadrilateral grid structures and demonstrates isotropy, guaranteeing uniform properties in all directions. This feature is beneficial for maintaining the model’s geometric and physical coherence during the simulation of complex terrain and flow dynamics.
- We compared the accuracy and efficiency of the IDW, bilinear, and cubic interpolation methods. The results show that cubic interpolation has the highest interpolation accuracy, and IDW interpolation accuracy is poor. When the lattice is finely divided, bilinear interpolation has obvious efficiency advantages over cubic interpolation. We recommend using bilinear or cubic interpolation methods as appropriate in the specific case.
- Building upon cellular automaton theory, transition rules define the process of debris flow. These transition rules focus on interactions among neighboring cells, avoiding the necessity of solving complex partial differential equations. The model utilizes the flow direction function, the sink-filling approach, the maximum length function, and the Monte Carlo iterative method to simulate the debris flow run-out extent, highlighting the model’s usefulness.
- The model has been applied to both simulate a water tank and replicate the Yohutagawa debris flow incident. In the -based evaluation framework, the values for the flume test simulation and the Yohutagawa debris flow incident are 0.5381 and 0.5642, respectively. These values represent improvements over the previous CA model’s values of 0.5054 and 0.5424. The score evaluation framework considers the varying impacts of missed judgments and misclassifications. The scores for the HCA model, 0.8488 and 0.8687, respectively, surpass those of the SCA model (0.8191 and 0. 8304) by 3.63% and 4.41%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Froehlich, D.C. Peak flood discharge from a landslide dam outburst. Nat. Hazards Rev. 2022, 23, 04022001. [Google Scholar] [CrossRef]
- Barrocu, G.; Eslamian, S. Geomorphology and Flooding. In Flood Handbook; CRC Press: Boca Raton, FL, USA, 2022; pp. 23–54. [Google Scholar]
- Alagumalai, A.; Anvari, S.; Awad, M.M. Water: A global grand challenge and a path forward. In Solar-Driven Water Treatment; Academic Press: Cambridge, MA, USA, 2022; pp. 1–35. [Google Scholar]
- Zou, Q.; Cui, P.; Zhou, G.G.; Li, S.; Tang, J.; Li, S. A new approach to assessing vulnerability of mountain highways subject to debris flows in China. Prog. Phys. Geogr. Earth Environ. 2018, 42, 305–329. [Google Scholar] [CrossRef]
- Liu, L.; Chen, H. Research Status and Trend about Dynamics of Debris Flow. J. Chongqing Jiaotong Univ. (Nat. Sci.) 2010, 29, 233–239. (In Chinese) [Google Scholar]
- Cui, P.; Wei, F.; Xie, H.; Yang, K.; He, Y.; Ma, D. Debris Flow and Disaster Reduction Strategies in Western China. Quat. Sci. 2003, 02, 142–151. (In Chinese) [Google Scholar]
- Thouret, J.-C.; Antoine, S.; Magill, C.; Ollier, C. Lahars and debris flows: Characteristics and impacts. Earth-Sci. Rev. 2020, 201, 103003. [Google Scholar] [CrossRef]
- Song, D.; Zhou, G.G.; Xu, M.; Choi, C.E.; Li, S.; Zheng, Y. Quantitative analysis of debris-flow flexible barrier capacity from momentum and energy perspectives. Eng. Geol. 2019, 251, 81–92. [Google Scholar] [CrossRef]
- Adedeji, O.H.; Odufuwa, B.O.; Adebayo, O.H. Building capabilities for flood disaster and hazard preparedness and risk reduction in Nigeria: Need for spatial planning and land management. J. Sustain. Dev. Afr. 2012, 14, 45–58. [Google Scholar]
- Iverson, R.M.; George, D.L. A depth-averaged debris-flow model that includes the effects of evolving dilatancy. I. Physical basis. In Proceedings of the Royal Society a Mathematical, Physical and Engineering Sciences; Royal Society: London, UK, 2014; Volume 470, 17p. [Google Scholar]
- Jakob, M. Debris-flow hazard assessments: A practitioner’s view. Environ. Eng. Geosci. 2021, 27, 153–166. [Google Scholar] [CrossRef]
- Pastor, M.; Tayyebi, S.M.; Stickle, M.M.; Yagüe, Á.; Molinos, M.; Navas, P.; Manzanal, D. A depth integrated, coupled, two-phase model for debris flow propagation. Acta Geotech. 2021, 16, 2409–2433. [Google Scholar] [CrossRef]
- Du, J.; Fan, Z.-J.; Xu, W.-T.; Dong, L.-Y. Research progress of initial mechanism on debris flow and related discrimination methods: A review. Front. Earth Sci. 2021, 9, 629567. [Google Scholar] [CrossRef]
- Khan, S.M.; Shafi, I.; Butt, W.H.; Diez, I.D.L.T.; Flores, M.A.L.; Galán, J.C.; Ashraf, I. A systematic review of disaster management systems: Approaches, challenges, and future directions. Land 2023, 12, 1514. [Google Scholar] [CrossRef]
- Kim, S.D.; Ahn, K.; Lee, H. Mathematical modeling of soil mixture flow surge and its application to coastal area. Mar. Georesources Geotechnol. 2017, 35, 610–620. [Google Scholar] [CrossRef]
- Ouyang, C.; He, S.; Tang, C. Numerical analysis of dynamics of debris flow over erodible beds in Wenchuan earthquake-induced area. Eng. Geol. 2015, 194, 62–72. [Google Scholar] [CrossRef]
- Kefayati, G.; Tolooiyan, A.; Dyson, A.P. Finite difference lattice Boltzmann method for modeling dam break debris flows. Phys. Fluids 2023, 35, 013102. [Google Scholar] [CrossRef]
- Han, Z.; Li, M.; Li, Y.; Zhao, M.; Li, C.; Xie, W.; Ding, H.; Ma, Y. An Integrated Approach for Simulating Debris-Flow Dynamic Process Embedded with Physically Based Initiation and Entrainment Models. Water 2023, 15, 1592. [Google Scholar] [CrossRef]
- Dai, Z.; Huang, Y.; Cheng, H.; Xu, Q. SPH model for fluid–structure interaction and its application to debris flow impact estimation. Landslides 2017, 14, 917–928. [Google Scholar] [CrossRef]
- Han, Z.; Su, B.; Li, Y.; Wang, W.; Wang, W.; Huang, J.; Chen, G. Numerical simulation of debris-flow behavior based on the SPH method incorporating the Herschel-Bulkley-Papanastasiou rheology model. Eng. Geol. 2019, 255, 26–36. [Google Scholar] [CrossRef]
- Liu, C.; Liang, L. A coupled SPH–DEM–FEM approach for modeling of debris flow impacts on flexible barriers. Arab. J. Geosci. 2022, 15, 420. [Google Scholar] [CrossRef]
- Choi, S.-K.; Park, J.-Y.; Lee, D.-H.; Lee, S.-R.; Kim, Y.-T.; Kwon, T.-H. Assessment of barrier location effect on debris flow based on smoothed particle hydrodynamics (SPH) simulation on 3D terrains. Landslides 2021, 18, 217–234. [Google Scholar] [CrossRef]
- Kafle, J. Dynamic Interaction between a Two-Phase Submarine Landslide and a Fluid Reservoir. Ph.D. Thesis, Kathmandu University, Dhulikhel, Nepal, 2014. [Google Scholar]
- Overton, D.E.; Meadows, M.E. Stormwater Modeling; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Pitilakis, K.; Crowley, H.; Kaynia, A.M. SYNER-G: Typology definition and fragility functions for physical elements at seismic risk. Geotech. Geol. Earthq. Eng. 2014, 27, 1–28. [Google Scholar]
- Carrara, A.; Crosta, G.; Frattini, P. Comparing models of debris-flow susceptibility in the alpine environment. Geomorphology 2008, 94, 353–378. [Google Scholar] [CrossRef]
- Liu, X.; Lei, J. A method for assessing regional debris flow risk: An application in Zhaotong of Yunnan province (SW China). Geomorphology 2003, 52, 181–191. [Google Scholar] [CrossRef]
- Wolfram, S. Statistical mechanics of cellular automata. Rev. Mod. Phys. 1983, 55, 601. [Google Scholar] [CrossRef]
- Chopard, B.; Droz, M. Cellular automata. Model. Phys. 1998, 1, 11–20. [Google Scholar]
- Vichniac, G.Y. Simulating physics with cellular automata. Phys. D Nonlinear Phenom. 1984, 10, 96–116. [Google Scholar] [CrossRef]
- Avolio, M.V.; Errera, A.; Lupiano, V.; Mazzanti, P.; Di Gregorio, S. VALANCA: A Cellular Automata Model for Simulating Snow Avalanches. J. Cell. Autom. 2017, 12, 309–330. [Google Scholar]
- Liucci, L.; Melelli, L.; Suteanu, C.; Ponziani, F. The role of topography in the scaling distribution of landslide areas: A cellular automata modeling approach. Geomorphology 2017, 290, 236–249. [Google Scholar] [CrossRef]
- Zhong, G.; Zhai, G.; Chen, W. Evacuation simulation of multi-story buildings during earthquakes based on improved cellular automata model. J. Asian Archit. Build. Eng. 2023, 22, 1007–1027. [Google Scholar] [CrossRef]
- Xie, J.; Zhang, L. Application of cellular automata with improved dynamic analysis in evacuation management of sports events. J. Sens. 2022, 2022, 8782865. [Google Scholar] [CrossRef]
- Byun, G.; No, W.; Park, C.; Lee, H.-K.; Kim, Y. Predicting the Potential of Rainfall Disaster Risk using Cellular Automata in Small Urban Declining Areas. KIEAE J. 2022, 22, 29–35. [Google Scholar] [CrossRef]
- Gamma, P. Dwalk-Ein Murgang-Simulationsprogramm zur Gefahrenzonierung; Geographisches Institut der Universität Bern: Bern, Switzerland, 2000. [Google Scholar]
- Horton, P.; Jaboyedoff, M.; Rudaz, B.E.A.; Zimmermann, M. Flow-R, a model for susceptibility mapping of debris flows and other gravitational hazards at a regional scale. Nat. Hazards Earth Syst. Sci. 2013, 13, 869–885. [Google Scholar] [CrossRef]
- Chiari, M.; Scheidl, C. Application of a new cellular model for bedload transporting extreme events at steep slopes. Geomorphology 2015, 246, 413–419. [Google Scholar] [CrossRef]
- Gregoretti, C.; Degetto, M.; Boreggio, M. GIS-based cell model for simulating debris flow runout on a fan. J. Hydrol. 2016, 534, 326–340. [Google Scholar] [CrossRef]
- Prochaska, A.B.; Santi, P.M.; Higgins, J.D.; Cannon, S.H. Debris-flow runout predictions based on the average channel slope (ACS). Eng. Geol. 2008, 98, 29–40. [Google Scholar] [CrossRef]
- Scheidl, C.; Rickenmann, D. Empirical prediction of debris-flow mobility and deposition on fans. Earth Surf. Process. Landf. J. Br. Geomorphol. Res. Group 2010, 35, 157–173. [Google Scholar] [CrossRef]
- Han, Z.; Li, Y.; Huang, J.; Chen, G.; Xu, L.; Tang, C.; Zhang, H.; Shang, Y. Numerical simulation for run-out extent of debris flows using an improved cellular automaton model. Bull. Eng. Geol. Environ. 2017, 76, 961–974. [Google Scholar] [CrossRef]
- Ma, Y.; Han, Z.; Li, Y.; Chen, G.; Wang, W.; Chen, N.; Hu, G.; Zhao, L.; Dou, J. Robustness evaluation of the probability-based HTCA model for simulating debris-flow run-out extent: Case study of the 2010 Hongchun event, China. Eng. Geol. 2023, 312, 106918. [Google Scholar] [CrossRef]
- Wolfram, S. Cellular automaton fluids 1: Basic theory. In Lattice Gas Methods for Partial Differential Equations; CRC Press: Boca Raton, FL, USA, 2019; pp. 19–74. [Google Scholar]
- de Sousa, L.; Nery, F.; Sousa, R.; Matos, J. Assessing the accuracy of hexagonal versus square tilled grids in preserving DEM surface flow directions. In Proceedings of the 7th International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences, Lisbon, Portugal, 5–7 July 2006. [Google Scholar]
- Frisch, U.; Hasslacher, B.; Pomeau, Y. Lattice-gas automata for the Navier-Stokes equation. In Lattice Gas Methods for Partial Differential Equations; CRC Press: Boca Raton, FL, USA, 2019; pp. 11–18. [Google Scholar]
- D’Ambrosio, D.; Di Gregorio, S.; Iovine, G. Simulating debris flows through a hexagonal cellular automata model: Sciddica s 3–hex. Nat. Hazards Earth Syst. Sci. 2003, 3, 545–559. [Google Scholar] [CrossRef]
- Avolio, M.V.; Di Gregorio, S.; Lupiano, V.; Mazzanti, P. SCIDDICA-SS 3: A new version of cellular automata model for simulating fast moving landslides. J. Supercomput. 2013, 65, 682–696. [Google Scholar] [CrossRef]
- Mersereau, R.M. The processing of hexagonally sampled two-dimensional signals. Proc. IEEE 1979, 67, 930–949. [Google Scholar] [CrossRef]
- Gallant, J.C.; Wilson, J.P. TAPES-G: A grid-based terrain analysis program for the environmental sciences. Comput. Geosci. 1996, 22, 713–722. [Google Scholar] [CrossRef]
- Wichmann, V. The Gravitational Process Path (GPP) model (v1.0)—A GIS-based simulation framework for gravitational processes. Geosci. Model Dev. 2017, 10, 3309–3327. [Google Scholar] [CrossRef]
- Wang, Y. Rheological properties and migration characteristics of debris fluids. Mt. Res. 2015, 04, 472. (In Chinese) [Google Scholar]
- Liu, J.; Ou, G.; You, Y. Experimental Study of Fan Development Process of Viscous Debris Flow. J. Catastrophology 2012, 02, 13–18. (In Chinese) [Google Scholar]
- Zhang, Y.; Ge, T.; Tian, W.; Liou, Y.-A. Debris flow susceptibility mapping using machine-learning techniques in Shigatse area, China. Remote Sens. 2019, 11, 2801. [Google Scholar] [CrossRef]



| Incoming Cell | Forward Direction | Oblique Direction |
|---|---|---|
| 1 | 4 | 3, 5 |
| 2 | 5 | 4, 6 |
| 3 | 6 | 5, 1 |
| 4 | 1 | 6, 2 |
| 5 | 2 | 1, 3 |
| 6 | 3 | 2, 4 |
| Parameters | SCA Model | HCA Model |
|---|---|---|
| Cell size | 2.5 m | 2.5 m |
| Unit depth | 0.25 m | 0.25 m |
| Collapse amount | 5843 m3 | 5843 m3 |
| Iterations number | 3740 | 4320 |
| Step correction | 1 | 1.3 |
| Maximum step | 300 | 403 |
| Event | Total Area | HCA Model | SCA Model | ||||
|---|---|---|---|---|---|---|---|
| TP | FN | FP | TP | FN | FP | ||
| ) | 6155 | 5439.79 | 715.21 | 1251.93 | 5006.25 | 1148.75 | 518.75 |
| Flume Test () | 120.344 | 102.485 | 17.859 | 19.869 | 96.733 | 23.611 | 12.407 |
| Event | HCA Model | SCA Model | ||||
|---|---|---|---|---|---|---|
| Yohutagawa Debris Flow | 0.5642 | 0.8469 | 0.8687 | 0.5424 | 0.8572 | 0.8304 |
| Flume Test | 0.5381 | 0.8445 | 0.8488 | 0.5045 | 0.8430 | 0.8191 |
| Interpolation Ratio | Bilinear | IDW | Cubic |
|---|---|---|---|
| 0.3 | 0.0100 | 0.0933 | 0.00042 |
| 0.5 | 0.0093 | 0.0603 | 0.00021 |
| 0.7 | 0.0100 | 0.0931 | 0.00042 |
| 0.9 | 0.0099 | 0.0941 | 0.00042 |
| 1.1 | 0.0092 | 0.0900 | 0.00036 |
| 1.3 | 0.0099 | 0.0928 | 0.00042 |
| 1.5 | 0.0092 | 0.0650 | 0.00020 |
| 1.7 | 0.0098 | 0.0922 | 0.00042 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.; Fu, Q.; Jiang, N.; Ma, Y.; Zhang, X.; Li, Y. Optimizing the Numerical Simulation of Debris Flows: A New Exploration of the Hexagonal Cellular Automaton Method. Water 2024, 16, 1536. https://doi.org/10.3390/w16111536
Han Z, Fu Q, Jiang N, Ma Y, Zhang X, Li Y. Optimizing the Numerical Simulation of Debris Flows: A New Exploration of the Hexagonal Cellular Automaton Method. Water. 2024; 16(11):1536. https://doi.org/10.3390/w16111536
Chicago/Turabian StyleHan, Zheng, Qiang Fu, Nan Jiang, Yangfan Ma, Xiulin Zhang, and Yange Li. 2024. "Optimizing the Numerical Simulation of Debris Flows: A New Exploration of the Hexagonal Cellular Automaton Method" Water 16, no. 11: 1536. https://doi.org/10.3390/w16111536
APA StyleHan, Z., Fu, Q., Jiang, N., Ma, Y., Zhang, X., & Li, Y. (2024). Optimizing the Numerical Simulation of Debris Flows: A New Exploration of the Hexagonal Cellular Automaton Method. Water, 16(11), 1536. https://doi.org/10.3390/w16111536










