Estimating Effective Light Exposure by Property-Tracking Tracers
Abstract
1. Introduction
2. Materials and Methods
2.1. Property Exposure
2.2. Exposure Time to the Euphotic Zone
2.3. Effective Light Exposure
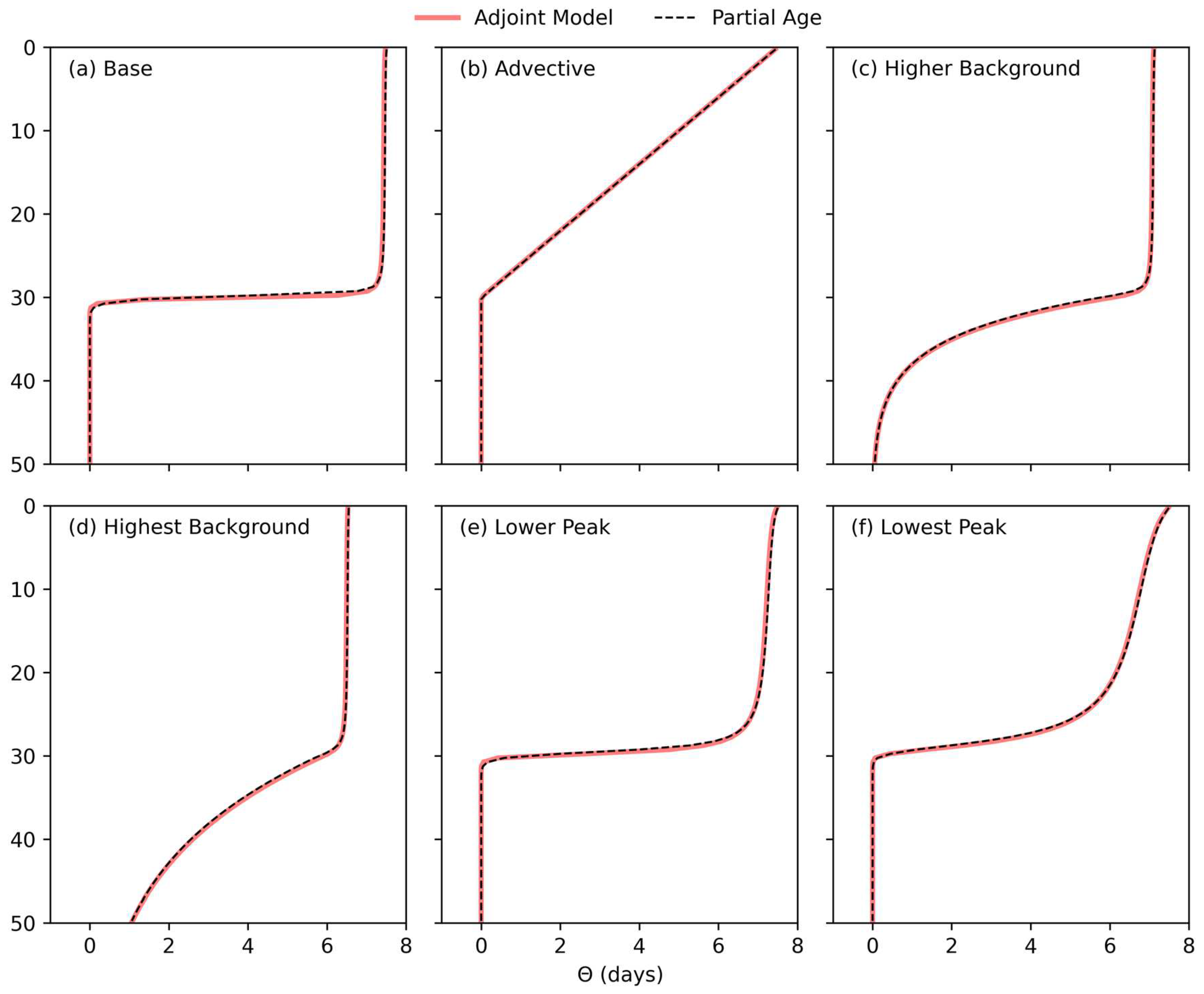
2.4. Numerical Test Cases
3. Results
3.1. Exposure Time to the Euphotic Zone
3.2. Effective Light Exposure
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Summary of Theoretical Aspects of Property-Tracking Approach
References
- Delhez, E.J.M.; Lacroix, G.; Deleersnijder, E. The age as a diagnostic of the dynamics of marine ecosystem models. Ocean Dyn. 2004, 54, 221–231. [Google Scholar] [CrossRef]
- Delhez, E.J.; Campin, J.-M.; Hirst, A.C.; Deleersnijder, E. Toward a general theory of the age in ocean modelling. Ocean Model. 1999, 1, 17–27. [Google Scholar] [CrossRef]
- Mouchet, A.; Cornaton, F.; Deleersnijder, E.; Delhez, J.M. Partial ages: Diagnosing transport processes by means of multiple clocks. Ocean Dyn. 2016, 66, 367–386. [Google Scholar] [CrossRef]
- Gross, E.; Andrews, S.; Bergamaschi, B.; Downing, B.; Holleman, R.; Burdick, S.; Durand, J. The Use of Stable Isotope-Based Water Age to Evaluate a Hydrodynamic Model. Water 2019, 11, 2207. [Google Scholar] [CrossRef]
- Gross, E.; Holleman, R.; Kimmerer, W.; Munger, S.; Burdick, S.; Durand, J. Using Age Tracers to Estimate Ecological Rates in a Phytoplankton Model. Water 2023, 15, 2097. [Google Scholar] [CrossRef]
- Deleersnijder, E. On the Method for Estimating the Mean Property Experienced by a Tracer Pioneered by Gross et al. 2019. 2021, p. 30. Available online: https://dial.uclouvain.be/pr/boreal/object/boreal:247973 (accessed on 10 March 2024).
- Delhez, J.; Deleersnijder, E. Residence time and exposure time of sinking phytoplankton in the euphotic layer. J. Theor. Biol. 2010, 262, 505–516. [Google Scholar] [CrossRef] [PubMed]
- Cloern, J.E. Habitat Connectivity and Ecosystem Productivity: Implications from a Simple Model. Am. Nat. 2007, 169, E21–E33. [Google Scholar] [CrossRef] [PubMed]
- Kida, S.; Ito, T. A Lagrangian View of Spring Phytoplankton Blooms. J. Geophys. Res. Oceans 2017, 122, 9160–9175. [Google Scholar] [CrossRef]
- Kamykowski, D.; Yamazaki, H.; Janowitz, G.S. A Lagrangian model of phytoplankton photosynthetic response in the upper mixed layer. J. Plankton Res. 1994, 16, 1059–1069. [Google Scholar] [CrossRef]
- Jönsson, B.F.; Watson, J.R. The timescales of global surface-ocean connectivity. Nat. Commun. 2016, 7, 11239. [Google Scholar] [CrossRef] [PubMed]
- Streeter, H.; Phelps, E. A Study of the Pollution and Natural Purification of the Ohio River; US Department of Health, Education, and Welfare: Boston, MA, USA, 1925; pp. 1–75. [Google Scholar]
- Deleersnijder, E.; Campin, J.-M.; Delhez, E.J.M. The Concept of Age in Marine Modelling I. Theory and Preliminary Model Results. J. Mar. Syst. 2001, 28, 229–267. [Google Scholar] [CrossRef]
- van Leer, B. Towards the ultimate conservative difference scheme. II. Monotonicity and conservation combined in a second-order scheme. J. Comput. Phys. 1974, 14, 361–370. [Google Scholar] [CrossRef]
- Steele, J.H. Environmental control of photosynthesis in the sea. Limnol. Oceanogr. 1962, 7, 137–150. [Google Scholar] [CrossRef]
- Deleersnijder, E.; Draoui, I.; Lambrechts, J.; Legat, V.; Mouchet, A. Consistent Boundary Conditions for Age Calculations. Water 2020, 12, 1274. [Google Scholar] [CrossRef]
- Lucas, L.V.; Deleersnijder, E. Timescale Methods for Simplifying, Understanding and Modeling Biophysical and Water Quality Processes in Coastal Aquatic Ecosystems: A Review. Water 2020, 12, 2717. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, H.; Shen, J.; Ye, F.; Zhang, Y.; Chai, F.; Liu, Z.; Du, J. An analytical phytoplankton model and its application in the tidal freshwater James River. Estuar. Coast. Shelf Sci. 2019, 224, 228–244. [Google Scholar] [CrossRef]
- Bolin, B.; Rodhe, H. A note on the concepts of age distribution and transit time in natural reservoirs. Tellus 1973, 25, 58–62. [Google Scholar] [CrossRef]

| Variable | Unit | Description |
|---|---|---|
| g m−3 | Concentration of tracer from specific source location | |
| d g m−3 | Age concentration of tracer | |
| d | Mean age of tracer | |
| d g m−3 | Partial age concentration tracking exposure to euphotic zone | |
| d | Mean partial age representing exposure time to euphotic zone | |
| d g m−3 | Property age concentration, where property is | |
| - | Mean value of tracer exposure to property | |
| g m−3 | Phytoplankton biomass concentration | |
| g | Initial phytoplankton biomass | |
| d | Time | |
| d | Time of insertion of biomass in simulation | |
| d | End time of the simulation | |
| m2 d−1 | Vertical eddy diffusivity | |
| m | Vertical coordinate increasing downward from surface | |
| m d−1 | Vertical (sinking) speed, positive downward | |
| m | Location of insertion of initial tracer mass | |
| d | Cumulative exposure time to the euphotic zone | |
| m | Surface mixed-layer depth and euphotic zone depth | |
| m | Depth of bottom layer with faster sinking | |
| - | Characteristic function of the euphotic layer | |
| - | Light inhibition factor for phytoplankton growth | |
| μmol photons m−2 s−1 | Light intensity | |
| μmol photons m−2 s−1 | Light intensity for optimal phytoplankton growth | |
| μmol photons m−2 s−1 | Surface light intensity | |
| m−1 | Light extinction coefficient | |
| d | Effective light exposure time | |
| m2 d−1 | Background eddy diffusivity | |
| m2 d−1 | Maximum increase from background eddy diffusivity | |
| m d−1 | Vertical (sinking) speed, positive downward | |
| m d−1 | Sinking speed in surface layer | |
| m d−1 | Sinking speed in bottom layer | |
| d | Predicted exposure time to the euphotic zone | |
| d | Predicted effective light exposure time |
| Test Case Name | (m2 d−1) | (m2 d−1) |
|---|---|---|
| Base | 1 | 8000 |
| Advective | 0 | 0 |
| Higher background | 20 | 8000 |
| Highest background | 60 | 8000 |
| Lower peak | 1 | 1000 |
| Lowest peak | 1 | 200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gross, E.; Holleman, R.; Deleersnijder, E.; Delhez, E.J.M. Estimating Effective Light Exposure by Property-Tracking Tracers. Water 2024, 16, 1469. https://doi.org/10.3390/w16111469
Gross E, Holleman R, Deleersnijder E, Delhez EJM. Estimating Effective Light Exposure by Property-Tracking Tracers. Water. 2024; 16(11):1469. https://doi.org/10.3390/w16111469
Chicago/Turabian StyleGross, Edward, Rusty Holleman, Eric Deleersnijder, and Eric J. M. Delhez. 2024. "Estimating Effective Light Exposure by Property-Tracking Tracers" Water 16, no. 11: 1469. https://doi.org/10.3390/w16111469
APA StyleGross, E., Holleman, R., Deleersnijder, E., & Delhez, E. J. M. (2024). Estimating Effective Light Exposure by Property-Tracking Tracers. Water, 16(11), 1469. https://doi.org/10.3390/w16111469








