A Computational Tool to Track Sewage Flow Discharge into Rivers Based on Coupled HEC-RAS and DREAM

Abstract

Worldwide abatement of untreated sewage discharge into surface water is a challenging task. Sewage discharging into surface waters has a detrimental impact on water quality. This paper presents a MATLAB (R2018b) framework designed to identify sewage flow discharges into rivers from an inverse problem-solving perspective. The computational tool integrates a hydrodynamic model using the Hydrologic Engineering Center’s River Analysis System (HEC-RAS 5.0.0) and an open-source toolbox for Differential Evolution Adaptive Metropolis (DREAM) as the inverse problem method. The proposed framework can effectively infer discharge sources in scenarios of highly transient flow based on hydraulic data at pre-set monitoring sites. To validate its capabilities, one hypothetical case and two real cases of sewage flow discharges entering a river were used to test the developed modeling framework. The results based on three performance metrics showed that this mathematical tool can be extended to simulate complex hydrodynamic flow patterns. This accomplishment underscores its potential as a valuable asset for environmental monitoring and water quality restoration efforts.

1. Introduction

Urban rivers are an essential factor in the sustainable development of urban society and economies. Nevertheless, the persistent issue of untreated and illegal discharges poses a significant threat to the surface water quality of these vital urban waterways [1,2]. Therefore, there is a pressing need to develop an efficient tool for tracking sewage flow discharges to tackle the challenges posed by river pollution and to achieve pollution interception and water quality restoration.

Mathematical modeling serves as a critical tool in the identification of pollutant sources. Employing an inverse problem-solving approach, it uses measurements of contaminant concentration data at monitoring sites to infer the features of emissions, such as the volume, location, and time of the emissions. This tracking methodology has been widely used in groundwater and atmospheric studies [3,4,5,6,7]. In recent years, the technique has also found increasing application in the field of sewage source identification in surface water systems [8,9,10,11,12,13]; water quality sensors have already been employed by many countries. Basically, the combination of optimization methods and model governing equations in the field of water quality can provide deterministic solutions for unknown source parameters. For instance, Zhang and Xin [14] utilized the basic Genetic Algorithm (GA) to pinpoint the spill location and contaminant mass of sources in a small river channel. Jiang et al. [15] estimated the characteristics of the pollutant source and determined where, when, and how much of the pollutant was released into a surface stream by developing an integration of Genetic Algorithm and Simulated Annealing Algorithm (IGSAA) as a pollutant source inverse method. However, the reliability of these optimization methods may be compromised due to high uncertainties in their deterministic processes and the data employed [16]. Alternatively, stochastic methods based on Bayesian inference have been suggested to overcome the disadvantages of deterministic optimization. These methods quantify the uncertainty in inverse modeling by estimating probability distributions of source parameters. Zhu et al. [17] applied genetic algorithms and Bayesian methods separately to identify instantaneous point sources and compared the performance of both methods. Jiang et al. [18] implemented a Bayesian framework for tracing the source of a significant nitrobenzene spill in the Songhua River, exploring the uncertainty factors affecting the inversion results. To enhance the performance of stochastic models, differential evolution has also been integrated into the Bayesian framework [19,20]. The generated Differential Evolution and Metropolis (DREAM) algorithm as well as the Differential Evolution and Metropolis–Hastings Markov Chain Monte Carlo (DEMH-MCMC) algorithm are capable of efficiently and accurately identifying sources of multi-point sudden water pollution incidents [11,12]. As a result, stochastic-based methods, such as the aforementioned DREAM algorithm, have been demonstrated to be more suitable for contaminant source identification due to their superior handling of uncertainty in identification results and unknown source parameters compared to deterministic-based methods like GA.

However, the previous studies have a disadvantage [11,12,14,15,16,17,18] because source tracking based on the water quality model usually assumes that the water flow velocity is relatively constant, which may not accurately reflect the real hydrodynamic conditions in rivers. Conversely, in cases where side flow discharge cannot be ignored compared to upstream inflow, the incorporation of a hydrodynamic model can inversely track side discharges by comparing simulated water level and flow discharge with the measured data. This enables accurate identification of flow discharge from sewage sources under varying flow velocities, as the pollutant discharge also brings side flow discharge that triggers water flow and water stage change at monitoring stations. Additionally, online hydraulic data monitoring proves to be more cost-effective than online water quality monitoring.

Therefore, there is a notable interest in the integration of inverse problem-solving methods with hydrodynamic models using low-cost hydraulic monitoring data. Recently, the integration of the hydrodynamic diffusion wave equation and the Bayesian–Markov Chain Monte Carlo (MCMC) algorithm has enabled a hydrodynamic-based river source tracing method. This approach utilizes hydraulic data to inversely estimate the location, flow rate, and timing of sewage discharges [21]. Nevertheless, the limitations of the diffusion wave equation, which only applies to single-direction flow, restrict its ability to simulate complex hydrodynamic flow patterns, such as backwater flow, tidal water flow, and highly transient flows during wet weather events or sudden sewage discharges. In contrast, HEC-RAS can be applied in the aforementioned situations, expanding its range of applications to better align with real-world scenarios [22,23,24,25]. Introducing complex hydrodynamic models like HEC-RAS that incorporate the software platform can provide more powerful tools for solving source-tracking problems.

Currently, comprehensive model systems that integrate HEC-RAS and inverse problem-solving techniques within an optimization framework are still scarce. Establishing such an integrated framework requires a programming platform that can effectively combine multiple software and open-source codes. A notable example of such a state-of-the-art programming platform is MATLAB. Recognized for its capabilities in technical computing, MATLAB integrates computation, visualization, and programming in a user-friendly environment [26]. This robust platform holds great promise in advancing the development of comprehensive solutions to address water quality challenges through the amalgamation of hydrodynamic modeling and inverse problem methodologies.

This paper presents a MATLAB framework for inverse tracking sewage flow discharges in river systems. The remainder of this paper is organized as follows: (1) Section 2 illustrates the core modules and the framework rationale; (2) Section 3 presents one hypothetical case and two real case studies under transient flow conditions to demonstrate the practical application of the modeling system. Finally, the main results are summarized in Section 4.

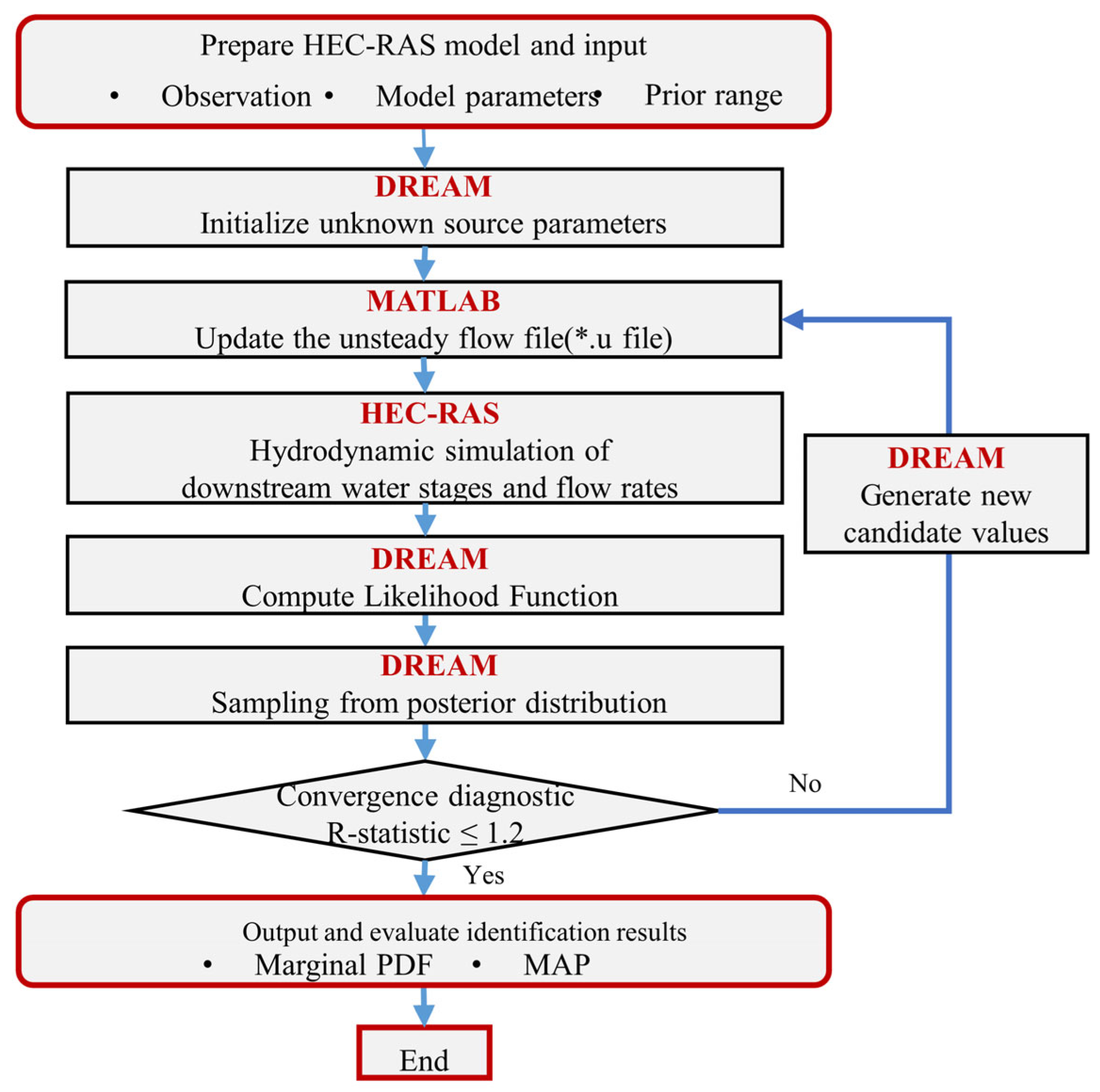
2. Framework Design

The MATLAB modeling system is comprised of a hydrodynamic model and an inverse problem method, which together form the basis for constructing a framework to address the inverse tracking of sewage flow discharges. The framework is built on two core modules: HEC-RAS, serving as the hydrodynamic model, and DREAM, functioning as the stochastic inverse problem algorithm. The integration of these two modules enables inverse tracking, allowing for the estimation of source discharges and discharge patterns in the river system.

2.1. HEC-RAS Modeling

A highly adopted hydrodynamic model for river flow simulation is HEC-RAS (v5.0), which was developed by the Hydrological Engineering Center/U.S. Army Corps of Engineers [27]. HEC-RAS software is a computer application crafted to simulate the flow of rivers through natural, open channels and to estimate the water surface profile [28,29].

Governing Equations

In the context of urban rivers, hydrodynamics can often be simplified to a one-dimensional (1D) model because the primary concern is the flow gradient along the longitudinal scale of the river. In this study, the HEC-RAS software performs hydrodynamic simulation with the complete 1D Saint-Venant equations, which are suitable for simulating complex hydrodynamic flow patterns during wet weather events or sudden sewage discharges. The relevant governing equations are as follows:

$$\frac{\partial A}{\partial t}+\frac{\partial Q}{\partial x}=q_L$$

(1)

$$\frac{\partial Q}{\partial t}+\frac{\partial }{\partial x}\left(\frac{Q^2}{A}\right)+gA\frac{\partial h}{\partial x}-gA(S_0-S_f)=0$$

(2)

where $A$ represents the cross-sectional area (m²); $t$ is time (s); $Q$ denotes flow rate (m³/s); $x$ is the longitudinal distance in the channel (m); $q_L$ is the lateral inflow per unit length of the river channel (m²/s); $h$ is the water depth of the channel (m); $g$ is the acceleration due to gravity (m²/s); $S_0$ is the channel slope; $S_f$ is the friction slope.

To construct a hydrodynamic model and solve the 1D Saint-Venant equations, input data related to the parameters mentioned above are required. This includes topographic data of cross-sectional shapes, channel slopes, and hydraulic data such as flow rate, water level, and Manning coefficients. In this study, the flow regime was assumed to be unsteady, nonuniform flow within the river reach, considering dynamic upstream flow in addition to lateral inflow from sewage outlets. The established model generates simulated downstream hydraulic values (water level and flow rate) based on different combinations of lateral inflow caused by sewage sources. These values are then compared with observed data in the inverse problem algorithm to trace the source parameters of side flow discharge.

2.2. DREAM Algorithm

The stochastic inverse problem method employed in this study utilizes the DREAM Toolbox, integrated within the MATLAB environment [20]. DREAM solves complex optimization problems of water resources based on the Bayesian–Markov Chain Monte Carlo (MCMC) method [11,30,31,32]. In each iteration, the DREAM simultaneously runs multiple Markov chains to explore the global space and automatically adjusts the scale and orientation of the proposal distribution through differential evolution and Metropolis selection. The process aims to sample from the target posterior distribution, achieved as the Markov chains, guided by an adaptive proposal distribution, converge towards the true posterior distribution.

2.2.1. Bayesian Theorem

According to Bayes’ theorem, the posterior distribution of uncertain source parameters can be estimated from the time series of observed data [33]:

$$p\left(\theta |O_t\right)\propto p\left(\theta \right)p\left(O_t|\theta \right)$$

(3)

where $p\left(\theta |O_t\right)$ is the posterior distribution of the model parameters $\theta$ given the observed data $O_t$. $p\left(\theta \right)$ is the prior distribution of the parameters, while $p\left(O_t|\theta \right)$ represents the likelihood function of the observed data with given $\theta$.

The likelihood function $p\left(O_t|\theta \right)$ characterizes the error between simulated data and the observation data. The log-form of the likelihood function is given as [34]:

$$p\left(O_t|\theta \right)=-\frac{n}{2}\mathit{Log}\left(2\pi \right)-{\sum }_{t=1}^n\left[\mathit{Log}\left(\sigma \right)\right]-\frac{1}{2}{\left(\frac{M_t\left(\theta \right)-O_t}{\sigma }\right)}^2$$

(4)

where $\sigma$ indicates model errors variance, $n$ is the number of observed data, $t$ shows the index representing time series, $M_t$ and $O_t$ are the simulated and observed time-series data, respectively.

2.2.2. Differential-Evolution and Metropolis Estimator

Differential evolution is applied as a genetic algorithm for the evolution of new candidates in the DREAM algorithm in Equations (5) and (6). Additionally, a Metropolis selection rule [35] decides whether candidates can replace their corresponding old values in Equation (7):

$${\theta }_p^{i,j}={\theta }_{t-1}^{i,j}+\zeta +\left(1+\lambda \right){\gamma }_{(\delta ,d^{\ast })}{\sum }_{k=1}^{\delta }\left({\theta }_{t-1}^{{i,a}_k}-{\theta }_{t-1}^{i,b_k}\right)$$

(5)

where ${\theta }_p^{i,j}$ is the parameter vector at the current iteration $t$ for the $i$th parameter in the $j$th chain, ${\theta }_{t-1}^{i,j}$ signifies the state variable of the $j$th chain at the current iteration of $t-1$, ${\gamma }_{(\delta ,d^{\ast })}=\frac{2.38}{\sqrt{2\delta d^{\ast }}}$ is the jump rate, $\delta$ = 3 is the default number of pairs used to generate the new candidate with $d^{\ast }=d$, $a$ and $b$ are vectors from {1, …,$N$}, the value of $\lambda$ and $\zeta$ are sampled from uniform distribution, $U$ (−0.1, 0.1), and normal distribution, $N$ (0, 10⁻⁶), respectively.

$${\theta }_p^{i,j}=\left\{\begin{array}{c}{\theta }_{t-1}^{i,j} if U\le 1-CR,d^{\ast }=d^{\ast }-1\\ {\theta }_p^{i,j} otherwise \end{array}\right.$$

(6)

where $U$~(0, 1) follows a uniform distribution the value of crossover rate ($CR$) is sampled from a geometric sequence of different crossover probabilities, $CR$ = {1/$nCR$, 2/$nCR$, …, 1} with default setting of $nCR$ = 3.

A random value $U^{\ast }$ is sampled from a uniform distribution $U$~(0, 1). The Metropolis acceptance probability is calculated as follows:

$$p_{acc}({\theta }_{t-1}^{i,j}\to {\theta }_p^{i,j})=\left\{\begin{array}{c}\mathit{min}\left[1,\frac{p\left({\theta }_p^{i,j}\right)}{p\left({\theta }_{t-1}^{i,j}\right)}\right] if p\left({\theta }_{t-1}^{i,j}\right)>0\\ 1 if p\left({\theta }_{t-1}^{i,j}\right)=0\end{array}\right.$$

(7)

If ${U^{\ast }<p}_{acc}({\theta }_{t-1}^{i,j}\to {\theta }_p^{i,j})$, the candidates are accepted, the chain is updated, ${\theta }_t^{i,j}$ = ${\theta }_p^{i,j}$; otherwise, the old values are retained, ${\theta }_{t-1}^{i,j}$.

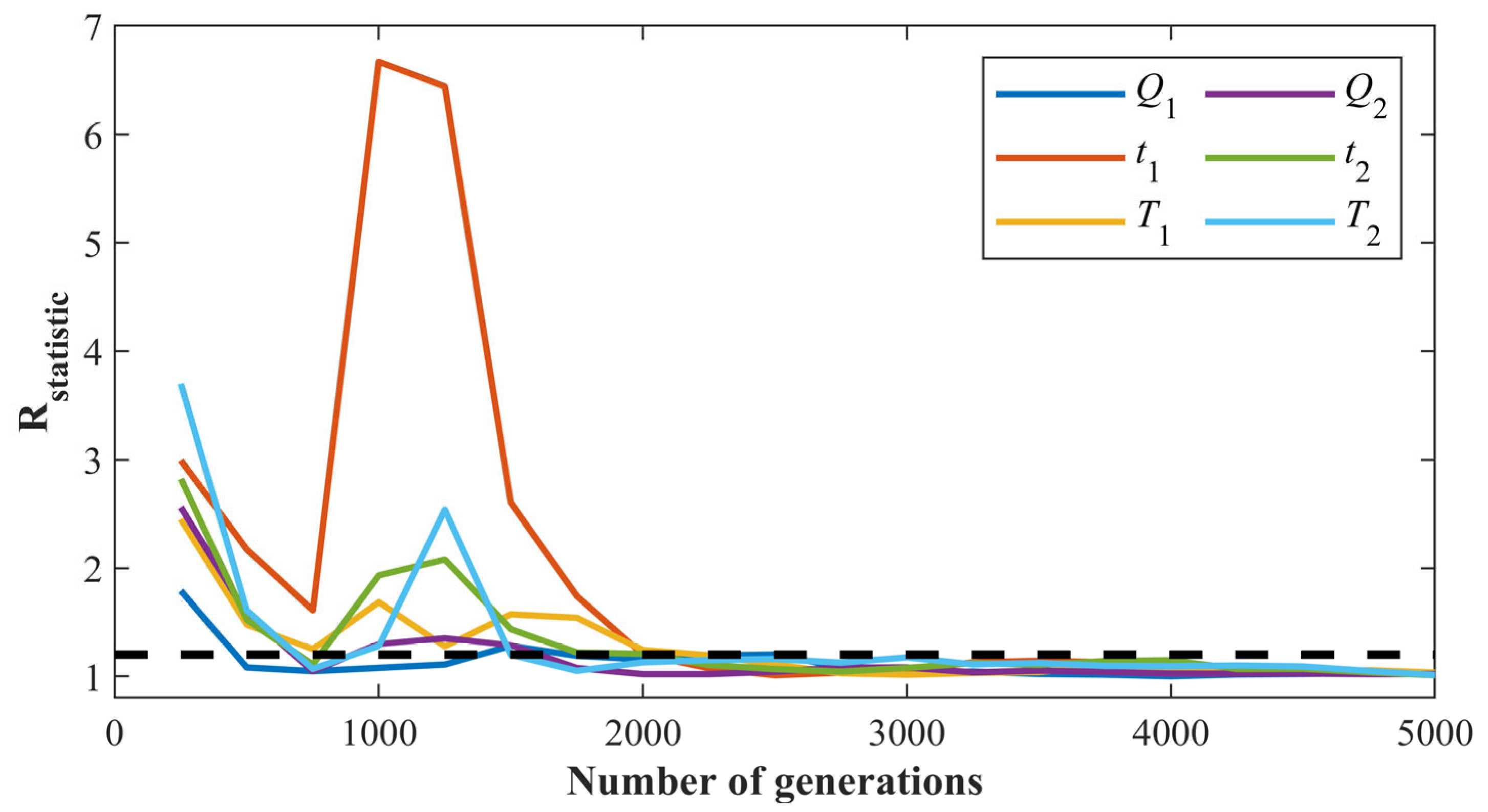
2.2.3. DREAM Algorithm

ThFe convergence of the DREAM algorithm is assessed by the R-statistic in Equations (8)–(10) [36]. It takes into account the convergence of different components and calculates them with weighted values. This ensures that not only the entire chain converges but also different components converge when the value of the R-statistic is less than 1.2 for each parameter. Thereby enhancing the performance and quality of the DREAM algorithm, as proposed by [37]:

$$R_{Statistic}^i=\sqrt{\frac{N+1}{N}\frac{\left(T-2\right)W^i+2B^i}{W^{i}T}-\frac{T-2}{NT}}$$

(8)

$$W^i=\frac{2}{N\left(T-2\right)}\sum _{j=1}^N\sum _{t=\left[\frac{T}{2}\right]}^T{\left({\theta }_t^{i,j}-{\overline{\theta }}^{i,j}\right)}^2$$

(9)

$$\frac{B^i}{T}=\frac{1}{2\left(N-1\right)}\sum _{j=1}^N{\left({\overline{\theta }}^{i,j}-\frac{1}{N}\sum _{j=1}^N{\overline{\theta }}^{i,j}\right)}^2$$

(10)

where $W^i$ is used to estimate the average level of parameter variation within each of the $N$ chains; $\frac{B^i}{T}$ is used to estimate the variation between the means of the $N$ chains, where $N$ is the number of chains and $T$ is the iteration number, and the remaining symbols are as previously defined.

It is important to analyze the convergence curves of the R-statistic. In many practical cases, the maximum number of iterations may be reached without convergence, evident when the R-statistic remains above 1.2. In such cases, if a decreasing trend in the R-statistic is observed, an increase in the maximum number of iterations should be considered. Alternatively, if the convergence curve lacks a consistent decreasing pattern, it may be necessary to add additional monitoring sites. This can be particularly effective in the case of high parameter dimensions, as it aids convergence by introducing additional constraints.

The marginal Probability Density Function (PDF) and Maximum A Posteriori (MAP) estimation are used to describe the statistical characteristics of the estimated source parameters, all of which are generated by the DREAM toolbox. The mathematical representation of the MAP can be expressed as follows:

$$MAP=\mathit{arg}{max}_{\theta }p\left(\theta |O_t\right)$$

(11)

2.3. Coupling HEC-RAS with DREAM in MATLAB

The architecture of the coupled HEC-RAS and DREAM system for identifying sewage inputs and their discharge flows is depicted in Figure 1. In the initial preparation phase, a hydrodynamic model is established using HEC-RAS based on field surveys and data provided by local water authorities. Time series of observations, including upstream and downstream water levels and flow rates, are collected from an existing monitoring system. Corresponding DREAM parameters are set based on the actual problem, and prior distributions for inverse modeling of source parameters are defined.

The inverse modeling process is accomplished within the MATLAB system. Initially, the DREAM algorithm generates initial combination values for source parameters (discharge flow and discharge pattern) from prior information. These values are then utilized to update the unknown source parameters of lateral flows in the HEC-RAS unsteady flow file. Subsequently, the HEC-RAS model simulates changes in downstream water levels and flow rates at the monitoring site in response to sewage source discharges. A comparison between the simulated and observed time series values is then conducted to calculate the likelihood function necessary for the posterior distribution required by DREAM. The DREAM algorithm then generates samples from the Bayesian posterior distribution in Equation (3) to analyze unknown source parameters. Employing differential evolution and Metropolis selection, it generates new candidate source parameters for further iteration cycles. This iterative process continues until the optimization termination criterion is satisfied. Finally, the results of the inversion process within the designed framework are expressed using marginal PDFs and MAP estimates. In summary, the described steps illustrate the systematic approach used by the coupled HEC-RAS and DREAM system to identify sewage flow inputs and their discharge patterns.

To facilitate a clear understanding of the workflow, the scripts for running the aforementioned models and the links between these models are briefly described in Figure S1 and Listing S1–S8.

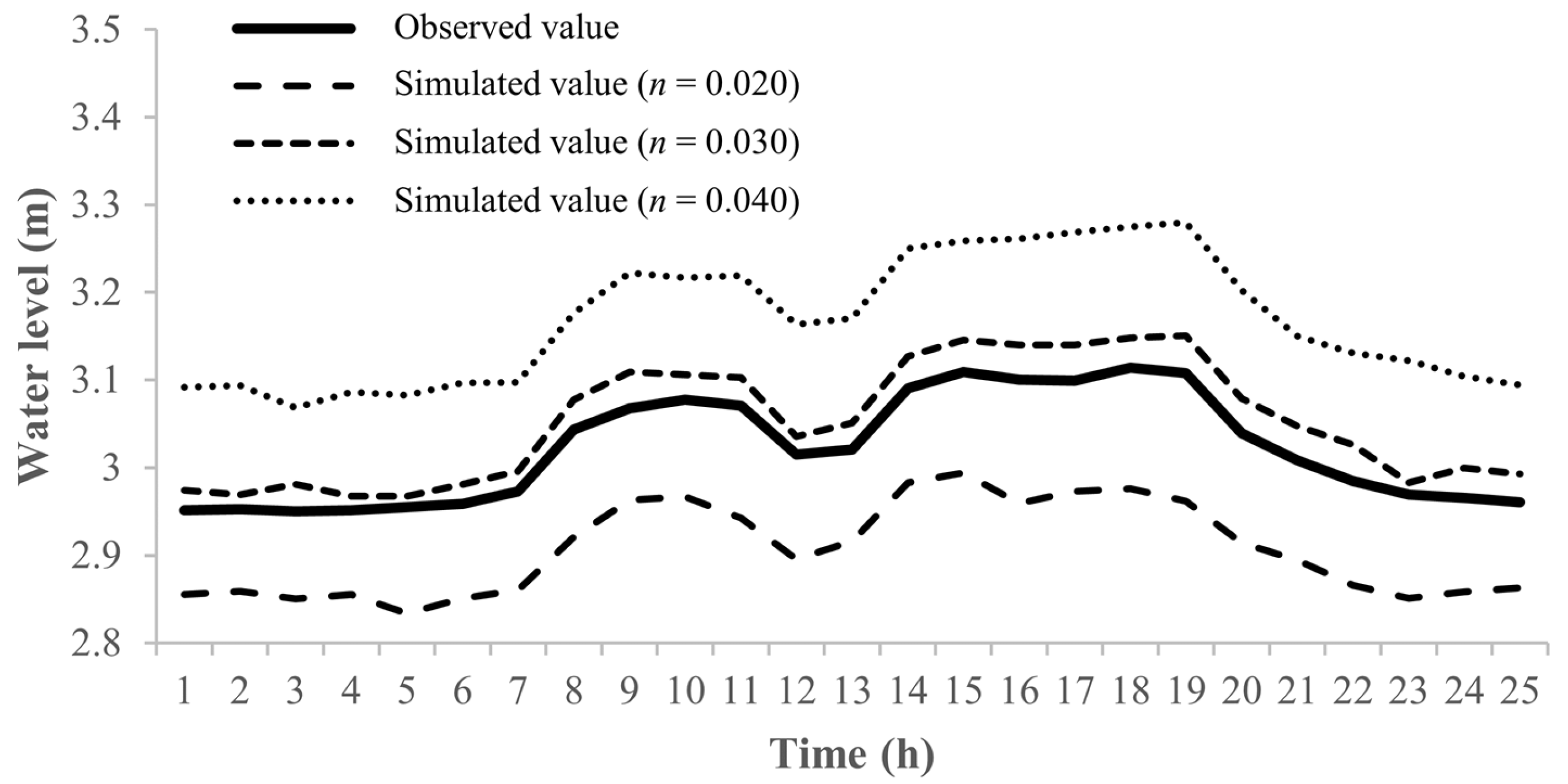
2.4. Modeling Performance Metrics

To validate the computational tool developed in this study, three error metrics were employed to assess and analyze the results of the forward computations, including the Means Relative Error (MRE), Coefficient of Determinism (R²), the Root Mean Squared Error (RMSE), and the Nash–Sutcliffe Efficiency (NSE). These metrics allow for the reconstruction of discharge events in real cases, enabling a comparison between the hydraulic data simulated by the model and actual measurements from observed sections. If the simulated and measured values align closely, it lends credibility to the inverse problem results. The calculation formulas for these metrics are presented in Equations (12)–(14):

$$R^2={\left(\frac{{\sum }_{t=1}^T\left(O_t-\overline{O}\right)\left(M_t-\overline{M}\right)}{\sqrt{{\sum }_{t=1}^T{(O_t-\overline{O})}^2}\sqrt{{\sum }_{t=1}^T{(M_t-\overline{M})}^2}}\right)}^2$$

(12)

$$RMSE=\sqrt{\frac{1}{T}\sum _{t=1}^T{\left(O_t-M_t\right)}^2}$$

(13)

$$NSE=1-\frac{\sum _{t=1}^T{\left(O_t-M_t\right)}^2}{\sum _{t=1}^T{\left(O_t-\overline{O}\right)}^2}$$

(14)

where $M_t$ represents the simulated values, $O_t$ represents the measured values, and $\overline{M}$ and $\overline{O}$ represent the mean values of simulated and measured data, respectively.

3. Modeling Tool Demonstration

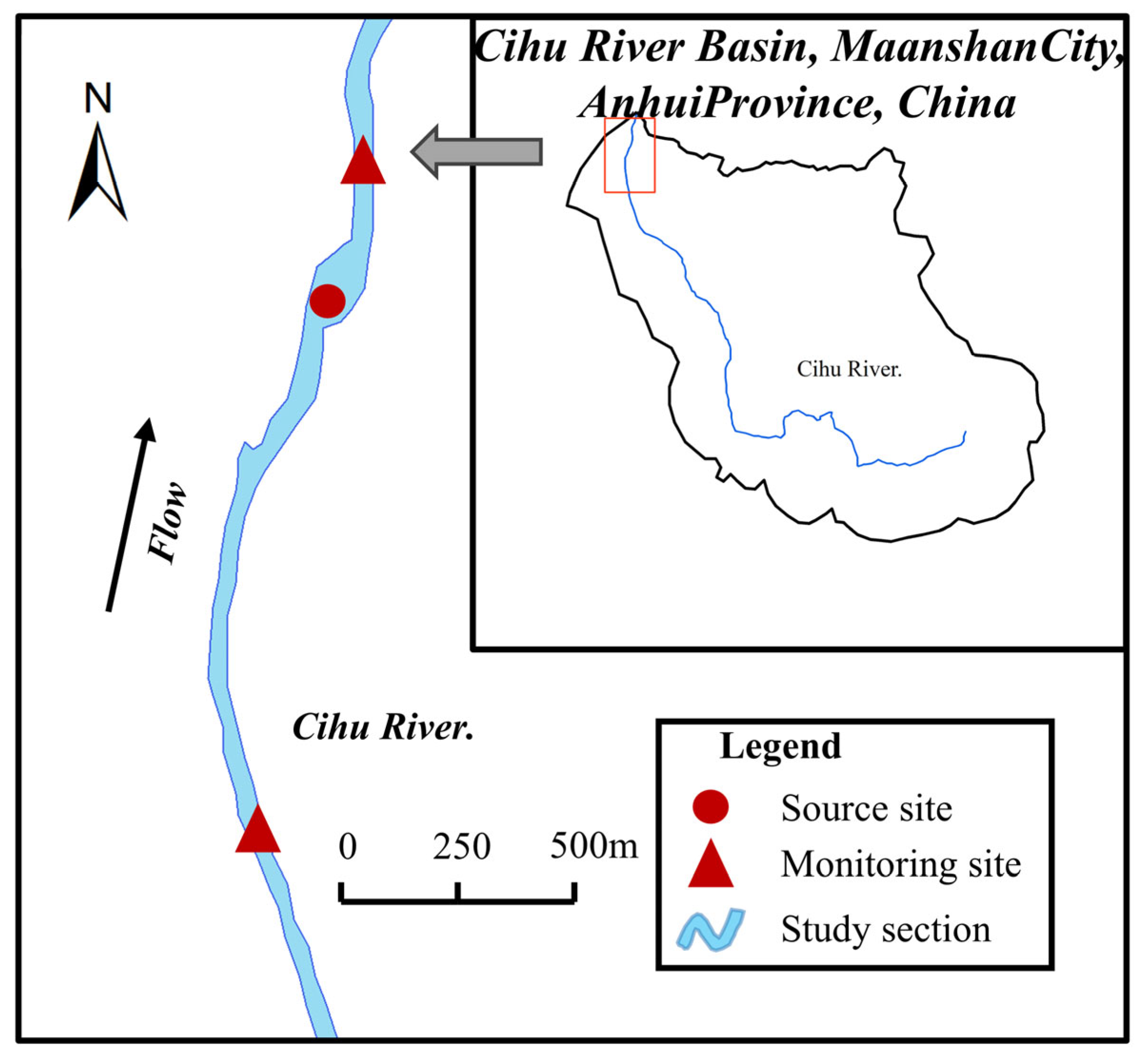
3.1. Hypothetical Case

The hypothetical case was a simulated scenario, which was intended to test the performance of the reliability of the proposed framework. This case simulated the sudden release of industrial wastewater in a non-steady state within an open channel. This study site is a 4000-m-long trapezoidal channel with other key parameters of water depth at 0.72 m, bottom width of 10.0 m, side slope of 0.4, channel gradient of 5 × 10⁻⁵, and an upstream inflow of 2.0 m³/s. In positive problem, this case was pulse discharges of sewage flow at $x_1$ = 1200 m and $x_2$ = 2600 m. The discharge flow ($q$) was set at 0.3 m³/s, occurring from 1:00 ($T_1$) to 2:59 ($T_2$) and at 0.2 m³/s, occurring from 6:00 ($T_1$) to 8:59 ($T_2$). Key parameters for the sewage discharge included average flow, initiation time, and duration. The pulse discharge model is represented by the following equation:

$$q\left(t\right)=\left\{\begin{array}{c}q,T_1<t<T_2 \\ 0,t<T_1 or t>T_2\end{array}\right.$$

(15)

Therefore, three source parameters for each sewage flow source needed to be determined in the DREAM-based framework, specifically denoted as {$Q_i$, $t_i$, $T_i$}. $Q_i$ represented the average emission rate of the source, $t_i$ represented the starting time of emission, and $T_i$ represented the duration of the emission. Through HEC-RAS modeling with a spatial grid size of 200 m, time-variable water levels and flow rates at the downstream boundary ($x$ = 4000 m) were simulated. In the context of the inverse problem, using the previously obtained values as continuous observed values of water levels at the downstream boundary, the source discharge (flow rate and temporal pattern) can be inferred using the proposed framework.

Regarding the prior distributions for each source parameter, an even distribution was assumed within the range of [0, 1] for the flow rate, [0, 1440] for the starting time of emission and the duration (recorded in minutes from 0:00 to 24:00). Hence, the dimension of source parameters in this case was set at 6 (d = 6), for the three parameters associated with the two sewage sources. In the DREAM computation, 7 Markov chains ($N$ = 7) were employed, and the pre-set number of iterations was 5000 ($T$ = 5000). The model error variance of the likelihood function was set at 0.001 ($\sigma$ = 0.001), while for the GA, the number of generations, the population size, the initial crossover rate, and the mutation rate for this case were set to 2000, 200, 0.8, and 0.01, respectively. For each method, simulations were conducted to reach a fit between the simulated hydrodynamic data $M_t$ and the observed data $O_t$ at the downstream monitoring site.

After the optimization termination criterion had been satisfied or a predefined maximum number of generations had been reached, the plot of a typical converging process of the DREAM-based optimization was automatically generated. Figure 2 illustrates the R-statistic, which is used to measure the convergence of the sampled chains for each of the unknown source parameters. The maximum R-statistic briefly reached nearly 7. However, with the correction of the outlier chains using the DREAM algorithm, this value rapidly decreased. Eventually, after approximately 2000 iterations, the R-statistic values for each parameter were found to be less than 1.2, indicating that the Markov chains had converged to the limit distribution with a high degree of accuracy.

Figure 3 provides the performance enhancement by the DREAM compared to GA. Specifically, GA methods exhibited higher uncertainty and lower accuracy. Even after averaging the results from 10 calculations, the mean relative errors in GA simulations stood at 2.1%, with the highest relative error for one simulation reaching 11.3% for $T_1$. Conversely, the MAP values of DREAM closely matched the true values, displaying a mean relative error of merely 0.3% across the six parameters. This remarkable difference in performance signified an 85.7% improvement in the tracking accuracy of source parameters by DREAM compared to GA, thereby validating the effectiveness of the inverse algorithm. Misleading outcomes arose as GA got trapped in local optima, failing to explore the full parameter space, unlike the comprehensive exploration ensured by DREAM.

As for the grid independence solution, it was crucial to determine the spatial grid size required for a stable numerical solution that minimizes the computational load while maintaining errors in the simulated outcome at a nearly constant level. To achieve this, inverse simulations were conducted with spatial grid sizes of 100 m and 200 m.

Table 1. Modeling performances for the simulated water levels for hypothetical case.

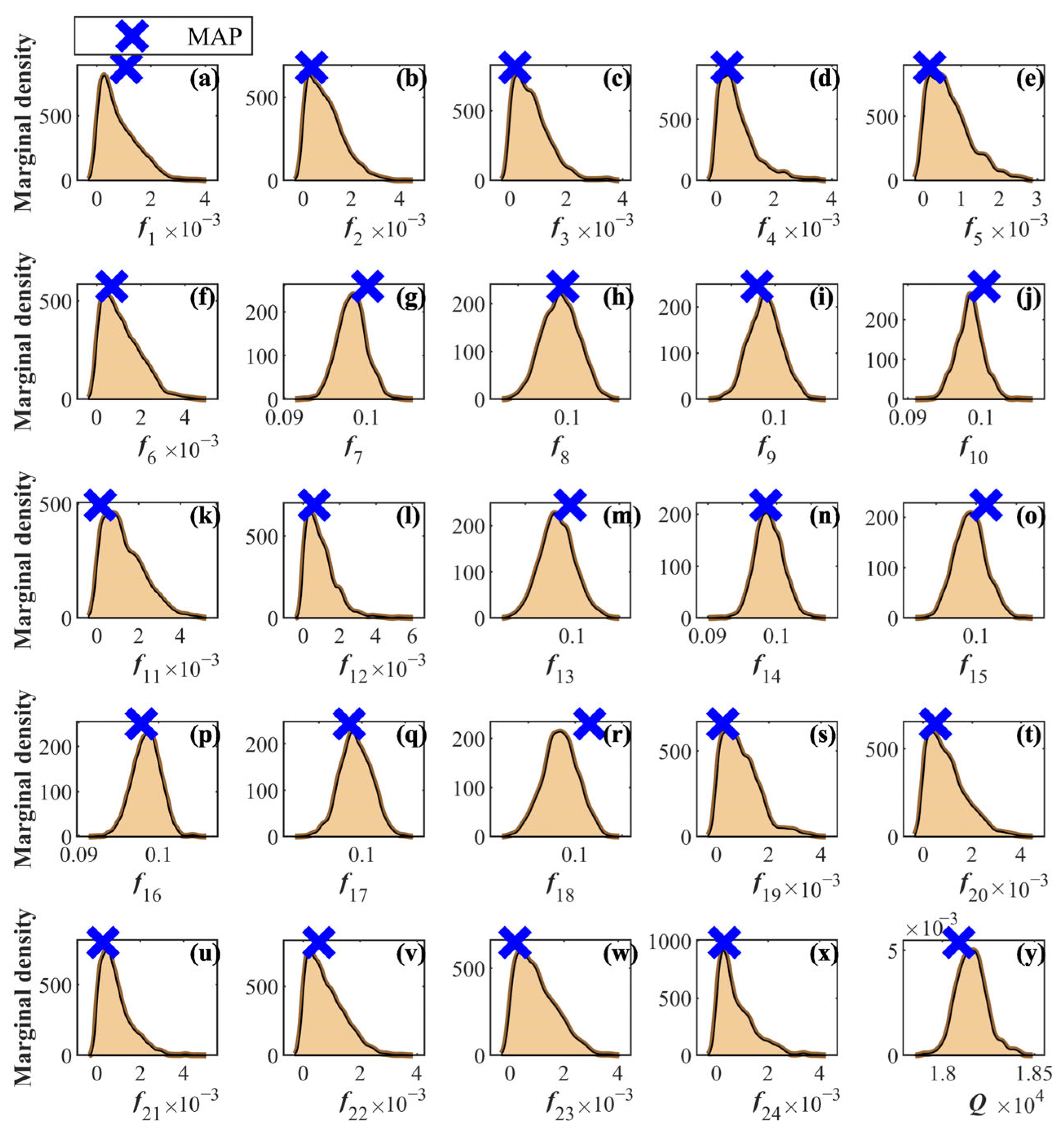
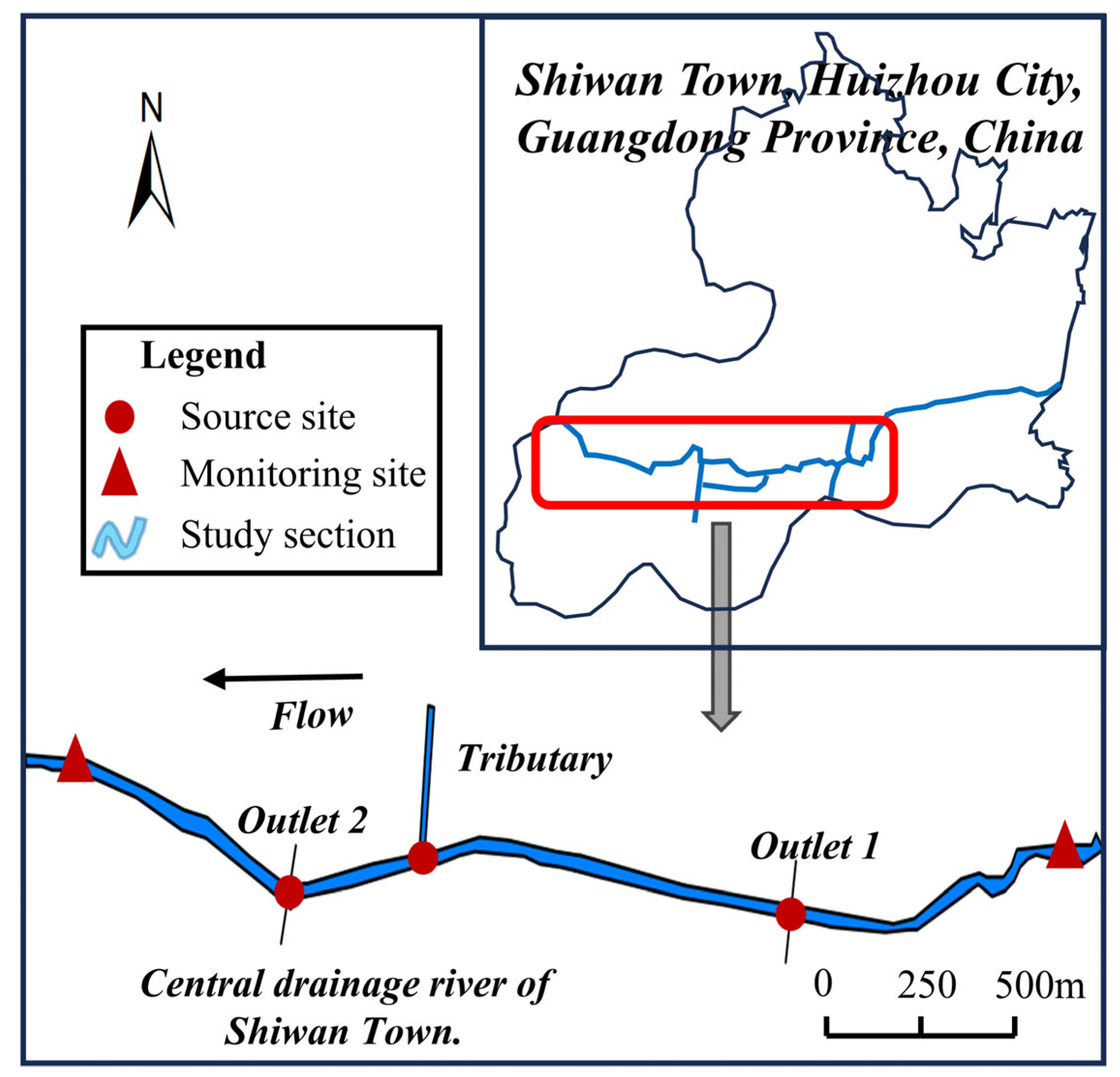
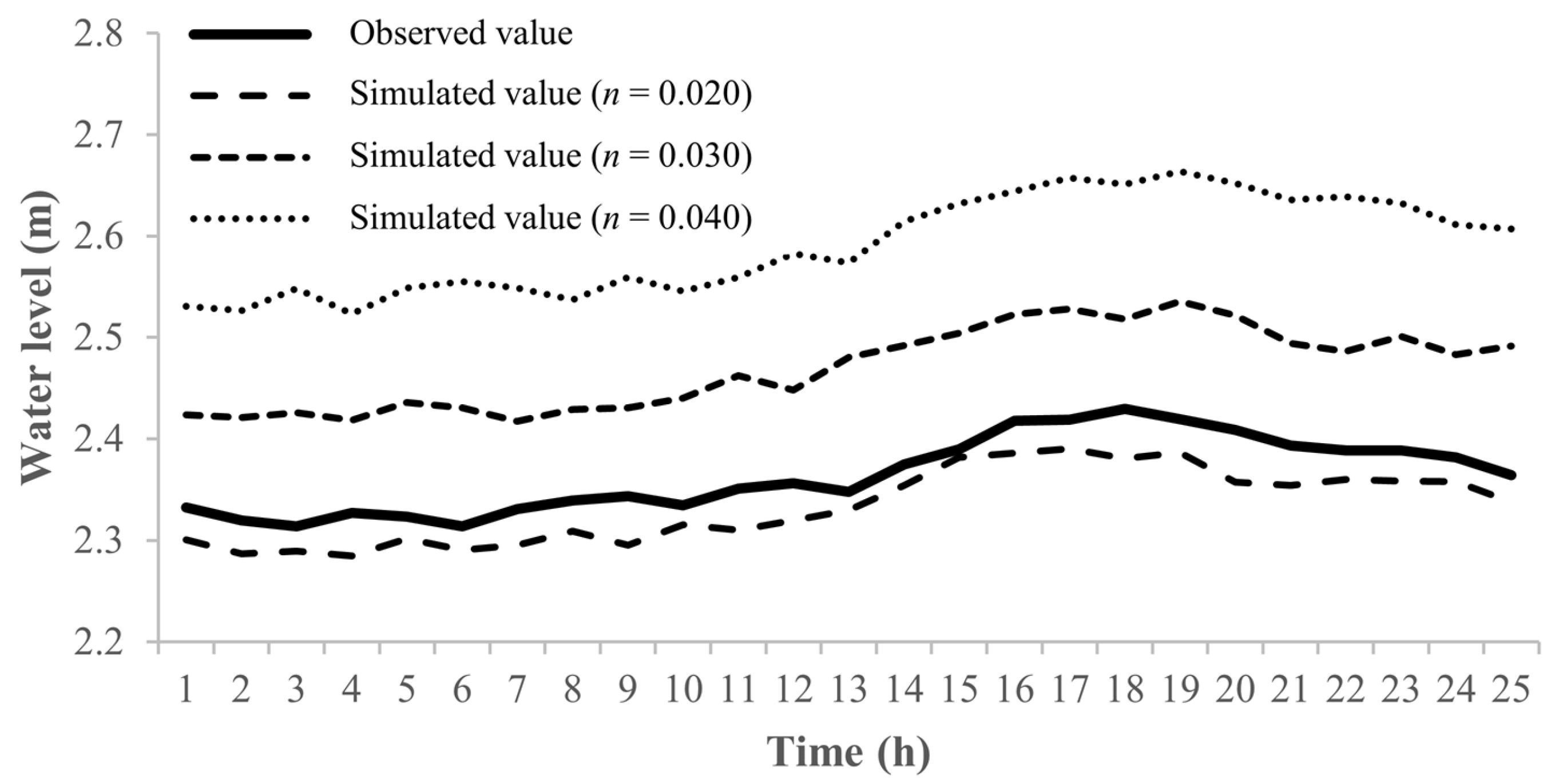
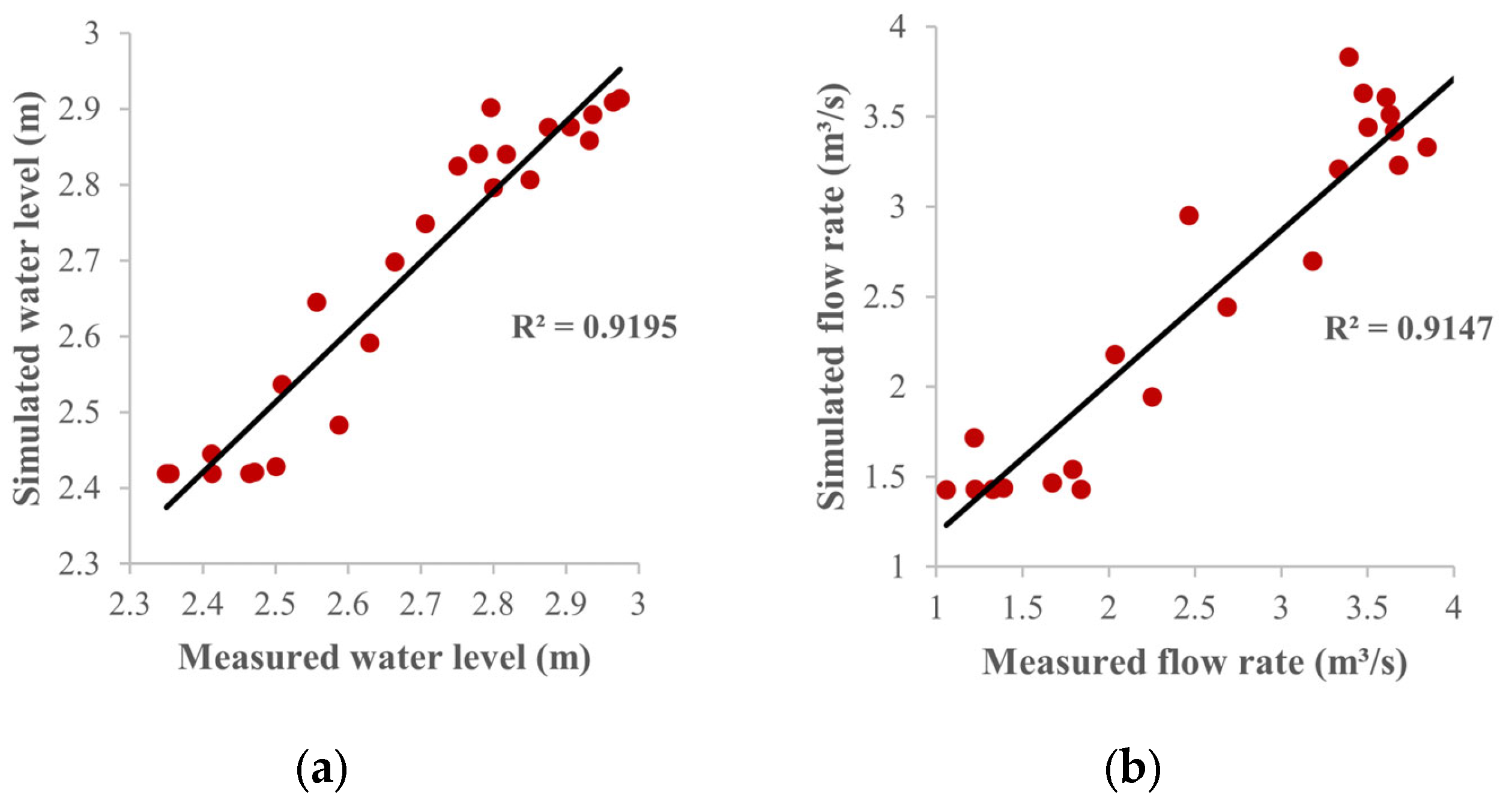
Grid Size (m)	Computation Time (s)	R2	RMSE	NSE
100 m	18,020	0.986	0.001	0.985
200 m	15,350	0.985	0.001	0.985

shows the downstream water levels achieved an R² of 0.985, an RMSE of 0.001, and an NSE of 0.985 with a 200-m grid, indicating a satisfactory tracking accuracy. If the spatial grid size was further refined to 100 m, the R², RMSE, and NSE remained almost unchanged compared to the 200-m grid solution, but the computational time increased by about 17%. Therefore, for source tracing scenarios at known discharge points, further grid refinement on the basis of 200 m did not notably enhance computational accuracy but significantly elevated computational load. Balancing the computational load and the tracking accuracy, a 200-m grid was the acceptable spatial dividing for this numerical solution.

3.2. Real Case

Two real cases, including one case of sewage source tracking of hourly variable sudden discharge and the other case for multiple sewage sources tracking of discharge flows and periods during both dry and wet weather, were employed to demonstrate and verify the robustness of the above framework.

3.2.1. Real Case 1: Source Tracking of a Time-Variable Industrial Discharge into the River

The developed computation tool was demonstrated in a 1.6 km river reach within the Ci Hu River Basin of Ma’anshan City, situated in Anhui Province. Ma’anshan is an industrial city located along the Yangtze River Economic Belt. The Cihu River, which is the longest river entering the city of Ma’anshan, flows through the Cihu Economic Development Zone in its downstream region, with industrial land dominating on both sides. A schematic representation of the generalized model for a demonstration river reach is depicted in Figure 4, with two monitoring devices located upstream and downstream, as well as one time-varying sudden discharge source within the river reach.

The establishment and calibration of the HEC-RAS model relied on topographic data, including river channel elevations, channel slopes, cross-sectional areas, and time-series hydraulic data like upstream and downstream water levels and flow rates. The topographic data were obtained directly from local water authorities to build the geometric model. The accuracy of these cross-sectional profiles was verified by conducting measurements across the river, using a river vessel equipped with an Acoustic Doppler Current Profiler, from the left bank to the right bank. Based on the survey results, the geometry and topography for this river included bottom width from 4.23 to 10.07 m, bottom slope from −0.0007 to 0.0025, bottom elevation from 2.298 to 2.503 m, and the cross-sectional areas from 4.43 to 9.55 square meters. The hydraulic data, involving time series of upstream and downstream water levels and flow rates, were measured at 1-h intervals using ultrasonic time-difference flow meters to set unsteady flow simulations. The upstream boundary and initial conditions were configured as flow hydrographs, with their values matching the measured data. Downstream boundary conditions were initially set as normal water depth to generate simulated downstream values. These simulated values were subsequently refined during the optimization process to align with observed data.

The Manning’s roughness coefficient ($n$) for the HEC-RAS model needed to be calibrated. Figure 5 shows an example of a sensitivity analysis for the calibration of roughness for the Cihu River. It can be observed that the simulated water level converges to the observed water level with a systematic selection of the $n$-value, showing that model calibration of roughness can improve the accuracy of model simulation significantly. Based on such sensitivity analysis, Manning’s roughness coefficient was calibrated to $n$ = 0.028 for the demonstrated river reach.

The unknown side discharge parameter was considered as a time-varying lateral flow whose boundary conditions needed to be optimized in the subsequent DREAM-based framework (i.e., discharge pattern and discharge flow). Based on Equations (3)–(7), the DREAM algorithm was configured as follows. The inverse problem aimed to determine the daily discharge flow and hourly varying coefficients for a known industrial outlet over a 24-h period, resulting in a 25-dimensional $(d$ = 25) source parameter matrix {$Q,f1,f2\dots f24$}. Here, $Q$ represented the average daily flow, and $f1,f2\dots f24$ represented the hourly time coefficients of variation. The prior distribution for each source parameter was assumed to follow a uniform distribution within the range of [0, 20,000] for the flow rate and [0, 1] for the time coefficients of variation. Similarly, 7 Markov chains ($N$ = 7) were employed, and the pre-set number of iterations was 10,000 ($T$ = 10,000). The model error variance of the likelihood function was set at 0.001 ($\sigma$ = 0.001), and the likelihood function observations $O_t$ were determined based on the online water levels and flow rates at the downstream boundary of the channel.

Once the HEC-RAS model was constructed and validated, and the setup of the DREAM algorithm was configured, the inverse problem framework was ready for execution. During the iterative process, the previously defined 25-dimensional source parameters were continuously updated with each iteration. This iteration process was repeated until convergence was achieved. All simulations involving HEC-RAS were executed in parallel, making use of the 7 available processors in the Intel^® Xeon^® W-2245 CPU @ 3.90 GHz (Intel, Santa Clara, CA, USA), which corresponds to running 7 parallel Markov chains in the DREAM algorithm.

Figure S2 presents the R-statistics used to measure the convergence of the sampled chains during the iterations. The R-statistics of each source parameter was less than 1.2 after 7000 iterations, representing the convergence precision of the Markov chains or the officially declared convergence to the limit distribution. In addition, Figure 6 shows the marginal PDFs of the source parameters from the DREAM-based inverse model for this case, including 24 parameters of hourly varying coefficients within a day and 1 parameter of average daily flow. As shown in Figure 5, the solid brown line represents the density of marginal PDFs, and the blue cross marks the MAP estimate. The marginal PDFs of all source parameters followed unimodal distributions with narrow posterior ranges, indicating the high reliability of the integrated pollution tracking framework.

Utilizing the MAP values of each source parameter as the model identification results and sending these values back into the HEC-RAS model, the outcomes of the forward hydrodynamic model were compared with observed data. As shown in Figure 7, it highlights that the inverse model developed in this study can accurately reproduce the changes in water levels and flow rates caused by source flow discharges. Additionally, as illustrated in

Table 2. Modeling performances for the simulated downstream values.

	R2	RMSE	NSE
Water level	0.960	0.012	0.959
Flow Rate	0.950	0.072	0.949

, the calculation of three error indices reveals an R² range of 0.950 to 0.960, an RMSE ranging only between 0.012 and 0.072, and an NSE spanning from 0.949 to 0.959. These results indicated a close agreement between the water level data and flow rate data generated through forward simulation using the inverse problem results and the actual measured data. The impressive level of accuracy demonstrated the feasibility of the developed computational tool to identify hourly variable sudden discharge flows under transient flow conditions.

3.2.2. Real Case 2: Source Tracking of Multiple Sewage Discharges into the River

Real case 2 involves the inverse tracking of multiple sewage flow discharges along a 4 km river reach in Shiwan Town of Huizhou City, Guangdong Province. Huizhou City is situated in the southeastern part of Guangdong, within the northeastern region of the Pearl River Delta. Based on the on-site investigation, it was found that this river reach exhibited black water and a noticeable odor. The model domain was confined to the main river channel. A schematic representation of the generalized model for a demonstration river reach is depicted in Figure 8, with two monitoring devices located upstream and downstream, as well as three discharge sources within the river reach. This case served to validate the effectiveness of the computation tool in tracking multiple sewage sources under both dry and wet weather conditions.

To build the HEC-RAS model in this case, river topographic data, meteorological data, and hydraulic data were required. The topographic data and meteorological data were obtained from local water authorities and on-site surveys. The specific topographic data and meteorological data within the studied reach included bottom width from 12.47 to 29.88 m, bottom slope from −0.0004 to 0.0005, bottom elevation from 2.298 to 2.503 m, and the cross-sectional areas from 6.72 to 24.87 square meters. Hydraulic data, including water level and flow rate, were available from the existing monitoring system in the study area. The input of upstream and downstream monitoring data for dry and wet weather conditions served as boundary conditions and observation targets for the subsequent inverse modeling process. Similarly, as shown in Figure 9, Manning’s roughness coefficient was calibrated to $n$ = 0.026 for the demonstrated river reach based on sensitivity analysis.

In this case of multiple sewage discharges, the unknown side discharge was considered as a pulse discharge. Similarly, three source parameters had to be determined for each wastewater flow source, specifically denoted as {$Q_i$, $t_i$, $T_i$}. The prior distribution of the three source parameters was set as a uniform distribution, with [0, 1] for the flow rate, [0, 23] for the emission start time, and [0, 24] for the duration. Therefore, the dimension of the source parameters in this case was set to 9 (d = 9) for the three parameters associated with the three sewage sources. Otherwise, the number of Markov chains was 7 ($N$ = 7), and the pre-set number of iterations was 10,000 ($T$ = 10,000). The observed water levels and flow rates at the downstream monitoring sites were used as observation data $O_t$ to inversely estimate the unknown source parameters.

Validation was performed under both dry and wet weather conditions to test the effectiveness of the proposed framework. In both scenarios, three lateral flows (two known outlets and one tributary flow) underwent variations at each generation throughout the optimization process. The R-statistics used to measure the convergence of the sampled chains during the iterations are presented in Figure S2, and the evolutions of the seven parallel Markov chains, as well as the resulting marginal PDFs, are presented in Figure S3.

Table 3. Identification results of source parameters from the DREAM-based model.

(a) Dry weather
Dry weather	$\mathit{Q}$ (m3/s)	$\mathit{t}$ (h)	$\mathit{T}$ (h)
Outlet 1	0.123	7	11
Outlet 2	0.219	12	4
Tributary	0.292	0	24
(b) Wet weather
Wet weather	$\mathit{Q}$ (m3/s)	$\mathit{t}$ (h)	$\mathit{T}$ (h)
Outlet 1	0.254	6	12
Outlet 2	0.330	7	10
Tributary	0.426	0	24

shows the MAP estimations of the source parameters from the DREAM-based inverse model for this case, including estimated flow rates, starting time, and duration of the two outlets and tributary. It is evident from the table that during rainfall events (based on data from the local water authority, with a daily rainfall of 19.7 mm), the flow values at each discharge outlet significantly increased compared to dry weather conditions, with an increase ranging from 45.8% to 106.4%.

Similarly, through the utilization of MAP values obtained from the inverse model and their integration into the HEC-RAS model, downstream values were simulated. As depicted in Figure 10 and Figure 11, a linear regression analysis comparing observed values to simulated values revealed a robust fit. Additionally, as outlined in

Table 4. Modeling performances for the simulated downstream values for Case 2.

(a) Dry weather
Dry weather	R2	RMSE	NSE
Water level	0.935	0.010	0.933
Flow Rate	0.930	0.043	0.924
(b) Wet weather
Wet weather	R2	RMSE	NSE
Water level	0.920	0.057	0.919
Flow Rate	0.915	0.333	0.901

, the analysis of performance metrics revealed R² values ranging from 0.915 to 0.935, RMSE values spanning from 0.010 to 0.333, and NSE values between 0.901 and 0.933. Notably, the proposed model demonstrated high reliability and accuracy in inversely estimating multiple discharge sources based on both dry and wet weather observations.

4. Conclusions

This paper presents an innovative open-source framework designed for the inverse tracking of emission patterns from known outlets in rivers under transient flow conditions based on observed river water levels and flow rates at pre-set monitoring sites. This framework is characterized by the integration of two key modules: HEC-RAS, serving as the hydrodynamic model, and DREAM, serving as the inverse problem method. Compared to diffusion wave equations that are only suitable for single-direction flow, the coupled HEC-RAS and DREAM algorithm within MATLAB can be extended to simulate source tracking under highly transient flow conditions, such as sudden discharges or in complex hydraulic conditions caused by rainfall, as demonstrated in this study. The paper also provides relevant code and scripts, serving as resources for reference and practical application in the field.

The proposed DREAM-based framework was first checked by the hypothetical case with pre-set known source parameters. The MAP values of DREAM closely matched the true values, with an average relative error of only 0.3% across the six parameters, indicating an 85.7% enhancement in tracking performance compared to GA. Further, by employing real cases, the inverse framework successfully estimated source discharges, including a real scenario involving the tracking of hourly variable sudden discharge from a sewage source and another scenario involving the tracking of discharge flows and periods from multiple sewage sources under both dry and wet weather conditions. With R² values ranging from 0.915 to 0.960, RMSE values from 0.010 to 0.333, and NSE values between 0.901 and 0.959, a strong agreement was observed between simulated values and actual measurements. These case study results revealed that the proposed approach served as an effective tool for inverse tracking sewage flow discharge in real-world scenarios of highly transient flow, showcasing its practical utility in pollution interception and water quality restoration.

The limitation of this study is that the presented cases only focus on the main river channel, but it is possible to extend the source tracking to the entire river network, including its tributaries, by increasing the number of monitoring points. To address this concern, future work will conduct additional cases within the river network by deploying more monitoring stations to expand the application scope of the proposed framework.