Rivers under Ice: Evaluating Simulated Morphodynamics through a Riffle-Pool Sequence
Abstract
:1. Introduction
2. Study Site and Field Measurements
3. Pre-Processing, Data Analysis, and Model Validation
4. Results
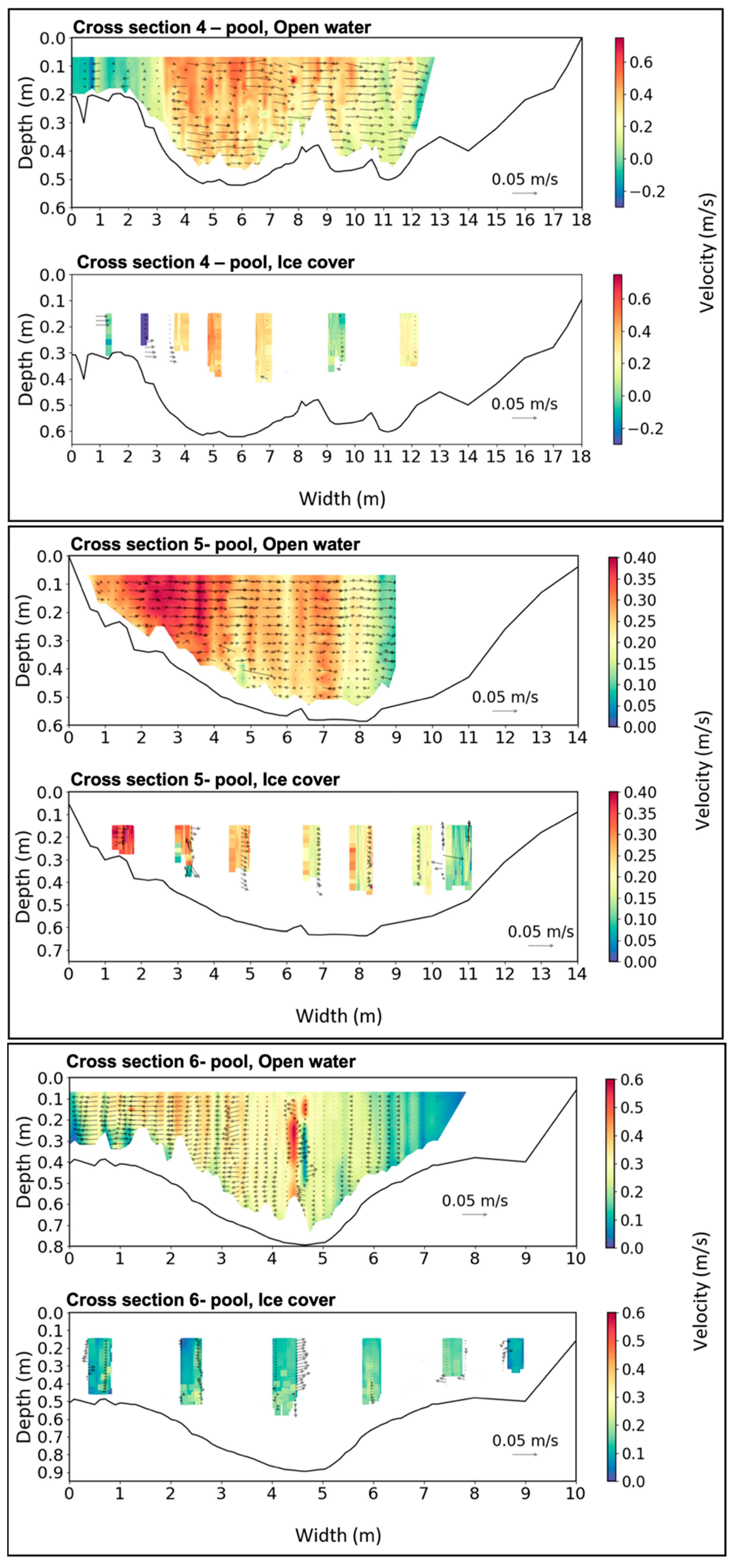
4.1. Cross-Section Velocity Distribution
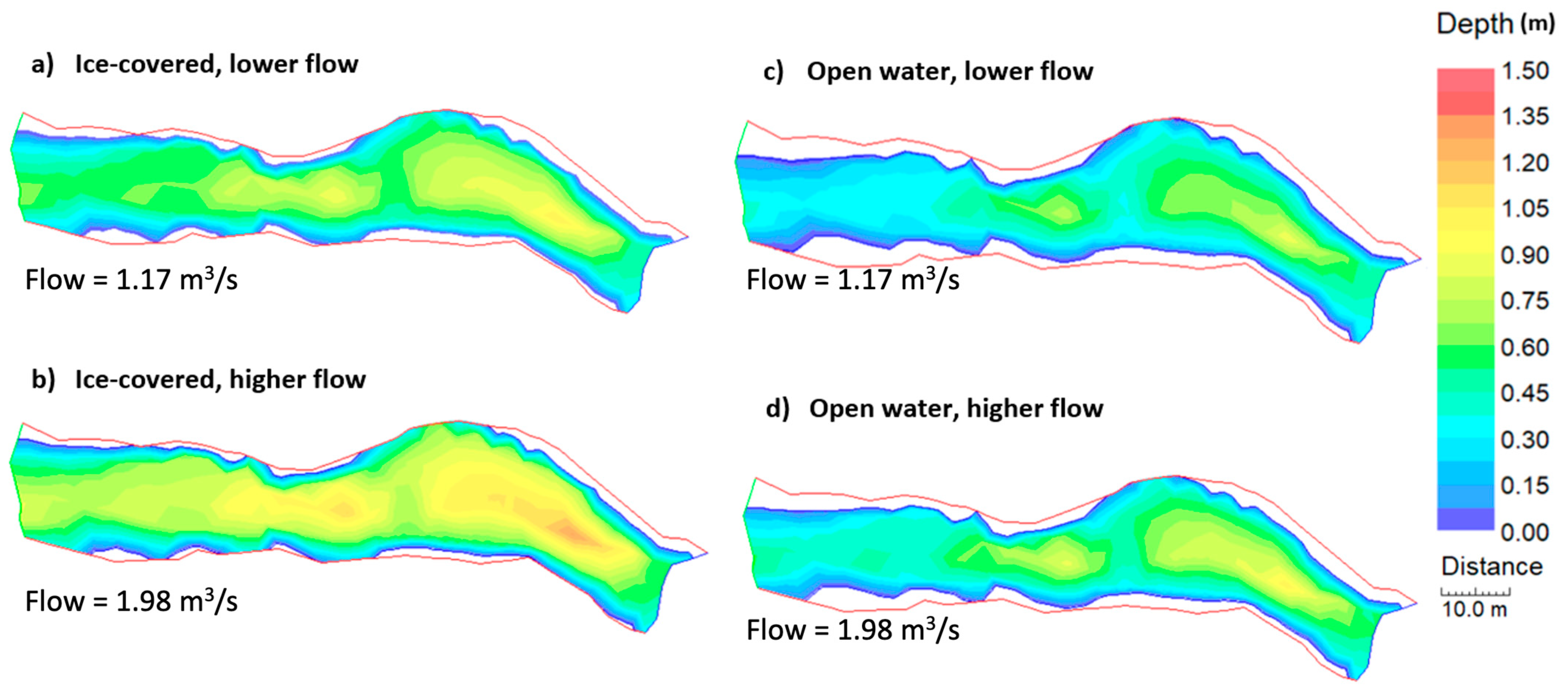
4.2. Water Depth Distribution and Depth-Averaged Velocity
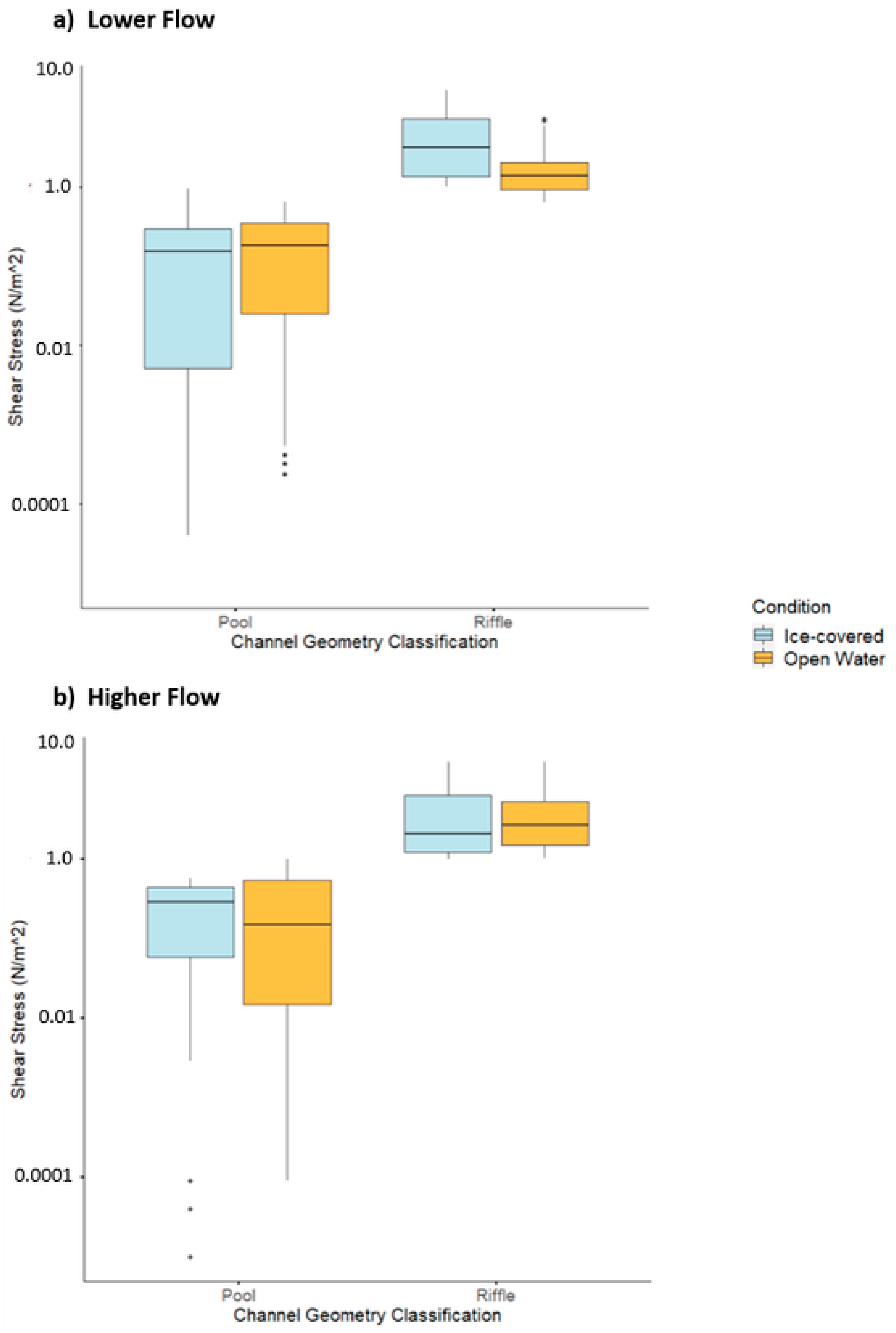
4.3. Shear Stress Magnitude and Distribution
4.4. Model Validation Results
5. Discussion
5.1. Spatial Distribution of Depth-Averaged Velocities and Bed Shear Stress under Ice Cover
5.2. Implications for Ecosystem Services
5.3. Modeled Shear Stress Distribution and Magnitude: Advantages and Drawbacks
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nicholas, A.P. Modelling the Continuum of River Channel Patterns. Earth Surf. Process. Landf. 2013, 38, 1187–1196. [Google Scholar] [CrossRef]
- Lotsari, E.; Lintunen, K.; Kasvi, E.; Alho, P.; Blåfield, L. The Impacts of Near-Bed Flow Characteristics on River Bed Sediment Transport under Ice-Covered Conditions in 2016–2021. J. Hydrol. 2022, 615, 128610. [Google Scholar] [CrossRef]
- Lotsari, E.; Thorndycraft, V.; Alho, P. Prospects and Challenges of Simulating River Channel Response to Future Climate Change. Prog. Phys. Geogr. Earth Environ. 2015, 39, 483–513. [Google Scholar] [CrossRef]
- Aghaji Zare, S.G.; Moore, S.A.; Rennie, C.D.; Seidou, O.; Ahmari, H.; Malenchak, J. Boundary Shear Stress in an Ice-Covered River during Breakup. J. Hydraul. Eng. 2016, 142, 04015065. [Google Scholar] [CrossRef]
- Smith, K.; Cockburn, J.; Villard, P.V. The Effect of Ice Cover on Velocity and Shear Stress in a Riffle-pool Sequence. Earth Surf. Process. Landf. 2023, esp.5557. [Google Scholar] [CrossRef]
- Lotsari, E.; Tarsa, T.; Kämäri, M.; Alho, P.; Kasvi, E. Spatial Variation of Flow Characteristics in a Subarctic Meandering River in Ice-Covered and Open-Channel Conditions: A 2D Hydrodynamic Modelling Approach. Earth Surf. Process. Landf. 2019, 44, 1509–1529. [Google Scholar] [CrossRef]
- Lotsari, E.; Kasvi, E.; Kämäri, M.; Alho, P. The Effects of Ice Cover on Flow Characteristics in a Subarctic Meandering River. Earth Surf. Process. Landf. 2017, 42, 1195–1212. [Google Scholar] [CrossRef]
- Demers, S.; Buffin-Bélanger, T.; Roy, A.G. Helical Cell Motions in a Small Ice-Covered Meander River Reach. River Res. Appl. 2011, 27, 1118–1125. [Google Scholar] [CrossRef]
- Schwartz, J.S.; Neff, K.J. Use of River2D Hydrodynamic Model for Stream Restoration Assessment and Design. In Proceedings of the World Environmental and Water Resources Congress 2011: Bearing Knowledge for Sustainability, Palm Springs, CA, USA, 22–26 May 2011; pp. 2593–2602. [Google Scholar] [CrossRef]
- Turcotte, B.; Morse, B.; Bergeron, N.E.; Roy, A.G. Sediment Transport in Ice-Affected Rivers. J. Hydrol. 2011, 409, 561–577. [Google Scholar] [CrossRef]
- Kämäri, M.; Alho, P.; Colpaert, A.; Lotsari, E. Spatial Variation of River-Ice Thickness in a Meandering River. Cold Reg. Sci. Technol. 2017, 137, 17–29. [Google Scholar] [CrossRef]
- Robert, A.; Tran, T. Mean and Turbulent Flow Fields in a Simulated Ice-Covered Channel with a Gravel Bed: Some Laboratory Observations. Earth Surf. Process. Landf. 2012, 37, 951–956. [Google Scholar] [CrossRef]
- Wang, J.; Sui, J.-Y.; Karney, B.W. Incipient Motion of Non-Cohesive Sediment under Ice Cover—An Experimental Study. J. Hydrodyn. 2008, 20, 117–124. [Google Scholar] [CrossRef]
- Turcotte, B.; Morse, B.; Pelchat, G. Impact of Climate Change on the Frequency of Dynamic Breakup Events and on the Risk of Ice-Jam Floods in Quebec, Canada. Water 2020, 12, 2891. [Google Scholar] [CrossRef]
- Lindenschmidt, K.-E. RIVICE—A Non-Proprietary, Open-Source, One-Dimensional River-Ice Model. Water 2017, 9, 314. [Google Scholar] [CrossRef]
- Morales-Marín, L.A.; Sanyal, P.R.; Kadowaki, H.; Li, Z.; Rokaya, P.; Lindenschmidt, K.E. A Hydrological and Water Temperature Modelling Framework to Simulate the Timing of River Freeze-up and Ice-Cover Breakup in Large-Scale Catchments. Environ. Model. Softw. 2019, 114, 49–63. [Google Scholar] [CrossRef]
- Shen, H.T. Mathematical Modeling of River Ice Processes. Cold Reg. Sci. Technol. 2010, 62, 3–13. [Google Scholar] [CrossRef]
- Namaee, M.R.; Sui, J. Local Scour Around Two Side-by-Side Cylindrical Bridge Piers under Ice-Covered Conditions. Int. J. Sediment Res. 2019, 34, 355–367. [Google Scholar] [CrossRef]
- Parsapour-Moghaddam, P.; Rennie, C.D. Calibration of a 3D Hydrodynamic Meandering River Model Using Fully Spatially Distributed 3D ADCP Velocity Data. J. Hydraul. Eng. 2018, 144, 04018010. [Google Scholar] [CrossRef]
- Peters, M.; Dow, K.; Clark, S.P.; Malenchak, J.; Danielson, D. Experimental Investigation of the Flow Characteristics beneath Partial Ice Covers. Cold Reg. Sci. Technol. 2017, 142, 69–78. [Google Scholar] [CrossRef]
- Vietz, G.J.; Rutherfurd, I.D.; Stewardson, M.J.; Finlayson, B.L. Hydrodynamics and Sedimentology of Concave Benches in a Lowland River. Geomorphology 2012, 147–148, 86–101. [Google Scholar] [CrossRef]
- Steffler, P.; Blackburn, J. Two-Dimensional Depth Averaged Model of River Hydrodynamics and Fish Habitat. Available online: https://relicensing.pcwa.net/documents/Library/PCWA-L%20452.pdf (accessed on 30 June 2021).
- Environment and Climate Change Water Survey of Canada. Available online: https://www.canada.ca/en/environment-climate-change/services/water-overview/quantity/monitoring/survey.html (accessed on 1 April 2022).
- Robert, A. Characteristics of Velocity Profiles along Riffle-Pool Sequences and Estimates of Bed Shear Stress. Geomorphology 1997, 19, 89–98. [Google Scholar] [CrossRef]
- Smith, K. Investigating Ice-Impacted Fluvial Processes in a Small Riffle-Pool Sequence in Southern Ontario. Master’s Thesis, University of Guelph, Guelph, ON, Canada, 2022. [Google Scholar]
- Crowder, D.W.; Diplas, P. Using Two-Dimensional Hydrodynamic Models at Scales of Ecological Importance. J. Hydrol. 2000, 230, 172–191. [Google Scholar] [CrossRef]
- Sontek Flowtracker 2 Wading Discharge Measurement Instrument. 2019. Available online: https://www.sontek.com/media/pdfs/flowtracker2-brochure-s19-02-1219.pdf (accessed on 9 September 2021).
- Sontek RiverSuveyor Discharge, Bathymetry and Current Profiling. 2015. Available online: https://info.xylem.com/rs/240-UTB-146/images/riversurveyor-m9-s5-brochure.pdf?_ga=2.67666392.894680228.1648847751-199850675.1648847751 (accessed on 9 September 2021).
- Parsons, D.R.; Jackson, P.R.; Czuba, J.A.; Engel, F.L.; Rhoads, B.L.; Oberg, K.A.; Best, J.L.; Mueller, D.S.; Johnson, K.K.; Riley, J.D. Velocity Mapping Toolbox (VMT): A Processing and Visualization Suite for Moving-Vessel ADCP Measurements. Earth Surf. Process. Landf. 2013, 38, 1244–1260. [Google Scholar] [CrossRef]
- Waddle, T.; Steffler, P. Mesh Generation Program for River2D Two Dimensional Depth Averaged Finite Element; US Geological Survey: Reston, VA, USA, 2002.
- Alabyan, A.M.; Lebedeva, S.V. Flow Dynamics in Large Tidal Delta of the Northern Dvina River: 2D Simulation. J. Hydroinform. 2018, 20, 798–814. [Google Scholar] [CrossRef]
- Robert, A. River Processes: An Introduction to Fluvial Dynamics; Routledge: London, UK, 2003. [Google Scholar]
- Waddle, T. Simulation of Flow Habitat Conditions Under Ice, Cache La Poudre River—January 2006; Open-File Report; US Geological Survey: Reston, VA, USA, 2007.
- Church, M.; Hassan, M.A. Size and Distance of Travel of Unconstrained Clasts on a Streambed. Water Resour. Res. 1992, 28, 299–303. [Google Scholar] [CrossRef]
- Lepelletier, T.; Araud, Q. Implicit Formulation for 1D and 2D St Venant Equations—Presentation of the Method, Validation and Applications. In Advances in Hydroinformatics, Proceedings of the Advances in Hydroinformatics: SimHydro 2017—Choosing The Right Model in Applied Hydraulics, Nice, France, 14–16 June 2017; Gourbesville, P., Cunge, J., Caignaert, G., Eds.; Springer: Singapore, 2018; pp. 91–103. [Google Scholar]
- Beltaos, S.; Prowse, T. River-Ice Hydrology in a Shrinking Cryosphere. Hydrol. Process. 2009, 23, 122–144. [Google Scholar] [CrossRef]
- Mosley, M.P. Analysis of the Effect of Changing Discharge on Channel Morphology and Instream Uses in a Braided River, Ohau River, New Zealand. Water Resour. Res. 1982, 18, 800–812. [Google Scholar] [CrossRef]
- Hassan, M.A.; Radić, V.; Buckrell, E.; Chartrand, S.M.; McDowell, C. Pool-Riffle Adjustment Due to Changes in Flow and Sediment Supply. Water Resour. Res. 2021, 57, e2020WR028048. [Google Scholar] [CrossRef]
- Urroz, G.E.; Ettema, R. Application of Two-Layer Hypothesis to Fully Developed Flow in Ice-Covered Curved Channels. Can. J. Civ. Eng. 1994, 21, 101–110. [Google Scholar] [CrossRef]
- Blanckaert, K.; de Vriend, H.J. Meander Dynamics: A Nonlinear Model without Curvature Restrictions for Flow in Open-Channel Bends. J. Geophys. Res. 2010, 115, F04011. [Google Scholar] [CrossRef]
- Bathhurst, J.C. Distribution of Boundary Shear Stress in Rivers. In Adjustments of the Fluvial System; Routledge: Oxfordshire, UK, 2020; pp. 95–116. [Google Scholar]
- Tokyay, T.; Sinha, S. Channel Width, Bedform Length and Turbulence: Numerical Investigation of Flow Dynamics over Laboratory-Scale Pool–Riffle Sequences. Environ. Fluid Mech. 2020, 20, 819–842. [Google Scholar] [CrossRef]
- Zabilansky, L.J.; Hains, D.B.; Remus, J.I. Increased Bed Erosion Due to Ice. In Current Practices in Cold Regions Engineering; ASCE: Reston, VA, USA, 2006; pp. 1–12. [Google Scholar] [CrossRef]
- Kang, S.; Sotiropoulos, F. Flow Phenomena and Mechanisms in a Field-Scale Experimental Meandering Channel with a Pool-Riffle Sequence: Insights Gained via Numerical Simulation. J. Geophys. Res. 2011, 116, F03011. [Google Scholar] [CrossRef]
- Booker, D.J.; Sear, D.A.; Payne, A.J. Modelling Three-Dimensional Flow Structures and Patterns of Boundary Shear Stress in a Natural Pool–Riffle Sequence. Earth Surf. Process. Landf. 2001, 26, 553–576. [Google Scholar] [CrossRef]
- Ministry of the Environment, Conservation and Parks. Silver Shiner; Government of Ontario: Toronto, ON, Canada, 2021.
- Bunt, C. Silver Shiner (Notropis Photogenis) Size-Class Structure, Habitat Utilization, Movement and Persistence in an Urbanized Fragment of a Great Lakes Tributary. Am. Midl. Nat. 2016, 176, 200–209. [Google Scholar] [CrossRef]
- Huusko, A.; Greenberg, L.; Stickler, M.; Linnansaari, T.; Nykänen, M.; Vehanen, T.; Koljonen, S.; Louhi, P.; Alfredsen, K. Life in the Ice Lane: The Winter Ecology of Stream Salmonids. River Res. Appl. 2007, 23, 469–491. [Google Scholar] [CrossRef]
- Sawyer, A.H.; Bayani Cardenas, M.; Buttles, J. Hyporheic Exchange Due to Channel-Spanning Logs. Water Resour. Res. 2011, 47, W08502. [Google Scholar] [CrossRef]
- Church, M. Channel Stability: Morphodynamics and the Morphology of Rivers. In Rivers—Physical, Fluvial and Environmental Processes; GeoPlanet: Earth and Planetary Sciences; Springer: Cham, Switzerland, 2015; pp. 281–321. ISBN 978-3-319-17718-2. [Google Scholar]
- Salmela, J.; Kasvi, E.; Vaaja, M.T.; Kaartinen, H.; Kukko, A.; Jaakkola, A.; Alho, P. Morphological Changes and Riffle-Pool Dynamics Related to Flow in a Meandering River Channel Based on a 5-Year Monitoring Period Using Close-Range Remote Sensing. Geomorphology 2020, 352, 106982. [Google Scholar] [CrossRef]
- MacWilliams, M.L., Jr.; Wheaton, J.M.; Pasternack, G.B.; Street, R.L.; Kitanidis, P.K. Flow Convergence Routing Hypothesis for Pool-Riffler Maintenance in Alluvial. Water Resour. Res. 2006, 42, W10427. [Google Scholar] [CrossRef]
- Cockburn, J.M.H.; Villard, P.V.; Hutton, C. Assessing Instream Habitat Suitability and Hydraulic Signatures of Geomorphic Units in a Reconstructed Single Thread Meandering Channel. Ecohydrology 2016, 9, 1094–1104. [Google Scholar] [CrossRef]
- Hjulström, F. Studies of the Morphological Activity of Rivers as Illustrated by the River Fyris. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 1935. [Google Scholar]
- Shamloo, H.; Rajaratnam, N.; Katopodis, C. Hydraulics of Simple Habitat Structures. J. Hydraul. Res. 2001, 39, 351–366. [Google Scholar] [CrossRef]
- Jay Lacey, R.W.; Millar, R.G. Reach Scale Hydraulic Assessment of Instream Salmonid Habitat Restoration. JAWRA J. Am. Water Resour. Assoc. 2004, 40, 1631–1644. [Google Scholar] [CrossRef]
- Franca, M.J.; Ferreira, R.M.L.; Lemmin, U. Parameterization of the Logarithmic Layer of Double-Averaged Streamwise Velocity Profiles in Gravel-Bed River Flows. Adv. Water Resour. 2008, 31, 915–925. [Google Scholar] [CrossRef]
- Rickenmann, D.; Recking, A. Evaluation of Flow Resistance in Gravel-Bed Rivers through a Large Field Data Set. Water Resour. Res. 2011, 47, W07538. [Google Scholar] [CrossRef]
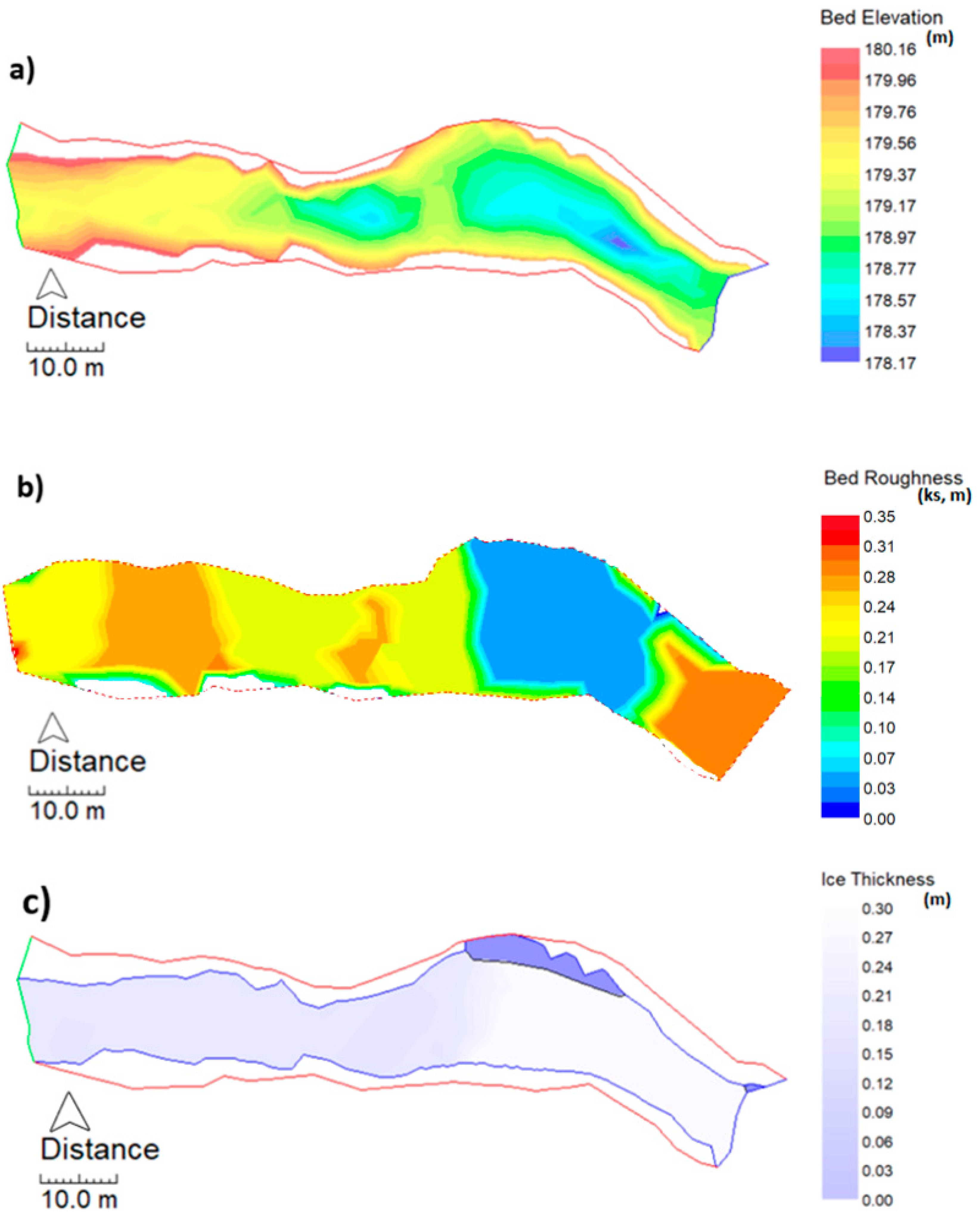
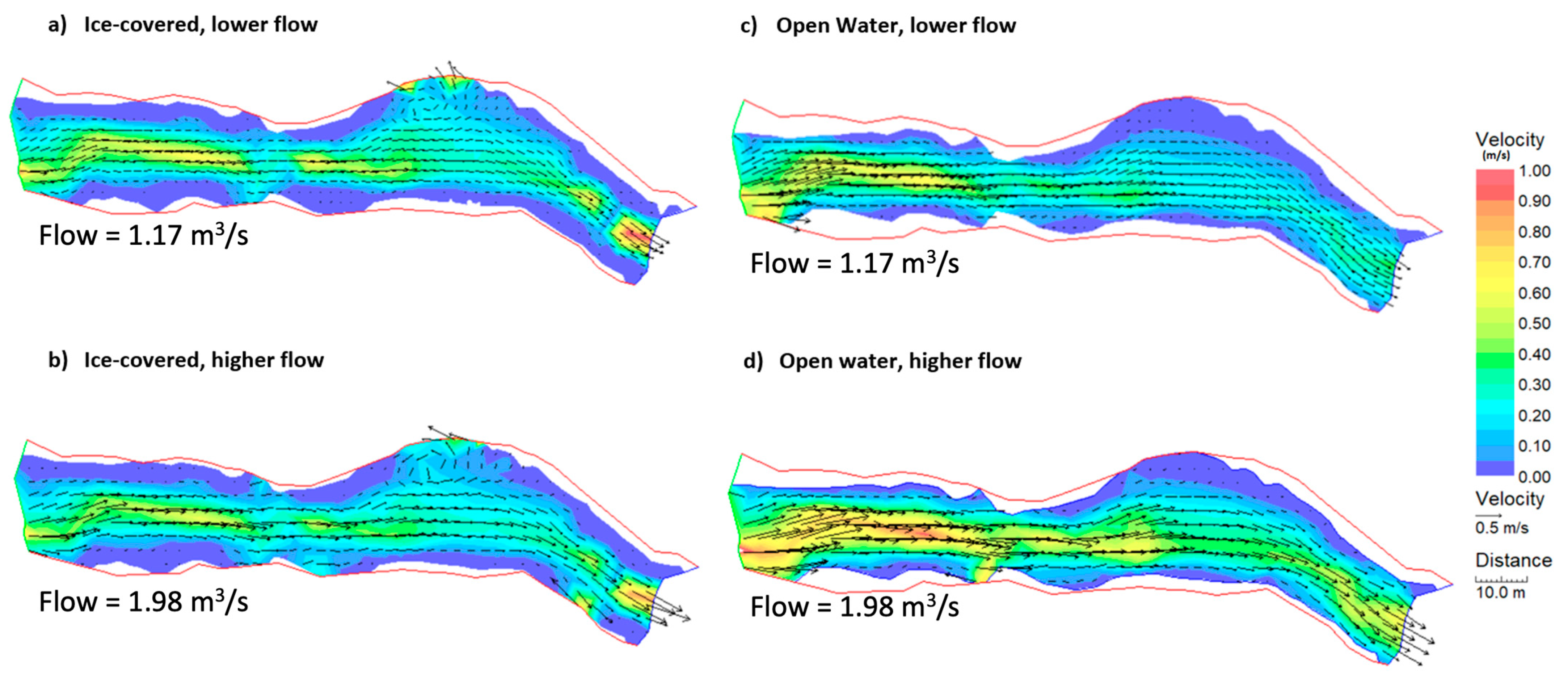
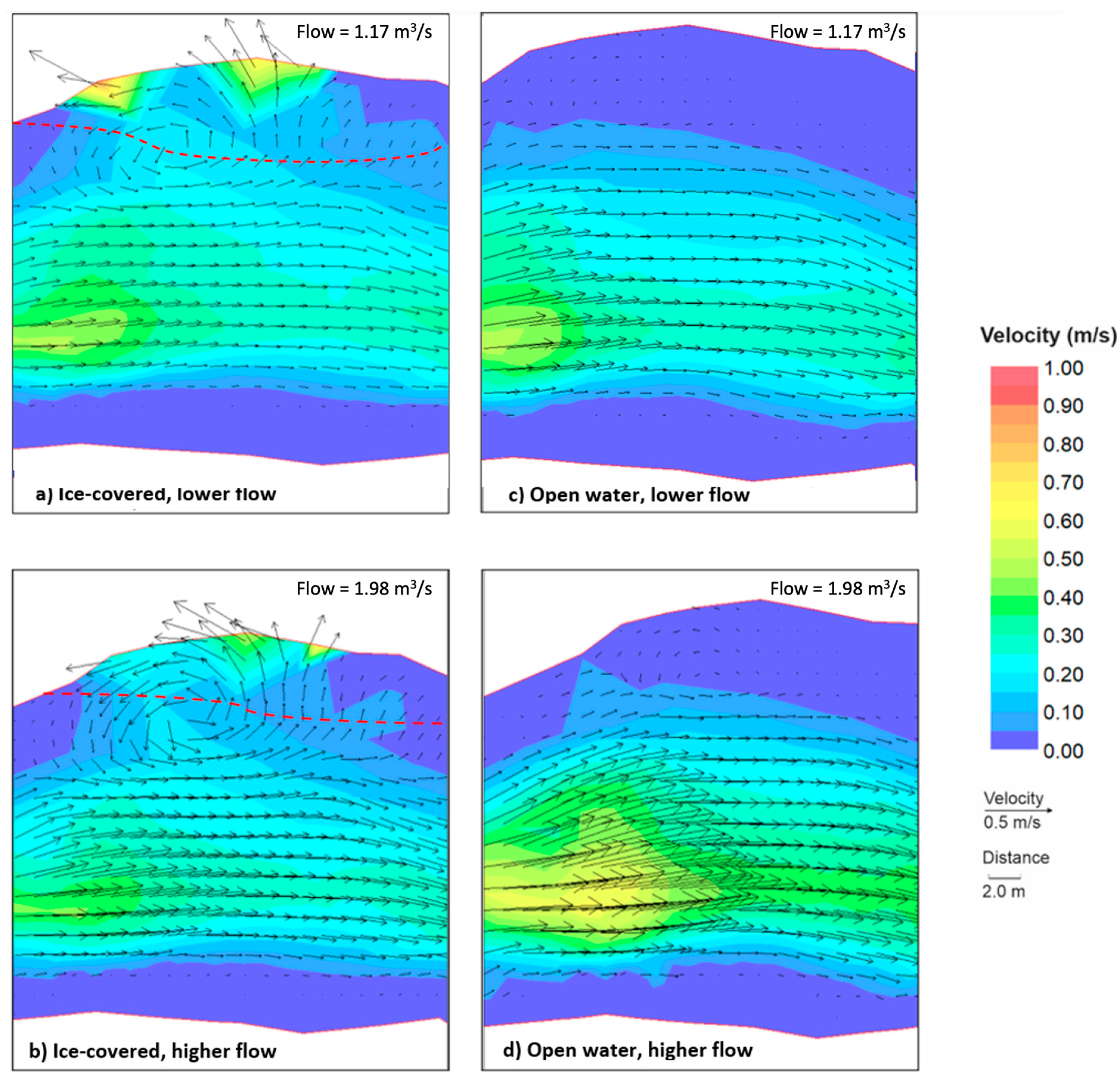
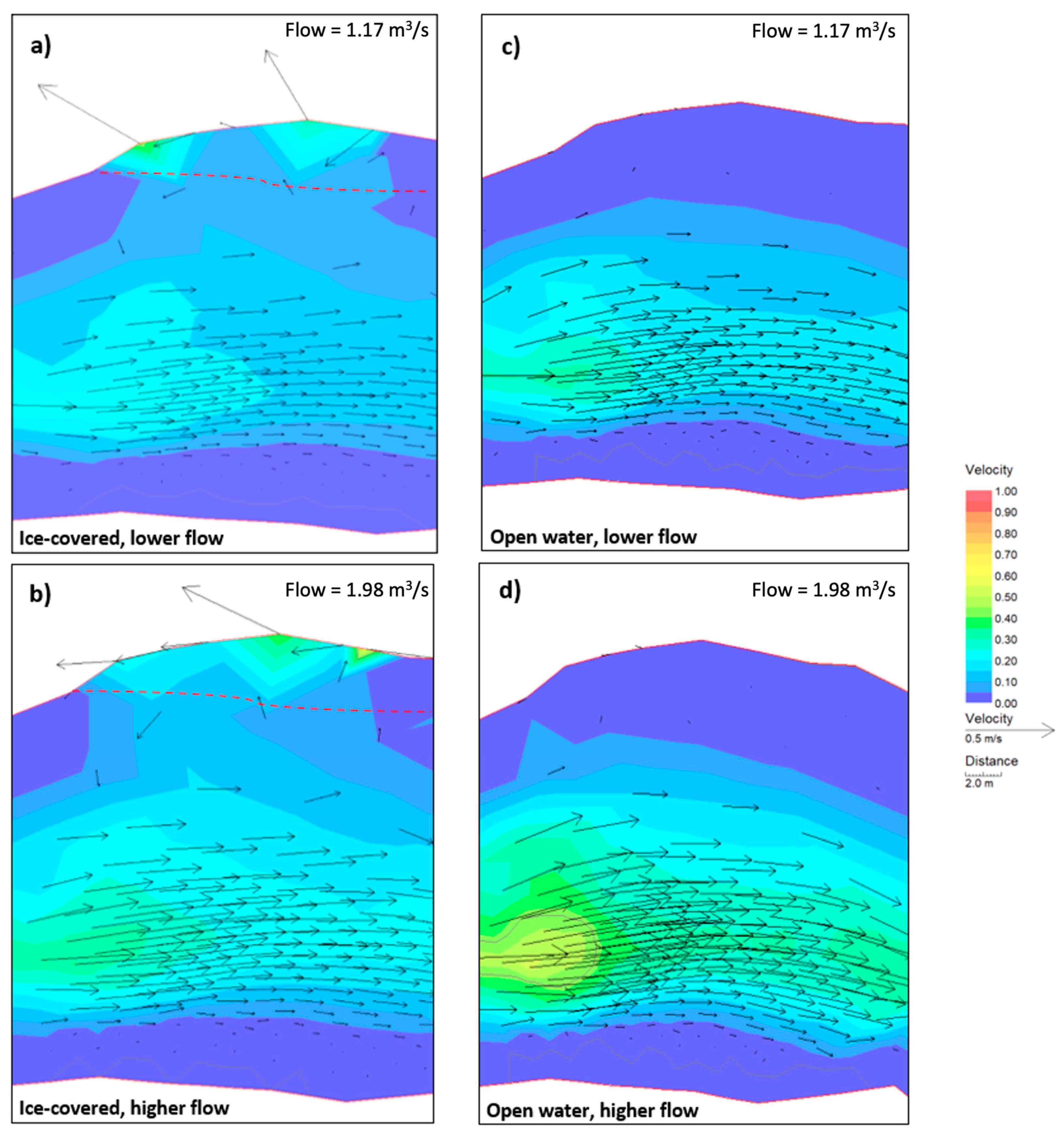
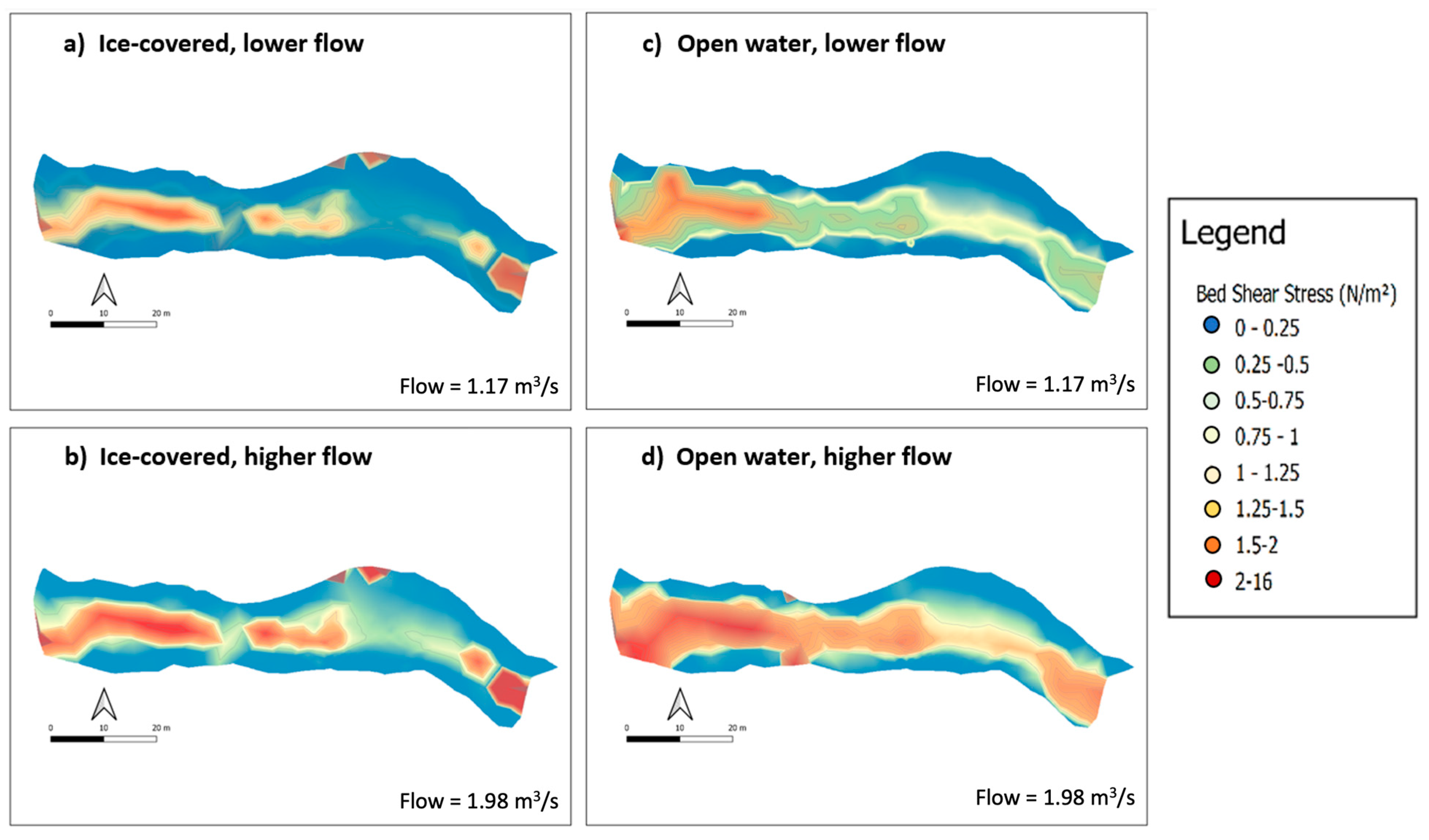
| Cross-Section | Width | Average Depth | d/D | Median Grain Size (D50) | Roughness Lengths | Notes |
|---|---|---|---|---|---|---|
| 1—Riffle | 12 m | 0.35 m | 0.85 | 412 mm | 2 mm | Large boulders near left bank |
| 2—Riffle | 10 m | 0.45 m | 3 | 150 mm | 2–2.5 mm | Embedded, poorly sorted fine material found between cobles |
| 3—Riffle | 10 m | 0.28 m | 0.95 | 295 mm | 2.4–2.8 mm | Large, flat boulder 3 m from the right bank, ~25% embedded |
| 4—Pool | 18 m | 0.48 m | 10 | 48 mm | 0.5–0.7 mm | Fine material (sand sized and fine) along the left bank, embedded gravel, cobbles, and boulders toward the right bank |
| 5—Pool | 14 m | 0.52 m | 100 | 5.2 mm | 0.5 mm | Dominated by fine-grained bed material (sand-sized and smaller) |
| 6—Pool | 10 m | 0.6 m | 125 | 4.8 mm | 0.4 mm | Dominated by fine-grained bed material (sand-sized and smaller) |
| 7—Riffle | 9 m | 0.5 m | 1.14 | 439 mm | 2.5–2.7 mm | Cobbles and boulders with embedded pebbles and coarse sand |
| Lower Flow | Higher Flow | |
|---|---|---|
| Pool (d/D > 10) | 0.26 | 0.041 |
| Riffle (d/D < 10) | <0.0001 | 0.053 |
| Cross-Section | Ice-Covered Conditions, Feb 23 Field Data (Lower Flow) | Open-Water Conditions, Mar 2 Field Data (Higher Flow) | ||||
|---|---|---|---|---|---|---|
| Water Depth (m) | Depth-Averaged Velocity (m/s) | Shear Stress (N/m2) | Water Depth (m) | Depth-Averaged Velocity (m/s2) | Shear Stress (N/m2) | |
| 1 | 0.038 (0.12) | 0.018 | 0.22 | 0.035 | 0.018 | 0.25 |
| (0.19) | (0.36) | (0.15) | (0.13) | (0.17) | ||
| 2 | 0.162 | 0.065 | 0.25 | 0.098 | 0.033 | 0.13 |
| (0.22) | (0.18) | (0.27) | (0.11) | (0.16) | (0.20) | |
| 3 | 0.177 | 0.079 | 0.39 | 0.063 | 0.14 | 0.36 |
| (0.24) | (0.21) | (0.19) | (0.18) | (0.15) | (0.39) | |
| 4 | 0.043 | 0.036 | 0.11 | 0.031 | 0.026 | 0.073 |
| (0.17) | (0.13) | (0.23) | (0.12) | (0.09) | (0.16) | |
| 5 | 0.134 | 0.058 | 0.15 | 0.012 | 0.011 | 0.11 |
| (0.23) | (0.16) | (0.18) | (0.08) | (0.10) | (0.13) | |
| 6 | 0.157 | 0.077 | 0.098 | 0.014 | 0.052 | 0.093 |
| (0.28) | (0.21) | (0.21) | (0.15) | (0.14) | (0.18) | |
| 7 | 0.066 | 0.016 | 0.083 | 0.091 | 0.012 | 0.047 |
| (0.15) | (0.11) | (0.14) | (0.11) | (0.09) | (0.16) | |
| Reach Average | 0.11 | 0.050 | 0.19 | 0.047 | 0.041 | 0.152 |
| (0.20) | (0.17) | (0.23) | (0.129) | (0.123) | (0.199) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smith, K.; Cockburn, J.M.H.; Villard, P.V. Rivers under Ice: Evaluating Simulated Morphodynamics through a Riffle-Pool Sequence. Water 2023, 15, 1604. https://doi.org/10.3390/w15081604
Smith K, Cockburn JMH, Villard PV. Rivers under Ice: Evaluating Simulated Morphodynamics through a Riffle-Pool Sequence. Water. 2023; 15(8):1604. https://doi.org/10.3390/w15081604
Chicago/Turabian StyleSmith, Karine, Jaclyn M. H. Cockburn, and Paul V. Villard. 2023. "Rivers under Ice: Evaluating Simulated Morphodynamics through a Riffle-Pool Sequence" Water 15, no. 8: 1604. https://doi.org/10.3390/w15081604
APA StyleSmith, K., Cockburn, J. M. H., & Villard, P. V. (2023). Rivers under Ice: Evaluating Simulated Morphodynamics through a Riffle-Pool Sequence. Water, 15(8), 1604. https://doi.org/10.3390/w15081604






