A High-Robust Displacement Prediction Model for Super-High Arch Dams Integrating Wavelet De-Noising and Improved Random Forest
Abstract
:1. Introduction
2. Statistical Model Construction and Pre-Processing Technique for Dam Displacement Data
2.1. The Selection of the Influencing Factors of Dam Deformation
- Water pressure component
- Temperature and aging component
2.2. Wavelet De-Noising for Displacement Signal Processing
2.2.1. Wavelet Threshold De-Noising Principle
2.2.2. Selection of Wavelet Bases, Threshold, and Threshold Function
3. Random Forests for Monitoring Model Construction
3.1. Random Forests
3.2. The Construction Process of Random Forest
- Select samples randomly. Bootstrap is used for sampling with the replacement method, and a training set is constructed for each decision tree.
- Select features randomly to construct a decision tree. Each node of the decision tree is formed by selecting a part of the total features continuously.
- All decision trees are combined into a random forest. At the prediction stage, each decision tree votes with the weight Select the tree with the most votes to get the equal-weighted vote model of the basic learning model as follows:
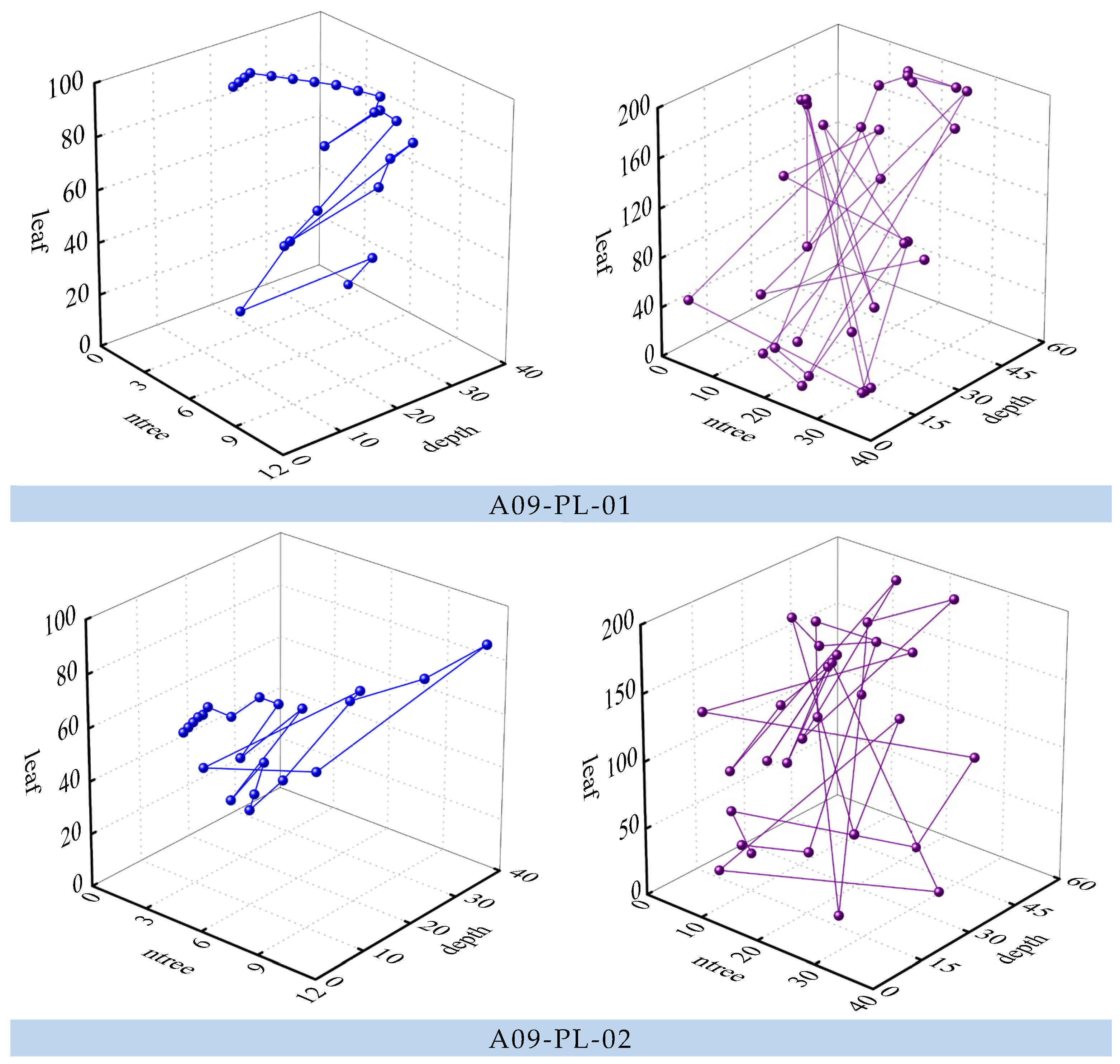
3.3. Relevant Parameters of the Random Forest Model
- Number of basic decision trees (ntree) is according to the training environment of the model.
- Maximum number of features (features) is the maximum number of the candidate features when building the basic decision tree model.
- Depth of the base decision tree (depth) controls the maximum value of the lower limit of subtree growth in a random forest model.
- Minimum sample number of leaf nodes (leaf) is used for pruning the subtree of the random forest model. This parameter determines whether to retain leaf nodes and sibling leaf nodes
- Evaluation criteria for node feature selection (criteria) include entropy, Gini coefficient, and so on.
4. Improved Salp Swarm Algorithm
4.1. Mathematical Model of the Salp Swarm
4.2. Performance-Improved Salp Swarm Algorithm
4.2.1. Elite Opposition-Based Learning Strategy
4.2.2. Differential Strategy
4.2.3. Gaussian Mutation Strategy
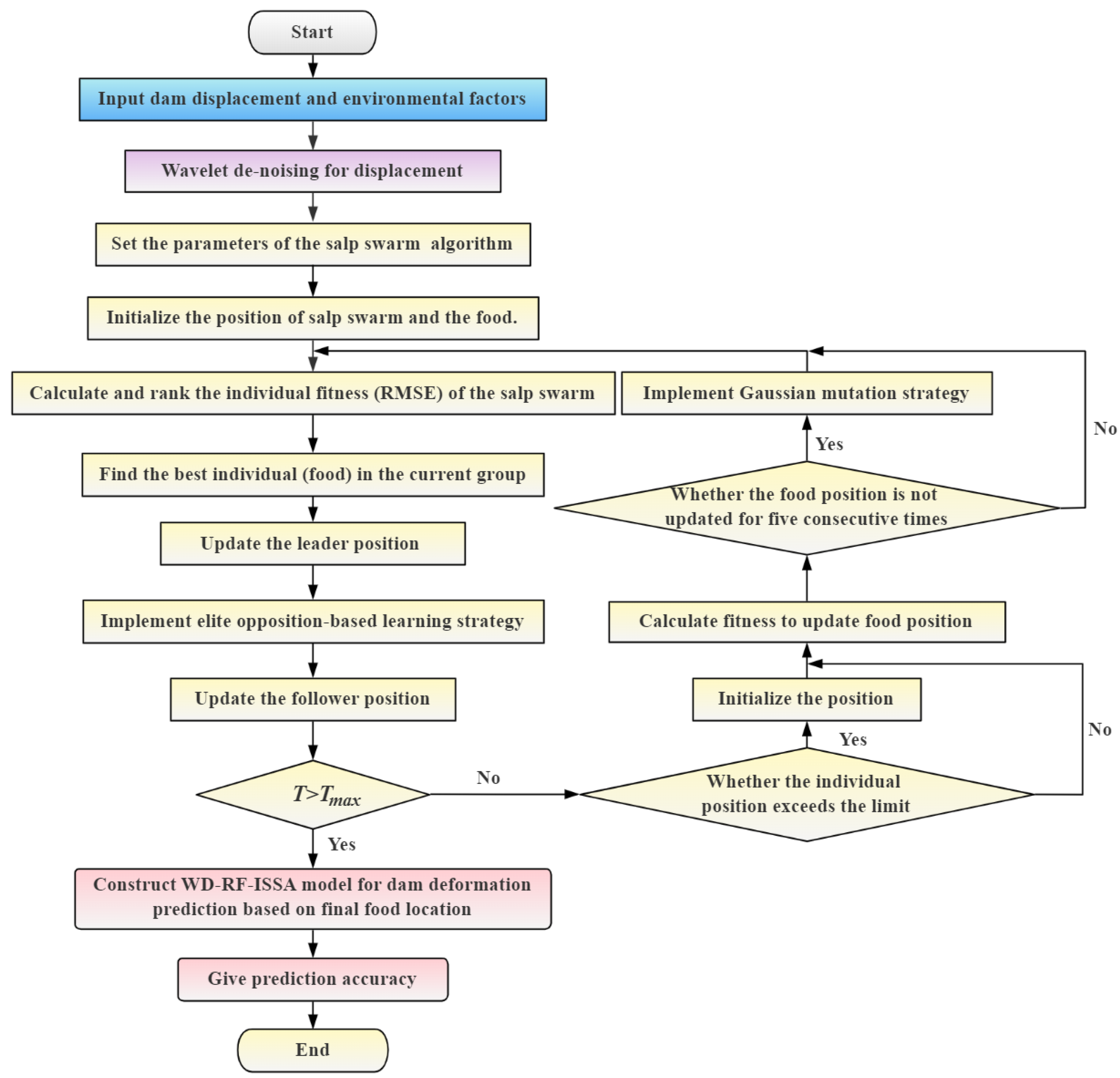
5. Construction Process of Prediction Model and Performance Evaluation Criterions
6. Engineering Example
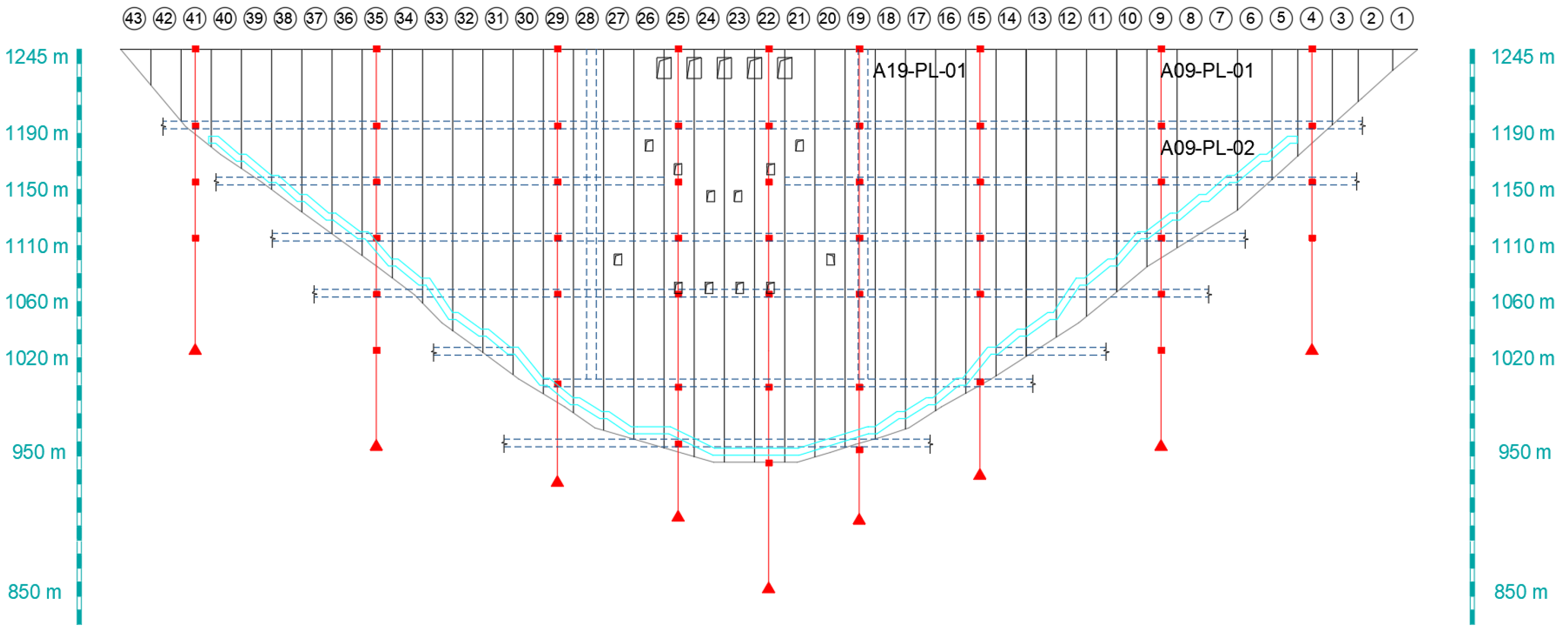
6.1. Project Background and Deformation Monitoring
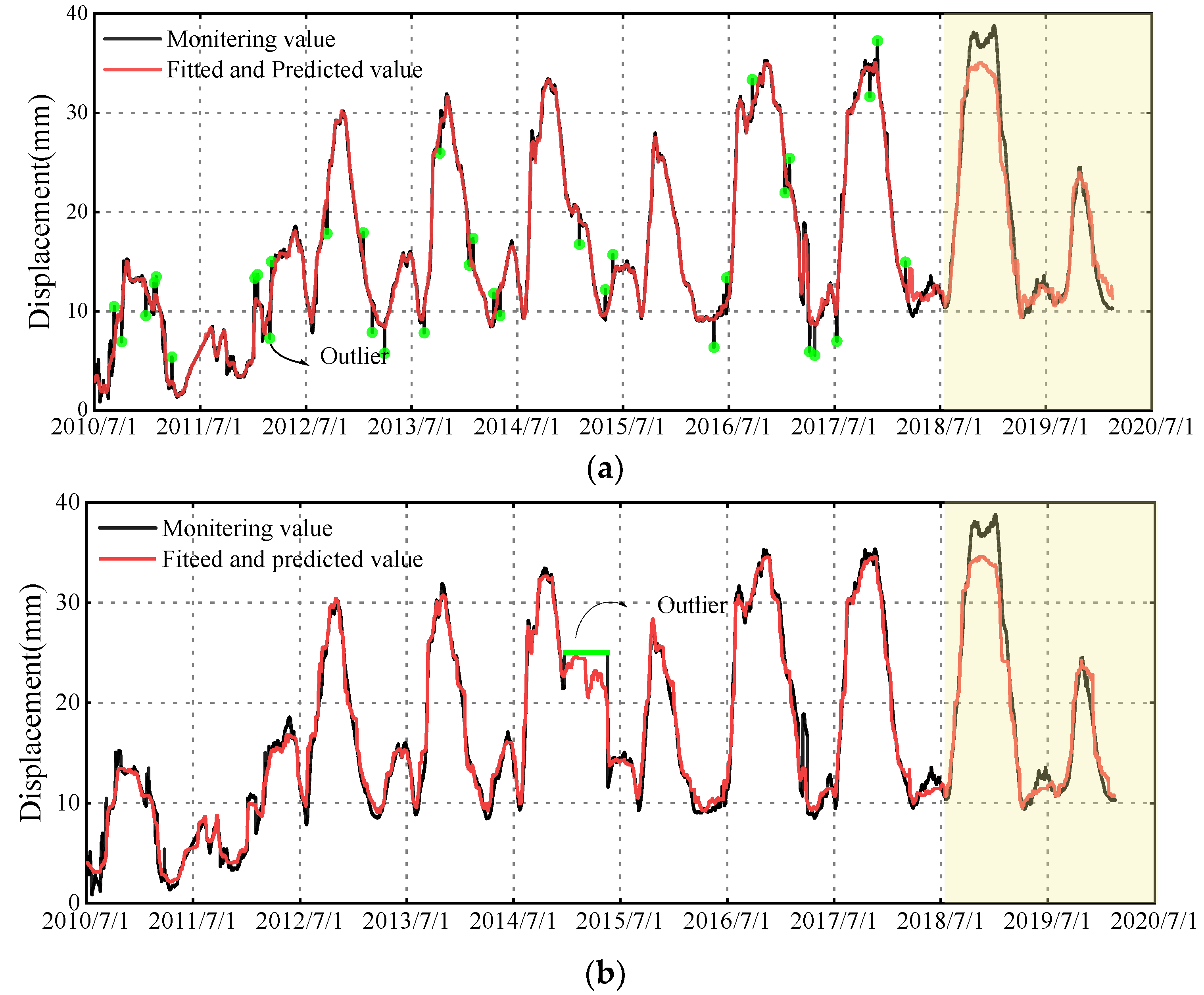
6.2. Performance Analysis of the Proposed Model Considering Wavelet De-Noising Technique and ISSA Algorithm
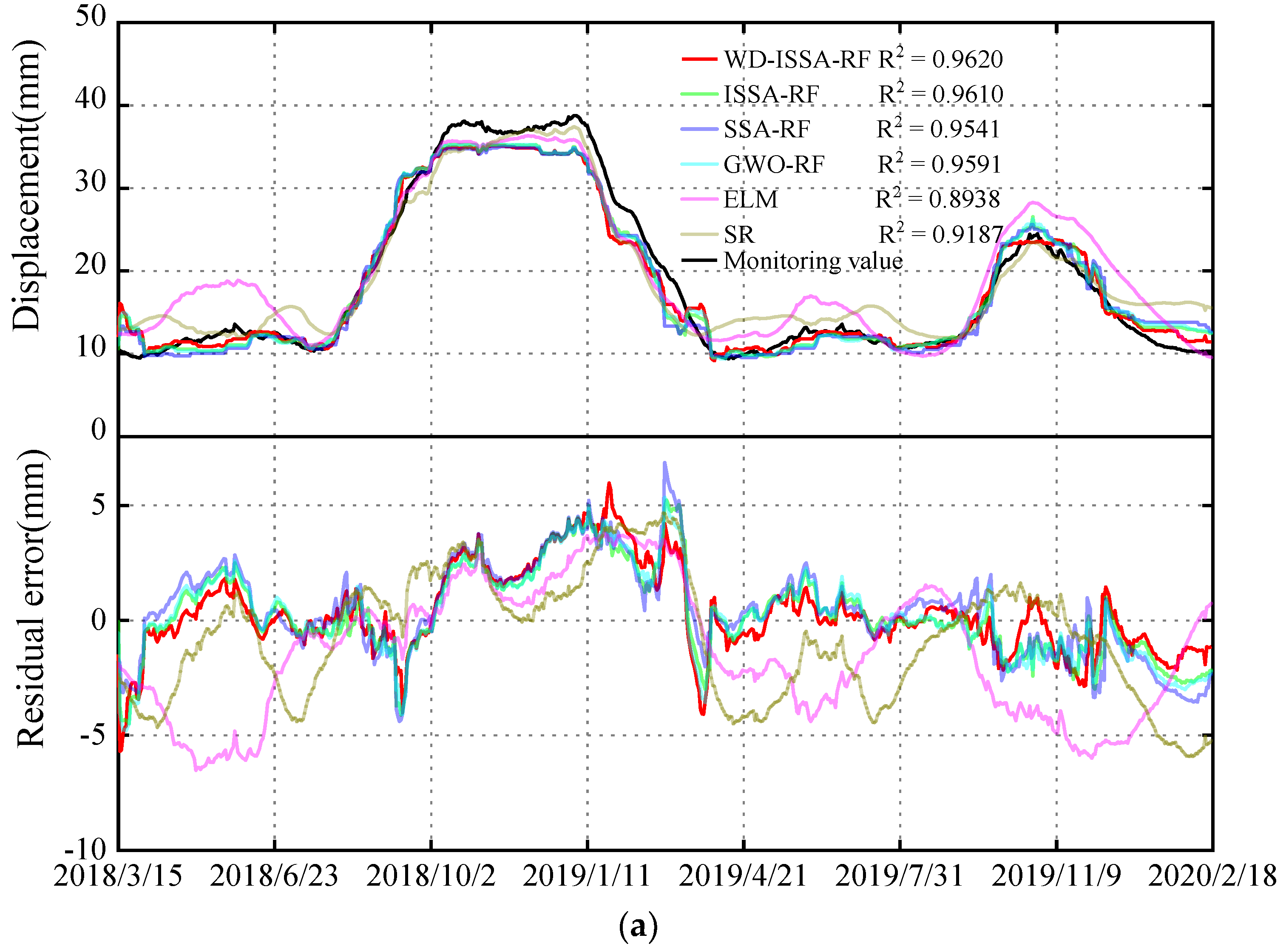
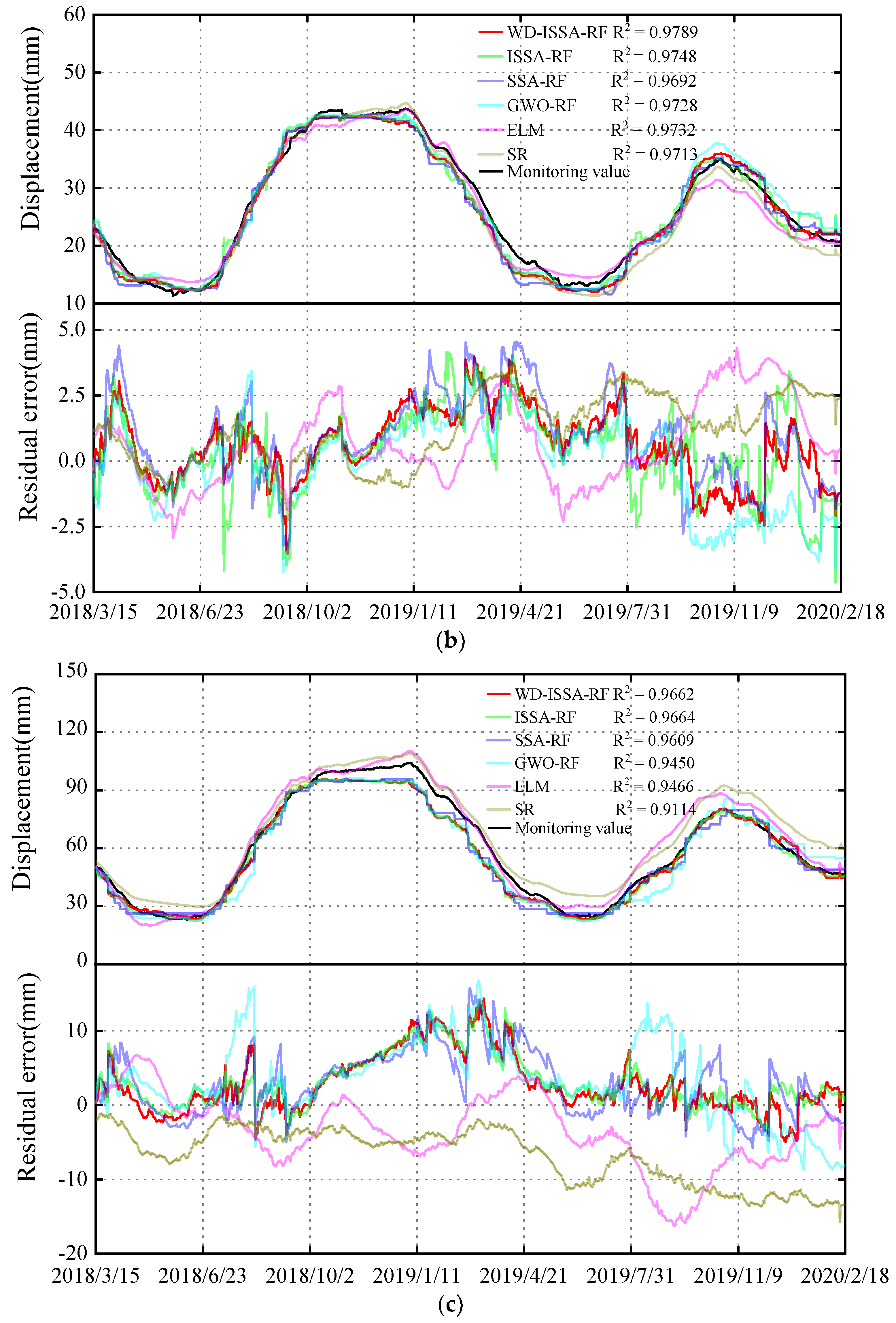
6.3. Accuracy Evaluation of the Prediction Models
- (1)
- Comparison of performance between the proposed model and the ISSA-RF model: The results presented in Figure 10 and Figure 11 and Table 1 indicate that for measuring point A09-PL-02, the WD-ISSA-RF model exhibits a higher multiple correlation coefficient (R2) of 97.89% as compared to 97.48% for the ISSA-RF model. Moreover, the WD-ISSA-RF model has smaller MAE, MSE, and MAPE values than the ISSA-RF model. Similar trends were observed for the other two measuring points. Therefore, it can be concluded that the WD-ISSA-RF model outperforms the ISSA-RF model in terms of modeling accuracy, and wavelet de-noising is an effective technique for enhancing prediction capability.
- (2)
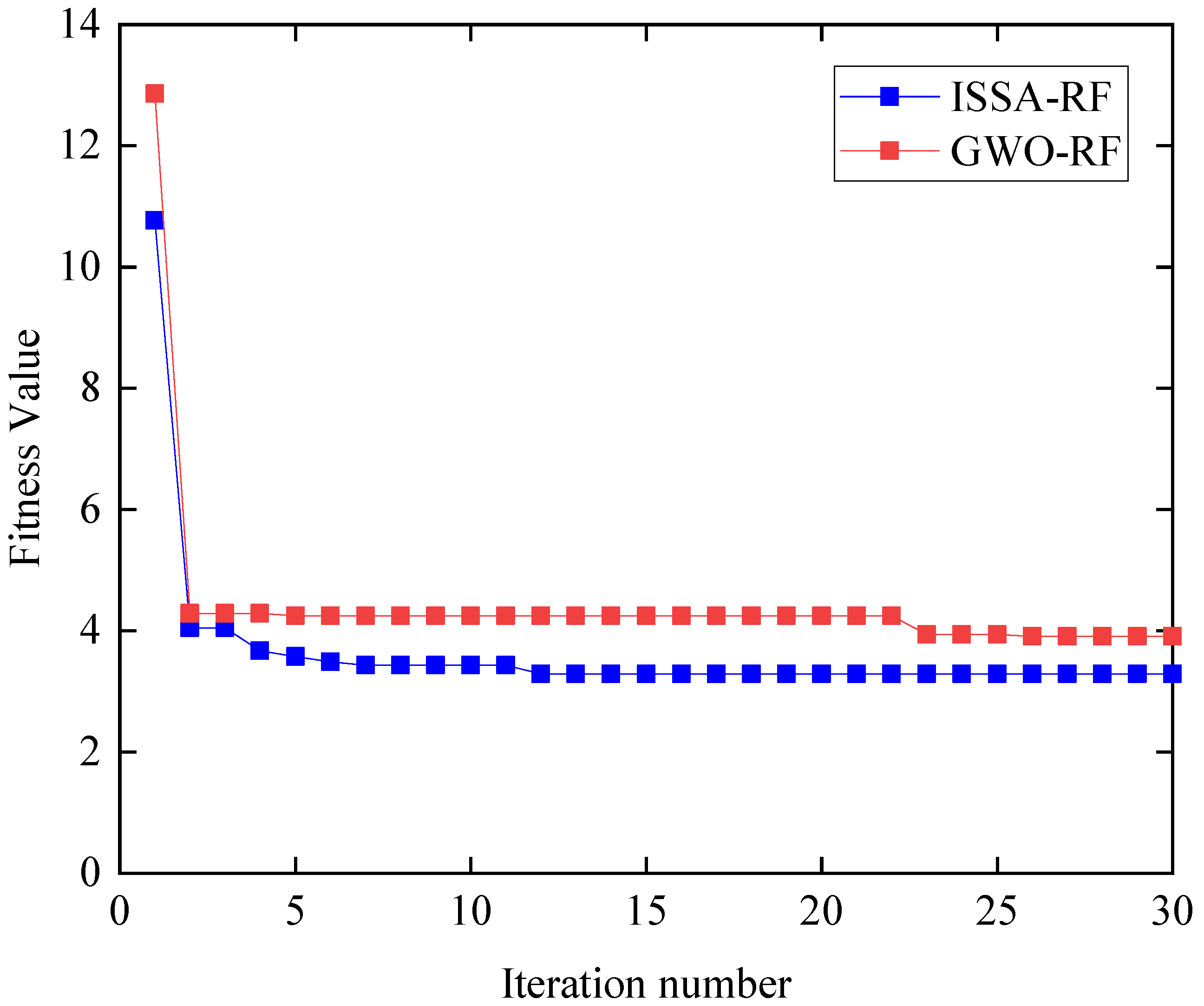
- Comparison of performance between the ISSA-RF model and the SSA-RF model: The ISSA-RF model employs the elite opposition-based learning strategy, difference strategy, and Gaussian mutation strategy to enhance the global search ability and avoid local optimization. From Figure 10, it can be observed that ISSA maintains a roughly similar convergence speed but exhibits a better global search ability as compared to SSA. The results presented in Figure 11 and Table 1 indicate that the ISSA-RF model has smaller MAE, MSE, and MAPE values than the SSA-RF model at all three measuring points. Hence, the ISSA-RF model demonstrates stronger predicting, learning, and generalization ability than the SSA-RF model. Although the ME of the ISSA-RF model on A09-PL-02 is slightly higher than that of the SSA-RF model, this does not affect the overall conclusion since the maximum error is an outlier value.
- (3)
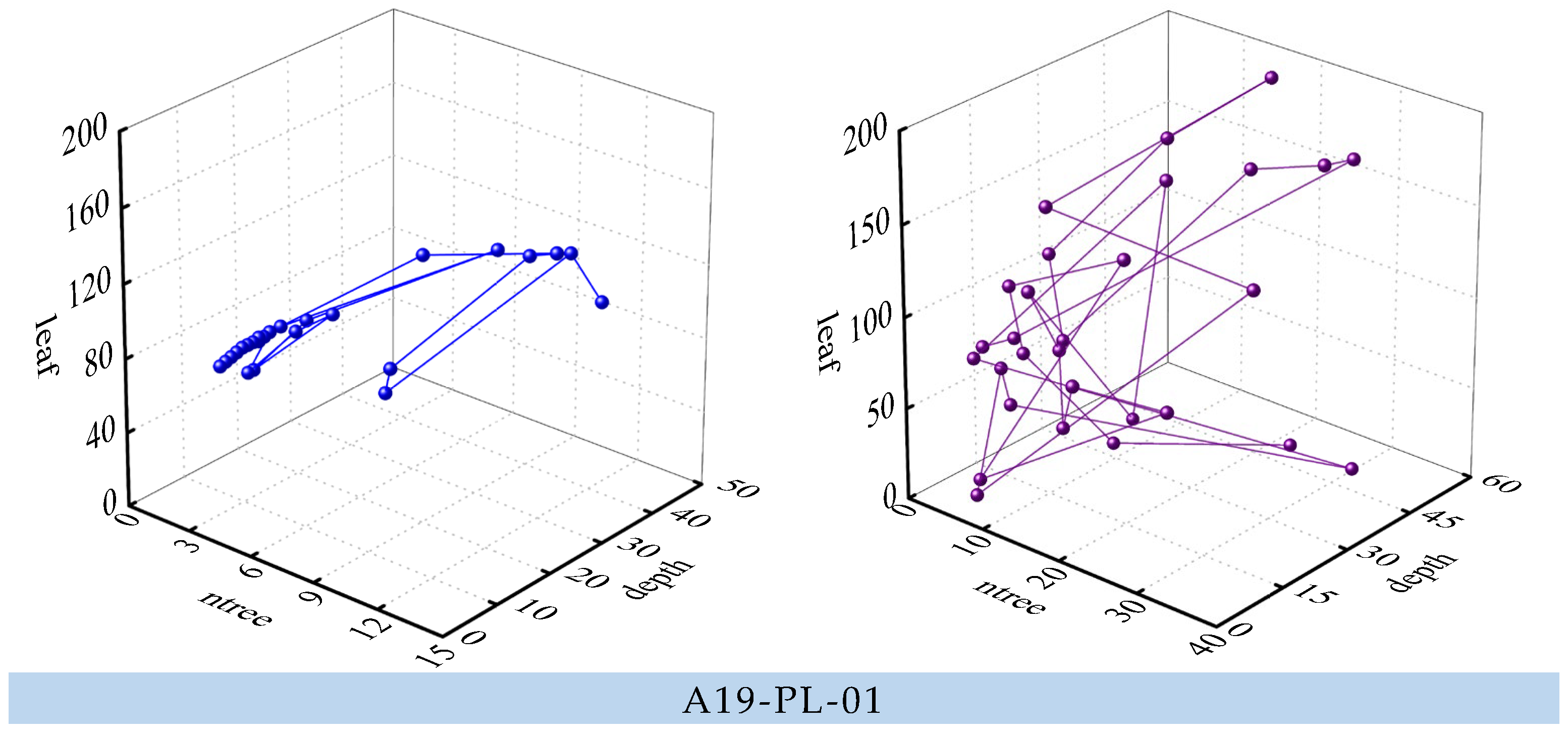
- Comparison of performance between the SSA-RF model and the GWO-RF model. As a swarm intelligence algorithm, GWO achieves global optimization according to behavior of gray wolves [41]. GWO divides the wolves into four groups, including , , and common gray wolf according to their social rank. Wolf , and are the leaders of the gray wolf group, with the highest adaptability. The common gray wolf obeys wolf , and , according to their location, and is constantly approaching the prey, which is the optimal solution. Figure 12 reveals the relationship curve (A19-PL-01) between the fitness value and the number of iterations of the SSA and GWO. Figure 12 reveals that the best fitness of SSA is better than that of GWO and the SSA algorithm has a faster convergence speed.
- (4)
- Comparison of performance between the RF model and the ELM model. The ELM model proposes a novel hidden layer forward-type network based on the theory of generalized inverse [42]. By changing the hidden layer nodes, the optimal fitness value is obtained. From Table 1 and Figure 11, the prediction accuracy of the ELM model at the three measuring points varies. Although the R2 of the ELM model on A9-PL-02 and A19-PL-01 is equal to or slightly better than that of the GWO-RF model, the R2 on A9-PL-01 is 0.893, far less than that of the GWO-RF model on A9-PL-01. This situation has also occurred in other monitoring indicators, indicating that the stability and generalization performance of the RF model surpasses the ELM model. Data samples may have the problem of multicollinearity, and this can lead to random fluctuations in the output of the ELM model. This problem is well overcome by the RF model.
- (5)
- Comparison of performance between the RF model and SR model. The SR model adaptively screens variables with high importance on the basis of multiple regression, to establish a prediction model with selected variables [1]. From Table 1 and Figure 11, it is clear that each performance index of the ISSA-RF model is better than that of the SR model at the three different measuring points. Therefore, the ISSA-RF model is more accurate in prediction than the SR model, and has stronger learning and generalization ability.
6.4. Robustness Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| WD | Wavelet De-noising |
| RF | Random Forests |
| SSA | Salp Swarm Algorithm |
| ISSA | Improved Salp Swarm Algorithm |
| ANN | Artificial Neural Networks |
| LSTM | Long Short-Term Memory Model |
| SVM | Support Vector Machine |
| PSO | Particle Swarm Optimization |
| GSA | Gravity Search Algorithm |
| GWO | Gray Wolf Optimization |
| R2 | Multiple Correlation Coefficient |
| ME | Maximum Error |
| RMSE | Root Mean Squared Error |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| ELM | Extreme Learning Machine |
| SR | Stepwise Regression Model |
References
- Wu, Z.R.; Su, H.Z.; Guo, H.Q. Risk assessment method of major unsafe hydroelectric project. Sci. Chin. Ser. E Technol. Sci. 2008, 51, 1345–1352. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Xuan, G.; Wang, X.; Li, J. Overtopping breaching of cohesive homogeneous earth dam with different cohesive strength. Sci. Chin. Ser. E Technol. Sci. 2009, 52, 3024–3029. [Google Scholar] [CrossRef]
- Longwell, C.R. Lessons from the St. Francis Dam. Science 1928, 68, 36–37. [Google Scholar] [CrossRef]
- Liu, W.M.; Carling, P.A.; Hu, K.H.; Wang, H.; Zhou, Z.; Zhou, L.Q.; Liu, D.Z.; Lai, Z.P.; Zhang, X.B. Outburst floods in China: A review. Earth-Sci. Rev. 2019, 197, 14. [Google Scholar] [CrossRef]
- Hervouet, J.M.; Petitjean, A. Malpasset dam-break revisited with two-dimensional computations. J. Hydraul. Res. 1999, 37, 777–788. [Google Scholar] [CrossRef]
- Zhong, D.H.; Sun, Y.F.; Li, M.C. Dam break threshold value and risk probability assessment for an earth dam. Nat. Hazards 2011, 59, 129–147. [Google Scholar] [CrossRef]
- Su, H.Z.; Li, X.; Yang, B.B.; Wen, Z.P. Wavelet support vector machine-based prediction model of dam deformation. Mech. Syst. Signal Proc. 2018, 110, 412–427. [Google Scholar] [CrossRef]
- Ribas, J.R.; Severo, J.C.R.; Guimaraes, L.F.; Perpetuo, K.P.C. A fuzzy FMEA assessment of hydroelectric earth dam failure modes: A case study in Central Brazil. Energy Rep. 2021, 7, 4412–4424. [Google Scholar] [CrossRef]
- Prakash, G.; Sadhu, A.; Narasimhan, S.; Brehe, J.M. Initial service life data towards structural health monitoring of a concrete arch dam. Struct. Control Health Monit. 2018, 25, e2036. [Google Scholar] [CrossRef]
- Wei, B.W.; Yuan, D.Y.; Xu, Z.K.; Li, L.H. Modified hybrid forecast model considering chaotic residual errors for dam deformation. Struct. Control Health Monit. 2018, 25, 16. [Google Scholar] [CrossRef]
- Mostafapour, A.; Davoodi, S. Acoustic emission source locating in two-layer plate using wavelet packet decomposition and wavelet-based optimized residual complexity. Struct. Control Health Monit. 2018, 25, 12. [Google Scholar] [CrossRef]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet filter-based weak signature detection method and its application on rolling element bearing prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Sendur, L.; Selesnick, I.W. Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency. IEEE Trans. Signal Process. 2002, 50, 2744–2756. [Google Scholar] [CrossRef] [Green Version]
- Gao, H.Y. Wavelet shrinkage denoising using the non-negative garrote. J. Comput. Graph. Stat. 1998, 7, 469–488. [Google Scholar]
- Zaminpardaz, S.; Teunissen, P.J.G.; Tiberius, C. A risk evaluation method for deformation monitoring systems. J. Geod. 2020, 94, 15. [Google Scholar] [CrossRef] [Green Version]
- Ma, C.H.; Yang, J.; Cheng, L.; Ran, L. Research on slope reliability analysis using multi-kernel relevance vector machine and advanced first-order second-moment method. Eng. Comput. 2022, 38, 3057–3068. [Google Scholar] [CrossRef]
- Li, Y.; Chen, W. Landslide Susceptibility Evaluation Using Hybrid Integration of Evidential Belief Function and Machine Learning Techniques. Water 2020, 12, 113. [Google Scholar] [CrossRef] [Green Version]
- Bui, D.T.; Khosravi, K.; Li, S.J.; Shahabi, H.; Panahi, M.; Singh, V.P.; Chapi, K.; Shirzadi, A.; Panahi, S.; Chen, W.; et al. New Hybrids of ANFIS with Several Optimization Algorithms for Flood Susceptibility Modeling. Water 2018, 10, 1210. [Google Scholar] [CrossRef] [Green Version]
- Hu, Y.T.; Gu, C.S.; Meng, Z.Z.; Shao, C.F.; Min, Z.Z. Prediction for the Settlement of Concrete Face Rockfill Dams Using Optimized LSTM Model via Correlated Monitoring Data. Water 2022, 14, 2157. [Google Scholar] [CrossRef]
- Chen, Y.J.; Gu, C.S.; Shao, C.F.; Gu, H.; Zheng, D.J.; Wu, Z.R.; Fu, X. An Approach Using Adaptive Weighted Least Squares Support Vector Machines Coupled with Modified Ant Lion Optimizer for Dam Deformation Prediction. Math. Probl. Eng. 2020, 2020, 23. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Niazmardi, S. A Novel Multiple-Kernel Support Vector Regression Algorithm for Estimation of Water Quality Parameters. Nat. Resour. Res. 2021, 30, 3761–3775. [Google Scholar] [CrossRef]
- Kang, F.; Liu, X.; Li, J.J. Temperature effect modeling in structural health monitoring of concrete dams using kernel extreme learning machines. Struct. Health Monit. 2020, 19, 987–1002. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Liu, Y.R.; Wang, L.; Li, M. Kalman filter-random forest-based method of dynamic load identification for structures with interval uncertainties. Struct. Control Health Monit. 2022, 29, 25. [Google Scholar] [CrossRef]
- Chen, X.; Ishwaran, H. Random forests for genomic data analysis. Genomics 2012, 99, 323–329. [Google Scholar] [CrossRef] [Green Version]
- Tesfamariam, S.; Liu, Z. Earthquake induced damage classification for reinforced concrete buildings. Struct. Saf. 2010, 32, 154–164. [Google Scholar] [CrossRef]
- Dai, B.; Gu, C.S.; Zhao, E.F.; Qin, X.N. Statistical model optimized random forest regression model for concrete dam deformation monitoring. Struct. Control Health Monit. 2018, 25, 15. [Google Scholar] [CrossRef]
- Li, X.; Wen, Z.P.; Su, H.Z. An approach using random forest intelligent algorithm to construct a monitoring model for dam safety. Eng. Comput. 2021, 37, 39–56. [Google Scholar] [CrossRef]
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev.-Data Min. Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef] [Green Version]
- Wei, B.W.; Liu, B.; Yuan, D.Y.; Mao, Y.; Yao, S.Y. Spatiotemporal hybrid model for concrete arch dam deformation monitoring considering chaotic effect of residual series. Eng. Struct. 2021, 228, 111488. [Google Scholar] [CrossRef]
- Khatibinia, M.; Khosravi, S. A hybrid approach based on an improved gravitational search algorithm and orthogonal crossover for optimal shape design of concrete gravity dams. Appl. Soft. Comput. 2014, 16, 223–233. [Google Scholar] [CrossRef]
- Li, M.J.; Pan, J.Y.; Liu, Y.L.; Wang, Y.Z.; Zhang, W.C.; Wang, J.X. Dam deformation forecasting using SVM-DEGWO algorithm based on phase space reconstruction. PLoS ONE 2022, 17, e0267434. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Faris, H.; Mafarja, M.M.; Heidari, A.A.; Aljarah, I.; Al-Zoubi, A.M.; Mirjalili, S.; Fujita, H. An efficient binary Salp Swarm Algorithm with crossover scheme for feature selection problems. Knowl.-Based Syst. 2018, 154, 43–67. [Google Scholar] [CrossRef]
- Sayed, G.I.; Khoriba, G.; Haggag, M.H. A novel chaotic salp swarm algorithm for global optimization and feature selection. Appl. Intell. 2018, 48, 3462–3481. [Google Scholar] [CrossRef]
- Wang, S.; Ding, L.; Xie, C.; Guo, Z.; Hu, Y. A Hybrid Differential Evolution with Elite Opposition-Based Learning. J. Wuhan Univ. Nat. Sci. Ed. 2013, 59, 111–116. [Google Scholar]
- Li, C.S.; Zhang, N.; Lai, X.J.; Zhou, J.Z.; Xu, Y.H. Design of a fractional-order PID controller for a pumped storage unit using a gravitational search algorithm based on the Cauchy and Gaussian mutation. Inf. Sci. 2017, 396, 162–181. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Y.; Ji, Z. Permanent Magnet Synchronous Motor Multi-parameter Identification Based on Improved Salp Swarm Algorithm. J. Syst. Simul. 2018, 30, 4284. [Google Scholar]
- Gu, Y.; Zheng, D.; Guo, H.; He, X. Regression analysis of 3D initial geostress field for dam site of Xiaowan Hydropower Station. Rock Soil Mech. 2008, 29, 1015. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Huang, G.B.; Zhou, H.M.; Ding, X.J.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. B-Cybern. 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed] [Green Version]







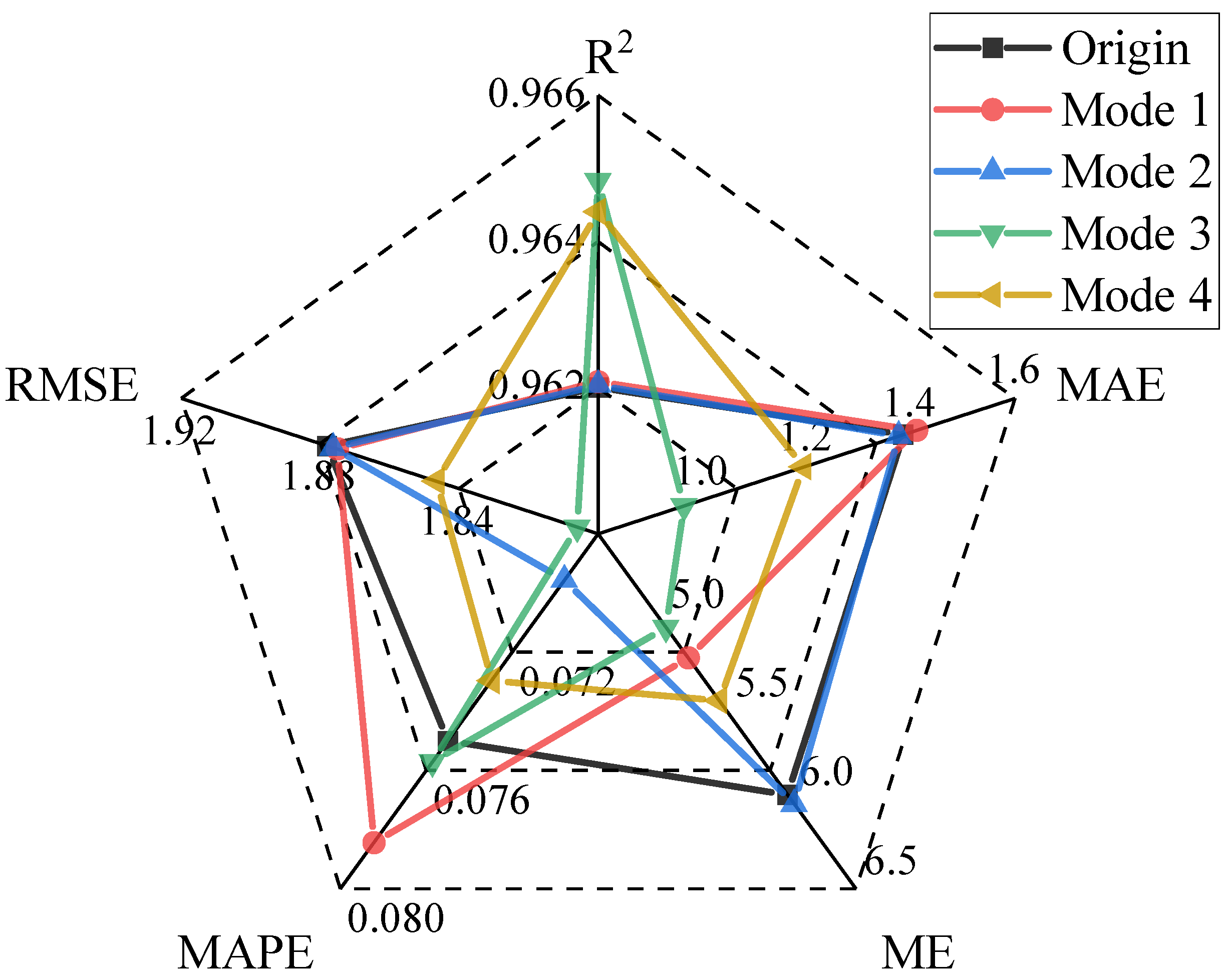
| Statistical Indicators | WD-ISSA-RF | ISSA-RF | SSA-RF | GWO-RF | ELM | SR | |
|---|---|---|---|---|---|---|---|
| A09-PL-01 | R2 | 0.962 | 0.961 | 0.954 | 0.959 | 0.893 | 0.919 |
| MAE | 1.386 | 1.451 | 1.625 | 1.521 | 2.599 | 2.248 | |
| ME | 5.970 | 5.240 | 6.868 | 5.364 | 6.520 | 5.919 | |
| MAPE | 0.075 | 0.082 | 0.093 | 0.088 | 0.174 | 0.165 | |
| RMSE | 1.878 | 1.901 | 2.063 | 1.946 | 3.137 | 2.744 | |
| A09-PL-02 | R2 | 0.979 | 0.975 | 0.969 | 0.972 | 0.973 | 0.971 |
| MAE | 1.235 | 1.327 | 1.442 | 1.403 | 1.300 | 1.478 | |
| ME | 3.977 | 4.620 | 4.454 | 4.421 | 4.311 | 3.400 | |
| MAPE | 0.054 | 0.058 | 0.064 | 0.059 | 0.057 | 0.069 | |
| RMSE | 1.510 | 1.649 | 1.823 | 1.713 | 1.700 | 1.761 | |
| A19-PL-01 | R2 | 0.966 | 0.966 | 0.960 | 0.945 | 0.946 | 0.911 |
| MAE | 3.464 | 3.500 | 4.038 | 4.873 | 4.766 | 6.829 | |
| ME | 14.342 | 14.021 | 15.763 | 16.79 | 16.30 | 15.73 | |
| MAPE | 0.058 | 0.061 | 0.073 | 0.089 | 0.092 | 0.149 | |
| RMSE | 4.806 | 4.783 | 5.167 | 6.128 | 6.035 | 7.778 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, C.; Wu, B.; Chen, Y. A High-Robust Displacement Prediction Model for Super-High Arch Dams Integrating Wavelet De-Noising and Improved Random Forest. Water 2023, 15, 1271. https://doi.org/10.3390/w15071271
Gu C, Wu B, Chen Y. A High-Robust Displacement Prediction Model for Super-High Arch Dams Integrating Wavelet De-Noising and Improved Random Forest. Water. 2023; 15(7):1271. https://doi.org/10.3390/w15071271
Chicago/Turabian StyleGu, Chongshi, Binqing Wu, and Yijun Chen. 2023. "A High-Robust Displacement Prediction Model for Super-High Arch Dams Integrating Wavelet De-Noising and Improved Random Forest" Water 15, no. 7: 1271. https://doi.org/10.3390/w15071271
APA StyleGu, C., Wu, B., & Chen, Y. (2023). A High-Robust Displacement Prediction Model for Super-High Arch Dams Integrating Wavelet De-Noising and Improved Random Forest. Water, 15(7), 1271. https://doi.org/10.3390/w15071271







