The Influence of the Internal Properties of River Ice on Ground Penetrating Radar Propagation
Abstract
1. Introduction
2. Research Area and Methods
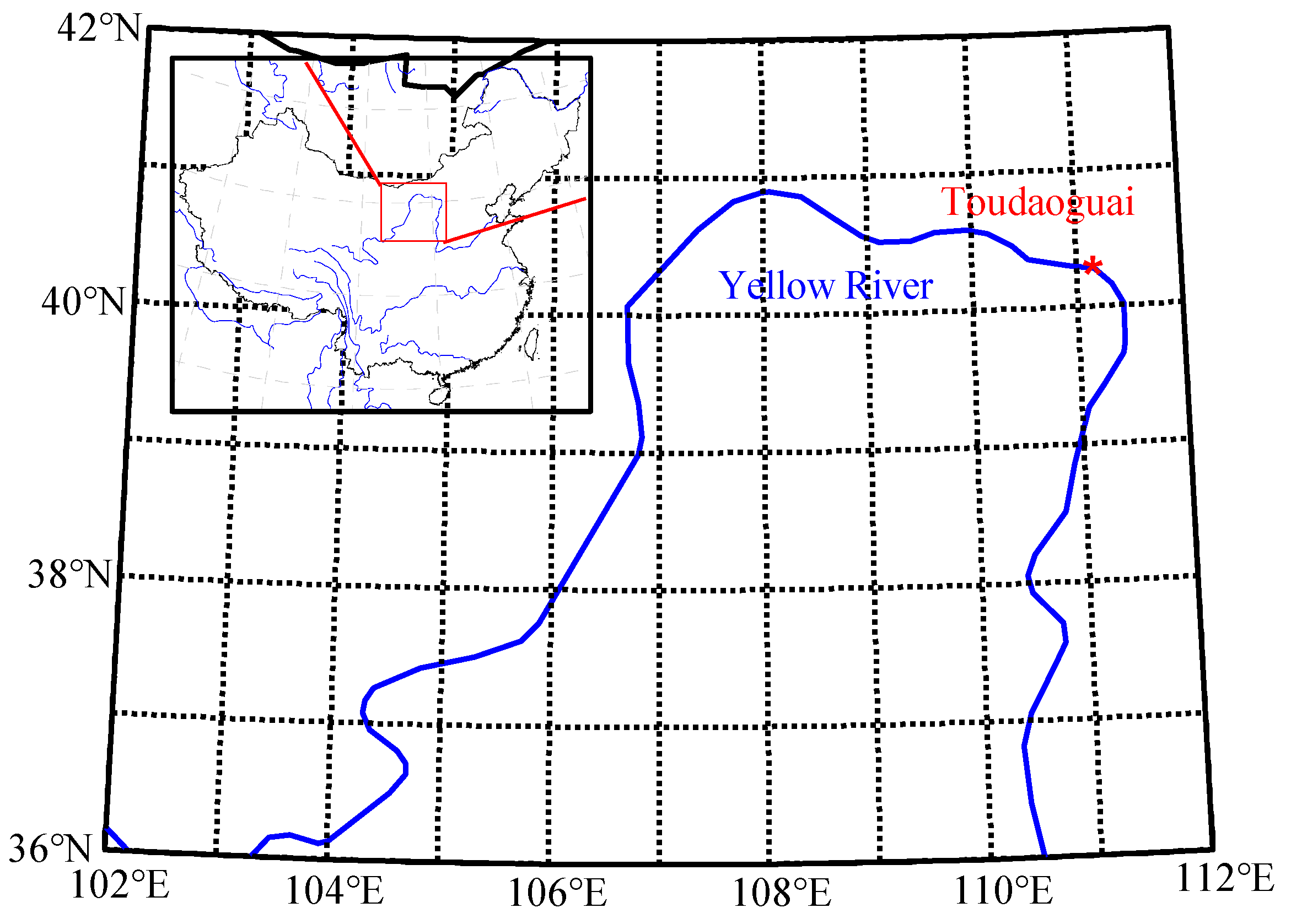
2.1. Overview of the Research Area
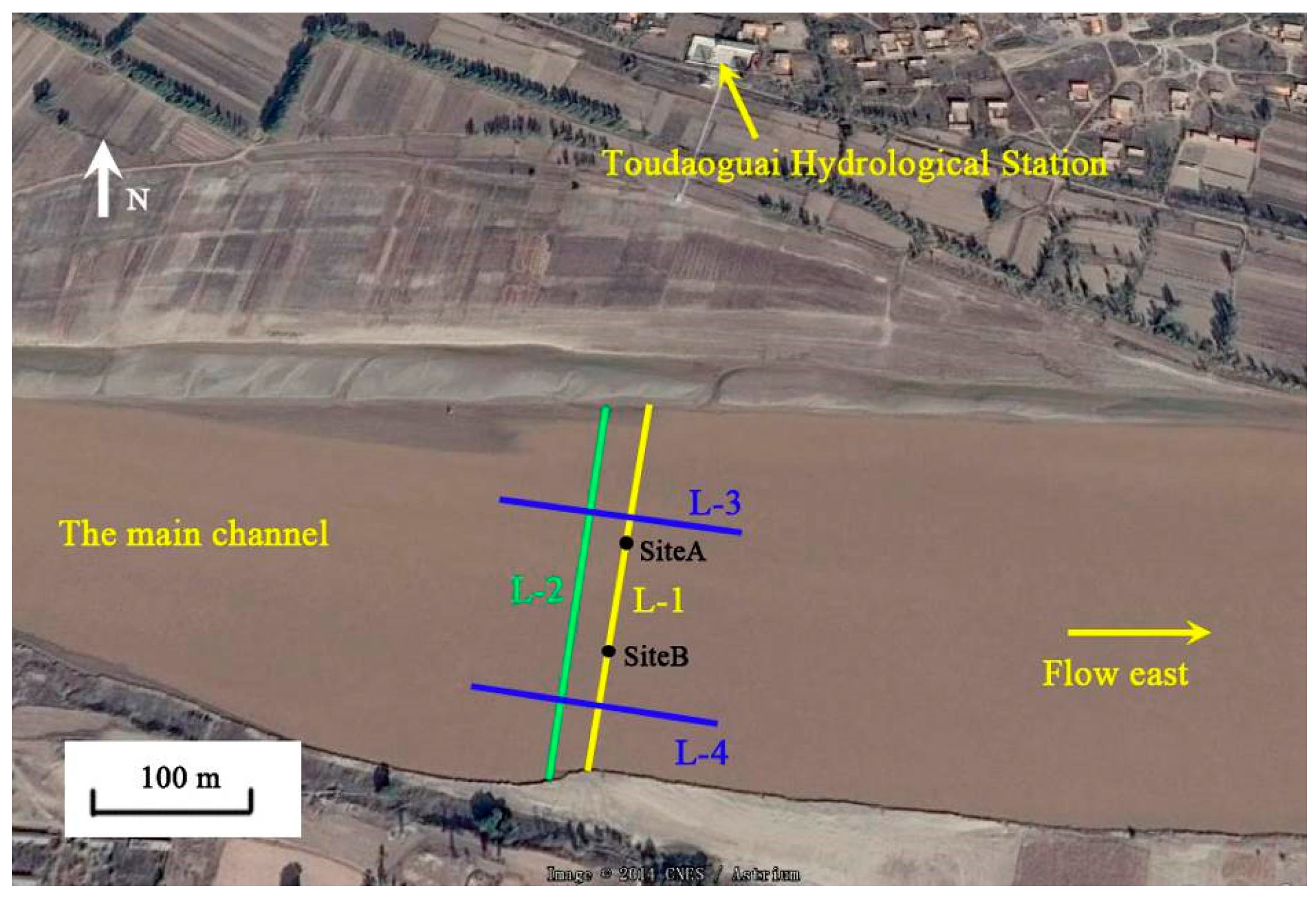
2.2. Research Method
3. Results
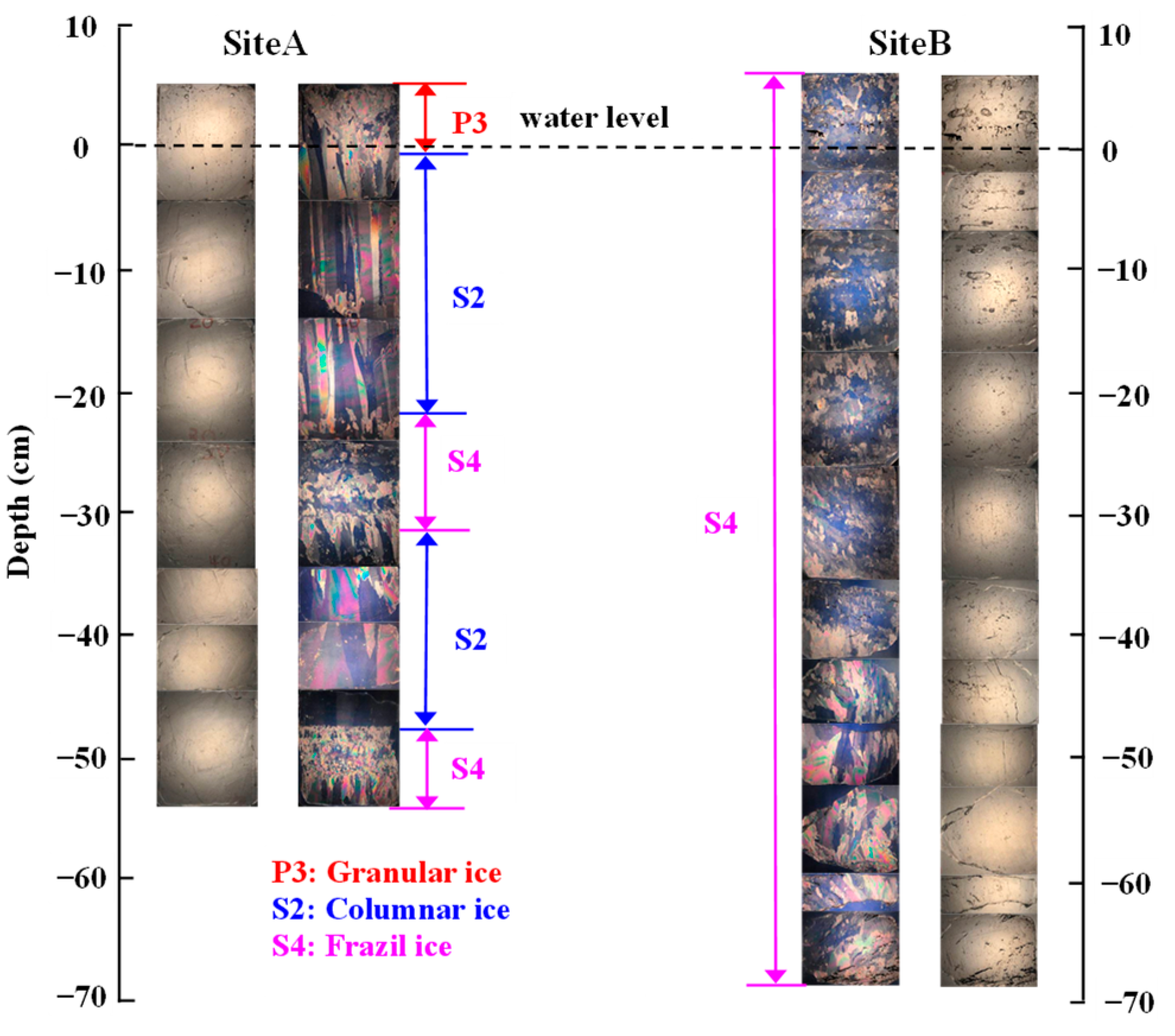
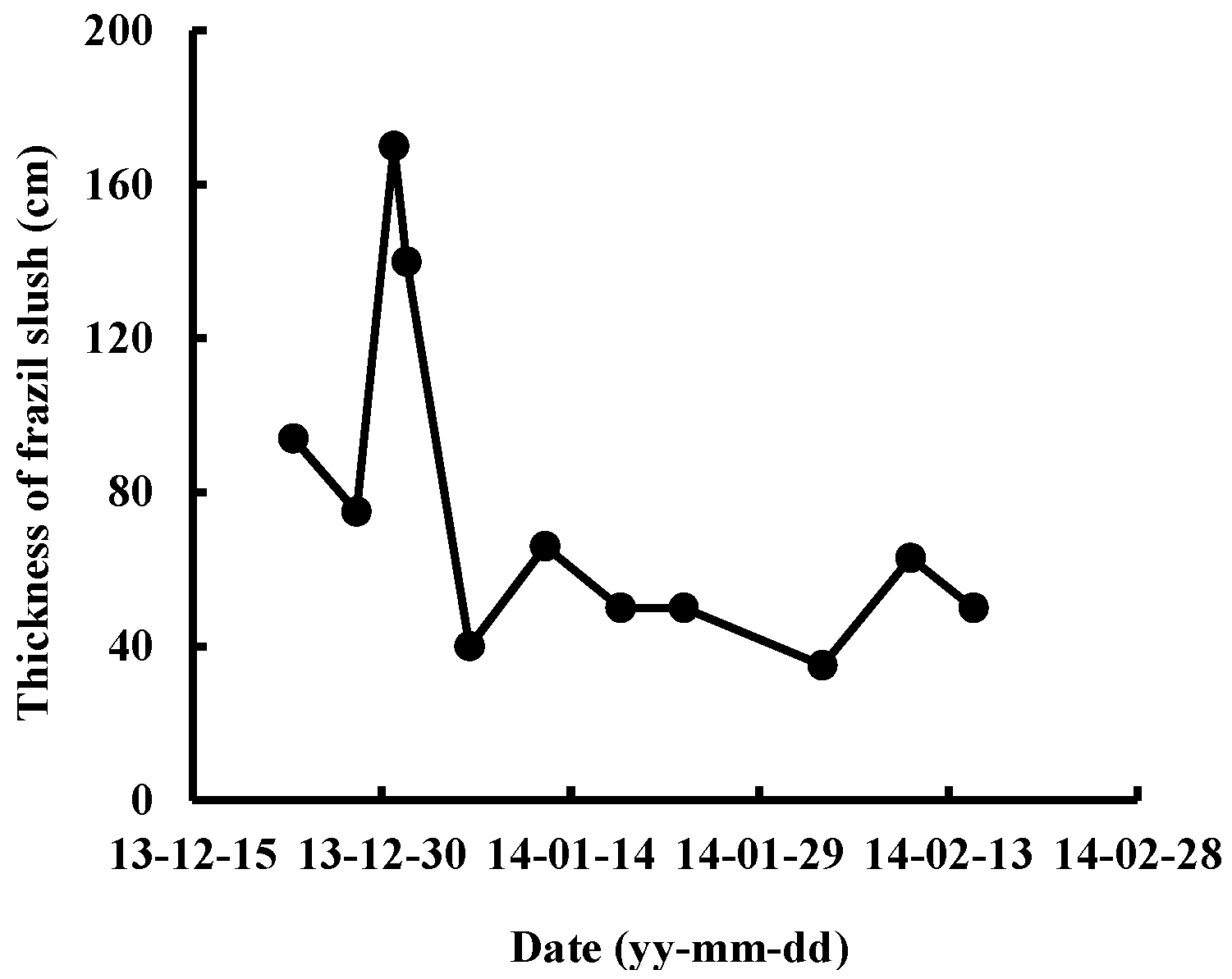
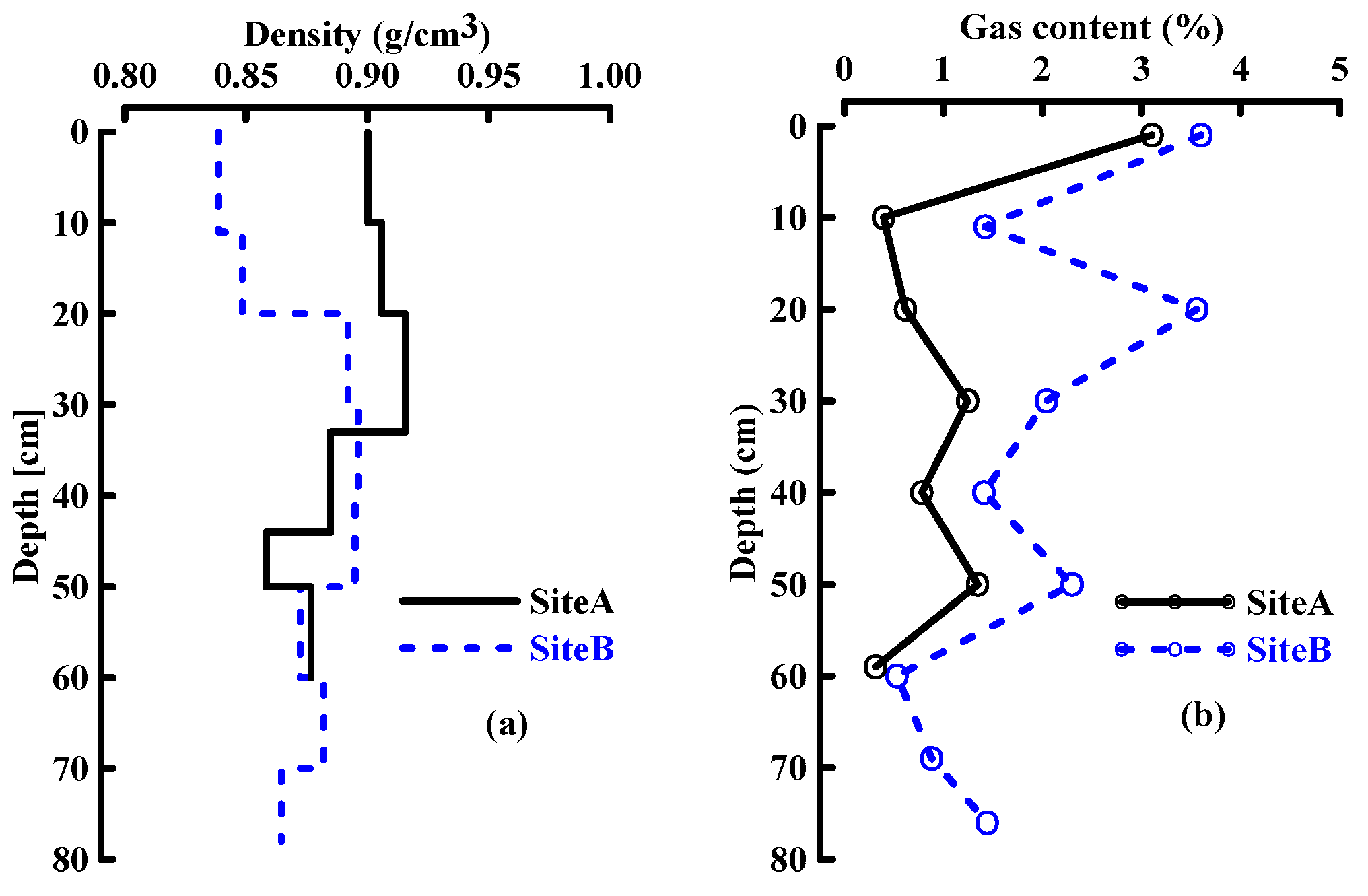
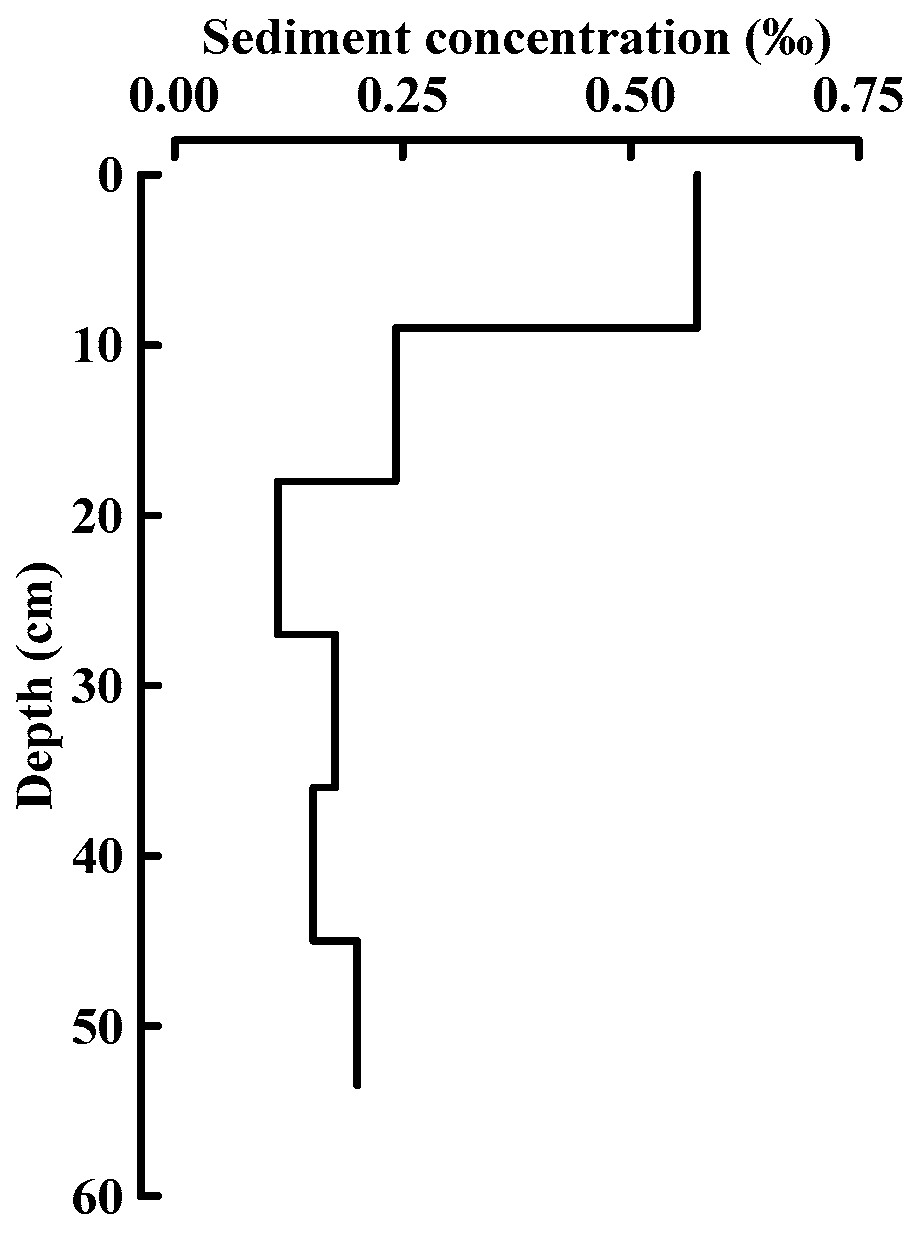
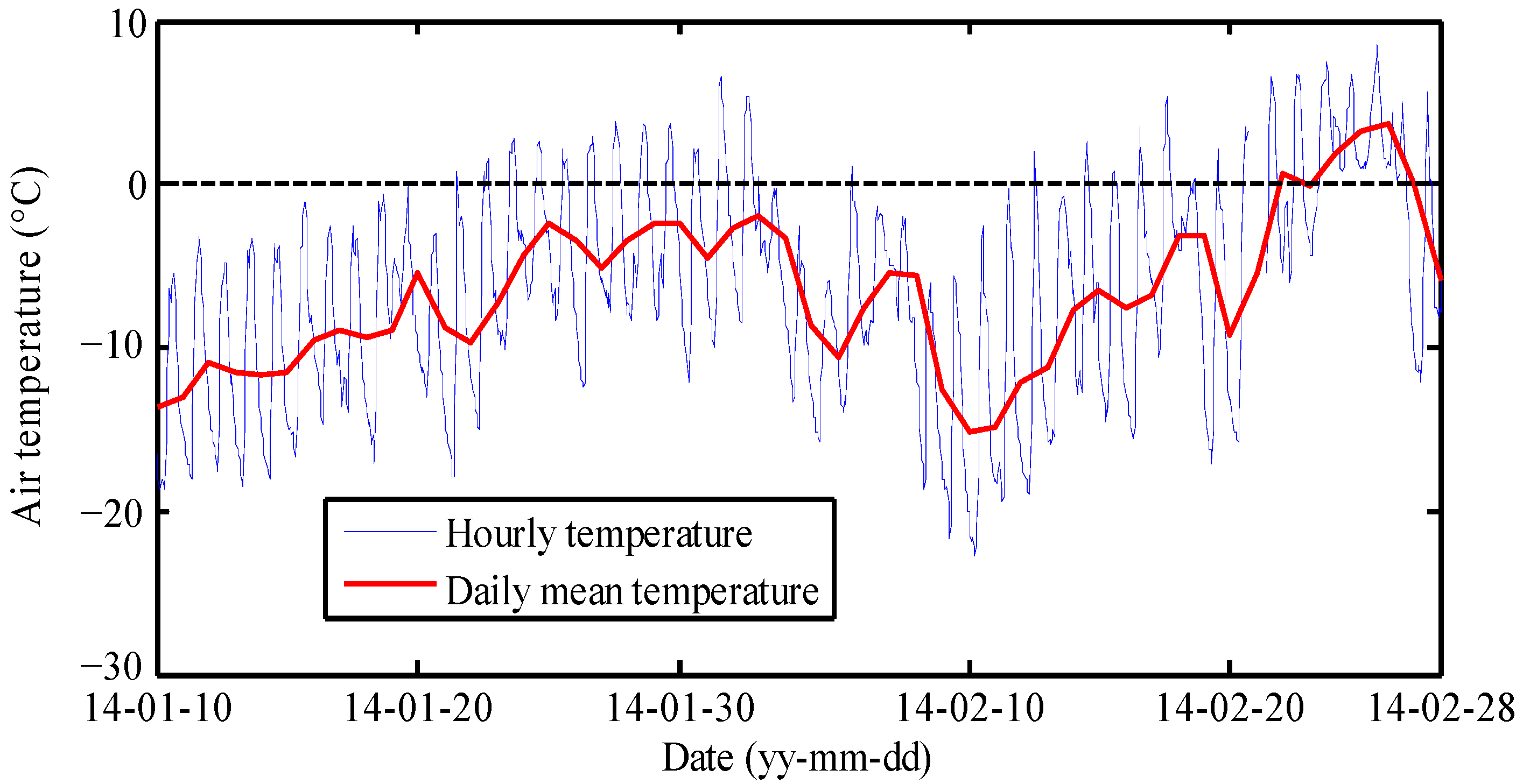
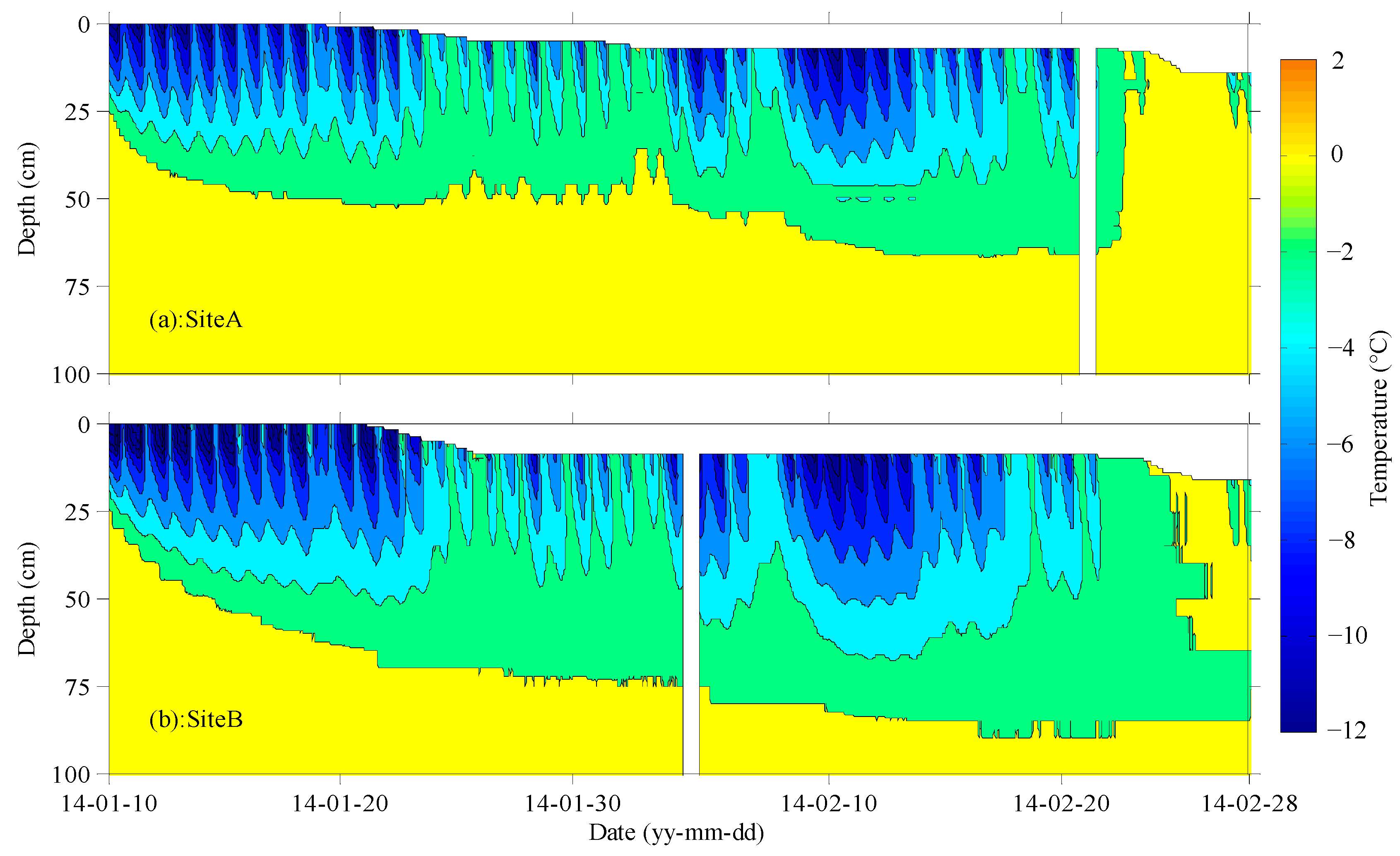
3.1. Ice Formation and Ice Physical Properties
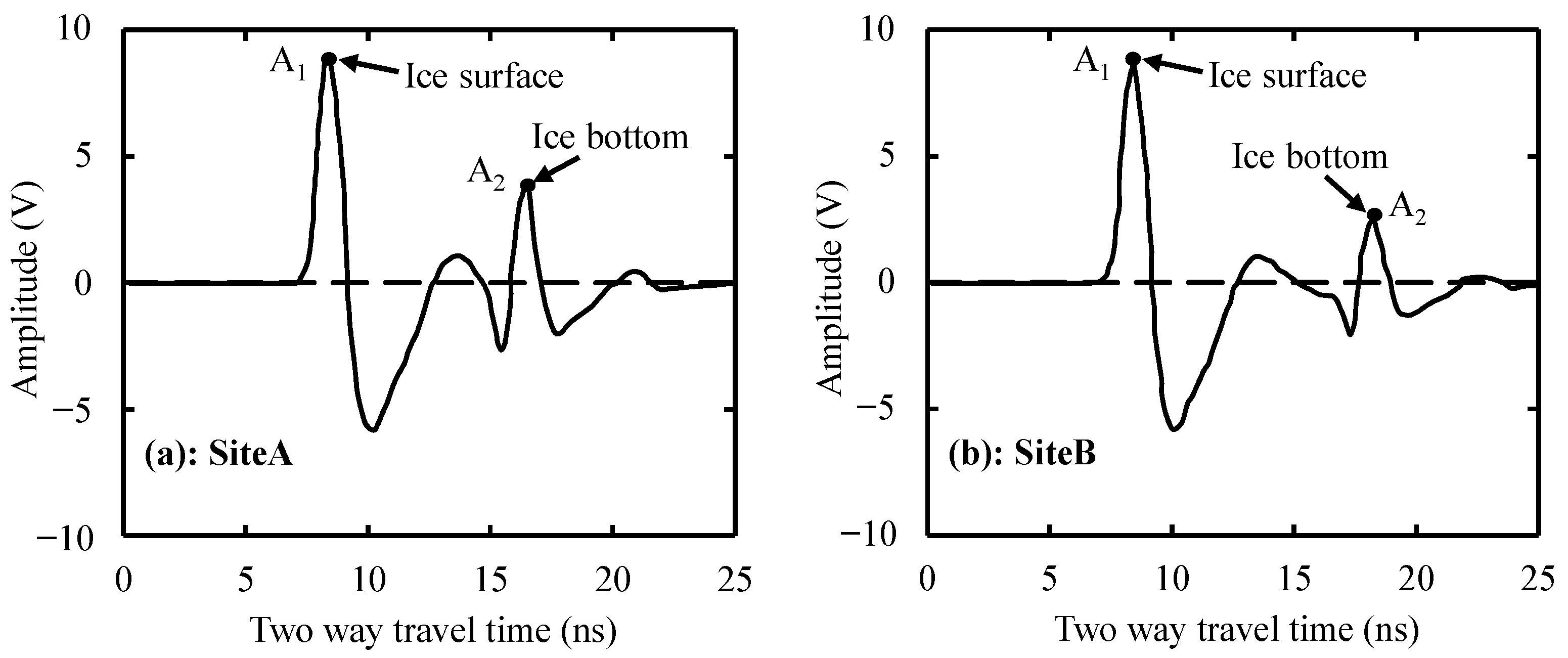
3.2. Interpretation of GPR Image
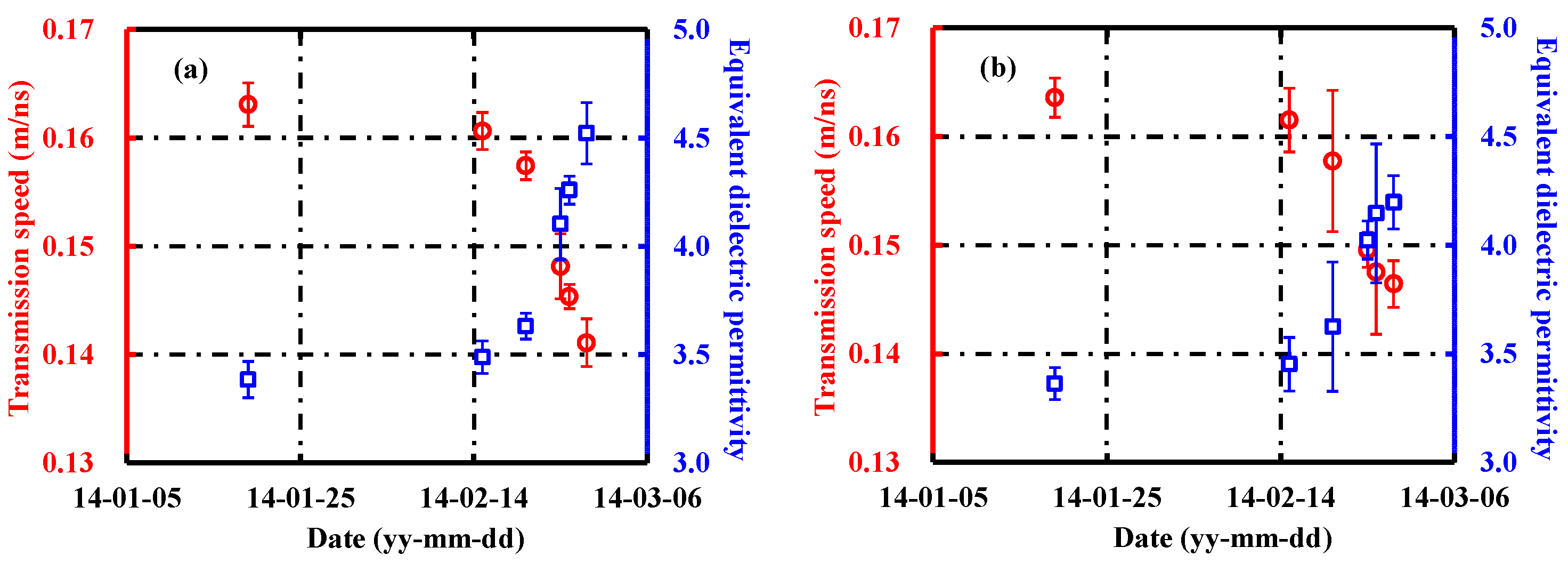
3.3. Dielectric Permittivities of River Ice
4. Discussion
5. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Frenette, J.J.; Thibeault, P.; Lapierre, J.F.; Hamilton, P.B. Presence of algae in freshwater ice cover of fluvial LAC Saint-Pierre (St. Lawrence River, Canada). J. Phycol. 2008, 44, 284–291. [Google Scholar] [CrossRef] [PubMed]
- Brooks, R.N.; Prowse, T.D.; O’Connell, I.J. Quantifying Northern Hemisphere freshwater ice. Geophys. Res. Lett. 2013, 40, 1128–1131. [Google Scholar] [CrossRef]
- Prowse, T.; Alfredsen, K.; Beltaos, S.; Bonsal, B.; Duguay, C.; Korhola, A.; McNamara, J.; Vincent, W.F.; Vuglinsky, V.; Weyhenmeyer, G.A. Arctic freshwater ice and its climatic role. AMBIO 2011, 40, 46–52. [Google Scholar] [CrossRef]
- Ferrick, M.G.; Mulherin, N.D. Framework for control of dynamic ice breakup by river regulation: Regulated Rivers. Res. Manag. 1989, 3, 79–92. [Google Scholar] [CrossRef]
- Mahabir, C.; Hicks, F.; Fayek, A.R. Neuro-fuzzy river ice breakup forecasting system. Cold Reg. Sci. Technol. 2006, 46, 100–112. [Google Scholar] [CrossRef]
- Reynolds, J.M. An Introduction to Applied and Environmental Geophysics; Wiley: New York, NY, USA, 1997; p. 796. [Google Scholar]
- Neal, A. Ground-penetrating radar and its use in sedimentology: Principles, problems and progress. Earth-Sci. Rev. 2004, 66, 261–330. [Google Scholar] [CrossRef]
- Annan, A.P.; Davis, J.L. Design and development of a digital ground penetrating radar system. In Ground Penetrating Radar; Canada Communication Group: Ottawa, ON, Canada, 1992; pp. 15–23. [Google Scholar]
- Binder, D.; Brückl, E.; Roch, K.H.; Behm, M.; Schöner, W.; Hynek, B. Determination of total ice volume and ice-thickness distribution of two glaciers in the Hohe Tauern region, Eastern Alps, from GPR data. Ann. Glaciol. 2009, 50, 71–79. [Google Scholar] [CrossRef]
- Cui, X.B.; Sun, B.; Tian, G.; Tang, X.Y.; Zhang, X.P.; Jiang, Y.Y.; Guo, J.X.; Li, X. Ice radar investigation at Dome A, East Antarctica: Ice thickness and subglacial topography. Chin. Sci. Bull. 2010, 55, 425–431. [Google Scholar] [CrossRef]
- Saintenoy, A.; Friedt, J.M.; Booth, A.D.; Tolle, F.; Bernard, E.; Laffly, D.; Marlin, C.; Griselin, M. Deriving ice thickness, glacier volume and bedrock morphology of Austre Lovénbreen (Svalbard) using GPR. Near Surf. Geophys. 2013, 11, 253–261. [Google Scholar] [CrossRef]
- Bohleber, P.; Sold, L.; Hardy, D.R.; Schwikowski, M.; Klenk, P.; Fischer, A.; Sirguey, P.; Cullen, N.J.; Potocki, M.; Hoffmann, H.; et al. Ground-penetrating radar reveals ice thickness and undisturbed englacial layers at Kilimanjaro’s Northern Ice Field. Cryosphere 2017, 11, 469–482. [Google Scholar] [CrossRef]
- Langhammer, L.; Rabenstein, L.; Bauder, A.; Maurer, H. Ground-penetrating radar antenna orientation effects on temperate mountain glaciers. Geophysics 2017, 82, H15–H24. [Google Scholar] [CrossRef]
- Mccarthy, M.; Pritchard, H.; Willis, I.; King, E. Ground-penetrating radar measurements of debris thickness on Lirung Glacier, Nepal. J. Glaciol. 2017, 63, 543–555. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Wang, N. Ice thickness sounded by ground penetrating radar on the Meikuang Glacier in the Eastern Kunlun Mountains. J. Glaciol. Geocryol. 2018, 40, 38–46. (in Chinese). [Google Scholar] [CrossRef]
- Mishra, A.; Negi, B.D.S.; Banerjee, A.; Nainwal, H.C.; Shankar, R. Estimation of ice thickness of the Satopanth Glacier, Central Himalaya using ground penetrating radar. Curr. Sci. India 2018, 114, 785–791. [Google Scholar] [CrossRef]
- Kanagaratnam, P.; Markus, T.; Lytle, V.; Heavey, B.; Jansen, P.; Prescott, G.; Gogineni, S.P. Ultrawideband radar measurements of thickness of snow over sea ice. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2715–2724. [Google Scholar] [CrossRef]
- Galley, R.J.; Trachtenberg, M.; Langlois, A.; Barber, D.G.; Shafai, L. Observations of geophysical and dielectric properties and ground penetrating radar signatures for discrimination of snow, sea ice and freshwater ice thickness. Cold Reg. Sci. Technol. 2009, 57, 29–38. [Google Scholar] [CrossRef]
- Liu, H.; Takahashi, K.; Sato, M. Measurement of dielectric permittivity and thickness of snow and ice on a brackish lagoon using GPR. IEEE J-STARS 2014, 7, 820–827. [Google Scholar] [CrossRef]
- Lundberg, A.; Thunehed, H. Snow wetness influence on impulse radar snow surveys: Theoretical and laboratory study. Nord. Hydrol. 2000, 31, 89–106. [Google Scholar] [CrossRef]
- Bradford, J.H.; Harper, J.T.; Brown, J. Complex dielectric permittivity measurements from ground-penetrating radar data to estimate snow liquid water content in the pendular regime. Water Resour. Res. 2009, 45, W08403. [Google Scholar] [CrossRef]
- Sundström, N.; Gustafsson, D.; Kruglyak, A. Lundberg, A. Field evaluation of a new method for estimation of liquid water content and snow water equivalent of wet snowpacks with GPR. Hydrol. Res. 2013, 44, 600–613. [Google Scholar] [CrossRef]
- Previati, M.; Godio, A.; Ferraris, S. Validation of spatial variability of snowpack thickness and density obtained with GPR and TDR methods. J. Appl. Geophys. 2011, 75, 284–293. [Google Scholar] [CrossRef]
- Forte, E.; Dossi, M.; Colucci, R.R.; Pipan, M. A new fast methodology to estimate the density of frozen materials by means of common offset GPR data. J. Appl. Geophys. 2013, 99, 135–145. [Google Scholar] [CrossRef]
- Godio, A.; Frigo, B.; Chiaia, B.; Maggioni, P.; Freppaz, M.; Ceaglio, E.; Dellavedova, P. Integration of upward GPR and water content reflectometry to monitor snow properties. Near Surf. Geophys. 2018, 16, 1–10. [Google Scholar] [CrossRef]
- Holbrook, W.S.; Miller, S.N.; Provart, M.A. Estimating snow water equivalent over long mountain transects using snowmobile-mounted ground-penetrating radar. Geophysics 2016, 81, WA183–WA193. [Google Scholar] [CrossRef]
- Webb, R.W. Using ground penetrating radar to assess the variability of snow water equivalent and melt in a mixed canopy forest, Northern Colorado. Front. Earth Sci. 2017, 11, 482–495. [Google Scholar] [CrossRef]
- Li, Z.; Li, C.; Yang, Y.; Zhang, B.; Deng, Y.; Li, G. Physical scheme and parametrization by using air temperature and ice thickness to improve accuracy of GPR propagation velocity in Yellow River ice. J. Hydraul. Eng. 2022, 53, 902–913. [Google Scholar] [CrossRef]
- Best, H.; Mcnamara, J.P.; Liberty, L. Association of ice and river channel morphology determined using ground-penetrating radar in the Kuparuk River, Alaska. Arct. Antarct. Alp. Res. 2005, 37, 157–162. [Google Scholar] [CrossRef]
- Fu, H.; Liu, Z.; Guo, X.; Cui, H. Double-frequency ground penetrating radar for measurement of ice thickness and water depth in rivers and canals: Development, verification and application. Cold Reg. Sci. Technol. 2018, 154, 85–94. [Google Scholar] [CrossRef]
- Li, T.; Zhao, J.; Jiao, Y.; Hou, J.; Mu, L. Regional characteristics of sea ice thickness in Canadian shelf and Arctic Archipelago measured by Ground Penetrating Radar. Acta Oceanol. Sin. 2015, 34, 110–116. [Google Scholar] [CrossRef]
- Li, Z.J.; Jia, Q.; Zhang, B.S.; Leppäranta, M.; Huang, W.F. Influences of gas bubble and ice density on ice thickness measurement by GPR. Appl. Geophys. 2010, 7, 105–113. [Google Scholar] [CrossRef]
- Stevens, C.W.; Moorman, B.J.; Solomon, S.M.; Hugenholtz, C.H. Mapping subsurface conditions within the near-shore zone of an Arctic delta using ground penetrating radar. Cold Reg. Sci. Technol. 2009, 56, 30–38. [Google Scholar] [CrossRef]
- Jones, B.M.; Gusmeroli, A.; Arp, C.D.; Strozzi, T.; Grosse, G.; Gaglioti, B.V.; Whitman, M.S. Classification of freshwater ice conditions on the Alaskan Arctic Coastal Plain using ground penetrating radar and TerraSAR-X satellite data. Int. J. Remote Sens. 2013, 34, 8267–8279. [Google Scholar] [CrossRef]
- Fantello, N.; Parsekian, A.D.; Anthony, K.M.W. Estimating winter ebullition bubble volume in lake ice using ground-penetrating radar. Geophysics 2017, 83, H13–H25. [Google Scholar] [CrossRef]
- Xu, J.; Cheng, D. Relation between the erosion and sedimentation zones in the Yellow River, China. Geomorphology 2002, 48, 365–382. [Google Scholar] [CrossRef]
- Ran, L.; Wang, S.; Fan, X. Channel change at Toudaoguai Station and its responses to the operation of upstream reservoirs in the upper Yellow River. J. Geogr. Sci. 2010, 20, 231–247. [Google Scholar] [CrossRef]
- Wang, T.; Yang, K.; Guo, Y. Application of artificial neural networks to forecasting ice conditions of the Yellow River in the Inner Mongolia Reach. J. Hydrol. Eng. 2008, 13, 811–816. [Google Scholar] [CrossRef]
- Ji, H.L.; Zhang, A.D.; Gao, R.Z.; Zhang, B.S.; Xu, J. Application of the break-up date prediction model in the Inner Mongolia Reach of the Yellow River. Adv. Sci. Technol. Water Resour. 2012, 32, 42–45. (in Chinese). [Google Scholar] [CrossRef]
- Kovacs, A.; Gow, A.J.; Morey, R.M. The in-situ dielectric constant of polar firn revisited. Cold Reg. Sci. Technol. 1995, 23, 245–256. [Google Scholar] [CrossRef]
- Shokr, M.E. Field observations and model calculations of dielectric properties of Arctic sea ice in the microwave C-band. IEEE Trans. Geosci. Remote Sens. 1998, 36, 463–478. [Google Scholar] [CrossRef]
- Gherboudj, I.; Bernier, M.; Hicks, F.; Leconte, R. Physical characterization of air inclusions in river ice. Cold Reg. Sci. Technol. 2007, 49, 179–194. [Google Scholar] [CrossRef]
- Evans, S. Dielectric properties of ice and snow-A review. J. Glaciol. 1965, 5, 773–792. [Google Scholar] [CrossRef]
- Ran, D.; Yao, W.; Shen, Z.; Ni, Y.; Dong, F. Analysis on the contribution rate of driving factors for the annual water and sediment variations at the Toudaoguai hydrological station in the Yellow River. Adv. Water Sci. 2015, 26, 769–778. (in Chinese). [Google Scholar] [CrossRef]
- Davis, J.L.; Annan, A.P. Ground-penetrating radar for high-resolution mapping of soil and rock stratigraphy. Geophys. Prospect. 1989, 37, 531–551. [Google Scholar] [CrossRef]
- Moorman, B.J.; Michel, F.A. Bathymetric mapping and sub-bottom profiling through lake ice with ground-penetrating radar. J. Paleolimnol. 1997, 18, 61–73. [Google Scholar] [CrossRef]
- Hausmann, H.; Behm, M. Imaging the structure of cave ice by ground-penetrating radar. Cryosphere 2011, 5, 329–340. [Google Scholar] [CrossRef]
- Stoyanovich, G.M.; Pupatenko, V.V.; Sukhobok, Y.A. Detection of ground ice using ground penetrating radar method. Sci. Cold Arid Reg. 2015, 7, 541–546. [Google Scholar] [CrossRef]
- Annan, A.P.; Diamanti, N.; Redman, J.D.; Jackson, S.R. Ground-penetrating radar for assessing winter roads. Geophysics 2016, 81, WA101–WA109. [Google Scholar] [CrossRef]
- You, Y.; Yang, M.; Yu, Q.; Pan, X.; Guo, L.; Wang, X.; Wu, Q. Factors influencing the reliability of grounded and floating ice distinguishing based on ground penetrating radar reflection amplitude. Cold Reg. Sci. Technol. 2018, 154, 1–8. [Google Scholar] [CrossRef]
- Bohleber, P.; Wagner, N.; Eisen, O. Permittivity of ice at radio frequencies: Part I. Coaxial transmission line cell. Cold Reg. Sci. Technol. 2012, 82, 56–67. [Google Scholar] [CrossRef]
- Bohleber, P.; Wagner, N.; Eisen, O. Permittivity of ice at radio frequencies: Part II. Artificial and natural polycrystalline ice. Cold Reg. Sci. Technol. 2012, 83, 13–19. [Google Scholar] [CrossRef]


| Regime | Site A | Site B | ||
|---|---|---|---|---|
| εdz1 | εavg2 | εdz1 | εavg2 | |
| Kovacs et al. [40] | 3.1 | 3.1 (±0.06) | 3.0 | 3.0 (±0.06) |
| Shokr [41] | 3.1 | 3.1 (±0.05) | 3.0 | 3.0 (±0.06) |
| Radar method | — | 3.5 (±0.06) | — | 3.3 (±0.03) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Li, Y.; Li, W.; Liu, X.; Wang, E.; Jiang, H. The Influence of the Internal Properties of River Ice on Ground Penetrating Radar Propagation. Water 2023, 15, 889. https://doi.org/10.3390/w15050889
Han H, Li Y, Li W, Liu X, Wang E, Jiang H. The Influence of the Internal Properties of River Ice on Ground Penetrating Radar Propagation. Water. 2023; 15(5):889. https://doi.org/10.3390/w15050889
Chicago/Turabian StyleHan, Hongwei, Yu Li, Wanyun Li, Xingchao Liu, Enliang Wang, and Haiqiang Jiang. 2023. "The Influence of the Internal Properties of River Ice on Ground Penetrating Radar Propagation" Water 15, no. 5: 889. https://doi.org/10.3390/w15050889
APA StyleHan, H., Li, Y., Li, W., Liu, X., Wang, E., & Jiang, H. (2023). The Influence of the Internal Properties of River Ice on Ground Penetrating Radar Propagation. Water, 15(5), 889. https://doi.org/10.3390/w15050889






