Coupled Model for Assessing the Present and Future Watershed Vulnerabilities to Climate Change Impacts
Abstract
:1. Introduction
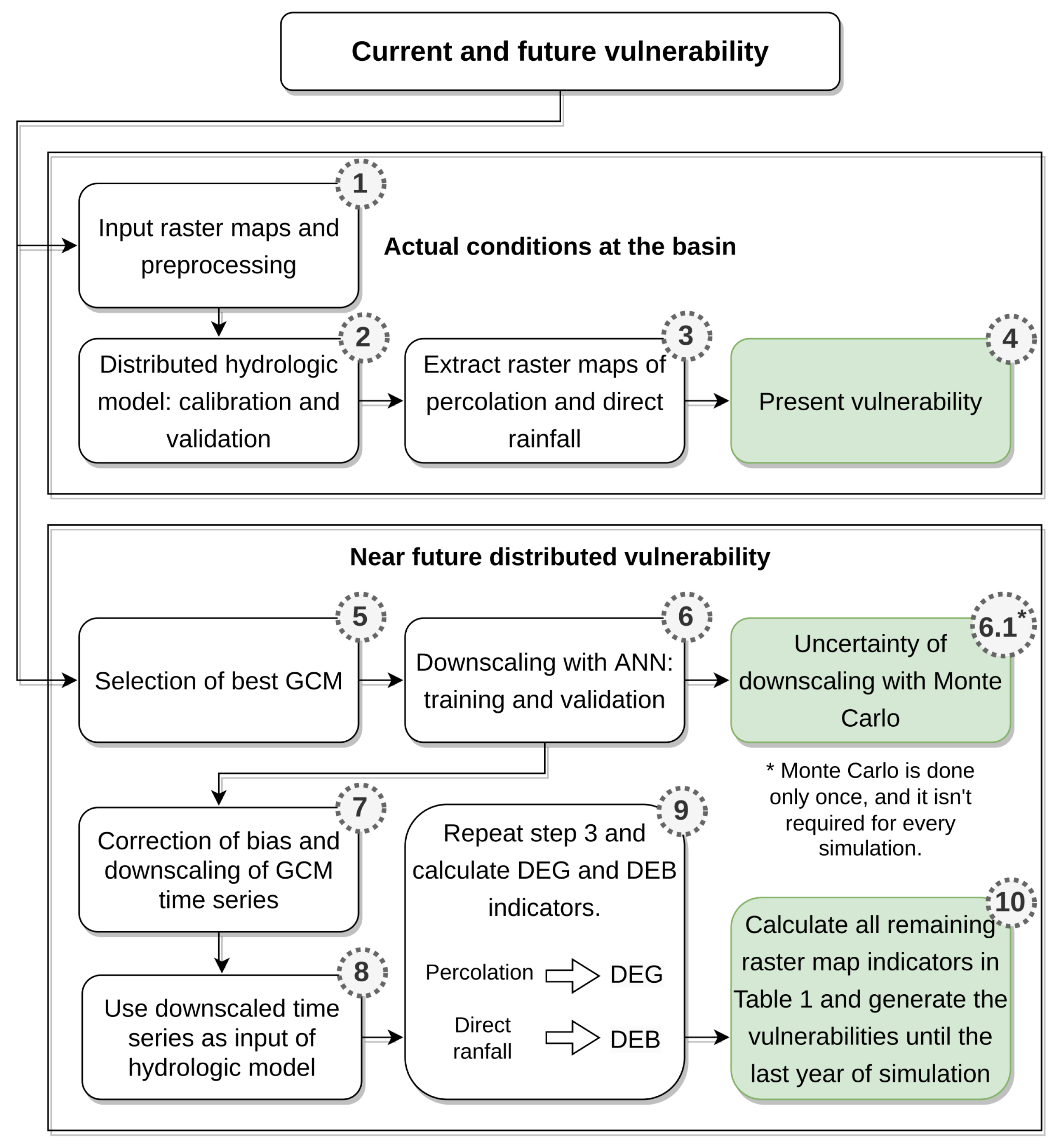
2. Methodology
2.1. Distributed Vulnerability Assessment
2.2. Spatially Distributed Indicators
2.3. Downscaling GCM Time Series
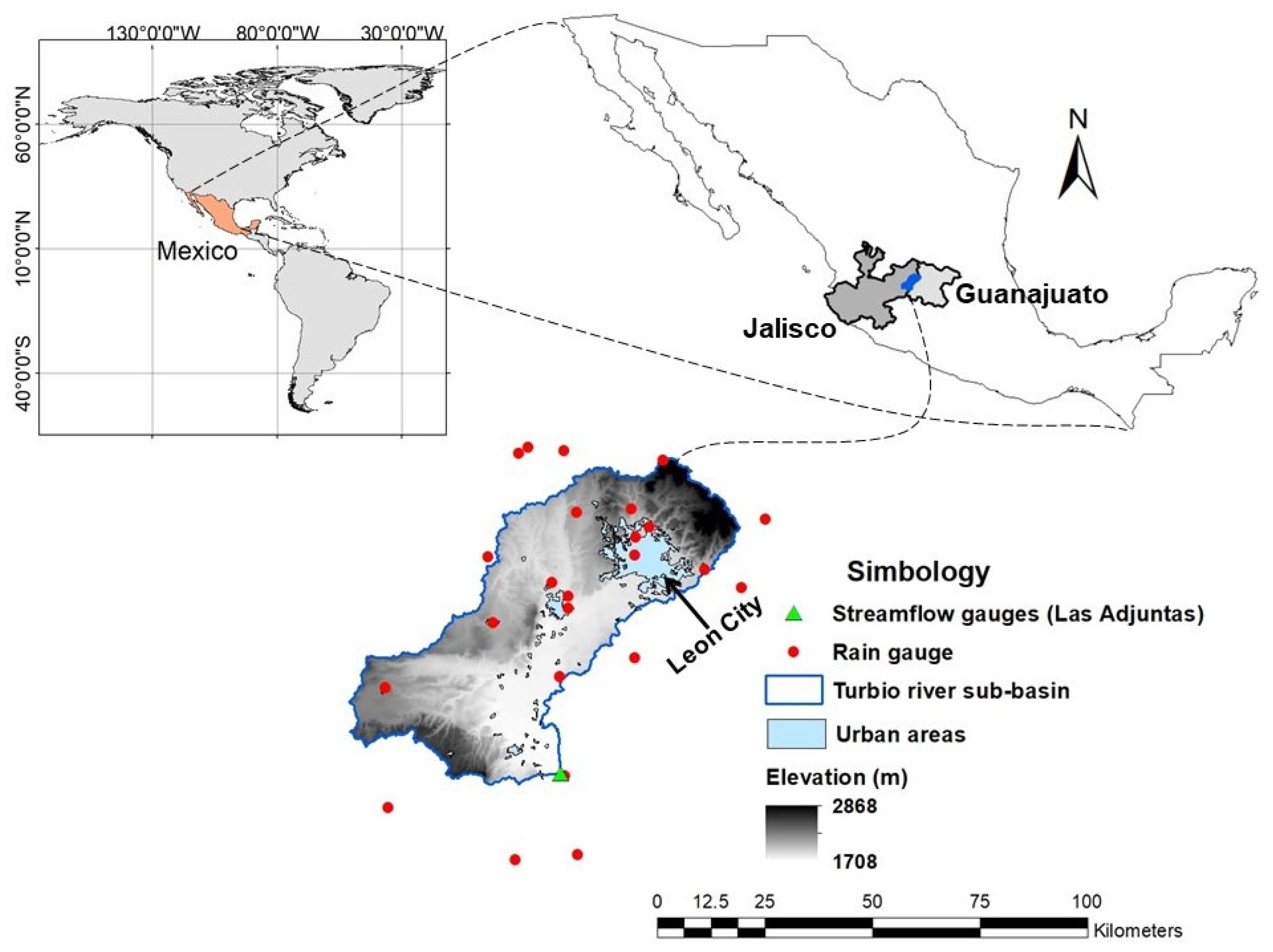
3. Case Study
4. Results and Discussion
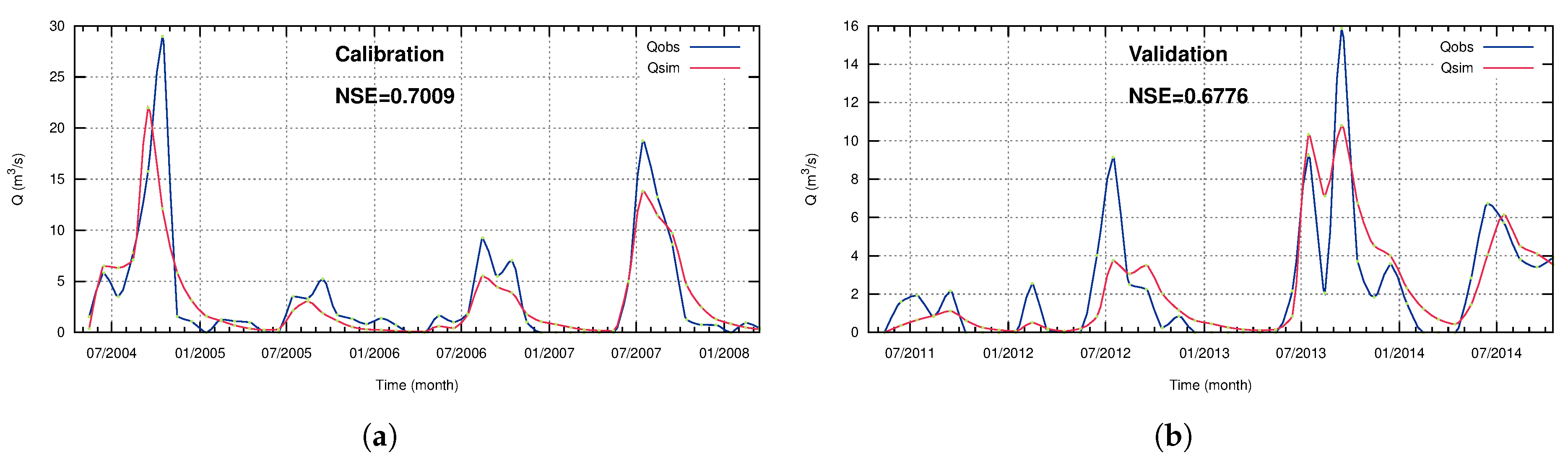
4.1. Hydrology Model Performance
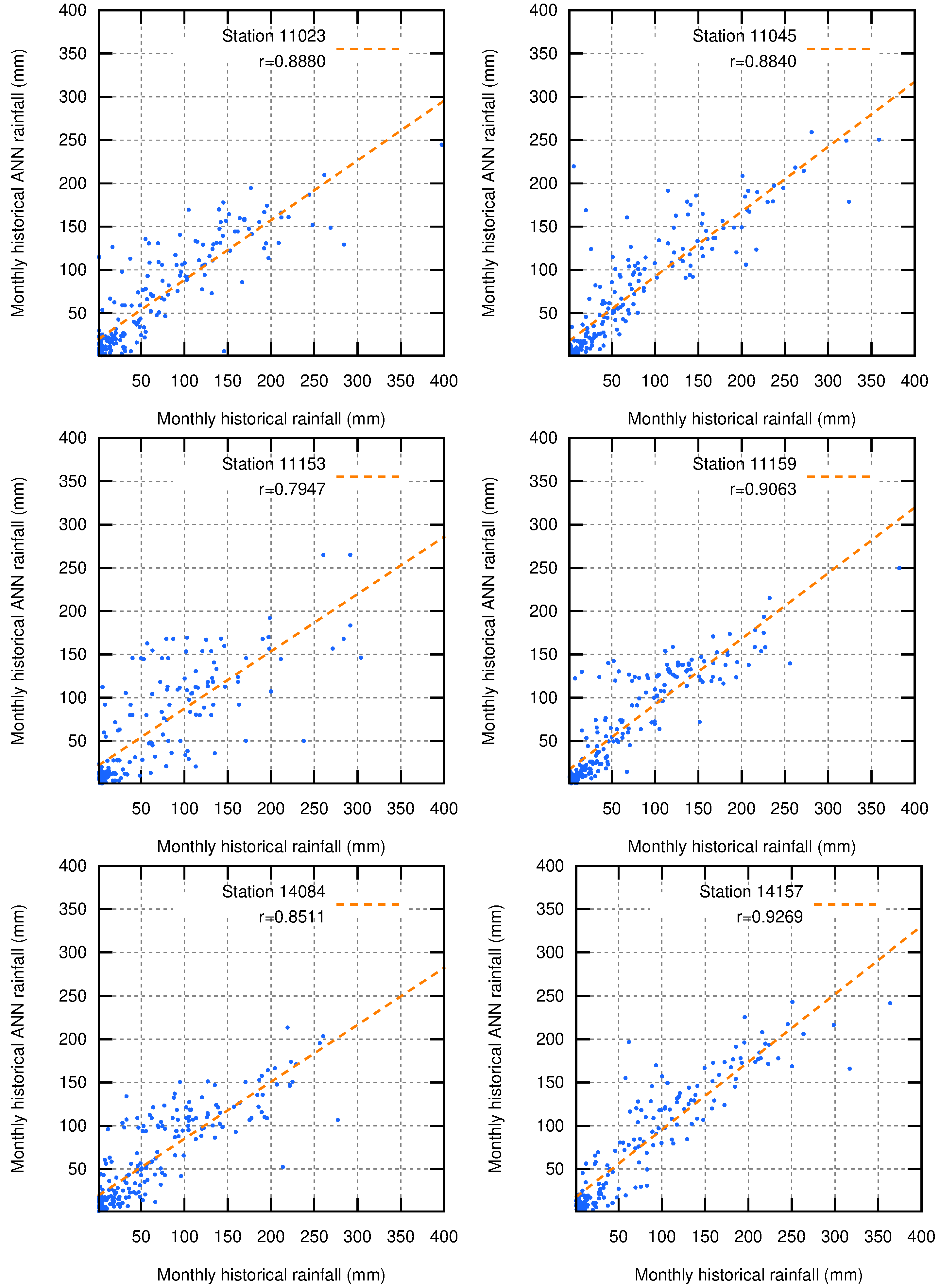
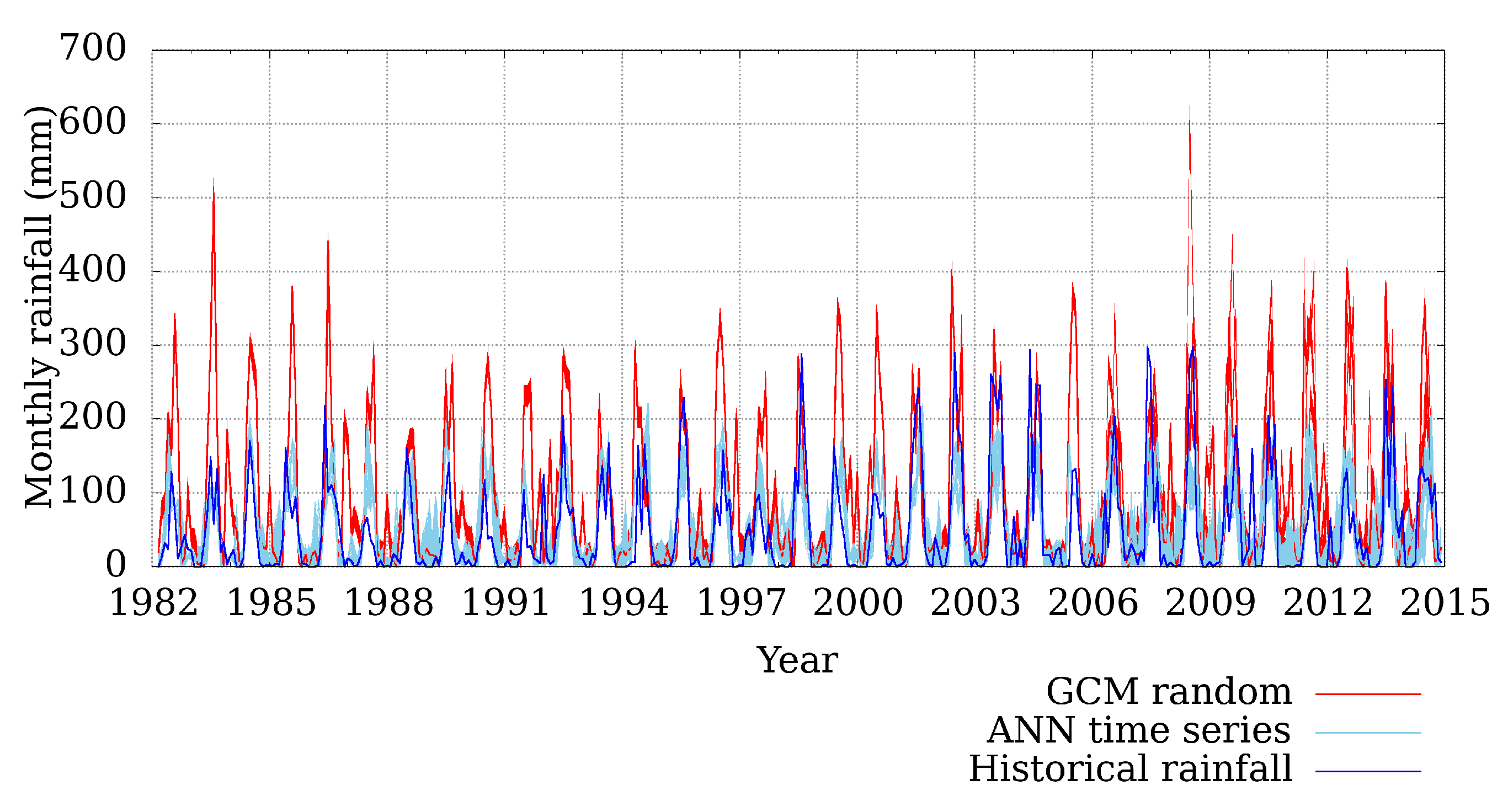
4.2. GCM Models and Downscaling
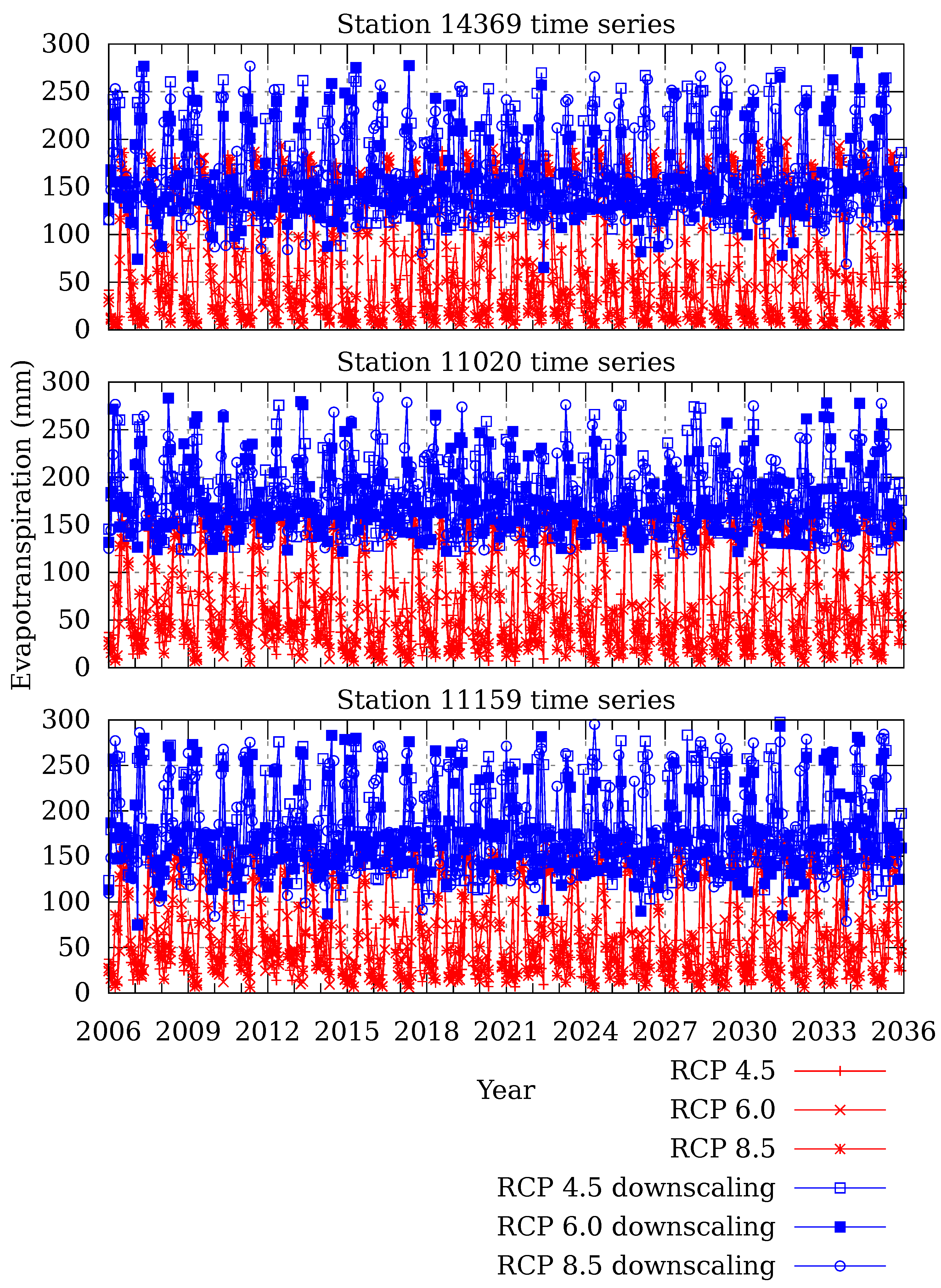
4.3. Uncertainty Analysis and Projections
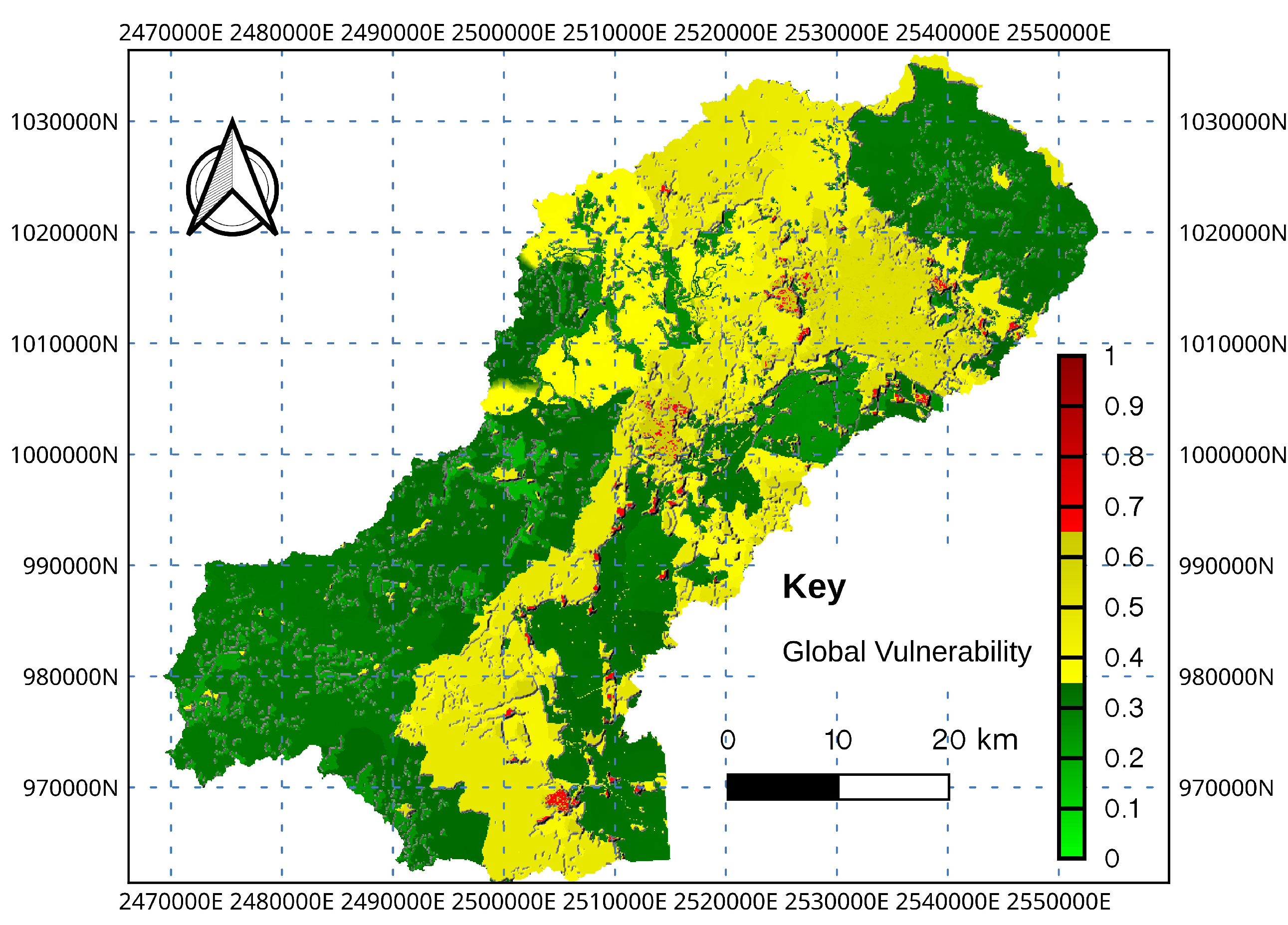
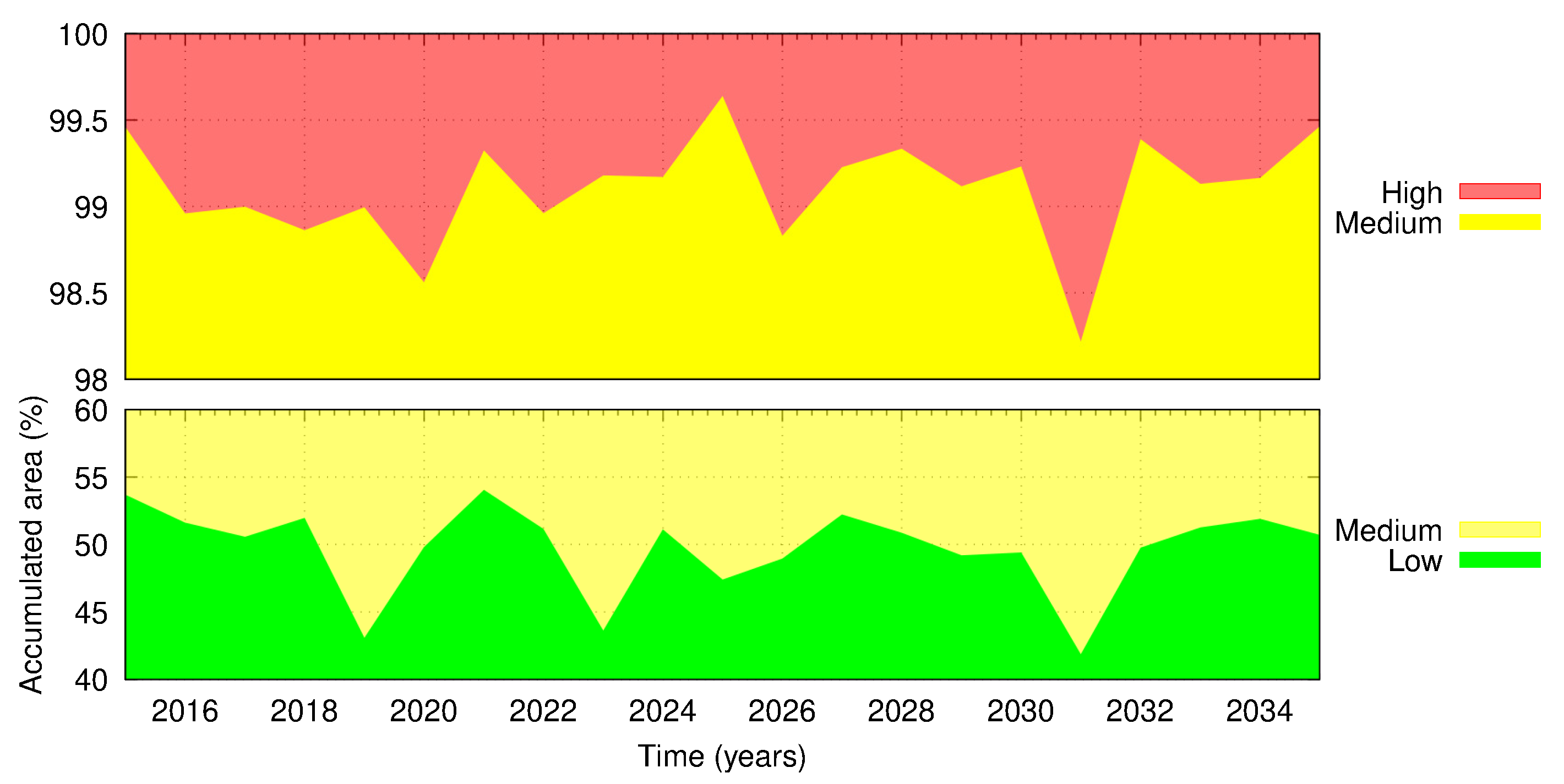
4.4. Vulnerability to Climate Change Impacts
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Green, T.R.; Taniguchi, M.; Kooi, H.; Gurdak, J.J.; Allen, D.M.; Hiscock, K.M.; Treidel, H.; Aureli, A. Beneath the surface of global change: Impacts of climate change on groundwater. J. Hydrol. 2011, 405, 532–560. [Google Scholar] [CrossRef]
- Lizarralde, G.; Bornstein, L.; Robertson, M.; Gould, K.; Herazo, B.; Petter, A.M.; Páez, H.; Díaz, J.H.; Olivera, A.; González, G.; et al. Does climate change cause disasters? How citizens, academics, and leaders explain climate-related risk and disasters in Latin America and the Caribbean. Int. J. Disaster Risk Reduct. 2021, 58, 102173. [Google Scholar] [CrossRef]
- Herrera, M.; Ferreira, A.A.; Coley, D.A.; De Aquino, R.R. SAX-quantile based multiresolution approach for finding heatwave events in summer temperature time series. AI Commun. 2016, 29, 725–732. [Google Scholar] [CrossRef]
- Hewitson, B.C.; Crane, R.G. Consensus between GCM climate change projections with empirical downscaling: Precipitation downscaling over South Africa. Int. J. Climatol. 2006, 26, 1315–1337. [Google Scholar] [CrossRef]
- Chung, E.S.; Park, K.; Lee, K.S. The relative impacts of climate change and urbanization on the hydrological response of a Korean urban watershed. Hydrol. Process. 2011, 25, 544–560. [Google Scholar] [CrossRef]
- Jun, K.S.; Chung, E.S.; Sung, J.Y.; Lee, K.S. Development of spatial water resources vulnerability index considering climate change impacts. Sci. Total. Environ. 2011, 409, 5228–5242. [Google Scholar] [CrossRef] [PubMed]
- Tulbure, M.G.; Broich, M. Spatiotemporal patterns and effects of climate and land use on surface water extent dynamics in a dryland region with three decades of Landsat satellite data. Sci. Total Environ. 2019, 658, 1574–1585. [Google Scholar] [CrossRef]
- Wiréhn, L.; Danielsson, Å.; Neset, T.S.S. Assessment of composite index methods for agricultural vulnerability to climate change. J. Environ. Manag. 2015, 156, 70–80. [Google Scholar] [CrossRef]
- Boy-Roura, M.; Nolan, B.T.; Menció, A.; Mas-Pla, J. Regression model for aquifer vulnerability assessment of nitrate pollution in the Osona region (NE Spain). J. Hydrol. 2013, 505, 150–162. [Google Scholar] [CrossRef]
- Abson, D.J.; Dougill, A.J.; Stringer, L.C. Using Principal Component Analysis for information-rich socio-ecological vulnerability mapping in Southern Africa. Appl. Geogr. 2012, 35, 515–524. [Google Scholar] [CrossRef]
- Cheng, J.; Ping Tao, J. Fuzzy Comprehensive Evaluation of Drought Vulnerability Based on the Analytic Hierarchy Process—An Empirical Study from Xiaogan City in Hubei Province. Agric. Agric. Sci. Procedia 2010, 1, 126–135. [Google Scholar] [CrossRef]
- Maiolo, M.; Martirano, G.; Morrone, P.; Pantusa, D. Assessment criteria for a sustainable management of the water resources. Water Pract. Technol. 2006, 1, wpt2006012. [Google Scholar] [CrossRef]
- Tixier, J.; Dandrieux, A.; Dusserre, G.; Bubbico, R.; Mazzarotta, B.; Silvetti, B.; Hubert, E.; Rodrigues, N.; Salvi, O. Environmental vulnerability assessment in the vicinity of an industrial site in the frame of ARAMIS European project. J. Hazard. Mater. 2006, 130, 251–264. [Google Scholar] [CrossRef] [PubMed]
- Brody, S.D.; Zahran, S.; Vedlitz, A.; Grover, H. Examining the Relationship Between Physical Vulnerability and Public Perceptions of Global Climate Change in the United States. Environ. Behav. 2008, 40, 72–95. [Google Scholar] [CrossRef]
- Dixon, B. Applicability of neuro-fuzzy techniques in predicting ground-water vulnerability: A GIS-based sensitivity analysis. J. Hydrol. 2005, 309, 17–38. [Google Scholar] [CrossRef]
- Cess, R.D.; Potter, G.L.; Blanchet, J.P.; Boer, G.J.; Del Genio, A.D.; Déqué, M.; Dymnikov, V.; Galin, V.; Gates, W.L.; Ghan, S.J.; et al. Intercomparison and interpretation of climate feedback processes in 19 atmospheric general circulation models. J. Geophys. Res. Atmos. 1990, 95, 16601–16615. [Google Scholar] [CrossRef]
- Song, Y.H.; Chung, E.S.; Shahid, S. Spatiotemporal differences and uncertainties in projections of precipitation and temperature in South Korea from CMIP6 and CMIP5 general circulation models. Int. J. Climatol. 2021, 41, 5899–5919. [Google Scholar] [CrossRef]
- Ali, S.; Eum, H.I.; Cho, J.; Dan, L.; Khan, F.; Dairaku, K.; Shrestha, M.L.; Hwang, S.; Nasim, W.; Khan, I.A.; et al. Assessment of climate extremes in future projections downscaled by multiple statistical downscaling methods over Pakistan. Atmos. Res. 2019, 222, 114–133. [Google Scholar] [CrossRef]
- Samanta, S.; Banerjee, S.; Patra, P.K.; Sehgal, V.K.; Chowdhury, A.; Kumar, B.; Mukherjee, A. Projection of future daily global horizontal irradiance under four RCP scenarios: An assessment through newly developed temperature and rainfall-based empirical model. Sol. Energy 2021, 227, 23–43. [Google Scholar] [CrossRef]
- Wilby, R.; Wigley, T. Downscaling general circulation model output: A review of methods and limitations. Prog. Phys. Geogr. Earth Environ. 1997, 21, 530–548. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Nathan, R.; Horne, A.; Peel, M.C.; Wei, Y.; Langford, J. Evaluating four downscaling methods for assessment of climate change impact on ecological indicators. Environ. Model. Softw. 2017, 96, 68–82. [Google Scholar] [CrossRef]
- Govindaraju, R.S.; Rao, A.R. Artificial Neural Networks in Hydrology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 36. [Google Scholar]
- Tiwari, M.K.; Chatterjee, C. Uncertainty assessment and ensemble flood forecasting using bootstrap based artificial neural networks (BANNs). J. Hydrol. 2010, 382, 20–33. [Google Scholar] [CrossRef]
- Gaume, E.; Gosset, R. Over-parameterisation, a major obstacle to the use of artificial neural networks in hydrology? Hydrol. Earth Syst. Sci. 2003, 7, 693–706. [Google Scholar] [CrossRef]
- Ajami, N.K.; Duan, Q.; Gao, X.; Sorooshian, S. Multimodel Combination Techniques for Analysis of Hydrological Simulations: Application to Distributed Model Intercomparison Project Results. J. Hydrometeorol. 2006, 7, 755–768. [Google Scholar] [CrossRef]
- Dixon, B.; Earls, J. Effects of urbanization on streamflow using SWAT with real and simulated meteorological data. Appl. Geogr. 2012, 35, 174–190. [Google Scholar] [CrossRef]
- Tegegne, G.; Kim, Y.O.; Seo, S.B.; Kim, Y. Hydrological modeling uncertainty analysis for different flow quantiles: A case study in two hydro-geographically different watersheds. Hydrol. Sci. J. 2019, 64, 473–489. [Google Scholar] [CrossRef]
- McMillan, H.K.; Westerberg, I.K.; Krueger, T. Hydrological data uncertainty and its implications. WIREs Water 2018, 5, e1319. [Google Scholar] [CrossRef]
- Pechlivanidis, I.; Jackson, B.; Mcintyre, N.; Wheater, H. Catchment scale hydrological modeling: A review of model types, calibration approaches and uncertainty analysis methods in the context of recent developments in technology and applications. Glob. NEST J. 2011, 13, 193–214. [Google Scholar]
- Orozco, I.; Martínez, A.; Ortega, V. Assessment of the Water, Environmental, Economic and Social Vulnerability of a Watershed to the Potential Effects of Climate Change and Land Use Change. Water 2020, 12, 1682. [Google Scholar] [CrossRef]
- Das, J.; Nanduri, U.V. Assessment and evaluation of potential climate change impact on monsoon flows using machine learning technique over Wainganga River basin, India. Hydrol. Sci. J. 2018, 63, 1020–1046. [Google Scholar] [CrossRef]
- Fazeli Farsani, I.; Farzaneh, M.R.; Besalatpour, A.A.; Salehi, M.H.; Faramarzi, M. Assessment of the impact of climate change on spatiotemporal variability of blue and green water resources under CMIP3 and CMIP5 models in a highly mountainous watershed. Theor. Appl. Climatol. 2019, 136, 169–184. [Google Scholar] [CrossRef]
- Harrison, P.A.; Dunford, R.W.; Holman, I.P.; Cojocaru, G.; Madsen, M.S.; Chen, P.Y.; Pedde, S.; Sandars, D. Differences between low-end and high-end climate change impacts in Europe across multiple sectors. Reg. Environ. Chang. 2019, 19, 695–709. [Google Scholar] [CrossRef]
- Wilson, K.; Newton, A.; Echeverría, C.; Weston, C.; Burgman, M. A vulnerability analysis of the temperate forests of south central Chile. Biol. Conserv. 2005, 122, 9–21. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, X.; Liu, S.; Liu, J.; Wang, Z.; Li, M. Regional assessment of environmental vulnerability in the Tibetan Plateau: Development and application of a new method. J. Arid. Environ. 2008, 72, 1929–1939. [Google Scholar] [CrossRef]
- Enea, M.; Salemi, G. Fuzzy approach to the environmental impact evaluation. Ecol. Model. 2001, 136, 131–147. [Google Scholar] [CrossRef]
- Nandy, S.; Singh, C.; Das, K.; Kingma, N.; Kushwaha, S. Environmental vulnerability assessment of eco-development zone of Great Himalayan National Park, Himachal Pradesh, India. Ecol. Indic. 2015, 57, 182–195. [Google Scholar] [CrossRef]
- Field, C.B.; Barros, V.; Stocker, T.F.; Dahe, Q. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Ortega-Gaucin, D.; Cruz, J.; Castellano Bahena, H. Peligro, vulnerabilidad y riesgo por sequía en el contexto del cambio climático en México. In Agua y Cambio Climático, 1st ed.; Lobato, R., Pérez, A.A., Eds.; Instituto Mexicano de Tecnología del Agua: Jiutepec, Mexico, 2018; pp. 78–103. [Google Scholar]
- Neelin, J.D.; Langenbrunner, B.; Meyerson, J.E.; Hall, A.; Berg, N. California Winter Precipitation Change under Global Warming in the Coupled Model Intercomparison Project Phase 5 Ensemble. J. Clim. 2013, 26, 6238–6256. [Google Scholar] [CrossRef]
- Montenegro, D.D.; Pérez Ortiz, M.A.; Vargas Franco, V.; Franco, V.V. Predicción de precipitación mensual mediante Redes Neuronales Artificiales para la cuenca del río Cali, Colombia. DYNA 2019, 86, 122–130. [Google Scholar] [CrossRef]
- Nourani, V.; Jabbarian Paknezhad, N.; Sharghi, E.; Khosravi, A. Estimation of prediction interval in ANN-based multi-GCMs downscaling of hydro-climatologic parameters. J. Hydrol. 2019, 579, 124226. [Google Scholar] [CrossRef]
- Okkan, U.; Kirdemir, U. Downscaling of monthly precipitation using CMIP5 climate models operated under RCPs. Meteorol. Appl. 2016, 23, 514–528. [Google Scholar] [CrossRef] [Green Version]
- Lorrentz, P. Artificial Neural Systems: Principle and Practice; Bentham Science Publishers: Sharjah, United Arab Emirates, 2015. [Google Scholar]
- Orozco, I.; Francés, F.; Mora, J. Parsimonious Modeling of Snow Accumulation and Snowmelt Processes in High Mountain Basins. Water 2019, 11, 1288. [Google Scholar] [CrossRef]
- Francés, F.; Vélez, J.I.; Vélez, J.J. Split-parameter structure for the automatic calibration of distributed hydrological models. J. Hydrol. 2007, 332, 226–240. [Google Scholar] [CrossRef]
- Bauwe, A.; Eckhardt, K.U.; Lennartz, B. Predicting dissolved reactive phosphorus in tile-drained catchments using a modified SWAT model. Ecohydrol. Hydrobiol. 2019, 19, 198–209. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Technical note: Inherent benchmark or not? Comparing Nash—Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Ruiz-Pérez, G.; González-Sanchis, M.; Campo, A.D.; Francés, F. Can a parsimonious model implemented with satellite data be used for modeling the vegetation dynamics and water cycle in water-controlled environments? Ecol. Model. 2016, 324, 45–53. [Google Scholar] [CrossRef] [Green Version]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]




| Name, Equation, and Units | ||
|---|---|---|
| Indicators | Economic | Population density: ; (habkm−2) |
| Economically active population: ; (%) | ||
| Length of rural roads: ; (km) | ||
| Agricultural area for irrigation: ; (ha) | ||
| Agriculture area with technified irrigation: ; (ha) | ||
| Social | Population without medical services: ; (%) | |
| Population in poverty: ; (%) | ||
| Illiterate population: ; (%) | ||
| Houses without drinking water: ; (%) | ||
| Houses without drainage and no restroom: ; (%) | ||
| Houses without electricity: ; (%) | ||
| Houses with land floor: ; (%) | ||
| Environmental | Degree of exploitation of the basin: ; | |
| Degree of exploitation of groundwater: ; | ||
| Deforestation: ; (%) | ||
| Protected natural areas: ; (%) | ||
| Water | Degree of exploitation of the basin: ; | |
| Degree of exploitation of groundwater: ; | ||
| Parameter | Correction Factor | Parameter Equation | Effective Parameter |
|---|---|---|---|
| Static storage | 382.090 (mm) | ||
| Vegetation cover index | 0.008 | ||
| Infiltration capacity | 113.981 (mmh−1) | ||
| Overland flow velocity | 5.158 (ms−1) | ||
| Percolation capacity | 7.216 (mmh−1) | ||
| Interflow velocity | 124.17 (mmh−1) | ||
| Deep aquifer permeability | 0.067 (mmh−1) | ||
| Connected aquifer permeability | 0.010 (mmh−1) | ||
| River channel velocity | 0.031 (mms−1) |
| GCM Model | Country |
|---|---|
| BCC-CSM1 | China |
| MIROC-ESM-CHEM MIROC-ESM MIROC5 | Japan |
| CanESM2 | Canada |
| CNRM-CM5 | France |
| CSIRO-MK3-6 | Australia |
| GFDL-CM3 GISS-E2-R | USA |
| HADGEM2-Es | United Kingdom |
| INM-CM4 | Russia |
| MPI-ESM-LR | Germany |
| MRI-CGCM3 | Japan |
| NCC-NorESM1 | Norway |
| IPSL-CMA-LR | France |
| CSIRO-Mk3-6-0 | ANNs and Monte Carlo | |||
|---|---|---|---|---|
| Minimum | Mean | Maximum | ||
| R | 0.6156 | 0.6520 | 0.7121 | 0.7713 |
| Bias | 101.3 | −4.9 | 2.0 | 9.1 |
| Variance | 13,538.2 | 3019.4 | 3430.2 | 3872.2 |
| Underestimation | −39.5 | −46.9 | −40.7 | −35.1 |
| Overestimation | 75.9 | 25.7 | 30.3 | 35.1 |
| RMSE | 100.2 | 43.8 | 48.6 | 53.1 |
| Rain Gauge | R | Bias | Variance | Underestimation | Overestimation | RMSE | Maximum | Mean | |
|---|---|---|---|---|---|---|---|---|---|
| 11,020 | MIN | 0.640 | −6.0 | 2621.4 | −44.8 | 24.0 | 44.9 | 176.7 | 46.3 |
| MEAN | 0.695 | 0.6 | 3029.3 | −39.3 | 28.6 | 49.5 | 205.9 | 49.5 | |
| MAX | 0.752 | 7.4 | 3425.3 | −33.6 | 33.8 | 53.5 | 221.2 | 52.9 | |
| 11,023 | MIN | 0.668 | −5.6 | 2751.4 | −47.0 | 25.7 | 41.3 | 217.0 | 50.1 |
| MEAN | 0.730 | 1.7 | 3022.3 | −39.4 | 29.1 | 45.8 | 241.0 | 53.2 | |
| MAX | 0.787 | 8.9 | 3302.2 | −33.7 | 33.4 | 50.4 | 244.6 | 56.4 | |
| 11,045 | MIN | 0.618 | −13.2 | 3420.1 | −52.4 | 26.8 | 49.8 | 206.4 | 50.0 |
| MEAN | 0.689 | −5.6 | 3972.4 | −45.4 | 32.5 | 56.6 | 251.2 | 54.4 | |
| MAX | 0.764 | 2.4 | 4458.6 | −40.2 | 38.2 | 62.2 | 259.2 | 59.0 | |
| 11,049 | MIN | 0.600 | −2.1 | 2818.6 | −44.3 | 27.8 | 44.2 | 215.1 | 52.5 |
| MEAN | 0.672 | 5.4 | 3342.4 | −38.4 | 33.1 | 50.1 | 284.2 | 56.9 | |
| MAX | 0.745 | 12.9 | 3837.6 | −32.3 | 39.5 | 55.7 | 371.9 | 60.9 | |
| 11,159 | MIN | 0.715 | −1.7 | 2881.8 | −41.0 | 21.7 | 39.4 | 179.0 | 49.7 |
| MEAN | 0.756 | 3.9 | 3179.6 | −35.4 | 26.4 | 44.2 | 214.0 | 52.6 | |
| MAX | 0.809 | 9.1 | 3501.3 | −30.9 | 29.8 | 47.6 | 249.7 | 55.2 | |
| 14,083 | MIN | 0.405 | −27.8 | 239.2 | −23.3 | 8.3 | 22.0 | 65.4 | 13.9 |
| MEAN | 0.539 | −20.1 | 343.2 | −20.5 | 10.4 | 24.7 | 131.0 | 15.2 | |
| MAX | 0.669 | −9.4 | 501.5 | −18.1 | 13.5 | 27.5 | 146.4 | 17.0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez, A.; Herrera, M.; de la Cruz, J.L.; Orozco, I. Coupled Model for Assessing the Present and Future Watershed Vulnerabilities to Climate Change Impacts. Water 2023, 15, 711. https://doi.org/10.3390/w15040711
Martínez A, Herrera M, de la Cruz JL, Orozco I. Coupled Model for Assessing the Present and Future Watershed Vulnerabilities to Climate Change Impacts. Water. 2023; 15(4):711. https://doi.org/10.3390/w15040711
Chicago/Turabian StyleMartínez, Adrián, Manuel Herrera, Jesús López de la Cruz, and Ismael Orozco. 2023. "Coupled Model for Assessing the Present and Future Watershed Vulnerabilities to Climate Change Impacts" Water 15, no. 4: 711. https://doi.org/10.3390/w15040711






