Intercomparing LSTM and RNN to a Conceptual Hydrological Model for a Low-Land River with a Focus on the Flow Duration Curve
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
2.3. Models
2.3.1. HBV
2.3.2. RNN
2.3.3. LSTM
2.4. Model Set-Up
2.4.1. RNN and LSTM Forcing Data
2.4.2. ML Model Architecture
2.4.3. Routing
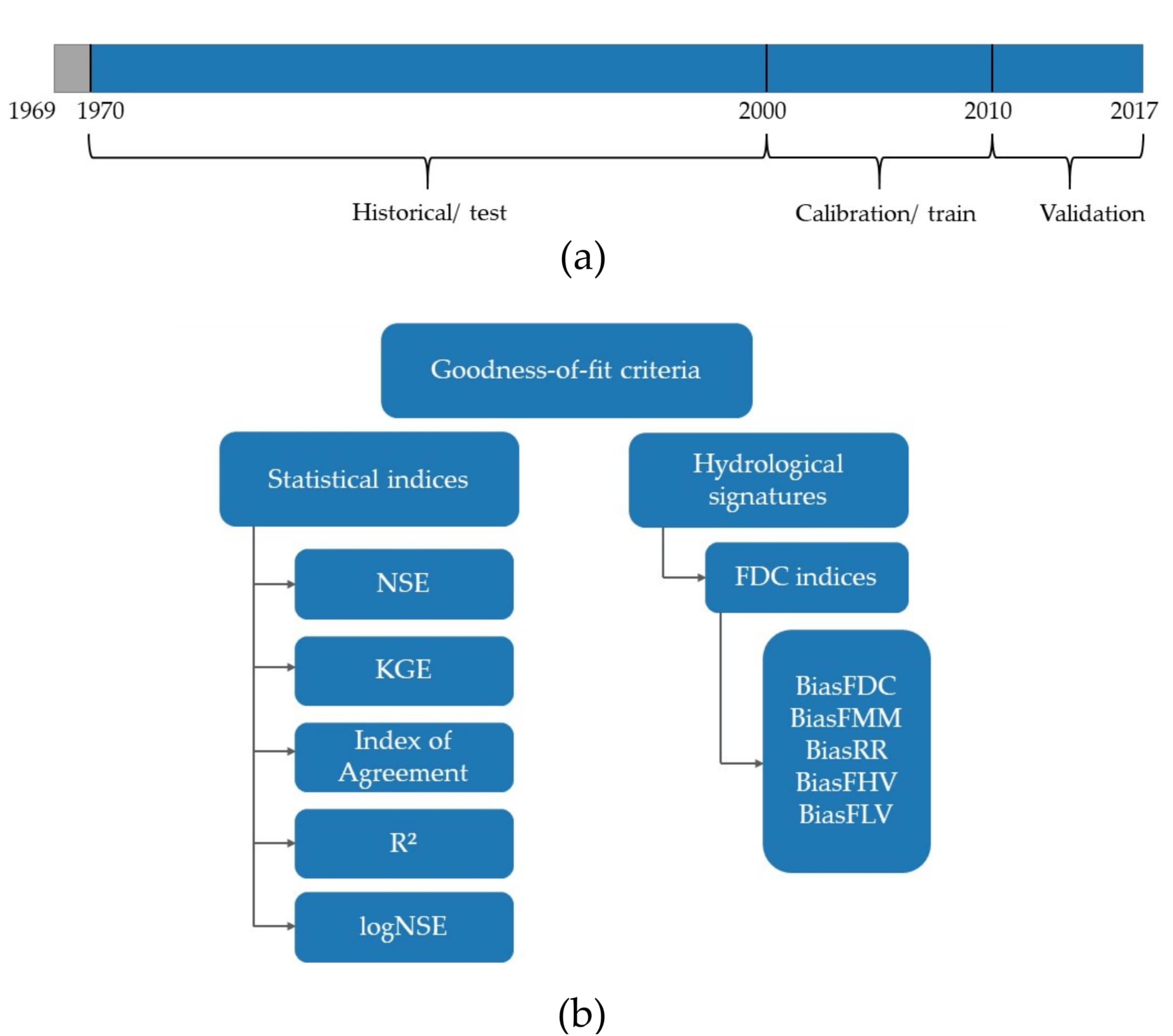
2.5. Calibration and Validation
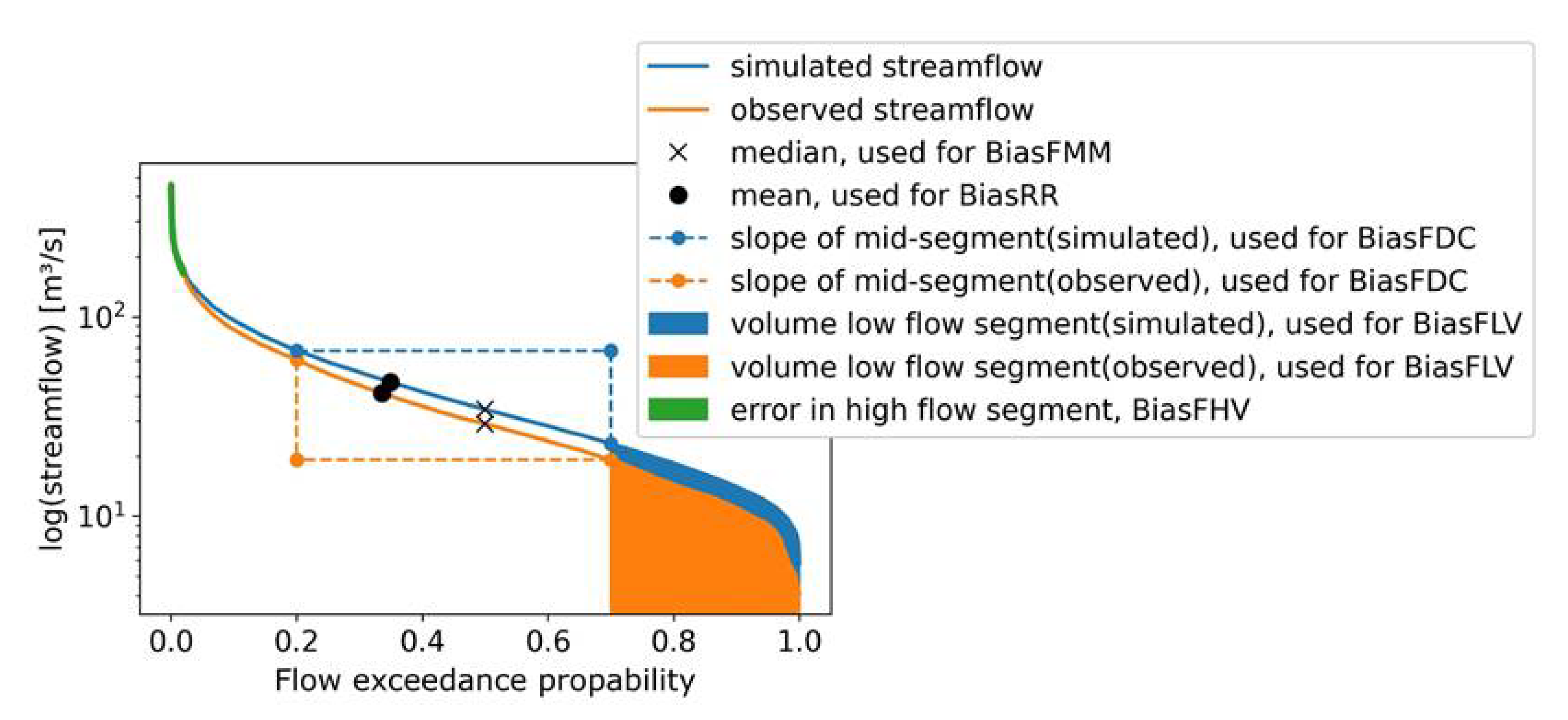
2.6. Model Evaluation
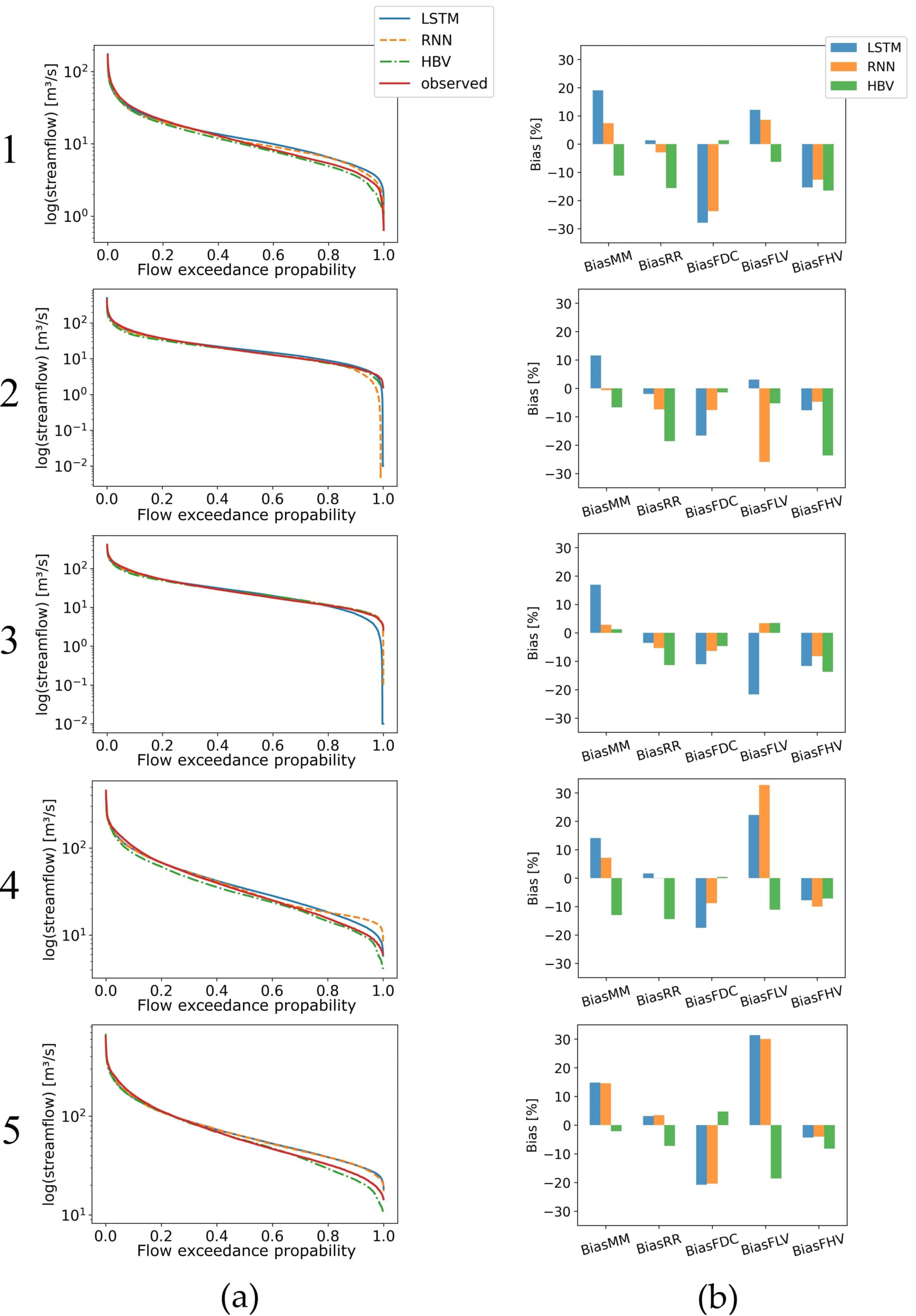
- 1.
- Bias RR: bias of the mean values in percent (black circles in Figure 4)
- 2.
- Bias MM: bias of the median values in percent (black crosses Figure 4)
- 3.
- Bias FDC midslope: bias of the mean slope in mid segment of FDC in percent (dashed lines in Figure 4)
- 4.
- Bias FLV: bias of the low segment of the FDC (orange and blue areas in Figure 4)
- 5.
- Bias FHV: bias of the high segment of the FDC (green area in Figure 4)
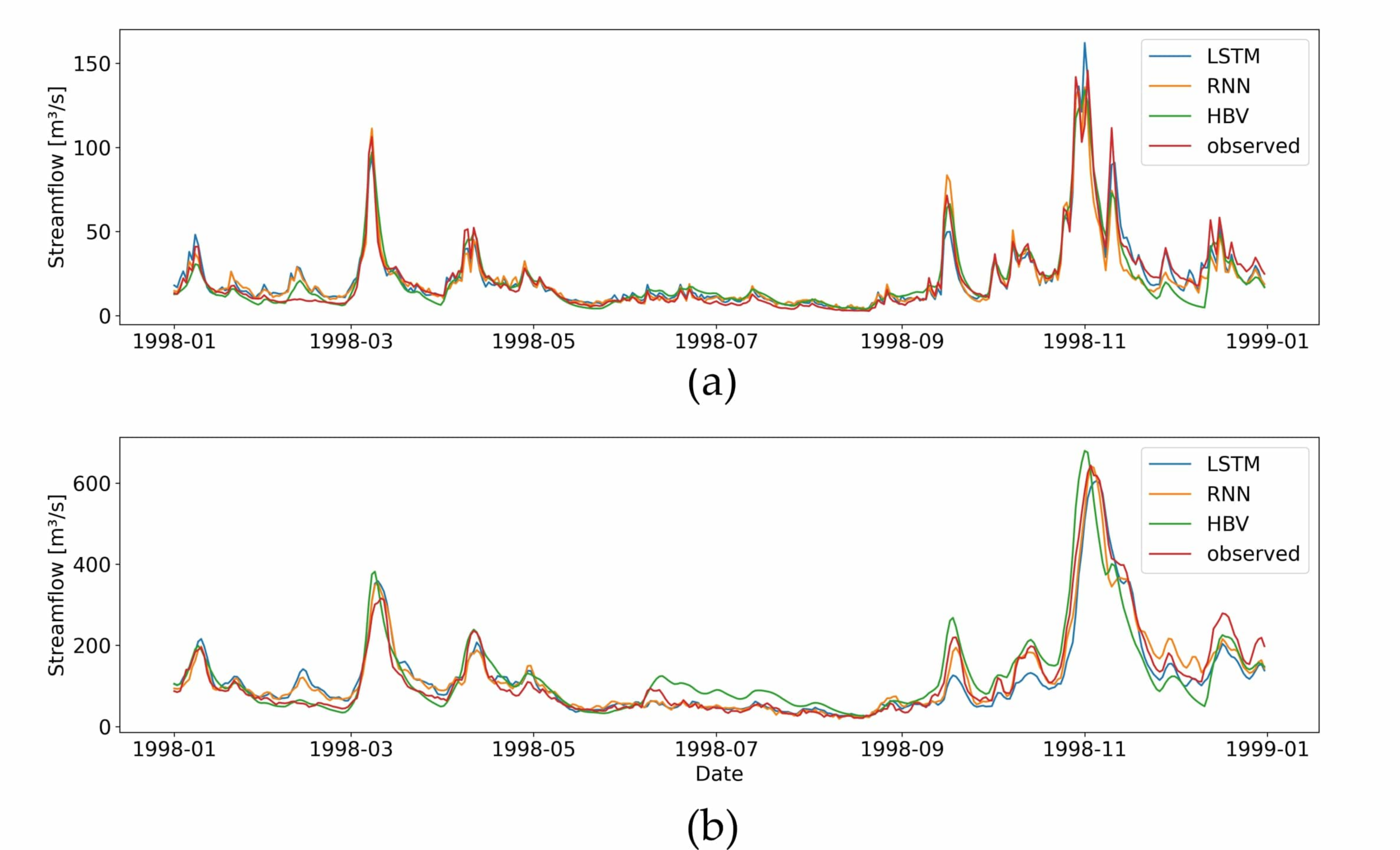
3. Results
3.1. Statistical Performance Indices
3.2. FDC and Signature Indices
4. Discussion
4.1. Statistical Performance Indices
4.2. FDC and Signature Indices
4.3. RNN Compared to LSTM
4.4. Routing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bergström, S.; Forsman, A. Development of a Conceptual Deterministic Rainfall-Runoff Model. Hydrol. Res. 1973, 4, 147–170. [Google Scholar] [CrossRef]
- Bergström, S. The HBV Model: Its Structure and Applications. SMHI Rep. Hydrol. 1992, 4, 35. [Google Scholar]
- Beven, K.; Binley, A. The Future of Distributed Models: Model Calibration and Uncertainty Prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Storm, B. Construction, Calibration and Validation of Hydrological Models. In Distributed Hydrological Modelling; Abbott, M.B., Refsgaard, J.C., Eds.; Water Science and Technology Library; Springer: Dordrecht, The Netherlands, 1996; pp. 41–54. ISBN 978-94-009-0257-2. [Google Scholar]
- Liu, Z.; Zhou, P.; Zhang, Y. A Probabilistic Wavelet–Support Vector Regression Model for Streamflow Forecasting with Rainfall and Climate Information Input. J. Hydrometeorol. 2015, 16, 2209–2229. [Google Scholar] [CrossRef]
- Duan, S.; Ullrich, P.; Shu, L. Using Convolutional Neural Networks for Streamflow Projection in California. Front. Water 2020, 2, 28. [Google Scholar] [CrossRef]
- Schmidt, L.; Heße, F.; Attinger, S.; Kumar, R. Challenges in Applying Machine Learning Models for Hydrological Inference: A Case Study for Flooding Events Across Germany. Water Resour. Res. 2020, 56, e2019WR025924. [Google Scholar] [CrossRef]
- Gao, C.; Gemmer, M.; Zeng, X.; Liu, B.; Su, B.; Wen, Y. Projected Streamflow in the Huaihe River Basin (2010–2100) Using Artificial Neural Network. Stoch Env. Res Risk Assess 2010, 24, 685–697. [Google Scholar] [CrossRef]
- Noori, N.; Kalin, L. Coupling SWAT and ANN Models for Enhanced Daily Streamflow Prediction. J. Hydrol. 2016, 533, 141–151. [Google Scholar] [CrossRef]
- Peng, T.; Zhou, J.; Zhang, C.; Fu, W. Streamflow Forecasting Using Empirical Wavelet Transform and Artificial Neural Networks. Water 2017, 9, 406. [Google Scholar] [CrossRef]
- Kisi, O.; Cimen, M. A Wavelet-Support Vector Machine Conjunction Model for Monthly Streamflow Forecasting. J. Hydrol. 2011, 399, 132–140. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y. Monthly Streamflow Prediction Using Modified EMD-Based Support Vector Machine. J. Hydrol. 2014, 511, 764–775. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Towards Learning Universal, Regional, and Local Hydrological Behaviors via Machine Learning Applied to Large-Sample Datasets. Hydrol. Earth Syst. Sci. 2019, 23, 5089–5110. [Google Scholar] [CrossRef]
- Le; Ho; Lee; Jung Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. [CrossRef]
- Feng, D.; Fang, K.; Shen, C. Enhancing Streamflow Forecast and Extracting Insights Using Long-Short Term Memory Networks With Data Integration at Continental Scales. Water Resour. Res. 2020, 56, e2019WR026793. [Google Scholar] [CrossRef]
- Scorzini, A.R.; Di Bacco, M.; De Luca, G.; Tallini, M. Deep Learning for Earthquake Hydrology? Insights from the Karst Gran Sasso Aquifer in Central Italy. J. Hydrol. 2023, 617, 129002. [Google Scholar] [CrossRef]
- Zhou, R.; Zhang, Y. On the Role of the Architecture for Spring Discharge Prediction with Deep Learning Approaches. Hydrol. Process. 2022, 36, e14737. [Google Scholar] [CrossRef]
- Chang, Y.-S.; Chiao, H.-T.; Abimannan, S.; Huang, Y.-P.; Tsai, Y.-T.; Lin, K.-M. An LSTM-Based Aggregated Model for Air Pollution Forecasting. Atmos. Pollut. Res. 2020, 11, 1451–1463. [Google Scholar] [CrossRef]
- Haq, M.; Jilani, A.; Prabu, P. Deep Learning Based Modeling of Groundwater Storage Change. CMC 2021, 70, 4599–4617. [Google Scholar] [CrossRef]
- Le, X.-H.; Nguyen, D.-H.; Jung, S.; Yeon, M.; Lee, G. Comparison of Deep Learning Techniques for River Streamflow Forecasting. IEEE Access 2021, 9, 71805–71820. [Google Scholar] [CrossRef]
- Solgi, R.; Loáiciga, H.A.; Kram, M. Long Short-Term Memory Neural Network (LSTM-NN) for Aquifer Level Time Series Forecasting Using in-Situ Piezometric Observations. J. Hydrol. 2021, 601, 126800. [Google Scholar] [CrossRef]
- Anul Haq, M. CDLSTM: A Novel Model for Climate Change Forecasting. Comput. Mater. Contin. 2022, 71, 2363–2381. [Google Scholar] [CrossRef]
- Seibert, J.; Bergström, S. A Retrospective on Hydrological Catchment Modelling Based on Half a Century with the HBV Model. Hydrol. Earth Syst. Sci. 2022, 26, 1371–1388. [Google Scholar] [CrossRef]
- Loganathan, P.; Mahindrakar, A.B. Intercomparing the Robustness of Machine Learning Models in Simulation and Forecasting of Streamflow. J. Water Clim. Change 2020, 12, 1824–1837. [Google Scholar] [CrossRef]
- Wheater, H.S.; Peach, D.; Binley, A. Characterising Groundwater-Dominated Lowland Catchments: The UK Lowland Catchment Research Programme (LOCAR). Hydrol. Earth Syst. Sci. 2007, 11, 108–124. [Google Scholar] [CrossRef]
- Geschäftsstelle Ems; Ministerie van Verkeer en Waterstaa; Geschäftsstelle Ems-NRW. Internationaler Bewirtschaftungplan nach Artikel 13 Wasserrahmenrichtlinie für die Flussgebietseinheit Ems; Geschäftsstelle der FGG Ems: Meppen, Germany, 2009. [Google Scholar]
- Wendland, F.; Bogena, H.; Goemann, H.; Hake, J.F.; Kreins, P.; Kunkel, R. Impact of Nitrogen Reduction Measures on the Nitrogen Loads of the River Ems and Rhine (Germany). Phys. Chem. Earth Parts A/B/C 2005, 30, 527–541. [Google Scholar] [CrossRef]
- DWD Climate Data Center. Available online: https://www.dwd.de/EN/climate_environment/cdc/cdc_node_en.html (accessed on 30 November 2022).
- BFG Global Runoff Data Centre. Available online: https://www.bafg.de/GRDC/EN/Home/homepage_node.html (accessed on 30 November 2022).
- European Environment Agency; European Union; Copernicus Land Monitoring Service. Corine Land Cover; European Environment Agency: Copenhagen, Denmark, 2018. [Google Scholar]
- Haude, W. Zur Bestimmung Der Verdunstung Auf Möglichst Einfache Weise. Mitt Dt Wetterd 1955, 11, 1–24. [Google Scholar]
- Götzinger, J.; Bárdossy, A. Comparison of Four Regionalisation Methods for a Distributed Hydrological Model. J. Hydrol. 2006, 333, 374–384. [Google Scholar] [CrossRef]
- Wrede, S.; Seibert, J.; Uhlenbrook, S. Distributed Conceptual Modelling in a Swedish Lowland Catchment: A Multi-Criteria Model Assessment. Hydrol. Res. 2013, 44, 318–333. [Google Scholar] [CrossRef]
- Booij, M.J.; Krol, M.S. Balance between Calibration Objectives in a Conceptual Hydrological Model. Hydrol. Sci. J. 2010, 55, 1017–1032. [Google Scholar] [CrossRef]
- Výleta, R.; Sleziak, P.; Hlavčová, K.; Danáčová, M.; Aleksić, M.; Szolgay, J.; Kohnová, S. An HBV-Model Based Approach for Studying the Effects of Projected Climate Change on Water Resources in Slovakia; Copernicus Meetings: Vienna, Austria, 2022. [Google Scholar]
- Breuer, L.; Huisman, J.A.; Willems, P.; Bormann, H.; Bronstert, A.; Croke, B.F.W.; Frede, H.-G.; Gräff, T.; Hubrechts, L.; Jakeman, A.J.; et al. Assessing the Impact of Land Use Change on Hydrology by Ensemble Modeling (LUCHEM). I: Model Intercomparison with Current Land Use. Adv. Water Resour. 2009, 32, 129–146. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Werbos, P.J. Generalization of Backpropagation with Application to a Recurrent Gas Market Model. Neural Netw. 1988, 1, 339–356. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning Long-Term Dependencies with Gradient Descent Is Difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–Runoff Modelling Using Long Short-Term Memory (LSTM) Networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Li, P.; Zhang, J.; Krebs, P. Prediction of Flow Based on a CNN-LSTM Combined Deep Learning Approach. Water 2022, 14, 993. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Gauch, M.; Klingler, C.; Nearing, G.; Hochreiter, S. Large-Scale River Network Modeling Using Graph Neural Networks. In Proceedings of the 23rd EGU General Assembly, Virtual, 19–30 April 2021. [Google Scholar]
- Lees, T.; Buechel, M.; Anderson, B.; Slater, L.; Reece, S.; Coxon, G.; Dadson, S.J. Benchmarking Data-Driven Rainfall–Runoff Models in Great Britain: A Comparison of Long Short-Term Memory (LSTM)-Based Models with Four Lumped Conceptual Models. Hydrol. Earth Syst. Sci. 2021, 25, 5517–5534. [Google Scholar] [CrossRef]
- Althoff, D.; Rodrigues, L.N.; Silva, D.D. da Addressing Hydrological Modeling in Watersheds under Land Cover Change with Deep Learning. Adv. Water Resour. 2021, 154, 103965. [Google Scholar] [CrossRef]
- Haq, M.A.; Ahmed, A.; Khan, I.; Gyani, J.; Mohamed, A.; Attia, E.-A.; Mangan, P.; Pandi, D. Analysis of Environmental Factors Using AI and ML Methods. Sci Rep 2022, 12, 13267. [Google Scholar] [CrossRef]
- Bormann, H.; De Brito, M.M.; Charchousi, D.; Chatzistratis, D.; David, A.; Grosser, P.F.; Kebschull, J.; Konis, A.; Koutalakis, P.; Korali, A.; et al. Impact of Hydrological Modellers’ Decisions and Attitude on the Performance of a Calibrated Conceptual Catchment Model: Results from a ‘Modelling Contest. Hydrology 2018, 5, 64. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.; Xie, J. Simulating Runoff under Changing Climatic Conditions: A Comparison of the Long Short-Term Memory Network with Two Conceptual Hydrologic Models. J. Hydrol. 2021, 592, 125779. [Google Scholar] [CrossRef]
- Van Werkhoven, K.; Wagener, T.; Reed, P.; Tang, Y. Sensitivity-Guided Reduction of Parametric Dimensionality for Multi-Objective Calibration of Watershed Models. Adv. Water Resour. 2009, 32, 1154–1169. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Gupta, H.V.; Wagener, T. A Process-Based Diagnostic Approach to Model Evaluation: Application to the NWS Distributed Hydrologic Model. Water Resour. Res. 2008, 44, 1–18. [Google Scholar] [CrossRef]
- Casper, M.C.; Grigoryan, G.; Gronz, O.; Gutjahr, O.; Heinemann, G.; Ley, R.; Rock, A. Analysis of Projected Hydrological Behavior of Catchments Based on Signature Indices. Hydrol. Earth Syst. Sci. 2012, 16, 409–421. [Google Scholar] [CrossRef]
- Ley, R.; Hellebrand, H.; Casper, M.C.; Fenicia, F. Comparing Classical Performance Measures with Signature Indices Derived from Flow Duration Curves to Assess Model Structures as Tools for Catchment Classification. Hydrol. Res. 2016, 47, 1–14. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.V.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Gauch, M.; Kratzert, F.; Klotz, D.; Nearing, G.; Lin, J.; Hochreiter, S. Rainfall–Runoff Prediction at Multiple Timescales with a Single Long Short-Term Memory Network. Hydrol. Earth Syst. Sci. 2021, 25, 2045–2062. [Google Scholar] [CrossRef]
- Zhang, L.; Bellugi, D.; Kadi, J.; Kamat, A.; Gorski, G.; Larsen, L. Physics-Informed LSTM for Streamflow Modeling Using a Dataset of Intensively-Monitored Watersheds in the USA. In Proceedings of the AGU Fall Meeting 2021, New Orleans, LA, USA, 13–17 December 2021. [Google Scholar]
- De Vos, N.J.; Rientjes, T.H.M. Multiobjective Training of Artificial Neural Networks for Rainfall-Runoff Modeling. Water Resour. Res. 2008, 44, W08434. [Google Scholar] [CrossRef]
- Hellwig, J.; Stahl, K. An Assessment of Trends and Potential Future Changes in Groundwater-Baseflow Drought Based on Catchment Response Times. Hydrol. Earth Syst. Sci. 2018, 22, 6209–6224. [Google Scholar] [CrossRef]


| Data | Number of Stations | Source | Required For |
|---|---|---|---|
| Precipitation (daily sum) | 142 | DWD | HBV, LSTM, RNN |
| Rel. Humidity (hourly mean) | 10 | DWD | HBV (pET estimation after Haude [31]) |
| Maximum Temperature (daily) | 25 | DWD | LSTM, RNN |
| Minimum Temperature (daily) | 25 | DWD | LSTM, RNN |
| Temperature (daily mean) | 33 | DWD | HBV |
| Temperature (hourly mean) | 8 | DWD | HBV (pET estimation after Haude [31]) |
| Vapor Pressure (daily mean) | 29 | DWD | LSTM, RNN |
| Streamflow (daily mean) | 5 | GRDC | HBV, LSTM, RNN |
| Number of Sub-catchment | Area (km2) | Flow Length (km) | BFI (%) |
|---|---|---|---|
| 1 | 1448 | 87 | 55 |
| 2 | 1283 | 26 | 51 |
| 3 | 871 | 40 | 57 |
| 4 | 1150 | 59 | 61 |
| 5 | 3324 | 22 | 55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ley, A.; Bormann, H.; Casper, M. Intercomparing LSTM and RNN to a Conceptual Hydrological Model for a Low-Land River with a Focus on the Flow Duration Curve. Water 2023, 15, 505. https://doi.org/10.3390/w15030505
Ley A, Bormann H, Casper M. Intercomparing LSTM and RNN to a Conceptual Hydrological Model for a Low-Land River with a Focus on the Flow Duration Curve. Water. 2023; 15(3):505. https://doi.org/10.3390/w15030505
Chicago/Turabian StyleLey, Alexander, Helge Bormann, and Markus Casper. 2023. "Intercomparing LSTM and RNN to a Conceptual Hydrological Model for a Low-Land River with a Focus on the Flow Duration Curve" Water 15, no. 3: 505. https://doi.org/10.3390/w15030505
APA StyleLey, A., Bormann, H., & Casper, M. (2023). Intercomparing LSTM and RNN to a Conceptual Hydrological Model for a Low-Land River with a Focus on the Flow Duration Curve. Water, 15(3), 505. https://doi.org/10.3390/w15030505






