Bragg Resonance of Water Waves by Multiple Permeable Thin Barriers over Periodic Breakwaters
Abstract
:1. Introduction
2. Methodology
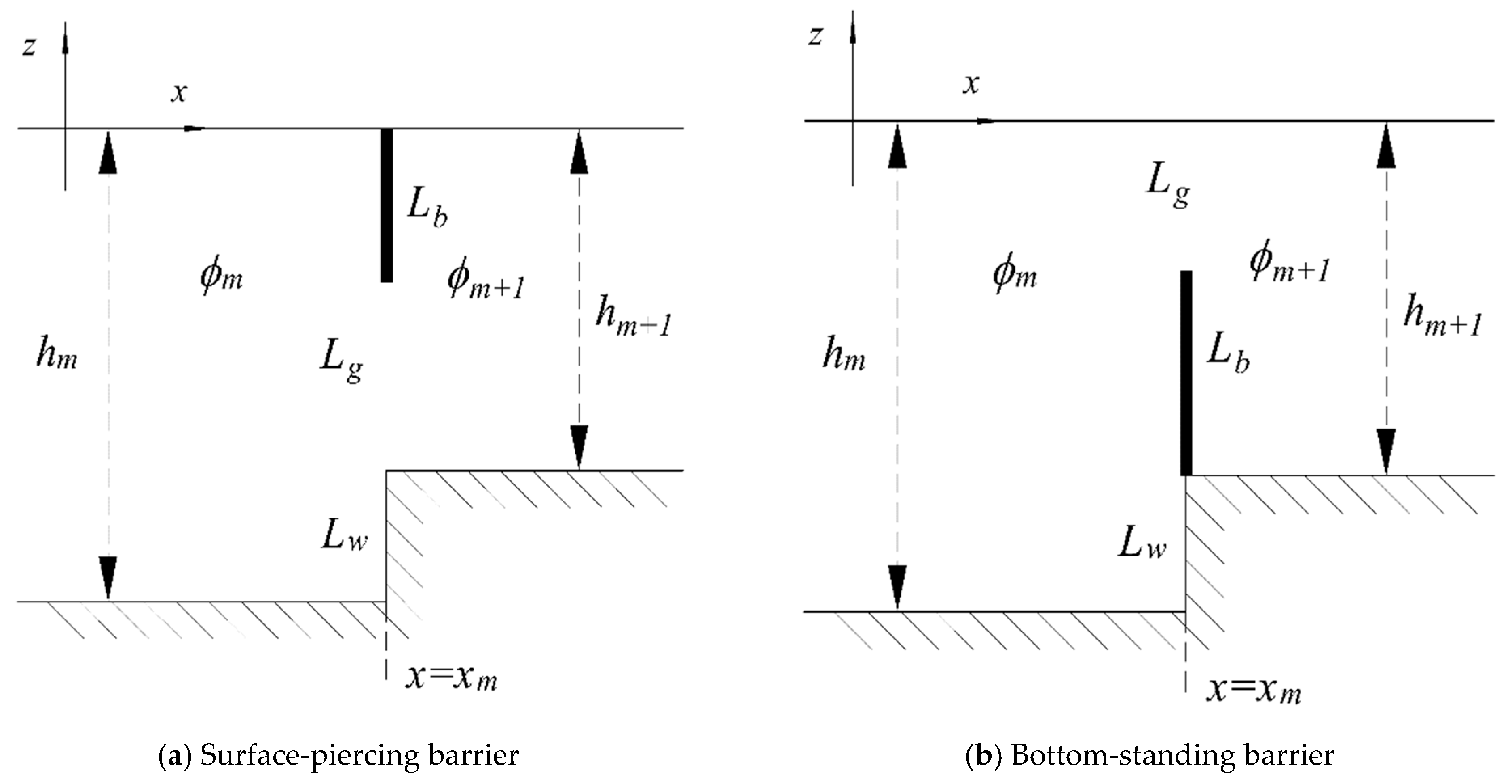
2.1. The Mathematical Model
2.2. Method of Solution
3. Results
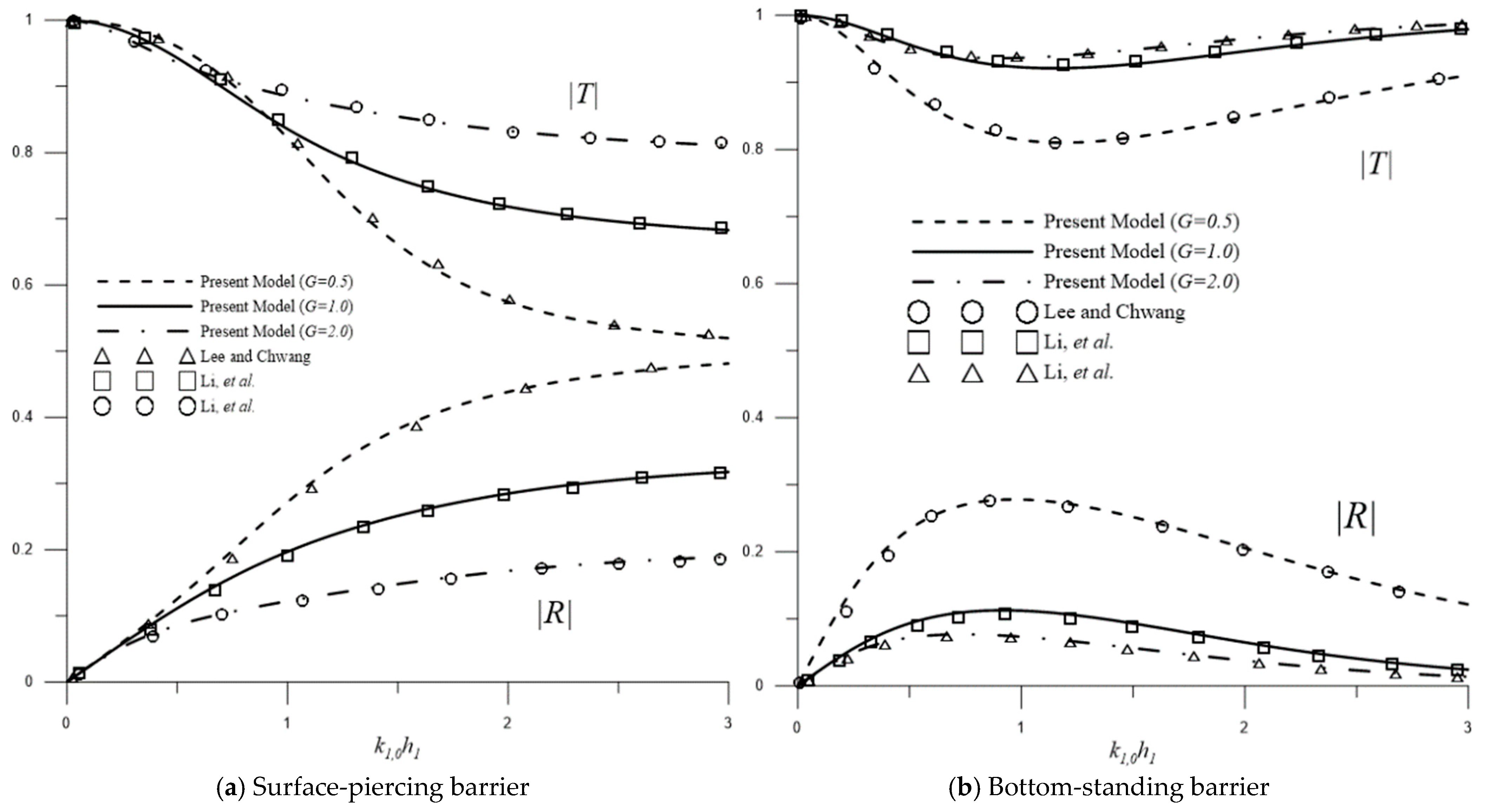
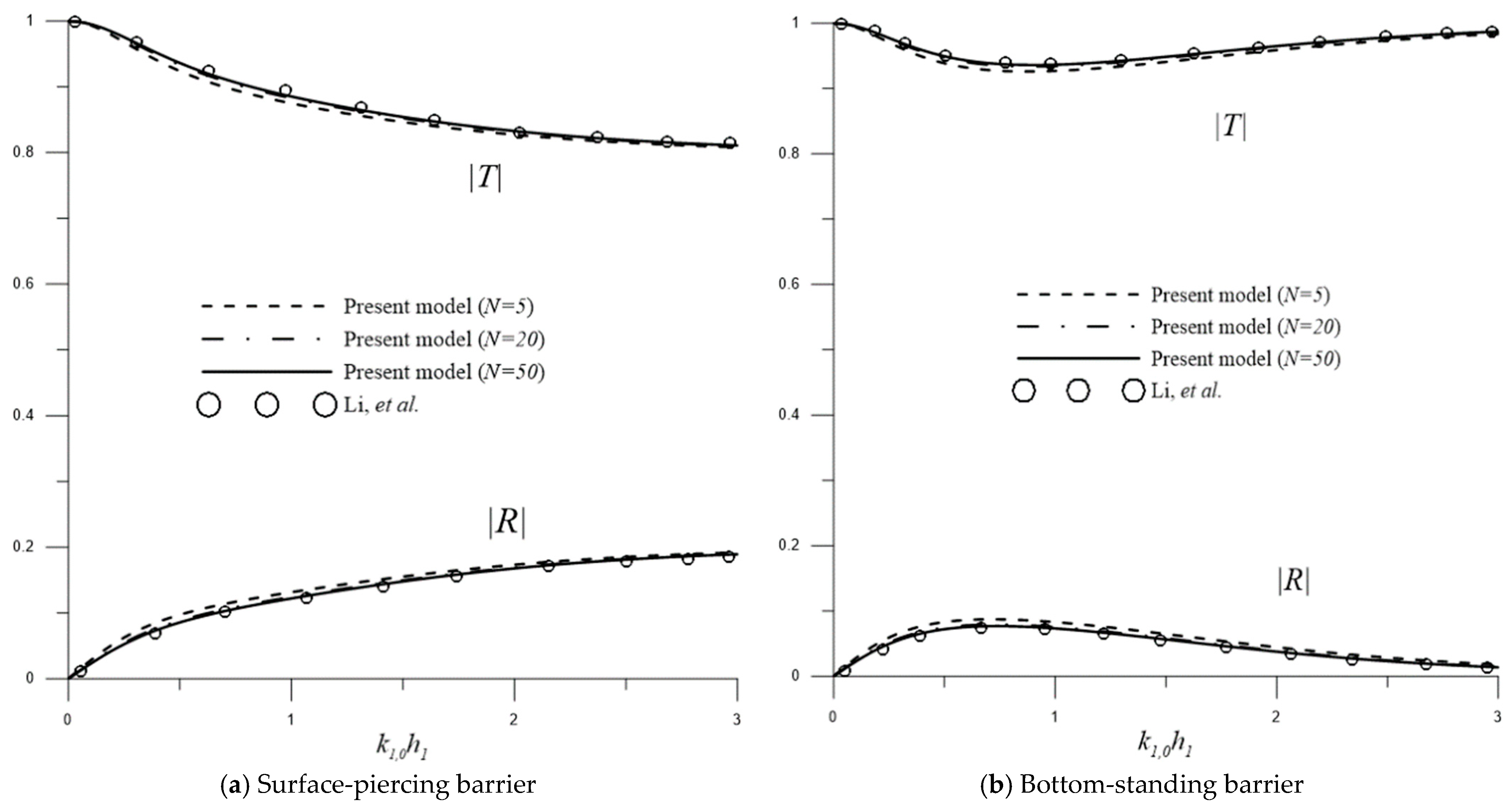
3.1. Water Wave Interactions with a Single Permeable Barrier over Flat Bottom Topography
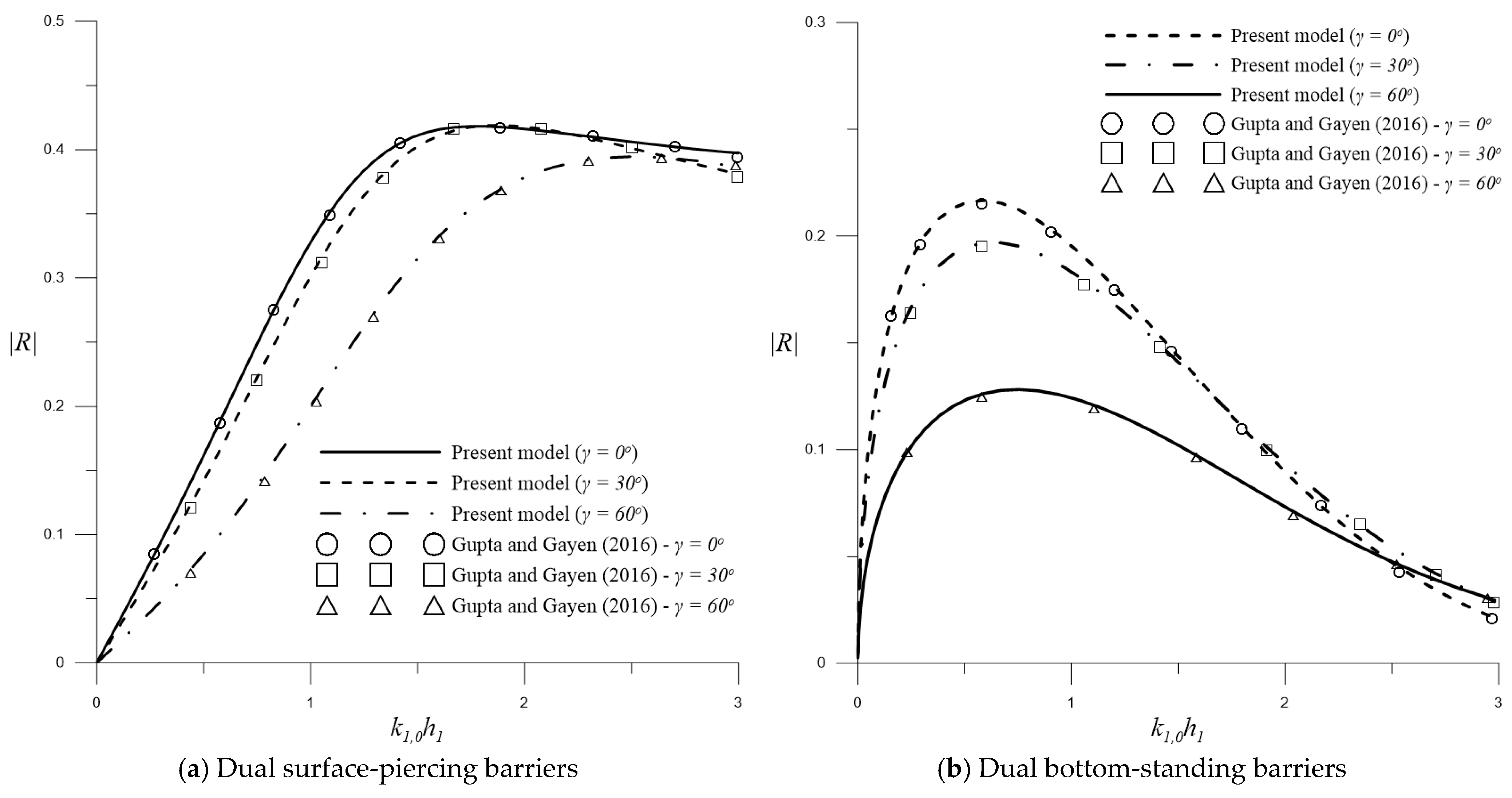
3.2. Water Wave Scattering by Dual Permeable Barriers over Uniform Bottom
3.3. Water Wave Scattering over Periodic Breakwaters
3.4. Water Scattering by Fully Submerged Barriers behind an Undulated Bottom
4. Discussion
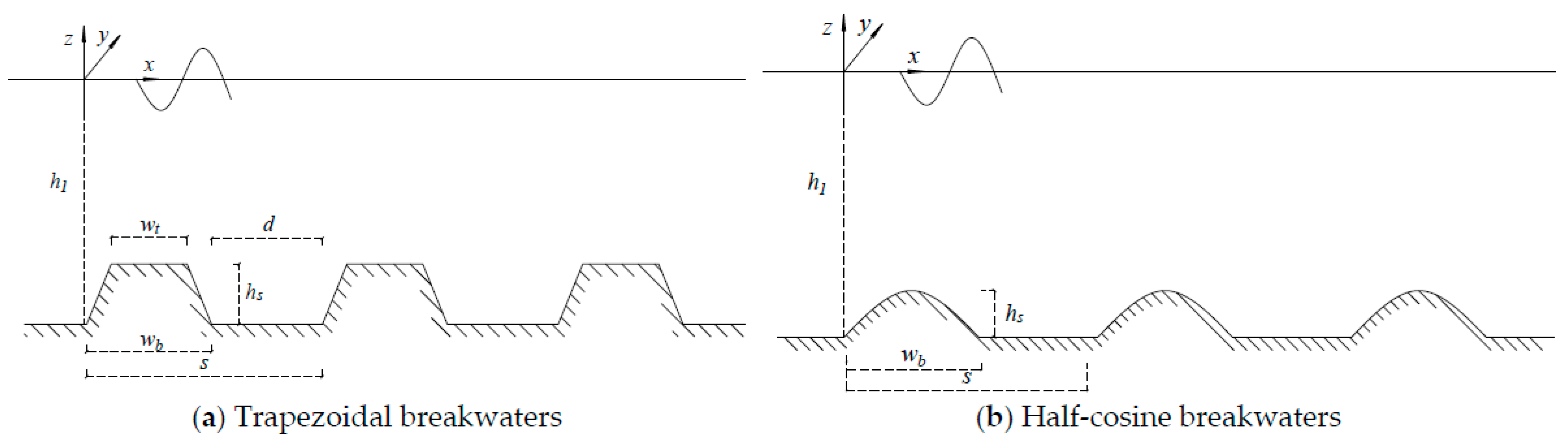
4.1. Permeable Thin Barriers with Trapezoidal Breakwaters
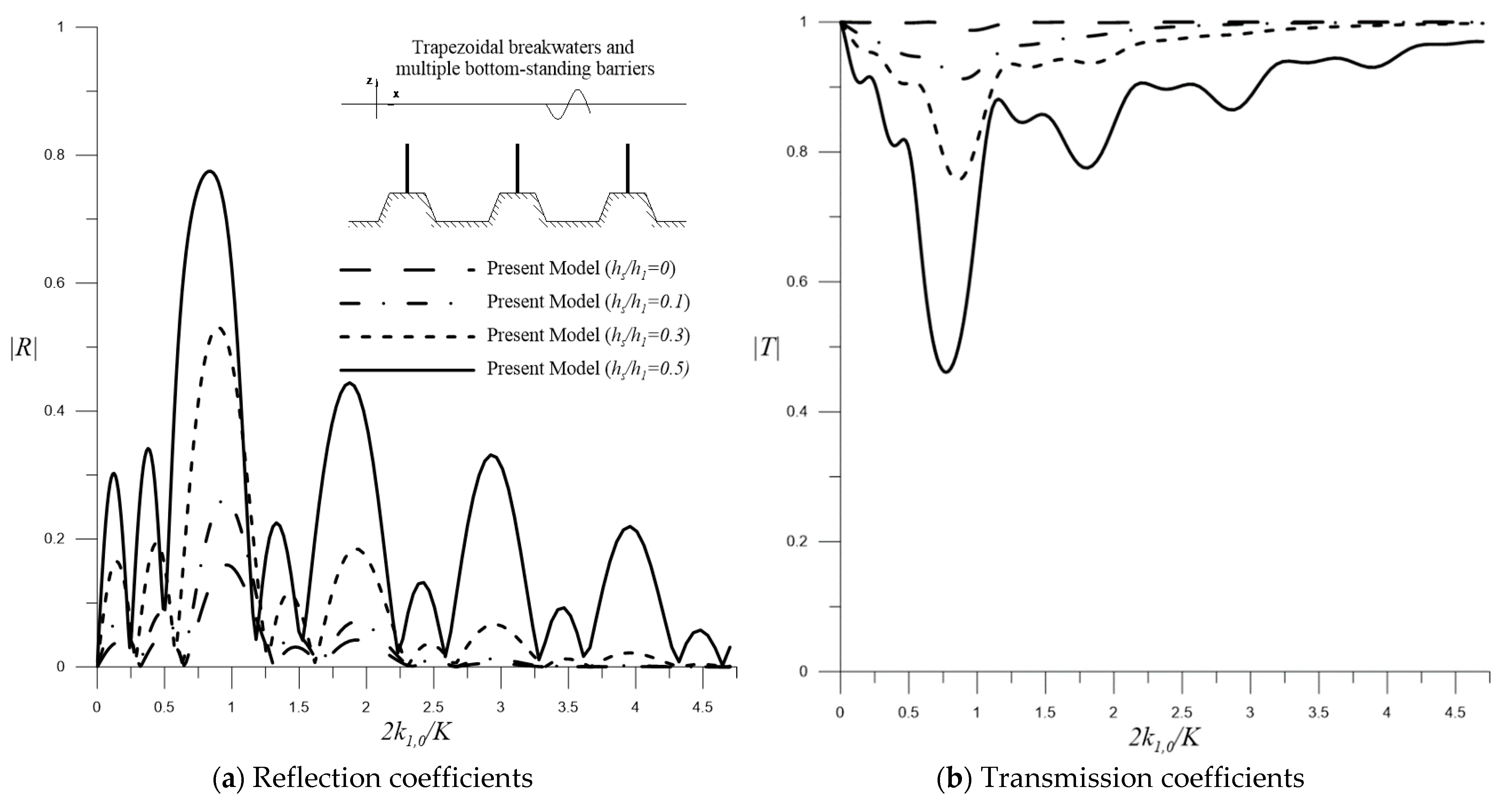
4.1.1. Bottom-Standing Barriers
Influence of Breakwater Amplitudes
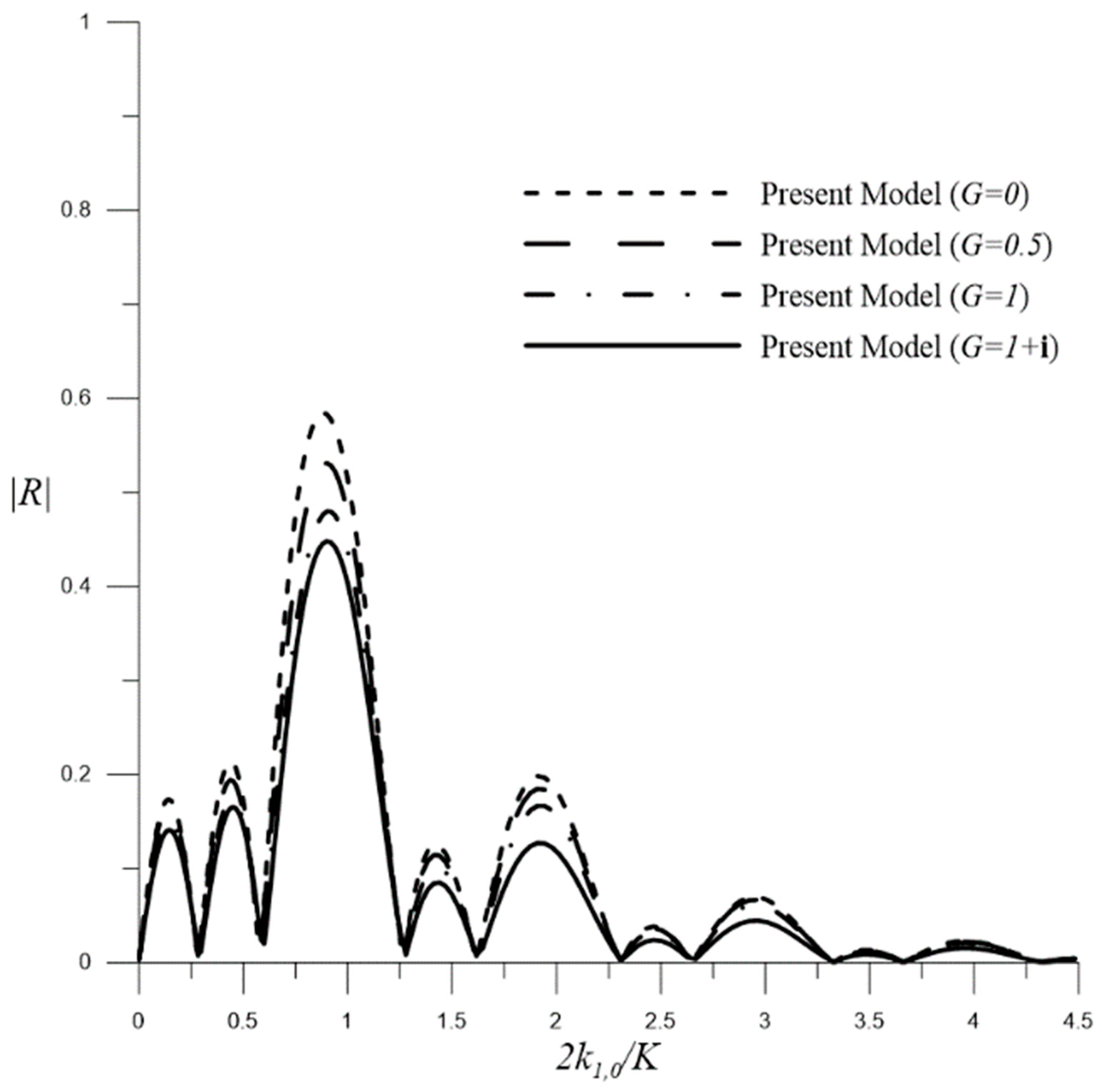
Influence of Permeable Parameters
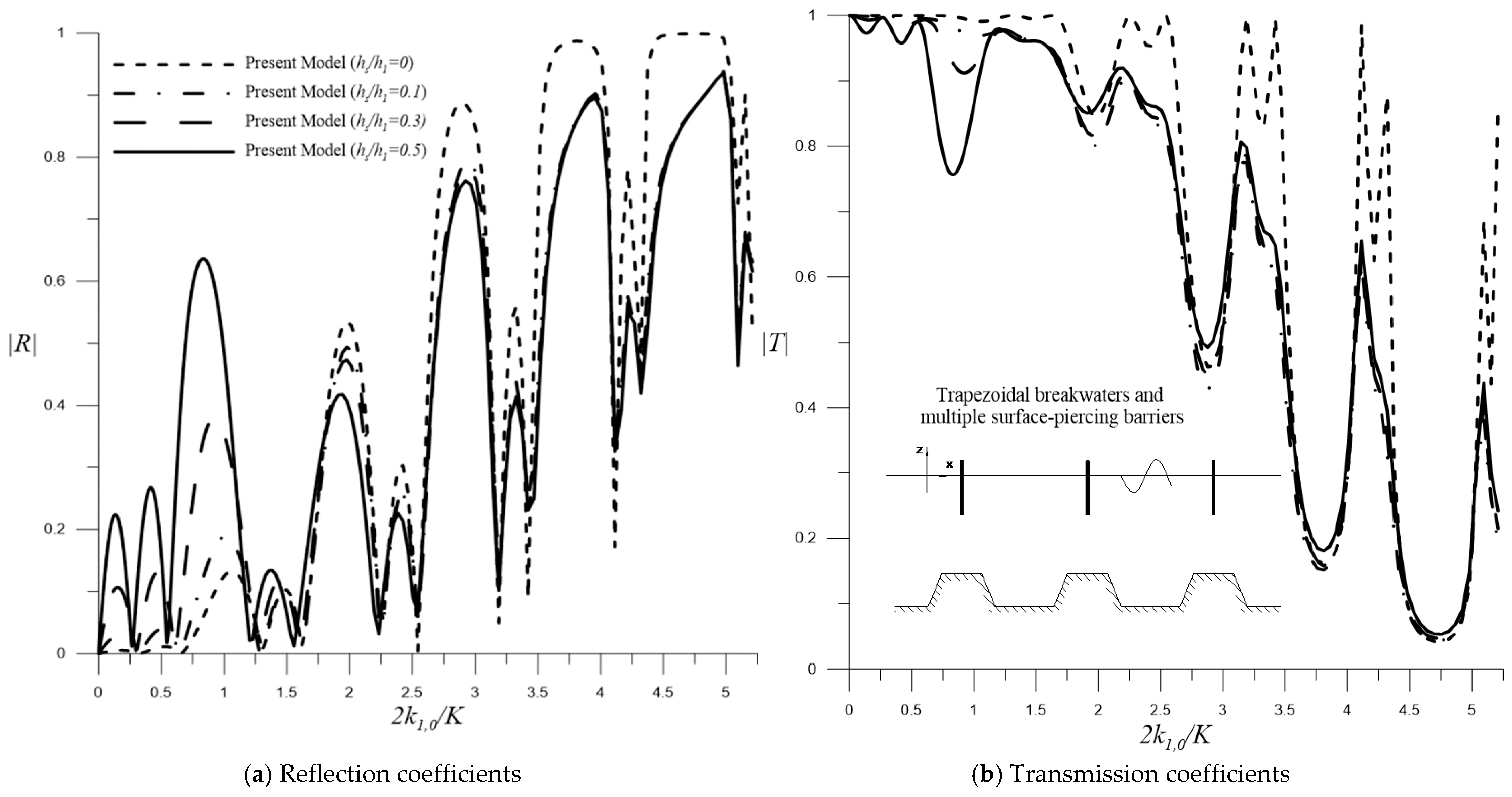
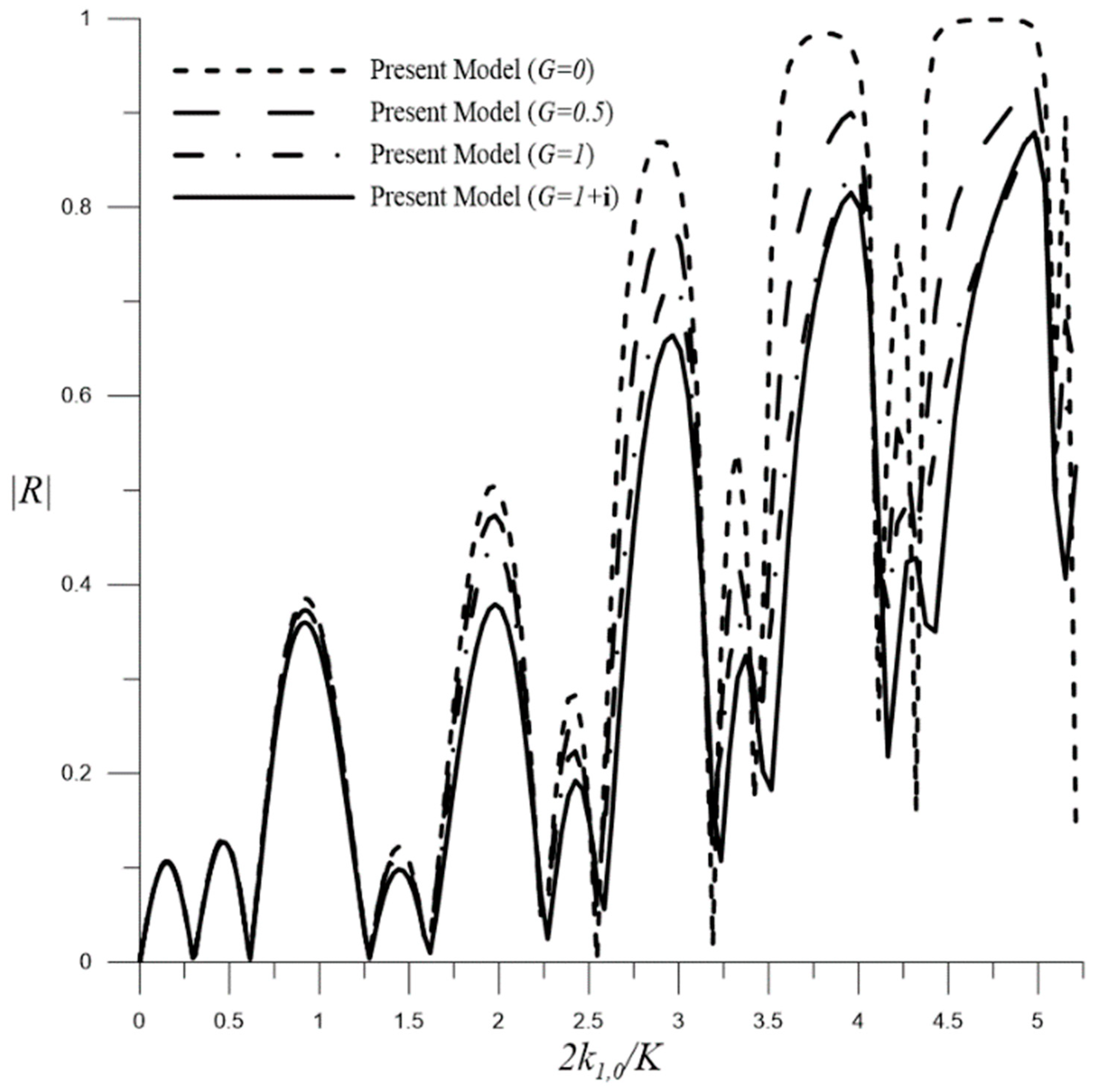
4.1.2. Surface-Piercing Barriers
Influence of Breakwater Amplitudes
Influence of Permeable Parameters
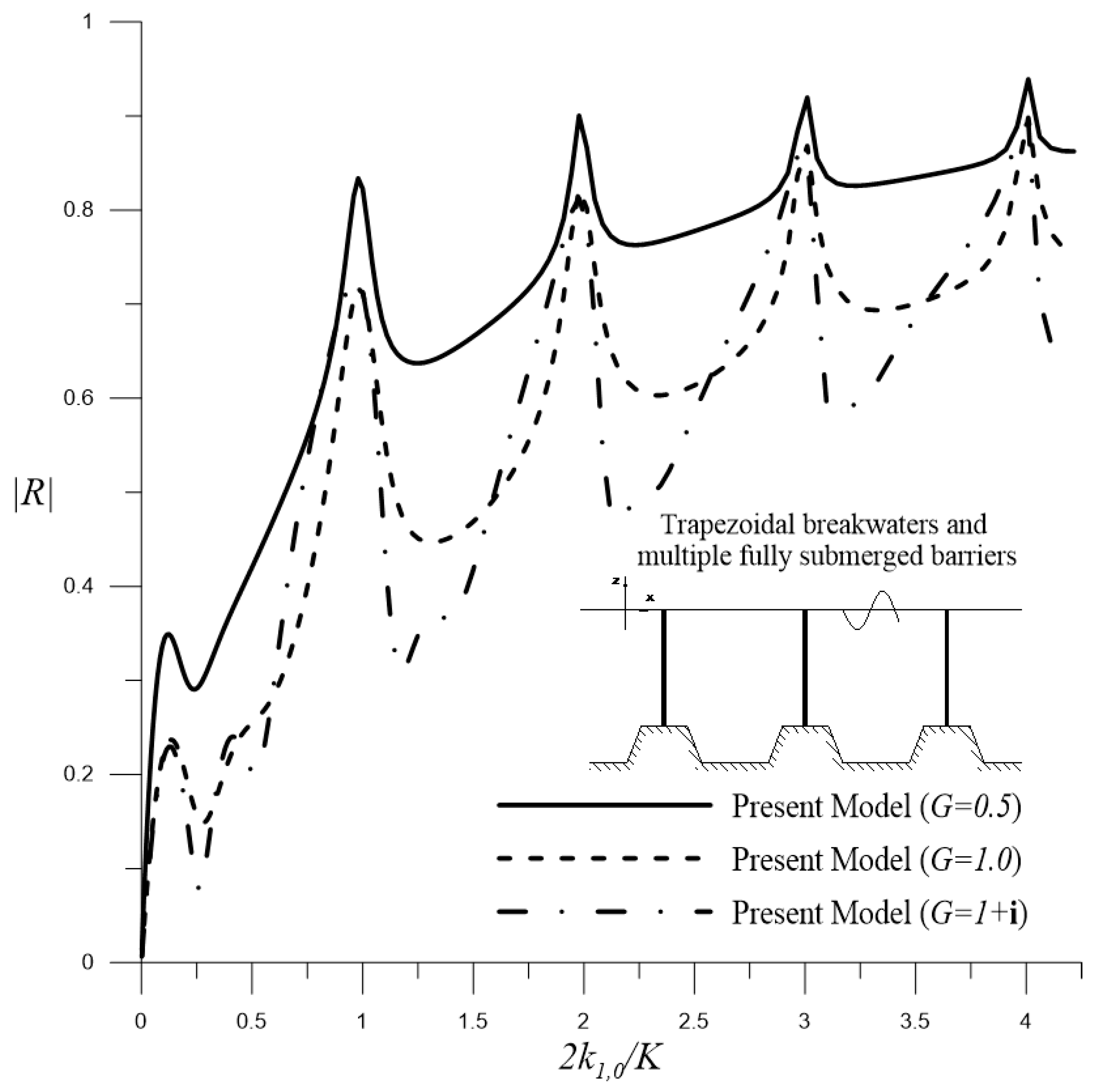
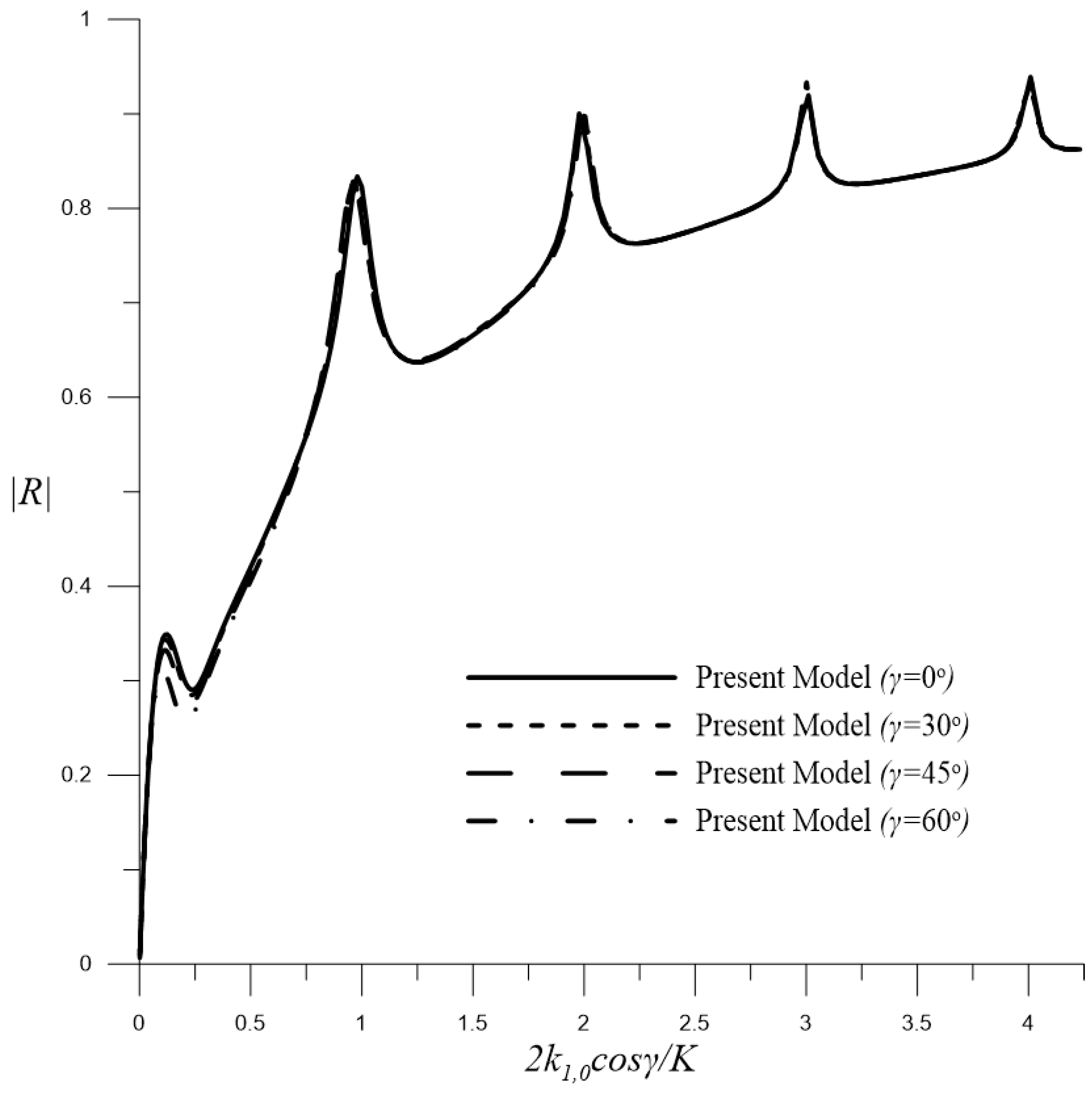
4.1.3. Fully Submerged Permeable Barriers
4.2. Permeable Thin Barriers with Half-Cosine Breakwaters
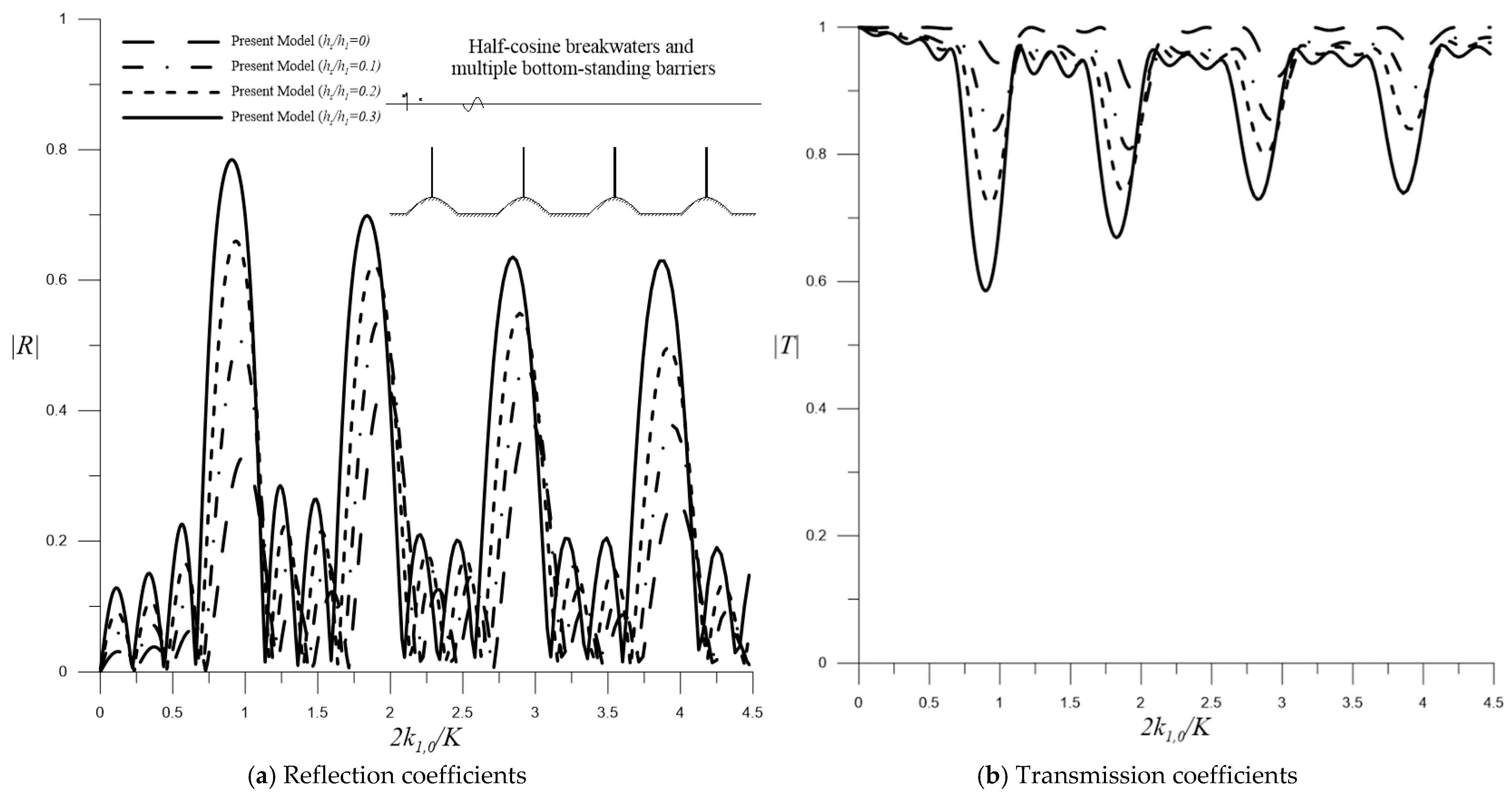
4.2.1. Bottom-Standing Barriers
Influence of Breakwater Amplitudes
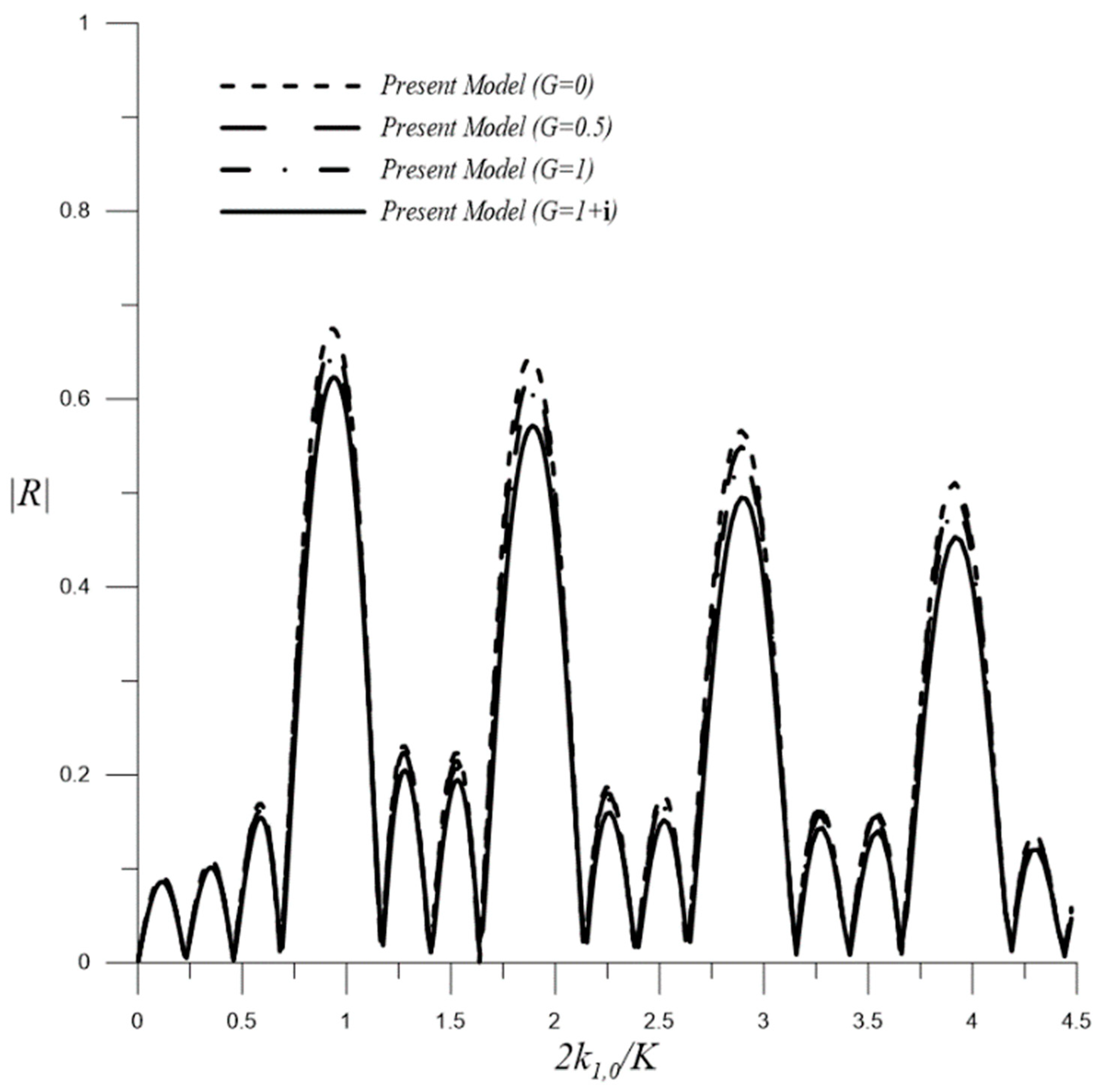
Influence of Permeable Parameters
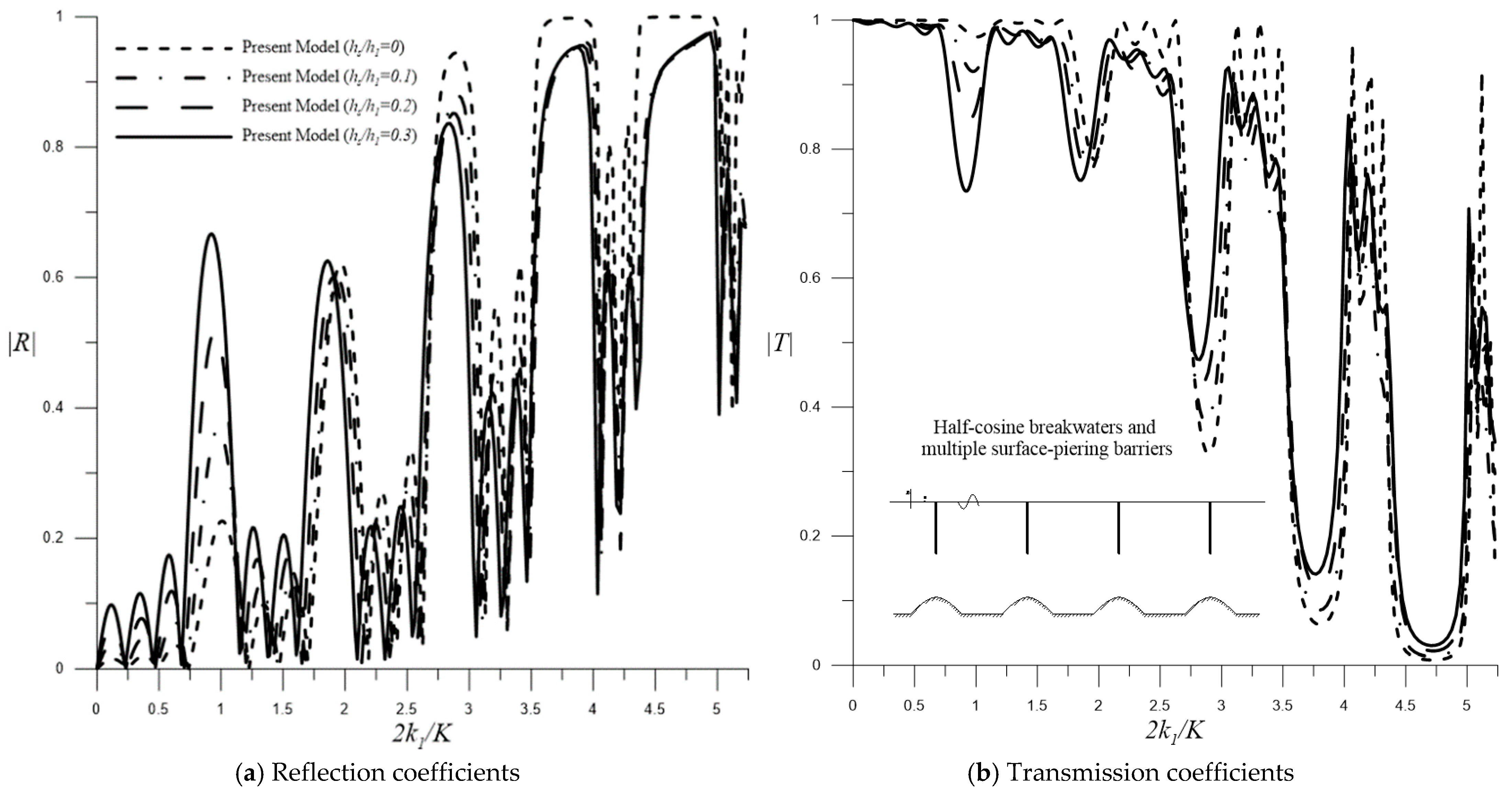
4.2.2. Surface-Piercing Barriers
Influence of Breakwater Amplitudes
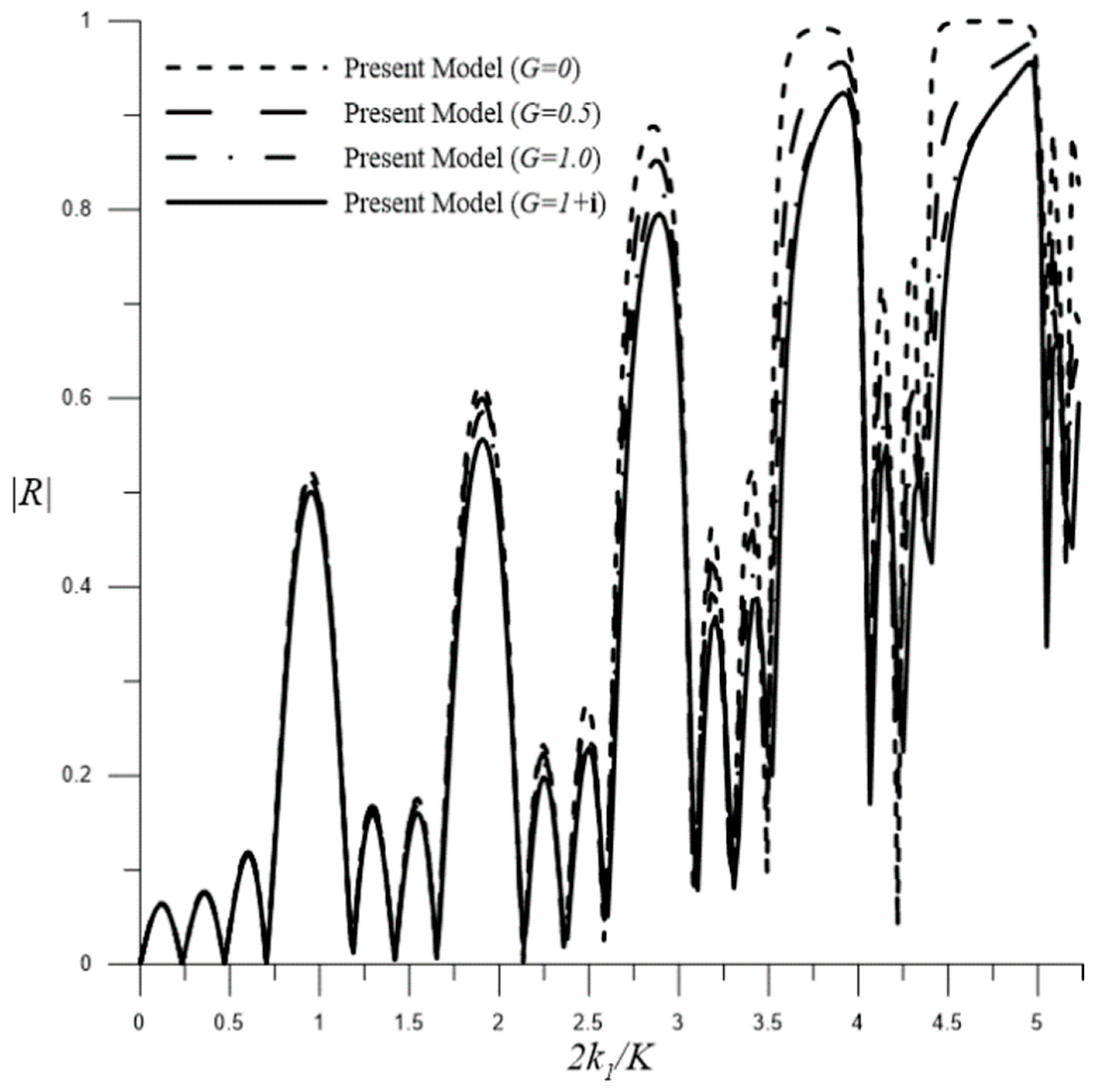
Influence of Permeable Parameters
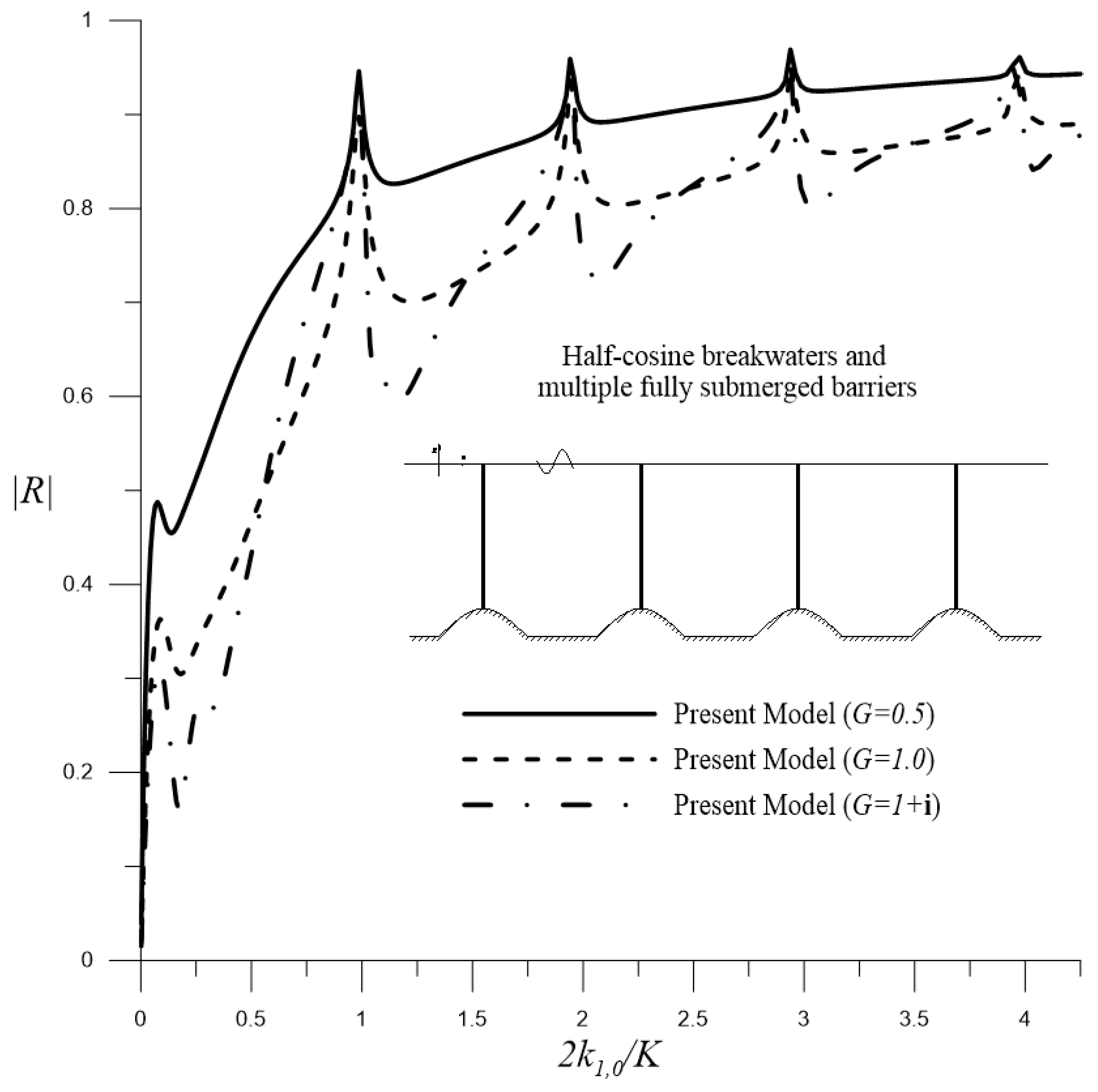
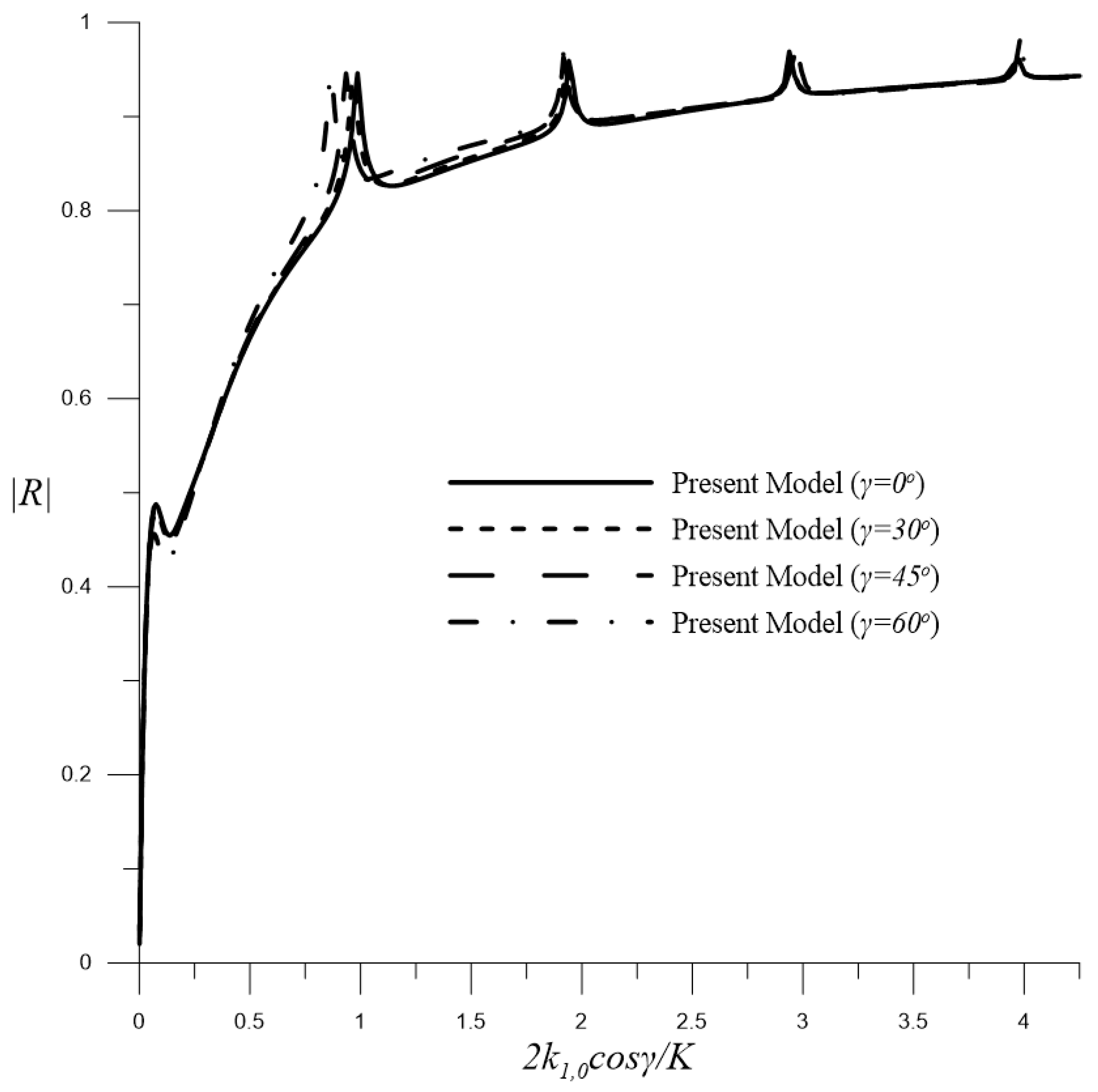
4.2.3. Fully Submerged Permeable Barriers
4.3. Energy Loss
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Porter, R.; Evans, D.V. Complementary approximations to wave scattering by vertical barriers. J. Fluid Mech. 1995, 294, 155–180. [Google Scholar] [CrossRef]
- Losada, I.J.; Losada, M.A.; Roldán, A. Propagation of oblique incident waves past rigid vertical thin barriers. Appl. Ocean Res. 1992, 14, 191–199. [Google Scholar] [CrossRef]
- Losada, M.A.; Losada, I.J.; Roldán, A.J. Propagation of oblique incident modulated waves past rigid, vertical thin barriers. Appl. Ocean Res. 1993, 15, 305–310. [Google Scholar] [CrossRef]
- Losada, I.J.; Losada, M.A.; Losada, R. Wave spectrum scattering by vertical thin barriers. Appl. Ocean Res. 1994, 16, 123–128. [Google Scholar] [CrossRef]
- Abul-Azm, A.G. Wave diffraction through submerged flexible breakwaters. Ocean Eng. 1996, 23, 403–422. [Google Scholar] [CrossRef]
- Ursell, F. The effect of a fixed vertical barrier on surface waves in deep water. Math. Proc. Camb. Philos. Soc. 1947, 43, 374–382. [Google Scholar] [CrossRef]
- Das, P.; Dolai, D.P.; Mandal, B.N. Oblique Wave Diffraction by Parallel Thin Vertical Barriers with Gaps. J. Waterw. 1997, 123, 163–171. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Losada, M.A.; Martin, P.A. Reflection and transmission from porous structures under oblique wave attack. J. Fluid Mech. 1991, 224, 625–644. [Google Scholar] [CrossRef]
- Lee, M.; Chwang, A.T. Scattering and radiation of water waves by permeable barriers. Phys. Fluids 2000, 12, 54–65. [Google Scholar] [CrossRef] [Green Version]
- Li, A.-J.; Liu, Y.; Li, H.-J. Accurate solutions to water wave scattering by vertical thin porous barriers. Math. Probl. Eng. 2015, 3, 985731. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.; Gayen, R. Scattering of oblique water waves by two thin unequal barriers with non-uniform permeability. J. Eng. Math. 2018, 112, 37–61. [Google Scholar] [CrossRef]
- Macaskill, C. Reflexion of water waves by a permeable barrier. J. Fluid Mech. 1979, 95, 141–157. [Google Scholar] [CrossRef]
- Takano, K. Effets d’un obstacle parallelepipedique sur la propagation de la houle. La Houille Blanche 1960, 15, 247–267. [Google Scholar] [CrossRef] [Green Version]
- Newman, J.N. Propagation of water waves over an infinite step. J. Fluid Mech. 1965, 23, 399–415. [Google Scholar] [CrossRef]
- Mei, C.C.; Black, J.L. Scattering of surface waves by rectangular obstacles in waters of finite depth. J. Fluid Mech. 1969, 38, 499–511. [Google Scholar] [CrossRef]
- Kirby, J.T.; Dalrymple, R.A. Propagation of obliquely incident water waves over a trench. J. Fluid Mech. 1983, 133, 47–63. [Google Scholar] [CrossRef] [Green Version]
- Kirby, J.T.; Dalrymple, R.A.; Seo, S.N. Propagation of obliquely incident water waves over a trench. Part 2. Currents flowing along the trench. J. Fluid Mech. 1987, 176, 95–116. [Google Scholar] [CrossRef]
- Devillard, P.; Dunlop, F.; Souillard, B. Localization of gravity waves on a channel with a random bottom. J. Fluid Mech. 1988, 186, 521–538. [Google Scholar] [CrossRef]
- O’Hare, T.J.; Davies, A. A new model for surface wave propagation over undulating topography. Coast. Eng. 1992, 18, 251–266. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Hsu, T.-W.; Lin, Y.-T. On step approximation for Roseau’s analytical solution of water waves. Math. Probl. Eng. 2011, 2011, 607196. [Google Scholar] [CrossRef] [Green Version]
- Tsai, C.-C.; Lin, Y.-T.; Hsu, T.-W. On step approximation of water-wave scattering over steep or undulated slope. Ocean Eng. 2014, 24, 98–105. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Chang, Y.-H.; Hsu, T.-W. Step approximation on oblique water wave scattering and breaking by variable porous breakwaters over uneven bottoms. Ocean Eng. 2022, 253, 111325. [Google Scholar] [CrossRef]
- Isaacson, M.; Premasiri, S.; Yang, G. Wave interactions with vertical slotted barrier. J. Waterw. 1998, 124, 118–126. [Google Scholar] [CrossRef]
- Poguluri, S.K.; Cho, I.H. Analytical and numerical study of wave interaction with a vertical slotted barrier. Ships Offshore Struct. 2021, 16, 1012–1024. [Google Scholar] [CrossRef]
- Tran, C.-T.; Chang, J.-Y.; Tsai, C.-C. Step approximation for water wave scattering by multiple thin barriers over undulated bottoms. J. Mar. Sci. Eng. 2021, 9, 629. [Google Scholar] [CrossRef]
- Bragg, W.H.; Bragg, W.L. The reflection of X-rays by crystals. Nature 1913, 88, 428–438. [Google Scholar] [CrossRef]
- Mei, C.C.; Hara, T.; Naciri, M. Note on Bragg scattering of water waves by parallel bars on the seabed. J. Fluid Mech. 1988, 186, 147–162. [Google Scholar] [CrossRef]
- Kirby, J.T. A note on Bragg scattering of surface waves by sinusoidal bars. Phys. Fluids A Fluid Dyn. 1993, 5, 858861. [Google Scholar] [CrossRef]
- Liu, H.-W.; Zeng, H.-D.; Huang, H.-D. Bragg resonant reflection of surface waves from deep water to shallow water by a finite array of trapezoidal bars. Appl. Ocean Res. 2020, 94, 101976. [Google Scholar] [CrossRef]
- Hao, J.; Li, J.; Liu, S.; Wang, L. Wave amplification caused by Bragg resonance on parabolic-type topography. Ocean Eng. 2022, 244, 110442. [Google Scholar] [CrossRef]
- Bailard, J.A.; de Vries, J.; Kirby, J.T.; Guza, R.T. Bragg Reflection Breakwater: A New Shore Protection Method? In Proceedings of the Coastal Engineering Proceedings, Delft, The Netherlands, 2–6 July 1990. [Google Scholar] [CrossRef]
- Bailard James, A.; de Vies Jack, W.; Kirby James, T. Considerations in Using Bragg Reflection for Storm Erosion Protection. J. Waterw. 1992, 118, 62–74. [Google Scholar] [CrossRef] [Green Version]
- Davies, A.; Heathershaw, A. Surface-wave propagation over sinusoidally varying topography. J. Fluid Mech. 1984, 144, 419–443. [Google Scholar] [CrossRef]
- Kirby, J.T. A general wave equation for waves over rippled beds. J. Fluid Mech. 1986, 162, 171–186. [Google Scholar] [CrossRef] [Green Version]
- Mei, C.C. Resonant reflection of surface water waves by periodic sandbars. J. Fluid Mech. 1985, 152, 315–335. [Google Scholar] [CrossRef]
- Kar, P.; Koley, S.; Sahoo, T. Scattering of surface gravity waves over a pair of trenches. Appl. Math. Model. 2018, 62, 303–320. [Google Scholar] [CrossRef]
- Kar, P.; Koley, S.; Sahoo, T. Bragg scattering of long waves by an array of trenches. Ocean Eng. 2020, 198, 107004. [Google Scholar] [CrossRef]
- Kar, P.; Sahoo, T.; Behera, H. Effect of Bragg scattering due to bottom undulation on a floating dock. Wave Motion 2019, 90, 121–138. [Google Scholar] [CrossRef]
- Kar, P.; Sahoo, T.; Meylan, M.H. Bragg scattering of long waves by an array of floating flexible plates in the presence of multiple submerged trenches. Phys. Fluids 2020, 32, 096603. [Google Scholar] [CrossRef]
- Ting, C.-L.; Lin, M.-C.; Kuo, C.-L. Bragg scattering of surface waves over permeable rippled beds with current. Phys. Fluids 2000, 12, 1382–1388. [Google Scholar] [CrossRef]
- Xie, J.-J. Long wave reflection by an array of submerged trapezoidal breakwaters on a sloping seabed. Ocean Eng. 2022, 252, 111138. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Chou, W.-R. Comparison between consistent coupled-mode system and eigenfunction matching method for solving water wave scattering. J. Mar. Sci. Technol. 2015, 23, 870–881. [Google Scholar] [CrossRef]
- Sahoo, T.; Chan, A.T.; Chwang, A.T. Scattering of oblique surface waves by permeable barriers. J. Waterw. 2000, 126, 196–205. [Google Scholar] [CrossRef]
- Cho, Y.-S.; Yoon, S.B.; Lee, J.-I.; Yoon, T.-H. A concept of beach protection with submerged breakwaters. J. Coast. Res. 2001, 34, 671–678. [Google Scholar]
- Tsai, C.-C.; Lin, Y.-T.; Chang, J.-Y.; Hsu, T.-W. A coupled-mode study on weakly viscous Bragg scattering of surface gravity waves. Ocean Eng. 2016, 122, 136–144. [Google Scholar] [CrossRef]
- Kirby, J.T.; Anton, J.P. Bragg reflection of waves by artifical bars. In Proceedings of the 22nd International Conference on Coastal Engineering, ICCE’90, Delft, The Netherlands, 29 January 1990. [Google Scholar] [CrossRef]
- Kaligatla, R.B.; Tabssum, S.; Sahoo, T. Effect of bottom topography on wave scattering by multiple porous barriers. Meccanica 2018, 53, 887–903. [Google Scholar] [CrossRef]
- Chwang, A.T. A porous-wavemaker theory. J. Fluid Mech. 1983, 132, 395–406. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tran, C.-T.; Lin, C.; Tsai, C.-C. Bragg Resonance of Water Waves by Multiple Permeable Thin Barriers over Periodic Breakwaters. Water 2023, 15, 495. https://doi.org/10.3390/w15030495
Tran C-T, Lin C, Tsai C-C. Bragg Resonance of Water Waves by Multiple Permeable Thin Barriers over Periodic Breakwaters. Water. 2023; 15(3):495. https://doi.org/10.3390/w15030495
Chicago/Turabian StyleTran, Chang-Thi, Chitsan Lin, and Chia-Cheng Tsai. 2023. "Bragg Resonance of Water Waves by Multiple Permeable Thin Barriers over Periodic Breakwaters" Water 15, no. 3: 495. https://doi.org/10.3390/w15030495





