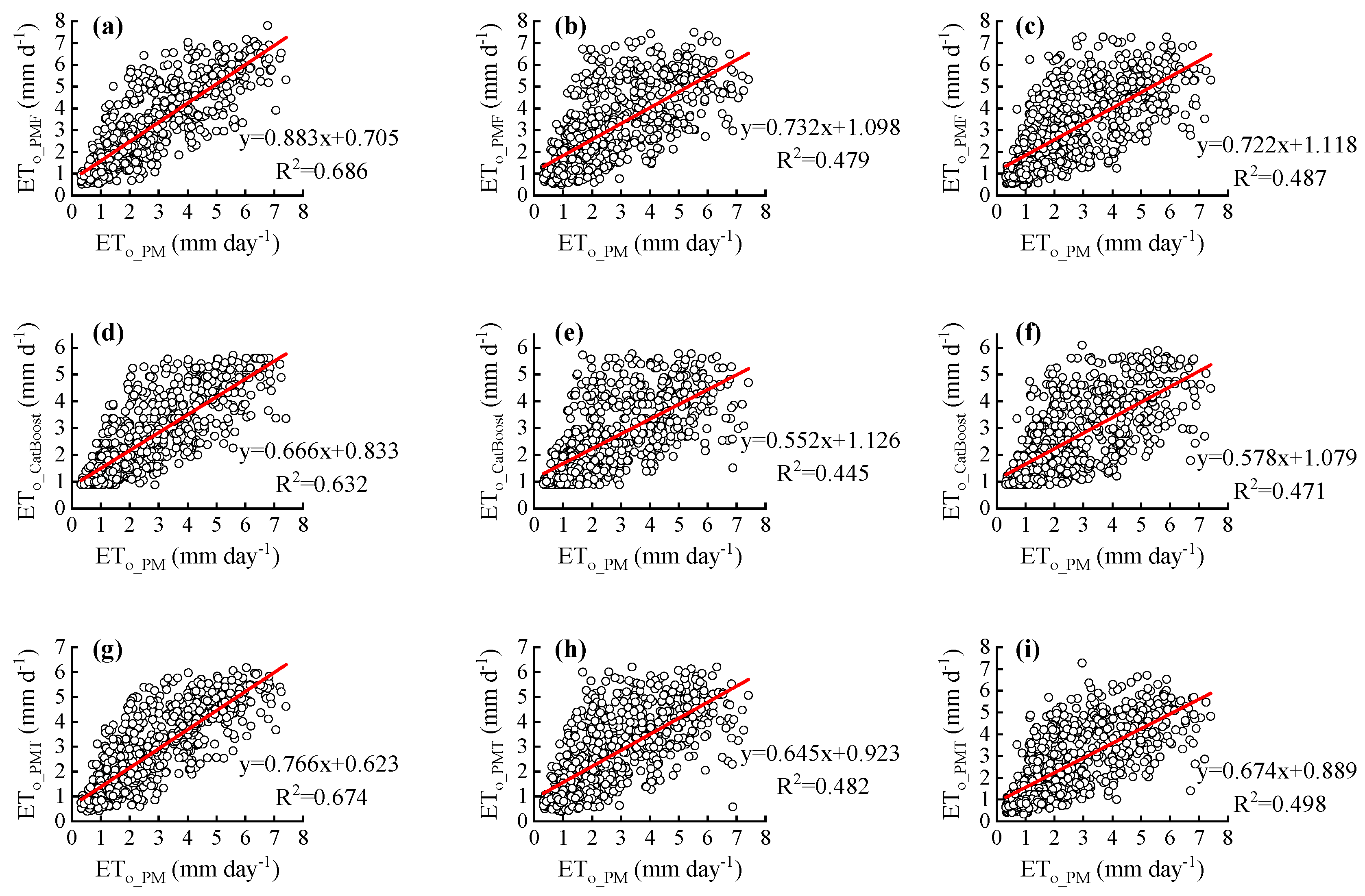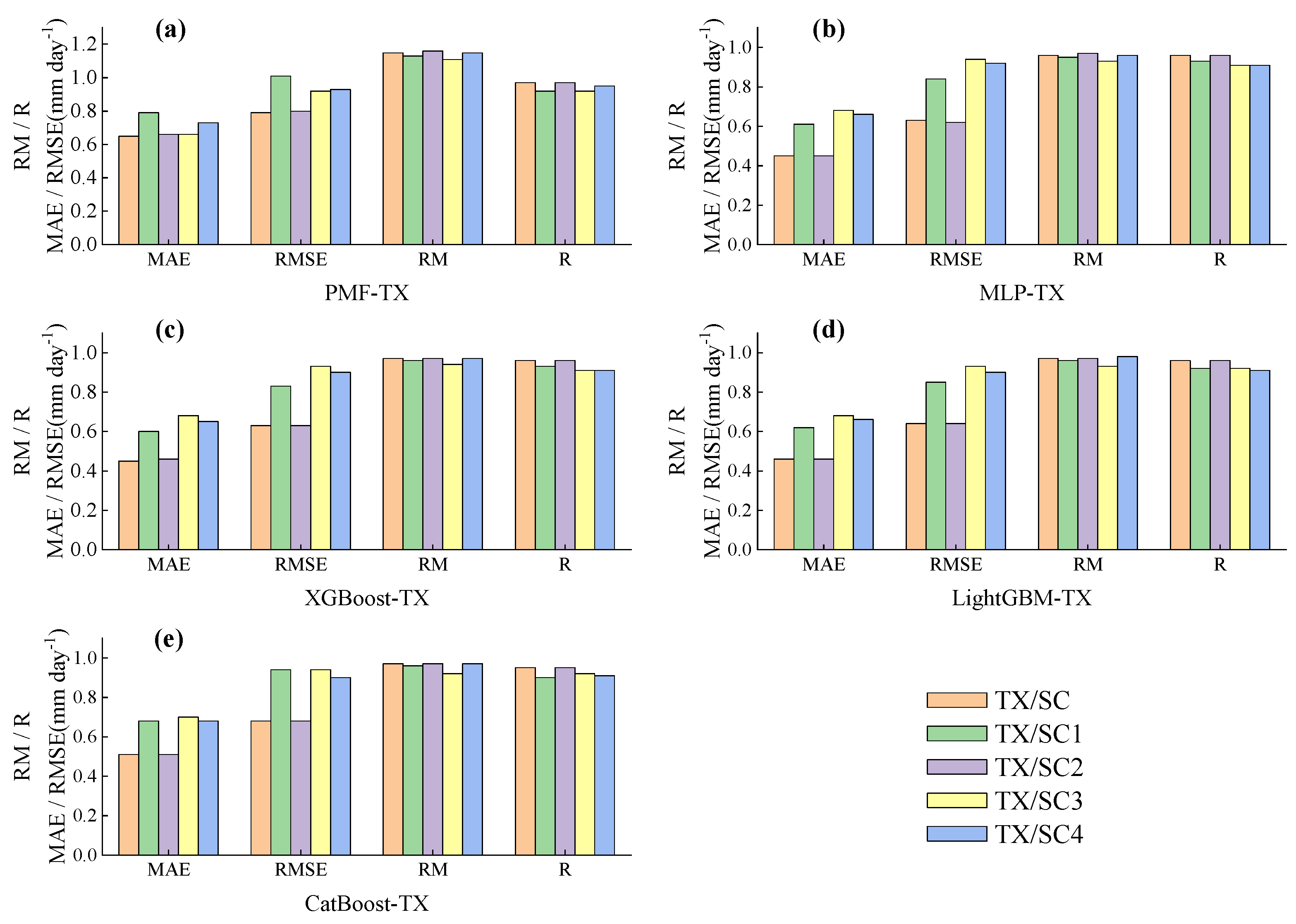1. Introduction
Evapotranspiration is a key link in the surface water cycle and an important basis for crop water demand determination. Evapotranspiration is generally obtained by multiplying the reference evapotranspiration (ET
o) by the crop coefficient. The determination of ET
o is not only a key factor in predicting and estimating crop water demand but also an important requirement for irrigation forecasting and irrigation decision making. Timely and accurate ET
o prediction has a notable reference value for real-time irrigation decision making [
1] and is very important for improving the real-time irrigation prediction accuracy, irrigation management level, crop yield, and water conservation [
2].
Depending on the adopted method and input data, ET
o prediction methods can be divided into direct and indirect methods [
1]. Among the direct methods, time series models, such as autoregressive (AR), moving average (MA), autoregressive moving average (ARMA), and autoregressive integrated moving average (ARIMA) models, have been used to forecast the daily ET
o using historical daily ET
o data calculated from historical daily measured meteorological data [
3]; alternatively, machine learning algorithms, such as the multilayer perceptron (MLP), multivariate relevance vector machine (MVRVM) [
4], multilayer perceptron–neural network model (MLP-NNM), Kohonen self-organizing feature maps–neural network model (KSOFM-NNM), gene expression programming (GEP) [
5], least-squares support vector machine (LSSVM), adaptive neuro-fuzzy inference system (ANFIS), generalized regression neural network (GRNN) [
3], deep learning models (long short-term memory (LSTM), one-dimensional convolutional neural network (1D CNN), and a combination of the two previous models (CNN-LSTM)), and traditional machine learning models (artificial neural network (ANN) and random forest (RF)) [
6], have been employed to predict the daily ET
o and the daily ET
o at a lead time of 1–7 days using historical data. In these studies, alternatives to time series models have been applied for future ET
o prediction based on historical meteorological data and ET
o calculated with historical meteorological data. In general, machine learning models using ET
o data computed from historical meteorological data outperform those directly using historical meteorological data [
3]. In addition, combined machine learning models, such as the fruit fly optimized GRNN model [
7] and autoencoder–decoder bidirectional LSTM (AED-BiLSTM) [
8], can predict ET
o more accurately than a single machine learning model (GRNN, XGBoost). However, in all these studies, so-called ET
o forecast data generated from long-term historical meteorological data were used, and since the short-term daily ET
o is mainly governed by weather conditions, direct methods may not be applicable [
9,
10,
11].
In the indirect method, ET
o can be calculated using weather variables predicted via numerical weather prediction (NWP) or public weather forecasts, such as those obtained using the Food and Agriculture Organization (FAO)-56 Penman–Monteith (PM) equation [
1,
12,
13,
14,
15,
16], the Hargreaves–Samani (HS) and Priestley (PT) equations [
12], or multivariate time series models [
17], and the numerical weather forecasts output by forecast systems or models (COSMO, Australian Community Climate and Earth System Simulator–Global (ACCESS-G), Global Ensemble Forecast System (GEFS) model, European Centre for Medium-Range Weather Forecasts (EC), National Centers for Environmental Prediction Global Forecast System (NCEP), and United Kingdom Meteorological Office (MO) forecasts) can be used to predict the daily ET
o, weekly ET
o, and daily ET
o with a lead time of 1–16 days. Although NWP can generate forecasts of the full range of meteorological variables needed by the FAO-56 PM equation and can be used for ET
o prediction, NWP data are not available to the public in some developing countries. For example, the numerical forecast products of the China Meteorological Data Network are only available to registered users for education and research purposes, while numerical forecast products require expert downscaling and bias correction [
16] or postprocessing methods [
14] to improve their reliability.
In China, the public can easily access free public weather forecasts up to 40 days in advance in real time from China Weather (
http://www.weather.com.cn (accessed on 31 December 2022)). These free public weather forecasts include four variables: maximum temperature, minimum temperature, wind scale, and weather type. Over the past decade, public weather forecasts have been widely used for ET
o prediction. For example, information retrieved from public weather forecasts has been converted into the variables needed to calculate ET
o using the FAO-56 PM equation and subsequently applied in daily ET
o prediction [
18,
19,
20,
21]. Given that temperature is the most accurate and only quantitative variable in public weather forecasts, many studies have used only temperature forecast data retrieved from public weather forecasts to predict ET
o. Based on temperature data retrieved from public weather forecasts, the daily ET
o has been predicted using locally calibrated versions of the HS equation [
9,
22,
23], the daily ET
o with a lead time of 1–7 days has been predicted using the monthly calibrated Blaney–Criddle (BC) model [
24], and four ANN models (linear regression (LR), probabilistic neural network (PNN), MLP, and generalized feedforward (GFF) models) [
10], and the GEP algorithm [
2] have been used to predict the daily ET
o with a lead time of 1–7 days at Gaoyou Station in Jiangsu Province of China. The above studies based on the adoption of public weather forecast models for daily ET
o prediction have achieved reasonable results, but there exists no evaluation model to determine the seasonal variation in the daily ET
o prediction performance, and there is a lack of comparative evaluation of machine learning models in daily ET
o prediction based on different input combinations of weather variables retrieved from public weather forecasts. These studies are aimed at a single model in a single region (or multiple regions) of China or a comparative study of similar models in a single region (or multiple regions) of China [
11]. The lack of comparative research on different types of models can lead to the inability to identify the best daily ET
o forecast model in a given region.
Recently, three tree models based on boosting algorithms, namely, extreme gradient boosting (XGBoost), light gradient boosting machine (LightGBM), and gradient boosting with categorical features support (CatBoost), have been widely used to estimate the daily ET
o [
25,
26,
27,
28,
29,
30,
31,
32,
33] and monthly ET
o [
34]. These studies have shown that the daily ET
o estimated by these three tree models is suitably accurate, with a better performance than that of other models. However, there are no studies on ET
o prediction with these three tree models. Compared with estimating historical daily ET
o by models and historical daily measured weather forecast data, it is more valuable to predict future daily ET
o by models and public weather forecasts because accurate prediction of ET
o is the key to crop water demand prediction and the premise of real-time irrigation prediction, which has important reference value and significance for real-time irrigation decision making.
In this paper, three empirical equations and four machine learning models for predicting daily ETo using public weather forecasts are evaluated to select the best daily ETo prediction model for the crop irrigation season in the study area. The objectives of this study were as follows: (1) In model assessment based on public weather forecasts, the optimal input combinations of the MLP, XGBoost, LightGBM, and CatBoost machine learning models were determined to obtain the best daily ETo prediction performance. (2) Three empirical equations (PMT, PMF, and HS) and four machine learning models (MLP, XGBoost, LightGBM, and CatBoost) were compared by determining the seasonal variation in the daily ETo prediction performance, and the best daily ETo prediction model was recommended for all four seasons at various research sites in three climate zones. The main error sources of daily ETo predicted by the PMF equation and four machine learning models were analyzed.
3. Results and Discussion
3.1. Prediction Performance of the Weather Variables in the Public Weather Forecast Information
3.1.1. Single-Parameter Performance
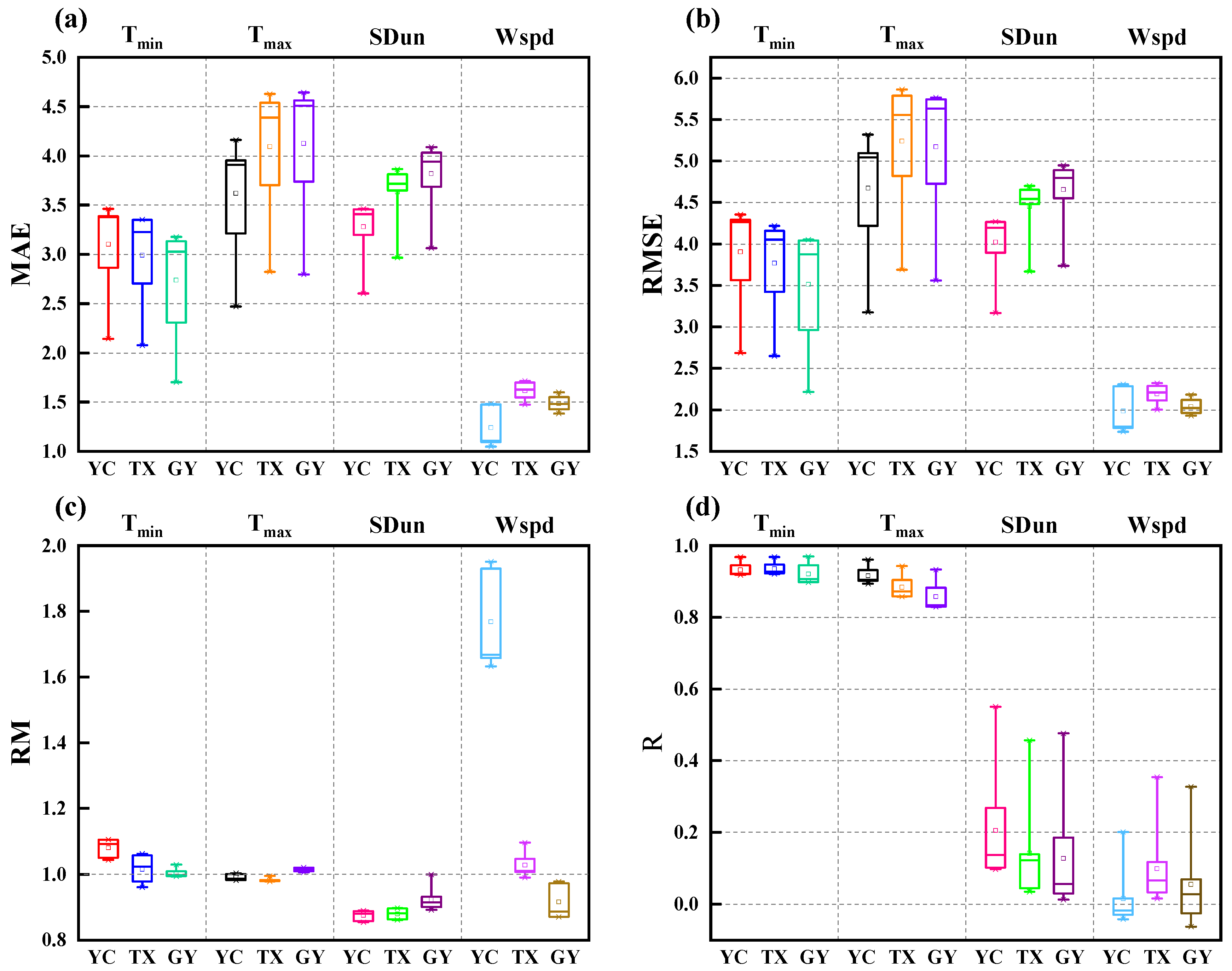
The performance indicators of the daily scale forecast weather variables at the three study sites obtained from public weather forecasts with a lead time of 1–7 days for 2020–2021 are shown in
Figure 3. The mean MAE and RMSE of T
min ranged from 2.73–3.10 °C and 3.51–3.90 °C, respectively. At the three sites, the mean MAE and RMSE of T
max ranged from 3.62–4.12 °C and 4.67–5.24 °C, respectively, while the mean R values of T
min and T
max were higher than 0.92 and 0.85, respectively. The accuracy of the T
min forecasts at all three sites was higher than that of the T
max forecasts, and the T
min and T
max prediction performance decreased with increasing forecast period, which is consistent with most previous studies in China [
9,
10,
11,
20,
21,
23,
24,
42,
58,
63]. In addition, the mean RM values of T
min and T
max ranged from 1.00–1.08 and 0.98–1.01, respectively, indicating that T
min was slightly overestimated at the three sites, T
max was slightly overestimated at GY, and T
max was slightly underestimated at YC and TX.
The mean MAE and RMSE of SDun at the three sites ranged from 3.28–3.82 h and 4.02–4.65 h, respectively, and the mean R and RM ranged from 0.13–0.20 and 0.88–0.92, respectively. The SDun forecast performance decreased in the order of YC, TX, and GY. SDun was underestimated by 12.51% (YC), 12.03% (TX), and 7.65% (GY). Compared to the temperature prediction performance, the SDun prediction performance was very poor, which may be due to the large error in the calculation process of converting the weather type in public weather forecast information into SDun [
11,
18,
20,
21,
58].
The mean MAE and RMSE of Wspd at the three sites ranged from 1.24–1.61 m s
−1 and 1.98–2.19 m s
−1, respectively, and the mean R and RM ranged from 0.02–0.08 and 0.92–1.77, respectively. The Wspd prediction performance was poor at all stations. Wspd was overestimated by 76.78% (YC) and 2.79% (TX) and underestimated by 8.44% (GY). Among the four variables in public weather forecasts, Wspd exhibited the worst prediction performance, which may be caused by inadequate forecasts of the wind scale in public weather forecasts and errors in the conversion of the wind scale into the wind speed [
18,
20,
21,
42].
3.1.2. Seasonality of the Prediction Performance
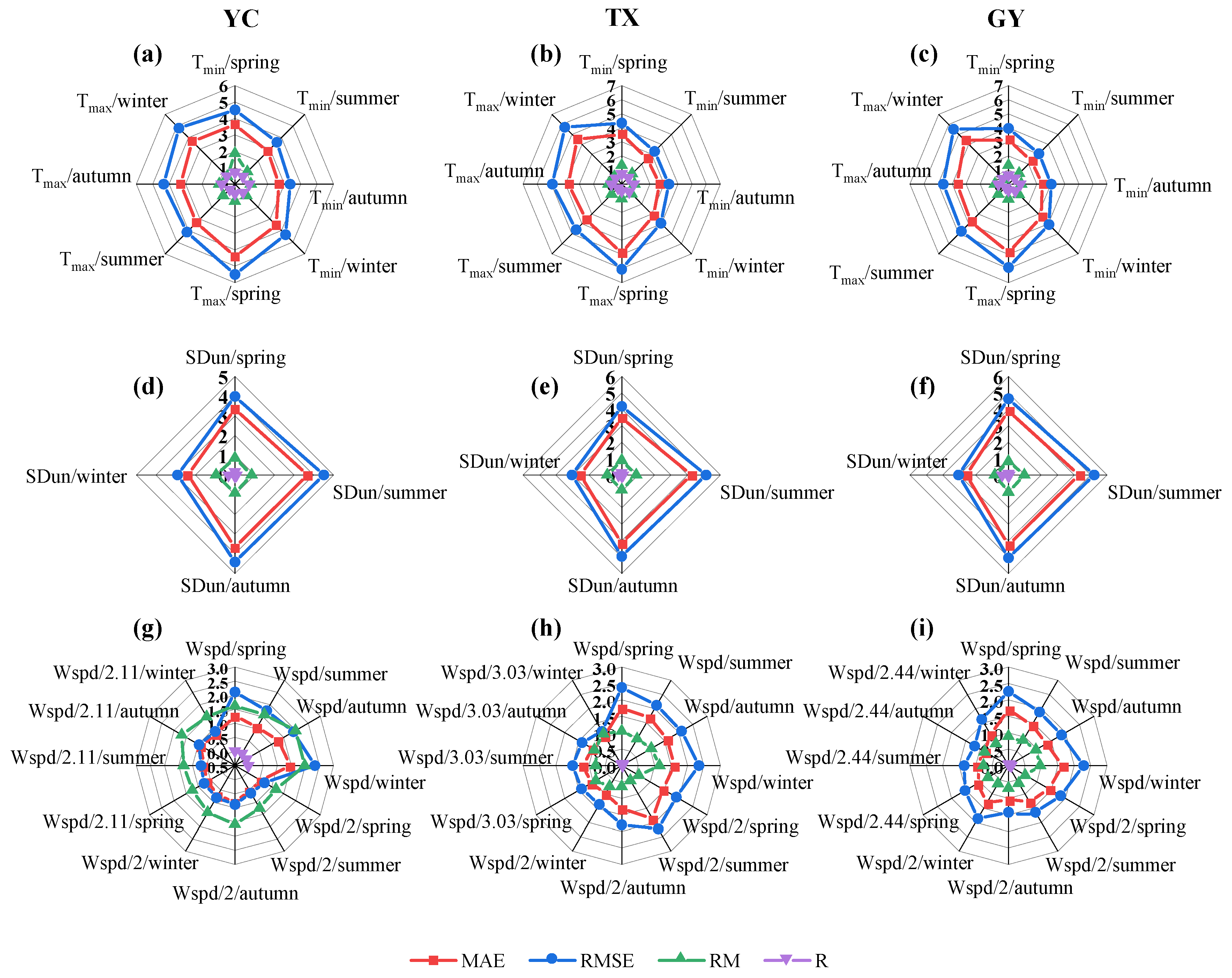
The average seasonal statistics of the performance indicators of the weather variables predicted by public weather forecasts with a lead time of 1–7 days at the three research stations from 2020 to 2021 are shown in
Figure 4. The average performance indicators of T
max at YC (GY) all decreased in the order of autumn, summer, winter, and spring. The average performance indicators of T
max at TX decreased in the order of summer, autumn, winter, and spring. At the three sites, T
max was overestimated within the range of 3.43–6.32% in spring (0.13–2.91% in summer) and underestimated within the range of 3.02–5.58% in autumn (26.21–57.24% in winter).
The average performance indicators of Tmin at YC decreased in the order of autumn, summer, winter, and spring (autumn, summer, spring, and winter for GY). The average performance indicators of Tmin in TX decreased in the order of summer, autumn, winter, and spring. At the three sites, Tmin was overestimated within the range of 32.43–85.75% in spring (4.33–5.84% in summer) and underestimated within the range of 4.15–9.13% in autumn (0.49–1.28% in winter) (except Tmin at GY, which was overestimated by 3.96% in winter).
The average performance indicators of SDun at the three sites decreased in the order of winter, spring, autumn, and summer. At the three sites, SDun was underestimated within the ranges of 11.89–18.08%, 3.52–15.18%, 8.96–8.99%, and 4.73–16.71% in spring, summer, autumn, and winter, respectively (except that SDun was overestimated by 3.76% in autumn at GY).
The predicted Wspd with a lead time of 1–7 days at the three research sites was defined as the predicted Wspd, a constant value (2 m s−1) or the long-term daily average wind speed (2.11 m s−1 at YC, 3.03 m s−1 at TX, and 2.44 m s−1 at GY). The average performance indicators of Wspd at YC during the four seasons decreased in the order of constant value, long-term daily average wind speed, and predicted Wspd. The average performance indicators when Wspd was defined as a constant value decreased in the order of summer, spring, winter, and autumn (summer, spring, autumn, and winter when the predicted Wspd was taken). Except in summer, the average performance indicators of Wspd at TX (GY) decreased in the order of long-term daily average wind speed, constant value, and predicted Wspd. Moreover, the average performance indicators at TX when Wspd was defined as a constant value decreased in the order of winter, autumn, spring, and summer (autumn, summer, winter, and spring when the predicted Wspd was taken). The average performance indicators at GY when Wspd was defined as a constant value and predicted Wspd decreased in the order of autumn, summer, winter, and spring. When Wspd was defined as a constant value (predicted Wspd), the predicted value at YC was overestimated by 17.92%, 24.84%, 59.04%, and 42.51% (62.03%, 59.62%, 98.80%, and 97.34%) in spring, summer, autumn, and winter, respectively, the predicted value at TX was underestimated by 39.96%, 47.71%, 36.30%, and 26.39% (overestimated by 5.13%, underestimated by 6.36%, overestimated by 4.14%, and overestimated by 14.78%) in spring, summer, autumn, and winter, respectively, and the predicted value at GY was underestimated by 40.96%, 37.80%, 31.30%, and 36.93% (11.06%, 10.99%, 3.98%, and 3.80%) in spring, summer, autumn, and winter, respectively.
In summary, according to the average seasonal statistics of the performance indicators of the weather variables predicted by the public weather forecasts with a lead time of 1–7 days at the three research sites from 2020 to 2021, the best Tmax and Tmin prediction performance occurred in autumn and summer, followed by winter and spring. The SDun prediction performance was consistent at the three sites, with the best performance in winter and spring, followed by autumn and summer, whereas the Wspd prediction performance greatly varied from site to site.
3.2. Calibration and Validation of the Three Empirical Equations
The calibration results of the three empirical equations of PMT, PMF, and HS at the three sites are provided in
Table 4. The C and E values of the HS equation at the three sites occurred within the range given by Hu et al. [
51].
The statistics of the ET
o prediction performance indicators of the three empirical equations (PMT, PMF, and HS) for the precalibration validation period and test period (a lead time of 1–7 days) and the postcalibration validation period and test period (a lead time of 1–7 days) are listed in
Table 5. During the test period, the mean MAE, RMSE, and RM of the PMT equation at YC decreased from 0.63 mm d
−1, 0.89 mm d
−1, and 1.03 before calibration to 0.61 mm d
−1 and 0.86 mm d
−1 and 1.02 after calibration, respectively, and the mean R increased from 0.88 before calibration to 0.89 after calibration. Moreover, the average MAE, RMSE, and RM of the PMF equation at YC decreased from 0.91 mm d
−1, 1.22 mm d
−1, and 1.24 before calibration to 0.86 mm d
−1, 1.17 mm d
−1, and 1.21 after calibration, respectively. The average R changed only slightly before and after calibration, reaching a value of 0.88. The average MAE, RMSE, and RM of the HS equation at YC decreased from 4.91 mm d
−1, 6.05 mm d
−1, and 2.70 before calibration to 0.68 mm d
−1, 0.97 mm d
−1, and 1.09 after calibration, respectively. The average R remained almost unchanged before and after calibration, reaching a value of 0.89. After calibration, the performance of the three empirical equations in ET
o prediction was improved. Among them, the average MAE, RMSE, and RM of the HS equation for ET
o prediction decreased by 86.15%, 83.97%, and 59.63%, respectively. The three empirical equations attained a similar performance at TX and GY during the test period. The three empirical equations after calibration could be used to predict ET
o with a lead time of 1–7 days.
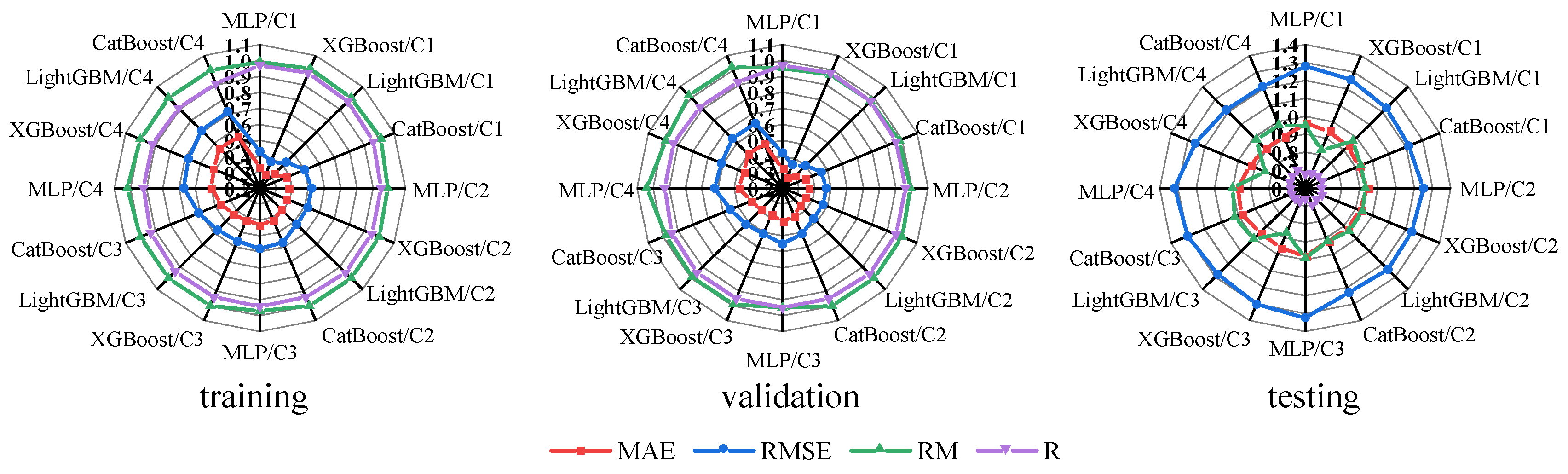
3.3. Performance Comparison of ETo Prediction by the Four Machine Learning Algorithms under the Various Input Combinations
The performance statistics of the four machine learning models for daily ET
o prediction at YC, TX, and GY with a lead time of 1–7 days under the different input combinations are provided in
Figure 5,
Figure 6 and
Figure 7, respectively, and the daily ET
o prediction performance significantly varied depending on the machine learning model, input combination of the machine learning model, and study site.
At YC, MLP and XGBoost performed best under the various input combinations during the training and validation periods. However, during the test period, the performance of the MLP, XGBoost, LightGBM, and CatBoost machine learning models in ETo prediction under the different input combinations decreased in the order of C2, C4, C1, and C3. LightGBM was the best model for ETo prediction under the C3 input combination (MAE = 0.83 mm d−1, RMSE = 1.09 mm d−1, and R = 0.85), while CatBoost attained the best prediction performance under all input combinations (MAE range: 0.69–0.77 mm d−1; RMSE range: 0.93–0.99 mm d−1; R range: 0.84–0.87). CatBoost achieved the highest performance with the C2 input combination (MAE = 0.69 mm d−1, RMSE = 0.93 mm d−1, and R = 0.86) during the testing phase at YC.
At TX, during the training and validation periods, MLP and XGBoost exhibited the best prediction performance under the C1 and C2 input combinations, while LightGBM and XGBoost achieved the best prediction performance under the C3 and C4 input combinations. However, during the test period, first, under the different input combinations, the ETo prediction performance of MLP and LightGBM decreased in the order of C2, C1, C4, and C3, the ETo prediction performance of XGBoost decreased in the order of C4, C2, C3, and C1, and the ETo prediction performance of CatBoost decreased in the order of C3, C4, C2, and C1. Second, LightGBM attained the best prediction performance under the C1 and C2 input combinations (MAE range: 0.985–1.009 mm d−1; RMSE range: 1.357–1.379 mm d−1; R range: 0.78–0.79), while CatBoost achieved the best prediction performance under the C3 and C4 input combinations (MAE range: 0.95–0.96 mm d−1; RMSE range: 1.279–1.31 mm d−1; R range: 0.80–0.81). CatBoost was the best performing machine learning model for the C3 input combination (MAE = 0.95 mm d−1, RMSE = 1.28 mm d−1, R = 0.81) at TX during the test period.
At GY, during the training and validation periods, XGBoost and LightGBM exhibited the best prediction performance under the C1, C2, and C3 input combinations, while MLP and XGBoost exhibited the best prediction performance under the C4 input combination. However, during the test period, first, the ETo prediction performance of the MLP under the different input combinations decreased in the order of C2, C1, C4, and C3, the ETo prediction performance of XGBoost under the different input combinations decreased in the order of C2, C4, C1, and C3, and the ETo prediction performance of LightGBM and CatBoost under the different input combinations decreased in the order of C4, C1, C2, and C3. Second, CatBoost was the best performing model for the C1, C2, and C4 input combinations (MAE range: 0.907–0.92 mm d−1; RMSE range: 1.213–1.228 mm d−1; R range: 0.699–0.707), and LightGBM was the best performing model for the C3 input combination (MAE = 0.95 mm d−1; RMSE = 1.28 mm d−1; R = 0.68). CatBoost was the best performing machine learning model for the C4 input combination (MAE = 0.907 mm d−1; RMSE = 1.213 mm d−1; R = 0.707) at GY during the test period.
The best input combinations of the four machine learning models, i.e., MLP, XGBoost, LightGBM, and CatBoost, and their model tuning information are provided in
Table 6. The best input combination of CatBoost at TX was C3 (8.33%). In contrast, the best input combination of the four machine learning models at the three sites was C2 (66.67%) or C4 (25.00%), indicating that the addition of SDun to the input combination positively affected the improvement in the ET
o prediction performance of the four machine learning models [
1,
11,
20,
31,
58,
63,
67,
68]. Since the predicted Wspd exhibits the worst prediction performance among the variables in the public weather forecasts, the addition of the predicted Wspd to the input combination could lead to a decrease in the daily ET
o prediction performance of the machine learning models (except for the CatBoost model at TX), which is consistent with previous research results [
42]. In addition, the MLP with two–three hidden layers performs better in predicting daily ET
o than the MLP with only one hidden layer [
10,
56,
58].
3.4. ETo Prediction Performance Evaluation of the Seven Models Based on Public Weather Forecasts
3.4.1. Daily ETo Prediction Performance of the Seven Models
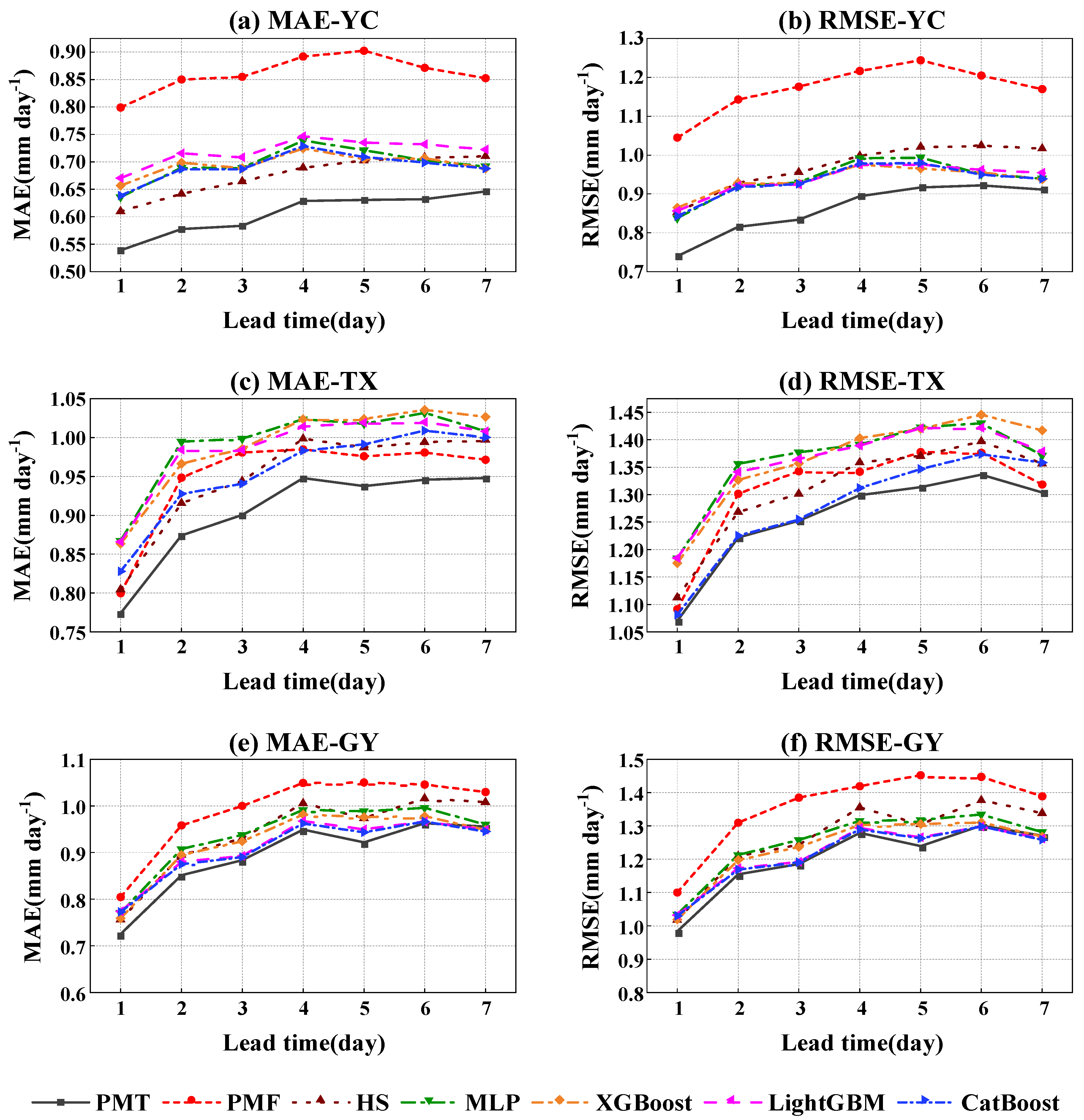
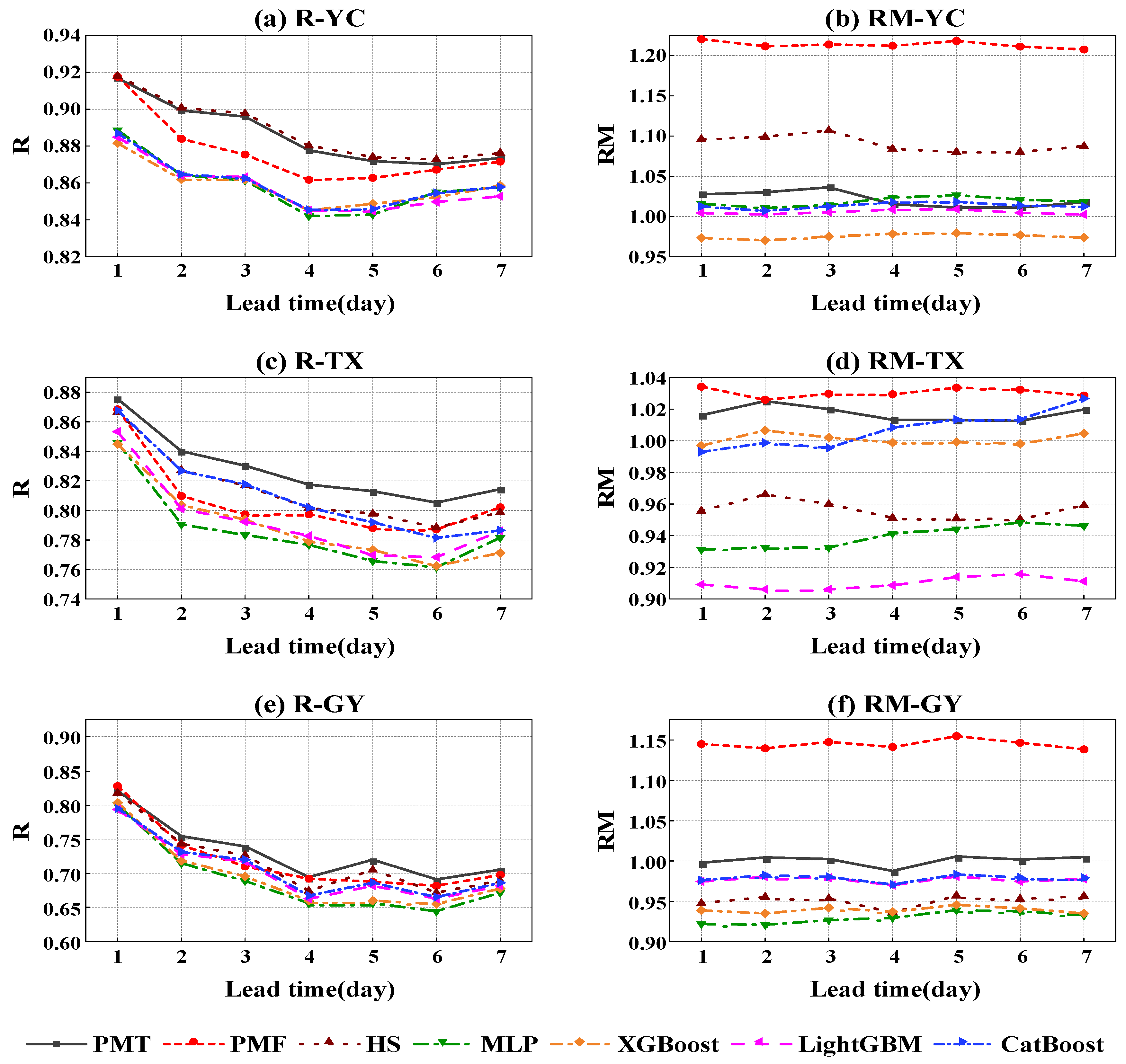
The daily ET
o prediction performance indicators of the three empirical equations and four machine learning models with a lead time of 1–7 days at the three sites are shown in
Figure 8 and
Figure 9, respectively. First, the daily ET
o prediction performance of the seven models at YC, TX, and GY decreased with increasing lead time, which is due to the decrease in the performance of the public weather forecast variables with increasing lead time, which is consistent with previous research results [
1,
2,
9,
10,
11,
17,
20,
23,
42,
58,
63]. Second, the RM values of the 7 models at YC ranged from 0.97 to 1.22, among which the XGBoost model slightly underestimated (2.04–2.96%) the daily ET
o, the PMF equation overestimated (20.74–22.03%) the daily ET
o, and the other models slightly overestimated (0.24–10.68%) the daily ET
o. The RM values of the seven models at TX ranged from 0.91 to 1.03, among which the HS, MLP, and LightGBM models slightly underestimated (3.39–9.38%) the daily ET
o, while the other models slightly overestimated (0.46–3.43%) the daily ET
o. The RM values of the seven models at GY ranged from 0.92 to 1.15. The PMF equation overestimated (13.83–15.46%) the daily ET
o, and the PMT equation slightly overestimated (0.19–0.47%) the daily ET
o, while the other models slightly underestimated (1.67–7.93%) the daily ET
o. The PMF model overestimated the daily ET
o at YC, which may be due to Wspd overestimation at this site. Under arid conditions, the drier the atmosphere is, the more small changes in wind speed could lead to large changes in the evapotranspiration rate and thus the greater the impact on evapotranspiration [
36]. The daily ET
o overestimation by the PMF model noted at GY may be due to T
max overestimation at this site. Moreover, the overestimation percentage of T
max at GY was higher than that of T
min, and the saturation vapor pressure was overestimated due to T
max overestimation, resulting in an increase in the saturation vapor pressure deficit and overestimation of the daily ET
o at GY.
Table 7 shows the mean statistics of the performance metrics for the predicted daily ET
o with a lead time of 1–7 days by the seven models at the three sites. Combining all indicators, first, the prediction performance of the seven models at YC was better than that at TX and GY, which is mainly due to the overall better forecast performance of the public weather forecast variables at YC than at TX and GY. Second, the top three models at YC were PMT, HS, and CatBoost, whereas PMF (the worst performing model) overestimated the daily ET
o (21.35%). The top three models at TX were PMT, CatBoost, and HS, whereas MLP (the worst performing model) underestimated the daily ET
o (6.05%), and the top three models at GY were PMT, CatBoost, and LightGBM, whereas PMF (the worst model) overestimated the daily ET
o (14.46%).
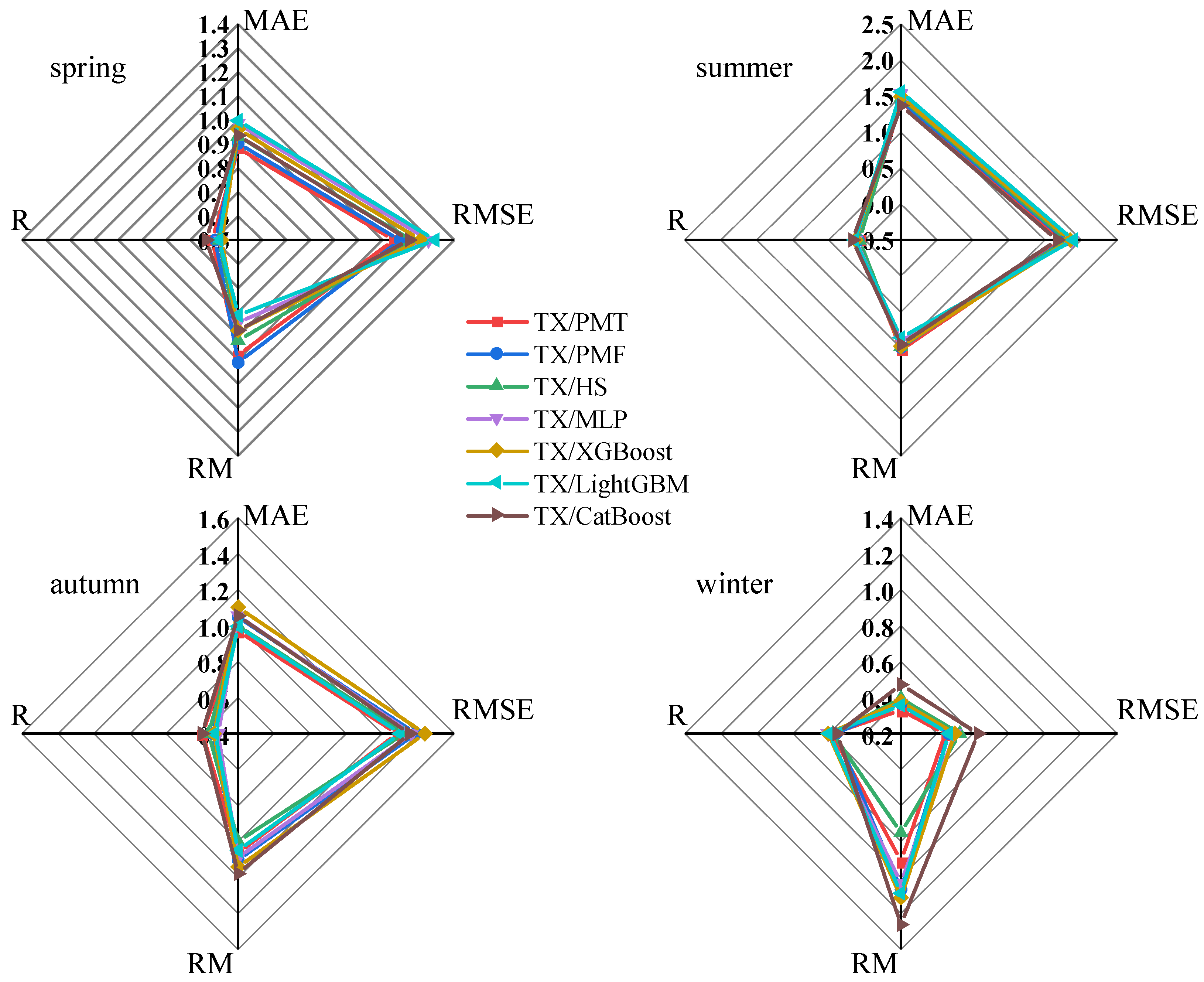
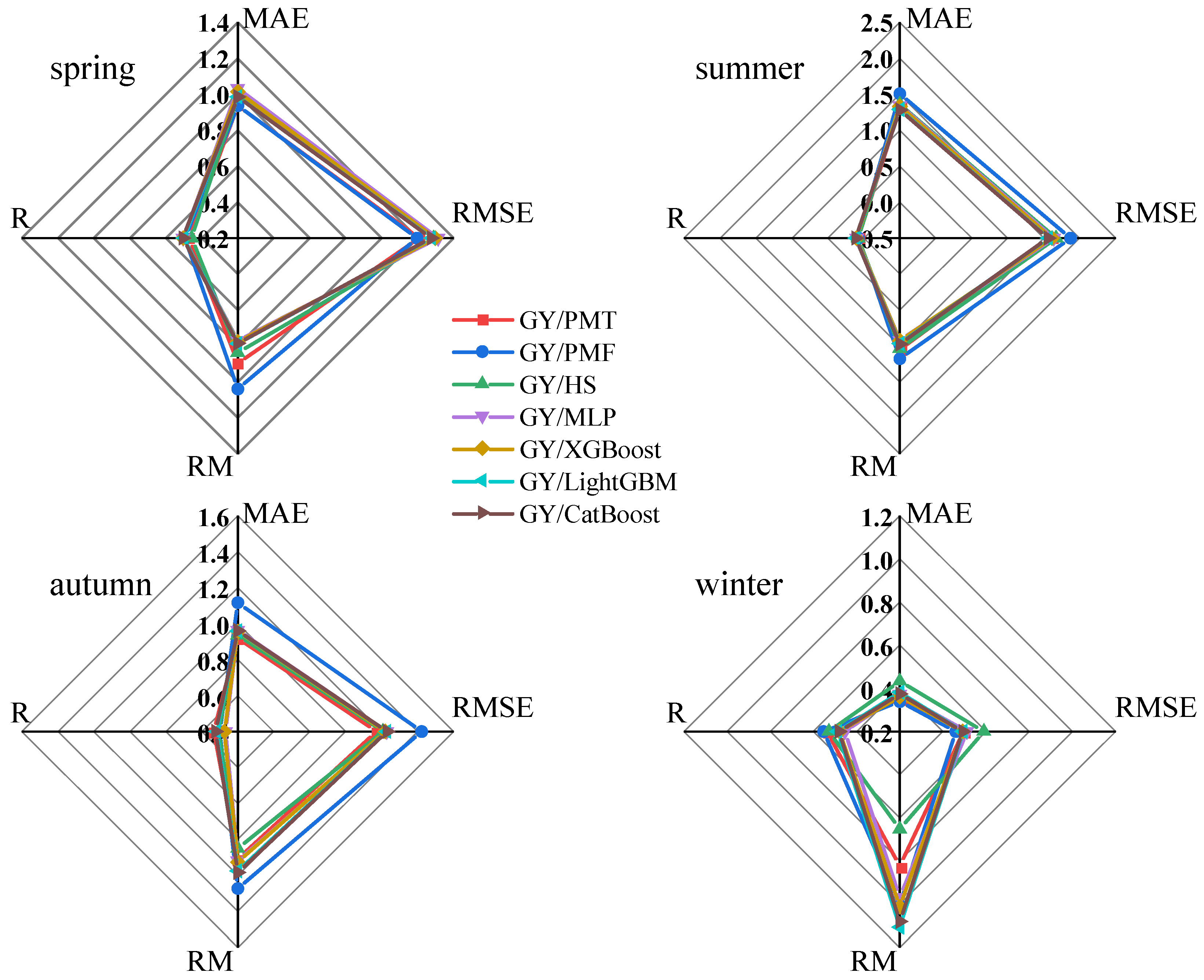
3.4.2. Seasonality of the Daily ETo Prediction Performance of the Seven Models
The sensitivity of weather variables varies with the different seasons and the microclimate at the studied site location [
15], while the irrigation area at the studied site location is associated with different field irrigation periods depending on the crop type, location, etc. [
1]. Therefore, it is necessary to evaluate the seasonality of the ET
o prediction performance. The average ET
o prediction performance indicators with a lead time of 1–7 days of the seven methods at the three station sites during the four seasons from 2020–2021 are shown in
Figure 10,
Figure 11 and
Figure 12, respectively.
First, during all four seasons, the daily ETo prediction performance of all seven models was higher at YC than at TX and GY (excluding the LightGBM model in winter), which was consistent with the results of evaluating the performance of daily ETo predicted by the seven models at three research sites (YC, TX, and GY) from a daily scale.
Second, except for the LightGBM model at TX, the seasonal MAE and RMSE values for ET
o prediction of all seven models at YC and six models at TX increased in the order of winter, spring, autumn, and summer, and the seasonal MAE and RMSE values in winter and spring were smaller than the annual values. At GY, except for the PMF model, the seasonal MAE and RMSE values for ET
o prediction of the other six models increased in the order of winter, autumn, spring, summer, and the seasonal MAE and RMSE values in winter were smaller than the annual values. This is consistent with previous studies [
1,
16,
20]. The seasonal R values for ET
o prediction of all models at the three sites were smaller than the annual values, and the seasonal R values were the smallest in summer. The seasonal R values at YC were the largest in autumn (except for the PMF model), the seasonal R values at TX were the largest in spring (the three empirical equations and the CatBoost model) and winter (MLP, XGBoost, and LightGBM), and the seasonal R values at GY were the largest in spring (MLP, XGBoost, and LightGBM), autumn (LightGBM and CatBoost), and winter (the three empirical equations). The seasonal RM values for daily ET
o prediction by the four machine learning models at the three sites were less than one in spring and summer and greater than one in autumn and winter, indicating that the daily ET
o in spring and summer was underestimated, while the daily ET
o was overestimated in autumn and winter (except at GY, where the MLP model underestimated the daily ET
o by 3.20%). The seasonal RM values for daily ET
o prediction by the three empirical models at YC and GY in summer and autumn and at TX in autumn were all greater than 1, indicating that the daily ET
o was overestimated during the corresponding season.
Finally, combining all indicators, at YC, the indicators of the predicted seasonal ET
o values with a lead time of 1–7 days by PMT were the best during all seasons, followed by HS (spring, autumn, and winter) and CatBoost (summer). At TX, the indicators of the predicted seasonal ET
o values with a lead time of 1–7 days by PMT were the best in spring, autumn, and winter. The indicators of the predicted seasonal ET
o values with a lead time of 1–7 days by CatBoost were the best in summer, followed by PMF (spring), PMT (summer), and LightGBM (autumn and winter). At GY, the indicators of the predicted seasonal ET
o values with a lead time of 1–7 days by PMF were the best in spring and winter, those of the predicted seasonal ET
o values with a lead time of 1–7 days by CatBoost were the best in summer, and those of the predicted seasonal ET
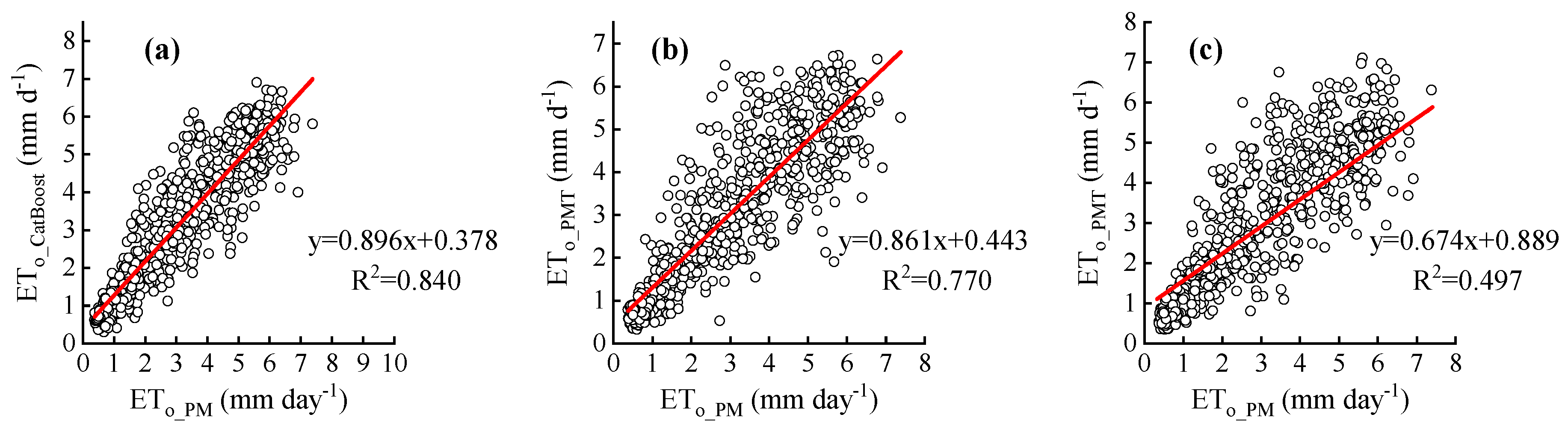
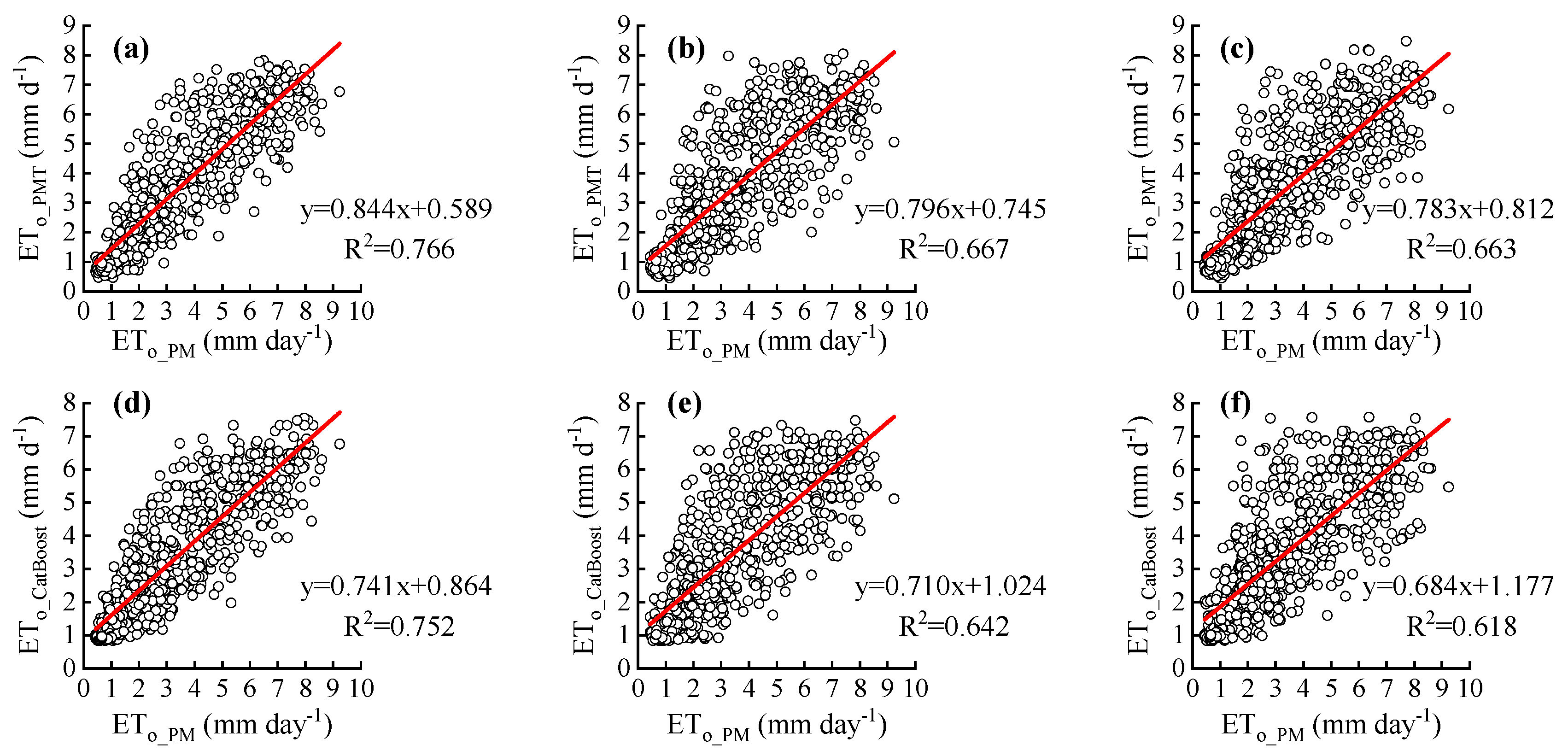
o values with a lead time of 1–7 days by PMT were the best in autumn, followed by PMT (spring and winter), LightGBM (summer), and HS (autumn). The scatter plots of the daily ET
o predicted by the PMT equations for the test period versus the daily ET
o computed by the PM equations for YC station; the scatter plots of the daily ET
o predicted by the PMT equations and the CatBoost model for the test period versus the daily ET
o computed by the PM equations for TX station; and the scatter plots of the daily ET
o predicted by the PMF equations, the CatBoost model, and the PMT equations for the test period versus the daily ET
o computed by the PM equations for GY station are given in
Figure 13,
Figure 14 and
Figure 15, respectively.
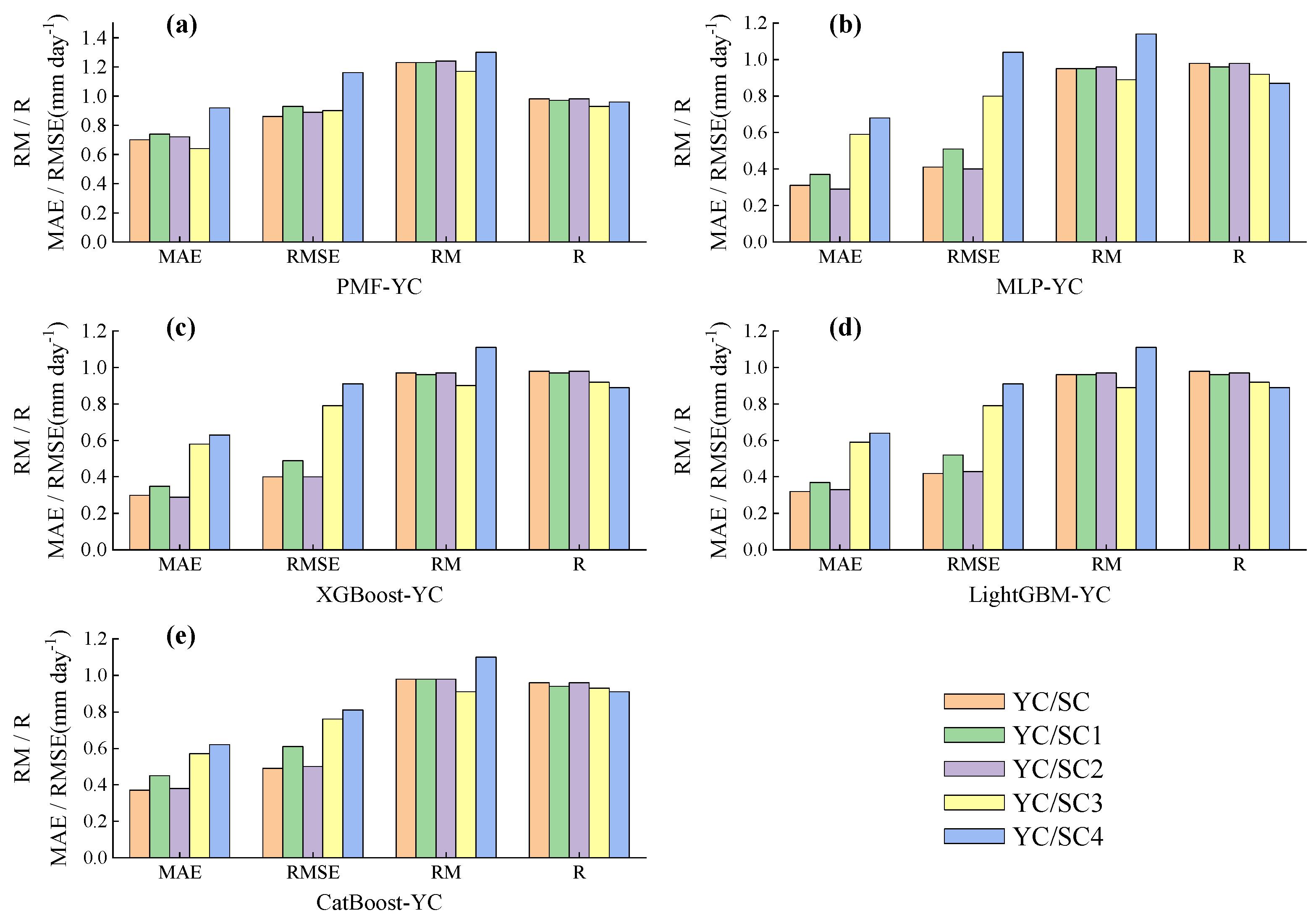
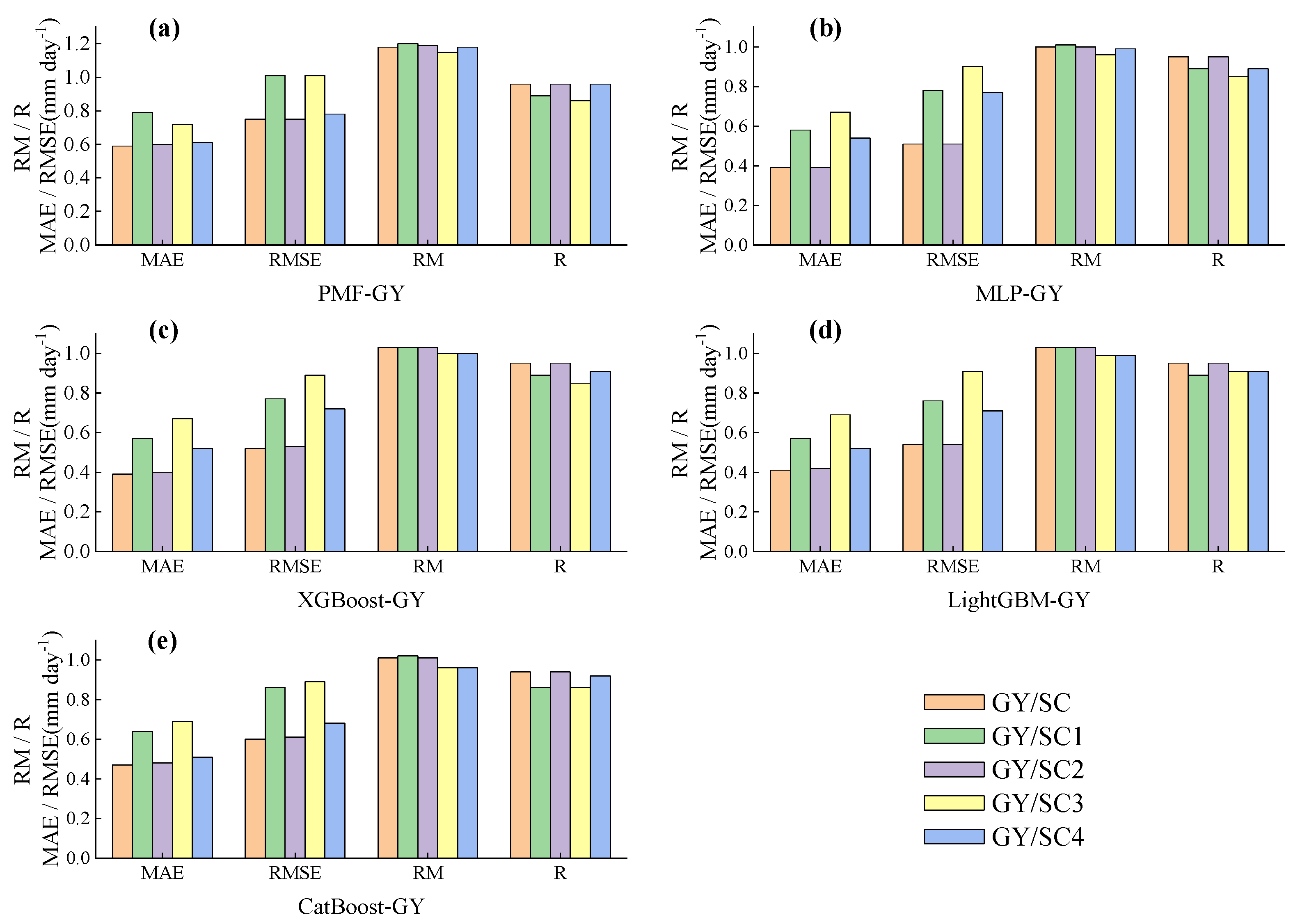
3.5. Impact of Weather Variable Prediction Based on Public Weather Forecasts on Daily ETo Prediction
To assess the impact of the weather variables in public weather forecasts on the performance of daily ET
o prediction, the four observed weather variables (T
max, T
min, SDun, and Wspd) were replaced in sequence with corresponding forecast values for a lead time of 1–7 days, such that a large change in the forecasted daily ET
o indicates that the forecasted weather variable would produce a large error in daily ET
o prediction [
1,
13,
16,
20].
Tmax,
Tmin,
Sdun, and
Wspd in public weather forecasts with a lead time of 1–7 days were used to replace the corresponding daily observed values of T
max, T
min, SDun, and Wspd, respectively, to form new combinations, namely, SC1 (
Tmax, T
min, SDun, and Wspd), SC2 (T
max,
Tmin, SDun, and Wspd), SC3 (T
max, T
min,
SDun, and Wspd), and SC4 (T
max, T
min, SDun, and
Wspd). The combination of all observations was denoted as SC (T
max, T
min, SDun, and Wspd). The mean values of the ET
o performance indicators of the five models at the three sites under the SC-SC4 input combinations are provided in
Figure 16,
Figure 17 and
Figure 18.
First, for the five models at all stations, the daily ETo slightly differed before and after replacing the observed Tmin with Tmin of the public weather forecasts. Notably, Tmin exhibited the smallest prediction error, and its contribution to the error in daily ETo prediction was minimal.
Second, for all models at YC,
Wspd yielded the largest contribution to the error in the predicted daily ET
o (first), and for the four machine learning models,
SDun and
Tmax yielded large (second) and relatively small (third) contributions, respectively, to the error in the predicted daily ET
o, which is consistent with previous findings [
20]. Regarding the PMF model,
Tmax and
SDun also yielded large (second) and relatively small (third) contributions, respectively, to the error in the predicted daily ET
o. At TX, among the four machine learning models,
n contributed the most to the error in the predicted daily ET
o (first), and
Wspd and
Tmax greatly contributed to the error in the predicted daily ET
o (second or third). Moreover,
Tmax contributed the most to the error in the predicted daily ET
o by the PMF model (first), while
Wspd and
SDun greatly contributed to the error in the predicted daily ET
o (second and third, respectively). For all models at GY,
SDun contributed the most to the error in the predicted daily ET
o (first), while
Tmax and
Wspd also greatly contributed (second and third, respectively) to the error in the predicted daily ET
o. This is consistent with previous studies [
12,
13,
16,
20].
These results indicate that the main source of error in daily ET
o prediction at YC in an arid region is
Wspd transformed from the wind scale in public weather forecasts. Due to regional differences, as well as the influences of the location of weather stations and local topographic features [
42], wind speed is one of the most difficult parameters to accurately predict [
20,
69]. Cai et al. [
18] stated that it is acceptable to estimate the wind speed from the wind scale in public weather forecasts, but the error in such estimates could be large in arid regions [
20]. George et al. [
70] showed that the discrepancy between predicted and measured reference crop evapotranspiration values largely resulted from erroneous predictions of the mean wind speed. Li and Beswick [
71] reported that wind speed represents a more serious source of error than solar radiation in ET
o estimation. Except in arid and windy areas, the effect of the wind speed on the estimated ET
o values is relatively limited [
72].
At TX in a semiarid region and GY in a semihumid region, SDun converted from the weather type in public weather forecasts was the main source of error in daily ET
o prediction. First, since the weather type in the public weather forecasts was converted into SDun using the sunshine duration coefficient values listed in
Table 3, obtained using 2004 measured solar radiation data for Daxing District, Beijing, which is located in a warm temperate semihumid continental monsoon climate zone, the application of sunshine duration coefficients derived from one region to other regions with different climate types could result in different degrees of error due to the climatic differences between these regions [
11,
21]. Second, the values of a
s and b
s in Equation (11) can vary depending on atmospheric conditions (humidity and dust) and solar declination (latitude and month), so the improved a
s and b
s parameters must be calibrated when calculating R
s with Equation (11) [
36]; in contrast, we directly used the recommended values of 0.25 and 0.5 without calibration, which could also cause errors. Perera et al. [
1] found that the largest error source between predicted and observed ET
o values is the prediction accuracy of the incident solar radiation. The results of Medina et al. [
13] showed that the error in radiation prediction imposed the greatest influence on ET
o prediction, followed by the error in wind prediction. Fan et al. [
16] noted that in the temperate continental zone (TCZ), temperate monsoon zone (TMZ), and other climate zones, the contribution of the R
s (solar radiation) prediction error to the ET
o prediction error was the greatest.
4. Conclusions
In this study, the performance of three empirical equations and four machine learning models for daily ETo prediction at three stations in three climatic regions of Ningxia, China, was evaluated using public weather forecasts with a lead time of 1–7 days. The prediction performance of weather variables in public weather forecasts and the prediction performance of the daily ETo of the seven models were analyzed and evaluated on daily and seasonal scales, respectively. The optimal input combination of the machine learning models was determined, and the weather forecast variables contributing to the error in the predicted daily ETo were clarified. The main conclusions of this study are as follows:
- (1)
At all stations, in the public weather forecast variables with a lead time of 1–7 days during the four seasons of spring, summer, autumn and winter from 2020–2021, Tmax followed the order of autumn > summer> winter > spring (or summer > autumn > winter > spring), Tmin followed the order of autumn > summer > winter > spring (or summer > autumn) > spring > winter), SDun followed the order of winter > spring > autumn > summer, and the average forecast performance decreased in sequence. The performance of wind speeds predicted by public weather forecasts was the worst, and their prediction performance showed great variation depending on the station. It was recommended that the model predict the daily ETo by considering the wind speed to take a constant value (2 m s−1) or the daily average wind speed over a long period;
- (2)
The calibrated PMT equation (kRs = 0.16, Tdew = Tmin − 1) with public weather forecasts of Tmax, Tmin, and 2 m s−1 of constant wind speed as inputs was recommended as the best model for the irrigation season at YC station for the predicted lead time of 1–7 day ETo for all three stations. The calibrated PMT equation (kRs = 0.21, Tdew = Tmin − 3) with public weather forecasts of Tmax, Tmin, and constant wind speed of 2 m s−1 as inputs and CatBoost with C3 (Tmax, Tmin, Wspd) as inputs were the best-performing models for the spring and autumn irrigation seasons and the summer irrigation season at station TX, respectively. The calibrated PMF equation (Tdew = Tmin) with Tmax, Tmin, SDun, and 2 m s−1 constant wind speed from the public weather forecast as inputs, CatBoost with C4 (Tmax, Tmin) as inputs, and the calibrated PMT equation (kr = 0.18, Tdew = Tmin−2) with Tmax, Tmin, and 2 m s−1 constant wind speed from the public weather forecast as inputs were the optimal models for the spring irrigation season, summer irrigation season, and autumn irrigation season, respectively, at the GY station;
- (3)
The four machine learning models MLP, XGBoost, LightGBM, and CatBoost are recommended to select C2 (Tmax, Tmin, SDun) or C4 (Tmax, Tmin) as the input combinations to predict the daily ETo of the three stations. However, for station YC located in the arid zone, the error in the model prediction of daily ETo is mainly caused by Wspd from the public weather forecast, followed by SDun. SDun from the public weather forecast is the main source of error in the model prediction of daily ETo for station TX located in the semiarid zone and station GY located in the semimoisture zone, followed by Wspd. Therefore, the combination of Wspd from public weather forecasts and SDun should be considered carefully when adding them to the input combination of the model.
The optimal predictive daily ETo model for the irrigation season recommended in this study has been successfully used in the irrigation forecast of 1–3 days in advance for 134 ha of Lycium barbarum crop in Tongxin, Ningxia, China. Compared with the local conventional irrigation, the irrigation forecasting of 1–3 days in advance using the ETo model of the optimal prediction day of the irrigation season realized the improvement of quality and yield, and water-saving irrigation of field Lycium barbarum, and improved the utilization of the limited rainfall during the fertility period of the Lycium barbarum crop.
Although the best models for predicting daily ETo during the irrigation season at the study stations were obtained, some stations had lower model prediction accuracy during certain irrigation seasons (e.g., the best models for the summer season at the TX and GY stations), and the combination of these machine learning models with optimization algorithms (ant colony optimization algorithms, cuckoo search algorithms, flower pollination algorithms, etc.) could be explored to optimize the model’s hyperparameters through optimization algorithms to further enhance the performance of the model to predict ETo and improve the accuracy of the model to predict ETo.