Evaluation of Extreme Climate Indices over the Three Northeastern Provinces of China Based on CMIP6 Models Outputs
Abstract
:1. Introduction
2. Materials and Methods
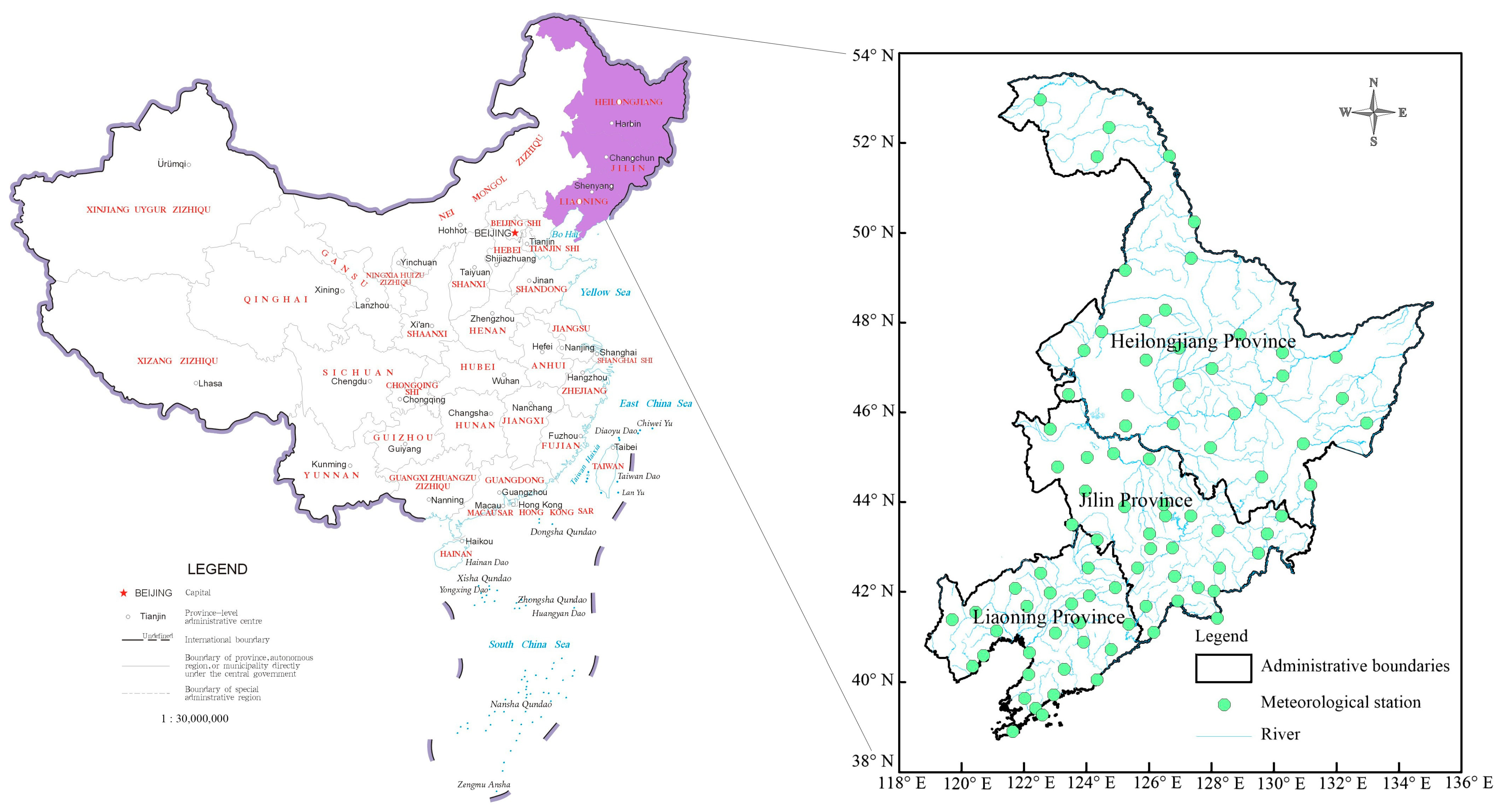
2.1. Study Area
2.2. Data
2.3. Extreme Climate Indices
2.4. Evaluation Methods
2.4.1. Biases
2.4.2. IVS
2.4.3. Taylor Diagram and S
3. Results
3.1. Spatial Bias Analysis
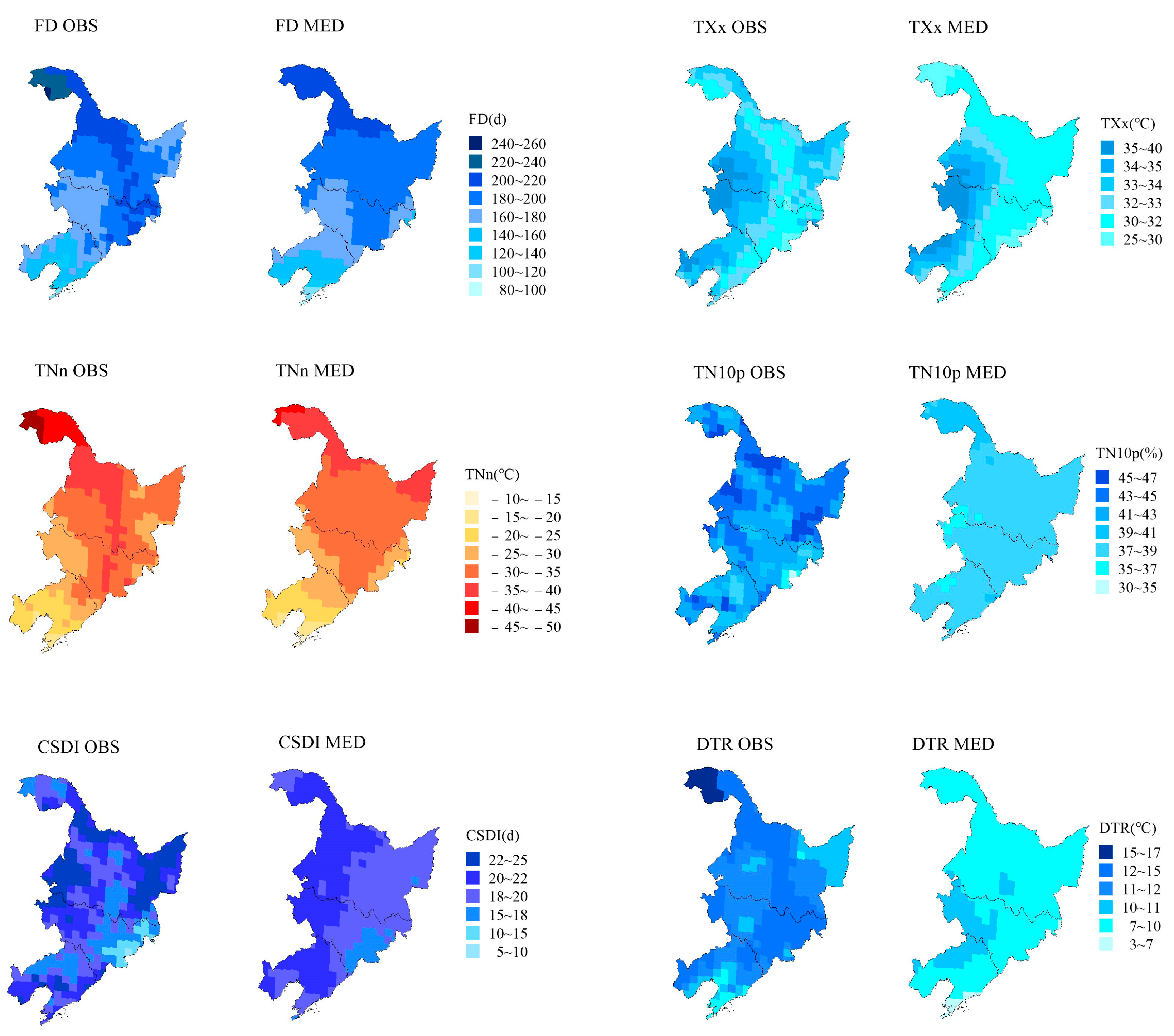
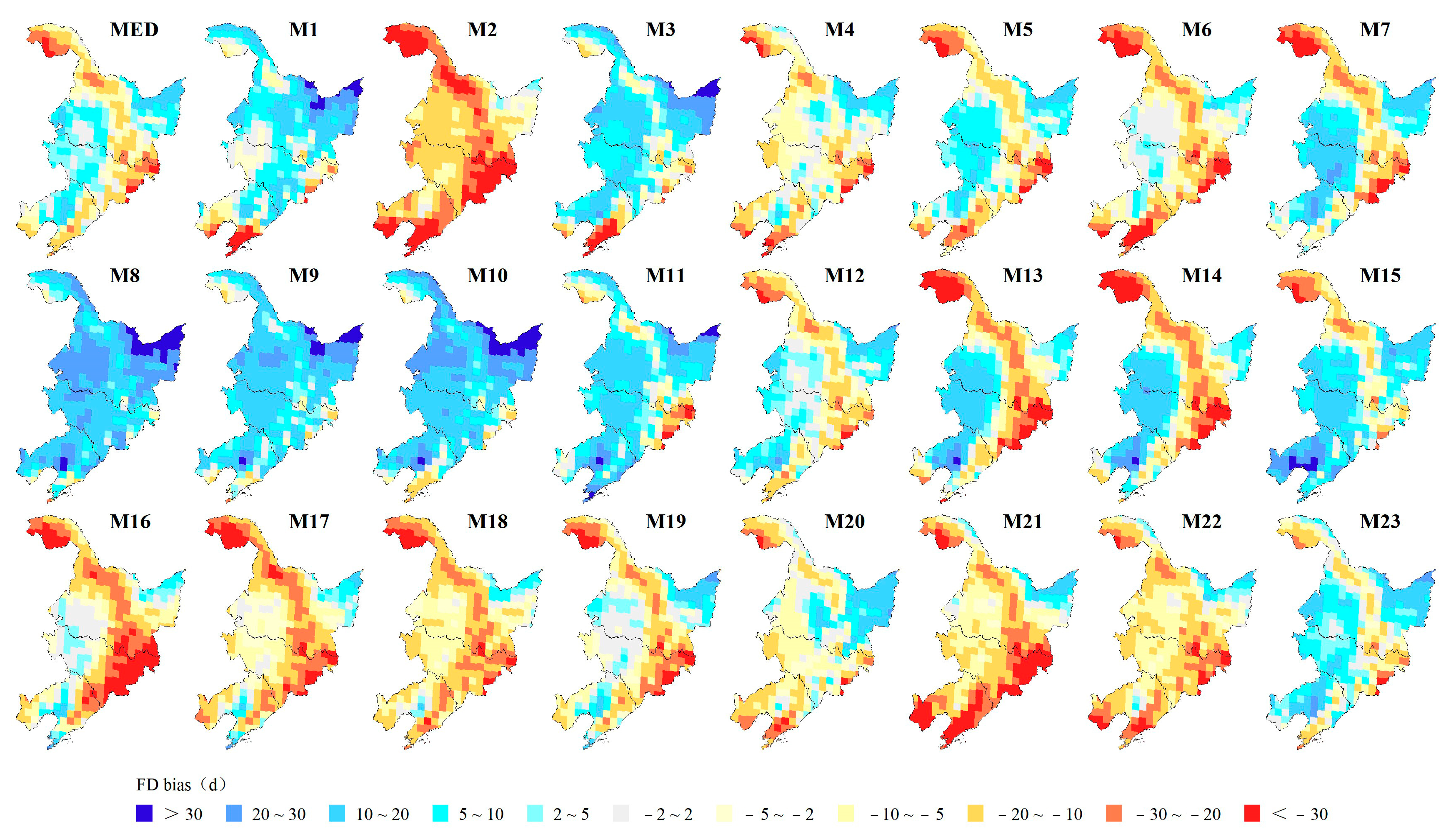
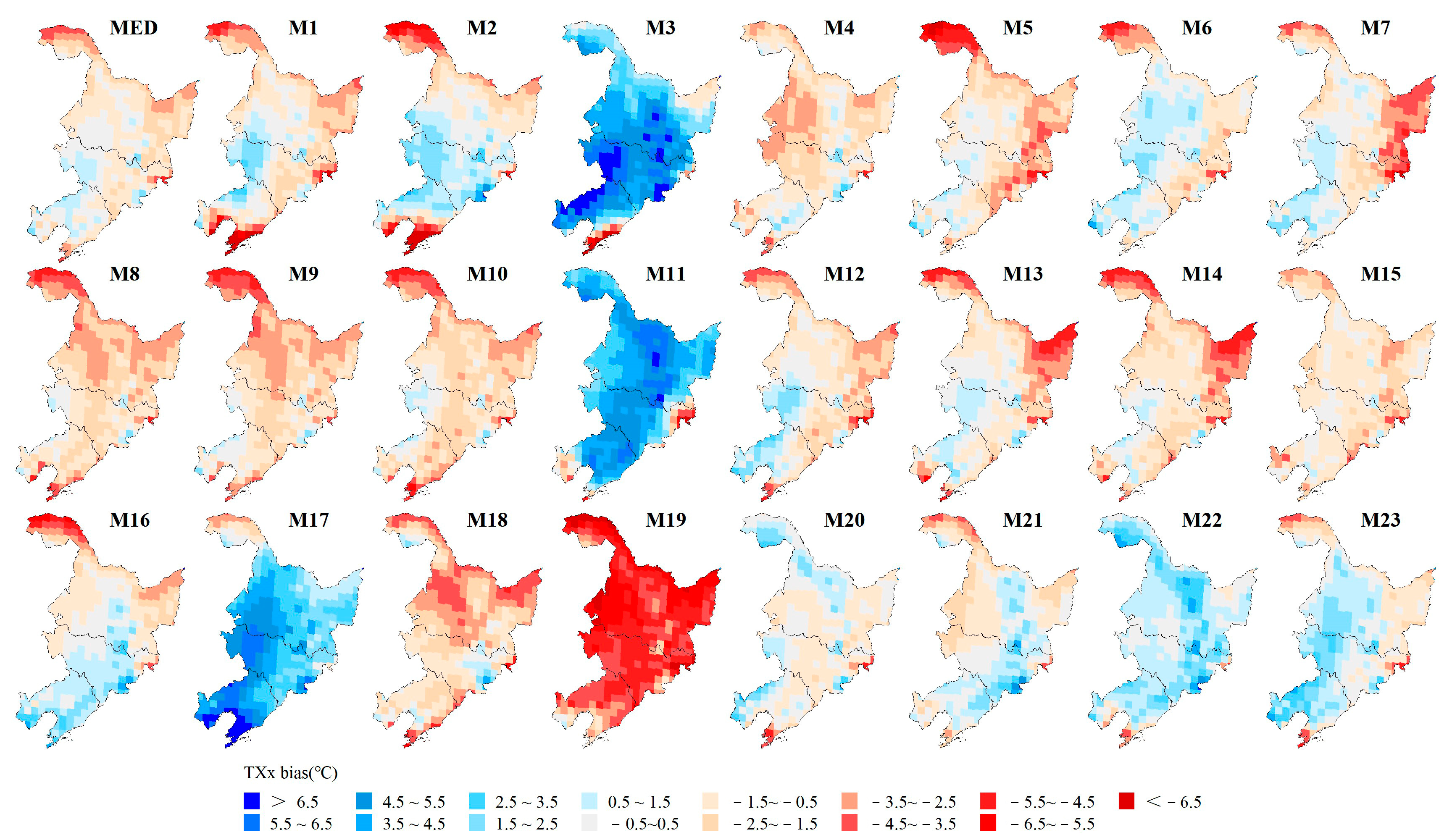
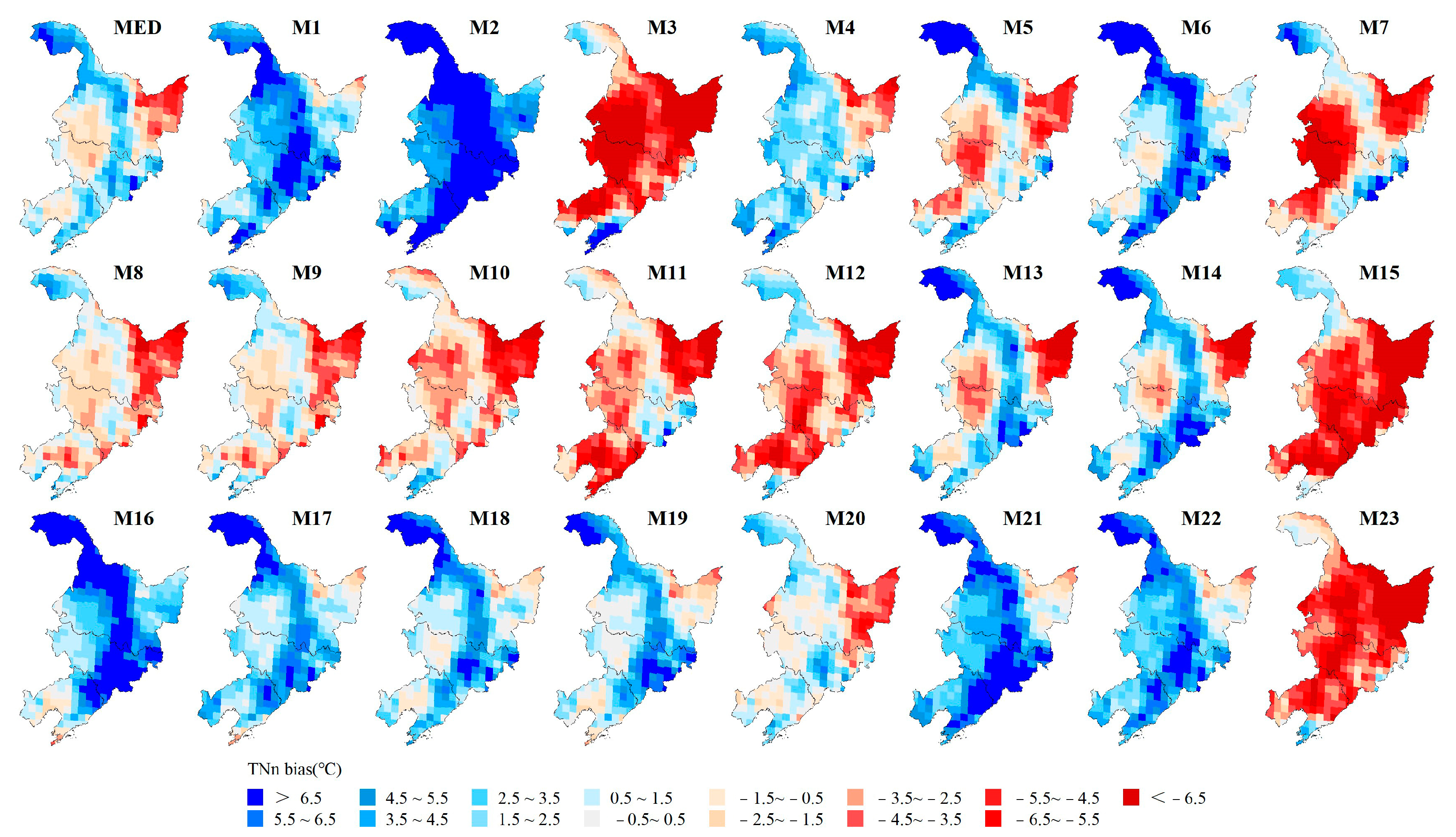
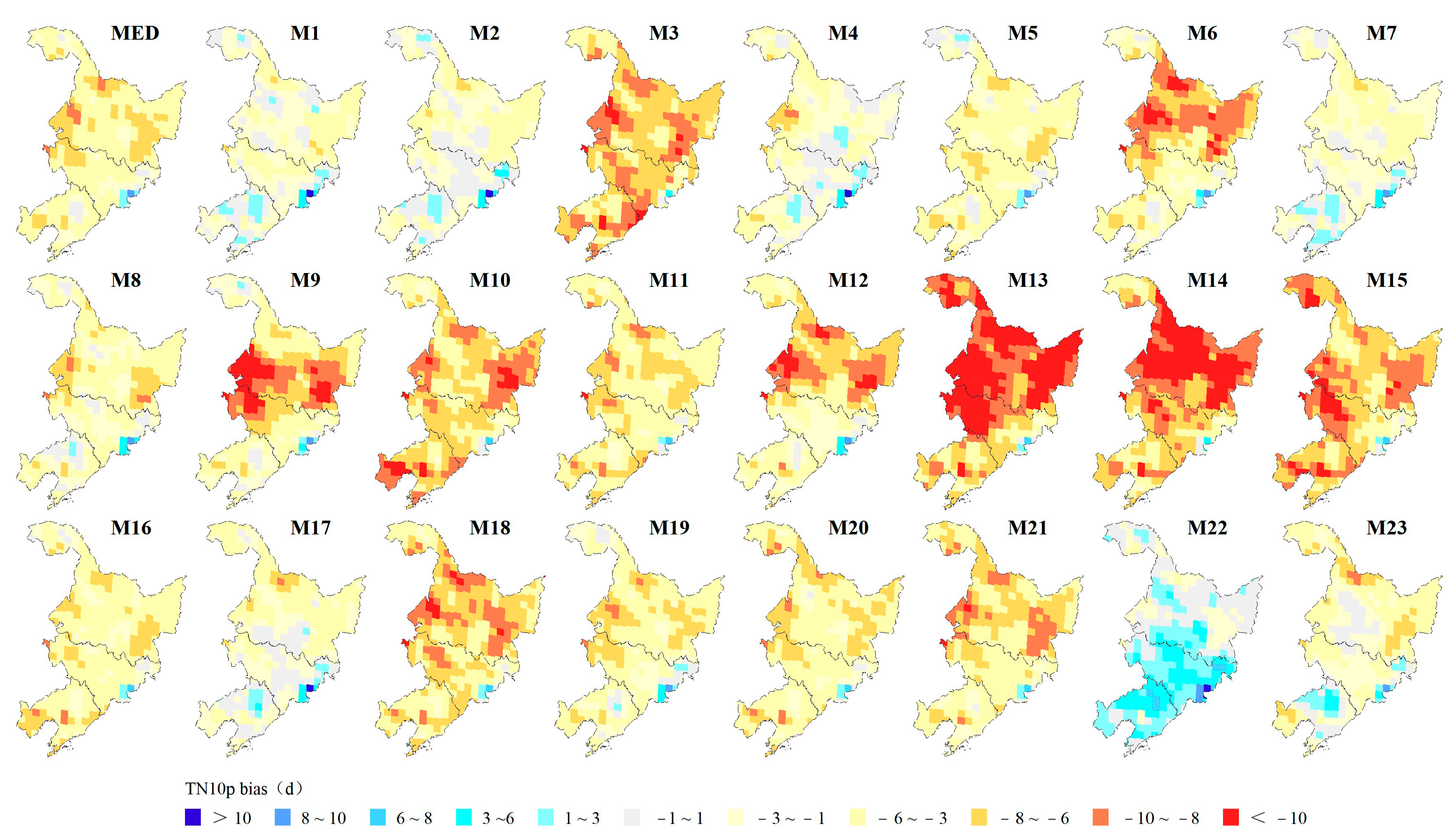
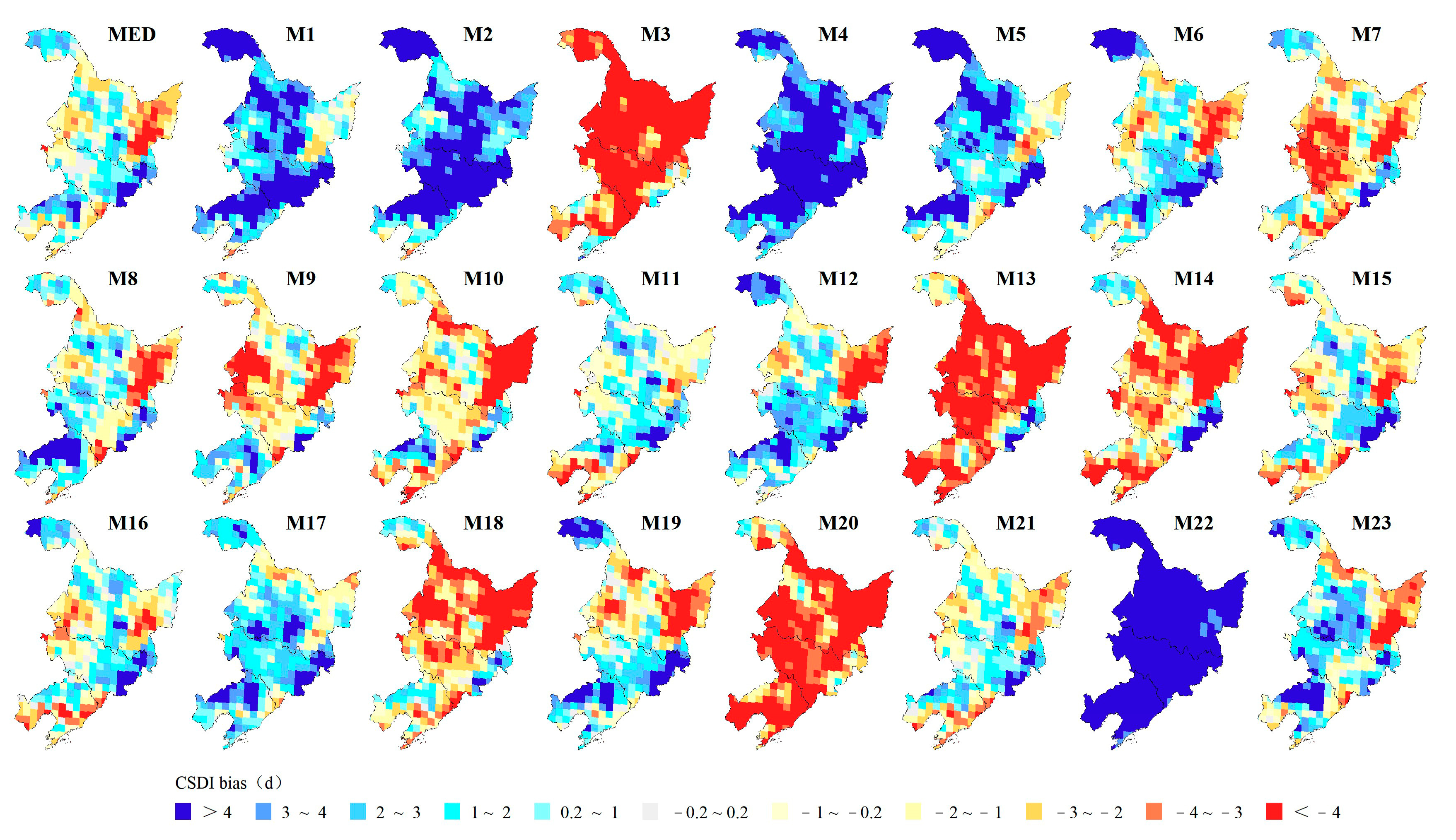
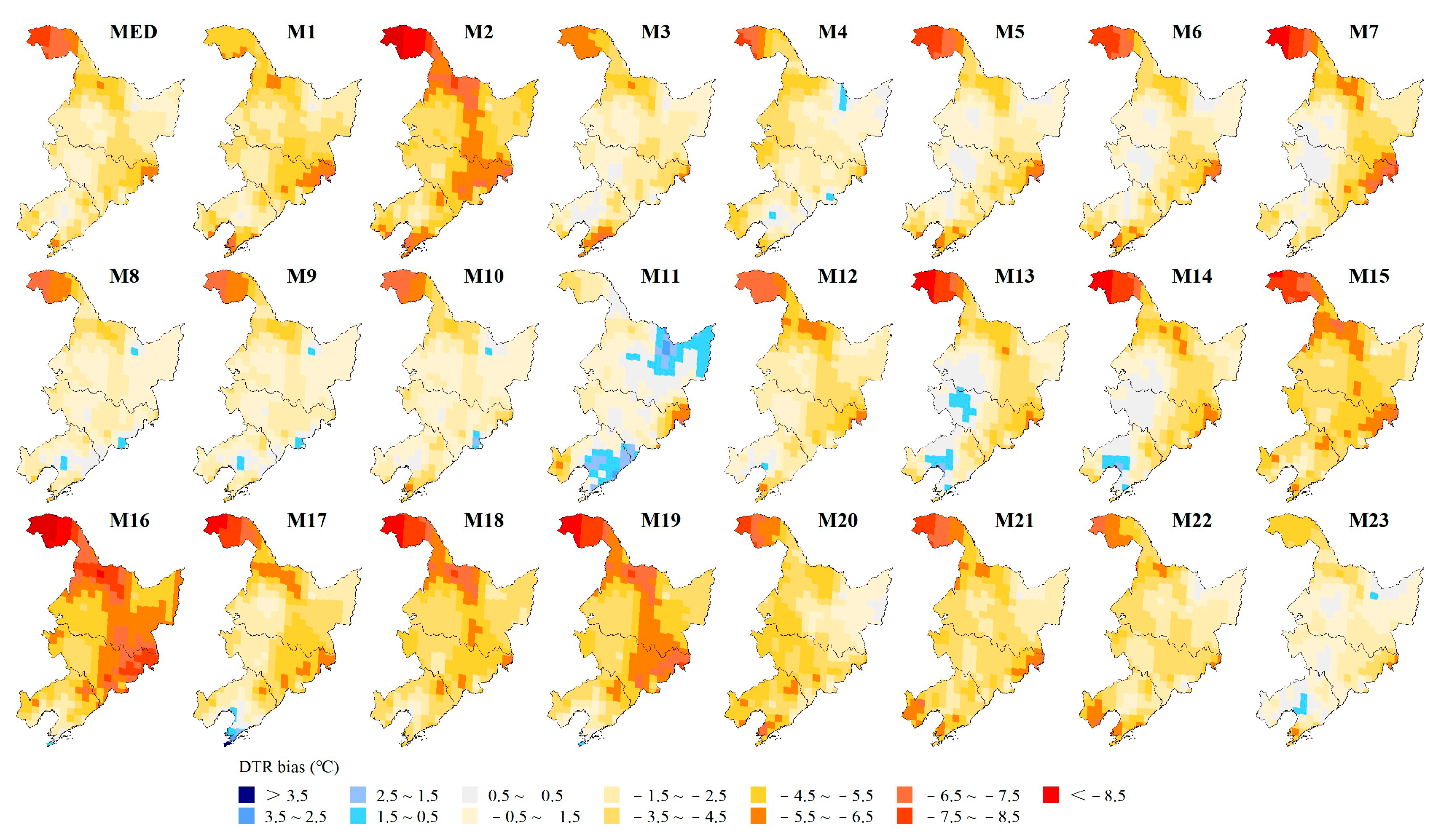
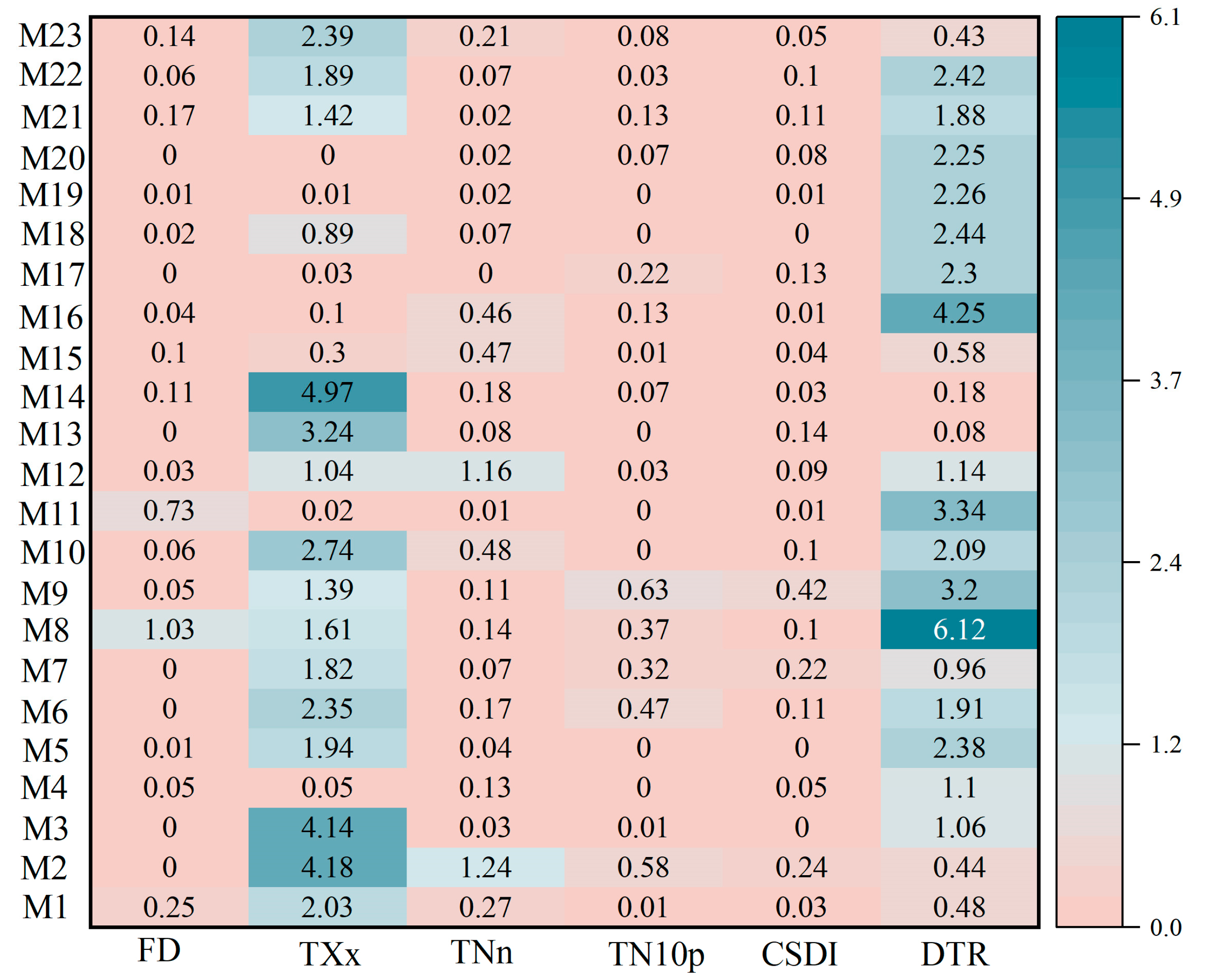
3.1.1. Spatial Biases of Extreme Temperature Indices
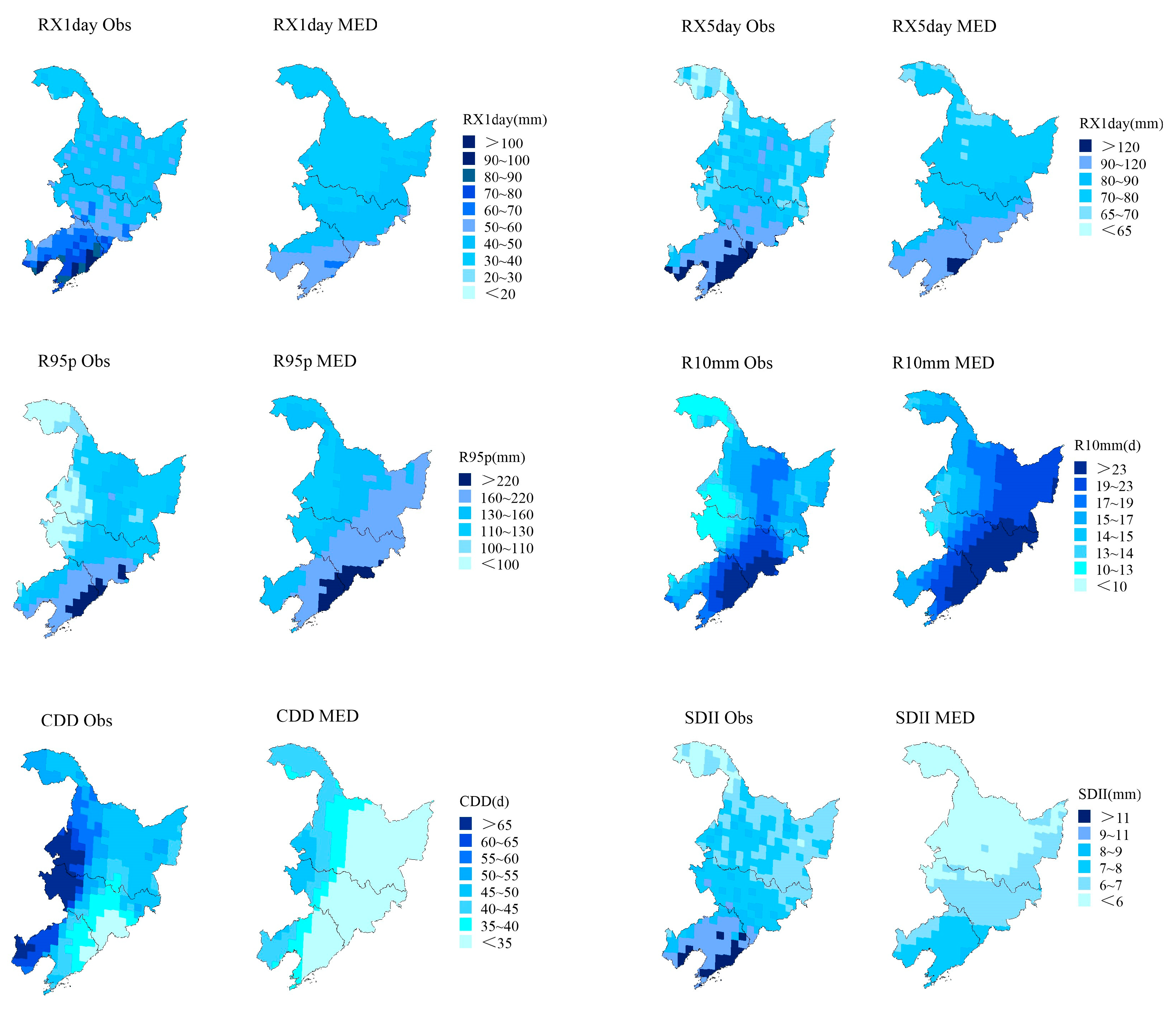
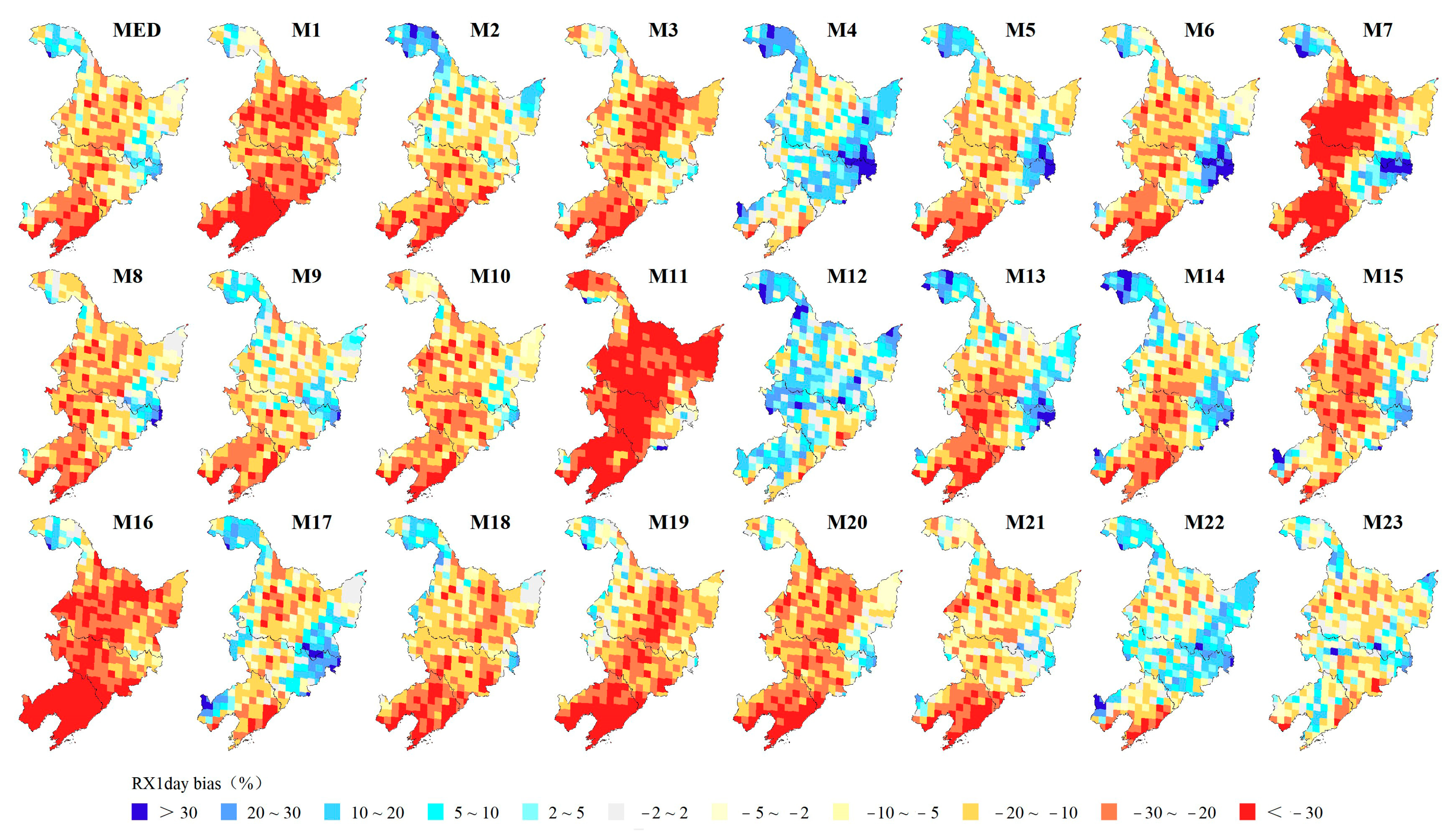
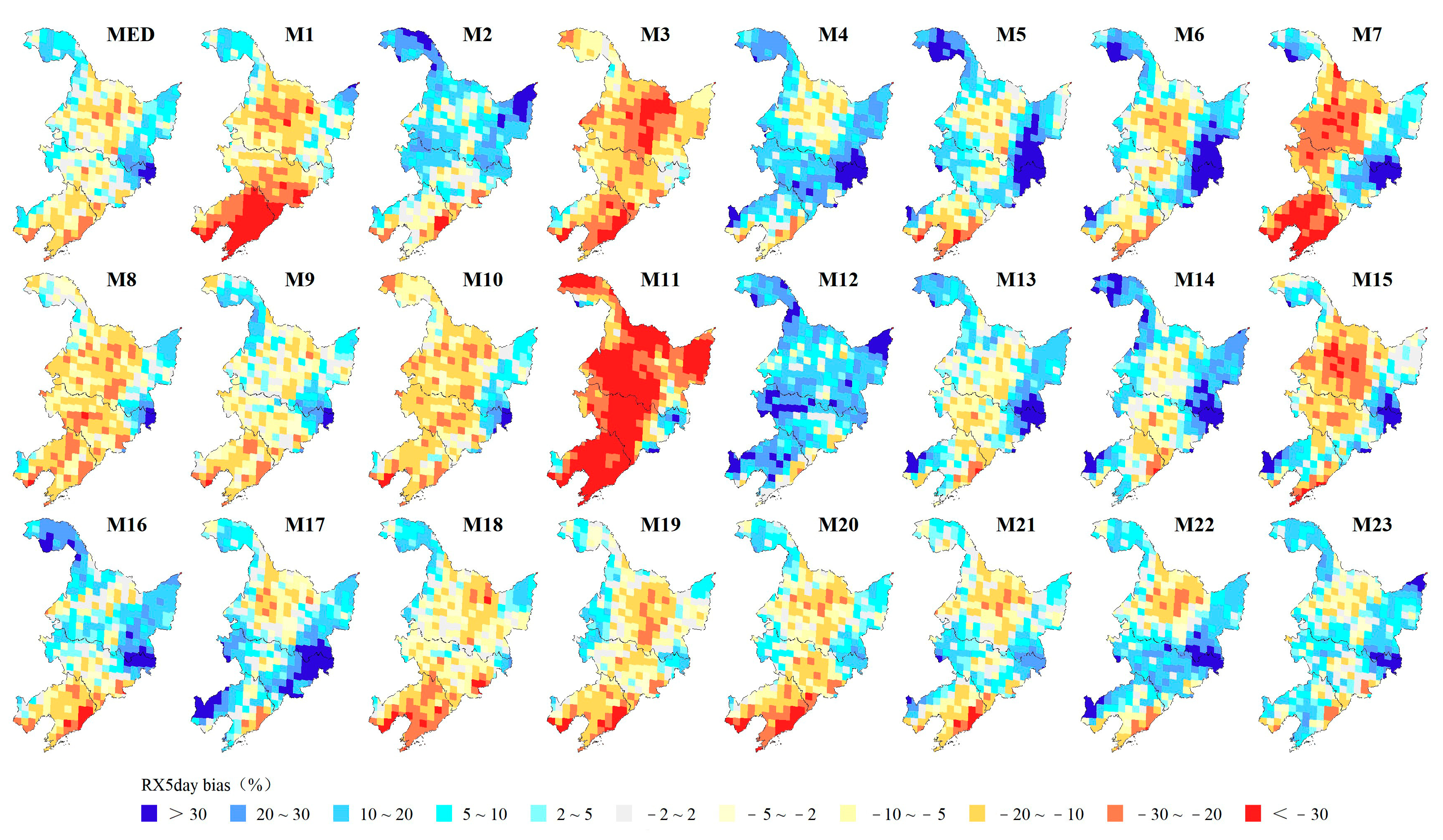
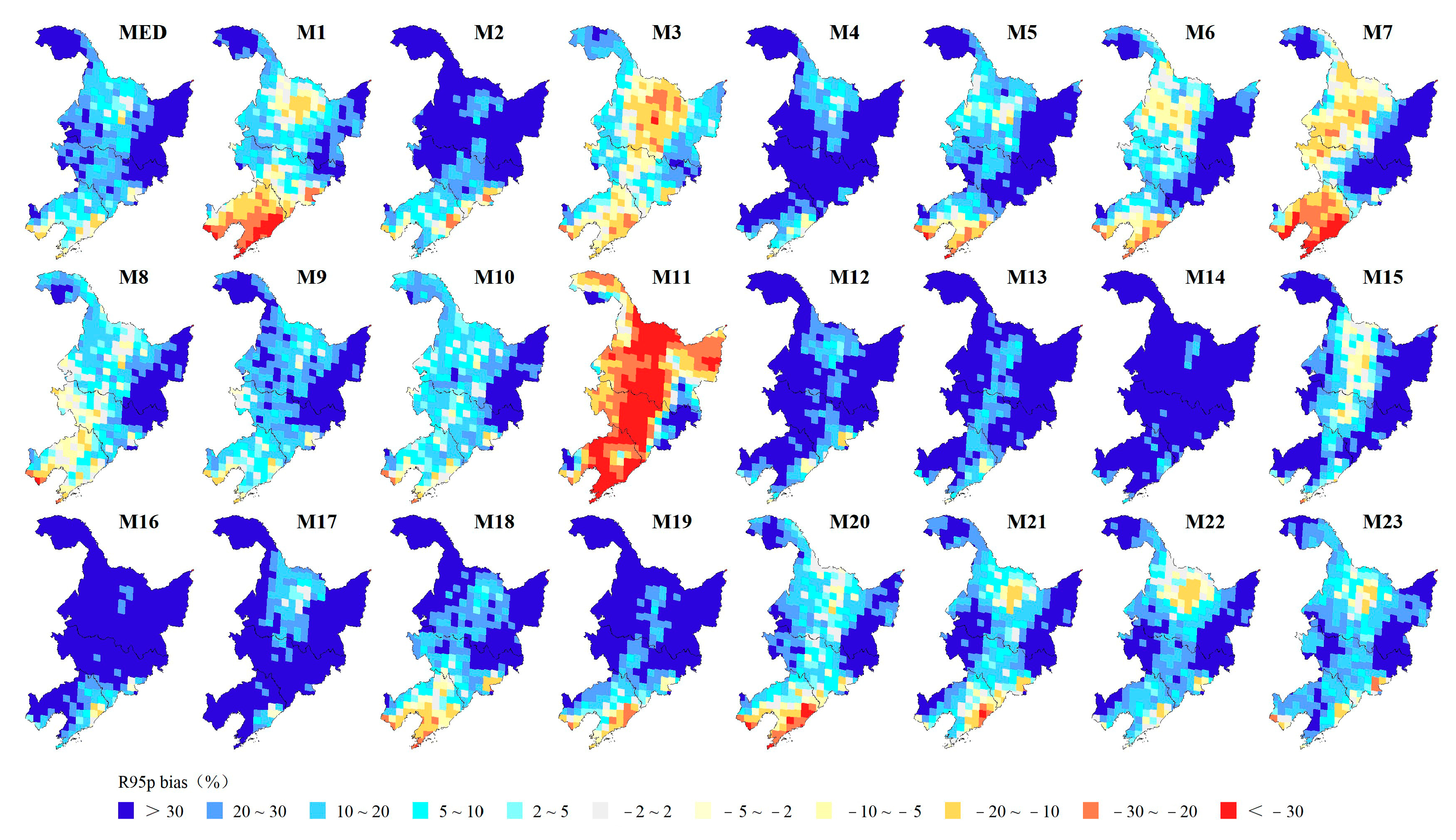
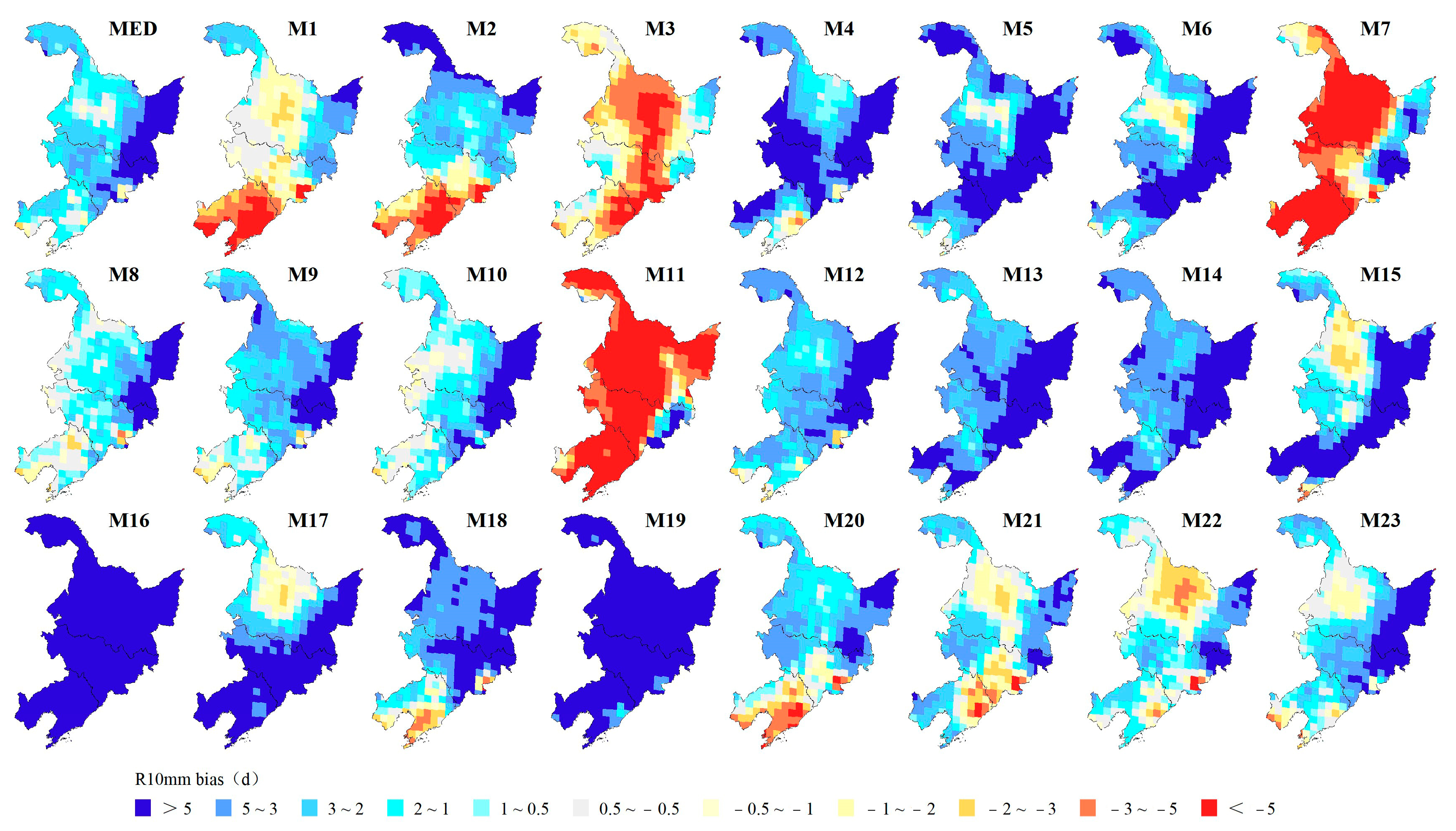
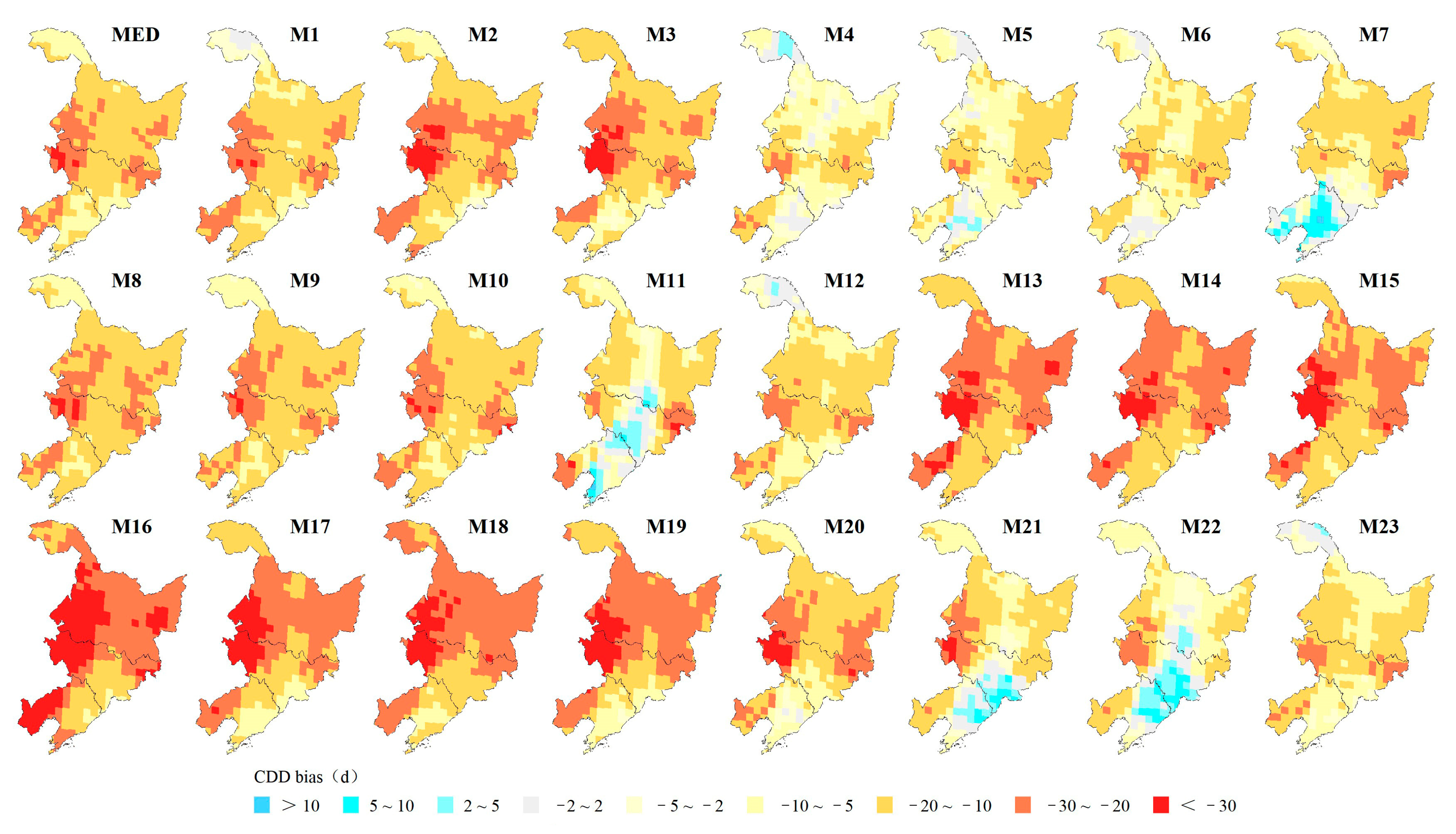
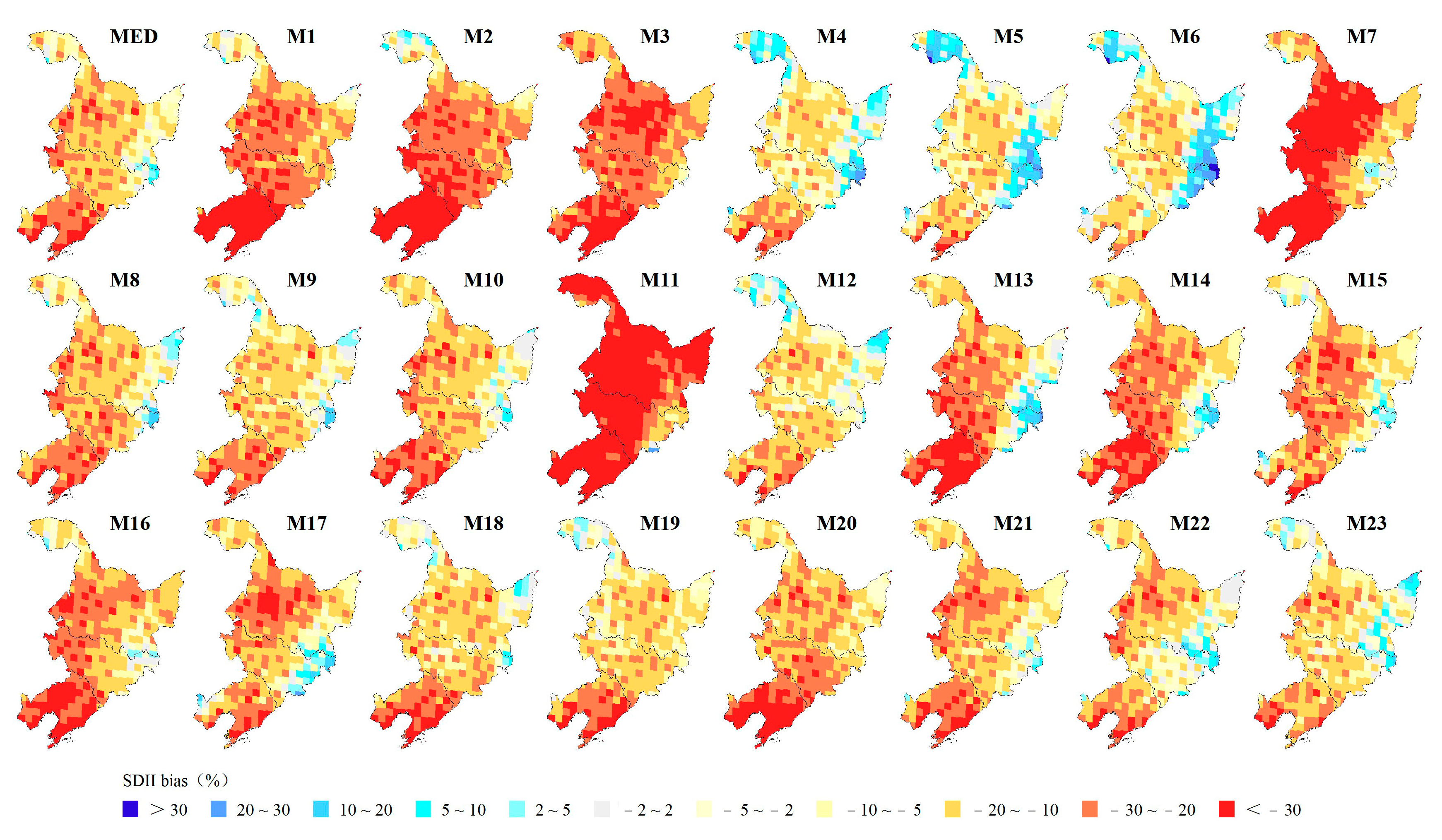
3.1.2. Spatial Biases of Extreme Precipitation Indices
3.2. Temporal Simulation Capability
3.2.1. Temporal Simulation Capabilities of GCMs for Extreme Temperature Indices
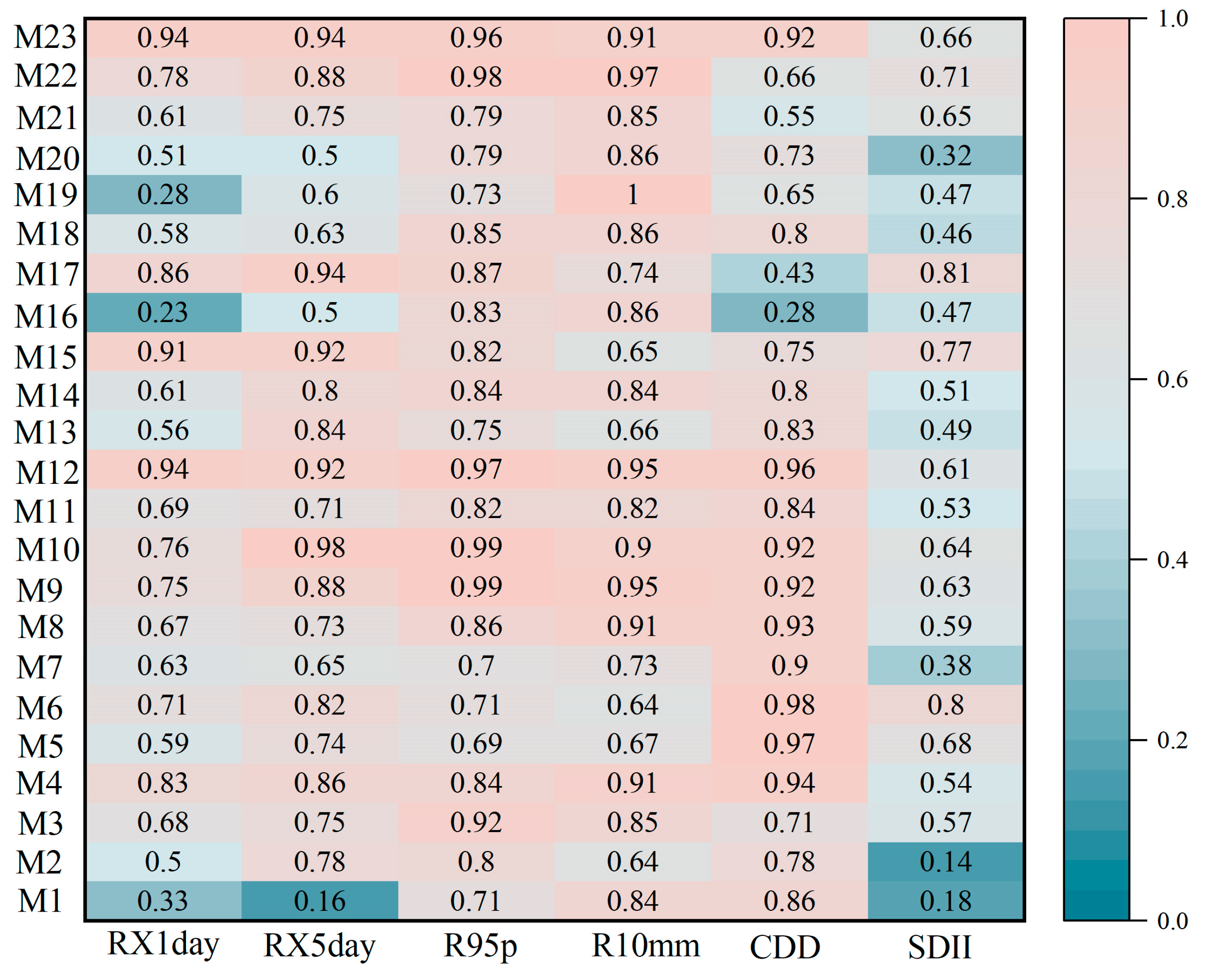
3.2.2. Temporal Simulation Capabilities of GCMs for Extreme Precipitation Indices
3.3. Spatial Simulation Capability
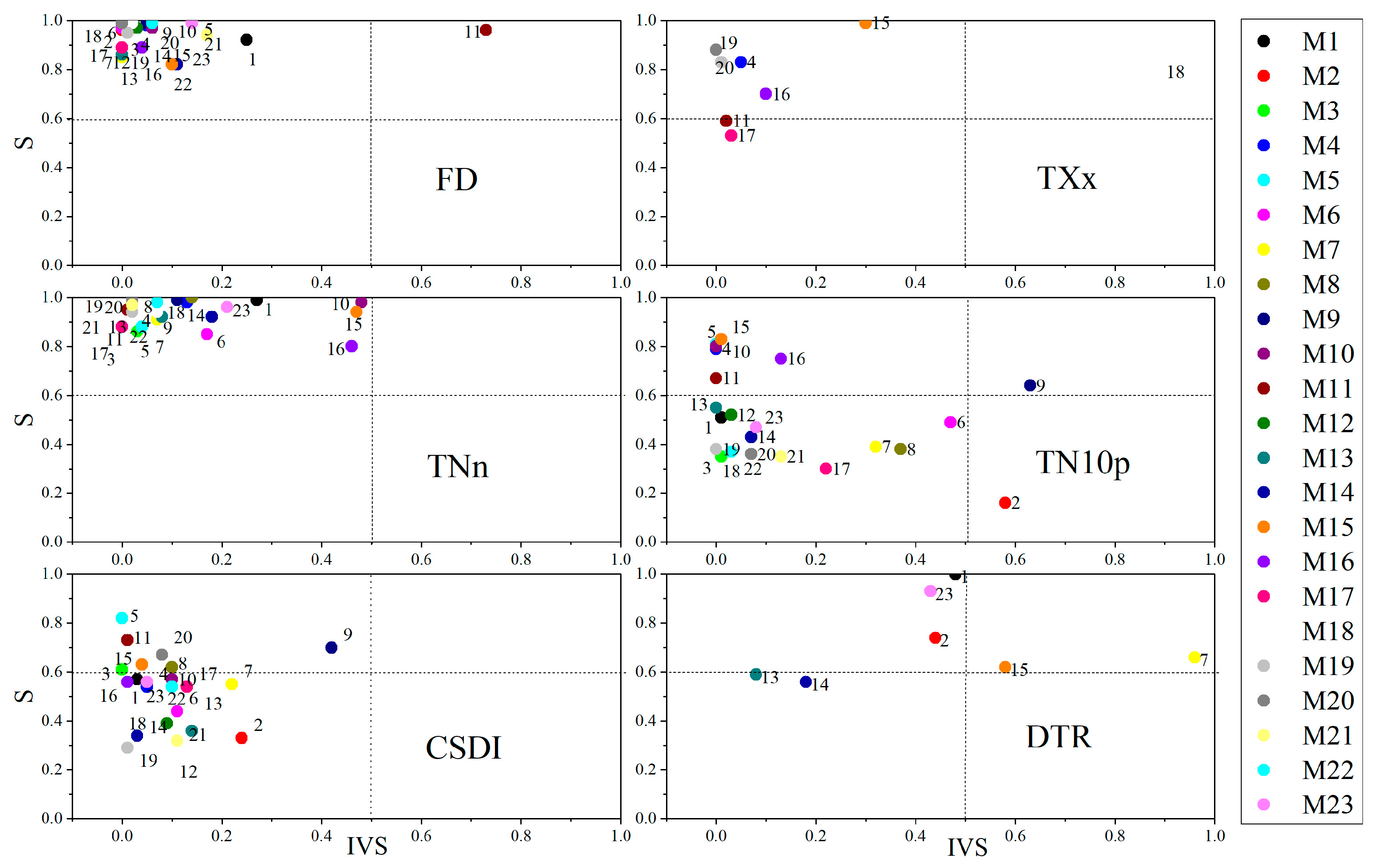
3.3.1. Spatial Simulation Capabilities of GCMs for Extreme Temperature Indices
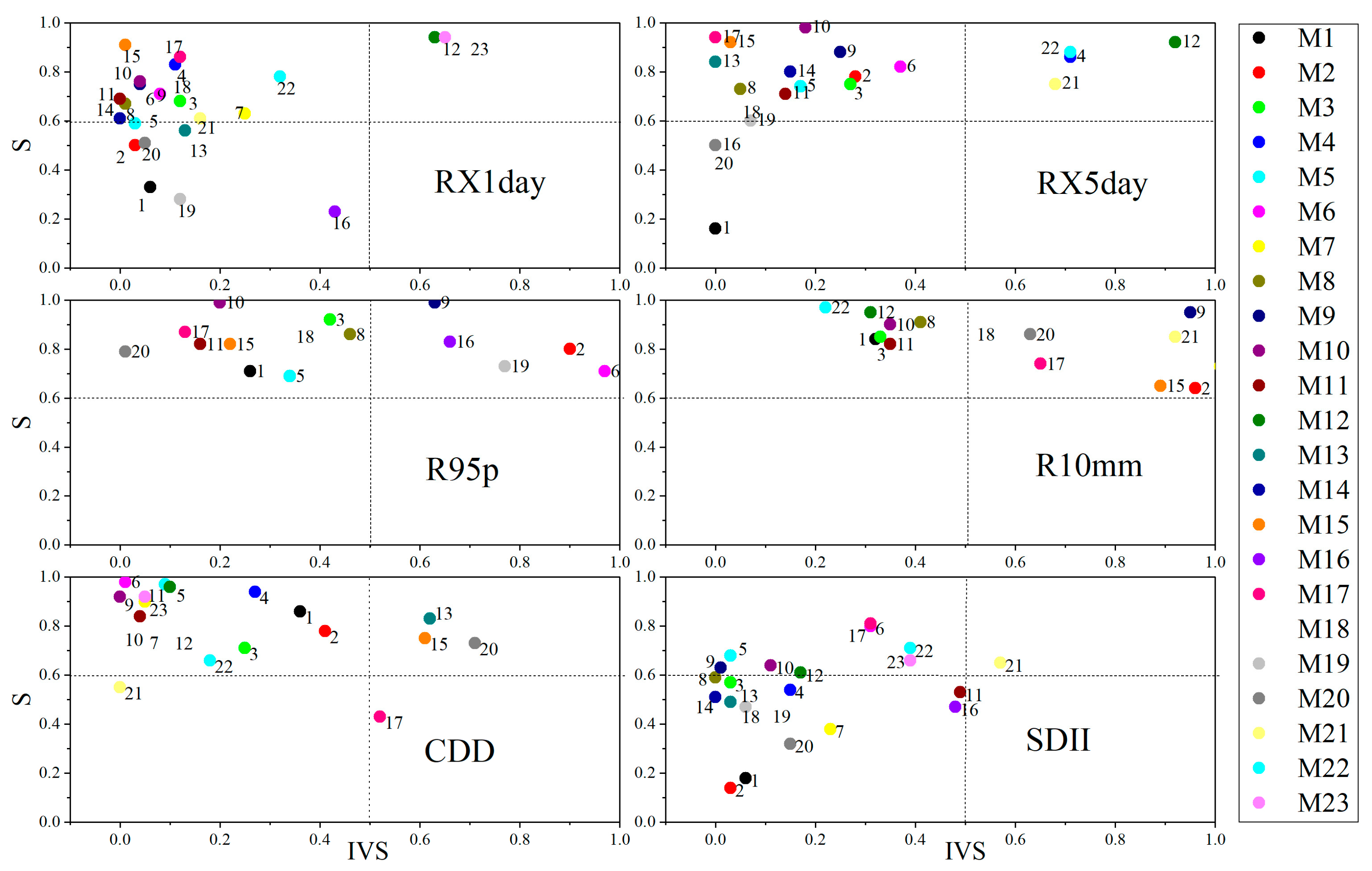
3.3.2. Spatial Simulation Capabilities of GCMs for Extreme Precipitation Indices
4. Discussion
5. Conclusions
- (1)
- The GCMs could generally reproduce the spatial distribution of the extreme temperature indices, but underestimate most indices, with the exception of TNn, which shows a positive bias in 55.7% of the regional grids. TN10p and DTR exhibit negative biases in over 95% of the regional grids. The GCMs may perform better for spatial simulations of TXx and CSDI, with regional spatial biases of 1.17 °C and 1.91 d, respectively, while performing poorly in the spatial simulation of FD, with a regional spatial bias of 9d. Regionally, the spatial biases of the GCMs are larger in the northern and central parts of Heilongjiang Province and in most parts of Jilin and Liaoning Provinces.
- (2)
- The GCMs perform better in the spatial simulation of RX5day and R10mm, with regional spatial biases of 10.66% and 3.24 d, respectively, while the GCMs perform worse in the spatial simulation of R95p, with a regional spatial bias of 29.10%. Over 90% of grid simulations show positive biases for R95p and R10mm, but negative biases for CDD and SDII. RX1day and RX5day also exhibit negative biases in over 80% and 54% of the regional grids, respectively. Regionally, the simulated extreme precipitation in northern and southeastern Heilongjiang Province and northeastern Jilin Province shows positive biases.
- (3)
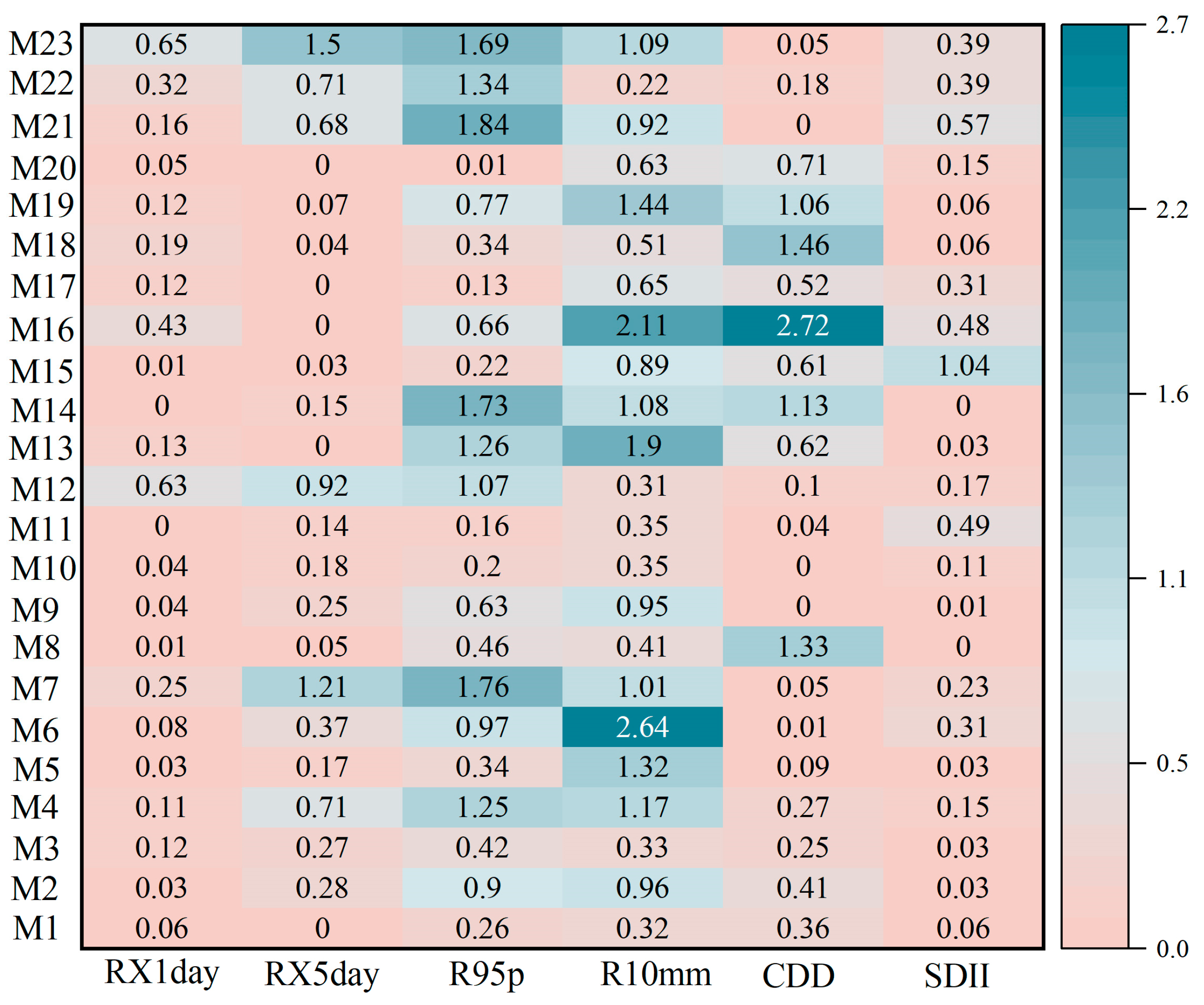
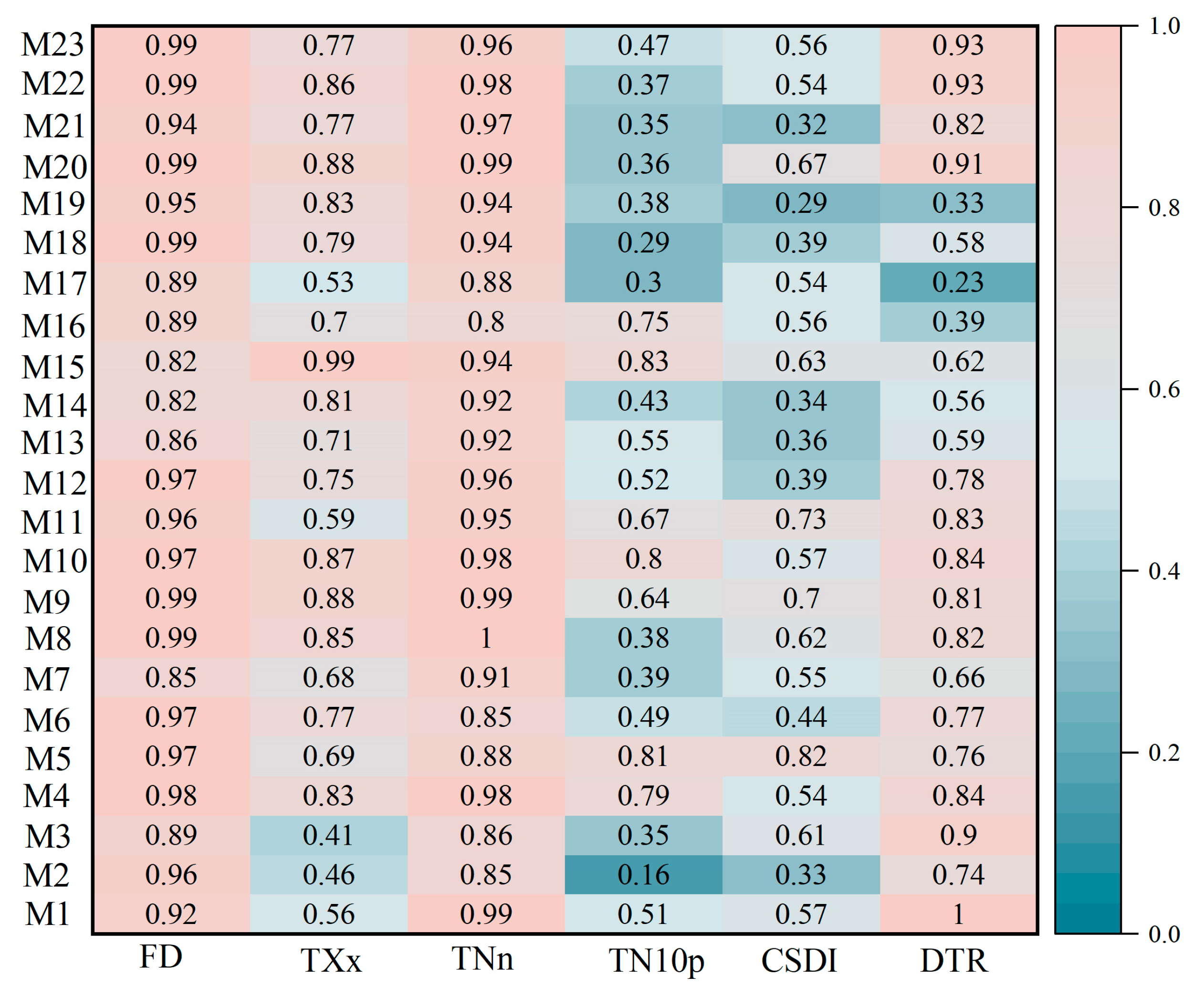
- The GCMs reproduce the interannual variability of FD, TNn, TN10p and CSDI (IVS < 0.5) but show inconsistency in capturing the interannual variabilities of TXx and DTR (IVS > 0.9). M15 has the best ability to reproduce interannual variability in six extreme temperature indices (IVS < 0.6). The GCMs perform well in temporal simulations of RX1day, RX5day, CDD and SDII (IVS < 0.65), but are poor in R95p and R10mm (IVS > 0.9). M1 and M10 reproduce the interannual variability well in six extreme precipitation indices (IVS < 0.4).
- (4)
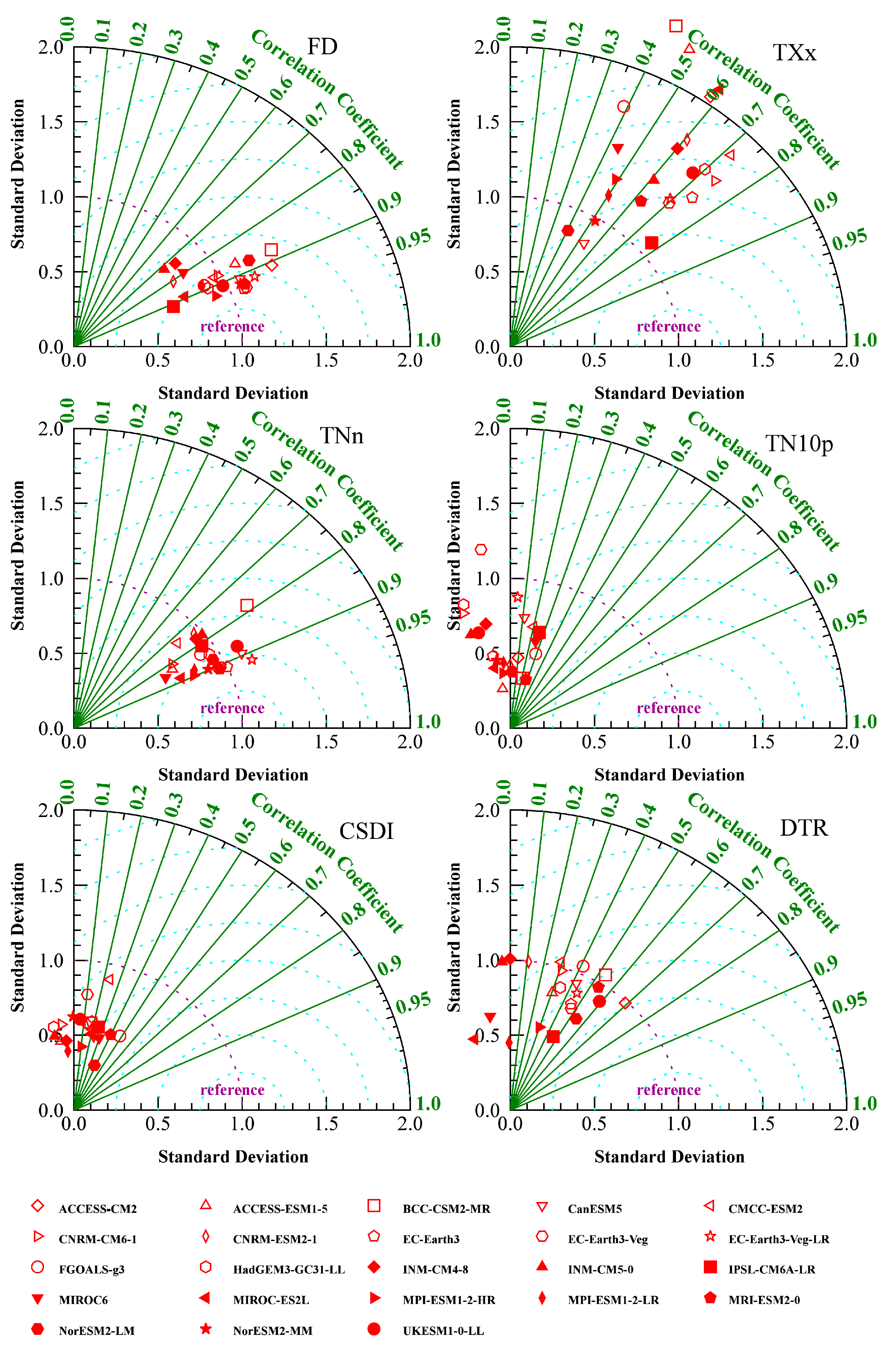
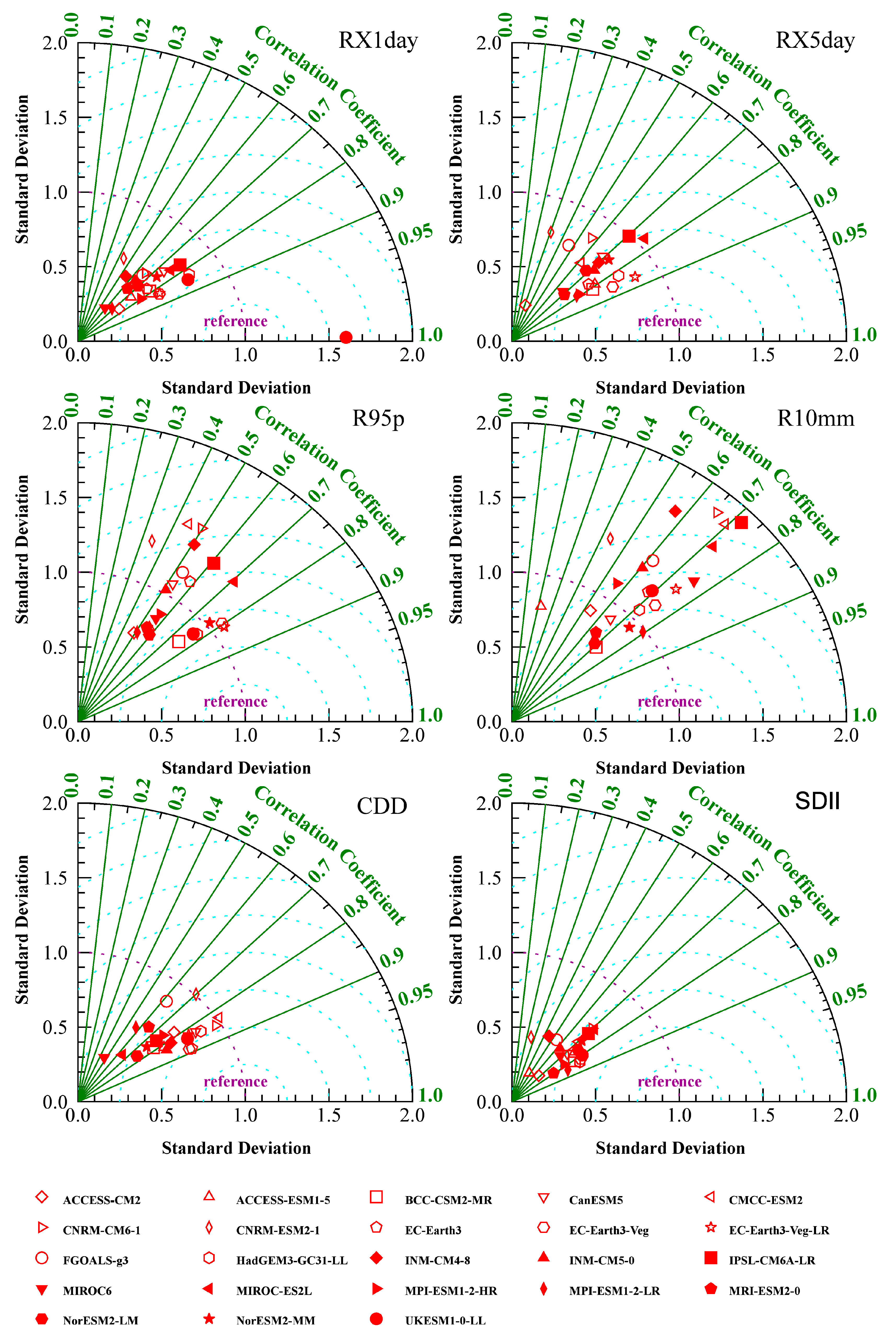
- The GCMs have the strongest spatial simulation for FD and TNn (R > 0.85, σ ≈ 1, 0.25 < E′ < 0.75, S > 8). For TN10p and CSDI, the agreement between GCMs outputs and observations is generally poor (R < 0.20, σ ≈ 0.5, E′ > 1, S < 0.5). The spatial simulation of extreme temperature indices is best for M5, M9 and M15, while M2, M17, M18 and M19 perform poorly. The spatial simulation of the RX1day, RX5day, CDD and SDII (0.6 < R < 0.9, 0.4 < σ < 0.7, E’ < 1.0) is generally good in most GCMs. Except M1, M16 and M19, the other GCMs perform well in the spatial simulation of the R95p and R10mm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IPCC Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; Available online: https://www.ipcc.ch/report/ar6/wg1/ (accessed on 1 June 2023).
- Sun, P.; Zou, Y.; Yao, R.; Ma, Z.; Bian, Y.; Ge, C.; Lv, Y. Compound and successive events of extreme precipitation and extreme runoff under heatwaves based on CMIP6 models. Sci. Total Environ. 2023, 878, 162980. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Huang, J.; Xiao, X.; Tong, X. The capability of CMIP6 models on seasonal precipitation extremes over Central Asia. Atmos. Res. 2022, 278, 106364. [Google Scholar] [CrossRef]
- World Meteorological Organization. State of Climate in 2021: Extreme Events and Major Impacts. 2021. Available online: https://public.wmo.int/en/media/press-release/state-of-climate-2021-extreme-events-and-major-impacts (accessed on 9 June 2023).
- Intergovernmental Panel on Climate Change, IPCC (Ed.) Global Warming of 15 °C: IPCC Special Report on Impacts of Global Warming of 1.5 °C above Pre-Industrial Levels in Context of Strengthening Response to Climate Change, Sustainable Development, and Efforts to Eradicate Roverty; Cambridge University Press: Cambridge, UK, 2018; pp. 601–616. [Google Scholar]
- Li, H.; Chen, H.; Wang, H.; Yu, E. Future precipitation changes over China under 1.5 °C and 2.0 °C global warming targets by using CORDEX regional climate models. Sci. Total Environ. 2018, 640–641, 543–554. [Google Scholar] [CrossRef] [PubMed]
- Qin, P.; Xie, Z.; Zou, J.; Liu, S.; Chen, S. Future Precipitation Extremes in China under Climate Change and Their Physical Quantification Based on a Regional Climate Model and CMIP5 Model Simulations. Adv. Atmos. Sci. 2021, 38, 460–479. [Google Scholar] [CrossRef]
- Fan, X.; Miao, C.; Duan, Q.; Shen, C.; Wu, Y. The performance of CMIP6 versus CMIP5 in simulating temperature extremes over the global land surface. J. Geophys. Res. Atmos. 2020, 125, e2020JD033031. [Google Scholar] [CrossRef]
- Liang, J.; Meng, C.; Wang, J.; Pan, X.; Pan, Z. Projections of mean and extreme precipitation over China and their resolution dependence in the HighResMIP experiments. Atmos. Res. 2023, 293, 106932. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Meehl, G.; Boer, G.; Covey, C.; Latif, M.; Ronald, S. CMIP Coupled Model Intercomparison Project. Bull. Am. Meteorol. Soc. 2000, 81, 313–318. [Google Scholar] [CrossRef]
- Raju, K.S.; Kumar, D.N. Review of approaches for selection and ensembling of GCMs. J. Water Clim. Chang. 2020, 11, 577–599. [Google Scholar] [CrossRef]
- Touzé-Peiffer, L.; Barberousse, A.; Le Treut, H. The Coupled Model Intercomparison Project: History, Uses, and Structural Effects on Climate Research. WIREs Clim. Chang. 2020, 11, e648. [Google Scholar] [CrossRef]
- Grose, M.R.; Narsey, S.; Delage, F.P.; Dowdy, A.J.; Bador, M.; Boschat, G.; Chung, C.; Kajtar, J.B.; Rauniyar, S.; Freund, M.B.; et al. Insights from CMIP6 for Australia’s Future Climate. Earths Future 2020, 8, e2019EF001469. [Google Scholar] [CrossRef]
- Zamani, Y.; Hashemi Monfared, S.A.; Azhdari Moghaddam, M.; Hamidianpour, M. A comparison of CMIP6 and CMIP5 projections for precipitation to observational data: The case of Northeastern Iran. Theor. Appl. Climatol. 2020, 142, 1613–1623. [Google Scholar] [CrossRef]
- Wyser, K.; van Noije, T.; Yang, S.; von Hardenberg, J.; O’Donnell, D.; Döscher, R. On the increased climate sensitivity in the EC-Earth model from CMIP5 to CMIP6. Geosci. Model Dev. 2020, 13, 3465–3474. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J.; Lin, W.; Xu, H. Comparison of CMIP6 and CMIP5 models in simulating climate extremes. Sci. Bull. 2020, 65, 1415–1418. [Google Scholar] [CrossRef] [PubMed]
- Cui, T.; Li, C.; Tian, F. Evaluation of temperature and precipitation simulations in CMIP6 models over the Tibetan Plateau. Earth Space Sci. 2021, 8, e2020EA001620. [Google Scholar] [CrossRef]
- Mequanint, F.; Streck, T.; Tesfaye, K.; Gayler, S.; Weber, T. Comprehensive assessment of climate extremes in high-resolution CMIP6 projections for Ethiopia. Front. Environ. Sci. 2023, 11, 1127265. [Google Scholar]
- Ha, T.T.V.; Fan, H.; Shuang, L. Climate change impact assessment on Northeast China’s grain production. Environ. Sci. Pollut. Res. 2021, 28, 14508–14520. [Google Scholar] [CrossRef]
- Yu, X.; Ma, Y. Spatial and temporal analysis of extreme climate events over Northeast China. Atmosphere 2022, 13, 1197. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, Z.; Liu, J.; Li, J.; Wang, P.; Li, C.; Xie, X.; Jia, Y.; Wang, H. Analysis of the runoff component variation mechanisms in the cold region of Northeastern China under climate change. Water 2022, 14, 3170. [Google Scholar] [CrossRef]
- Wei, J.; Liu, X.; Zhou, B. Sensitivity of vegetation to climate in mid-to-high latitudes of Asia and future vegetation projections. Remote Sens. 2023, 15, 2648. [Google Scholar] [CrossRef]
- He, X.; Jiang, C.; Wang, J.; Wang, X. Comparison of CMIP6 and CMIP5 models performance in simulating temperature in Northeast China. Chin. J. Geophys. 2022, 65, 4194–4207. (In Chinese) [Google Scholar]
- Xu, T.; Pang, H.; Zhan, Z.; Guo, H.; Wu, S.; Zhang, W.; Hou, S. Characteristics of water vapor isotopes and moisture sources for short-duration heavy rainfall events in Nanjing, eastern China. J. Hydrol. 2023, 622, 129731. [Google Scholar] [CrossRef]
- Guan, J.; Yao, J.; Li, M.; Li, D.; Zheng, J. Historical changes and projected trends of extreme climate events in Xinjiang, China. Clim. Dyn. 2022, 59, 1753–1774. [Google Scholar] [CrossRef]
- Chen, Y.D.; Li, J.; Zhang, Q.; Gu, X. Projected changes in seasonal temperature extremes across China from 2017 to 2100 based on statistical downscaling. Glob. Planet Chang. 2018, 166, 30–40. [Google Scholar] [CrossRef]
- Chen, F.; Liu, C. Estimation of the spatial rainfall distribution using inverse distance weighting (IDW) in the middle of Taiwan. Paddy Water Environ. 2012, 10, 209–222. [Google Scholar] [CrossRef]
- Mastyło, M. Bilinear interpolation theorems and applications. J. Funct. Anal. 2013, 265, 185–207. [Google Scholar] [CrossRef]
- PL, F.; Alexander, L.; Della-Marta, P.; Gleason, B.; Haylock, M.; Klein, T.; TC, P. Observed coherent changes in climatic extremes during 2nd half of the 20th century. Clim. Res. 2002, 19, 193–212. [Google Scholar]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. WIREs Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Zhu, C.; Yue, Q.; Huang, J. Projections of mean and extreme precipitation using the CMIP6 Model: A study of the Yangtze River Basin in China. Water 2023, 15, 3043. [Google Scholar] [CrossRef]
- Ávila, Á.; Guerrero, F.C.; Escobar, Y.C.; Justino, F. Recent precipitation trends and floods in the Colombian Andes. Water 2019, 11, 379. [Google Scholar] [CrossRef]
- Chen, W.; Jiang, Z.; Li, L. Probabilistic projections of climate change over China under the SRES A1B scenario using 28 AOGCMs. J. Clim. 2011, 24, 4741–4756. [Google Scholar] [CrossRef]
- Taylor, K. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Ullah, W.; Wang, G.; Lou, D.; Ullah, S.; Bhatti, A.S.; Ullah, S.; Karim, A.; Hagan, D.F.T.; Ali, G. Large-scale atmospheric circulation patterns associated with extreme monsoon precipitation in Pakistan during 1981–2018. Atmos. Res. 2021, 253, 105489. [Google Scholar] [CrossRef]
- Alexander, L.V.; Arblaster, J.M. Historical and projected trends in temperature and precipitation extremes in Australia in observations and CMIP5. Weather Clim. Extrem. 2017, 15, 34–56. [Google Scholar] [CrossRef]
- Schoof, J.T.; Robeson, S.M. Projecting changes in regional temperature and precipitation extremes in the United States. Weather Clim. Extrem. 2016, 11, 28–40. [Google Scholar] [CrossRef]
- Rojpratak, S.; Supharatid, S. Regional extreme precipitation index: Evaluations and projections from the multi-model ensemble CMIP5 over Thailand. Weather Clim. Extrem. 2022, 37, 100475. [Google Scholar] [CrossRef]
- Lei, X.; Xu, C.; Liu, F.; Song, L.; Cao, L.; Suo, N. Evaluation of CMIP6 Models and Multi-Model Ensemble for Extreme Precipitation over Arid Central Asia. Remote Sens. 2023, 15, 2376. [Google Scholar] [CrossRef]
- Zhu, H.; Jiang, Z.; Li, J.; Li, W.; Sun, C.; Li, L. Does CMIP6 inspire more confidence in simulating climate extremes over China? Adv. Atmos. Sci. 2020, 37, 1119–1132. [Google Scholar] [CrossRef]
- Hu, G.; Franzke, C.L.E. Evaluation of daily precipitation extremes in reanalysis and gridded observation-based data sets over Germany. Geophys. Res. Lett. 2020, 47, e2020GL089624. [Google Scholar] [CrossRef]
- Wei, L.; Xin, X.; Li, Q.; Wu, Y.; Tang, H.; Li, Y.; Yang, B. Simulation and projection of climate extremes in China by multiple Coupled Model Intercomparison Project Phase 6 models. Int. J. Climatol. 2023, 43, 219–239. [Google Scholar] [CrossRef]
- Dirmeyer, P.A. Land-sea geometry and its effect on monsoon circulations. J. Geophys. Res. Atmos. 1998, 103, 11555–11572. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, T. Significant increases in extreme precipitation and the associations with global warming over the global land monsoon regions. J. Clim. 2019, 32, 8465–8488. [Google Scholar] [CrossRef]
- Kong, X.; Wang, A.; Bi, X.; Wang, D. Assessment of temperature extremes in China using RegCM4 and WRF. Adv. Atmos. Sci. 2019, 36, 363–377. [Google Scholar] [CrossRef]
- Landwehrs, J.; Feulner, G.; Petri, S.; Sames, B.; Wagreich, M. Investigating mesozoic climate trends and sensitivities with a large ensemble of climate model simulations. Paleoceanogr. Paleoclimatol. 2021, 36, e2020PA004134. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, T.; Man, W.; Hu, H.; Long, Y.; Li, Z.; Pang, Z. Contribution of recycled moisture to precipitation: A modified D-Excess-Based Model. Geophys. Res. Lett. 2021, 48, e2021GL095909. [Google Scholar] [CrossRef]
- Zhang, W.; Furtado, K.; Wu, P.; Zhou, T.; Chadwick, R.; Marzin, C.; Rostron, J.; Sexton, D. Increasing precipitation varia-bility on daily-to-multiyear time scales in a warmer world. Sci. Adv. 2021, 7, f8021. [Google Scholar] [CrossRef]
- John, A.; Douville, H.; Ribes, A.; Yiou, P. Quantifying CMIP6 model uncertainties in extreme precipitation projections. Weather Clim. Extrem. 2022, 36, 100435. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y.; Gao, Z.; Pan, Z.; Zhang, X. Historical and projected changes in temperature extremes over China and the inconsistency between multimodel ensembles and individual models from CMIP5 and CMIP6. Earth Space Sci. 2023, 10, e2022EA002514. [Google Scholar] [CrossRef]
- Xu, Z.; Han, Y.; Tam, C.; Yang, Z.; Fu, C. Bias-corrected CMIP6 global dataset for dynamical downscaling of the historical and future climate (1979–2100). Sci. Data 2021, 8, 293. [Google Scholar] [CrossRef]
- Ma, Z.; Sun, P.; Zhang, Q.; Zou, Y.; Lv, Y.; Li, H.; Chen, D. The characteristics and evaluation of future droughts across China through the CMIP6 multi-model ensemble. Remote Sens. 2022, 14, 1097. [Google Scholar] [CrossRef]
| Serial Number | GCM | Institution | Atmospheric Resolution (Lat × Lon Grid Numbers) |
|---|---|---|---|
| M1 | ACCESS-CM2 | CSIRO, Australia | 144 × 192 |
| M2 | ACCESS-ESM1-5 | CSIRO, Australia | 145 × 192 |
| M3 | BCC-CSM2-MR | BCC, China | 160 × 320 |
| M4 | CanESM5 | CCCMA, Canada | 64 × 128 |
| M5 | CMCC-ESM2 | CMCC, Italy | 192 × 288 |
| M6 | CNRM-CM6-1 | CNRM, France | 128 × 256 |
| M7 | CNRM-ESM2-1 | CNRM, France | 128 × 256 |
| M8 | EC-Earth3 | EC-Earth-Consortium, European Union | 256 × 512 |
| M9 | EC-Earth3-Veg | EC-Earth-Consortium, European Union | 256 × 512 |
| M10 | EC-Earth3-Veg-LR | EC-Earth-Consortium, European Union | 160 × 320 |
| M11 | FGOALS-g3 | CAS, China | 80 × 180 |
| M12 | HadGEM3-GC31-LL | MOHC, UK | 144 × 192 |
| M13 | INM-CM4-8 | INM, Russia | 120 × 180 |
| M14 | INM-CM5-0 | INM, Russia | 120 × 180 |
| M15 | IPSL-CM6A-LR | IPSL, France | 143 × 144 |
| M16 | MIROC6 | MIROC, Japan | 128 × 256 |
| M17 | MIROC-ES2L | MIROC, Japan | 64 × 128 |
| M18 | MPI-ESM1-2-HR | MPI, Germany | 192 × 384 |
| M19 | MPI-ESM1-2-LR | MPI, Germany | 96 × 192 |
| M20 | MRI-ESM2-0 | MRI, Japan | 160 × 320 |
| M21 | NorESM2-LM | NCC, Norway | 96 × 144 |
| M22 | NorESM2-MM | NCC, Norway | 192 × 288 |
| M23 | UKESM1-0-LL | MOHC, UK | 144 × 192 |
| Categorization | Indicator | Indicator Definitions | Units |
|---|---|---|---|
| Extreme temperature indices | FD | Annual count when daily minimum temperature < 0 °C | d |
| TXx | Monthly maximum value of daily max temperature | °C | |
| TNn | Monthly minimum value of daily min temperature | °C | |
| TN10p | Percentage of time when daily min temperature < 10th percentile | % | |
| CSDI | Annual count when at least six consecutive days of min temperature < 10th percentile | d | |
| DTR | Monthly mean difference between daily max and min temperature | °C | |
| Extreme precipitation indices | RX1day | Monthly maximum 1-day precipitation | mm |
| RX5day | Monthly maximum consecutive 5-day precipitation | mm | |
| R95p | Annual total precipitation from days > 95th percentile | mm | |
| R10mm | Annual count when precipitation ≥ 10 mm | d | |
| CDD | Maximum number of consecutive days when precipitation < 1 mm | d | |
| SDII | The ratio of annual total precipitation to the number of wet days (≥1 mm) | mm/d |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, H.; Zhuo, Y.; Pang, K.; Sun, H.; An, Z.; Zhang, X. Evaluation of Extreme Climate Indices over the Three Northeastern Provinces of China Based on CMIP6 Models Outputs. Water 2023, 15, 3895. https://doi.org/10.3390/w15223895
Xiao H, Zhuo Y, Pang K, Sun H, An Z, Zhang X. Evaluation of Extreme Climate Indices over the Three Northeastern Provinces of China Based on CMIP6 Models Outputs. Water. 2023; 15(22):3895. https://doi.org/10.3390/w15223895
Chicago/Turabian StyleXiao, Heng, Yue Zhuo, Kaiwen Pang, Hong Sun, Zhijia An, and Xiuyu Zhang. 2023. "Evaluation of Extreme Climate Indices over the Three Northeastern Provinces of China Based on CMIP6 Models Outputs" Water 15, no. 22: 3895. https://doi.org/10.3390/w15223895





