Abstract
The thermal factor is the main reason for winter ice cover with a low Froude number flow, and the heat transfer to narrow and deep river banks accelerates ice cover formation and ice thickness change. The freezing of water flow to freezing thickening is a nonisothermal-flow phase transition process coupled with the water flow temperature, environment and riverbank. Here, the Nusselt number and viscous dissipation are used to consider the flow velocity influence on icing, and a thermodynamic model of static ice cover horizontal distribution considering riverbed heat transfer is established. The initial ice time, freezing time and static ice cover thickness formed by static and dynamic water calculated by the model were consistent with measured data. The model reflects the horizontal growth process of the static ice cover, which was significant for narrow and deep channels. The horizontal distribution of the static ice cover was thin in the center and thick on both sides. The maximum horizontal thickness difference of −20 °C indoor freezing for 24 h reached 15% of the central ice thickness. Compared with the degree-day method for calculating ice thickness, the numerical model and dimensionless formula better reflect the growth law and horizontal distribution characteristics of static ice cover and provide a theoretical basis for safe water conveyance under ice cover in winter and ice cover formation in reservoirs and lakes in cold regions.
1. Introduction
At high latitudes in the Northern Hemisphere, 60% of the rivers and reservoirs in the cold regions are significantly affected by the freezing phenomenon of the negative temperature environment [1,2]. For example, the water freezing period in the cold regions of China can last approximately two months, and the freezing period of water conveyance channels in northern Xinjiang can even reach half a year [3]. In winter, the water flow forms an ice cover with an increase in cumulative negative temperature. The ice cover grows synchronously along the horizontal and vertical thickness of the section due to hydraulic and thermal factors [4,5,6], which affect the hydraulic characteristics under the ice [7] and the stress distribution of the bank slope in the cold regions [8]. The maximum time difference between the initial ice time and the freezing time of the dynamic water can reach 20 days, and the maximum ice thickness difference between the canal center and the bank can reach 10 cm [9]. The significant horizontal ice thickness difference will aggravate the uneven distribution of the horizontal thrust generated by the frozen ice cover, resulting in obvious ice ridges at the weak ice cover points and slope lining damage on the bank slope, as shown in Figure 1a. In addition, the hydraulic characteristics of the water flow also change after freezing into ice, as shown in Figure 1b. Therefore, the accurate prediction of ice cover growth is important in ice prediction research [10].
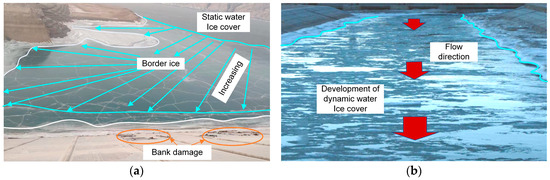
Figure 1.
Horizontal distribution of static and dynamic water ice cover: (a) reservoir, Karabelli Water Conservancy Project, which is located in Wuqia County, Kezhou, China; (b) canal, diversion canal of power station, which is located in Xie Tongmen County, Tibet, China.
Hydraulic and thermal factors are important factors affecting the development of ice cover [11,12]. In winter, the water flow of the water conveyance project is small, and water flow conditions with a low Froude number and low flow velocity result in freezing to form a static ice cover dominated by thermal growth. The duration of the initial freezing period and the initial sealing period of the static ice cover is short and the horizontal distribution is significant. The heat transfer of the riverbank is the main factor affecting the formation of a stable frozen ice cover in the initial stage of the river channel. In addition, local heat exchange is the basic factor affecting the growth of border ice, and the heat flux of the riverbank has a significant effect on the growth of border ice. At present, there is relatively little research on the impact of heat flux from riverbanks and the influx of groundwater recharge heat sources on static ice cover [5,13,14]. Michel et al. found that border ice can develop freely in low-velocity flows and thermal factors, such as river bank heat transfer, are important factors for the horizontal development of border ice [15]. The final thickness of the ice cover calculated by the degree day method and the one-dimensional vertical ice thickness model that requires water temperature and weather data can only be approximated as an equal thickness calculation [16,17,18,19], which is inconsistent with the phenomenon of horizontal differences in actual static and dynamic water flow icing time and frozen ice cover thickness. Therefore, the thermal growth of static ice cover formed by large canal reservoirs with low Froude numbers and small flow velocities and the heat flux of the riverbank will aggravate the horizontal difference affecting the growth of border ice and the horizontal thickness of the ice cover. The influence of riverbank heat transfer on the formation of initial stable ice cover and the horizontal distribution of the ice cover formation process are two factors that need to be elucidated in the existing ice cover thickness model.
This paper considered the impact of riverbank heat transfer on water flow icing, treating water as a typical phase change material and simulating the process of ice formation in water through temperature changes caused by the nonisothermal flow of water [20]. The Nusselt number and viscous dissipation were used to reflect the effect of flow velocity on ice formation, and a two-dimensional static ice cover model was established to simulate the entire horizontal and vertical development processes of ice cover. The model couples the temperature of water flow, riverbed and ice cover, which can completely simulate the process from the formation of static ice cover to initial freezing and analyze the difference in the horizontal distribution of ice cover and the influence degree of heat transfer in the riverbank. Finally, the numerical model was verified by experiments, summarizing the regression formula that reflects the horizontal distribution characteristics of the static ice cover and is convenient for engineering applications. This paper can provide theoretical support for the safe water delivery of canal reservoirs in cold regions.
2. Horizontal Distribution Model of Static Ice Cover Considering Heat Transfer of River Banks
The generation and disappearance of ice cover is a physical process of thermal exchange coupling among the atmosphere, ice cover, water body and river bank. The temperature simulation of water and river bank coupling is the premise for accurately simulating border ice and static ice cover generation [10]. The flow velocity influence on icing is reflected by the Nusselt number and viscous dissipation in the water temperature calculation, and the influence of environmental temperature and wind speed on water freezing is expressed by convective heat flux. The horizontal distribution model of static and dynamic water ice cover includes the water temperature model, water flow icing model and frozen soil hydrothermal model. The equivalent heat capacity method was used to simulate the temperature equation of water flow and river bank soil, and the water migration and ice-water phase transition of frozen soil caused by the negative temperature of the river bank were considered.
2.1. Temperature Control Equation
2.1.1. Water Flow Temperature Calculation Model
To calculate the fully mixed water temperature, the convection-diffusion equation can be used to represent heat conduction and heat convection in the water heat exchange process. The water body is approximately regarded as an incompressible fluid, as shown in Equation (1). Compared with the calculation of static water temperature, the nonisothermal flow in the cross section is more significant than that in the static water due to the difference in flow velocity in the dynamic water temperature [21]. The diffusion term in the direction of water flow is significantly enhanced due to water turbulence; the thermal conductivity of water flow is also significantly increased due to flow velocity, and the source term from viscous dissipation is generated. The solution process involved one-way coupling calculation of the velocity temperature. Equations (2) and (3) are mass and momentum equations, respectively. For the calculation of the velocity, we adopted the Boussinesq hypothesis for the influence of the density of the water flow, and assumed that the velocity caused by the ice-water phase change was very small and could be ignored.
where Tw is the water temperature, °C; Qvd is viscous dissipation, W/m3; q is the heat source term generated by electric heating and other related heating methods, W/m3; u is the velocity field of water flow, m/s; μ is fluid dynamic viscosity, (m2)/s; ρw is the density of water flow (kg/m3); p is water flow pressure, N/m2; I is the unit matrix; and F is an external force acting on the water and is calculated using the Boussinesq approximation. ρwi, Cpwi and kwi are the density of ice-water mixture flow (kg/m3), constant pressure heat capacity (J/(kg·K)) and thermal conductivity (W/(m·K)), respectively, and Nu is a dimensionless Nusselt number that represents the degree of convective heat transfer. It can be expressed as a function of the dimensionless Reynolds number Re and the dimensionless Prandtl number Pr related to the hydraulic characteristics according to the experimental data [22,23], as shown in Equation (4).
The dimensionless Prandtl number Pr is calculated by Kays–Crawford heat transfer turbulence [24], as shown in Equation (5).
where μT is defined by the flow interface, and PrT∞ = 0.85 depends on the heat transfer turbulence model.
The viscous dissipation of water flow is calculated as shown in Equation (6).
where τ is the viscous stress tensor of water flow.
2.1.2. Water Flow Icing Model
The supercooled water flow forms ice crystals as the water temperature decreases to the freezing point. The density, heat capacity and mass fraction of the ice-water mixture during the freezing process change with temperature. Water is regarded as a phase change material (PCM) [25]. It is assumed that the total heat per unit volume released during the phase change of ice water coincides with the latent heat. The freezing process of the water flow directly depends on the freezing point and the latent heat of the phase change. The equivalent heat capacity method was used to simulate the fluid heat transfer equation, including the phase change, to simulate the thermodynamic process of ice cover generation and disappearance, as shown in Equations (7)–(10). It was assumed that the ideal phase transition was in the phase transition temperature range of water flow, and the water phase was transformed into the ice phase. The corresponding volume fraction was obtained by the second-order smooth Heaviside function [26], as shown in Figure 2. The effective density, heat capacity and mass fraction of the ice-water mixture obtained by the equivalent heat capacity method were substituted into the water flow temperature calculation model to simulate the water flow freezing process. The calculated ice volume fraction was related to the ice concentration. The model does not consider the secondary nucleation phenomenon caused by the collision of ice particles.
where ρwi is the effective density of the ice-water mixture; Cpwi is the apparent heat capacity of the ice-water mixture; αm is the mass fraction; L is the latent heat of ice water phase change, kJ/kg; and θw and θi are the volume fractions of water and ice, respectively. ρw and ρi are the densities of water and ice, respectively. Cpw and Cpi are the constant pressure heat capacities of water and ice, respectively.
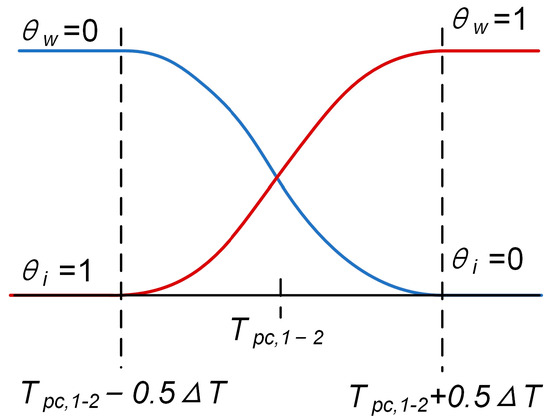
Figure 2.
Phase volume fractions using the Heaviside phase transition function.
2.1.3. Coupled Moisture-Heat Transport Model of Frozen Soil on Banks
Due to small gaps among soil particles, the soil on the bank of the river is mainly considered to produce heat conduction. The soil pore water is frozen by the influence of the negative temperature in the environment, and the temperature gradient and soil matrix potential further cause the pore water to migrate to the cold side [27,28]. Therefore, in the hydrothermal coupling equation of frozen soil we adopted the Fourier heat conduction equation considering the ice-water phase transition [29,30], Equation (11), and the Richards equation [31,32] for describing the water migration in the variable saturated porous media with ice phase was added, as Equation (12). Considering the surface energy of soil particles, the unfrozen water content of soil was expressed by the temperature-dependent soil freezing characteristic curve (SFCC), in the form of Equation (13) [33].
where T is the soil temperature, °C; H is the matric potential, m; λ and Cv are the equivalent constant pressure heat capacity J/(kg·K) and the equivalent thermal conductivity W/(m·K) of the soil, respectively, which are expressed by the calculated average of each component, Equations (14) and (15); and the subscripts sp, sw, si and sa represent soil particles, pore water, pore ice and gas phase, respectively. C is the specific water capacity, and the van Genuchten model (VG model) was used to describe the relationship between the unfrozen water content and the matrix potential and the permeability coefficient [34], Equations (16)–(19). a and b are the experimental fitting parameters of the freezing characteristic curve; ρd is the dry density of soil, kg/m3.
where α and m are soil fitting parameters and θs and θr are the soil saturation and residual water content, respectively. Se is the equivalent saturation; Ks is the permeability coefficient of saturated soil, m/s; i is the ice impedance factor; and GwT is the temperature correction factor of the soil water characteristic curve (SWCC). γ is the surface tension of pore water, J/m3. Klh is the hydraulic conductivity, m/s, and KlT is the permeability coefficient caused by the thermal gradient, m2/(K·s).
2.2. Model Boundary Condition and Solving Process
In considering the heat exchange between the riverbank, the water flow temperature and the external environment, we adopted the convective heat flux as the boundary condition, Equation (20). The cumulative negative temperature of the environment is the most important factor affecting the vertical growth of ice cover. The model does not consider the influence of snow and other pollutants (dust) covering the surface ice layer on albedo. The influence of wind speed on icing is reflected by the convective heat transfer coefficient related to wind speed. The lower boundary of the model is the constant temperature layer at the bottom of the riverbed, which is taken as the constant temperature Dirichlet boundary. The bottom groundwater of the riverbed is mainly affected by the temperature gradient and the matrix potential gradient migrates to the bank interface, and affects the development of soil temperature and freezing depth. The left and right boundaries of the model are set as adiabatic boundaries.
where n is the normal vector of the upper surface; Tamb and Tin are the external environment temperature and the upper surface temperature of the river bank and water flow, respectively, °C; and h is the convective heat transfer coefficient, W/(m2·°C). The convective heat transfer coefficient on the surface of the water flow comprehensively considers the evaporation and convection of the water surface. The evaporation heat flux is expressed as the wind speed and the saturated water vapor pressure-related term [35,36], Equation (21). The convective heat transfer coefficient of the riverbed is only related to the wind speed, 15 W/(m2·°C) [27].
where the saturated water vapor pressure increases with increasing water surface temperature [37]. A and B are constants for the water surface: A = 17.62, B = 35.86; for the ice surface: A = 21.88, B = 7.66 [38]. Convective heat transfer coefficient of the water surface, T < 0 °C, 18 W/(m2·°C) [38]; T > 0 °C, 10 W/(m2·°C) [27].
An annular flume verification test was carried out to verify the accuracy of the model and parameter calibration. The model test focused on the analysis of the freezing process and the initial ice thickening process in narrow and deep channels. The water depth, soil depth and slope ratio of the river bank model were 0.2 m, 1.1 m and 1:1, respectively. A freezing process of static and dynamic water with flow rates of 0 m/s and 0.2 m/s (Fr ≤ 0.15 for static ice covers) was analyzed. The specific model size is shown in Figure 3a. Prior to commencing the model test, the initial temperature and the bottom plate of the model were set at 4 °C. After achieving the water temperature and temperature of bank soil stabilization, the environmental temperature decreased from 4 °C to −20 °C. The ice thickness of the monitoring point was measured according to the principle of the resistance wire thermal melting method and compared with the simulated value. The flow velocity of water was adjusted by the pump with external frequency conversion control. The model must be solved numerically because of the nonlinear equations, and was solved by using COMSOL Multiphysics v5.2 for the finite element analysis of the coupled systems of partial differential equations. The numerical model solving process is shown in Figure 3b, and the basic hydraulic, thermal and soil parameters of the model are shown in Table 1.
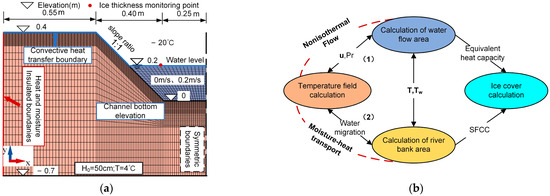
Figure 3.
Model geometric dimensions and the numerical analysis process.

Table 1.
Model parameter values used in the simulation [27].
3. Results
3.1. Analysis of Ice Thickness Growth Generated by Static and Dynamic Water
The ice thickness calculated by the model was consistent with the measured ice thickness, as shown in Figure 4. To facilitate the description of the flow conditions of 0 m/s and 0.2 m/s, the flow is referred to as static water and dynamic water in the results. The ice thickness growth period of static and dynamic water mainly presented two stages. In the initial stage, the surface temperature of the ice cover was greatly different from the air temperature, and the heat exchange between the ice and the atmosphere was relatively large, so the growth rate of the ice cover was rapid. As the ice thickness increased, the heat loss of the water under the ice cover decreased, and the growth rate of the ice cover slowed and tended to stabilize. The freezing rates of the two stages were three times different. The greater the flow velocity of the same temperature, the smaller the growth rate of the ice thickness was. The initial icing rate of the static water monitoring point was 0.86 cm/h, and the stable icing rate was 0.25 cm/h. The initial icing rate of the dynamic water monitoring point was 0.60 cm/h, and the stable icing rate was 0.21 cm/h. The flow velocity inhibited the growth of ice thickness. The freezing time of dynamic water was longer than that of static water. The initial freezing time of dynamic water was slower than that of static water by 1.7 h. The difference in ice thickness at 24 h monitoring points was 1.6 cm. Simultaneously, the dynamic water was affected by the turbulence of the supercooled water flow, and some ice crystals at the bottom of the ice thickness were constantly neutralized by the latent heat released and the heat generated by viscous dissipation. The ice thickness in the steady growth stage fluctuated slightly compared with that in the static water.
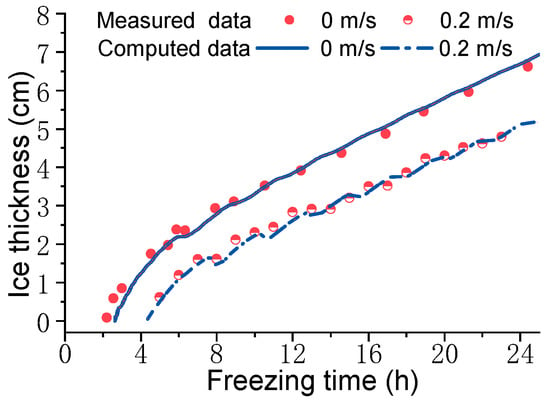
Figure 4.
The variation of ice thickness at monitoring points over time.
Compared with the analysis of the ice thickness growth process at different locations in the transverse direction of water flow, the ice cover thickness of static and dynamic water flow showed obvious transverse distribution characteristics. The ice thicknesses on both sides of the canal center near point A of monitoring point B and point C near the riverbank were not equal, as shown in Figure 5a. The water depth on the bank of the river was small, the heat storage reservoir of the water was small, and the water depth was different. After the ‘bottom-uncovering freezing’ of the water flow near the bank side of Point C, the water flow at Point C was frozen by temperature and two-way freezing, the stable freezing rate increased and the ice thickness increased rapidly to the bottom of Point C. Simultaneously, the freezing rate of point C increased rapidly to 0.29 cm/h, which was higher than that of point A and point B, and the ice thickness was also significantly greater than that of point A and point B. At this time, the freezing rate of point A was also slightly higher than that of point B. However, due to the large and equal water depth of point A and point B near the center of the canal, there was little difference in ice thickness and icing rate. The ice thickness difference between point A and point B in static water was only 0.2 cm.
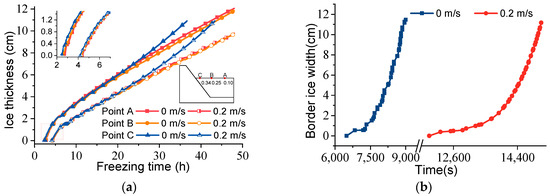
Figure 5.
Horizontal ice thickness distribution. (a) Development of ice thickness. (b) Development of width of border ice.
The vertical ice cover thickening process of static and dynamic water flow had an obvious transverse distribution of river bank–canal center water. The difference in ice thickness in dynamic water was only slightly greater than that in static water, which was mainly caused by the transverse difference in ice cover caused by velocity. In comparing the horizontal difference in static ice cover of static and dynamic water, the heat transfer of the riverbank was the main factor affecting the horizontal difference in static ice thickness. In addition, the initial stage of horizontal icing showed a process of gradual development from the river bank to the canal center. After bank ice appeared in static and dynamic water, the transverse width of the bank ice first increased rapidly, and the growth rate slowed. When border ice developed to a certain width, ice cover was rapidly generated due to the reduction of the cross section of the water flow. Taking the transverse width of bank ice as an example, as shown in Figure 5b, the initial icing at point A of the canal center was approximately 0.25 h later than that at point C of the riverbank. Although the initial freezing time of dynamic water was significantly slower than that of static water, the total time of ice cover formation was less than 2 h because the ice cover was still a static ice cover (Fr < 0.15), and the transverse development time of dynamic water border ice was slightly slower than that of static water. The freezing time of a 12 cm border of ice in static water was 0.70 h, and the freezing time of a 12 cm border of ice in dynamic water was only 0.17 h longer than that in static water.
3.2. Coupling Analysis of Ice Thickness Growth and Riverbank Freezing Process
The formation of static ice cover mainly includes two stages: the initial period and freezing period, as shown in Figure 6. The formation and development process of static ice cover, especially its initial stage in the form of border ice, was dependent on coupling water flow and riverbank heat. The freezing depth of the river bank soil was closely related to the development of ice cover. A negative environmental temperature is the main factor in water freezing, but the upper surface of the river bank and the water surface are both subject to heat exchange heat loss. When the temperature of the river bank soil dropped to a negative temperature and the water surface formed ice crystals, the initial border ice formed. Therefore, the frozen soil on the riverbank was also a cold source affecting the transverse distribution of the ice cover. In addition, the water depth of the riverbank was shallow, so the horizontal characteristics of the ice cover were significant.
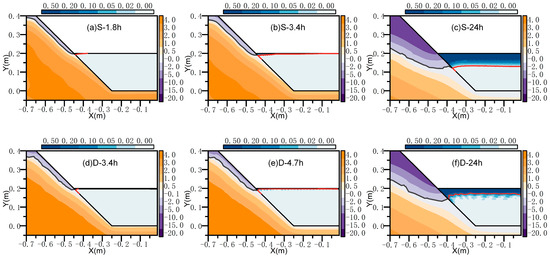
Figure 6.
Distribution of bank temperature during the development of ice cover.
The development of the initial ice time and thickness of the border ice was synchronized with the development of the corresponding negative temperature isotherm of the river bank, but the growth of the ice cover in the dynamic water and the static water was slightly different from the law of the river bank temperature. The initial ice time of static water was 1.8 h, and the initial freeze-up time was 3.4 h. The initial ice time of the dynamic water was 3.4 h, and the initial freeze-up time was 4.7 h. The initial freeze-up time of the whole ice cover in dynamic water was longer than that in static water. Static and dynamic water bodies with low ice volume fractions gather to form the initial ice on the bank, and the turbulence of the water body significantly inhibits ice crystals from forming ice cover [39]. The ice volume fraction of the border ice at the initial ice time of static water was 0.02, and the ice volume fraction of the border ice at the initial ice time of dynamic water was 0.2. The initial ice formation of dynamic water requires a larger ice volume fraction. The nucleation phenomenon of dynamic water and static water ice leads to a difference in the ice volume fraction. In addition, the static water border ice contour coincided with the river bank −0.01 °C isotherm, and the dynamic water bank ice contour coincided with the river bank −0.03 °C isotherm. During the freezing period, the supercooled water mass releases latent heat at the ice-water interface so that the ice thickness continues to grow, and the ice thickness bank shape develops with the corresponding negative temperature line. With the passage of freezing time, the horizontal ice thickness difference formed by the negative temperature line of the riverbank was more significant. After 24 h of freezing, the ice cover of static and dynamic water had the characteristics of thick border ice and thin ice in the center of the canal, and the shape showed an eyebrow distribution. Figure 7 shows half of the measured transverse profile of the ice cover. The ice cover not only shows the difference in the transverse thickness distribution but also the difference in the classification of the vertical ice [40,41]. The primary ice on the upper layer of the ice cover was P2-type ice formed by a large temperature gradient on the calm water surface. The ice under the ice cover was characterized by S1-type columnar ice with static water and low-velocity water flowing parallel to the heat flow. The thermodynamics and latent heat release of different types of ice formation are not much different, and the model does not consider the differences in the formation of different types of ice, so there was not much analysis of the formation and development of different types of ice.

Figure 7.
Measured horizontal section of ice cover.
The vertical water temperature distribution of the canal center of static and dynamic water is shown in Figure 8a,b. When the water temperature is 4 °C, the density is the largest, and the water body is less affected by the lateral nonisothermal flow formed by the surface and bottom water temperatures [42]. Therefore, the initial water temperature of 4 °C was evenly distributed along the vertical direction, and there was no obvious phenomenon in which the surface water body sank due to the decrease in temperature and the lower water body floated on the surface. As the water lost heat, the surface water temperature gradually decreased, forming a large temperature gradient. Compared with static water, the decrease rate of the surface water temperature in the flow state was significantly slower. The water of the canal center was not frozen at the initial time of ice formation. The water temperature of the canal center was lower than that of the static water at the initial ice time and the freezing time of the dynamic water. The turbulent effect of the dynamic water evenly mixed the vertical water temperature. After the water temperature dropped to 0 °C, the heat loss of the water flow did not continue to decrease the water temperature but formed a low volume fraction of the ice phase to maintain near 0 °C. After the freezing period, the stable ice cover changed the form of heat exchange, from water vapor heat exchange during the freezing period to heat exchange between the surface water and the bottom of the ice cover and between the atmosphere and upper surface of the ice cover. The vertical distribution of temperature on both sides of the interface between ice cover and water significantly differed. The temperature in the ice was linearly distributed, and the temperature gradient was large. With the process of ice cover thickening, the interface water between the ice cover and the water flow froze to release latent heat, causing the interface temperature to rise slightly. At the same time, due to the heat preservation effect of the ice cover, the temperature of the water under the ice was more uniform.
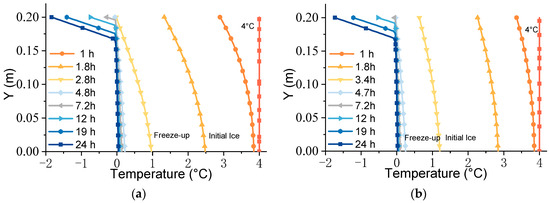
Figure 8.
Vertical temperature distribution of (a) static water and (b) dynamic water.
4. Discussion
4.1. The Influence of Temperature and Water Velocity on the Formation of Static Ice Cover
4.1.1. Analysis of Model Coupling Parameters
The Nusselt number and the viscous dissipation term are the coupling terms of the water flow temperature calculation. The environmental temperature and the water velocity change the water temperature by enhancing the heat transfer through the Nusselt number and viscous dissipation [43]. The difference between the water temperature and the environmental temperature is the main factor affecting the difference in heat transfer. According to the measured temperature of static water flow, the variation of the Nusselt number with temperature calculated by Equation (1) is shown in Figure 9a. The lower the negative temperature environment during the freezing period, the greater the Nusselt number of the water flow and the stronger the heat exchange. The difference in flow heat transfer in flowing water is mainly affected by the flow velocity turbulence, and the heat transfer coefficient increases with increasing flow turbulence. It can be expressed as a function of the dimensionless Reynolds number Re and the dimensionless Prandtl number Pr related to the hydraulic characteristics according to the experimental data [35]. According to the principle of thermodynamics, the Nusselt number of dynamic water flow can be expressed by the dimensionless Prandtl number reflecting the relative size of the water flow viscosity and heat conduction and the dimensionless Reynolds number reflecting the relative size of the water flow viscous force and inertial force, as shown in Figure 9b. Simultaneously, the higher the flow velocity of the dynamic water, the greater the heat generated by viscous dissipation. The relationship between the viscous dissipation heat generated by the conversion of kinetic energy into internal energy caused by the flow velocity and the flow velocity is shown in Figure 10. The temperature and velocity of water flow under different conditions make the Nusselt number and viscous dissipation term different, so the heat exchange process between ice cover and water flow is different. The more violent the turbulence of the water flow and the higher the environmental temperature, the lower the cooling rate of the water flow temperature will be, and the water flow will be more difficult to freeze.
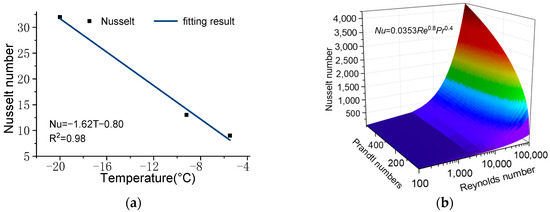
Figure 9.
The variation of the Nusselt number of static and dynamic water. (a) Static water; (b) dynamic water.
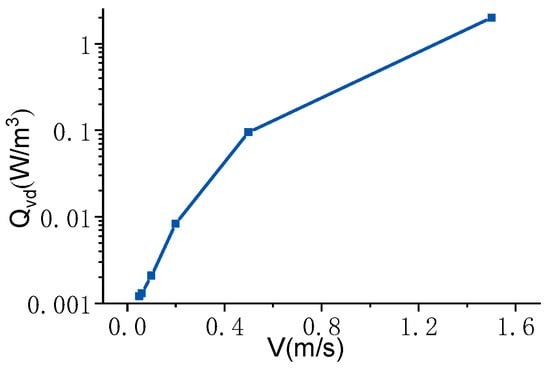
Figure 10.
The variation of viscous dissipation.
4.1.2. Analysis of the Horizontal Difference of Static Ice Cover
The numerical model can reflect the change process of water heat transfer. The Froude number is an important parameter for judging the type of ice cover growth. In addition to negative environmental temperature and water flow velocity, water flow depth is also an important factor affecting the growth of static ice cover [44]. Therefore, the simulation verified the static ice cover growth generated by static water of −5 °C, −10 °C and −20 °C of the numerical model size at different environmental temperatures (recorded as condition 1); the growth of static water ice cover with an environmental temperature of −20 °C and a water depth of 0.3 m (recorded as condition 2); and a slope ratio m of 1.1 (recorded as condition 3) and 1.5 (recorded as condition 4). The experimental model had a −20 °C environment temperature flow rate of 0.12 m/s (recorded as condition 5) and 0.2 m/s (recorded as condition 6) for the dynamic water static ice cover growth. The static ice cover growth characteristics are shown in Table 2. The initial ice time, freezing time and horizontal difference in the thickness of static ice cover all reflect the characteristics of its horizontal distribution.

Table 2.
Characteristics of ice cover growth.
The initial ice time and freezing time reflect the process of horizontal development of ice cover. The formation of border ice is the starting point of the formation of static ice cover. The influence of environmental temperature and velocity on the initial ice time are much greater than that of water depth and slope ratio, and the influence of water depth on the initial ice time is the smallest. The lower the environmental temperature is, the smaller the flow velocity and the larger the slope ratio, the shorter the initial ice time of the static ice cover, and the water depth has little effect on the initial ice time. The initial ice time of −5 °C static ice cover was 1.6 h later than that of −20 °C; the initial ice time of the static ice cover generated by the critical Froude number (Fr = 0.15) with a flow rate of 0.2 m/s was 1.5 h later than that of the static water.
The initial total heat of the water is affected by the water depth and slope ratio. The water depth of the slope ratio has a great influence on the initial ice time. The initial ice time of the static ice cover with a slope ratio of 1.0 was 0.4 h later than that with a slope ratio of 1.5. The difference in water depth had no significant effect on the initial ice time. The initial ice time of the static ice cover with a water depth of 0.2 m was 0.1 h later than the initial ice time with a water depth of 0.3. Considering the influence of water depth and slope ratio on the initial ice time, the larger the width–depth ratio is, the more rapid the two-way freezing of the top of the river bank soil is, and it is more conducive to the negative temperature heat exchange between the water surface and the environment. The shore water is easily affected by the negative temperature frozen soil and the ambient temperature to form border ice. Therefore, the larger the width–depth ratio is, the shorter the initial ice time is. The influence of environmental temperature and water flow velocity on the icing duration was consistent with the initial ice time, but the change in the width–depth ratio of the water flow affected both the total heat storage of the water flow and the water surface width of the direct heat exchange with the negative temperature environment. The width of the water surface was the most important factor affecting the freezing time, and the freezing time of the water body with the same slope ratio increased with increasing water depth. Simultaneously, the slope ratio of the same water depth also affected the width of the water surface. Although a larger slope ratio of the water accelerated the rate of heat exchange on the water surface, it also increased the width of the frozen water surface, and the freezing time of the water flow also increased slightly with increasing slope ratio.
The vertical thickness of the ice cover also varied with the horizontal distribution of water flow. The initial ice cover with unequal thickness better reflected the horizontal difference in ice thickness. The ice thickness difference of the static ice cover was analyzed by the ice thickness of the center of the water body and the ice thickness difference of 0.1 m (center) and 0.34 m (border) from the center of the water body for 48 h. The lower the environmental temperature was, the smaller the temperature gradient of the water body under the ice, the greater the ice thickness growth rate, and the greater the ice thickness difference between the river bank and the water center. After freezing for 48 h at −5 °C and −10 °C, the water 0.34 m (border) from the center of the water body was not completely frozen into ice. The maximum ice thickness difference between the center and the shore during the freezing period was small and appeared in the early stage of the freezing period, and the horizontal ice thickness difference was small. The environmental negative temperature was −20 °C, the ice thickness difference was significantly higher than the environmental negative temperatures of −5 °C and −10 °C in the early stage of freezing, and the shore water 0.34 m away from the center was completely frozen after 48 h.
The growth process of ice cover thickness is synchronized with the freezing depth of slope soil and the decrease of water temperature under ice. The depth, slope ratio and flow velocity of the water flow directly affected the ice cover thickness and thickness difference. The deeper the water depth of the same slope ratio was, the easier it was for the shore water to form shore ice due to the freezing of the soil, but the freezing area of the shore soil was difficult to expand due to the increase in the water depth. Therefore, the deeper the water depth was, the greater the ice thickness difference at the initial stage of freezing, and the smaller the ice thickness was at 48 h of freezing. The ice thickness after 48 h of freezing at a 0.3 m water depth was 0.59 cm lower than that at a 0.2 m water depth, and the maximum ice thickness difference at the initial stage of freezing was higher than 1.33 cm. The greater the slope ratio of the same water depth was, the more conducive it was to the direct heat exchange between the water surface and the negative temperature of the environment, and the soil on the bank was more likely to form negative temperature frozen soil. The 48 h ice thickness and the maximum ice thickness difference at the initial stage of freezing increased with increasing slope ratio. The characteristics of static ice cover formed by dynamic water were related not only to the negative temperature of the environment but also to the flow velocity of the water flow. The larger the water velocity was, the stronger the turbulence was, and ice crystals did not easily form in the early stage of freezing, so the maximum ice thickness difference decreased in the early stage of freezing. The maximum ice thickness difference at the initial stage of freezing with a flow rate of 0.20 m/s was 0.22 cm less than that at the initial stage of freezing with a flow rate of 0.12 m/s. In addition, the larger the initial flow velocity was, the more obvious the water flow velocity decrease after the ice cover was formed during the freezing period, and the supercooled water mass was more likely to form ice in the weakly turbulent part of the water flow. However, the overall effect on ice cover thickness was not obvious. The thickness of the ice cover after freezing at a flow rate of 0.20 m/s for 48 h was 0.02 cm greater than that after freezing at a flow rate of 0.12 m/s for 48 h.
The horizontal development process and volume difference of dynamic water were more significant than those of static water. The influence of temperature and flow velocity on the initial ice time was much greater than that of water depth and slope ratio, and the influence of water depth on the initial ice time was the smallest. The heat flux of narrow and deep river banks was larger than that of wide and shallow river banks. The interval between the initial ice period and the freezing period of the water flow on narrow and deep river banks is short, and the difference in the horizontal ice thickness is small. A stable ice cover forms easily, which makes them an excellent section for the operation of projects in the cold region.
4.1.3. The Influence of Riverbed Heat Transfer on Water and Heat Exchange
Combined with the factors analyzed in Table 2, the coupling effect of riverbank soil and water temperature affects the formation process of static ice cover. The frozen shallow water flow and the heat exchange between the water flow and the river bank soil are important thermal factors. The heat conduction of frozen soil on the bank of the river greatly influences the characteristics of ice and the distribution of horizontal ice cover [16]. The law of the maximum ratio of bank heat flux to water surface heat flux is shown in Figure 11, and the maximum bank heat flux can account for 0.42 of the water surface heat flux. The influence of riverbank heat flux on water surface icing increases linearly with increasing negative temperature. The maximum ratio of riverbank heat flux to water surface heat flux at −5 °C is 1.75 times that of the maximum ratio of river bank heat flux to water surface heat flux at −20 °C. The influence of bank heat flux on water surface icing decreases first and then increases with increasing flow velocity. When the water velocity is small, the temperature of the viscous bottom layer of the water flow is larger, and the influence of the bank heat flux on the water surface icing is slightly reduced. With the increase in velocity, the nonisothermal flow caused by the transverse flow velocity intensifies the convective heat flux of the riverbank to the water, and the influence of the riverbank heat flux on the water surface icing increases. The maximum ratio of heat flux to water surface heat flux on narrow and deep river banks is larger than that on wide and shallow river banks. The influence of bank heat flux on water surface icing decreases linearly with increasing bank slope ratio. When the bank slope ratio increases to 1.25, the maximum ratio of bank heat flux to water surface heat flux remains basically unchanged. Therefore, there is an optimal river channel slope ratio that can generate ice cover rapidly and stably. The influence of water depth on the proportion of heat flux on the bank is less than that of other factors. The influence of heat flux on the bank on the freezing of the water surface decreases linearly with increasing water depth, and the maximum ratio of heat flux on the bank to that on the water surface is basically maintained at 0.24.

Figure 11.
Maximum heat flux ratio between riverbed and water surface. (a) The variation of maximum heat flux ratio with environmental temperature; (b) The variation of maximum heat flux ratio with flow velocity; (c) The variation of maximum heat flux ratio with slope coefficient; (d) The variation of maximum heat flux ratio with water depth. The red line in (c) represents the variation of maximum heat flux ratio of low slope ratio.
4.2. Horizontal Distribution Regression Model of Ice Cover
The empirical model of ice cover thickness represented by the freezing degree-day method assumes that the ice surface temperature is equal to the atmospheric temperature [6,17]. The form of this kind of empirical model is simple, and the calculation of the vertical thickness of the ice cover has good accuracy, as shown in Figure 12a. The Stephen equation results were smaller than the numerical simulation and the measured values in this paper except at the initial freezing stage and the rapid growth stage of the border ice. Therefore, the empirical formula for describing the transverse distribution of ice cover needs to consider the influence of transverse water depth. According to the numerical simulation results, the regression formula generalized by the transverse distribution of the dimensionless ice thickness of the water depth and water surface width is shown in Equation (20). Since the negative temperature of the external environment of the test and numerical model in this paper is constant, the relationship between ice thickness and cumulative negative temperature can be equivalent to the relationship with time, as shown in Figure 12b. The regression Equation (22) of the ice cover horizontal distribution can better calculate the ice cover shape of the cross section.
where hice is the thickness of ice cover, cm; Hw is the water depth of the section, cm; x′ is the distance from the shore, m; B is the width of the water surface, m; and a and c are the parameters of the empirical formula to describe the transverse distribution of the ice cover. The fitting parameters and their correlation coefficients are shown in Table 3.

Figure 12.
Empirical formula for ice thickness. (a) Vertical thickening formula; (b) horizontal distribution formula. The red dash line in (b) represents the connecting part of the channel slope and the trough.

Table 3.
Regression model parameters for horizontal distribution of ice cover.
Further analysis of the physical meaning of the regression formula parameters showed that parameters a and c were related to the cumulative negative temperature of the initial ice. As shown in Table 3, parameter a was positively correlated with the ratio of cumulative negative temperature to initial ice cumulative negative temperature, and parameter c was negatively correlated with the ratio of initial ice cumulative negative temperature to cumulative negative temperature. As freezing progresses, the horizontal distribution shape parameters of the ice cover increased linearly with the multiple cumulative negative temperatures of the initial ice. The regression model based on numerical model generalization is a simple calculation, with clear physical meaning of fitting parameters and high accuracy, which is convenient for the direct application of practical engineering and design.
5. Conclusions
In this paper, a static ice cover horizontal distribution model considering riverbank heat transfer is proposed. The main feature of the model is the coupling analysis of the environmental temperature, the flow of the river channel and the temperature field of the river bank soil, reflecting the horizontal growth process of the static ice cover by the bank slope, which is very significant for narrow and deep river channels. The application of this model to simulate the initial ice time, freezing time and thickness of the static ice cover formed by static and dynamic water was consistent with the measured results. The numerical model in this paper has strong versatility and can provide a theoretical reference for the formation of ice cover in reservoirs, rivers and lakes.
(1) The ice thickness growth process of static water and dynamic water forming static ice cover was divided into two stages, and its change had obvious horizontal distribution characteristics. In the early stage of freezing, it was the ice cover growth mode of “first border ice, then channel center”; after freezing, the horizontal ice thickness of the static ice cover was unequally thickened, and the horizontal difference of the dynamic water ice cover was more significant than that of the static water.
(2) The freezing depth of bank soil is closely related to the development of ice cover. During the freezing period, the temperature of the river bank soil dropped to a negative temperature, and the water surface formed ice crystals to form the initial border ice. During the freezing period, the shape of the static ice cover coincided with the river bank isotherm. The coincidence isotherm of dynamic water affected by flow turbulence was lower than that of static water. The type of ice in the upper and lower layers of the ice cover was also different from the soil and environment of the riverbank.
(3) The growth difference of static ice cover was mainly due to the influence of environmental temperature and water flow characteristics on the initial Nusselt number. The influence of temperature and flow velocity on the initial ice time was much greater than that of water depth and slope ratio, and the influence of water depth on the initial ice time was the smallest. The heat flux of narrow and deep river banks was larger than that of wide and shallow river banks. The interval between the initial ice period and the freezing period of the water flow on the narrow and deep river bank was short, and the horizontal ice thickness difference was small, easily forming a stable ice cover. Narrow and deep sections are excellent sections for ice cover operation of water conveyance projects in cold regions.
(4) The heat exchange between the water and the river bank soil was the main reason for the horizontal distribution of the thick ice on the river bank slope and the thick and thin ice cover in the canal center. The regression model is simple to calculate, the physical meaning of the fitting parameters is clear and has high accuracy, and it is more convenient for practical engineering and design applications.
Author Contributions
Conceptualization, B.X. and Z.W.; methodology, B.X. and Z.W.; funding acquisition, Z.W.; software, B.X. and Q.L.; validation, B.X., Z.W., Q.L. and H.L.; formal analysis, B.X.; resources, B.X., Z.W., Q.L. and H.L.; data curation, B.X., Z.W., Q.L. and H.L.; writing—original draft preparation, B.X.; writing—review and editing, B.X. and Z.W.; visualization, B.X. and Q.L.; supervision, Z.W.; project administration, Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. U2003108; 51279168) awarded to Zhengzhong Wang, the National Key Research and Development Program of China (Grant No. 2017YFC0405103) awarded to Zhengzhong Wang, and the Water Conservancy Development Fund on Scientific Research Project of Shaanxi Province of China (Grant No. 2021slkj-1) awarded to Zhengzhong Wang.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The author would like to gratefully acknowledge Haoyuan Jiang and Jian Mao for their technical support.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationship that could have appeared to influence the work reported in this study.
References
- Saadé, R.G.; Sarraf, S. Simulation of Ice Cover Melting in Turbulent Flow. Int. J. Numer. Methods Heat Fluid Flow 1995, 5, 647–663. [Google Scholar] [CrossRef]
- Rokaya, P.; Budhathoki, S.; Lindenschmidt, K.-E. Trends in the Timing and Magnitude of Ice-Jam Floods in Canada. Sci. Rep. 2018, 8, 5834. [Google Scholar] [CrossRef]
- Adalaiti, H.J.; Yu, S.S. Study and Prospect of Ice Damage Prevention and Control in Xinjiang’s Water Conveyance Projects. J. Water Resour. Archit. Eng. 2010, 8, 46–49. (In Chinese) [Google Scholar]
- Yang, K. Advances of ice hydraulics, ice regime observation and forecasting in rivers. J. Hydraul. Eng. 2018, 49, 81–91. (In Chinese) [Google Scholar] [CrossRef]
- Guo, X.; Wang, T.; Fu, H.; Pan, J.; Lu, J.; Guo, Y.; Li, J. Progress and Trend in the Study of River Ice Hydraulics. Theor. Appl. Mech. 2021, 53, 655–671. (In Chinese) [Google Scholar]
- Shen, H.T. River Ice Processes. In Advances in Water Resources Management; Wang, L.K., Yang, C.T., Wang, M.-H.S., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 483–530. ISBN 978-3-319-22923-2. [Google Scholar]
- Peters, M.; Dow, K.; Clark, S.P.; Malenchak, J.; Danielson, D. Experimental Investigation of the Flow Characteristics beneath Partial Ice Covers. Cold Reg. Sci. Technol. 2017, 142, 69–78. [Google Scholar] [CrossRef]
- Pan, J.; Shen, H.T. Modeling Ice Cover Effect on River Channel Bank Stability. Environ. Fluid Mech. 2022, 22, 1121–1133. [Google Scholar] [CrossRef]
- Duan, W.; Huang, G.; Yang, J.; Liu, M. Ice regime analysis and safe dispatch research on long distance water diversion project in winter. South-North Water Transf. Water Sci. Technol. 2016, 14, 96–104. (In Chinese) [Google Scholar] [CrossRef]
- Shen, H.T. Mathematical Modeling of River Ice Processes. Cold Reg. Sci. Technol. 2010, 62, 3–13. [Google Scholar] [CrossRef]
- Svensson, U.; Billfalk, L.; Hammar, L. A Mathematical Model of Border-Ice Formation in Rivers. Cold Reg. Sci. Technol. 1989, 16, 179–189. [Google Scholar] [CrossRef]
- Huang, F.; Shen, H.T.; Knack, I. Modeling Border Ice Formation and Cover Progression in Rivers. In Proceedings of the IAHR International Symposium on Ice, Dalian, China, 11–15 June 2012. [Google Scholar]
- Mao, Z.; Dong, Z.; Chen, C. Review on mathematical simulation of river ice. Water Power 1996, 12, 58–61. (In Chinese) [Google Scholar]
- Mao, Z.; Chen, C. Simulation of Heat Transfer between Streambed and River Flow. Water Resour. Hydropower Eng. 1999, 5, 11–13. (In Chinese) [Google Scholar] [CrossRef]
- Bernard, M. Comparison of Field Data with Theories on Ice Cover Progression in Large Rivers. Can. J. Civ. Eng. 2011, 11, 798–814. [Google Scholar] [CrossRef]
- Shen, H.T.; Yapa, P.D. A Unified Degree-Day Method for River Ice Cover Thickness Simulation. Can. J. Civ. Eng. 1985, 12, 54–62. [Google Scholar] [CrossRef]
- Yang, K.; Guo, X.; Wang, T.; Fu, H.; Pan, J. Effects of solar radiation and ground temperature on water temperature under ice cover. J. Hydraul. Eng. 2022, 53, 530–538+548. (In Chinese) [Google Scholar] [CrossRef]
- Lian, J.; Zhao, X. Radiation degree-day method for predicting the development of ice cover thickness under the hydrostatic and non-hydrostatic conditions. J. Hydraul. Eng. 2011, 42, 1261–1267. (In Chinese) [Google Scholar] [CrossRef]
- Gordon, M. Greene Simulation of Ice-Cover Growth and Decay in One Dimension on the Upper St. Lawrence River. Available online: https://repository.library.noaa.gov/view/noaa/10432 (accessed on 30 June 2023).
- Khan, Z.H.; Ahmad, R.; Sun, L. Effect of Instantaneous Change of Surface Temperature and Density on an Unsteady Liquid–Vapour Front in a Porous Medium. Exp. Comput. Multiph. Flow 2020, 2, 115–121. [Google Scholar] [CrossRef]
- Peters, G.W.M.; Baaijens, F.P.T. Modelling of Non-Isothermal Viscoelastic Flows. J. Non-Newton. Fluid Mech. 1997, 68, 205–224. [Google Scholar] [CrossRef]
- Xiao, H.; Dong, Z.; Long, R.; Yang, K.; Yuan, F. A Study on the Mechanism of Convective Heat Transfer Enhancement Based on Heat Convection Velocity Analysis. Energies 2019, 12, 4175. [Google Scholar] [CrossRef]
- Lienhard, J.H. A Heat Transfer Textbook; Phlogiston Press: Cambridge, MA, USA, 2011; Available online: https://ahtt.mit.edu (accessed on 3 August 2023).
- Kays, W.M. Turbulent Prandtl Number—Where Are We? Asme Trans. J. Heat Transf. 1994, 116, 284–295. [Google Scholar] [CrossRef]
- Thonon, M.; Fraisse, G.; Zalewski, L.; Pailha, M. Towards a Better Analytical Modelling of the Thermodynamic Behaviour of Phase Change Materials. J. Energy Storage 2020, 32, 101826. [Google Scholar] [CrossRef]
- Moench, S.; Dittrich, R. Influence of Natural Convection and Volume Change on Numerical Simulation of Phase Change Materials for Latent Heat Storage. Energies 2022, 15, 2746. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, Q.; Wang, Z.; Gong, J.; Li, L. Frost Heave Modelling of the Sunny-Shady Slope Effect with Moisture-Heat-Mechanical Coupling Considering Solar Radiation. Sol. Energy 2022, 233, 292–308. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Z.; Li, Z.; Wang, Y. Transversely Isotropic Frost Heave Modeling with Heat–Moisture–Deformation Coupling. Acta Geotech. 2020, 15, 1273–1287. [Google Scholar] [CrossRef]
- Harlan, R.L. Analysis of Coupled Heat-Fluid Transport in Partially Frozen Soil. Water Resour. Res. 1973, 9, 1314–1323. [Google Scholar] [CrossRef]
- Hansson, K.; Imnek, J.; Mizoguchi, M.; Lundin, L.C.; Van Genuchten, M.T. Water Flow and Heat Transport in Frozen Soil: Numerical Solution and Freeze–Thaw Applications. Vadose Zone J. 2004, 3, 693–704. [Google Scholar] [CrossRef]
- Liu, X.; Liu, J.; Tian, Y.; Shen, Y.; Liu, J. A Frost Heaving Mitigation Method with the Rubber-Asphalt-Fiber Mixture Cylinder. Cold Reg. Sci. Technol. 2020, 169, 102912. [Google Scholar] [CrossRef]
- Li, S.; Zhang, M.; Tian, Y.; Pei, W.; Zhong, H. Experimental and Numerical Investigations on Frost Damage Mechanism of a Canal in Cold Regions. Cold Reg. Sci. Technol. 2015, 116, 1–11. [Google Scholar] [CrossRef]
- Xu, X. Physics of Frozen Soil; Physics of Frozen Soil: Beijing, China, 2010; ISBN 978-7-03-028867-7. [Google Scholar]
- Lu, N.; Likos, W.J. Unsaturated Soil Mechanics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; Available online: https://webapps.unitn.it/Biblioteca/it/Web/EngibankFile/5802626.pdf (accessed on 15 June 2023).
- Nan, L.I.; Tuo, Y.C.; Deng, Y.; Jia, L.I.; Liang, R.F.; Rui-Dong, A.N. Heat Transfer at Ice-Water Interface under Conditions of Low Flow Velocities. J. Hydrodyn. 2016, 28, 603–609. [Google Scholar] [CrossRef]
- Sarraf, S.; Zhang, X.T. Modeling Ice-Cover Melting Using a Variable Heat Transfer Coefficient. J. Eng. Mech. 1996, 122, 930–938. [Google Scholar] [CrossRef]
- Dong, S.; Cui, H. Analysis of Calculating Formula and Improvement of Empirical Formula for Saturation Vapour Pressure. Q. J. Appl. Meteorol. 1992, 3, 501–508. (In Chinese) [Google Scholar]
- Yang, K. Heat exchange model between river-lake and atmosphere during ice age. J. Hydraul. Eng. 2021, 52, 556–564+577. (In Chinese) [Google Scholar] [CrossRef]
- Hanley, T.O.; Michel, B. Laboratory Formation of Border Ice and Frazil Slush. Can. J. Civ. Eng. 1977, 4, 153–160. [Google Scholar] [CrossRef]
- Michel, B.; Ramseier, R.O. Classification of River and Lake Ice. Can. Geotech. J. 1971, 8, 36–45. [Google Scholar] [CrossRef]
- Turcotte, B.; Morse, B. A Global River Ice Classification Model. J. Hydrol. 2013, 507, 134–148. [Google Scholar] [CrossRef]
- Blokhina, N.S.; Ordanovich, A.E. The Influence of Ice Cover on a Reservoir on the Development of a Spring Thermal Bar. Mosc. Univ. Phys. 2012, 67, 109–115. [Google Scholar] [CrossRef]
- Marsh, P.; Prowse, T.D. Water Temperature and Heat Flux at the Base of River Ice Covers. Cold Reg. Sci. Technol. 1987, 14, 33–50. [Google Scholar] [CrossRef]
- Yu, S.; Li, Q.; Song, L. Forecast of Ice State in Open Canal with Water Delivered in Ice Periods. China Rural Water Hydropower 2008, 9, 108–109+113. (In Chinese) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).