An Analysis of Rainfall Characteristics and Rainfall Flood Relationships in Cities along the Yangtze River Based on Machine Learning: A Case Study of Luzhou
Abstract
:1. Introduction
2. Data and Methods
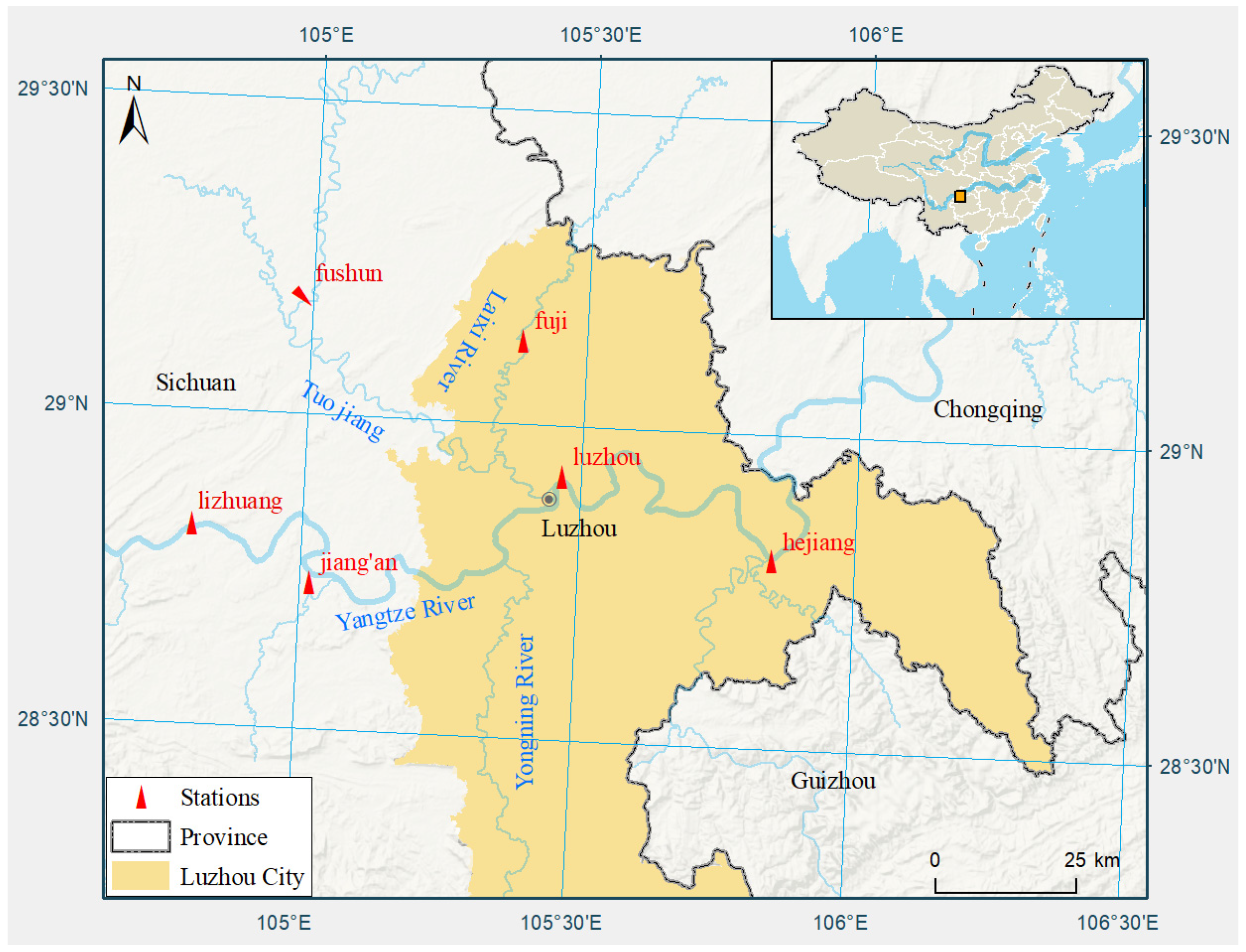
2.1. Data
2.2. Methods
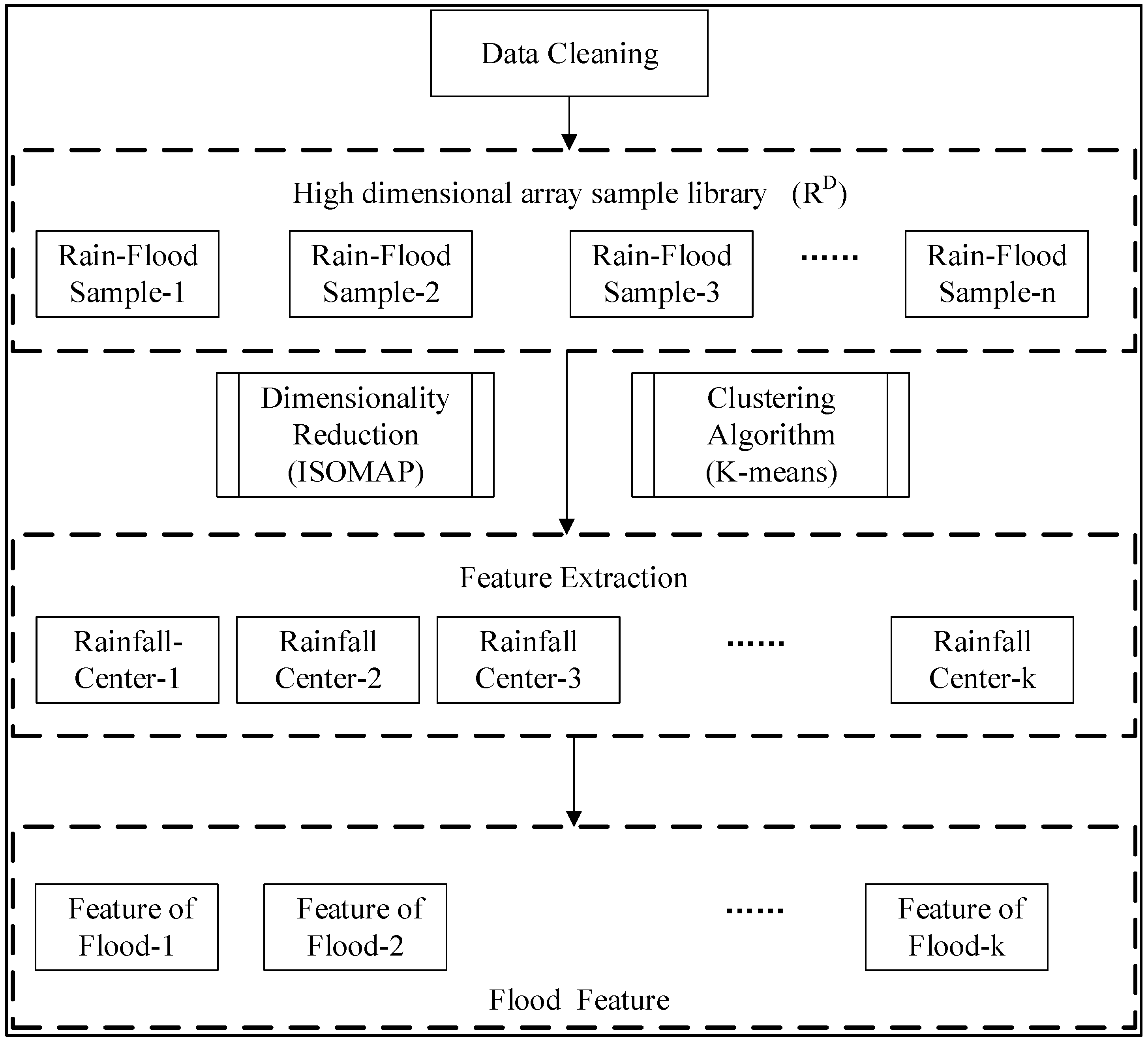
2.2.1. Construction of a Dynamic Characteristics Matrix for Space–Time Distribution of Heavy Rainfall
2.2.2. Dimensionality Reduction Analysis Based on the Isomap Algorithm
- (1)
- Build an adjacent graph, , by defining input space X as any two samples of vectors and . Calculate the Euclidean distance between them as . Then, select the k-nearest points of sample as its neighbors. If two samples, and , have neighboring points, they are connected. The connection length is the Euclidean distance between them, . This operation is repeated on all points to obtain graph G.
- (2)
- In graph G, for any two sample vectors and , set the distance between them as . Initialize if and are directly connected, otherwise set . Then, update . For all samples in graph G, calculate the shortest path via . After each iteration, we obtained the shortest path between the sample vectors as .
- (3)
- Let and solve the eigenvalue decomposition of matrix Bwhere the feature vector corresponding to is , and the feature vector corresponding to is . Subsequently, the -th component of the -dimensional embedding vector is equal to . Based on this, the sample set in the high-dimensional space is mapped to the low-dimensional space to represent :
2.2.3. Dynamic Clustering Analysis
3. Results and Discussion
4. Conclusions
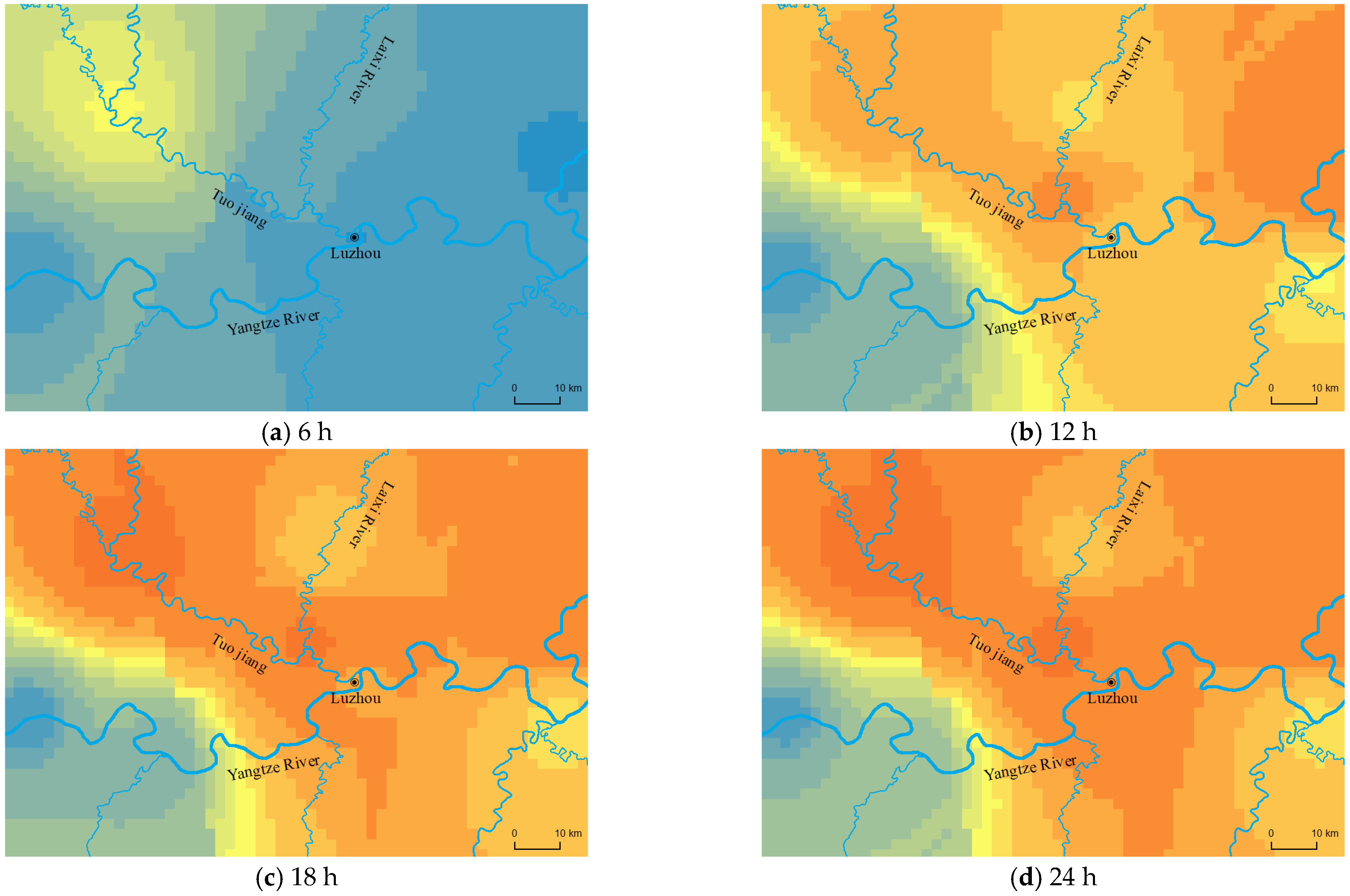
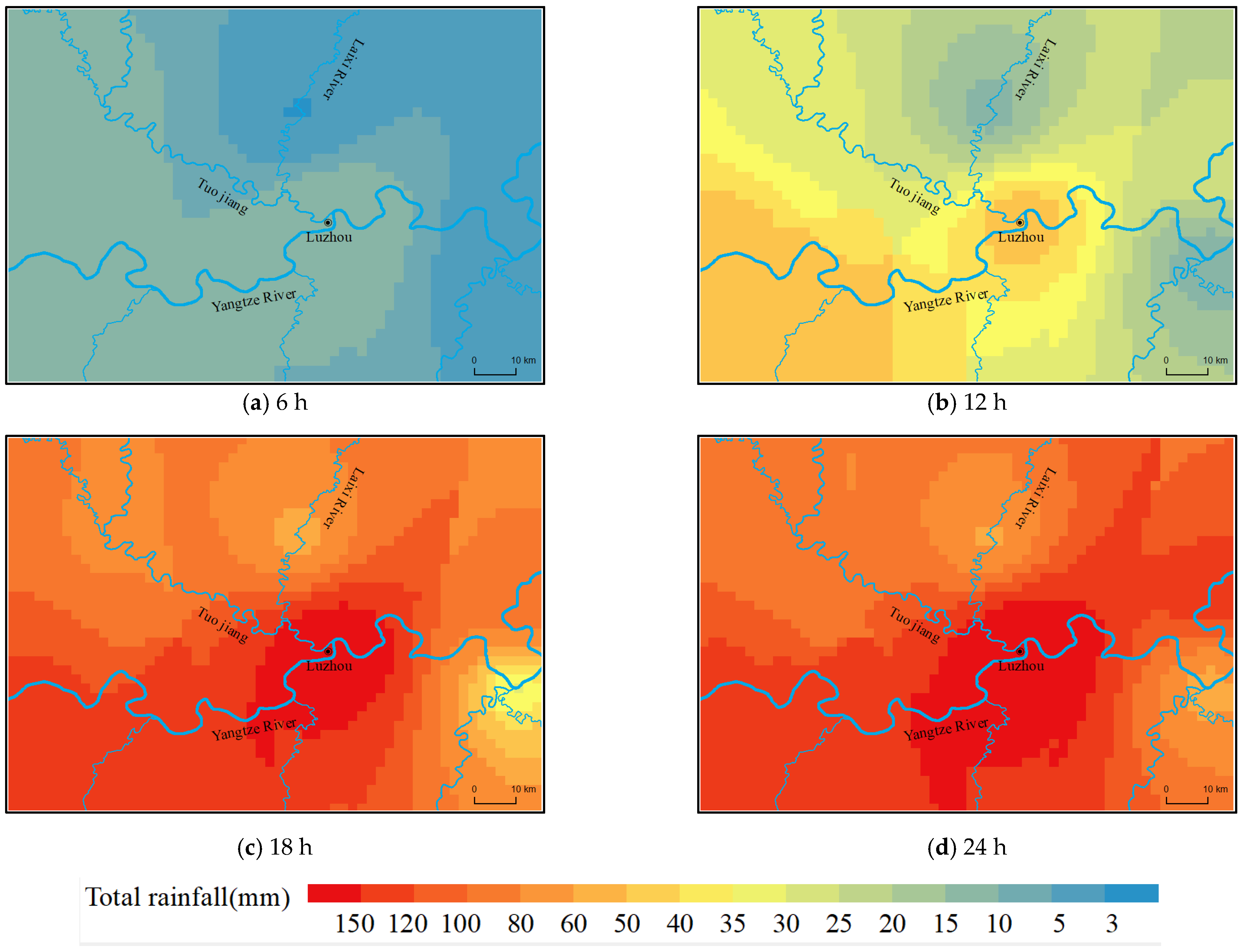
- Traditional methods of analyzing rainfall characteristics focus on rainfall data or surface rainfall at a single station. However, rainfall processes are characterized by spatial and temporal variation. Traditional methods cannot objectively express rainfall variations in time and space. Machine learning technology can quantitatively describe the dynamic temporal and spatial distributions of various types of rainfall. This is consistent with the climatic characteristics of the region. By comparing the featured rainfall process with the typical actual rainfall process, we found that the temporal and spatial distribution characteristics of the two were similar, and that the featured rainfall process was sufficiently representative of the actual rainfall process. Machine learning techniques can be effectively applied in the study and extraction of rainfall’s spatiotemporal distribution features.
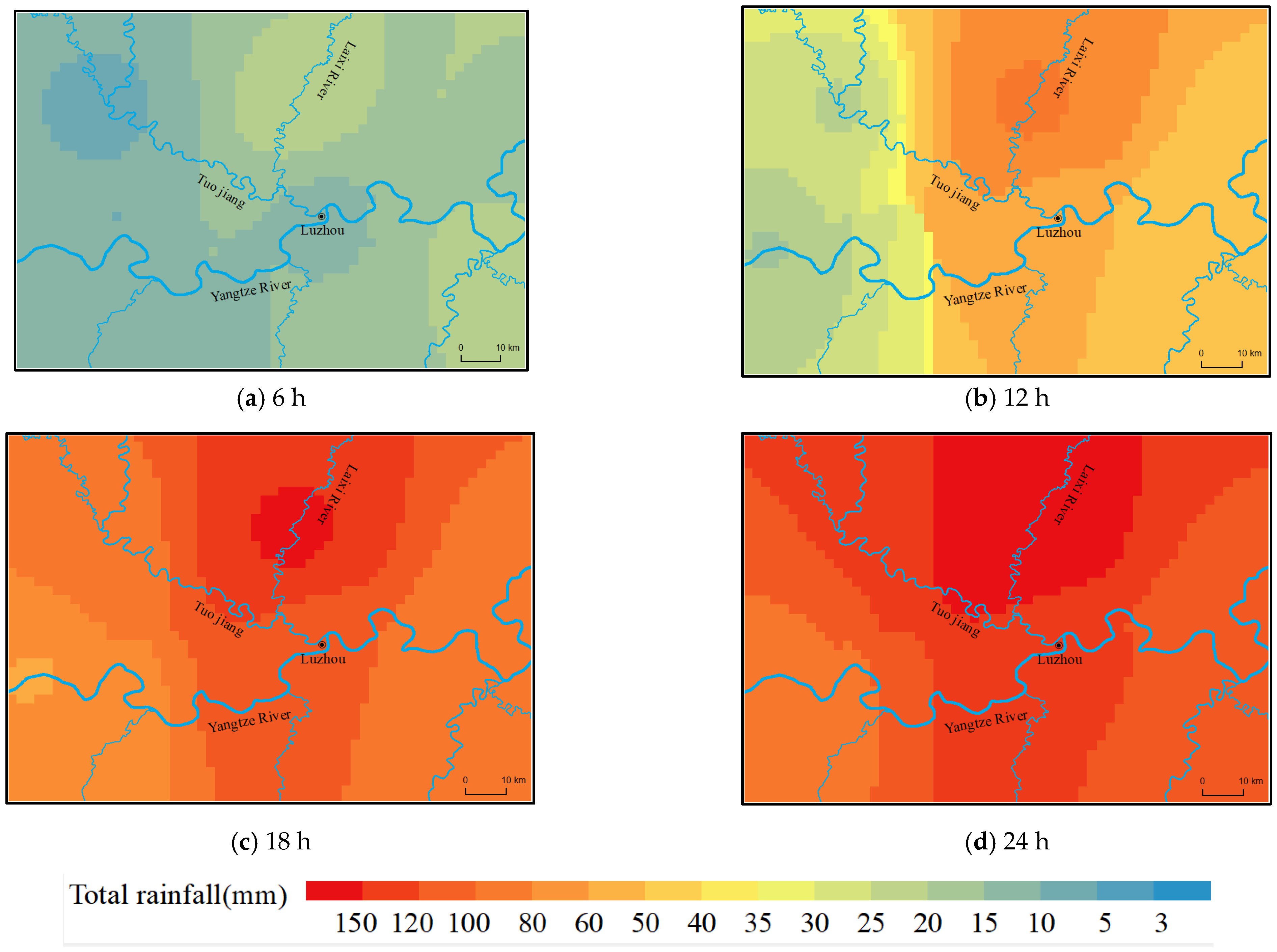
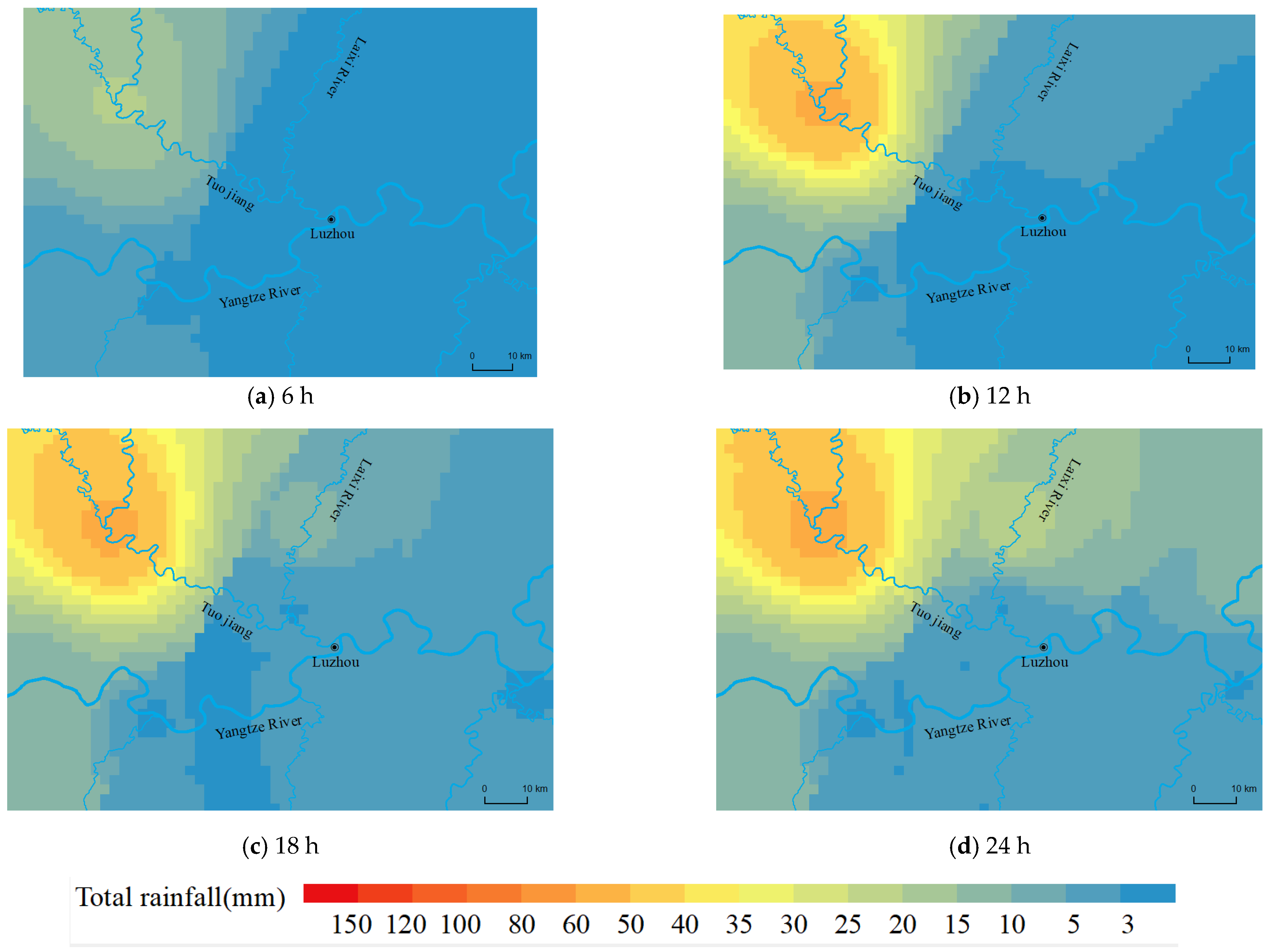
- Rainfall in the Luzhou area can be divided into three types according to the different spatial and temporal distributions. And the flood characteristics formed by different types of rainfall are also different. When analyzing flood characteristics, it is necessary to study the spatial and temporal distribution characteristics of rainfall in the area in order to obtain objective and reasonable conclusions.
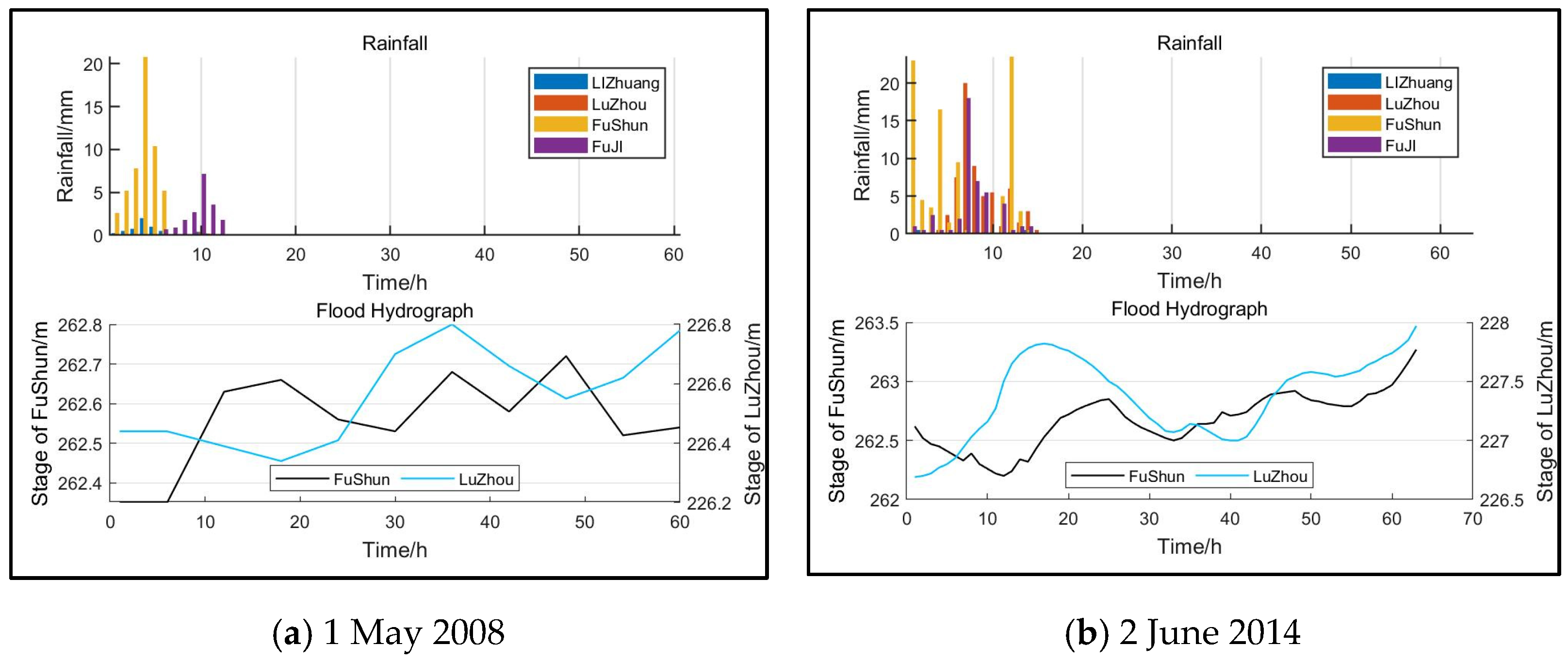
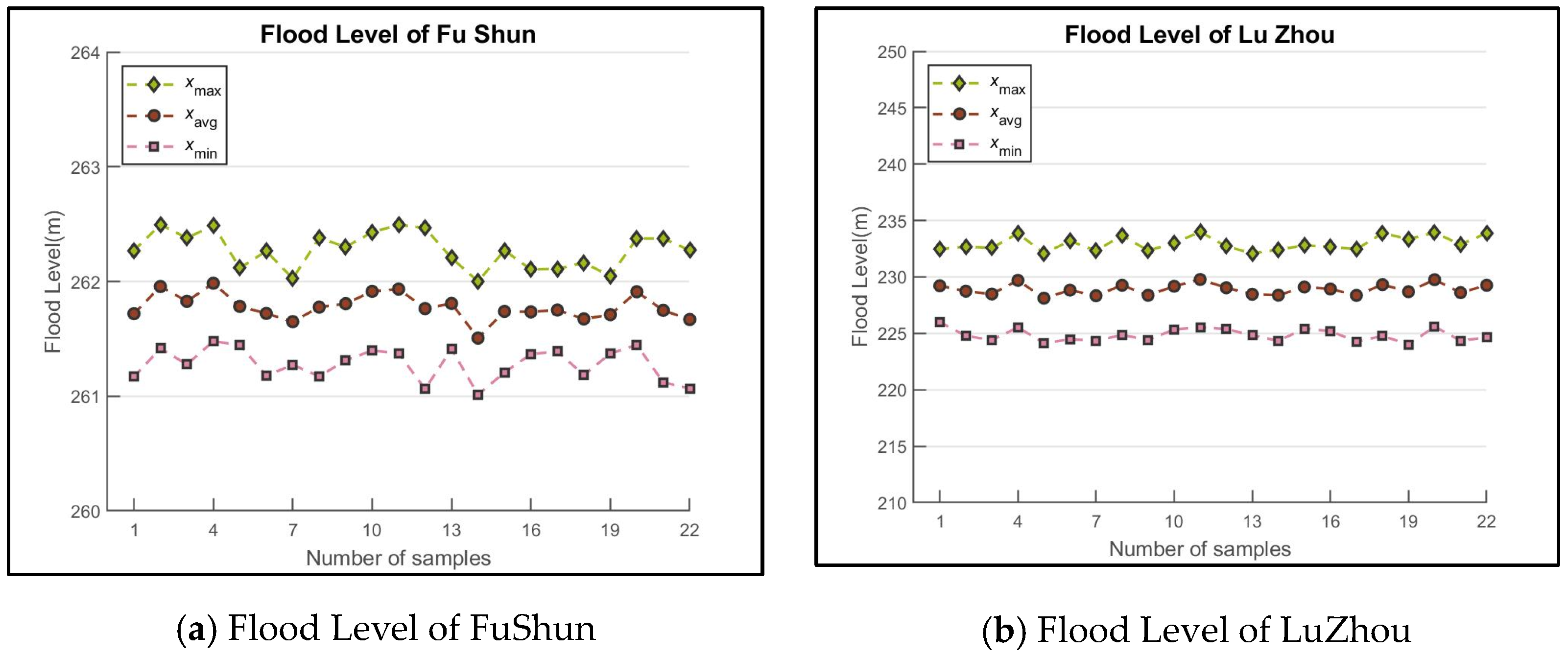
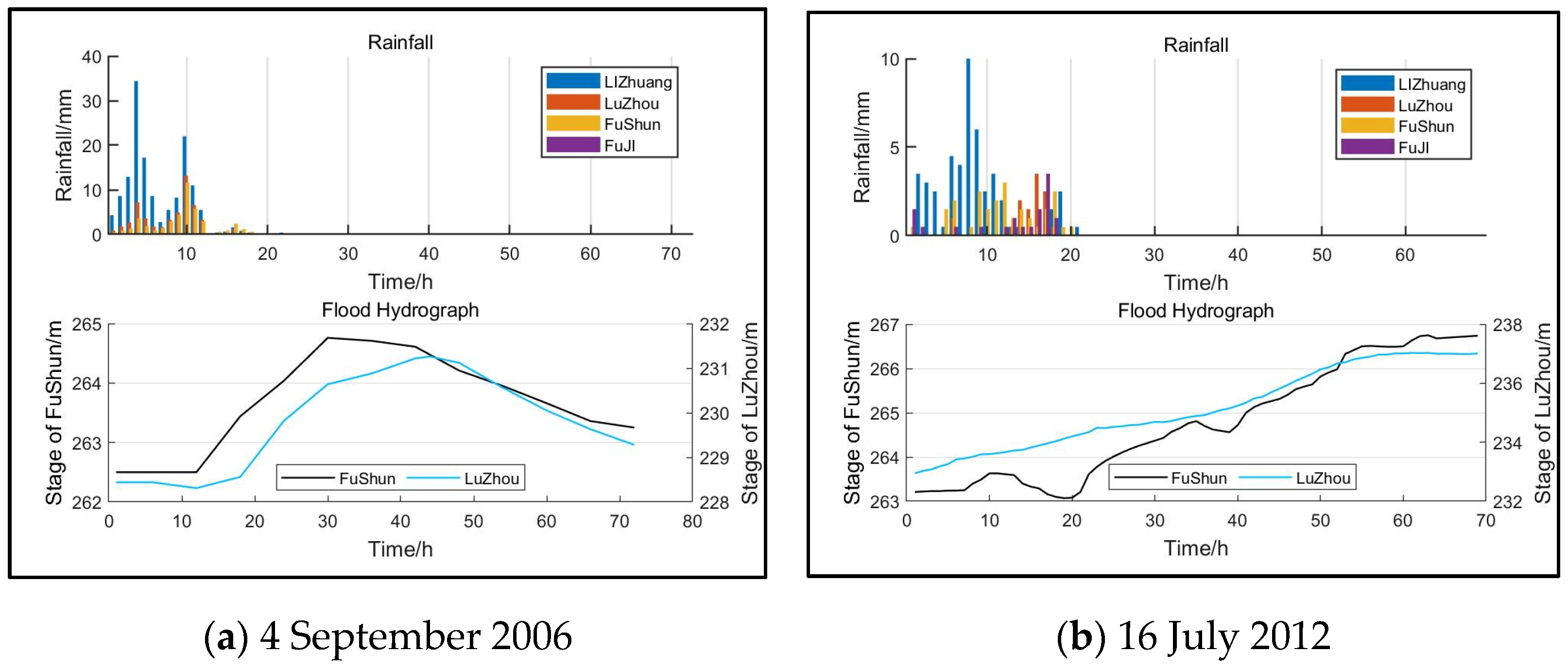
- River flooding had a negligible impact on urban flood control and drainage. When the rainstorm center was located upstream of the Yangtze and Tuojing rivers, the movement direction of the rainstorm center was consistent with the flood evolution direction of the Yangtze and Tuojing rivers. The Tuojing River was significantly affected by the top support of the Yangtze River, with flood level changes up to 7–8 m. Both the Yangtze and Tuojing rivers maintained high water levels with a high risk of flooding. This is the most unfavorable rainfall process and must be a focus for flood prevention.
- Although the rainfall–flood relationship obtained in this study applies only to Luzhou, the proposed method is universal. At present, this study only considers Luzhou as an example; the research scope can be further expanded to include the entire basin to obtain more objective results. The results of this study can provide technical support for urban storm risk management, as well as for the design of urban flood control and drainage systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Allen, M.R.; Ingram, W.J. Constraints on Future Changes in Climate and the Hydrologic Cycle. Nature 2002, 419, 228–232. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Wang, Y.T.; He, R.M.; Hu, Q.; Song, X. Discussion on the urban flood and waterlogging and causes analysis in China. Adv. Water Sci. 2016, 27, 485–491. [Google Scholar]
- Liu, Y.Y.; Zheng, J.W.; Liu, H.W. Warning and thoughts of extreme rainstorm on urban flood prevention. China Flood Drought Manag. 2021, 31, 21–24. [Google Scholar]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E.; Redman, C.L.; Wu, J.; Bai, X.; Briggs, J.M. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef]
- Camorani, G.; Castellarin, A.; Brath, A. Effects of land-use changes on the hydrologic response of reclamation systems. Phys. Chem. Earth 2005, 30, 561–574. [Google Scholar] [CrossRef]
- Mcdonald, R.I.; Green, P.; Balk, D.; Fekete, B.M.; Revenga, C.; Todd, M.; Montgomery, M. Urban growth, climate change, and freshwater availability. Proc. Natl. Acad. Sci. USA 2011, 108, 6312–6317. [Google Scholar] [CrossRef]
- Schubert, J.E.; Sanders, B.F.; Smith, M.J.; Wright, N.G. Unstructured mesh generation and landcover-based resistance for hydrodynamic modeling of urban flooding. Adv. Water Resour. 2008, 31, 1603–1621. [Google Scholar] [CrossRef]
- Cardoso, M.A.; Almeida, M.C.; Brito, R.S.; Gomes, J.L.; Beceiro, P.; Oliveira, A. 1D/2D stormwater modelling to support urban flood risk management in estuarine areas: Hazard assessment in the Dafundo case study. J. Flood Risk Manag. 2020, 13, e12663. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Li, L.; Liu, Y.S.; Chan, P.W.; Zhang, W.H. Dynamic spatial-temporal precipitation distribution models for short-duration rainstorms in Shenzhen, China based on machine learning. Atmos. Res. 2020, 237, 104861. [Google Scholar] [CrossRef]
- Wang, G.-Y.; Sun, G.-R.; Li, J.-K.; Li, J. The experimental study of hydrodynamic characteristics of the overland flow on a slope with three-dimensional Geomat. J. Hydron. 2018, 30, 153–159. [Google Scholar] [CrossRef]
- Cristiano, E.; Veldhuis, M.T.; Wright, D.B.; Smith, J.A.; van de Giesen, N. The Influence of Rainfall and Catchment Critical Scales on Urban Hydrological Response Sensitivity. Water Resour. Res. 2019, 55, 3375–3390. [Google Scholar] [CrossRef]
- Cristiano, E.; ten Veldhuis, M.-C.; van de Giesen, N. Spatial and temporal variability of rainfall and their effects on hydrological response in urban areas—A review. Hydrol. Earth Syst. Sci. 2017, 21, 3859–3878. [Google Scholar] [CrossRef]
- Cheng, X.T. Disasters and strategy of comprehensive control of water disaster. J. Catastrophology 2010, 25, 10–15. [Google Scholar]
- Berne, A.; Delrieu, G.; Creutin, J.D.; Obled, C. Temporal and spatial resolution of rainfall measurements required for urban hydrology. J. Hydrol. 2004, 299, 166–179. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Liu, H.W.; Huo, F.L. An application of machine learning on examining spatial and temporal distribution of short duration rainstorm. J. Hydraul. Eng. 2019, 50, 773–779. [Google Scholar]
- Kibler, D.F. Urban Stormwater Hydrology; American Geophysical Union: Washington, DC, USA, 1982. [Google Scholar]
- Keifer, C.J.; Chu, H.H. Synthetic storm pattern for drainage design. J. Hydraul. Div. 1957, 83, 1332-1–1332-25. [Google Scholar] [CrossRef]
- Huff, F.A. Time distribution of rainfall in heavy storms. Water Resour. Res. 1967, 3, 1007–1019. [Google Scholar] [CrossRef]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J.F. Coupling a Hybrid CNN-LSTM Deep Learning Model with a Boundary Corrected Maximal Overlap Discrete Wavelet Transform for Multiscale Lake Water Level Forecasting. J. Hydrol. 2021, 598, 126196. [Google Scholar] [CrossRef]
- Prodhan, F.A.; Zhang, J.; Hasan, S.S.; Sharma, T.P.P.; Mohana, H.P. A review of machine learning methods for drought hazard monitoring and forecasting: Current research trends, challenges, and future research directions. Environ. Model. Softw. 2022, 149, 105327.1–105327.14. [Google Scholar] [CrossRef]
- Supattra, P.; Paramate, H. Flood Forecasting System Based on Integrated Big and Crowdsource Data by Using Machine Learning Techniques. IEEE Access 2020, 8, 5885–5905. [Google Scholar]
- Liu, Y.Y.; Liu, Y.S.; Zheng, J.W. Intelligent rapid prediction method of urban flooding based on BP neural network and numerical simulation model. J. Hydraul. Eng. 2022, 53, 284–295. [Google Scholar]
- Morshed-Bozorgdel, A.; Kadkhodazadeh, M.; Valikhan Anaraki, M.; Farzin, S. A Novel Framework Based on the Stacking Ensemble Machine Learning (SEML) Method: Application in Wind Speed Modeling. Atmosphere 2022, 13, 758. [Google Scholar] [CrossRef]
- Farzin, S.; Chianeh, F.N.; Anaraki, M.V.; Mahmoudian, F. Introducing a framework for modeling of drug electrochemical removal from wastewater based on data mining algorithms, scatter interpolation method, and multi criteria decision analysis (DID). J. Clean. Prod. 2020, 266, 122075. [Google Scholar] [CrossRef]
- Adnan, M.S.G.; Siam, Z.S.; Kabir, I.; Kabir, Z.; Ahmed, M.R.; Hassan, Q.K.; Rahman, R.M.; Dewan, A. A novel framework for addressing uncertainties in machine learning-based geospatial approaches for flood prediction. J. Environ. Manag. 2023, 326, 116813. [Google Scholar] [CrossRef]
- Bao, Z.; Zhang, J.; Wang, G.; He, R.; Jin, J.; Wang, J.; Wu, H. Quantitative assessment of the attribution of runoff and sediment changes based on hydrologic model and machine learning: A case study of the Kuye River in the Middle Yellow River basin. Adv. Water Sci. 2021, 32, 485–496. [Google Scholar]
- Bengio, Y.; Paiement, J.F.; Vincent, P.; Delalleau, O.; Roux, N.; Ouimet, M. Out-of-Sample Extensions for LLE, Isomap, MDS, Eigenmaps, and Spectral Clustering. In Advances in Neural Information Processing Systems 16; MIT Press: Cambridge, MA, USA, 2004; Volume 6, pp. 177–184. [Google Scholar]
- Tenenbaum, J.B.; de Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Paiement, A. Integrated Registration, Segmentation, and Interpolation for 3D/4D Sparse Data. Electron. Lett. Comput. Vis. Image Anal. 2015, 14, 6–8. [Google Scholar] [CrossRef]

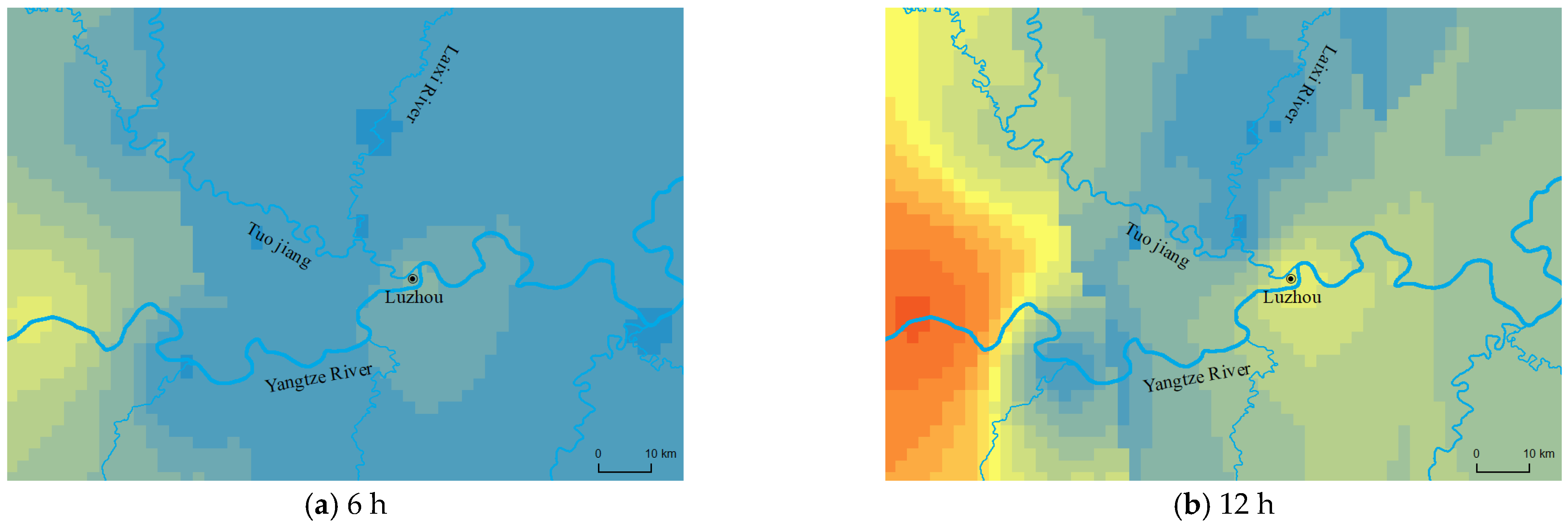
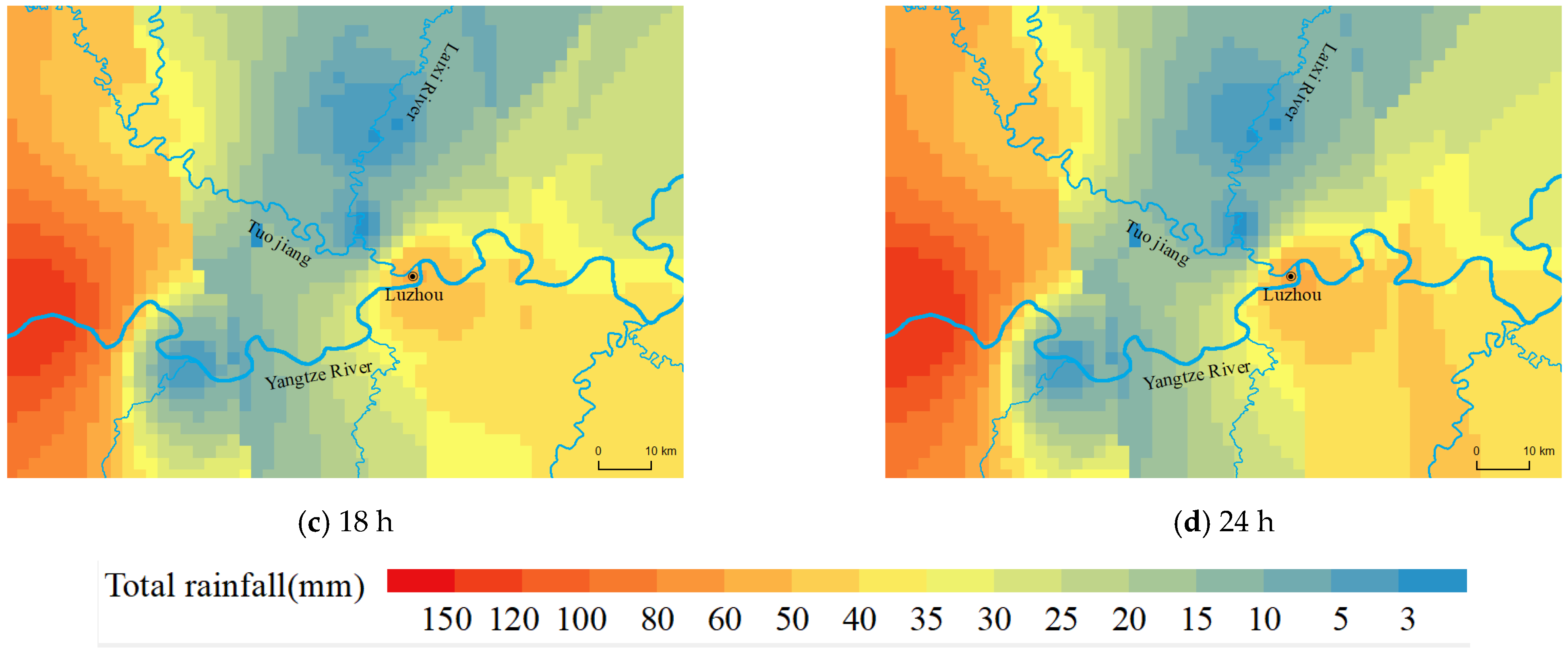
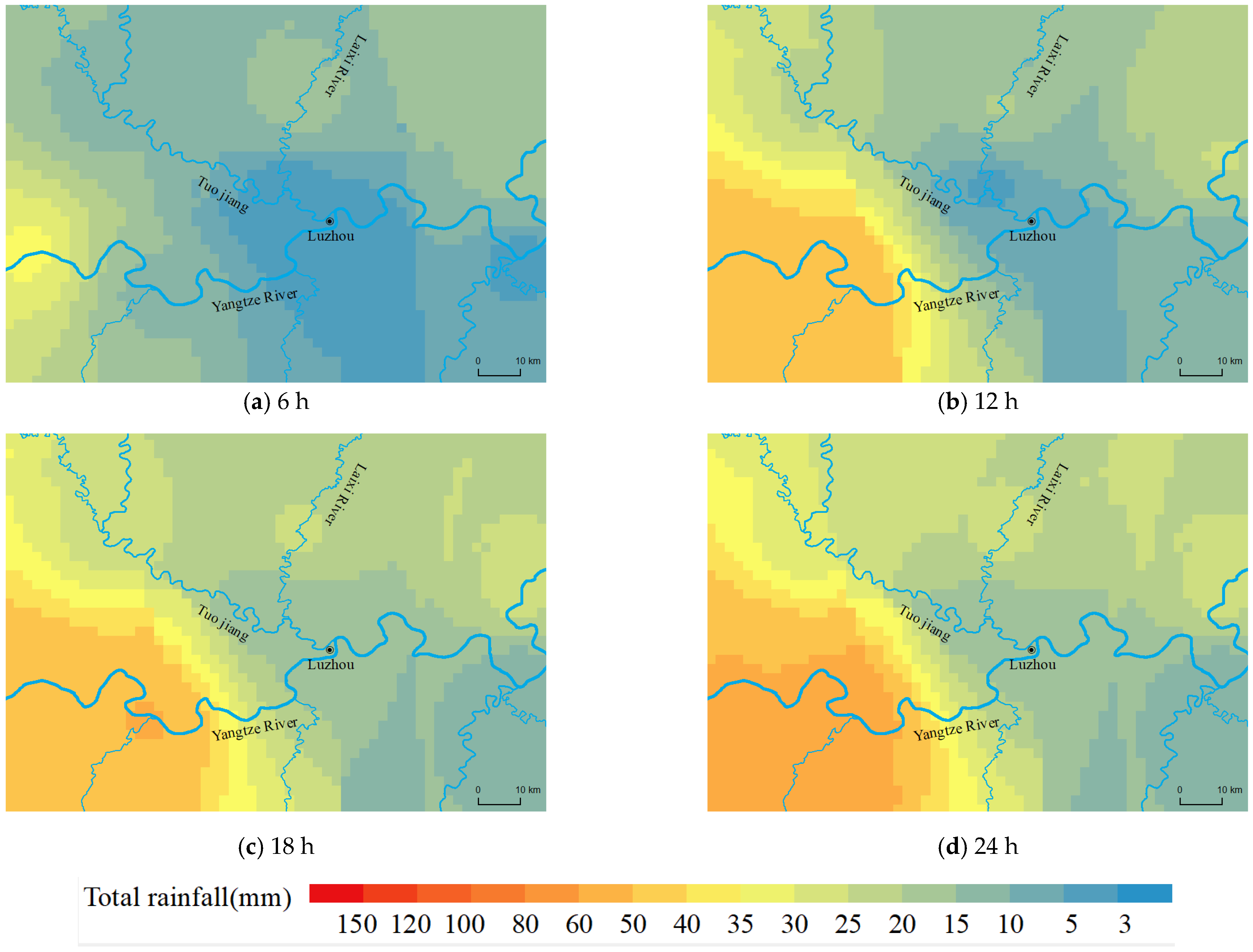

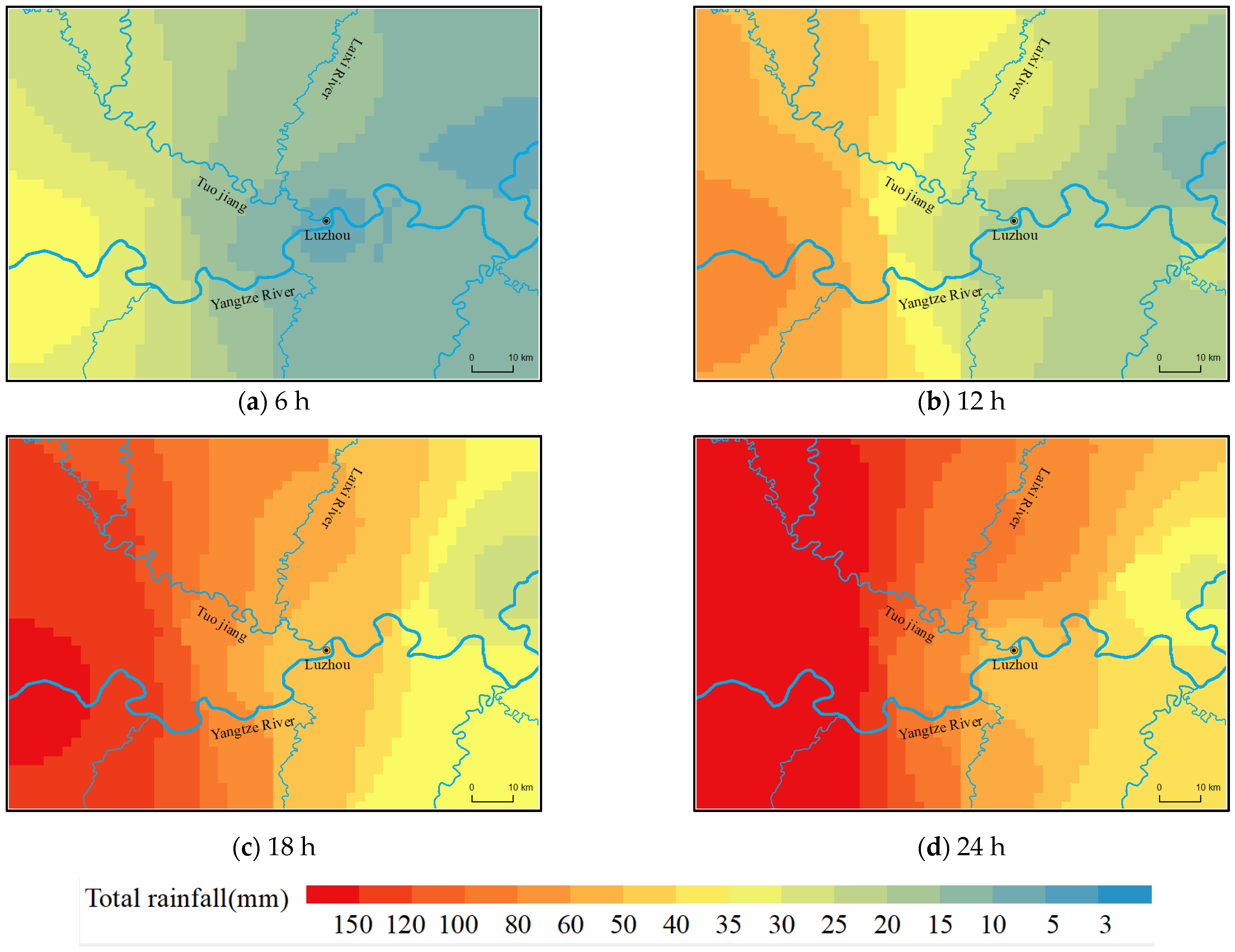

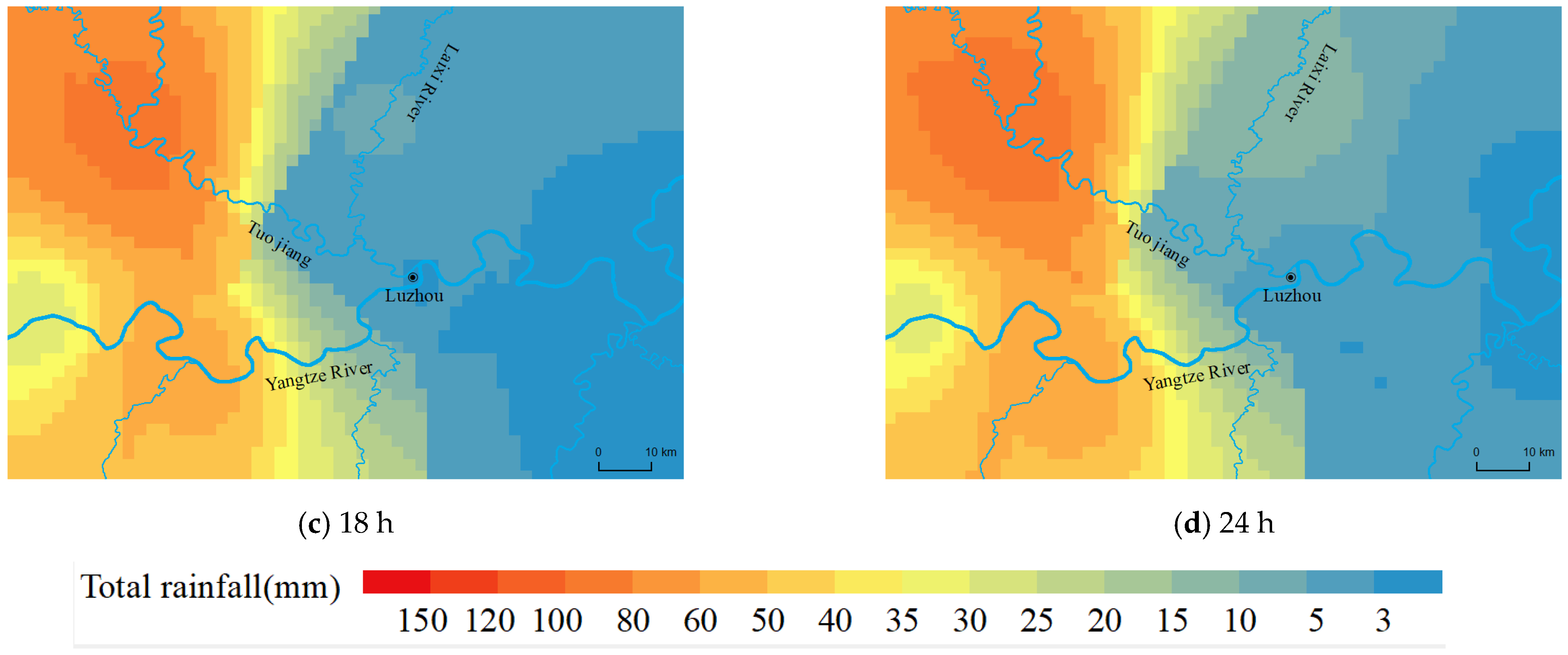
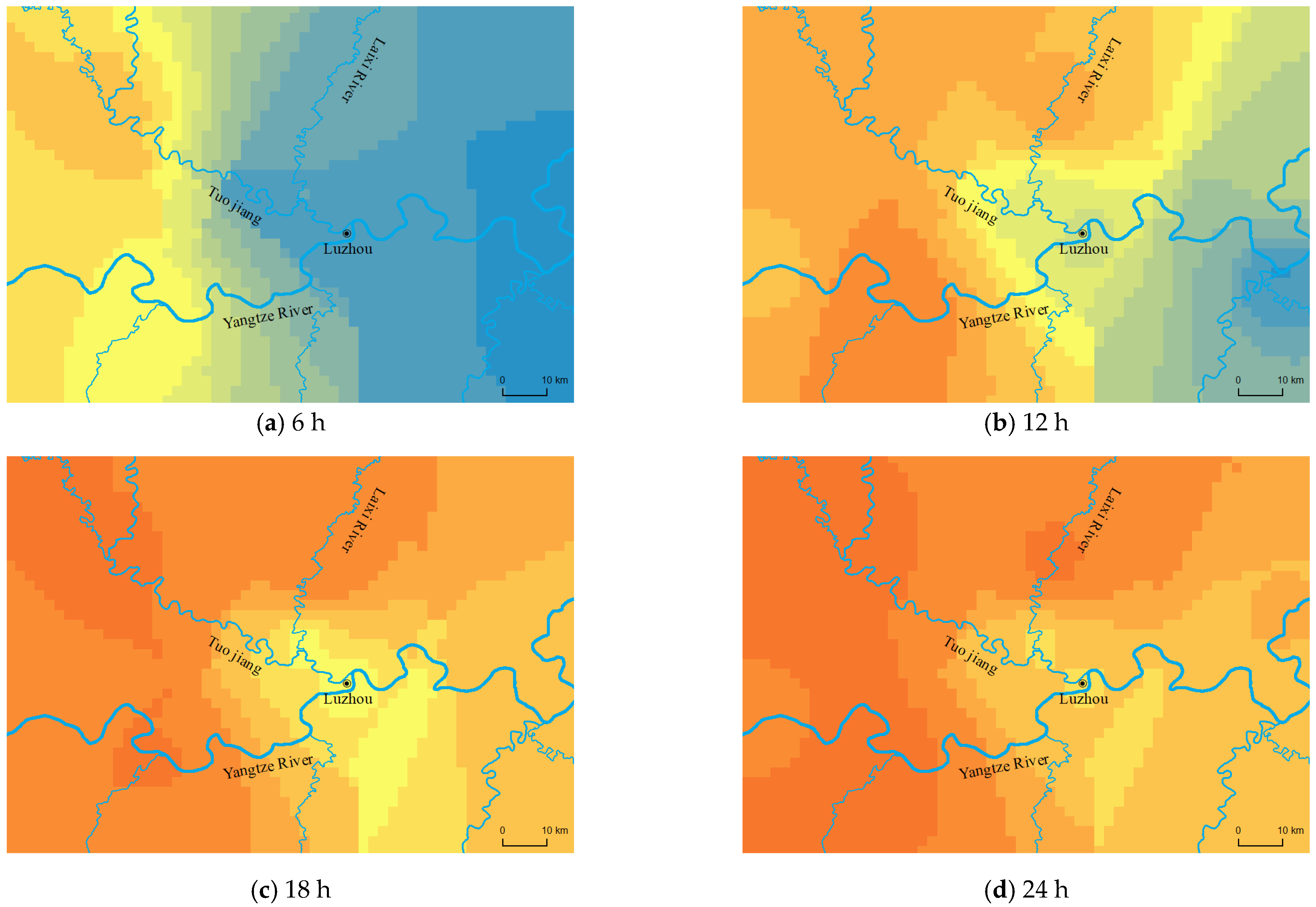
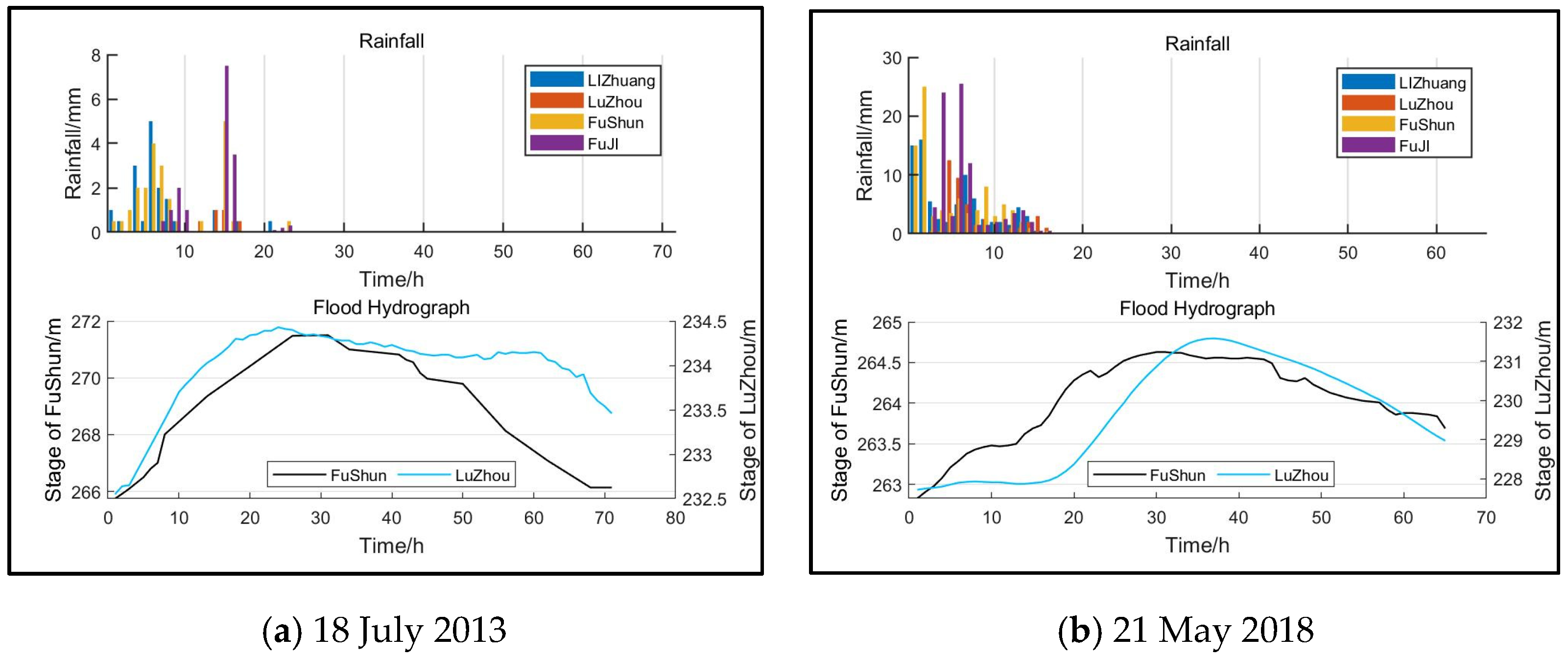

| Type of Rainfall | Spatial and Temporal Characteristics of Rainfall | Morphological Characteristics of Flood Processes | Characterization of Maximum and Minimum Flood Levels |
|---|---|---|---|
| Type I | The center of the storm moved upstream from the Tuogang River toward Luzhou | The flooding process is mostly of the single-peak type, and this type of rainfall mainly affects the flood level of the Tuojiang River. | The water level of the Tuo River fluctuated between 1 and 2 m due to rainfall, and the flood level of the Yangtze River remained stable. |
| Type II | The center of the storm moved from the upper reaches of the Yangtze River to Luzhou. | The flooding process was mostly a single peak, and this type of rainfall mainly affects the flood level of the Yangtze River. | The water level of the Tuo River is greatly influenced by the water level of the Yangtze River. The water level of the Tuo River fluctuated greatly, with an average change of about 4–8 m. |
| Type III | The center of the storm moved toward Luzhou from the upper Yangtze River and the upper Tuo River, respectively. | The flooding process was mostly a single peak. The rainfall process in the upper reaches of the Tuojian River overlapped with that in the upper reaches of the Yangtze River and moved towards Luzhou. | The direction of movement of the rainstorm center was consistent with the flood evolution direction of the Yangtze and Tuojian rivers, which was the most unfavorable rainfall process. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liu, Y.; Wang, J.; Ren, H.; Liu, S.; Hu, W. An Analysis of Rainfall Characteristics and Rainfall Flood Relationships in Cities along the Yangtze River Based on Machine Learning: A Case Study of Luzhou. Water 2023, 15, 3755. https://doi.org/10.3390/w15213755
Liu Y, Liu Y, Wang J, Ren H, Liu S, Hu W. An Analysis of Rainfall Characteristics and Rainfall Flood Relationships in Cities along the Yangtze River Based on Machine Learning: A Case Study of Luzhou. Water. 2023; 15(21):3755. https://doi.org/10.3390/w15213755
Chicago/Turabian StyleLiu, Yuanyuan, Yesen Liu, Jiazhuo Wang, Hancheng Ren, Shu Liu, and Wencai Hu. 2023. "An Analysis of Rainfall Characteristics and Rainfall Flood Relationships in Cities along the Yangtze River Based on Machine Learning: A Case Study of Luzhou" Water 15, no. 21: 3755. https://doi.org/10.3390/w15213755
APA StyleLiu, Y., Liu, Y., Wang, J., Ren, H., Liu, S., & Hu, W. (2023). An Analysis of Rainfall Characteristics and Rainfall Flood Relationships in Cities along the Yangtze River Based on Machine Learning: A Case Study of Luzhou. Water, 15(21), 3755. https://doi.org/10.3390/w15213755





