The Large Rivers of the Past in West Siberia: Unknown Hydrological Regimen
Abstract
:1. Introduction
- Calculating the discharge in a paleoriver from paleoclimatic reconstructions with water budget equations.
- Calculating the flow velocity and discharge in a paleoriver for a given level based on the cross-section geometry and the paleoriver slope and bed resistance to flow.
- Calculating the flow discharge of a certain return period based on hydraulic geometry of the paleochannel.
- 1 .
- Reduced air temperature
- 2 .
- Increased total precipitation
- 3 .
- Changed regimen of precipitation
- 4 .
- Increased extent of frozen ground
- 5 .
- Changed regimen of runoff
- 6 .
- Increased size of individual rains
- 7 .
- Increased frequency of storms
- 8 .
- Increased wetness of soil
- 9 .
- Changed vegetation cover.
2. Materials and Methods
2.1. General Information
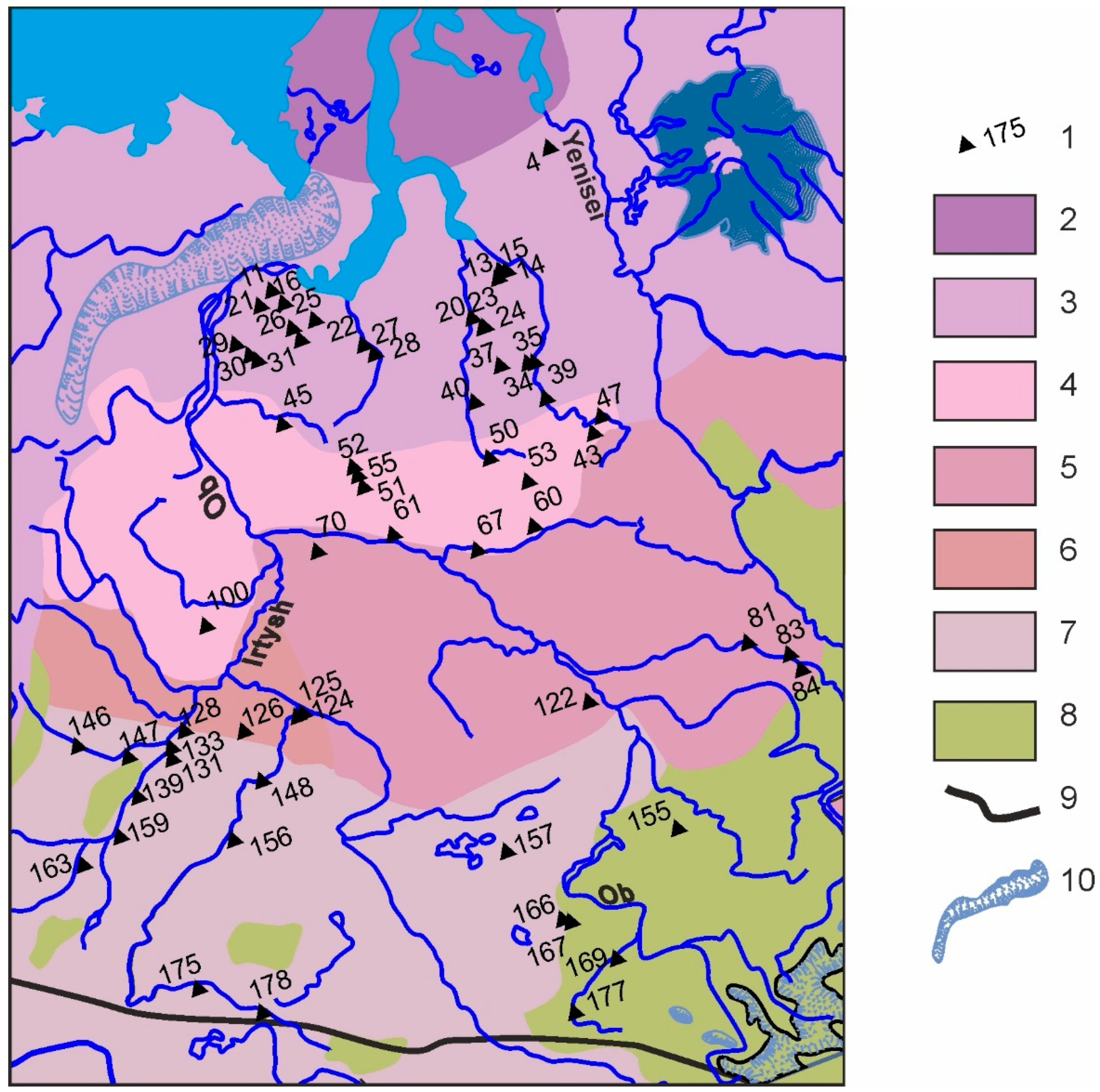
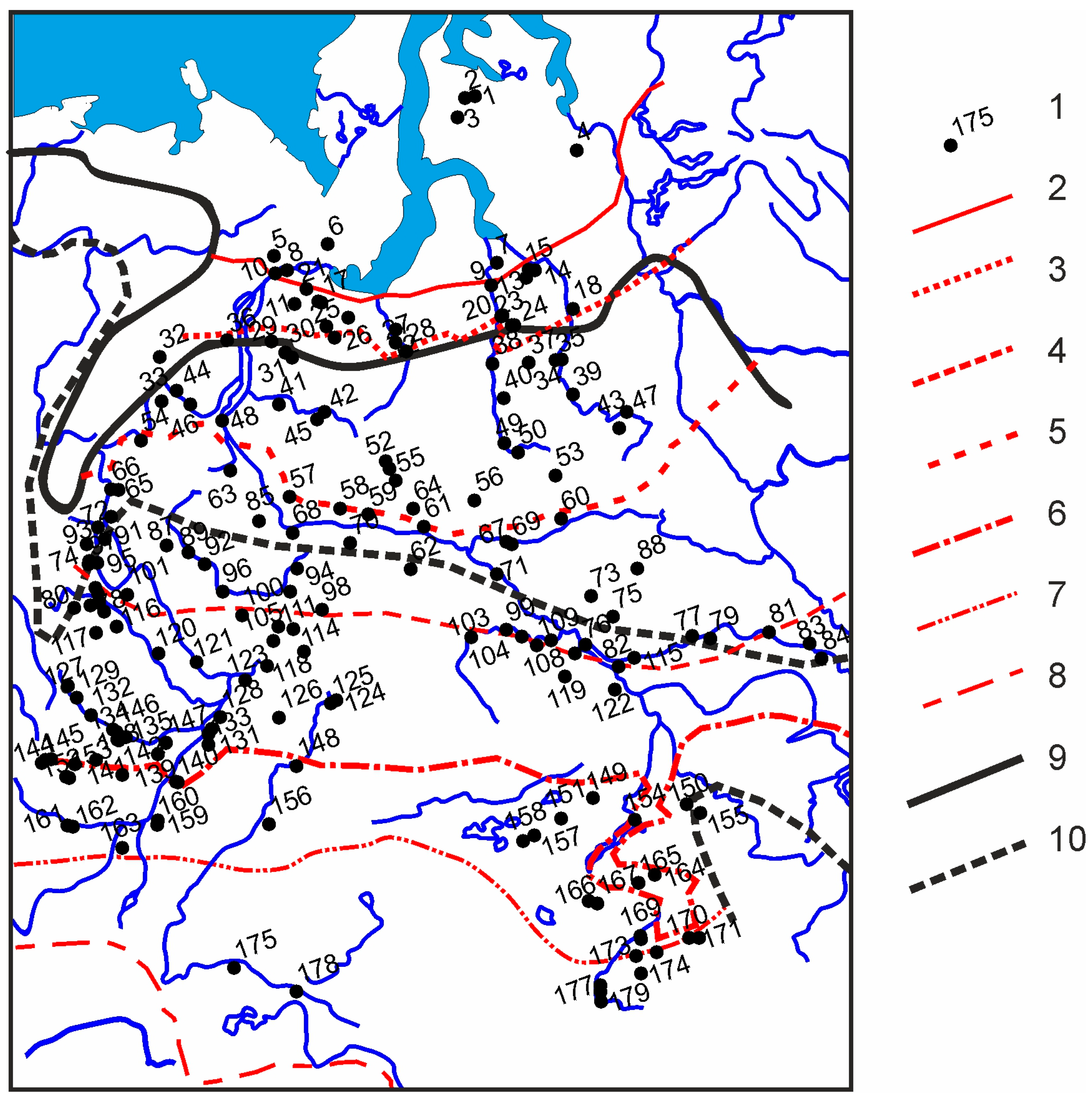
2.2. Large Ancient Meandering Rivers in the West Siberian Plain
2.3. The Modern Rivers of West Siberia
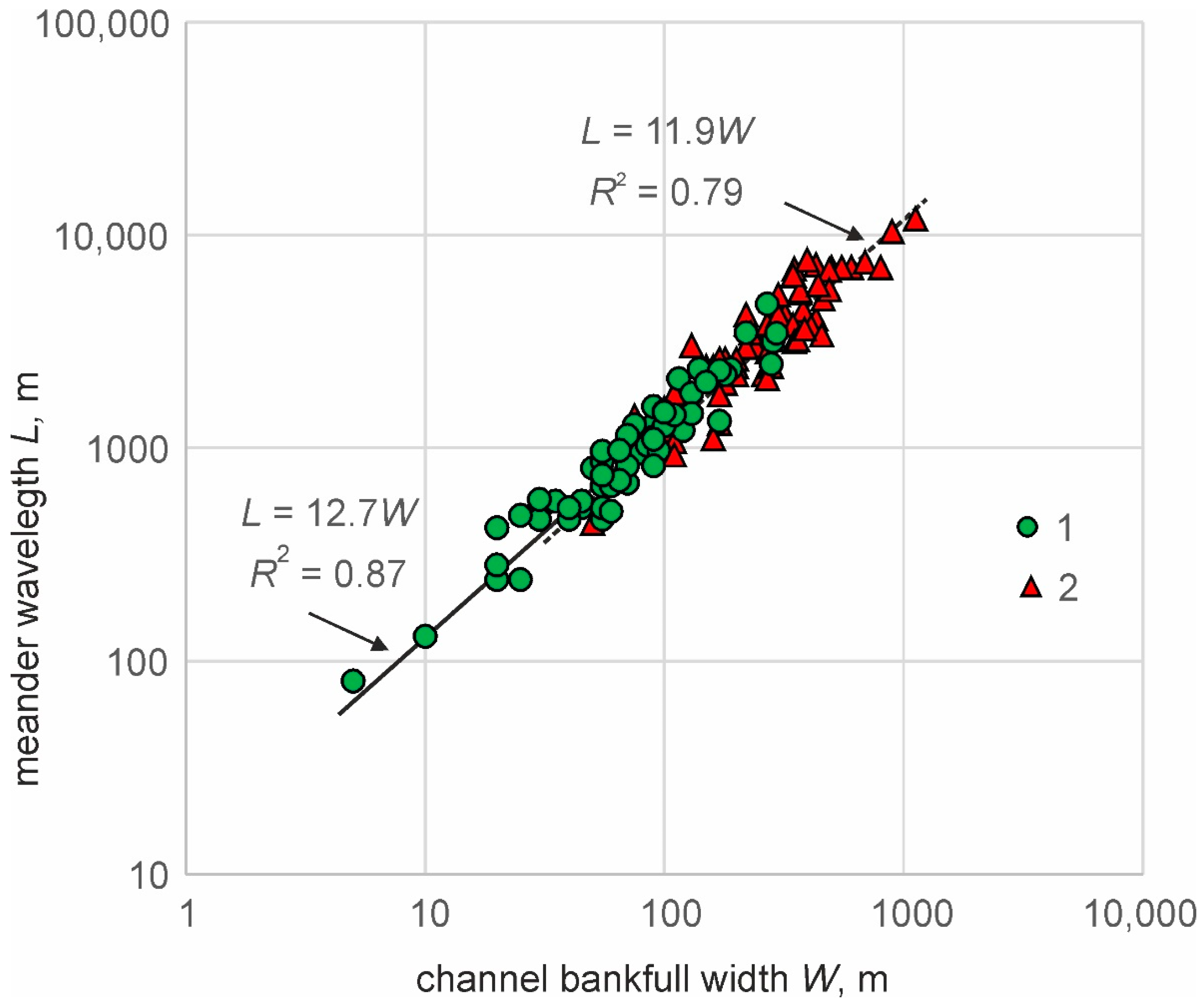
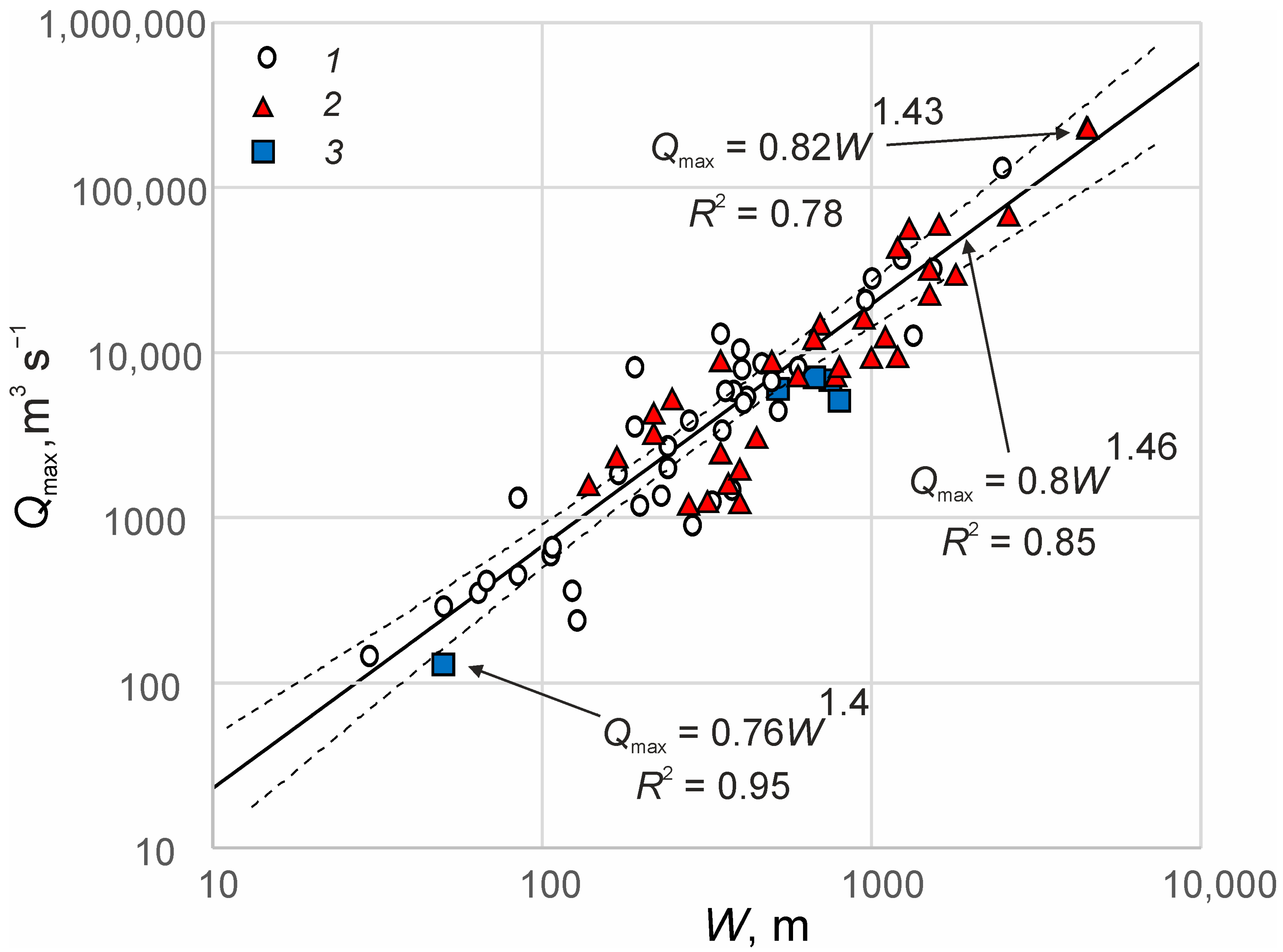
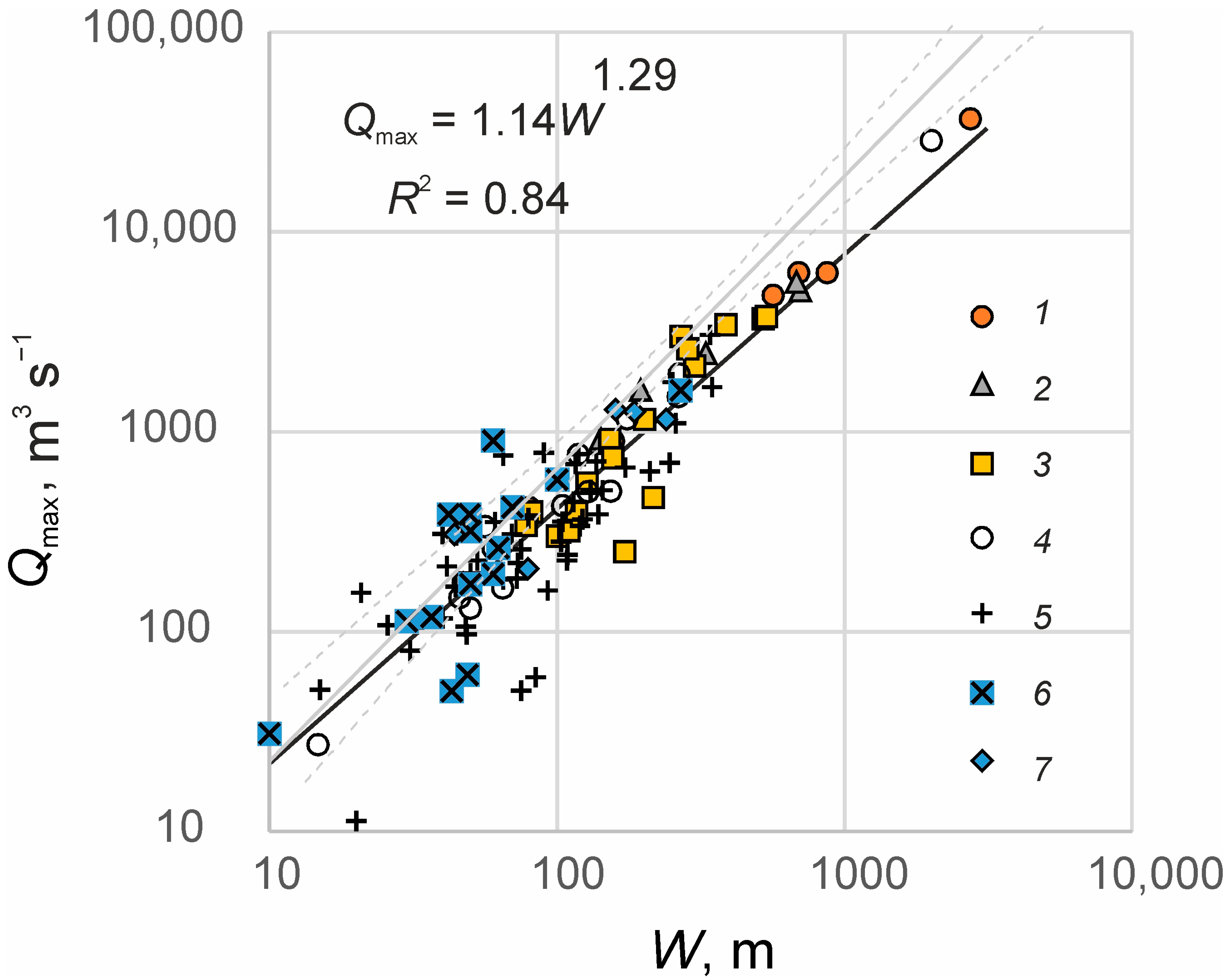
2.4. Relationships between River Channel Width and Discharge
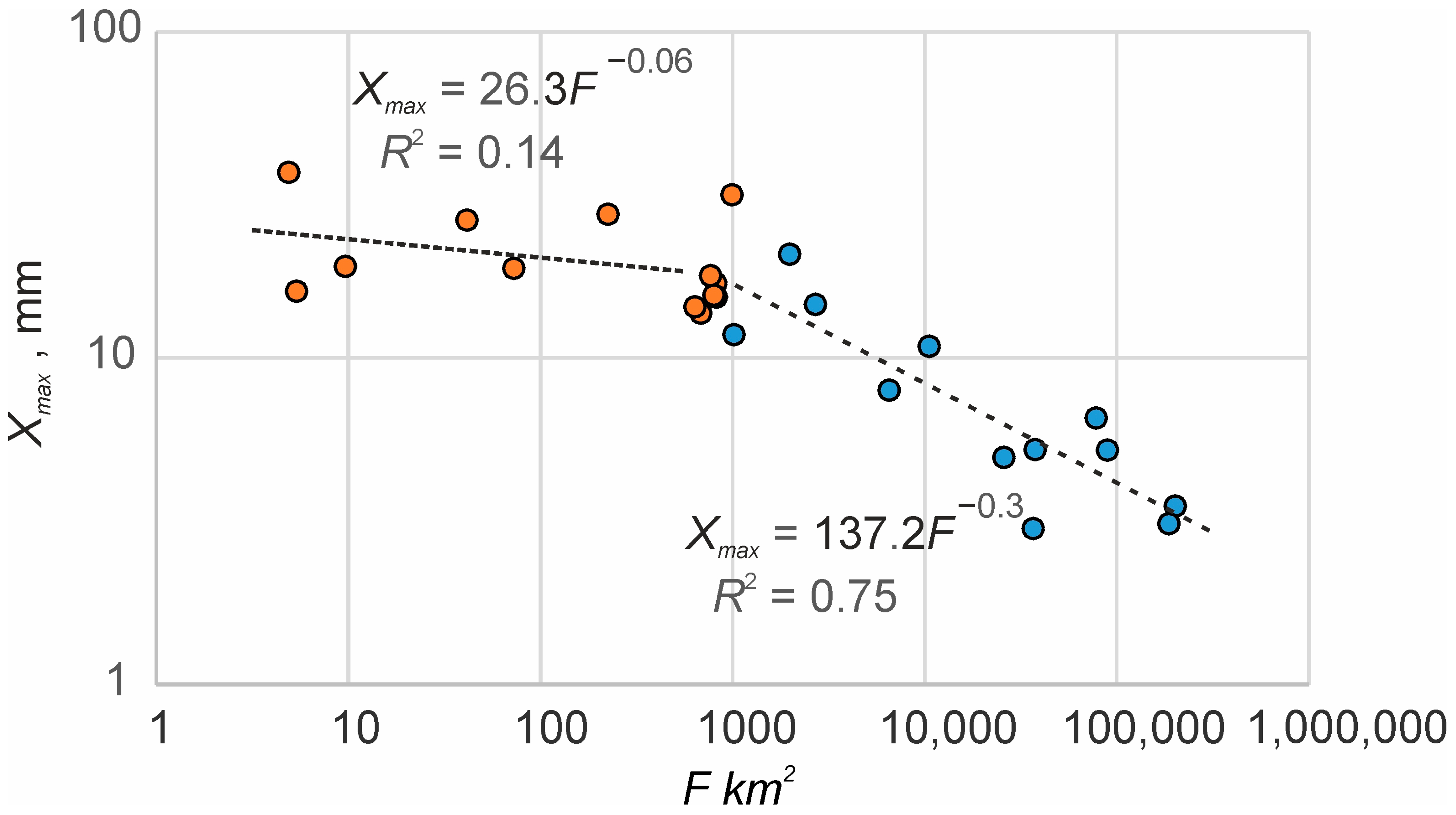
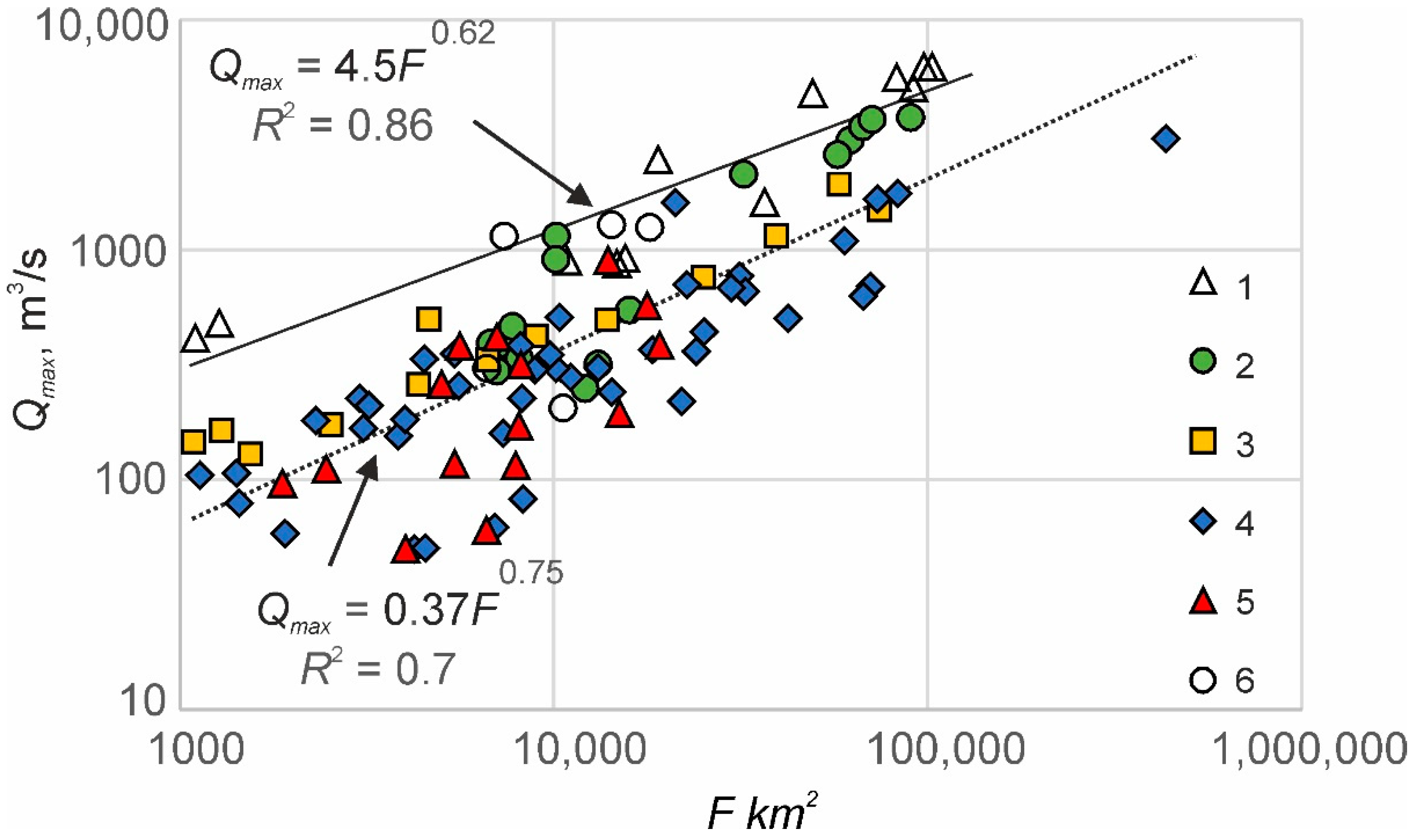
2.5. Relationships between Mean Maximum Discharge and Basin Area
3. Results
3.1. The Regime Equation between River Channel Width and Discharge
3.1.1. General Assumptions
3.1.2. Equation (2) for the West Siberian Plain
3.2. Relationships between River Channel Width and Contributing Basin Area for West Siberia
3.2.1. The Modern Rivers
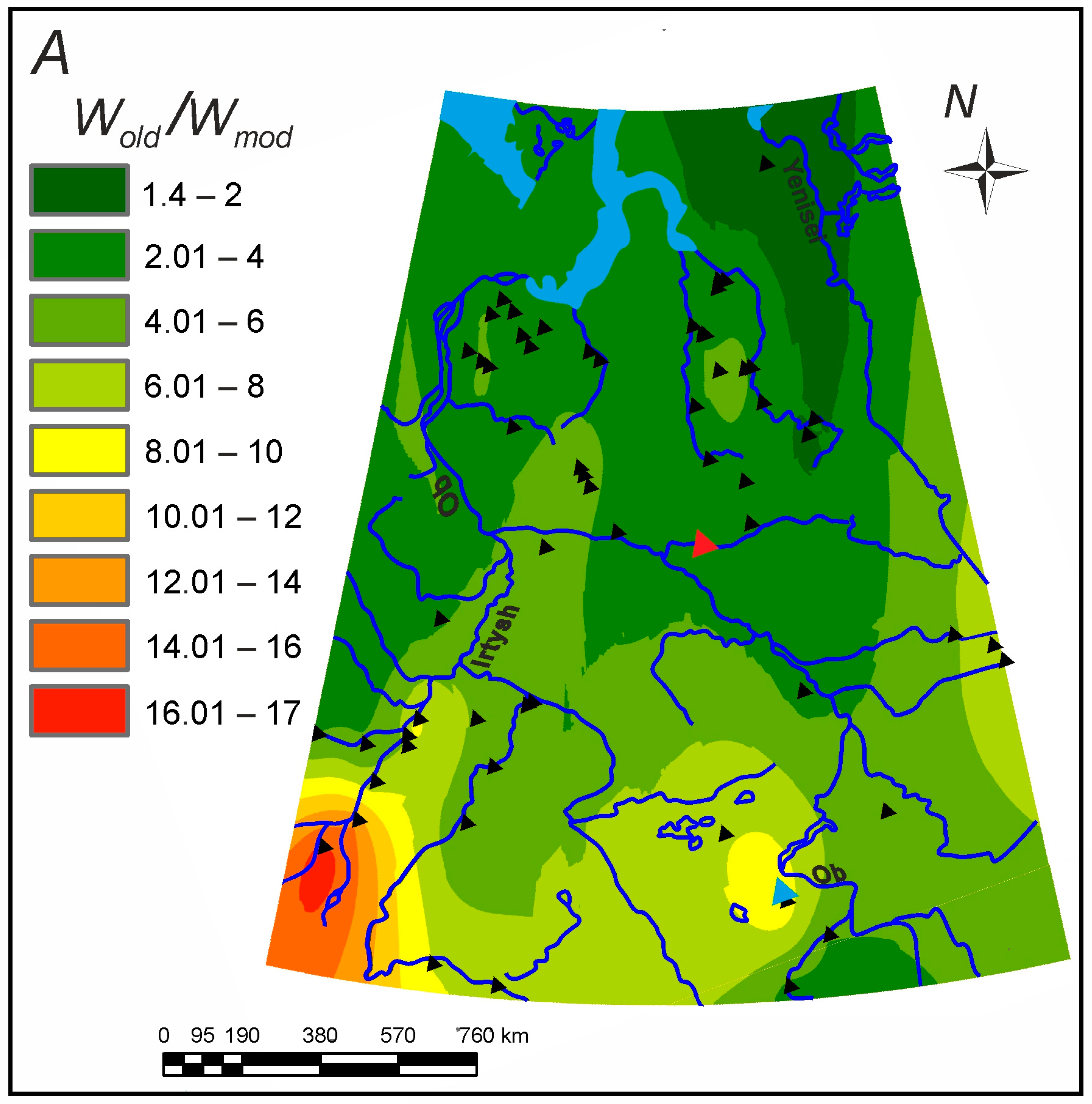
3.2.2. The Ancient Rivers
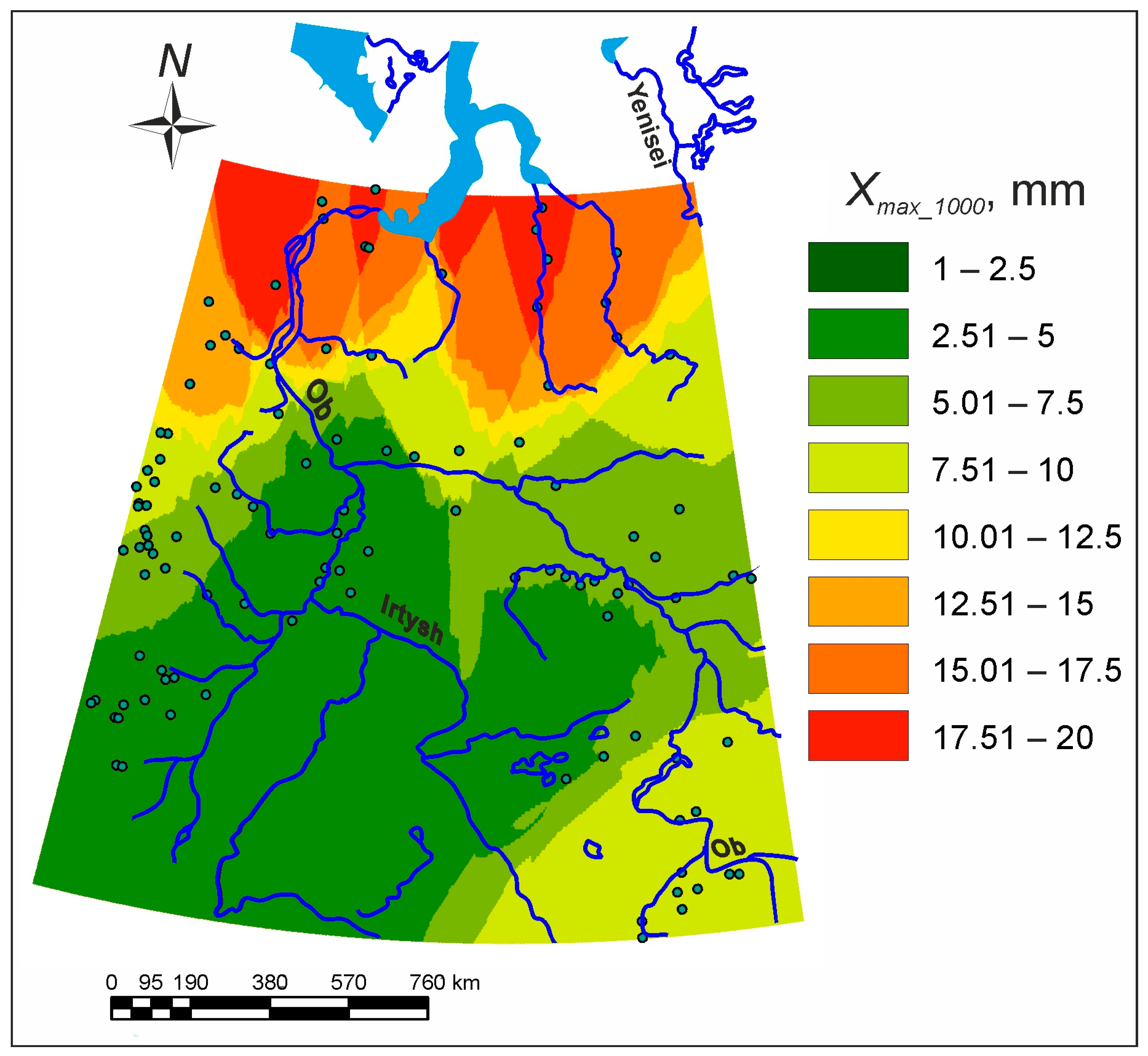
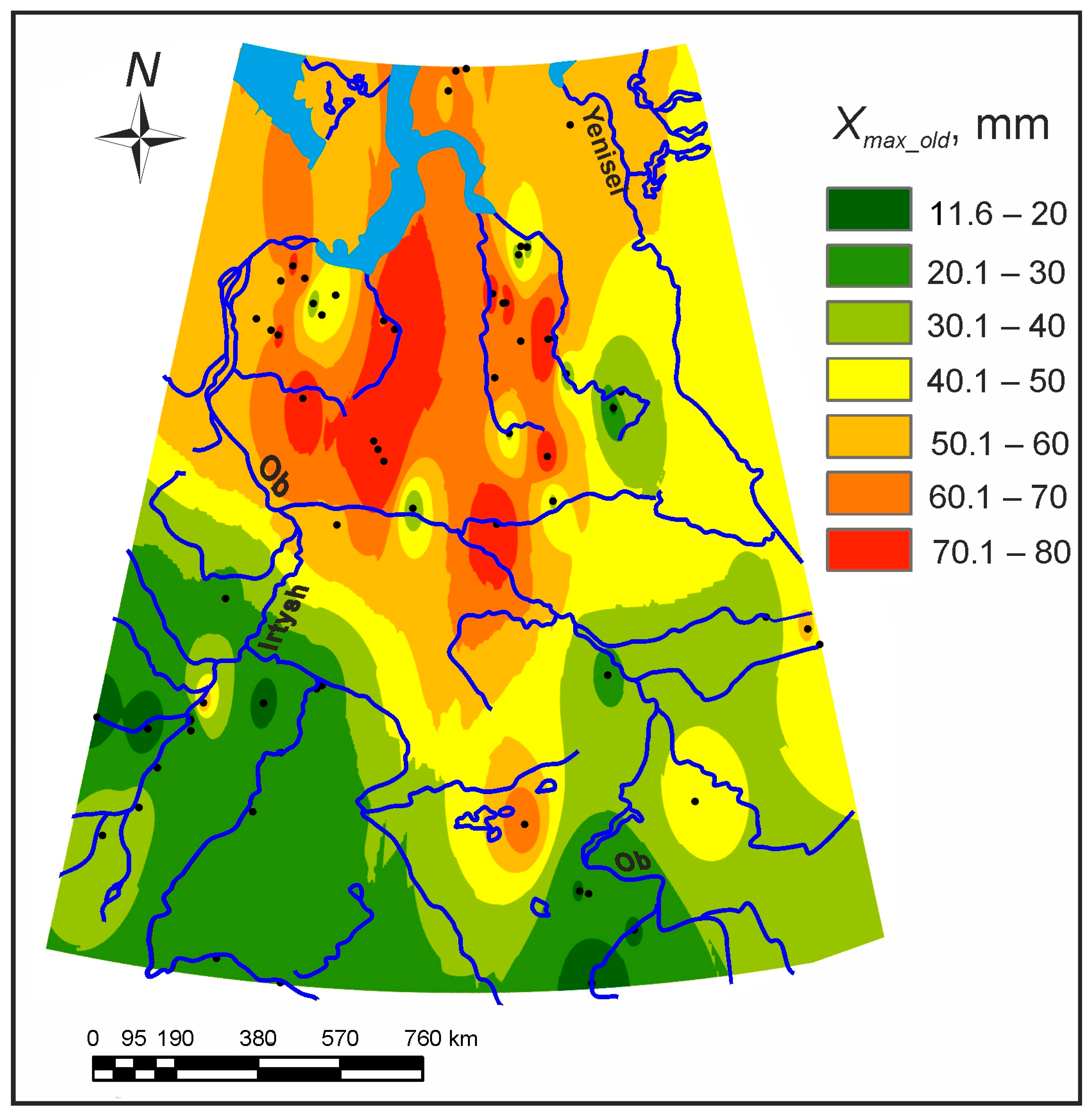
3.3. The Ancient Maximum Surface Runoff in West Siberia
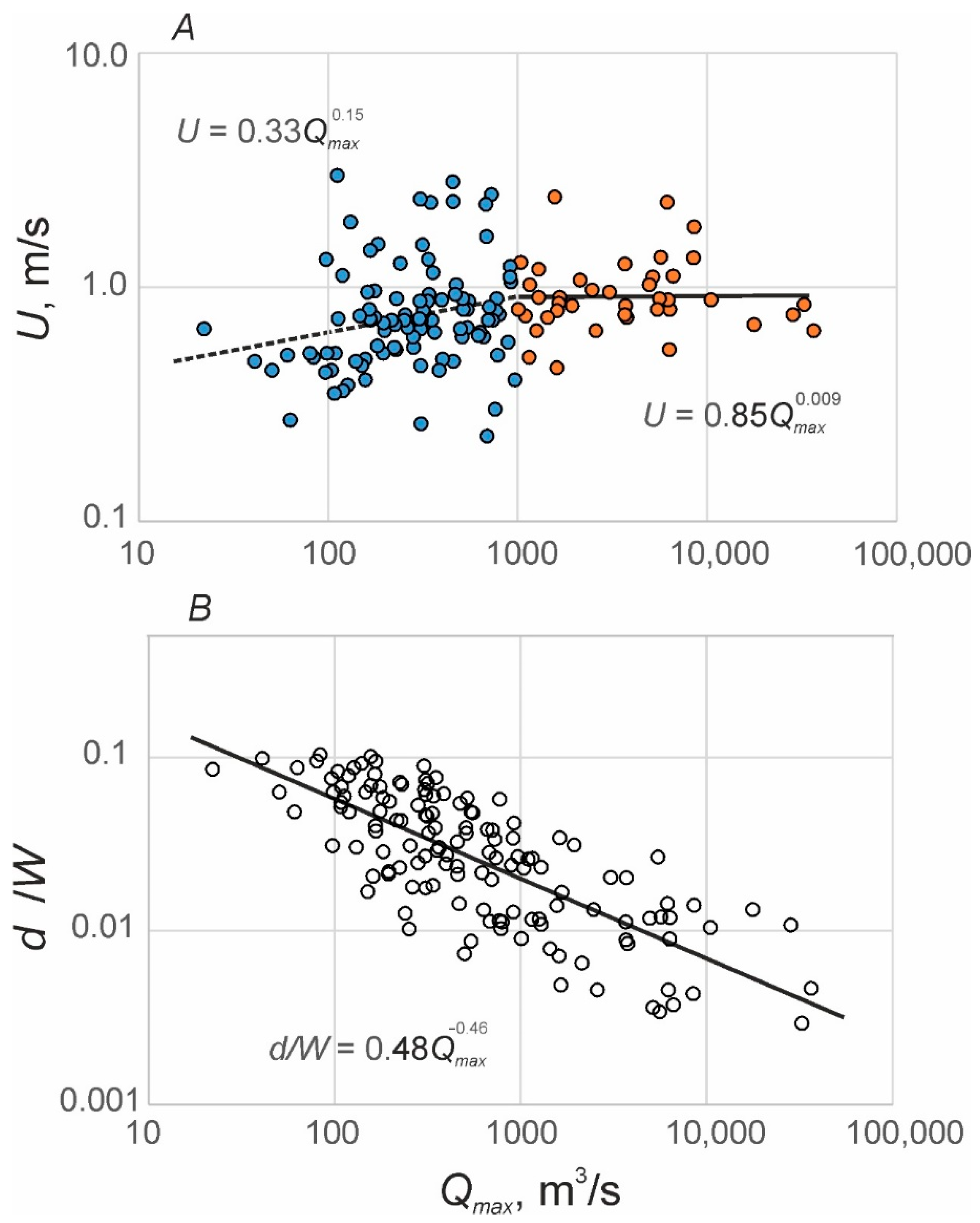
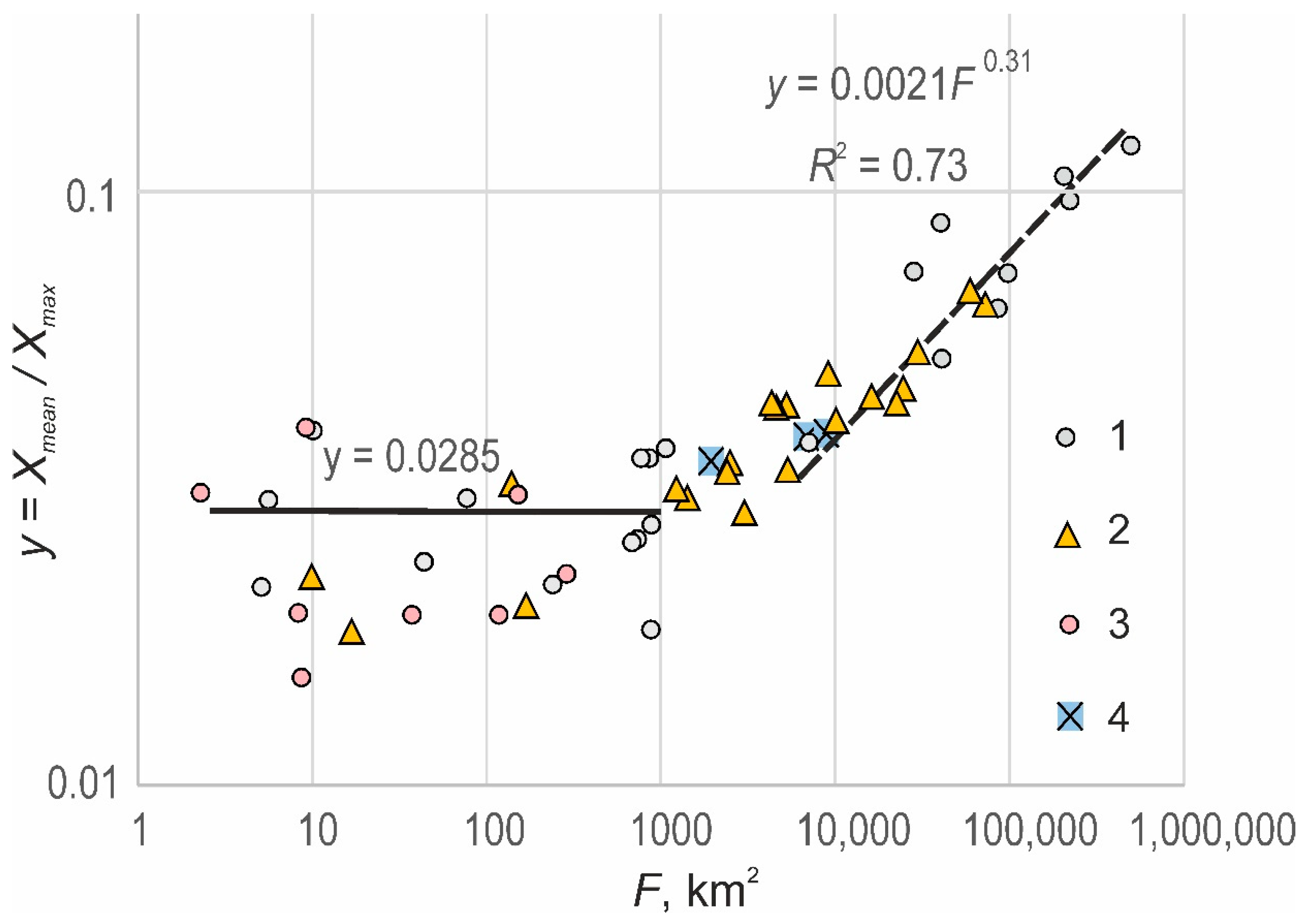
3.4. The Possibility to Estimate Mean Annual Flow Characteristics
4. Discussion
4.1. Parameters of the Relationship between Channel Width and Discharge in Downstream Direction
4.2. Estimations of the Mean Annual Flow Characteristics
5. Conclusions
- The West Siberian Plain is the territory with numerous remnants of large meandering paleochannels formed during the Late Pleniglacial/Late Glacial time. Their widths are 2–16 times greater than those of the modern rivers with the same basins.
- The relationship between river bankfull width and mean maximum discharge is relatively close for the rivers with very different regimes of water runoff and different ages. This observation allows for the use of the main hypothesis of the paleohydrology: the hydraulic geometry equations, designed for the modern rivers, are valid for the ancient rivers. The main limitation of this approach is the possible change in the morphological type of the river channel in time.
- The hydraulic geometry of the modern rivers of West Siberia was used to reconstruct the mean maximum discharges of the ancient rivers based on their ancient bankfull widths. Mean maximum discharges were recalculated to the mean flood surface runoff depth from a unit basin. The ancient daily water input intensity during snow thaw was 60–75 mm/day in the north of the plain occupied by tundra and sparse forest and 20–40 mm/day in the south (so-called periglacial steppe with sparse forest), with the mean value for the entire plain of 46 mm. This is more than five times larger than the modern value.
- Maximum daily water input intensity during snow thaw was recalculated into mean annual river runoff using assumptions of the paleohydrological analogy. The average annual depth of the river runoff was 430 mm for the Ob basin, except for floodplains and mountains. The total annual flow of the Ob into the ocean was about 1000 km3. This is three times the current flow from the same basin, so the river was a significant source of fresh water to the Arctic Ocean during the last period of deglaciation.
- Almost all factors listed by Dury [5] (further in italics) were important for the changes in hydrologic regime and flood runoff increase in West Siberia in the Late Pleniglacial. Data from analogous regions show that the winter air temperature reduced by 8–10 °C, but that of the snowmelt period (June–July) was approximately the same as the current one. Total precipitation increased, and the regimen of precipitation changed, with a shift to the winter months. The extent of frozen ground increased dramatically: the southern boundary of the continuous permafrost was then at about 50° northern latitude instead of the modern 66°N. The regimen of runoff changed along with the regime of precipitation, with high floods during the snow thaw period and nearly empty channels during all the rest of the year. Increased size of individual rains, increased frequency of storms and increased wetness of soil were probable but not proved. Vegetation cover changed within the area of boreal forest (taiga), largely replaced by sparse forest and tundra–steppe landscapes.
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Davis, W.M. La Seine, la Meuse et la Moselle. Ann. Géogr. 1895, 4, 25–49. [Google Scholar] [CrossRef] [Green Version]
- Dokuchaev, V.V. The Ways of the River Valleys Formation at the European Russia [Sposoby Obrazovaniya Rechnykh Dolin Evropeiskoi Rossii]; Tipografiya V. Dermakova: St. Petersburg, Russia, 1878; p. 221. (In Russian) [Google Scholar]
- Dury, G.H. Contribution to a general theory of meandering valleys. Am. J. Sci. 1954, 252, 193–224. [Google Scholar] [CrossRef]
- Dury, G.H. Principles of Underfit Streams; US Geological Survey Professional Paper; United States Government Printing Office: Washington, DC, USA, 1964; Volume 452, p. 67.
- Dury, G.H. Theoretical Implications of Underfit Streams; US Geological Survey Professional Paper; United States Government Printing Office: Washington, DC, USA, 1965; Volume 452, p. 43.
- Schumm, S.A. Quaternary paleohydrology. In The Quaternary of the United States; Wright, H.E., Jr., Frey, D.G., Eds.; Princeton University Press: Princeton, NY, USA, 1965; pp. 783–794. [Google Scholar]
- Schumm, S.A. River Adjustment to Altered Hydrologic Regimen—Murrumbidgee River and Paleochannels; US Geological Survey Professional Paper; United States Government Printing Office: Washington, DC, USA, 1968; Volume 598, p. 65.
- Volkov, I.A. On the recent past of the rivers Ishim and Nura [O nedavnem proshlom rek Ishima i Nury]. Tr. Lab. Aerometod. AN SSSR 1960, 9, 15–19. (In Russian) [Google Scholar]
- Volkov, I.A. Sledy moschnogo stoka v dolinakh rek yuga Zapadnoy Sibiri [Remnants of powerful flow in the valleys of the southern West Siberia]. Dokl. AN SSSR 1963, 151, 23–25. (In Russian) [Google Scholar]
- Maizels, J.K. Palaeovelocity and palaeodischarge determination for coarse gravel deposits. In Background to Paleohydrology: A Perspective; Gregory, K.J., Ed.; John Wiley and Sons: New York, NY, USA, 1983; pp. 101–139. [Google Scholar]
- Sidorchuk, A.Y.; Panin, A.V. Geomorphological approach to the river runoff evaluation in the geological past. Paper 4. Sediment particle size analysis for estimation of paleoflow velocities. Geomorfologiya 2018, 3, 40–51. (In Russian) [Google Scholar]
- Rotnicki, K. Retrodiction of palaeodischarges of meandering and sinuous rivers and its palaeoclimatic implications. In Temperate Palaeohydrology; John Wiley and Sons: Chichester, UK, 1991; pp. 431–470. [Google Scholar]
- Popov, D.; Markovic, S.B.; Strbac, D. Generations of meanders in Serbian part of Tisa valley. J. Geogr. Inst. 2008, 58, 29–41. [Google Scholar] [CrossRef]
- Sidorchuk, A.Y.; Borisova, O.K.; Panin, A.V. Fluvial response to the Late Valdai/Holocene environmental change on the East European Plain. Glob. Planet. Chang. 2001, 28, 303–318. [Google Scholar] [CrossRef]
- Sidorchuk, A.Y.; Panin, A.V.; Borisova, O.K. The Late Glacial and the Holocene palaeohydrology of the Northern Eurasia. In Palaeohydrology: Understanding Global Change; Gregory, K.J., Benito, G., Eds.; Wiley and Sons: Chichester, UK, 2003; pp. 61–76. [Google Scholar]
- Sidorchuk, A.Y.; Panin, A.V.; Borisova, O.K. Climate-induced changes in surface runoff on the north-Eurasian plains during the Late Glacial and Holocene. Water Resour. 2008, 35, 386–396. [Google Scholar] [CrossRef]
- Sidorchuk, A.Y.; Panin, A.V.; Borisova, O.K. Morphology of river channels and surface runoff in the Volga River basin (East European Plain) during the Late Glacial period. Geomorphology 2009, 113, 137–157. [Google Scholar] [CrossRef]
- Sidorchuk, A.Y.; Panin, A.V.; Borisova, O.K. Surface runoff to the Black Sea from the East European Plain during Last Glacial Maximum–Late Glacial time. In Geology and Geoarchaeology of the Black Sea Region: Beyond the Flood Hypothesis; Buynevich, I., Yanko-Hombach, V., Gilbert, A.S., Martin, R.E., Eds.; Geological Society of America: Boulder, CO, USA, 2011; Volume 473, pp. 1–25. [Google Scholar]
- Leigh, D.S.; Feeney, T.P. Paleochannels indicating wet climate and lack of response to lower sea level, southeast Georgia. Geology 1995, 23, 687–690. [Google Scholar] [CrossRef]
- Page, K.J.; Kemp, J.; Nanson, G.C. Late Quaternary evolution of Riverine Plain paleochannels, Southeastern Australia. Aust. J. Earth Sci. 2009, 56, 19–33. [Google Scholar] [CrossRef]
- Borodko, A.V. (Ed.) National Atlas of Russia (Maps) [Natsional’nyi Atlas Rossii (Karty)]; Roskartografiya: Moscow, Russia, 2004; Volume 2. [Google Scholar]
- Velichko, A.A. (Ed.) Dynamics of Landscape Components and Internal Marine Basins of Northern Eurasia over the Past 130,000 Years: Atlas-Monograph. Part 2. Development of Landscapes and Climate of Northern Eurasia. Late Pleistocene—Holocene—Forecast Elements [Dinamika Landshaftnykh Komponentov i Vnutrennikh Morskikh Basseynov Severnoy Yevrazii za Posledniye 130 000 Let: Atlas-Monografiya. Ch. 2. Razvitiye Landshaftov i Klimata Severnoy Yevrazii. Pozdniy Pleystotsen—Golotsen—Elementy Prognoza]; GEOS: Moscow, Russia, 2002; p. 231. (In Russian) [Google Scholar]
- Vandenberghe, J.; Sidorchuk, A. Large palaeomeanders in Europe: Distribution, formation process, age, environments and significance. In Palaeohydrology. Geography of the Physical Environment; Springer: Cham, Switzerland, 2019; pp. 169–186. [Google Scholar]
- Zykina, V.S.; Volkov, I.A.; Dergacheva, M.I. Upper Quaternary Deposits and Fossil Soils of the Novosibirsk Ob Region [Verkhnechetvertichnyye Otlozheniya i Iskopayemyye Pochvy Novosibirskogo Priob’ya]; Nauka: Moscow, Russia, 1981; p. 203. (In Russian) [Google Scholar]
- Sidorchuk, A.Y.; Panin, A.V.; Borisova, O.K. Late glacial palaeochannels in West Siberia. Izv. Akad. Nauk. Seriya Geogr. 2008, 2, 67–75. (In Russian) [Google Scholar]
- Automated Information System for State Monitoring of Water Bodies (AIS GMVO) [Avtomatizirovannaya Informatsionnaya Sistema Gosudarstvennogo Monitoringa Vodnykh Ob”yektov (AIS GMVO)]. Available online: https://gmvo.skniivh.ru/ (accessed on 22 November 2022).
- Hydrological Yearbook Volume 6 of the Kara Sea Basin. Issue 0–9. [Gidrologicheskiy Yezhegodnik Tom 6 Basseyn Karskogo Morya. Vyp. 0–9]; Gidrometeoizdat: Leningrad, Russia, 1949–1986. (In Russian)
- Global Runoff Data Centre. Available online: https://www.bafg.de/GRDC/EN/Home/homepage_node.html (accessed on 22 November 2022).
- Leopold, L.B.; Maddock, T. The Hydraulic Geometry of Stream Channels and Some Physiographic Implications; US Geological Survey Professional Paper; United States Government Printing Office: Washington, DC, USA, 1953; Volume 252, p. 57.
- Velikanov, M.A. The Dynamics of the Open Flow. V. 2. Sediment and the Channel [Dinamika Ruslovyh Potokov. T. 2: Nanosy i Ruslo]; Gostekhizdat: Moscow, Russia, 1955; p. 323. (In Russian) [Google Scholar]
- Blom, A.; Arkesteijn, L.; Chavarrias Borras, V.; Viparelli, E. The equilibrium alluvial river under variable flow and its channel-forming discharge. J. Geophys. Res. Earth Surf. 2017, 122, 1924–1948. [Google Scholar] [CrossRef] [Green Version]
- Wolman, M.G.; Miller, J.P. Magnitude and frequency of forces in geomorphic processes. J. Geol. 1960, 68, 54–74. [Google Scholar] [CrossRef]
- Perdios, A.; Langousis, A. Revisiting the statistical scaling of annual discharge maxima at daily resolution with respect to the basin size in the light of rainfall climatology. Water 2020, 12, 610. [Google Scholar] [CrossRef] [Green Version]
- Novikov, S.M. (Ed.) Hydrology of the Wetlands of the Permafrost Zone of Western Siberia [Gidrologiya Zabolochennykh Territoriy Zony Mnogoletney Merzloty Zapadnoy Sibiri]; VVM: St. Petersburg, Russia, 2009; p. 536. (In Russian) [Google Scholar]
- Sidorchuk, A.Y.; Panin, A.V.; Borisova, O.K. Geomorphological approaches to assessing the value of river flow in the geological past. Paper 5. Comparative analysis of the results obtained by different methods [Geomorfologicheskiye podkhody k otsenke velichiny rechnogo stoka v geologicheskom proshlom. Statya 5. Sravnitel’nyi analiz rezul’tatov, poluchennykh raznymi metodami]. Geomorfologiya 2019, 1, 66–79. (In Russian) [Google Scholar]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Velichko, A.A. Natural Process in the Pleistocene [Prirodnyi Protsess v Pleystotsene]; Nauka: Moscow, Russia, 1973; p. 256. (In Russian) [Google Scholar]
- Sidorchuk, A.Y.; Borisova, O.K. Method of paleogeographical analogues in paleohydrological reconstructions. Quat. Int. 2000, 72, 95–106. [Google Scholar] [CrossRef]
- Chytrý, M.; Horsák, M.; Danihelka, J.; Ermakov, N.; German, D.A.; Hájek, M.; Hájková, P.; Kočí, M.; Kubešová, S.; Lustyk, P.; et al. A modern analogue of the Pleistocene steppe-tundra ecosystem in southern Siberia. Boreas 2019, 48, 36–56. [Google Scholar] [CrossRef] [Green Version]
- Gurina, A.A.; Dudko, R.Y.; Prosvirov, A.S.; Tshernyshev, S.E.; Legalov, A.A.; Zinovyev, E.V. Coleoptera assemblages from the Quaternary deposits of Kizikha river, the southernmost late Pleistocene insects of the West Siberian Plain. Invert. Zool. 2019, 16, 165–182. [Google Scholar] [CrossRef]
- Baker, V.R.; Benito, G.; Rudoy, A.N. Paleohydrology of late Pleistocene superflooding, Altay Mountains, Siberia. Science 1993, 259, 348–350. [Google Scholar] [CrossRef] [PubMed]
- Bohorquez, P.; Carling, P.A.; Herget, J. Dynamic simulation of catastrophic late Pleistocene glacial-lake drainage, Altai Mountains, central Asia. Int. Geol. Rev. 2016, 58, 1795–1817. [Google Scholar] [CrossRef]
- Inglis, C.C. Meanders and their bearing on river training. Inst. Civ. Eng. Mar. Waterways Eng. Div. 1947, 7, 3–54. [Google Scholar]
- Leopold, L.B.; Wolman, M.G. River Channel Patterns: Braided, Meandering and Straight; US Geological Survey Professional Paper; United States Government Printing Office: Washington, DC, USA, 1957; Volume 282-B.
- Leopold, L.B.; Langbein, W.B. The Concept of Entropy in Landscape Evolution; US Geological Survey Professional Paper; United States Government Printing Office: Washington, DC, USA, 1962; Volume 500-A.
- Nachtergaele, J.; Poesen, J.; Sidorchuk, A.; Torri, D. Prediction of concentrated flow width in ephemeral gully channels. Hydrol. Process. 2002, 16, 1935–1953. [Google Scholar] [CrossRef]
- Schumm, S.A. The Shape of Alluvial Channels in Relation to Sediment Type; US Geological Survey Professional Paper; United States Government Printing Office: Washington, DC, USA, 1960; Volume 353 B, pp. 17–30.
- Schumm, S.A. Sinuosity of Alluvial Rivers in the Great Plains. Bull. Geol. Soc. Am. 1963, 74, 1089–1100. [Google Scholar] [CrossRef]
- Sidorchuk, A.Y.; Panin, A.V. Geomorphological approach to the river runoff evaluation in the geological past. Paper 1. Regime equations. [Geomorfologicheskiye podkhody k otsenke velichiny rechnogo stoka v geologicheskom proshlom (st. 1. morfometricheskiye zavisimosti)]. Geomorfologiya 2017, 1, 55–65. (In Russian) [Google Scholar]
- Sidorchuk, A.Y.; Ukraintsev, V.Y.; Panin, A.V. Estimating annual Volga runoff in the Late Glacial epoch from the size of river paleochannels. Water Resour. 2021, 48, 864–876. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sidorchuk, A. The Large Rivers of the Past in West Siberia: Unknown Hydrological Regimen. Water 2023, 15, 258. https://doi.org/10.3390/w15020258
Sidorchuk A. The Large Rivers of the Past in West Siberia: Unknown Hydrological Regimen. Water. 2023; 15(2):258. https://doi.org/10.3390/w15020258
Chicago/Turabian StyleSidorchuk, Aleksey. 2023. "The Large Rivers of the Past in West Siberia: Unknown Hydrological Regimen" Water 15, no. 2: 258. https://doi.org/10.3390/w15020258
APA StyleSidorchuk, A. (2023). The Large Rivers of the Past in West Siberia: Unknown Hydrological Regimen. Water, 15(2), 258. https://doi.org/10.3390/w15020258





