Novel Ocean Wave Height and Energy Spectrum Forecasting Approaches: An Application of Semi-Analytical and Machine Learning Models
Abstract
:1. Introduction
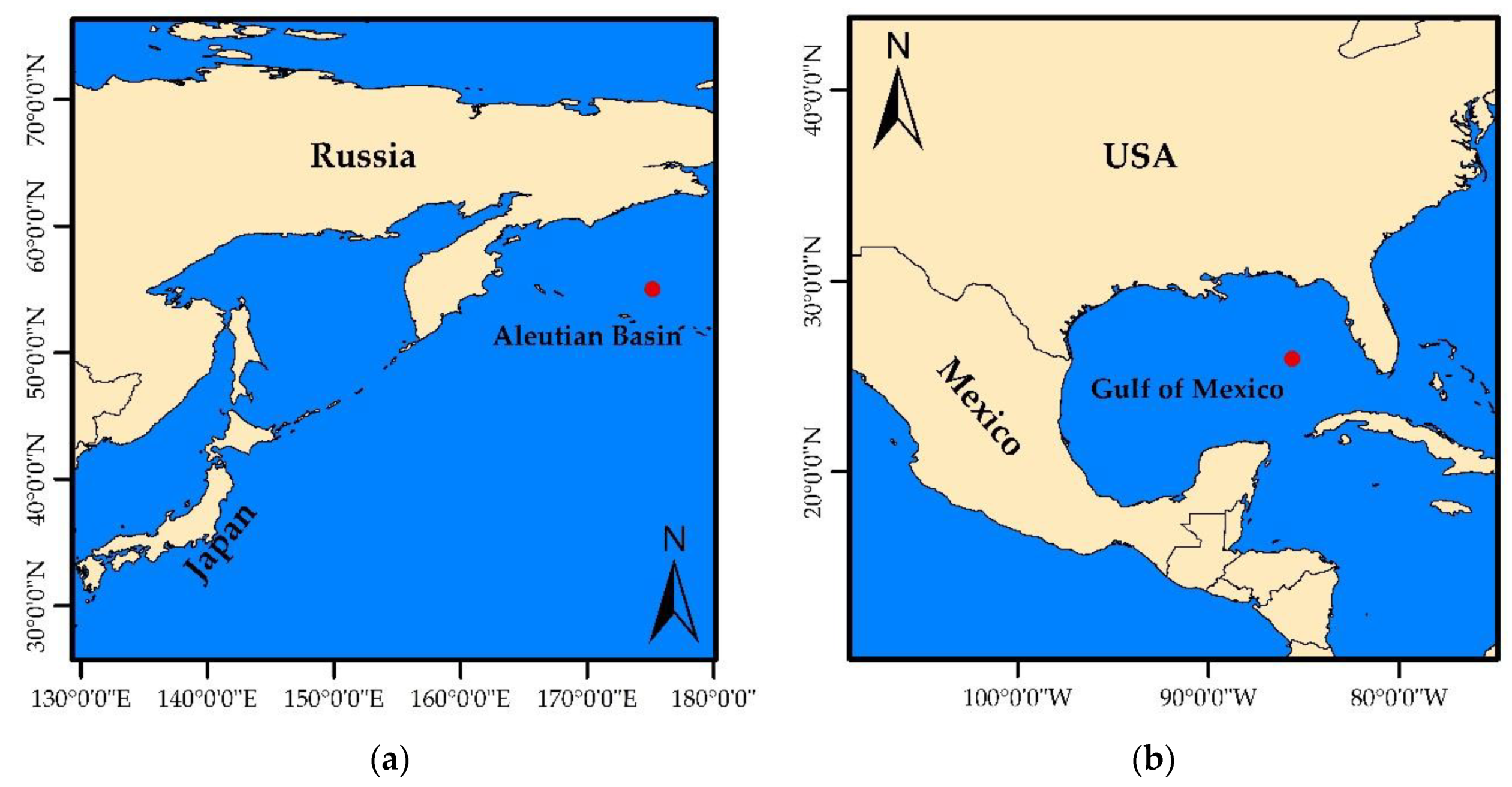
2. Study Area and Dataset
3. Materials and Methods
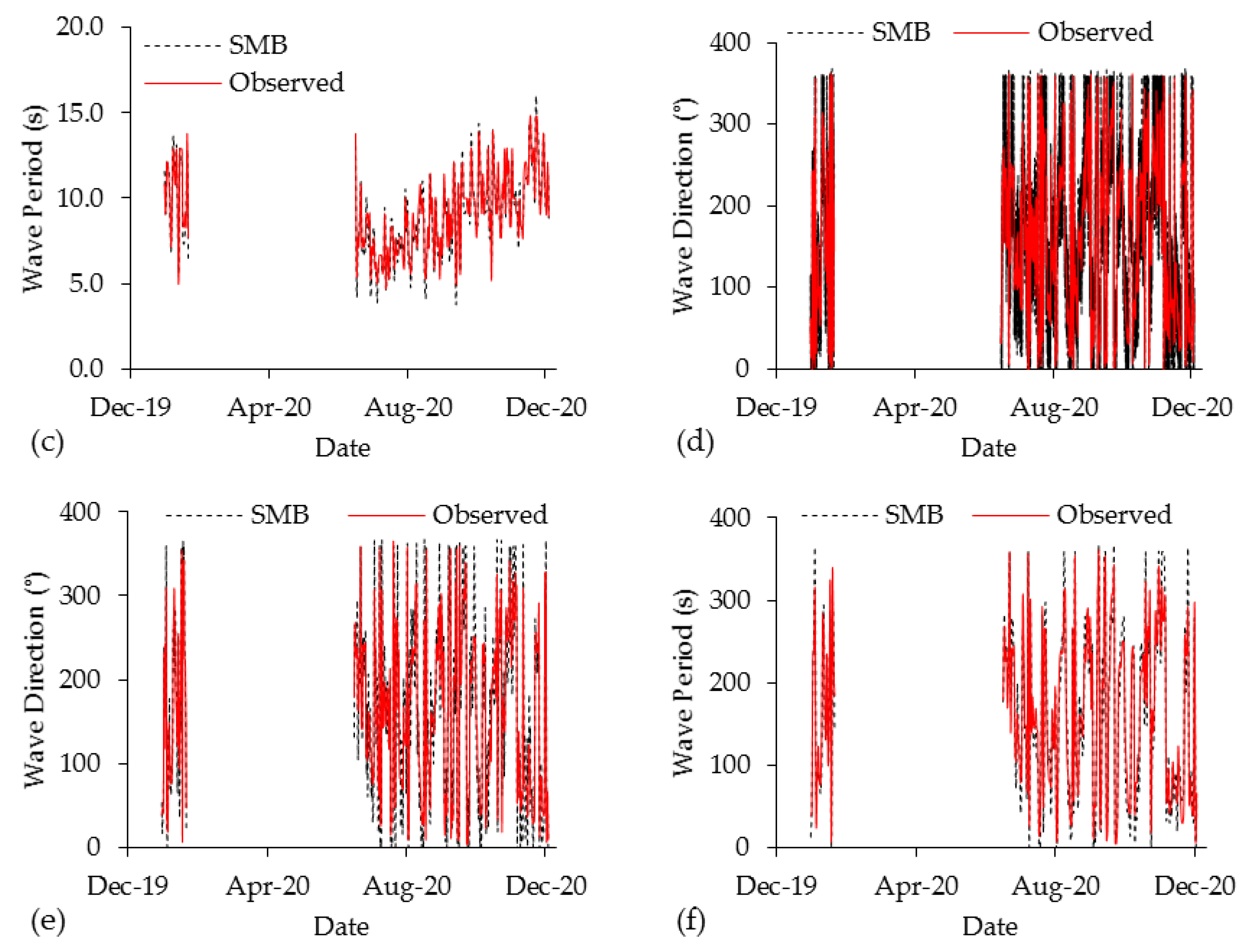
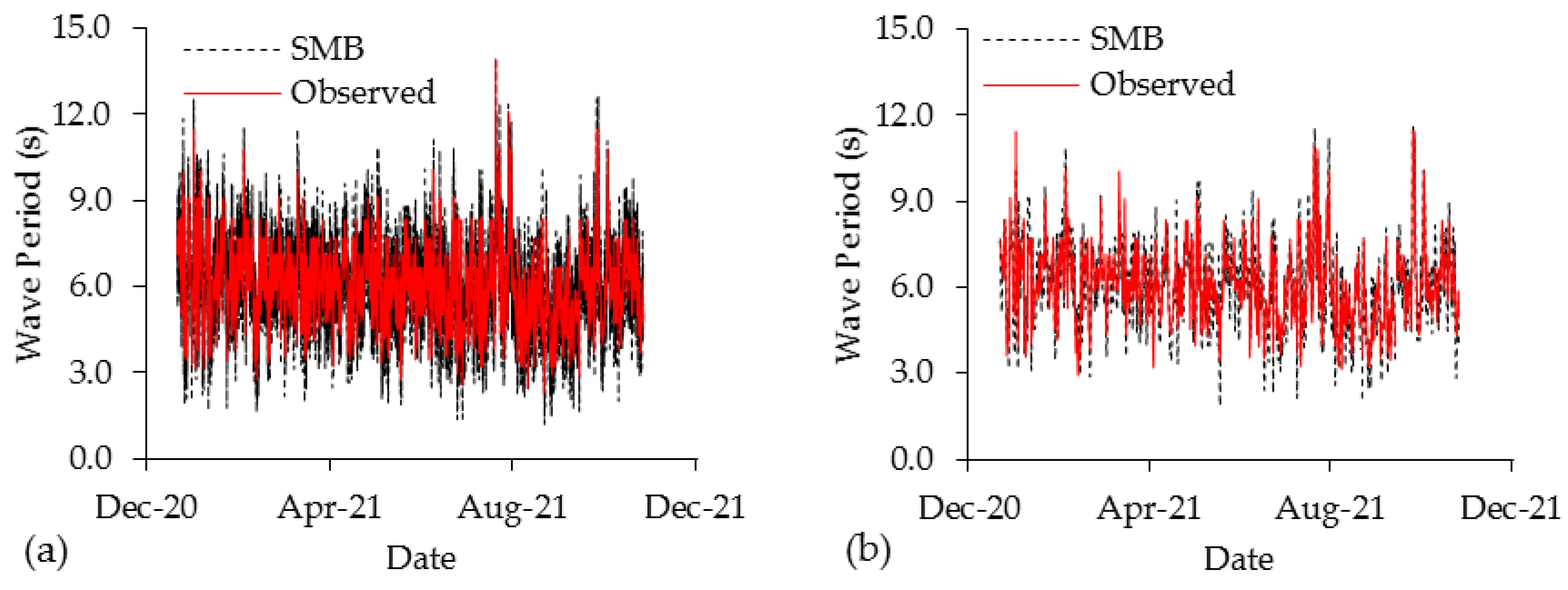
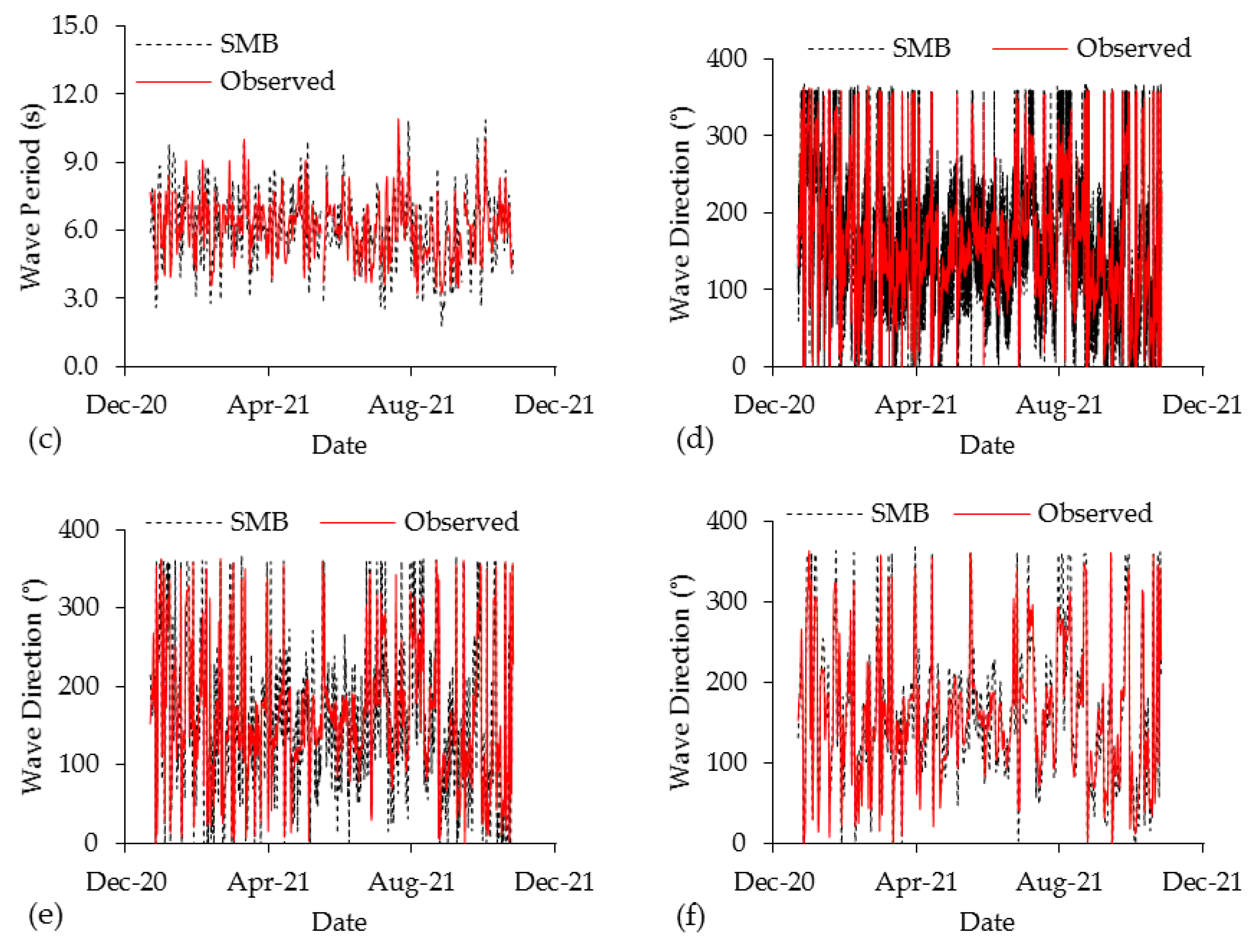
3.1. Sverdrup Munk Bretschneider
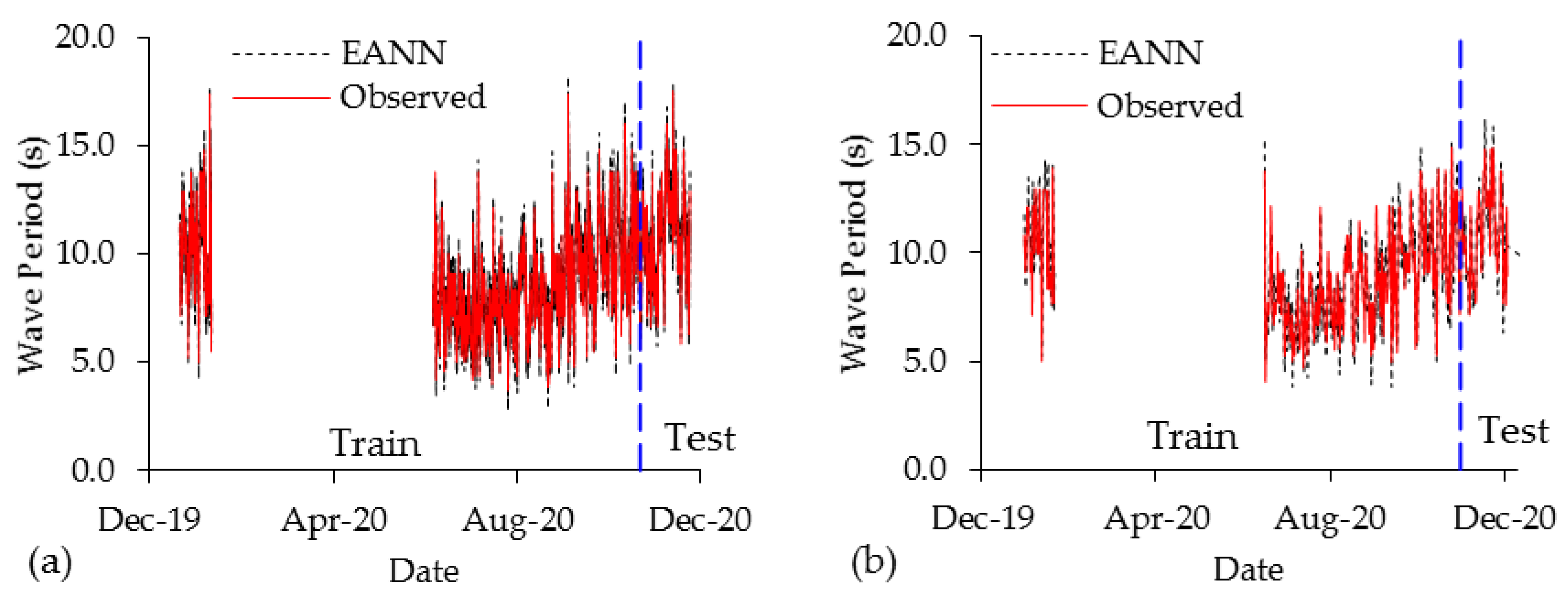
3.2. Emotional Artificial Neural Network
3.3. Wavelet Artificial Neural Network
- The input data are used for training and validating the network;
- b—Under the specified conditions, the mother wavelet is transformed into the daughter wavelet by applying the transfer coefficients and the appropriate scale;
- Types of child wavelets replace the activation functions of the neurons in the hidden layer of the neural network;
- The created violet neural network is trained with the training-related dataset.
- The overall performance of the wavelet network is analyzed by examining the method for estimating the precision of measurement data, and with the part of the network’s approval, the training phase is concluded. Otherwise, the steps leading up to the optimal state are evaluated. It has been demonstrated as an example of a three-layer network structure with an input layer, a hidden layer, and an output layer. Meanwhile, the Levenberg–Marquardt algorithm was applied to train the model.
3.4. Wave Energy Density Spectrum
3.5. Efficiency Criteria
4. Results and Discussion
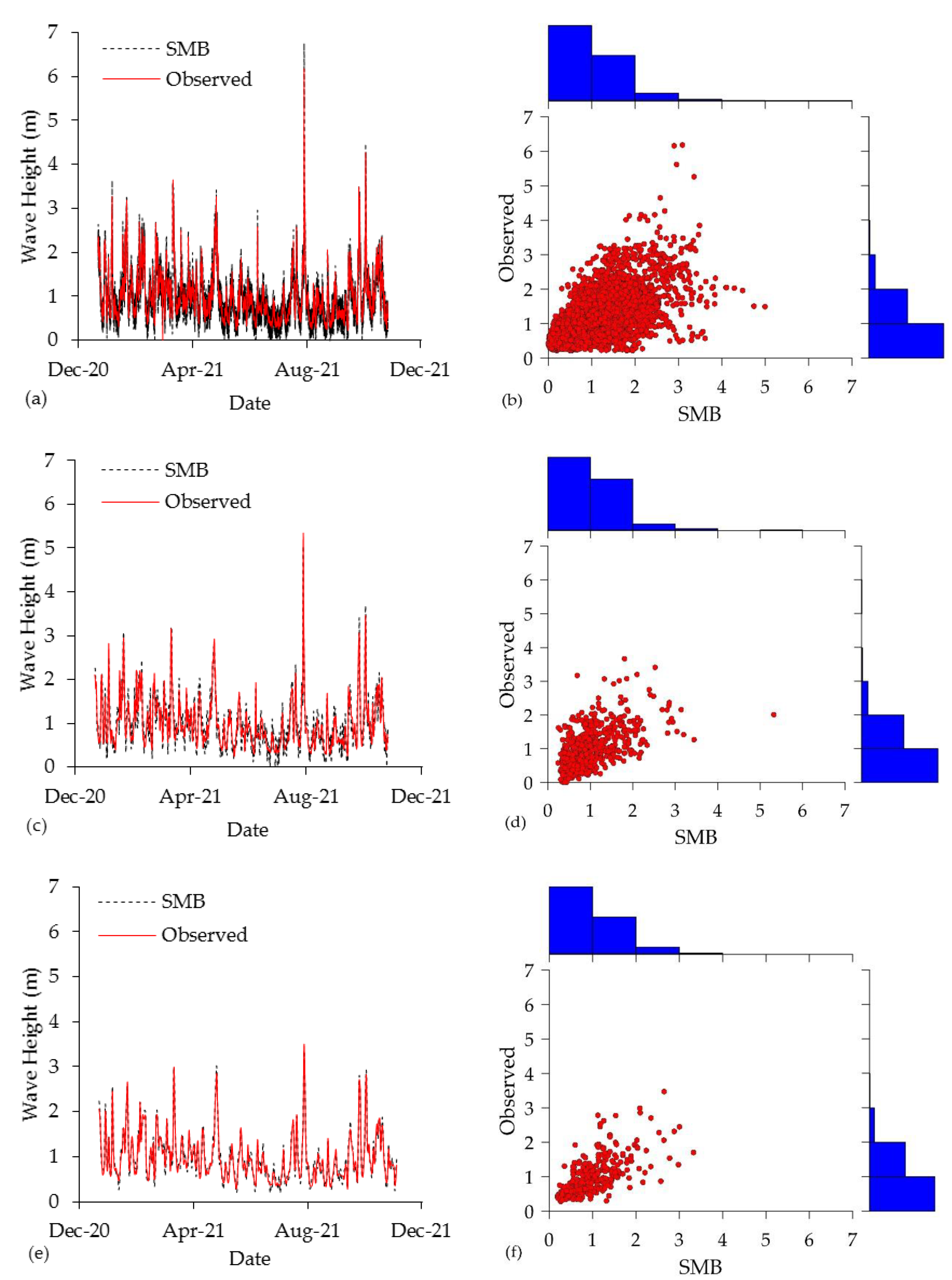
4.1. Sverdrup Munk Bretschneider
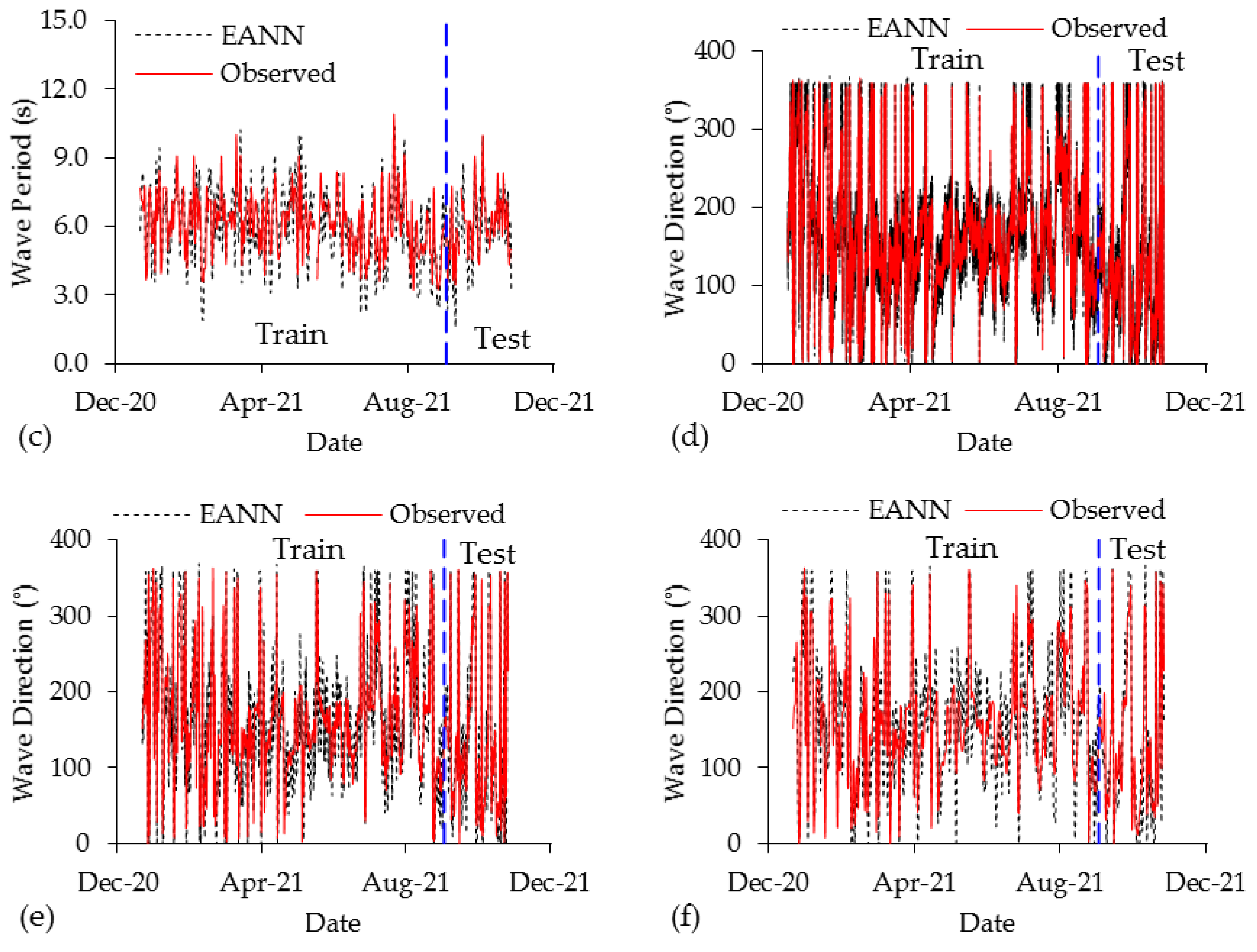
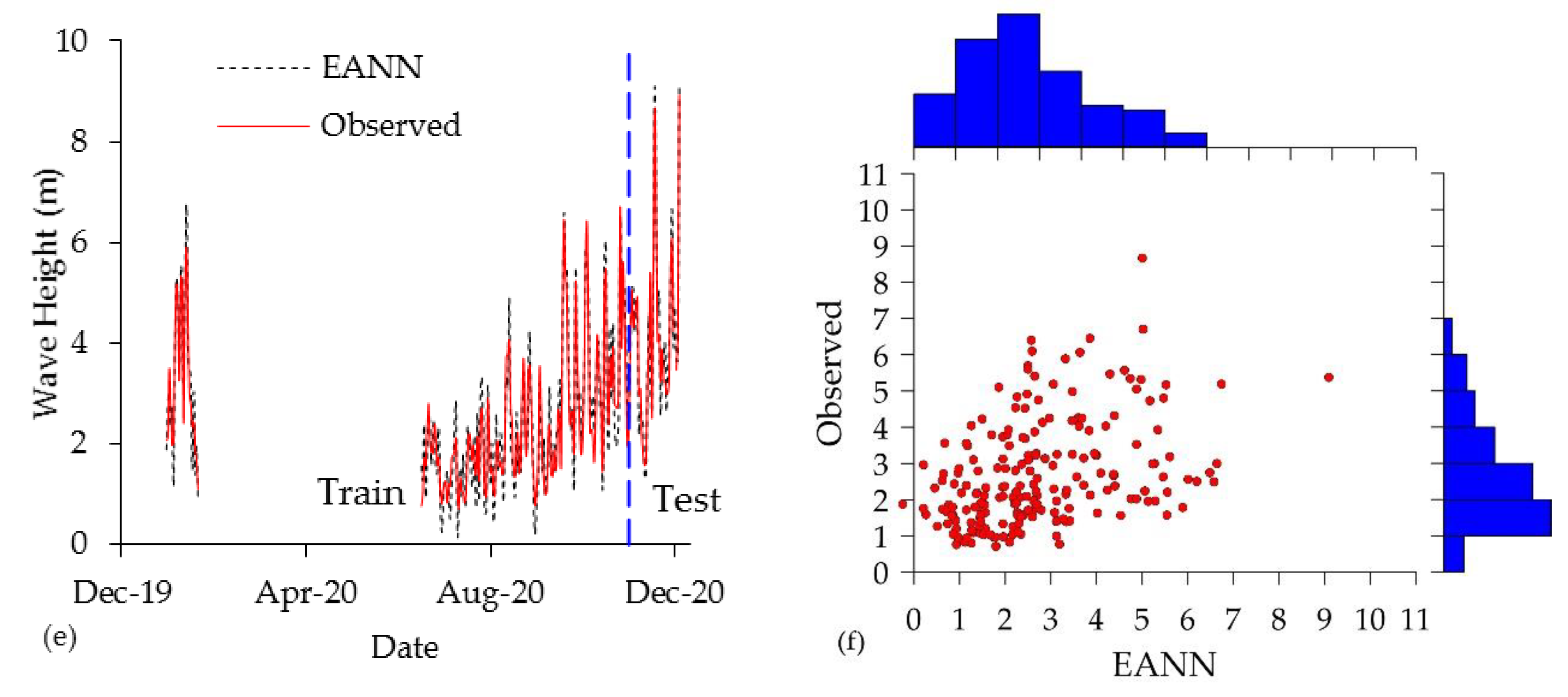
4.2. Emotional Artificial Neural Network
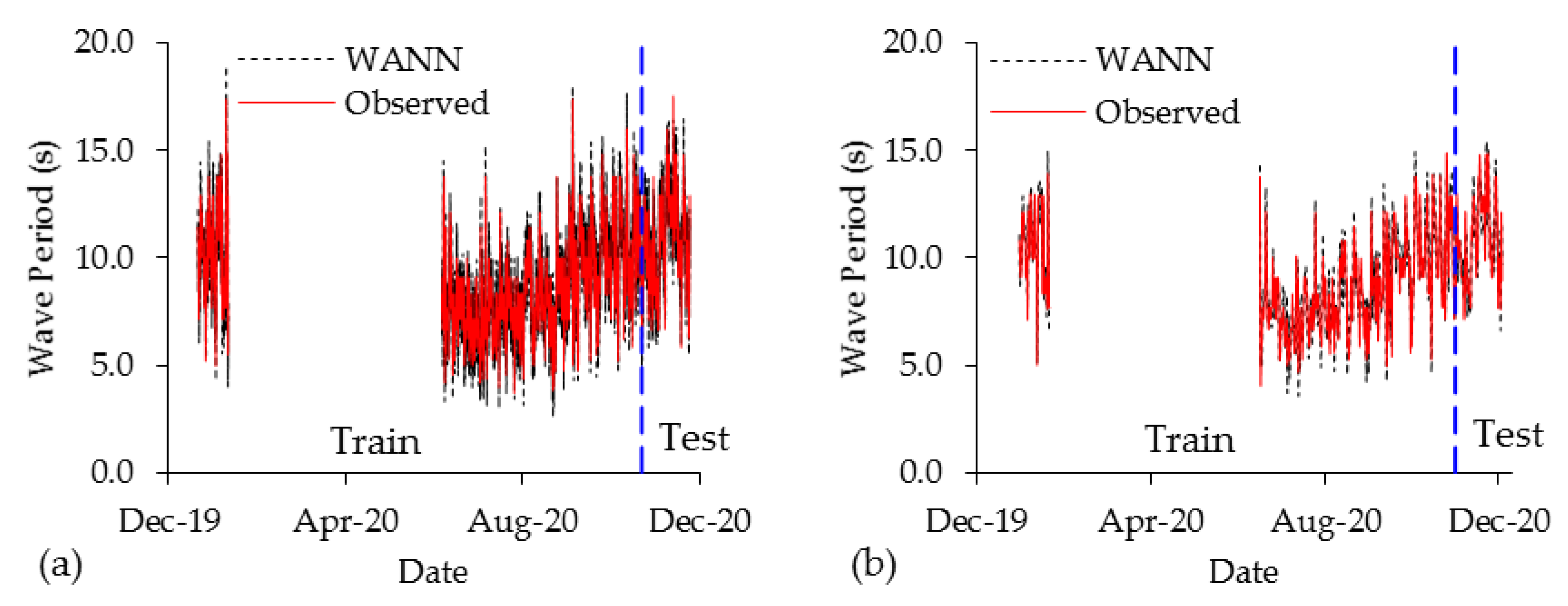
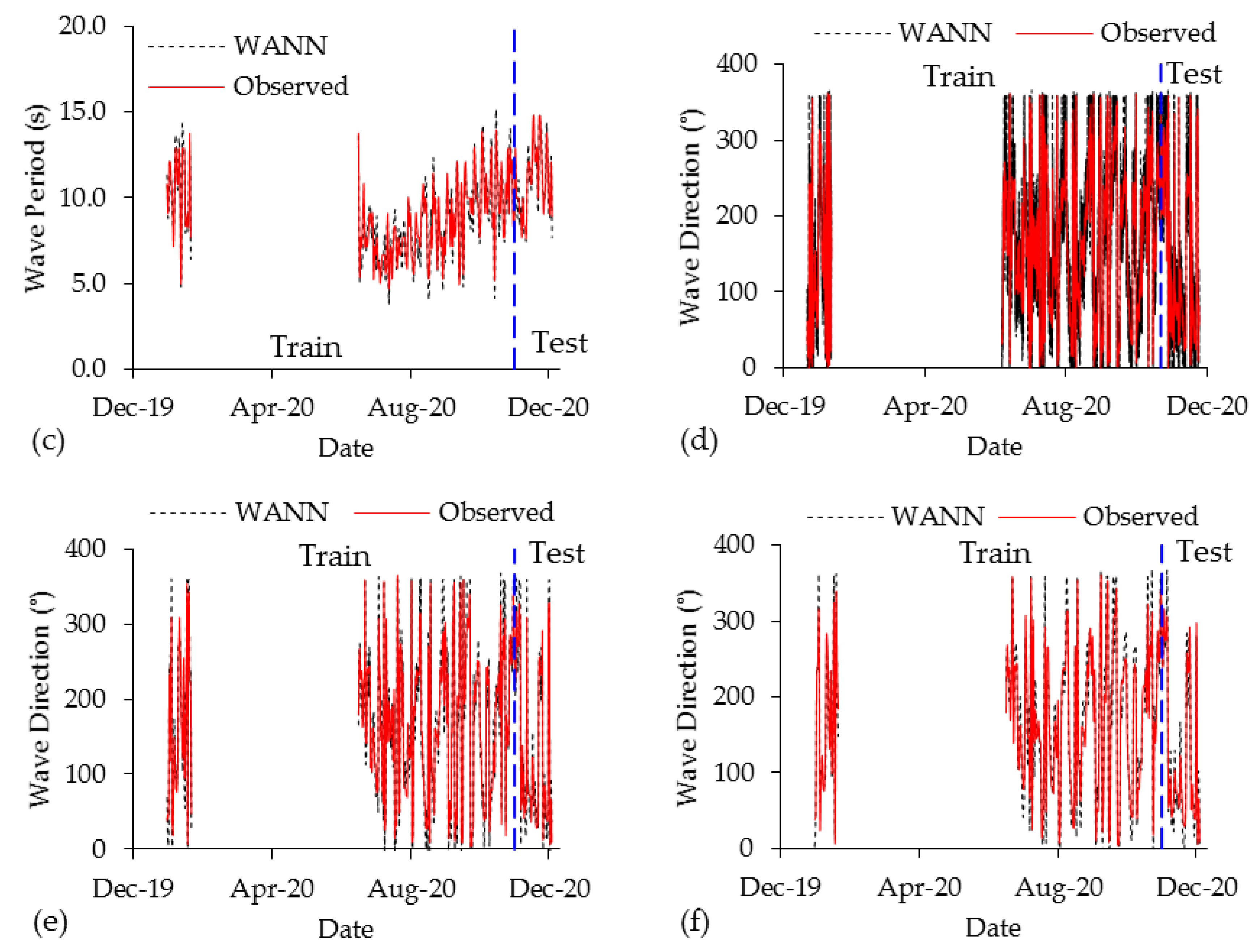
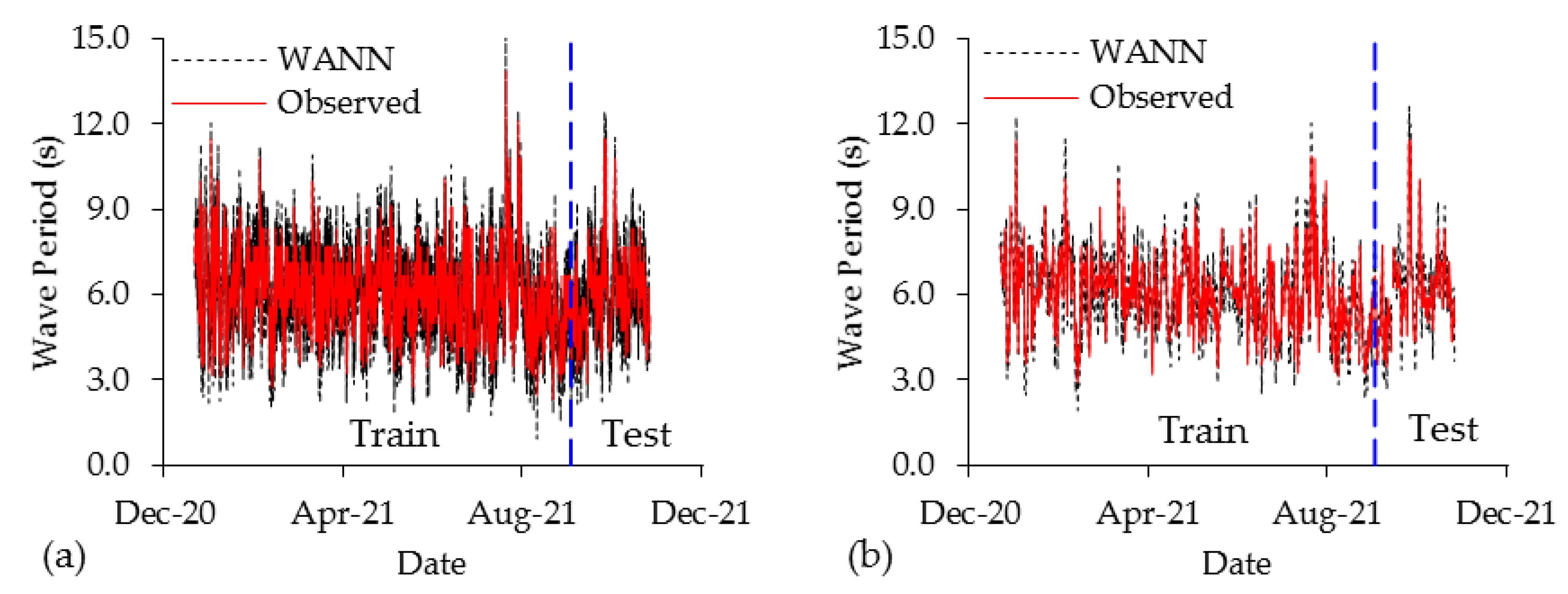
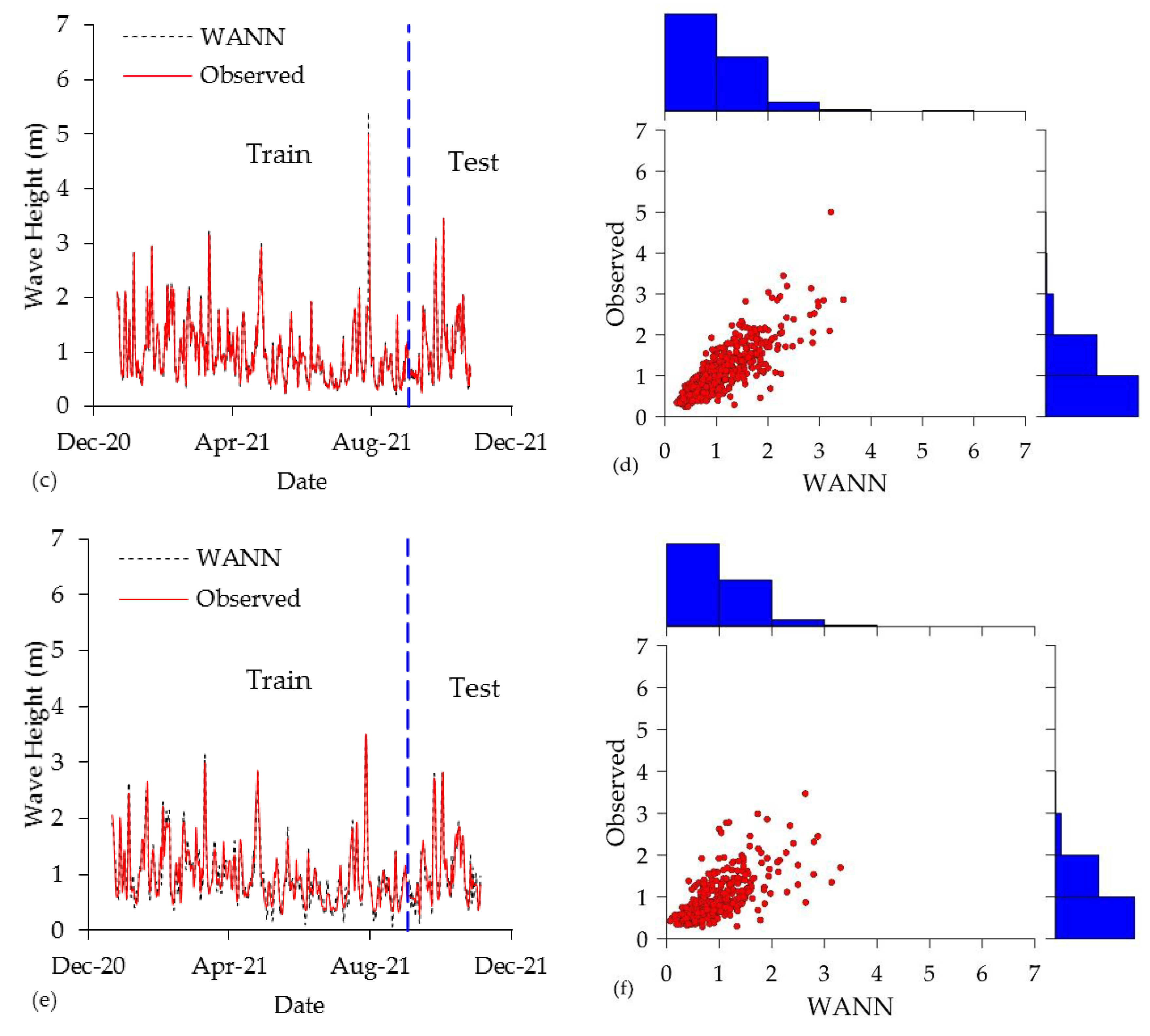
4.3. Wavelet Artificial Neural Network
4.4. Model Performance Comparison
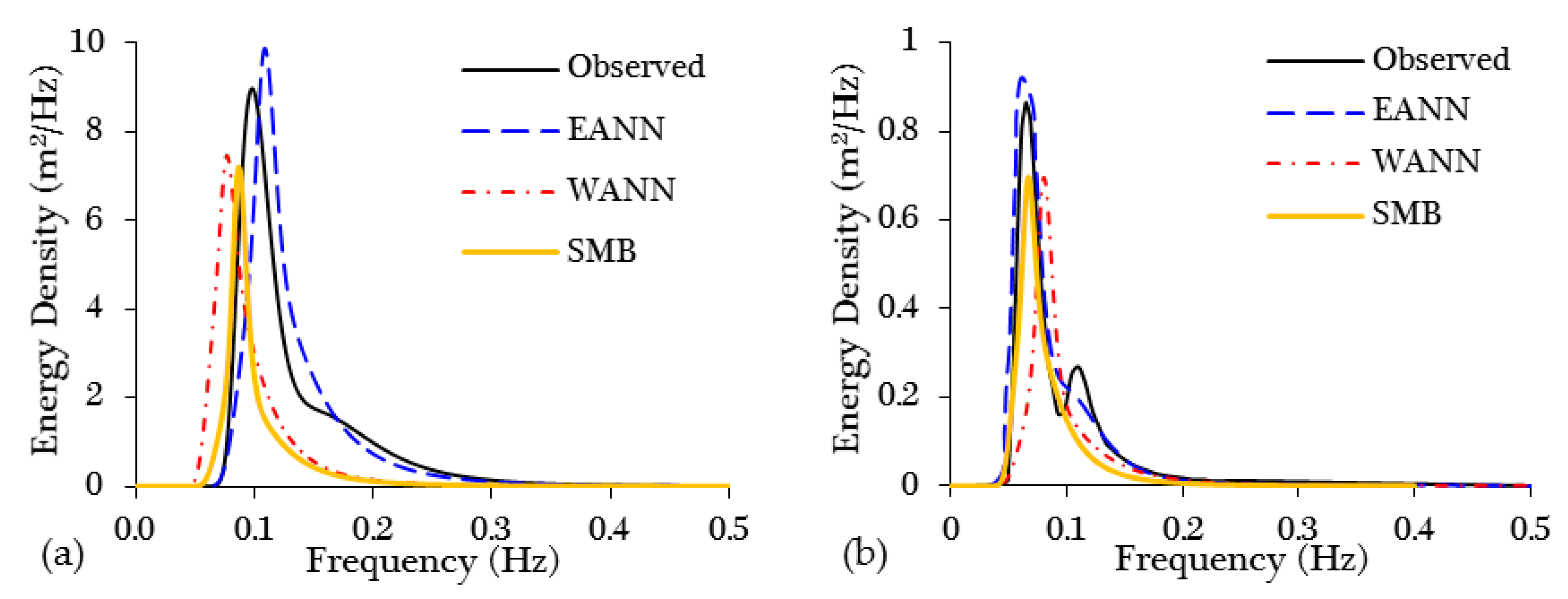
4.5. Wave Energy Density Spectrum
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A




References
- Bateman, W.J.D.; Katsardi, V.; Swan, C. Extreme Ocean Waves. Part I. The Practical Application of Fully Nonlinear Wave Modelling. Appl. Ocean Res. 2012, 34, 209–224. [Google Scholar] [CrossRef]
- Golshani, A.; Banan-Dallalian, M.; Shokatian-Beiragh, M.; Samiee-Zenoozian, M.; Sadeghi-Esfahlani, S. Investigation of Waves Generated by Tropical Cyclone Kyarr in the Arabian Sea: An Application of ERA5 Reanalysis Wind Data. Atmosphere 2022, 13, 1914. [Google Scholar] [CrossRef]
- Mojtahedi, A.; Beiragh, M.S.; Farajpour, I.; Mohammadian, M. Investigation on Hydrodynamic Performance of an Environmentally Friendly Pile Breakwater. Ocean Eng. 2020, 217, 107942. [Google Scholar] [CrossRef]
- Zhao, L.; Li, Z.; Zhang, J.; Teng, B. An Integrated Complete Ensemble Empirical Mode Decomposition with Adaptive Noise to Optimize LSTM for Significant Wave Height Forecasting. J. Mar. Sci. Eng. 2023, 11, 435. [Google Scholar] [CrossRef]
- Yin, Y.; Le Guen, V.; Dona, J.; de Bézenac, E.; Ayed, I.; Thome, N.; Gallinari, P. Augmenting Physical Models with Deep Networks for Complex Dynamics Forecasting. J. Stat. Mech. Theory Exp. 2021, 2021, 124012. [Google Scholar] [CrossRef]
- Sadeghifar, T.; Lama, G.F.C.; Sihag, P.; Bayram, A.; Kisi, O. Wave Height Predictions in Complex Sea Flows through Soft-Computing Models: Case Study of Persian Gulf. Ocean Eng. 2022, 245, 110467. [Google Scholar] [CrossRef]
- Wu, L.; Breivik, Ø.; Rutgersson, A. Ocean-Wave-Atmosphere Interaction Processes in a Fully Coupled Modeling System. J. Adv. Model. Earth Syst. 2019, 11, 3852–3874. [Google Scholar] [CrossRef]
- Chaichitehrani, N.; Allahdadi, M.N.; Li, C. Simulation of Low Energy Waves during Fair-Weather Summer Conditions in the Northern Gulf of Mexico: Effect of Whitecapping Dissipation and the Forcing Accuracy. Atmosphere 2022, 13, 2047. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Santoso, A.; Cai, W. Introduction to El Niño Southern Oscillation in a Changing Climate. In Geophysical Monograph Series; Wiley Online Library: Hoboken, NJ, USA, 2020; pp. 1–19. [Google Scholar]
- Wang, P.; Tian, X.; Peng, T.; Luo, Y. A Review of the State-of-the-Art Developments in the Field Monitoring of Offshore Structures. Ocean Eng. 2018, 147, 148–164. [Google Scholar] [CrossRef]
- Davidson, F.; Alvera-Azcárate, A.; Barth, A.; Brassington, G.B.; Chassignet, E.P.; Clementi, E.; De Mey-Frémaux, P.; Divakaran, P.; Harris, C.; Hernandez, F.; et al. Synergies in Operational Oceanography: The Intrinsic Need for Sustained Ocean Observations. Front. Mar. Sci. 2019, 6, 450. [Google Scholar] [CrossRef]
- Remya, P.G.; Rabi Ranjan, T.; Sirisha, P.; Harikumar, R.; Balakrishnan Nair, T.M. Indian Ocean Wave Forecasting System for Wind Waves: Development and Its Validation. J. Oper. Oceanogr. 2022, 15, 1–16. [Google Scholar] [CrossRef]
- Tajfar, I.; Pazoki, M.; Pazoki, A.; Nejatian, N.; Amiri, M. Analysis of Heating Value of Hydro-Char Produced by Hydrothermal Carbonization of Cigarette Butts. Pollution 2023, 9, 1273–1280. [Google Scholar] [CrossRef]
- Bento, P.M.R.; Pombo, J.A.N.; Mendes, R.P.G.; Calado, M.R.A.; Mariano, S.J.P.S. Ocean Wave Energy Forecasting Using Optimised Deep Learning Neural Networks. Ocean Eng. 2021, 219, 108372. [Google Scholar] [CrossRef]
- Chen, T.-C.; Najat Rashid, Z.; Theruvil Sayed, B.; Sari, A.; Kateb Jumaah Al-Nussairi, A.; Samiee-Zenoozian, M.; Shokatian-Beiragh, M. Evaluation of Hybrid Soft Computing Model’s Performance in Estimating Wave Height. Adv. Civ. Eng. 2023, 2023, 8272566. [Google Scholar] [CrossRef]
- Squire, V.A. Ocean Wave Interactions with Sea Ice: A Reappraisal. Annu. Rev. Fluid Mech. 2020, 52, 37–60. [Google Scholar] [CrossRef]
- Muscarella, P.; Brunner, K.; Walker, D. Estimating Coastal Winds by Assimilating High-Frequency Radar Spectrum Data in SWAN. Sensors 2021, 21, 7811. [Google Scholar] [CrossRef]
- Ali, M.; Prasad, R. Significant Wave Height Forecasting via an Extreme Learning Machine Model Integrated with Improved Complete Ensemble Empirical Mode Decomposition. Renew. Sustain. Energy Rev. 2019, 104, 281–295. [Google Scholar] [CrossRef]
- Silam Siregar, G.R.; Alfarizi, H.; Purnomo, F.M.; Ginanjar, S.; Wirasatriya, A. Validation of Wave Forecasting with the Sverdrup, Munk, and Bretschneider (SMB) Method Using Easywave Algorithm. In Proceedings of the 2020 IEEE Asia-Pacific Conference on Geoscience, Electronics and Remote Sensing Technology (AGERS), Jakarta, Indonesia, 7–8 December 2020; pp. 11–15. [Google Scholar]
- Benetazzo, A.; Barbariol, F.; Davison, S. Short-Term/Range Extreme-Value Probability Distributions of Upper Bounded Space-Time Maximum Ocean Waves. J. Mar. Sci. Eng. 2020, 8, 679. [Google Scholar] [CrossRef]
- Rahimian, M.; Beyramzadeh, M.; Siadatmousavi, S.M.; Allahdadi, M.N. Simulating Meteorological and Water Wave Characteristics of Cyclone Shaheen. Atmosphere 2023, 14, 533. [Google Scholar] [CrossRef]
- Ramos, M.S.; Farina, L.; Faria, S.H.; Li, C. Relationships between Large-Scale Climate Modes and the South Atlantic Ocean Wave Climate. Prog. Oceanogr. 2021, 197, 102660. [Google Scholar] [CrossRef]
- Li, M.; Liu, K. Probabilistic Prediction of Significant Wave Height Using Dynamic Bayesian Network and Information Flow. Water 2020, 12, 2075. [Google Scholar] [CrossRef]
- Banan-Dallalian, M.; Shokatian-Beiragh, M.; Golshani, A.; Mojtahedi, A.; Lotfollahi-Yaghin, M.A.; Akib, S. Study of the Effect of an Environmentally Friendly Flood Risk Reduction Approach on the Oman Coastlines during the Gonu Tropical Cyclone (Case Study: The Coastline of Sur). Eng 2021, 2, 141–155. [Google Scholar] [CrossRef]
- Gao, J.; Ji, C.; Gaidai, O.; Liu, Y. Numerical Study of Infragravity Waves Amplification during Harbor Resonance. Ocean Eng. 2016, 116, 90–100. [Google Scholar] [CrossRef]
- Gao, J.; Shi, H.; Zang, J.; Liu, Y. Mechanism Analysis on the Mitigation of Harbor Resonance by Periodic Undulating Topography. Ocean Eng. 2023, 281, 114923. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Chen, H.; Liu, Q.; Zang, J. Investigation on the Effects of Bragg Reflection on Harbor Oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Gao, J.; Zhou, X.; Zhou, L.; Zang, J.; Chen, H. Numerical Investigation on Effects of Fringing Reefs on Low-Frequency Oscillations within a Harbor. Ocean Eng. 2019, 172, 86–95. [Google Scholar] [CrossRef]
- Wang, J.; Shen, Y. Development and Validation of a Three-Dimensional, Wave-Current Coupled Model on Unstructured Meshes. Sci. China Phys. Mech. Astron. 2011, 54, 42–58. [Google Scholar] [CrossRef]
- Kim, S.; Barth, J.A. Connectivity and Larval Dispersal along the Oregon Coast Estimated by Numerical Simulations. J. Geophys. Res. 2011, 116, C06002. [Google Scholar] [CrossRef]
- Meng, Z.; Hu, Y.; Ancey, C. Using a Data Driven Approach to Predict Waves Generated by Gravity Driven Mass Flows. Water 2020, 12, 600. [Google Scholar] [CrossRef]
- Liu, F.; Chao, J.; Huang, G.; Feng, L. A Semi-Analytical Model for the Propagation of Rossby Waves in Slowly Varying Flow. Chin. Sci. Bull. 2011, 56, 2727–2731. [Google Scholar] [CrossRef]
- Alifdini, I.; Sugianto, D.N.; Andrawina, Y.O.; Widodo, A.B. Identification of Wave Energy Potential with Floating Oscillating Water Column Technology in Pulau Baai Beach, Bengkulu. IOP Conf. Ser. Earth Environ. Sci. 2017, 55, 012040. [Google Scholar] [CrossRef]
- Young, I.R. Wind Generated Ocean Waves; Elsevier: Amsterdam, The Netherlands, 1999; ISBN 978-0-08-043317-2. [Google Scholar]
- Joensen, B.; Niclasen, B.A.; Bingham, H.B. Wave Power Assessment in Faroese Waters Using an Oceanic to Nearshore Scale Spectral Wave Model. Energy 2021, 235, 121404. [Google Scholar] [CrossRef]
- Akpinar, A.; Özger, M.; Bekiroglu, S.; Komurcu, M.I. Performance Evaluation of Parametric Models in the Hindcasting of Wave Parameters along the South Coast of Black Sea. Indian J. Geo-Mar. Sci. 2014, 43, 899–914. [Google Scholar]
- Soomere, T. Numerical Simulations of Wave Climate in the Baltic Sea: A Review. Oceanologia 2023, 65, 117–140. [Google Scholar] [CrossRef]
- Bishop, C.T. Comparison of Manual Wave Prediction Models. J. Waterw. Port Coast. Ocean Eng. 1983, 109, 1–17. [Google Scholar] [CrossRef]
- Malekmohamadi, I.; Bazargan-Lari, M.R.; Kerachian, R.; Nikoo, M.R.; Fallahnia, M. Evaluating the Efficacy of SVMs, BNs, ANNs and ANFIS in Wave Height Prediction. Ocean Eng. 2011, 38, 487–497. [Google Scholar] [CrossRef]
- Chang, H.-K.; Liou, J.-C.; Liu, S.-J.; Liaw, S.-R. Simulated Wave-Driven ANN Model for Typhoon Waves. Adv. Eng. Softw. 2011, 42, 25–34. [Google Scholar] [CrossRef]
- Suursaar, Ü. Locally Calibrated Wave Hindcasts in the Estonian Coastal Sea in 1966–2011. Est. J. Earth Sci. 2013, 62, 42–56. [Google Scholar] [CrossRef]
- Suursaar, Ü.; Jaagus, J.; Tõnisson, H. How to Quantify Long-Term Changes in Coastal Sea Storminess? Estuar. Coast. Shelf Sci. 2015, 156, 31–41. [Google Scholar] [CrossRef]
- Domala, V.; Lee, W.; Kim, T. Wave Data Prediction with Optimized Machine Learning and Deep Learning Techniques. J. Comput. Des. Eng. 2022, 9, 1107–1122. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, X.; Jin, S.; Greaves, D. Phase-Resolved Real-Time Ocean Wave Prediction with Quantified Uncertainty Based on Variational Bayesian Machine Learning. Appl. Energy 2022, 324, 119711. [Google Scholar] [CrossRef]
- den Bieman, J.P.; van Gent, M.R.A.; van den Boogaard, H.F.P. Wave Overtopping Predictions Using an Advanced Machine Learning Technique. Coast. Eng. 2021, 166, 103830. [Google Scholar] [CrossRef]
- Fan, S.; Xiao, N.; Dong, S. A Novel Model to Predict Significant Wave Height Based on Long Short-Term Memory Network. Ocean Eng. 2020, 205, 107298. [Google Scholar] [CrossRef]
- Dai, H.; Shang, S.; Lei, F.; Liu, K.; Zhang, X.; Wei, G.; Xie, Y.; Yang, S.; Lin, R.; Zhang, W. CRBM-DBN-Based Prediction Effects Inter-Comparison for Significant Wave Height with Different Patterns. Ocean Eng. 2021, 236, 109559. [Google Scholar] [CrossRef]
- Londhe, S.N.; Shah, S.; Dixit, P.R.; Nair, T.M.B.; Sirisha, P.; Jain, R. A Coupled Numerical and Artificial Neural Network Model for Improving Location Specific Wave Forecast. Appl. Ocean Res. 2016, 59, 483–491. [Google Scholar] [CrossRef]
- James, S.C.; Zhang, Y.; O’Donncha, F. A Machine Learning Framework to Forecast Wave Conditions. Coast. Eng. 2018, 137, 1–10. [Google Scholar] [CrossRef]
- Tsai, C.-P.; Lin, C.; Shen, J.-N. Neural Network for Wave Forecasting among Multi-Stations. Ocean Eng. 2002, 29, 1683–1695. [Google Scholar] [CrossRef]
- Makarynskyy, O.; Pires-Silva, A.A.; Makarynska, D.; Ventura-Soares, C. Artificial Neural Networks in Wave Predictions at the West Coast of Portugal. Comput. Geosci. 2005, 31, 415–424. [Google Scholar] [CrossRef]
- Gopinath, D.I.; Dwarakish, G.S. Wave Prediction Using Neural Networks at New Mangalore Port along West Coast of India. Aquat. Procedia 2015, 4, 143–150. [Google Scholar] [CrossRef]
- Ahn, H.; Kim, K. Bankruptcy Prediction Modeling with Hybrid Case-Based Reasoning and Genetic Algorithms Approach. Appl. Soft Comput. 2009, 9, 599–607. [Google Scholar] [CrossRef]
- Dixit, P.; Londhe, S.N.; Dandawate, Y.H. Wave Forecasting Using Neuro Wavelet Technique. Int. J. Ocean Clim. Syst. 2014, 5, 237–247. [Google Scholar] [CrossRef]
- Sharghi, E.; Nourani, V.; Najafi, H.; Gokcekus, H. Conjunction of a Newly Proposed Emotional ANN (EANN) and Wavelet Transform for Suspended Sediment Load Modeling. Water Sci. Technol. Water Supply 2019, 19, 1726–1734. [Google Scholar] [CrossRef]
- Nourani, V.; Molajou, A.; Uzelaltinbulat, S.; Sadikoglu, F. Emotional Artificial Neural Networks (EANNs) for Multi-Step Ahead Prediction of Monthly Precipitation; Case Study: Northern Cyprus. Theor. Appl. Climatol. 2019, 138, 1419–1434. [Google Scholar] [CrossRef]
- Nourani, V.; Molajou, A.; Najafi, H.; Danandeh Mehr, A. Emotional ANN (EANN): A New Generation of Neural Networks for Hydrological Modeling in IoT. In Artificial Intelligence in IoT; Springer: Cham, Switzerland, 2019; pp. 45–61. [Google Scholar]
- Danielson, S.L.; Ahkinga, O.; Ashjian, C.; Basyuk, E.; Cooper, L.W.; Eisner, L.; Farley, E.; Iken, K.B.; Grebmeier, J.M.; Juranek, L.; et al. Manifestation and Consequences of Warming and Altered Heat Fluxes over the Bering and Chukchi Sea Continental Shelves. Deep Sea Res. Part II Top. Stud. Oceanogr. 2020, 177, 104781. [Google Scholar] [CrossRef]
- Danielson, S.L.; Weingartner, T.J.; Hedstrom, K.S.; Aagaard, K.; Woodgate, R.; Curchitser, E.; Stabeno, P.J. Coupled Wind-Forced Controls of the Bering–Chukchi Shelf Circulation and the Bering Strait Throughflow: Ekman Transport, Continental Shelf Waves, and Variations of the Pacific–Arctic Sea Surface Height Gradient. Prog. Oceanogr. 2014, 125, 40–61. [Google Scholar] [CrossRef]
- Katsuki, K.; Khim, B.-K.; Itaki, T.; Harada, N.; Sakai, H.; Ikeda, T.; Takahashi, K.; Okazaki, Y.; Asahi, H. Land—Sea Linkage of Holocene Paleoclimate on the Southern Bering Continental Shelf. Holocene 2009, 19, 747–756. [Google Scholar] [CrossRef]
- Roden, G.I. Aleutian Basin of the Bering Sea: Thermohaline, Oxygen, Nutrient, and Current Structure in July 1993. J. Geophys. Res. 1995, 100, 13539. [Google Scholar] [CrossRef]
- Sallenger, A.H., Jr. Storm Impact Scale for Barrier Islands. J. Coast. Res. 2000, 16, 890–895. [Google Scholar]
- Sheng, Y.P.; Zhang, Y.; Paramygin, V.A. Simulation of Storm Surge, Wave, and Coastal Inundation in the Northeastern Gulf of Mexico Region during Hurricane Ivan in 2004. Ocean Model. 2010, 35, 314–331. [Google Scholar] [CrossRef]
- Harris, C.; Syvitski, J.; Arango, H.G.; Meiburg, E.H.; Cohen, S.; Jenkins, C.J.; Birchler, J.; Hutton, E.W.H.; Kniskern, T.A.; Radhakrishnan, S.; et al. Data-Driven, Multi-Model Workflow Suggests Strong Influence from Hurricanes on the Generation of Turbidity Currents in the Gulf of Mexico. J. Mar. Sci. Eng. 2020, 8, 586. [Google Scholar] [CrossRef]
- Sharghi, E.; Nourani, V.; Najafi, H.; Molajou, A. Emotional ANN (EANN) and Wavelet-ANN (WANN) Approaches for Markovian and Seasonal Based Modeling of Rainfall-Runoff Process. Water Resour. Manag. 2018, 32, 3441–3456. [Google Scholar] [CrossRef]
- Molajou, A.; Nourani, V.; Afshar, A.; Khosravi, M.; Brysiewicz, A. Optimal Design and Feature Selection by Genetic Algorithm for Emotional Artificial Neural Network (EANN) in Rainfall-Runoff Modeling. Water Resour. Manag. 2021, 35, 2369–2384. [Google Scholar] [CrossRef]
- Haruna, S.I.; Malami, S.I.; Adamu, M.; Usman, A.G.; Farouk, A.; Ali, S.I.A.; Abba, S.I. Compressive Strength of Self-Compacting Concrete Modified with Rice Husk Ash and Calcium Carbide Waste Modeling: A Feasibility of Emerging Emotional Intelligent Model (EANN) Versus Traditional FFNN. Arab. J. Sci. Eng. 2021, 46, 11207–11222. [Google Scholar] [CrossRef]
- Sharghi, E.; Paknezhad, N.J.; Najafi, H. Assessing the Effect of Emotional Unit of Emotional ANN (EANN) in Estimation of the Prediction Intervals of Suspended Sediment Load Modeling. Earth Sci. Inform. 2021, 14, 201–213. [Google Scholar] [CrossRef]
- Yadav, A.; Chithaluru, P.; Singh, A.; Joshi, D.; Elkamchouchi, D.; Pérez-Oleaga, C.; Anand, D. An Enhanced Feed-Forward Back Propagation Levenberg–Marquardt Algorithm for Suspended Sediment Yield Modeling. Water 2022, 14, 3714. [Google Scholar] [CrossRef]
- Farooq, M.U.; Zafar, A.M.; Raheem, W.; Jalees, M.I.; Aly Hassan, A. Assessment of Algorithm Performance on Predicting Total Dissolved Solids Using Artificial Neural Network and Multiple Linear Regression for the Groundwater Data. Water 2022, 14, 2002. [Google Scholar] [CrossRef]
- Zuccaro, G.; Leone, M.F.; Zuber, S.Z.; Nawi, M.N.M.; Nifa, F.A.; Zou, Y.; Kiviniemi, A.; Jones, S.W.; Zou, P.X.W.; Lun, P.; et al. Productivity of Digital Fabrication in Construction: Cost and Time Analysis of a Robotically Built Wall. Autom. Constr. 2019, 92, 297–311. [Google Scholar]
- Tariq, R.; Alhamrouni, I.; Rehman, A.U.; Tag Eldin, E.; Shafiq, M.; Ghamry, N.A.; Hamam, H. An Optimized Solution for Fault Detection and Location in Underground Cables Based on Traveling Waves. Energies 2022, 15, 6468. [Google Scholar] [CrossRef]
- Qin, Y.; Tang, B.; Wang, J. Higher-Density Dyadic Wavelet Transform and Its Application. Mech. Syst. Signal Process. 2010, 24, 823–834. [Google Scholar] [CrossRef]
- Nourani, V.; Molajou, A.; Tajbakhsh, A.D.; Najafi, H. A Wavelet Based Data Mining Technique for Suspended Sediment Load Modeling. Water Resour. Manag. 2019, 33, 1769–1784. [Google Scholar] [CrossRef]
- Dixit, P.; Londhe, S. Prediction of Extreme Wave Heights Using Neuro Wavelet Technique. Appl. Ocean Res. 2016, 58, 241–252. [Google Scholar] [CrossRef]
- Saber, A.; James, D.E.; Hayes, D.F. Long-term Forecast of Water Temperature and Dissolved Oxygen Profiles in Deep Lakes Using Artificial Neural Networks Conjugated with Wavelet Transform. Limnol. Oceanogr. 2020, 65, 1297–1317. [Google Scholar] [CrossRef]
- Jacovides, C.P. Model Comparison for the Calculation of Linke’s Turbidity Factor. Int. J. Climatol. 1997, 17, 551–563. [Google Scholar] [CrossRef]
- Wang, N.; Chen, Q.; Zhu, L.; Sun, H. Integration of Data-Driven and Physics-Based Modeling of Wind Waves in a Shallow Estuary. Ocean Model. 2022, 172, 101978. [Google Scholar] [CrossRef]
- Nourani, V. An Emotional ANN (EANN) Approach to Modeling Rainfall-Runoff Process. J. Hydrol. 2017, 544, 267–277. [Google Scholar] [CrossRef]
- Sharghi, E.; Nourani, V.; Molajou, A.; Najafi, H. Conjunction of Emotional ANN (EANN) and Wavelet Transform for Rainfall-Runoff Modeling. J. Hydroinform. 2019, 21, 136–152. [Google Scholar] [CrossRef]
- Nourani, V.; Hosseini Baghanam, A.; Adamowski, J.; Kisi, O. Applications of Hybrid Wavelet–Artificial Intelligence Models in Hydrology: A Review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]









| Scale | Time Series | Statistical Characteristic | Aleutian Basin (1 January 2020 12:00:00 a.m. to 21 December 2020 07:00:00 p.m.) | Gulf of Mexico (1 January 2021 12:00:00 a.m. to 30 November 2021 12:00:00 a.m.) | ||
|---|---|---|---|---|---|---|
| Calibration | Verification | Calibration | Verification | |||
| Hourly | Significant Wave Height (m) | Root Mean Squared Mean | 1.74 | 2.73 | 0.70 | 0.74 |
| Maximum | 9.39 | 10.79 | 6.64 | 4.27 | ||
| Minimum | 0.5 | 1.21 | 0.22 | 0.22 | ||
| Standard Deviation | 1.42 | 1.15 | 0.57 | 0.61 | ||
| Mean Wave Period (s) | Root Mean Squared Mean | 6.15 | 7.86 | 4.87 | 4.04 | |
| Maximum | 17.39 | 17.39 | 13.79 | 11.43 | ||
| Minimum | 3.70 | 5.56 | 2.35 | 2.86 | ||
| Standard Deviation | 2.17 | 2.01 | 1.33 | 1.32 | ||
| Wind Speed (m/s) | Root Mean Squared Mean | 5.50 | 6.07 | 3.72 | 4.00 | |
| Maximum | 19.60 | 21.70 | 19.40 | 15.80 | ||
| Minimum | 0.1 | 0.2 | 0.1 | 0.1 | ||
| Standard Deviation | 3.57 | 1.60 | 2.47 | 2.24 | ||
| 12 Hourly | Significant Wave Height (m) | Root Mean Squared Mean | 1.73 | 2.76 | 0.70 | 0.73 |
| Maximum | 9.39 | 10.79 | 5.32 | 3.44 | ||
| Minimum | 0.57 | 1.42 | 0.24 | 0.25 | ||
| Standard Deviation | 1.38 | 1.60 | 0.56 | 0.60 | ||
| Mean Wave Period (s) | Root Mean Squared Mean | 5.30 | 7.80 | 4.19 | 4.06 | |
| Maximum | 14.81 | 14.81 | 11.43 | 11.43 | ||
| Minimum | 4.17 | 7.14 | 2.94 | 3.32 | ||
| Standard Deviation | 2.15 | 2.01 | 1.34 | 1.42 | ||
| Wind Speed (m/s) | Root Mean Squared Mean | 5.03 | 6.41 | 3.74 | 3.99 | |
| Maximum | 17.60 | 19.37 | 18.50 | 3.44 | ||
| Minimum | 1.31 | 1.56 | 0.96 | 0.85 | ||
| Standard Deviation | 3.32 | 4.20 | 2.35 | 2.00 | ||
| Daily | Significant Wave Height (m) | Root Mean Squared Mean | 1.72 | 2.85 | 0.71 | 0.72 |
| Maximum | 6.70 | 8.93 | 3.47 | 2.78 | ||
| Minimum | 0.71 | 1.56 | 0.28 | 0.29 | ||
| Standard Deviation | 1.31 | 1.63 | 0.53 | 0.56 | ||
| Mean Wave Period (s) | Root Mean Squared Mean | 6.29 | 8.05 | 4.56 | 3.89 | |
| Maximum | 13.79 | 14.81 | 11.81 | 11.00 | ||
| Minimum | 4.76 | 7.69 | 3.33 | 3.23 | ||
| Standard Deviation | 2.20 | 1.99 | 1.33 | 1.37 | ||
| Wind Speed (m/s) | Root Mean Squared Mean | 5.48 | 6.26 | 3.72 | 4.00 | |
| Maximum | 16.18 | 19.37 | 14.03 | 11.15 | ||
| Minimum | 1.72 | 2.03 | 1.34 | 2.16 | ||
| Standard Deviation | 3.03 | 4.04 | 2.15 | 1.84 | ||
| Case Study | Time Scale | Criteria | |||||
|---|---|---|---|---|---|---|---|
| RMSE | bias | SI | t | NSE | DCpeak | ||
| Wave Height (m) | |||||||
| Buoy 46070 (Aleutian Basin) | Hourly | 1.87 | −2.87 | 0.68 | 91.62 | 0.11 | 0.50 |
| 12-Hourly | 1.24 | 2.12 | 0.45 | 24.78 | 0.30 | 0.51 | |
| Daily | 0.91 | 1.95 | 0.32 | 16.06 | 0.62 | 0.54 | |
| Buoy 42003 (Gulf of Mexico) | Hourly | 0.42 | 1.19 | 0.41 | 94.39 | 0.50 | 0.46 |
| 12-Hourly | 0.39 | −1.02 | 0.40 | 27.62 | 0.54 | 0.52 | |
| Daily | 0.33 | 0.99 | 0.33 | 19.09 | 0.64 | 0.55 | |
| Wave Period (s) | |||||||
| Buoy 46070 (Aleutian Basin) | Hourly | 1.21 | 2.45 | 0.20 | 79.96 | 0.17 | 0.54 |
| 12-Hourly | 1.02 | 2.21 | 0.10 | 22.63 | 0.45 | 0.44 | |
| Daily | 0.89 | 2.00 | 0.15 | 15.87 | 0.57 | 0.61 | |
| Buoy 42003 (Gulf of Mexico) | Hourly | 1.82 | −1.91 | 0.41 | 291.24 | 0.14 | 0.55 |
| 12-Hourly | 1.70 | 1.75 | 0.40 | 107.42 | 0.33 | 0.51 | |
| Daily | 1.44 | 1.52 | 0.33 | 56.31 | 0.53 | 0.59 | |
| Wave Direction (°) | |||||||
| Buoy 46070 (Aleutian Basin) | Hourly | 81.82 | −22.52 | 81.82 | −22.52 | 0.56 | - |
| 12-Hourly | 92.4 | 20.15 | 92.40 | 20.15 | 0.59 | - | |
| Daily | 76.6 | 15.12 | 76.60 | 15.12 | 0.51 | - | |
| Buoy 42003 (Gulf of Mexico) | Hourly | 102.11 | 39.12 | 102.11 | 39.12 | 0.41 | - |
| 12-Hourly | 95.80 | 25.01 | 95.80 | 25.01 | 0.40 | - | |
| Daily | 92.15 | −21.18 | 92.15 | −21.18 | 0.33 | - | |
| Case Study | Time Scale | Input | Hormone | Hidden Neuron | Epoch | Computational Cost (s) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Buoy 46070 (Aleutian Basin) | Hourly | W(t), W(t−1), W(t−2), W(t−3), W(t−4), W(t−5), W(t−6), f(t) | 15 | 10 | 10 | 1300 | |||||||
| 12-Hourly | W(t), W(t−6), W(t−12), f(t) | 10 | 7 | 20 | 700 | ||||||||
| Daily | W(t), W(t−12), W(t−24), f(t) | 8 | 6 | 30 | 1100 | ||||||||
| Buoy 42003 (Gulf of Mexico) | Hourly | W(t), W(t−1), W(t−2), W(t−3), W(t−4), W(t−5), W(t−6), f(t) | 12 | 8 | 20 | 1800 | |||||||
| 12-Hourly | W(t), W(t−6), W(t−12), f(t) | 8 | 4 | 20 | 1500 | ||||||||
| Daily | W(t), W(t−12), W(t−24), f(t) | 6 | 3 | 30 | 900 | ||||||||
| Case Study | Time Scale | Criteria | |||||||||||
| RMSE | bias | SI | t | NSE | DCpeak | ||||||||
| Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | ||
| Wave Height (m) | |||||||||||||
| Buoy 46070 (Aleutian Basin) | Hourly | 0.90 | 0.99 | −0.37 | 0.48 | 0.33 | 0.36 | 31.36 | 38.54 | 0.60 | 0.53 | 0.88 | 0.81 |
| 12-Hourly | 1.89 | 2.02 | 1.92 | −1.98 | 0.68 | 0.73 | 114.01 | 99.37 | 0.37 | 0.40 | 0.72 | 0.61 | |
| Daily | 1.92 | 2.05 | 1.95 | −1.99 | 0.68 | 0.73 | 81.34 | 57.45 | 0.46 | 0.44 | 0.68 | 0.59 | |
| Buoy 42003 (Gulf of Mexico) | Hourly | 0.71 | 0.92 | 0.29 | 0.32 | 0.71 | 0.92 | 39.53 | 32.78 | 0.80 | 0.67 | 0.82 | 0.79 |
| 12-Hourly | 0.85 | 0.99 | −1.02 | 1.21 | 0.86 | 1.00 | 46.12 | 44.34 | 0.70 | 0.62 | 0.71 | 0.69 | |
| Daily | 1.22 | 1.41 | 1.18 | −1.44 | 1.23 | 1.42 | 68.66 | 88.78 | 0.36 | 0.18 | 0.73 | 0.68 | |
| Wave Period (s) | |||||||||||||
| Buoy 46070 (Aleutian Basin) | Hourly | 1.19 | 1.37 | 1.86 | −1.96 | 0.20 | 0.23 | 90.46 | 97.22 | 0.98 | 1.02 | 0.78 | 0.72 |
| 12-Hourly | 1.36 | 1.84 | 1.91 | 2.03 | 0.14 | 0.19 | 28.59 | 47.52 | 1.26 | 1.24 | 0.71 | 0.69 | |
| Daily | 1.51 | 1.69 | 2.15 | −1.99 | 0.25 | 0.28 | 19.97 | 26.92 | 1.31 | 1.35 | 0.74 | 0.65 | |
| Buoy 42003 (Gulf of Mexico) | Hourly | 1.73 | 1.89 | −1.12 | 1.19 | 0.18 | 0.19 | 75.04 | 71.60 | 0.88 | 1.29 | 0.69 | 0.60 |
| 12-Hourly | 1.91 | 2.06 | −1.65 | 1.69 | 0.32 | 0.34 | 43.72 | 36.58 | 1.91 | 1.96 | 0.63 | 0.58 | |
| Daily | 2.02 | 2.32 | −1.91 | 2.09 | 0.20 | 0.24 | 52.37 | 37.41 | 1.87 | 1.82 | 0.62 | 0.53 | |
| Wave Direction (°) | |||||||||||||
| Buoy 46070 (Aleutian Basin) | Hourly | 51.12 | 63.02 | 42.42 | 46.82 | 8.51 | 10.49 | 103.39 | 77.17 | 0.58 | 0.56 | - | - |
| 12-Hourly | 62.35 | 71.13 | 43.21 | 50.11 | 6.34 | 7.24 | 19.30 | 19.93 | 0.39 | 0.47 | - | - | |
| Daily | 66.31 | 79.12 | −55.02 | 57.14 | 11.01 | 13.13 | 21.13 | 14.84 | 0.30 | 0.30 | - | - | |
| Buoy 42003 (Gulf of Mexico) | Hourly | 77.11 | 81.82 | −44.11 | −41.03 | 7.82 | 8.29 | 61.61 | 51.21 | 0.34 | 0.37 | - | - |
| 12-Hourly | 85.2 | 88.18 | 38.15 | 40.11 | 14.07 | 14.56 | 12.77 | 13.02 | 0.19 | 0.32 | - | - | |
| Daily | 72.15 | 81.19 | −51.09 | 44.81 | 7.31 | 8.23 | 18.08 | 11.93 | 0.53 | 0.29 | - | - | |
| Case Study | Time Scale | Input | Hidden Neuron | Epoch | Computational Cost (s) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Buoy 46070 (Aleutian Basin) | Hourly | Wa(t),Wd4(t),Wd5(t),fa(t),fd2(t) | 6 | 20 | 1000 | ||||||||
| 12-Hourly | Wa(t),Wd2(t),Wd4(t),fa(t) | 6 | 20 | 500 | |||||||||
| Daily | Wa(t),Wd4(t), fa(t),fd4(t) | 10 | 30 | 900 | |||||||||
| Buoy 42003 (Gulf of Mexico) | Hourly | Wa(t),Wd4(t),Wd5(t),fa(t),fd2(t) | 3 | 20 | 1800 | ||||||||
| 12-Hourly | Wa(t),Wd2(t),Wd4(t),fa(t) | 7 | 10 | 1100 | |||||||||
| Daily | Wa(t),Wd4(t), fa(t),fd4(t) | 6 | 10 | 700 | |||||||||
| Case Study | Time Scale | Criteria | |||||||||||
| RMSE (m) | bias (m) | SI | t | NSE | DCpeak | ||||||||
| Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | ||
| Wave Height (m) | |||||||||||||
| Buoy 46070 (Aleutian Basin) | Hourly | 1.19 | 1.29 | −1.17 | 1.48 | 0.43 | 0.47 | 374.43 | 141.84 | 0.30 | 0.21 | 0.66 | 0.62 |
| 12-Hourly | 0.89 | 1.02 | −0.62 | 0.78 | 0.32 | 0.37 | 19.49 | 23.82 | 0.86 | 0.85 | 0.68 | 0.61 | |
| Daily | 0.94 | 1.05 | 0.65 | −0.79 | 0.33 | 0.37 | 13.60 | 16.23 | 0.87 | 0.85 | 0.65 | 0.61 | |
| Buoy 42003 (Gulf of Mexico) | Hourly | 0.81 | 0.88 | 0.71 | 1.32 | 0.81 | 0.88 | 160.89 | 118.53 | 0.73 | 0.70 | 0.63 | 0.59 |
| 12-Hourly | 0.75 | 0.78 | 1.17 | −1.01 | 0.76 | 0.79 | 33.22 | 40.13 | 0.77 | 0.76 | 0.71 | 0.67 | |
| Daily | 0.8 | 0.83 | 1.08 | −1.42 | 0.81 | 0.84 | 26.84 | 22.22 | 0.73 | 0.72 | 0.58 | 0.61 | |
| Wave Period (s) | |||||||||||||
| Buoy 46070 (Aleutian Basin) | Hourly | 1.59 | 1.66 | −1.13 | −1.2 | 0.26 | 0.28 | 70.24 | 72.74 | 0.16 | 0.07 | 0.55 | 0.54 |
| 12-Hourly | 1.16 | 1.29 | 1.11 | 1.09 | 0.12 | 0.13 | 66.14 | 31.72 | 0.25 | 0.17 | 0.63 | 0.62 | |
| Daily | 1.22 | 1.3 | 2 | −2.18 | 0.20 | 0.22 | 17.94 | 17.71 | 0.16 | 0.10 | 0.59 | 0.55 | |
| Buoy 42003 (Gulf of Mexico) | Hourly | 1.43 | 1.53 | 1.81 | 2.02 | 0.14 | 0.16 | 144.11 | 135.31 | 0.31 | 0.42 | 0.50 | 0.52 |
| 12-Hourly | 1.19 | 1.36 | −1.55 | 1.61 | 0.20 | 0.22 | 39.79 | 47.64 | 0.69 | 0.54 | 0.64 | 0.61 | |
| Daily | 1.09 | 1.32 | 1.69 | 1.79 | 0.11 | 0.13 | 23.59 | 26.69 | 0.75 | 0.56 | 0.70 | 0.63 | |
| Wave Direction (°) | |||||||||||||
| Buoy 46070 (Aleutian Basin) | Hourly | 69 | 66.12 | 62.72 | 66.65 | 11.48 | 11.00 | 151.62 | 552.42 | 0.24 | 0.51 | - | - |
| 12-Hourly | 52.59 | 58.7 | 52.21 | 50.03 | 5.35 | 5.97 | 166.09 | 32.71 | 0.57 | 0.64 | - | - | |
| Daily | 49.68 | 53.5 | 48.11 | 51.57 | 8.25 | 8.88 | 55.18 | 51.47 | 0.61 | 0.68 | - | - | |
| Buoy 42003 (Gulf of Mexico) | Hourly | 67.01 | 70.09 | 58.78 | 61.91 | 6.79 | 7.10 | 161.40 | 166.45 | 0.50 | 0.54 | - | - |
| 12-Hourly | 59.23 | 66.51 | 35.45 | −39.17 | 9.78 | 10.98 | 19.05 | 18.58 | 0.61 | 0.61 | - | - | |
| Daily | 48.05 | 56.11 | 40.39 | 41 | 4.87 | 5.68 | 27.98 | 19.30 | 0.79 | 0.66 | - | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elkhrachy, I.; Alhamami, A.; Alyami, S.H.; Alviz-Meza, A. Novel Ocean Wave Height and Energy Spectrum Forecasting Approaches: An Application of Semi-Analytical and Machine Learning Models. Water 2023, 15, 3254. https://doi.org/10.3390/w15183254
Elkhrachy I, Alhamami A, Alyami SH, Alviz-Meza A. Novel Ocean Wave Height and Energy Spectrum Forecasting Approaches: An Application of Semi-Analytical and Machine Learning Models. Water. 2023; 15(18):3254. https://doi.org/10.3390/w15183254
Chicago/Turabian StyleElkhrachy, Ismail, Ali Alhamami, Saleh H. Alyami, and Aníbal Alviz-Meza. 2023. "Novel Ocean Wave Height and Energy Spectrum Forecasting Approaches: An Application of Semi-Analytical and Machine Learning Models" Water 15, no. 18: 3254. https://doi.org/10.3390/w15183254





