Service Pressure and Energy Consumption Mitigation-Oriented Partitioning of Closed Water Distribution Networks
Abstract
:1. Introduction
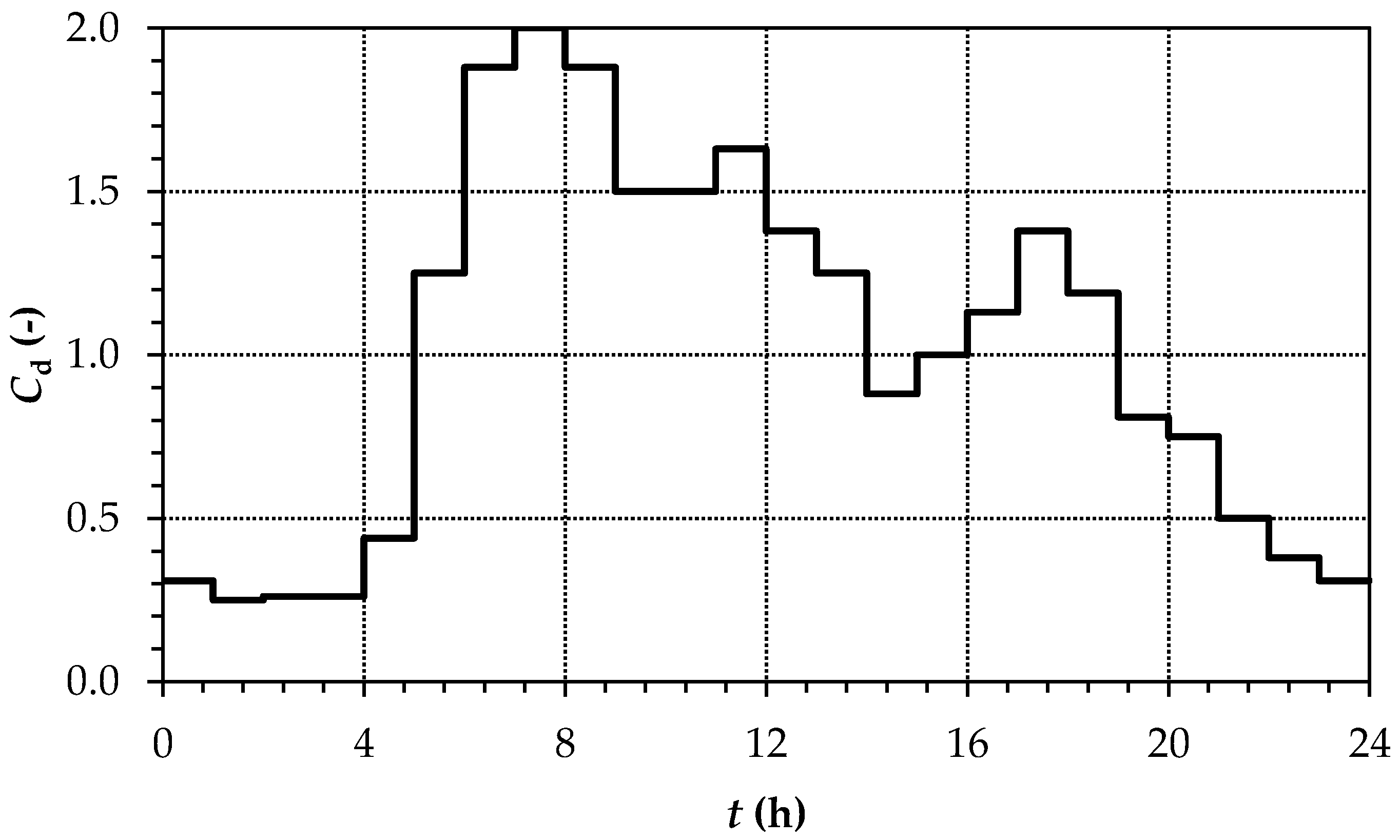
2. Case Study
3. Materials and Methods
- Partitioning (clustering and dividing) of the WDN;
- Optimization of the hourly settings of the pumping stations present in the WDN.
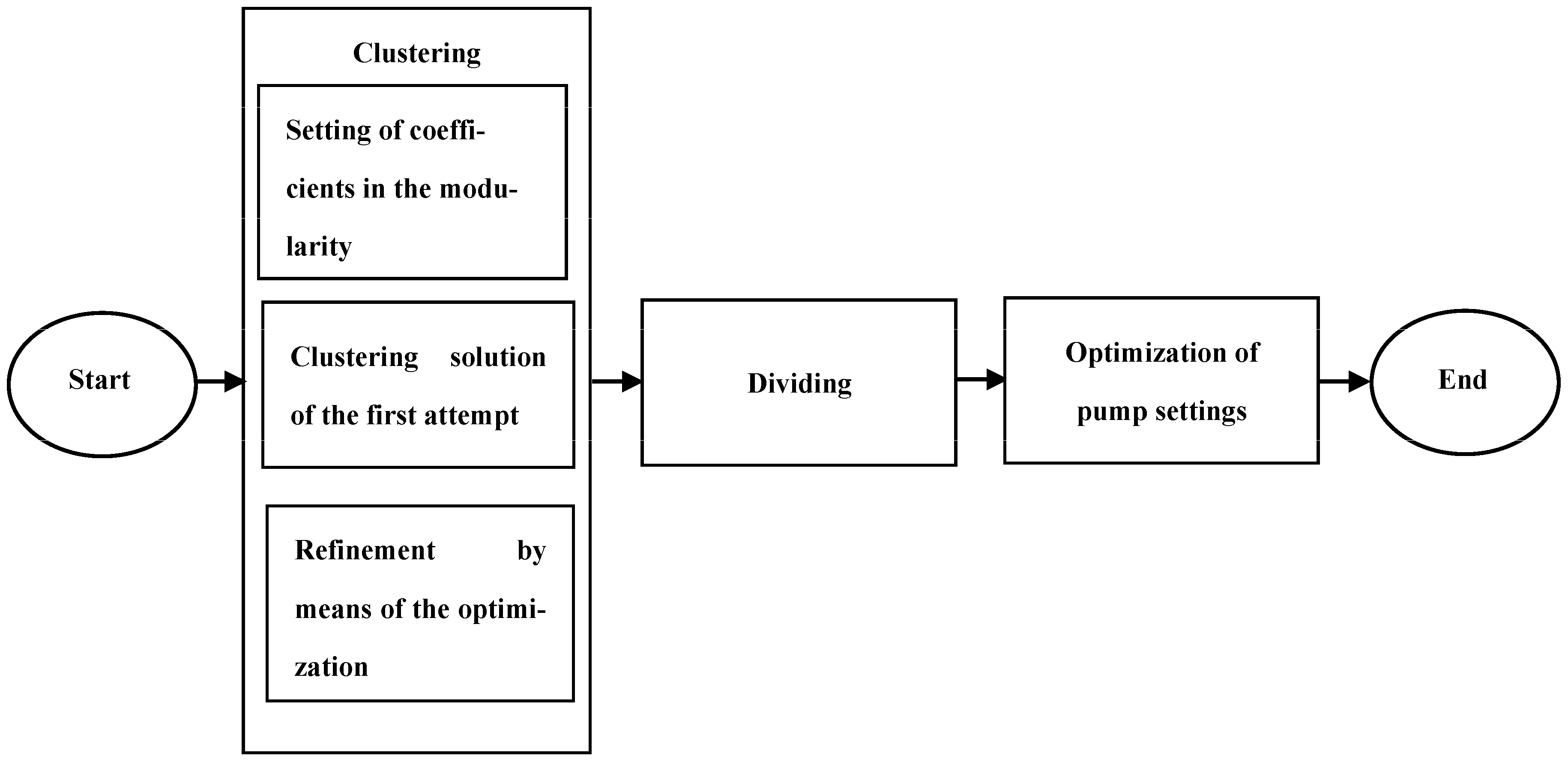
3.1. WDN Partitioning
3.1.1. Clustering
- Construction of a configuration of the first attempt with the desired number M of clusters;
- Refinement of the configuration by means of an algorithm inspired by simulated annealing to search for a configuration with a better value of Q, the number M of clusters being the same.
3.1.2. Dividing
3.2. The Optimization of Pump Settings
4. Results
4.1. Results of WDN Partitioning
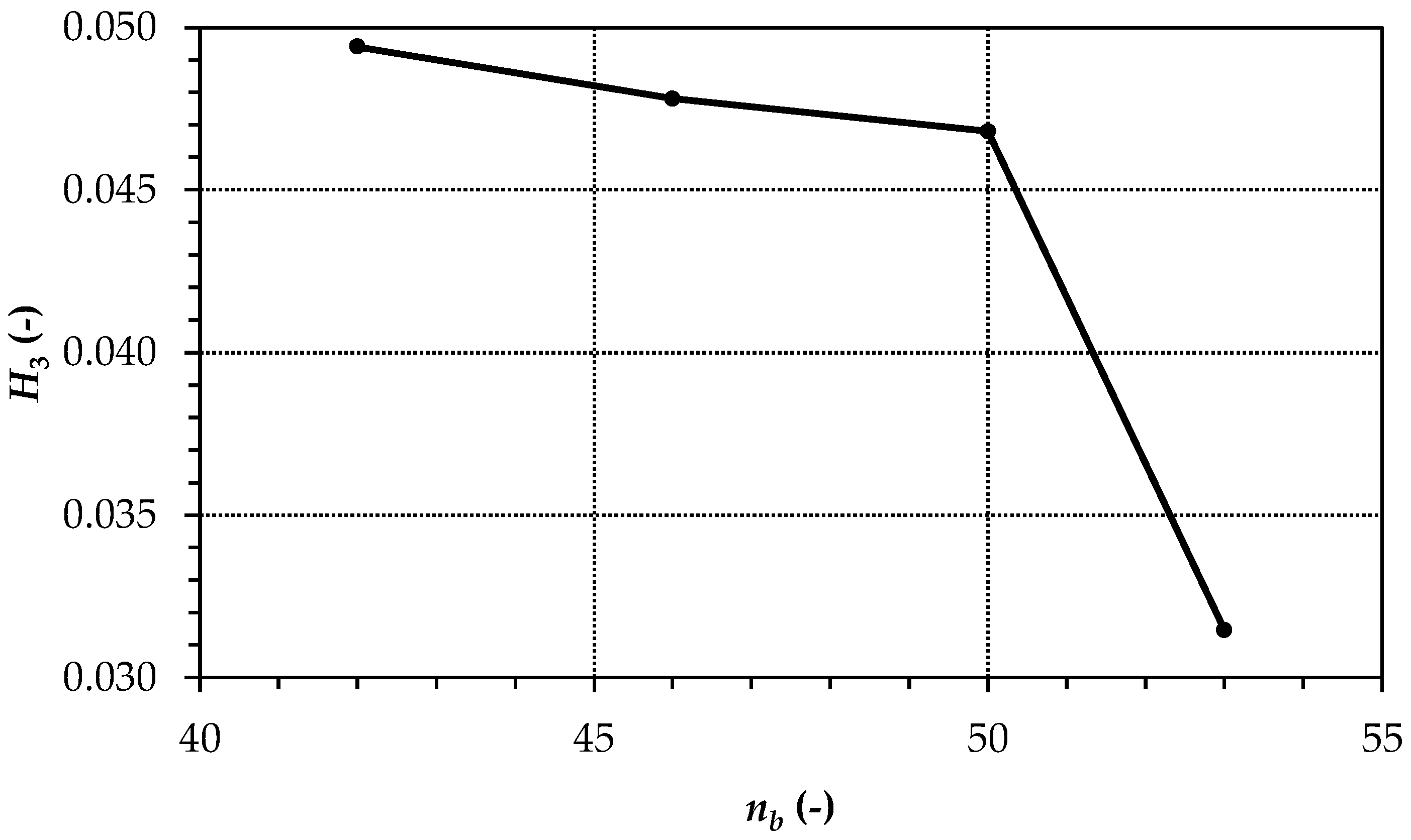
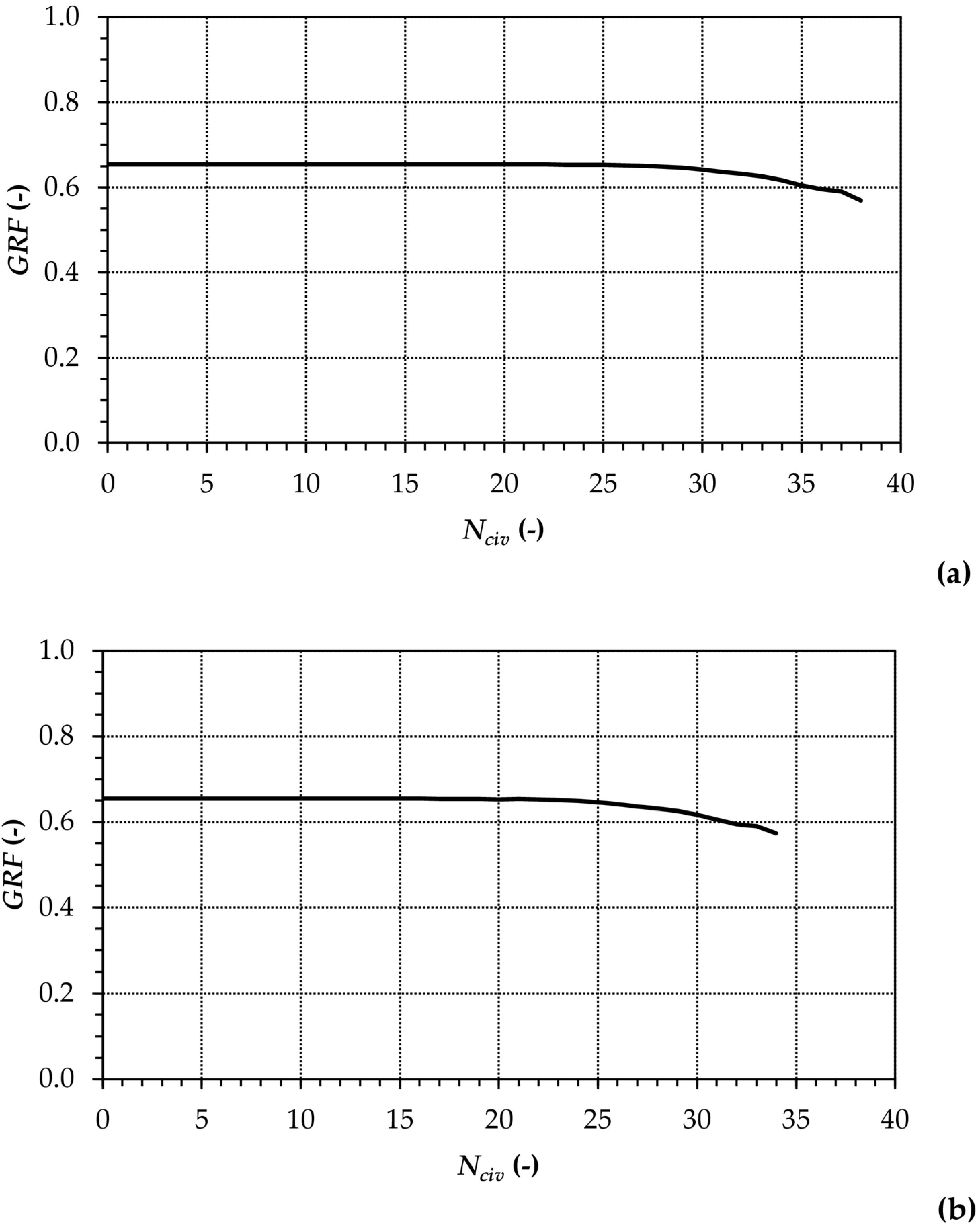
4.1.1. Results of Clustering
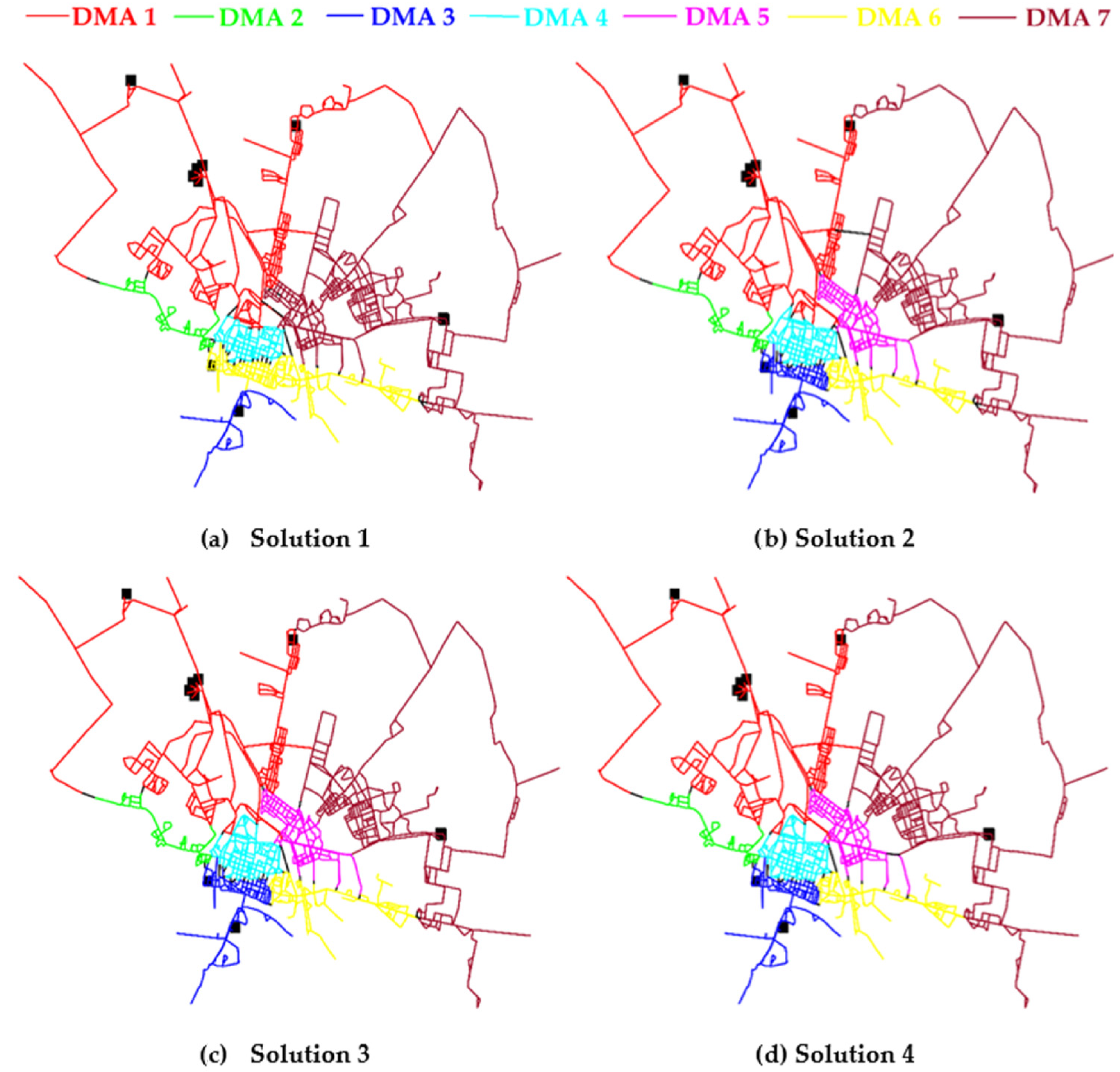
4.1.2. Results of Dividing
4.2. Results of the Optimization of Pump Settings
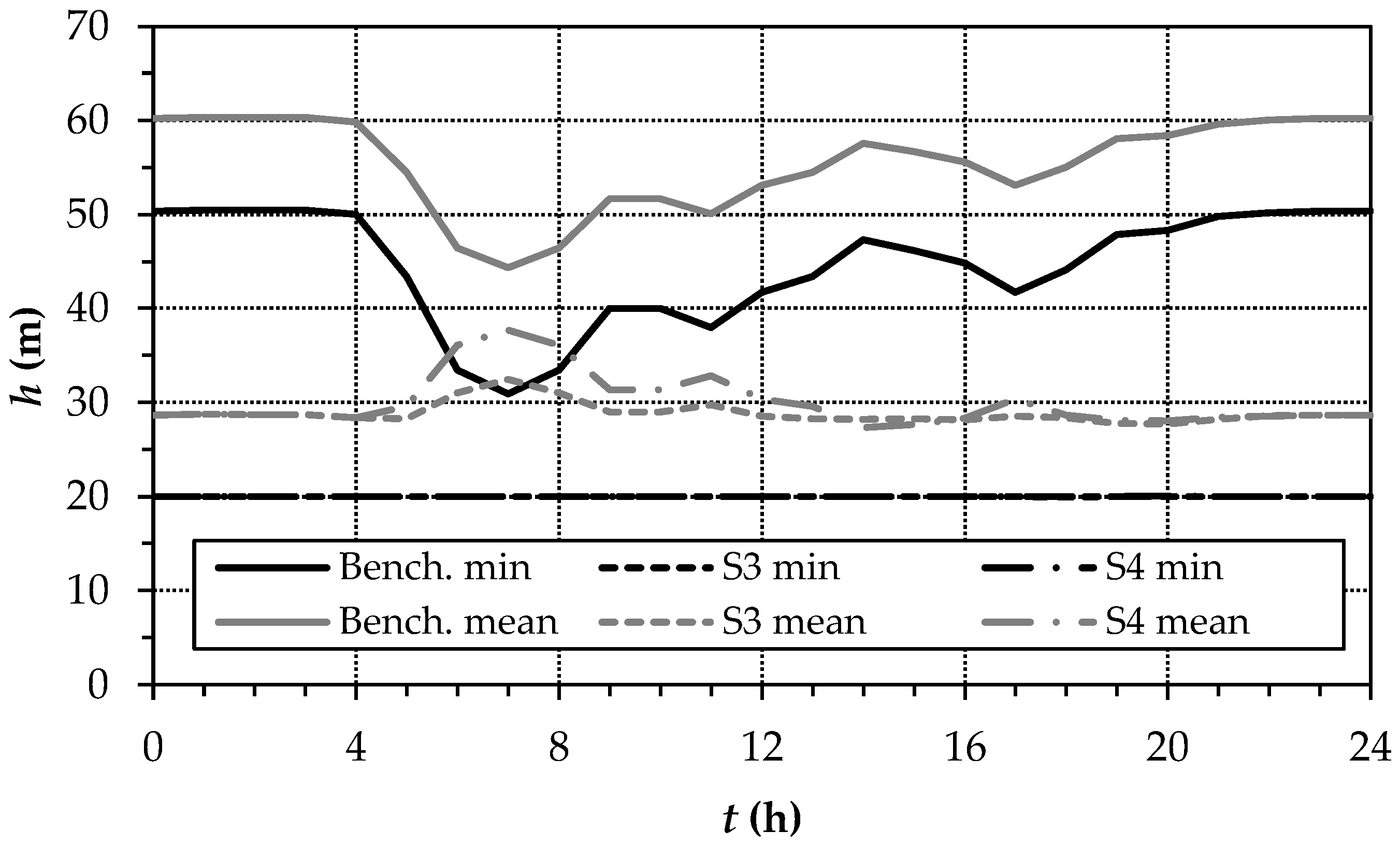
5. Discussion
- The modelled service pressure remained above the threshold of 20 m for full demand satisfaction.
- The rate of leakage in the real WDN is currently small.
- The number of nodes in the WDN layout is high, meaning that demand is always modelled close to its associated user along the pipe.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA. World Energy Outlook 2016—Special Report: Water-Energy Nexus; IEA: Paris, France, 2016. [Google Scholar]
- UK Water Industry Research Limited. A Manual of DMA Practice; UK Water Industry Research Limited: London, UK, 1999. [Google Scholar]
- Morrison, J.; Tooms, S.; Rogers, D. DMAs Guidance Notes; Water Loss Task Force; IWA Publications: London, UK, 2007. [Google Scholar]
- Campbell, E.; Izquierdo, J.; Montalvo, I.; Pérez-García, R. A novel water supply network sectorization methodology based on a complete economic analysis, including uncertainties. Water 2016, 8, 179. [Google Scholar] [CrossRef]
- Ciaponi, C.; Creaco, E.; Di Nardo, A.; Di Natale, M.; Giudicianni, C.; Musmarra, D.; Santonastaso, G.F. Reducing impacts of contamination in water distribution networks: A combined strategy based on network partitioning and installation of water quality sensors. Water 2019, 11, 1315. [Google Scholar] [CrossRef]
- Giudicianni, C.; Herrera, M.; Di Nardo, A.; Adeyeye, K. Automatic multiscale approach for water networks partitioning into dynamic district metered areas. Water Resour. Manag. 2020, 34, 835–848. [Google Scholar] [CrossRef]
- Gomes, R.; Sá Marques, A.; Sousa, J. Identification of the optimal entry points at District Metered Areas and implementation of pressure management. Urban Water J. 2012, 9, 365–384. [Google Scholar] [CrossRef]
- Khoa Bui, X.; Marlim, M.S.; Kang, D. Water network partitioning into district metered areas: A state-of-the-art review. Water 2020, 12, 1002. [Google Scholar] [CrossRef]
- Giustolisi, O.; Ridolfi, L. A novel infrastructure modularity index for the segmentation of water distribution networks. Water Resour. Res. 2014, 50, 7648–7661. [Google Scholar] [CrossRef]
- Creaco, E.; Haidar, H. Multiobjective optimization of control valve installation and DMA creation for reducing leakage in water distribution networks. J. Water Resour. Plan. Manag. 2019, 145, 04019046. [Google Scholar] [CrossRef]
- Sharma, A.N.; Dongre, S.R.; Gupta, R.; Ormsbee, L. Multiphase procedure for identifying district metered areas in water distribution networks using community detection, NSGA-III optimization, and multiple attribute decision making. J. Water Resour. Plan. Manag. 2022, 148, 4022040. [Google Scholar] [CrossRef]
- Clauset, A.; Newman, M.E.J.; Moore, C. Finding community structure in very large networks. Phys. Rev. E 2004, 70, 66111. [Google Scholar] [CrossRef] [PubMed]
- Creaco, E.; Giudicianni, C.; Mottahedin, A. Improved community detection for WDN partitioning in the dual topology based on segments and valves. J. Hydroinformatics 2023, 25, 1341–1357. [Google Scholar] [CrossRef]
- Hajebi, S.; Temate, S.; Barrett, S.; Clarke, A.; Clarke, S. Water distribution network sectorisation using structural graph partitioning and multi-objective optimization. Procedia Eng. 2014, 89, 1144–1151. [Google Scholar] [CrossRef]
- Brentan, B.M.; Campbell, E.; Meirelles, G.L.; Luvizotto, E.; Izquierdo, J. Social network community detection for DMA creation: Criteria analysis through multilevel optimization. Math. Probl. Eng. 2018, 144, 9053238. [Google Scholar] [CrossRef]
- Li, W.; Huang, Y.; Ji, L.; Ma, L.; Agarwal, R.K.; Awais, M. Prediction model for energy conversion characteristics during transient processes in a mixed-flow pump. Energy 2023, 271, 127082. [Google Scholar] [CrossRef]
- Li, W.; Huang, Y.; Ji, L.; Zhong, L.; Shi, W.; Zhu, Y. Mechanism and propagation characteristics of rotating stall in a mixed-flow pump. Renew. Energy 2020, 153, 74–92. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Paredes, A.; González, J.M.; Aguado, J.A. A three-layer game theoretic-based strategy for optimal scheduling of microgrids by leveraging a dynamic demand response program designer to unlock the potential of smart buildings and electric vehicle fleets. Appl. Energy 2023, 347, 121440. [Google Scholar] [CrossRef]
- Mansouri, S.A.; Nematbakhsh, E.; Jordehi, A.R.; Marzband, M.; Tostado-Véliz, M.; Jurado, F. An interval-based nested optimization framework for deriving flexibility from smart buildings and electric vehicle fleets in the TSO-DSO coordination. Appl. Energy 2023, 341, 121062. [Google Scholar] [CrossRef]
- Marchi, A.; Simpson, A.R.; Ertugrul, N. Assessing variable speed pump efficiency in water distribution systems. Drink. Water Eng. Sci. 2012, 5, 15–21. [Google Scholar] [CrossRef]
- Rossman, L.; Woo, H.; Tryby, M.; Shang, F.; Janke, R.; Haxton, T. EPANET 2.2 User Manual; EPA/600/R-20/133; U.S. Environmental Protection Agency: Washington, DC, USA, 2020. [Google Scholar]
- Laarhoven, P.J.M.; Aarts, E.H.L. Simulated Annealing: Theory and Applications; D. Reidel: Dordrecht, The Netherlands, 1987; ISBN 90-277-2513-6. [Google Scholar]
- MATLAB, version: 9.14.0 (R2023a); The MathWorks, Inc.: Natick, MA, USA, 2023.
- Creaco, E.; Zheng, F.; Pezzinga, G. Minimum transport driven algorithm for water distribution network partitioning. Aqua-Water Infrastruct. Ecosyst. Soc. 2022, 71, 120–138. [Google Scholar]
- Creaco, E.; Franchini, M.; Todini, E. Generalized resilience and failure indices for use with pressure-driven modeling and leakage. J. Water Resour. Plan. Manag. 2016, 142, 04016019. [Google Scholar] [CrossRef]
- Eliades, D.G.; Kyriakou, M.; Vrachimis, S. Polycarpou MMEPANET-MATLABToolkit: An Open-Source Software for Interfacing EPANET with, MATLAB. In Proceedings of the 14th International Conference on Computing and Control for the Water Industry (CCWI), Amsterdam, The Netherlands, 7–9 November 2016; p. 8. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef]
- Menapace, A.; Avesani, D. Global Gradient Algorithm Extension to Distributed Pressure Driven Pipe Demand Model. Water Resour. Manag. 2019, 33, 1717–1736. [Google Scholar] [CrossRef]
- Avesani, D.; Righetti, M.; Righetti, D.; Bertola, P. The extension of EPANET source code to simulate unsteady flow in water distribution networks with variable head tanks. J. Hydroinform. 2012, 14, 960–973. [Google Scholar] [CrossRef]
- Berardi, L.; Giustolisi, O.; Todini, E. Accounting for uniformly distributed pipe demand in WDN analysis: Enhanced GGA. Urban Water J. 2010, 7, 243–255. [Google Scholar] [CrossRef]

| Station ID | Station Name | Number of Pumps | Qmax (L/s) | Hmax (m) |
|---|---|---|---|---|
| 1 | Villalunga | 1 | 50 | 80 |
| 2 | Nord | 4 | 144 | 47 |
| 3 | Libertà | 1 | 38 | 85 |
| 4 | Borgo Ticino | 1 | 38 | 85 |
| 5 | Mirabello | 1 | 50 | 80 |
| 6 | Est | 4 | 144 | 47 |
| Solution | Weights | nb (-) | H1 (-) | H2 (-) | H3 (-) |
|---|---|---|---|---|---|
| 1 | α1 = 0.1; α2 = 0.0; α3 = 1.9 | 53 | 0.0112 | 0.2351 | 0.0315 |
| 2 | α1 = 0.5; α2 = 0.0; α3 = 1.5 | 50 | 0.0105 | 0.1668 | 0.0468 |
| 3 | α1 = 1.0; α2 = 0.0; α3 = 1.0 | 46 | 0.0097 | 0.1643 | 0.0478 |
| 4 | α1 = 1.5; α2 = 0.0; α3 = 0.5 | 42 | 0.0089 | 0.1642 | 0.0494 |
| Time (h) | Setting in Station 1 | Setting in Station 2 | Setting in Station 3 | Setting in Station 4 | Setting in Station 5 | Setting in Station 6 |
|---|---|---|---|---|---|---|
| 0–1 | 0.648 | 0.607 | 0.754 | 0.770 | 0.717 | 0.571 |
| 1–2 | 0.646 | 0.607 | 0.760 | 0.776 | 0.708 | 0.569 |
| 2–3 | 0.648 | 0.606 | 0.756 | 0.774 | 0.715 | 0.569 |
| 3–4 | 0.648 | 0.606 | 0.756 | 0.774 | 0.715 | 0.569 |
| 4–5 | 0.646 | 0.615 | 0.750 | 0.764 | 0.780 | 0.569 |
| 5–6 | 0.707 | 0.729 | 0.678 | 0.710 | 0.680 | 0.728 |
| 6–7 | 0.880 | 0.893 | 0.943 | 0.665 | 0.643 | 0.909 |
| 7–8 | 0.884 | 0.939 | 0.890 | 0.790 | 0.673 | 0.943 |
| 8–9 | 0.880 | 0.893 | 0.943 | 0.665 | 0.643 | 0.909 |
| 9–10 | 0.769 | 0.774 | 0.786 | 0.656 | 0.740 | 0.798 |
| 10–11 | 0.769 | 0.774 | 0.786 | 0.656 | 0.740 | 0.798 |
| 11–12 | 0.777 | 0.795 | 0.806 | 0.725 | 0.888 | 0.831 |
| 12–13 | 0.717 | 0.751 | 0.738 | 0.663 | 0.725 | 0.765 |
| 13–14 | 0.707 | 0.729 | 0.678 | 0.710 | 0.680 | 0.728 |
| 14–15 | 0.672 | 0.667 | 0.702 | 0.702 | 0.663 | 0.631 |
| 15–16 | 0.699 | 0.686 | 0.761 | 0.779 | 0.658 | 0.648 |
| 16–17 | 0.714 | 0.707 | 0.646 | 0.721 | 0.671 | 0.703 |
| 17–18 | 0.717 | 0.751 | 0.738 | 0.663 | 0.725 | 0.765 |
| 18–19 | 0.694 | 0.716 | 0.729 | 0.717 | 0.708 | 0.706 |
| 19–20 | 0.653 | 0.659 | 0.734 | 0.734 | 0.638 | 0.610 |
| 20–21 | 0.652 | 0.647 | 0.730 | 0.740 | 0.702 | 0.597 |
| 21–22 | 0.636 | 0.619 | 0.748 | 0.756 | 0.791 | 0.572 |
| 22–23 | 0.640 | 0.613 | 0.758 | 0.769 | 0.736 | 0.571 |
| 23–24 | 0.649 | 0.605 | 0.730 | 0.733 | 0.719 | 0.571 |
| Time (h) | Setting in Station 1 | Setting in Station 2 | Setting in Station 3 | Setting in Station 4 | Setting in Station 5 | Setting in Station 6 |
|---|---|---|---|---|---|---|
| 0–1 | 0.648 | 0.606 | 0.756 | 0.769 | 0.716 | 0.571 |
| 1–2 | 0.658 | 0.604 | 0.760 | 0.778 | 0.713 | 0.569 |
| 2–3 | 0.649 | 0.605 | 0.760 | 0.776 | 0.721 | 0.569 |
| 3–4 | 0.649 | 0.605 | 0.760 | 0.776 | 0.721 | 0.569 |
| 4–5 | 0.642 | 0.615 | 0.750 | 0.758 | 0.773 | 0.571 |
| 5–6 | 0.829 | 0.730 | 0.765 | 0.763 | 0.763 | 0.729 |
| 6–7 | 0.873 | 0.890 | 0.886 | 0.860 | 0.786 | 0.979 |
| 7–8 | 0.944 | 0.938 | 0.976 | 0.985 | 0.744 | 0.999 |
| 8–9 | 0.873 | 0.890 | 0.886 | 0.860 | 0.786 | 0.979 |
| 9–10 | 0.766 | 0.792 | 0.832 | 0.811 | 0.639 | 0.820 |
| 10–11 | 0.766 | 0.792 | 0.832 | 0.811 | 0.639 | 0.820 |
| 11–12 | 0.754 | 0.823 | 0.697 | 0.723 | 0.649 | 0.922 |
| 12–13 | 0.735 | 0.763 | 0.839 | 0.745 | 0.659 | 0.776 |
| 13–14 | 0.829 | 0.730 | 0.765 | 0.763 | 0.763 | 0.729 |
| 14–15 | 0.662 | 0.667 | 0.705 | 0.715 | 0.765 | 0.607 |
| 15–16 | 0.670 | 0.692 | 0.739 | 0.803 | 0.665 | 0.623 |
| 16–17 | 0.742 | 0.713 | 0.824 | 0.849 | 0.683 | 0.648 |
| 17–18 | 0.735 | 0.763 | 0.839 | 0.745 | 0.659 | 0.776 |
| 18–19 | 0.696 | 0.727 | 0.815 | 0.890 | 0.639 | 0.669 |
| 19–20 | 0.677 | 0.656 | 0.804 | 0.798 | 0.815 | 0.592 |
| 20–21 | 0.674 | 0.651 | 0.732 | 0.740 | 0.715 | 0.601 |
| 21–22 | 0.637 | 0.623 | 0.768 | 0.764 | 0.791 | 0.572 |
| 22–23 | 0.645 | 0.612 | 0.758 | 0.764 | 0.742 | 0.571 |
| 23–24 | 0.648 | 0.606 | 0.756 | 0.769 | 0.716 | 0.571 |
| Station | Benchmark | Solution 3 | Solution 4 |
|---|---|---|---|
| Station 1 | 29.62 | 11.40 | 12.10 |
| Station 2 | 138.95 | 66.17 | 67.29 |
| Station 3 | 19.71 | 9.00 | 9.92 |
| Station 4 | 19.25 | 7.49 | 9.84 |
| Station 5 | 30.22 | 13.45 | 12.24 |
| Station 6 | 145.64 | 67.62 | 71.69 |
| Total | 383.40 | 175.13 | 183.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Creaco, E.; Giudicianni, C.; Tosco, A. Service Pressure and Energy Consumption Mitigation-Oriented Partitioning of Closed Water Distribution Networks. Water 2023, 15, 3218. https://doi.org/10.3390/w15183218
Creaco E, Giudicianni C, Tosco A. Service Pressure and Energy Consumption Mitigation-Oriented Partitioning of Closed Water Distribution Networks. Water. 2023; 15(18):3218. https://doi.org/10.3390/w15183218
Chicago/Turabian StyleCreaco, Enrico, Carlo Giudicianni, and Alessandro Tosco. 2023. "Service Pressure and Energy Consumption Mitigation-Oriented Partitioning of Closed Water Distribution Networks" Water 15, no. 18: 3218. https://doi.org/10.3390/w15183218
APA StyleCreaco, E., Giudicianni, C., & Tosco, A. (2023). Service Pressure and Energy Consumption Mitigation-Oriented Partitioning of Closed Water Distribution Networks. Water, 15(18), 3218. https://doi.org/10.3390/w15183218








