Quantitative Diagnosis of Water Resources Carrying Capacity Obstacle Factors Based on Connection Number and TOPSIS in Huaibei Plain
Abstract
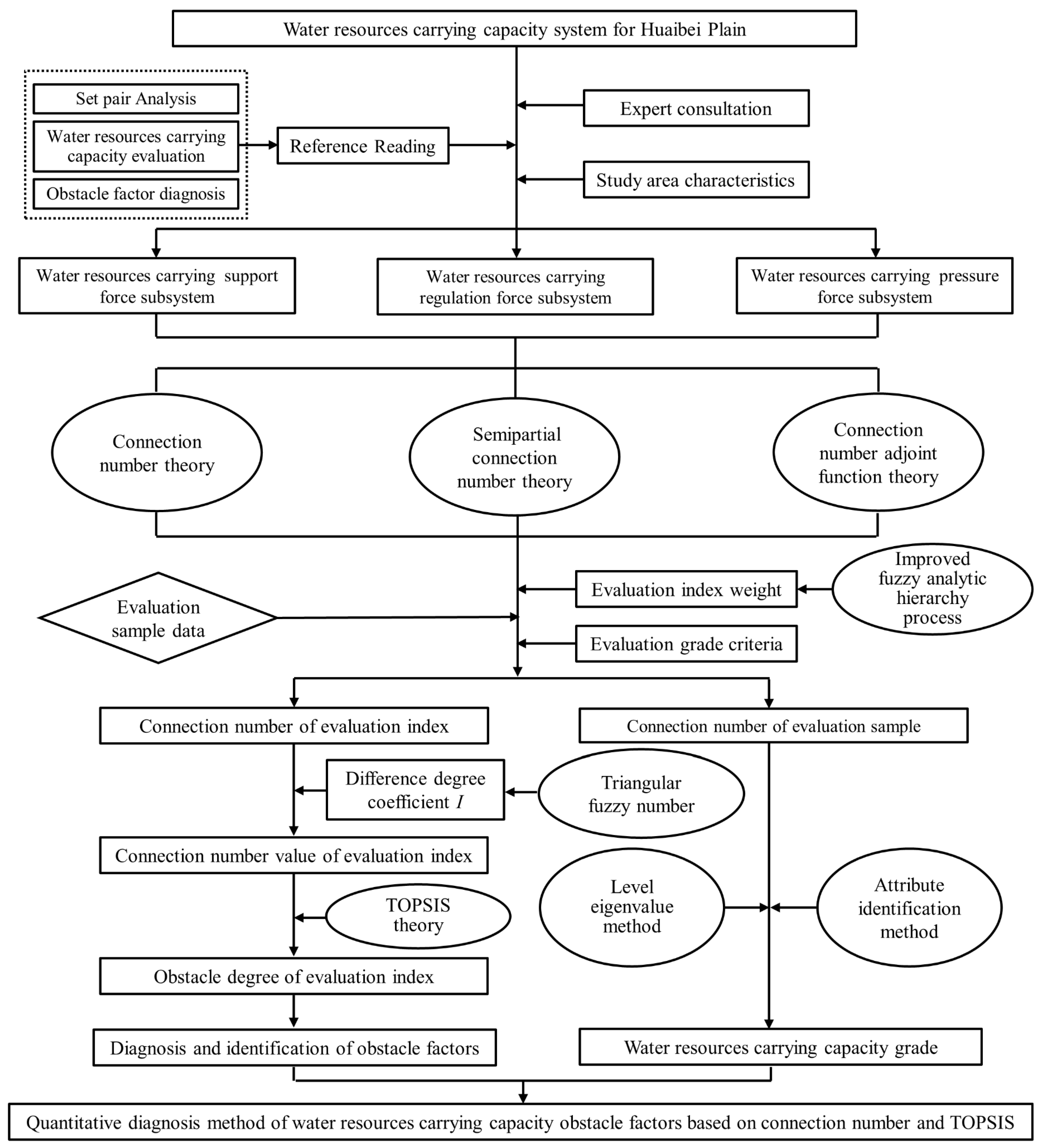
:1. Introduction
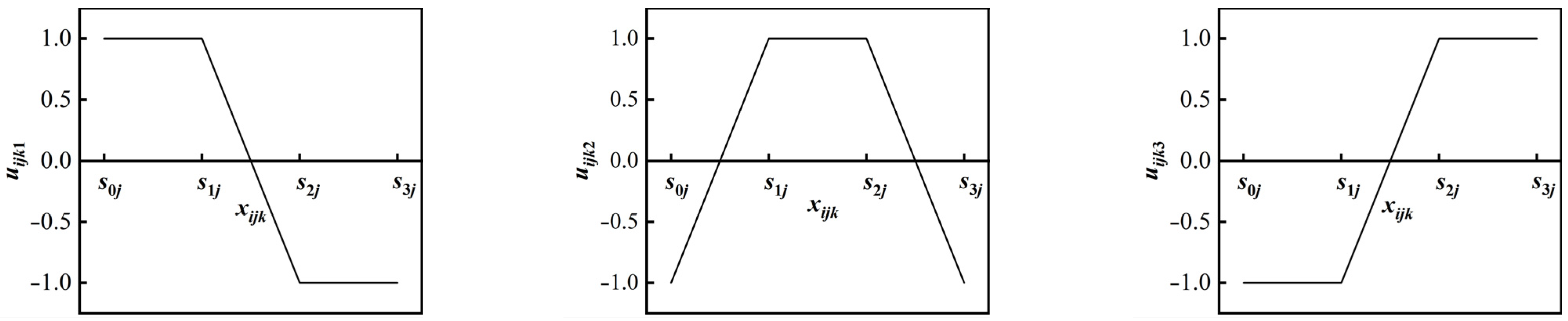
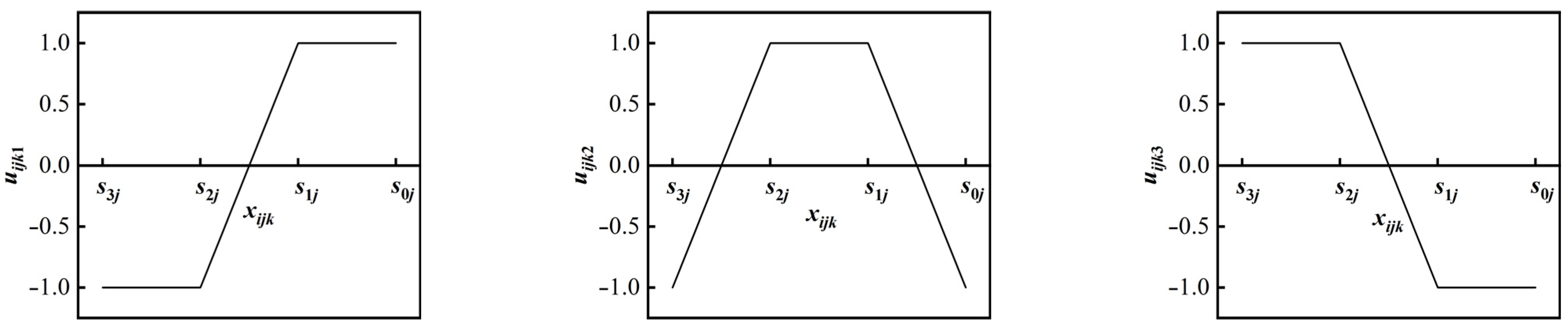
2. Materials and Methods
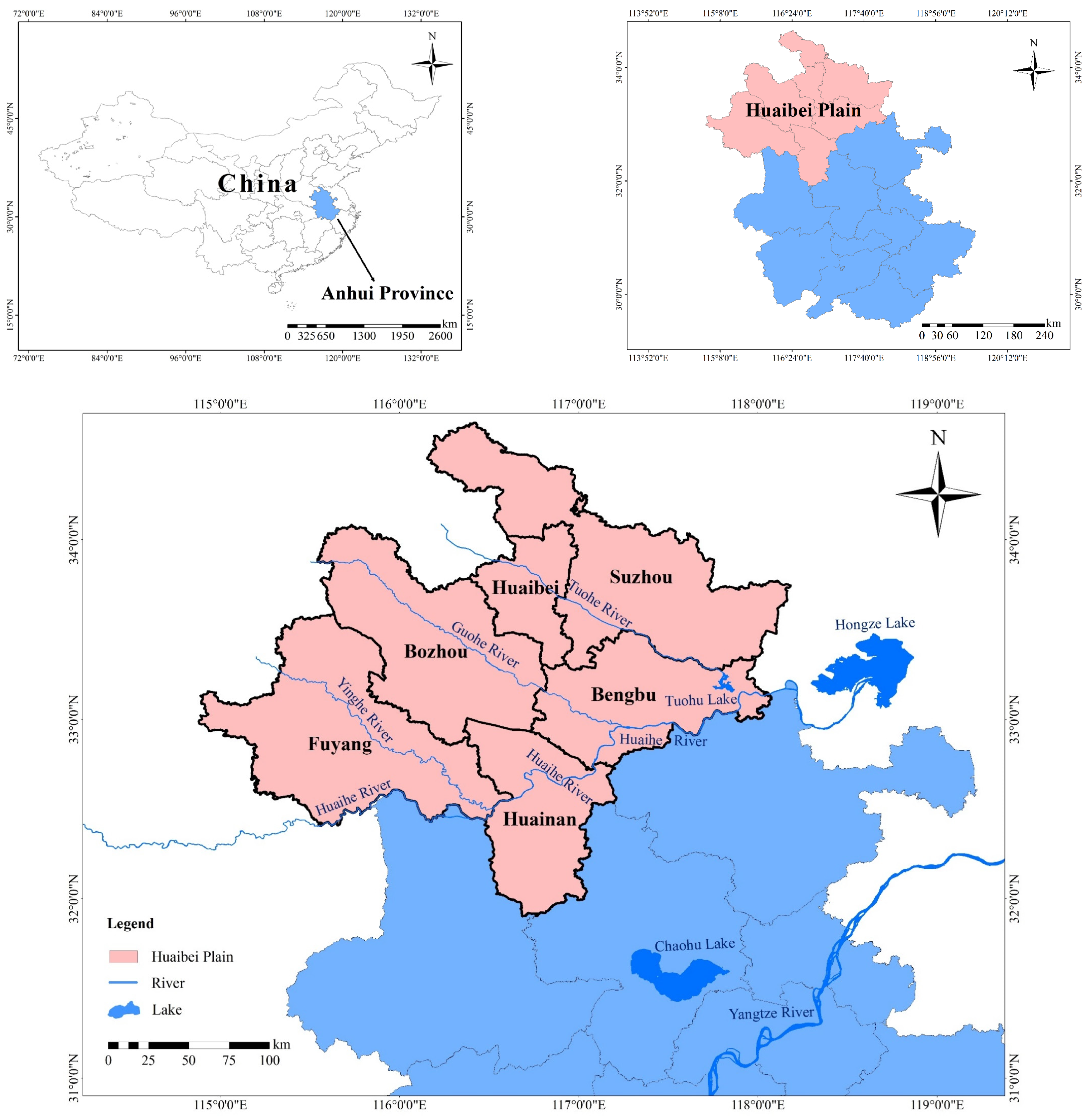
3. Study Area
4. Results and Discussion
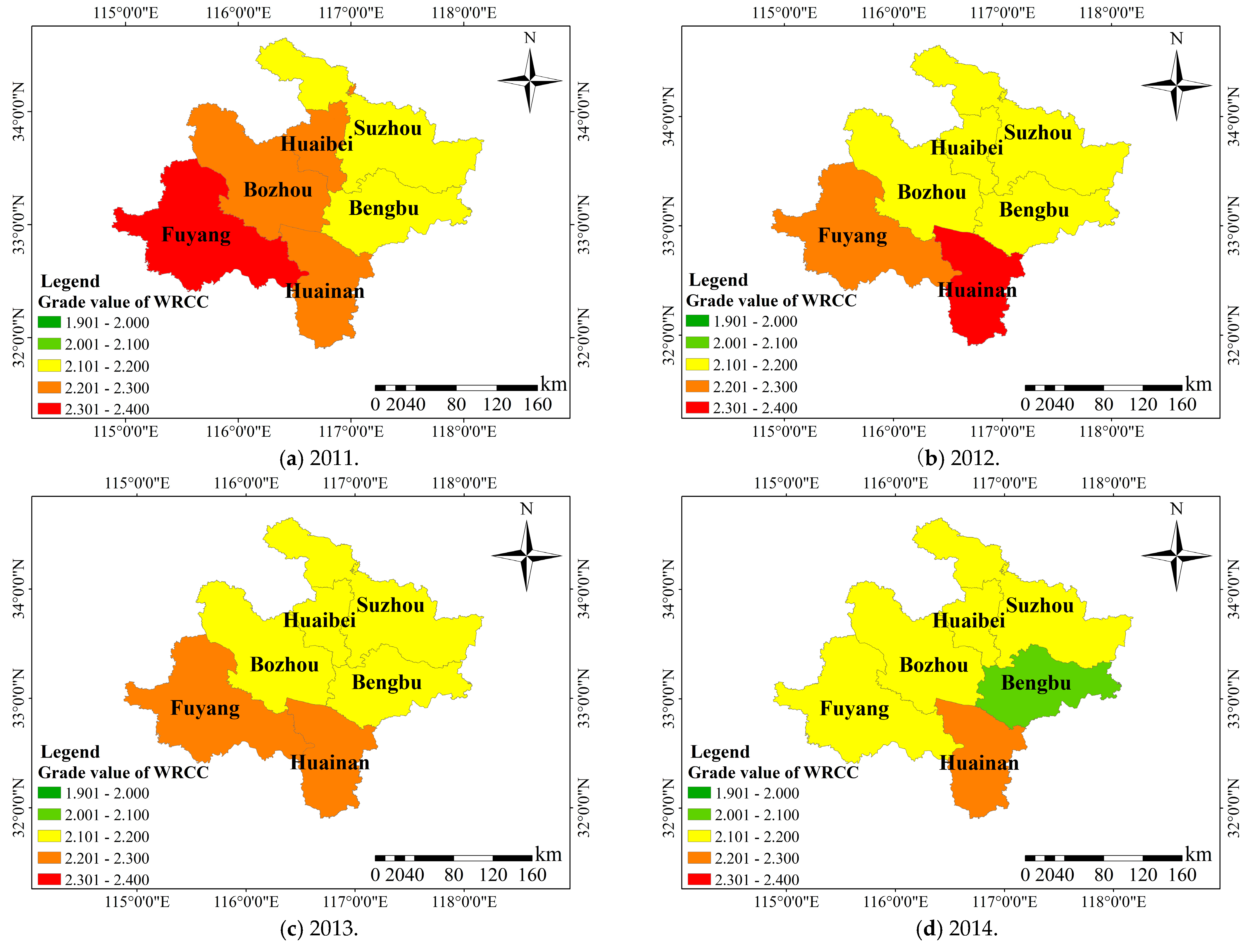
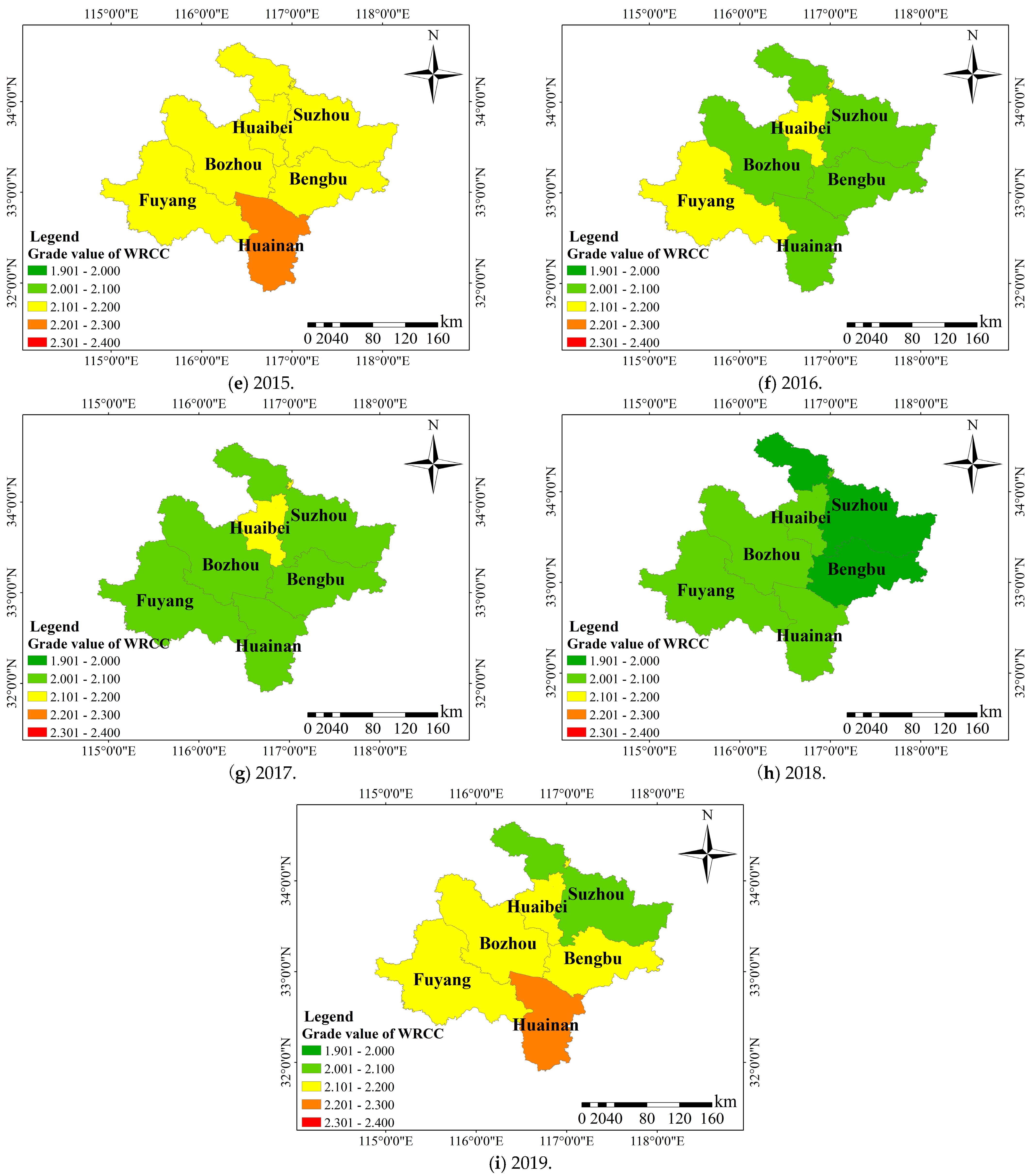
4.1. Evaluation of the Water Resources Carrying Capacity
- (1)
- From 2011 to 2019, the WRCC grades of Huaibei City, Bozhou City, Fuyang City, and Huainan City were 2.027–2.208, 2.038–2.232, 2.071–2.312, and 2.022–2.314, respectively, which were between critically overloaded and overloaded states; those of Suzhou City and Bengbu City, 1.990–2.160 and 1.975–2.160, respectively, were between loadable and critically overloaded states in 2018, and between critically overloaded and overloaded states in the remaining years. Overall, the WRCC of Huaibei Plain fluctuated around grade 2 from 2011 to 2019; the evaluation grades calculated using the attribute identification method were either grade 2 or grade 3. The grades of the two methods were in good agreement, indicating that the mobility matrix proposed in this paper, which quantitatively portrayed the microscopic movements among the connection number components, were feasible and effective, verifying the reliability of the proposed method. It provides a new insight into the accurate and reasonable determination of the connection number and the quantitative evaluation of the WRCC, and will provide technical support for regional water resources management with the goal of achieving sustainable utilization.
- (2)
- In time, the WRCC in Huaibei Plain as a whole showed a good development trend gradually, e.g., Bozhou City changed from 2.232 in 2011 to 2.038 in 2018 and to 2.171 in 2019. It is associated with the strictest water resource management system in Anhui Province since 2013. In space, the WRCC of Fuyang City and Huainan City was worse than that of the other four cities from 2011 to 2019. Over the nine years, the average grades for Fuyang City and Huainan City were 2.26 and 2.43, while the grades for Huaibei City, Bozhou City, Suzhou City, and Bengbu City were 2.19, 2.12, 2.05, and 2.05, respectively, which was mainly related to the water resources, the number of resident population, GDP, and the farmland irrigation quota; the WRCC of Huainan City was the poorest among the six cities in 2013–2015 and 2019, and Fuyang City was the poorest among the six cities in 2011, 2013, and 2016. These findings indicate that the method of this paper, in time, realized the dynamic analysis of the WRCC system and a judgment of its development trend; in space, the spatial difference in the WRCC in Huaibei Plain can be accurately identified. This will help to quantitatively and qualitatively analyze the WRCC system and grasp the development trend of the water resources system.
- (3)
- The WRCC in Huaibei Plain had a tendency to become worse during 2019 due to the drought in Anhui Province. By reviewing the available information, from March 2019, rainfall continued to be low, with 70% less rainfall than normal during the plum rainy period in Huaibei. From August 12th to November 11th, the weather in Anhui Province was sunny and hot with little rain, with the province’s average rainfall being 70% less than normal. In 2019, the annual rainfall in Huaibei City, Bozhou City, Suzhou City, Bengbu City, Fuyang City, and Huainan City was 611.7 mm, 566.8 mm, 593.4 mm, 614.9 mm, 552.1 mm, and 560.5 mm, accounting for 65.37%, 60.57%, 63.41%, 65.71%, 59.00%, and 59.90% of the province’s annual rainfall (935.8 mm), respectively. Soil moisture monitoring results showed that the area of Anhui Province undergoing severe drought was 2.0 × 104 km2, moderate drought was about 4.3 × 104 km2, and mild drought was about 4.7 × 104 km2, with the drought area of soil moisture accounting for about 79% of the total area of the province. The affected area in the province was 6793.3 km2, of which 1346.7 km2 was along the northern part of the Huaihe River. In addition, the per capita water resources in Huaibei Plain also decreased in 2019 compared to previous years, with the per capita water resources of Huaibei City, Bozhou City, Suzhou City, Bengbu City, Fuyang City, and Huainan City being 211.45 m3, 279.16 m3, 312.84 m3, 311.86 m3, 207.05 m3, and 222.39 m3, respectively, accounting for 24.93%, 32.92%, 36.89%, 36.77%, 24.41%, and 26.22% of the province’s per capita water resources (848.07 m3), respectively. From the perspective of the physical causes that form the water resources carrying state, as the factors affecting the water resources carrying state in Huaibei Plain (such as water resources) changed in 2019, its WRCC grade was bound to respond under the effect of a certain relationship’s structure; the response results were consistent with actual perceptions, meaning that the evaluation method constructed in this paper was more responsive under the changing conditions. This will provide the basis for managers to establish more targeted water management measures, as a more responsive approach has greater precision and more comprehensive information.
- (4)
- Cui et al. [22] constructed a set pair analysis evaluation model to obtain a WRCC grade value of 2.32 for Huaibei City, which was between critically overloaded and overloaded states. Gao et al. [48] reported that a fuzzy integrated model was used to estimate the WRCC in Suzhou City, which was close to being overloaded and had little potential for utilization of water resources. Wang [49] used a multi-level fuzzy-integrated evaluation model based on AHP assignment, and their evaluation results showed the largest affiliation to the overloaded state, indicating that the overall WRCC of Fuyang City is weak. Furthermore, Bai [50] used a coupled evaluation model based on gray correlation, and SPA calculated the WRCC grade of Bozhou City from 2012 to 2015, all of which were grade 2; Fuyang City was grade 3 from 2012 to 2013 and grade 2 from 2014 to 2015; Huainan City was grade 3 in 2012, 2013, and 2015 and grade 2 in 2014. The results of this paper were well consistent with available studies, all suggesting that the WRCC in Huaibei Plain is poor.
4.2. Diagnosis of the Water Resources Carrying Capacity Obstacle factors
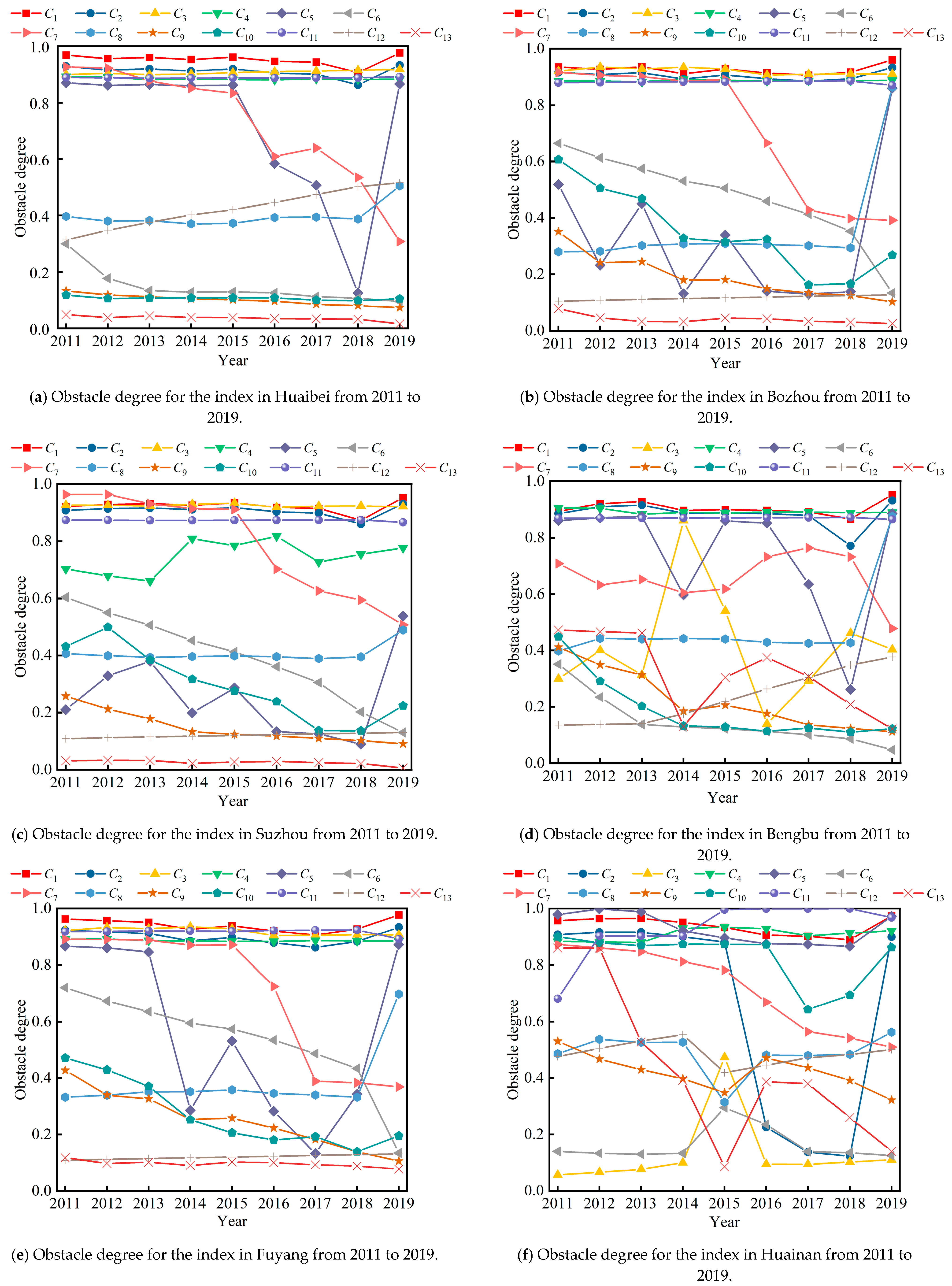
- (1)
- The WRCC obstacle degree of each index changed with the evaluation area and the evaluation year, and even for the same index, its obstacle degree changed with the evaluation sample, which showed that the method constructed in this paper can dynamically diagnose and identify obstacle factors. Taking Huainan City as an example, the obstacle degree was ranked from largest to smallest as C11 > C4 > C1 > C5 > C10 > C7 > C8 > C12 > C9 > C13 > C6 > C2 > C3 in 2018, and C1 > C5 > C11 > C4 > C2 > C10 > C8 > C7 > C12 > C9 > C13 > C6 > C3 in 2019, respectively. In terms of the evaluation indexes, the water resources carrying capacity state of six cities in the Huaibei Plain developed positively from 2011–2018, while the main reason for the deterioration in 2019 was attributed to the low precipitation in that year, the decrease in water resources, and the high degree of water resource utilization. The average obstacle degree of the per capita water resources C1 (average value of 2011–2018) of the six cities in the Huaibei Plain increased from 0.9263 to 0.9654 in 2019; the average obstacle degree of the annual water production modulus C2 increased from 0.8517 to 0.9271, the average obstacle degree of the utilization ratio of water resources C5 increased from 0.5567 to 0.8322, and the average obstacle degree of the per capita daily domestic water consumption increased from 0.3887 to 0.6655. These data showed that the precipitation in the cities of Huaibei Plain in the year 2019 ranged from 552.1 mm–614.9 mm, which was about 40% less compared to 2018 and about 30% less compared to the multi-year average. It can be seen that the quantitative diagnostic method of the regional WRCC obstacle factors based on the CN and TOPSIS constructed in this paper can effectively identify the change process of carrying capacity evaluation indexes, and the year-by-year change in the obstacle degree can quantitatively analyze the reasons for the change in the carrying state.
- (2)
- The main obstacle factors affecting the enhancement in the WRCC in Huaibei City were C1, C2, C3, C4, and C7 in 2011–2012, and C1, C2, C3, C4, and C11 in 2013–2019.The water consumption ratio of the ecological environment C7, has been improved, and its obstacle degree decreased from 0.9268 in 2011 to 0.3081 in 2019, and was no longer a key obstacle factor. From this, it can be determined that the key obstacle factors hindering the improvement in the WRCC in Huaibei City were the per capita water resources C1, the annual water production modulus C2, the per capita water supply C3, the vegetation coverage ratio C4, and the population density C11, of which there are four (4/4 × 100 = 100%), zero, and one (1/6 × 100% = 16.7%) in the support, regulation, and pressure force subsystems, respectively. At the same time, the per capita water resources C1, as the first obstacle factor, appeared eight times (years) in nine years, indicating that the main reason for the WRCC of Huaibei City to be between the critically overloaded and overloaded states for a long time was the insufficient support force. Based on the year-by-year changes in the obstacle degree of the indexes to analyze the causal mechanism of the carrying state, the obstacle degree of the utilization ratio of water resources C5, the per capita GDP C6, the water consumption ratio of the ecological environment C7, the water consumption per CNY 104 GDP C9, the water consumption per 104 yuan value-added by industry C10, and the farmland irrigation quota C13 in Huaibei City from 2011 to 2018 had been decreasing gradually, i.e., these indexes improved. In terms of the evaluation indexes, this was also an important reason why the city’s WRCC grade was decreasing from 2.208 in 2011 to 2.027 in 2018, showing an improving trend. It was found that the utilization ratio of water resources in Huaibei City was 98.45% in 2011, showing a downward trend in recent years, which was directly related to the control of the “three red lines” (the red line of control of water resources development and utilization, etc.), reflecting the science and effectiveness of the most stringent water resources management system. The water consumption ratio of the ecological environment increased from 2 × 106 m3 in 2011 to 1.8 × 107 m3 in 2019, and the water consumption ratio of the ecological environment (the proportion of ecological water consumption to total water consumption) increased from 0.39% to 4.27%. The above two indexes, as importants part of the water resources regulation force, improved the water resources carrying state of Huaibei City. In addition, the indexes of water consumption per CNY 104 GDP and water consumption per 104 yuan value-added by industry, which were the pressure forces of the water resources, were also continuing to develop in a favorable way, and the pressure force was reduced. Therefore, in terms of the evaluation subsystems, the WRCC of Huaibei City developed in a positive direction due to the weakness in the pressure force and the enhancement in the regulation force. The main reason for the deterioration in the water resources carrying state in Huaibei City in 2019 was the low precipitation, the decrease in the water resources, the over-exploitation of the water resources, and the increase in per capita daily domestic water consumption, coupled with the fact that this city is located far away from the Huaihe River, the conditions for the diversion and transfer of water are insufficient, and the relevant data showed that the total water resources of Huaibei City was 1.8 × 108 m3 in 2019. which was 63.5% less than that of 2018, and 42.3% less than the average value of many years. The diagnostic results of this city’s water resources carrying state were in line with the actual situation, which indicated that the quantitative diagnostic method of the WRCC factors based on the connection number and TOPSIS, which was constructed in this paper, was effective.
- (3)
- The main obstacle factors affecting the enhancement in the WRCC in Bozhou City were C1, C2, C3, C4, and C7 in 2011–2015, and C1, C2, C3, C4, and C11 in 2013–2019. The water consumption ratio of the ecological environment C7 increased from 0.36% in 2011 to 3.76% in 2019, and its obstacle degree declined from 0.9167 to 0.3920, and the index was no longer a key factor restricting the improvement in the WRCC. Therefore, the key obstacle factors hindering the enhancement in its WRCC were the per capita water resources C1, the annual water production modulus C2, the per capita water supply C3, the vegetation coverage ratio C4, and the population density C11, which was consistent with that of Huaibei City. Insufficient support force was still an important reason for Bozhou City’s WRCC to jump from a critically overloaded or overloaded to a loadable state. In Bozhou City, the obstacle degree of the per capita GDP C6, the water consumption ratio of the ecological environment C7, the water consumption per CNY 104 GDP C9, and the water consumption per 104 yuan value-added by industry C10 gradually decreased from 2011 to 2018, i.e., these indexes improved, while the overall obstacle degree of the per capita daily domestic water consumption C8 gradually increased, i.e., it deteriorated; the utilization ratio of water resources C5 fluctuated a lot. In terms of the evaluation indexes, the water resources carrying state of Bozhou City developed to a better state due to the degree in the improvements of C6, C7, C9, and C10 being greater than the degree of deterioration of C8, indicating that the increase in the per capita GDP, the increase in the water consumption ratio of the ecological environment, and the decrease in water consumption per CNY 104 GDP and water consumption per 104 yuan value-added by industry promoted its WRCC; meanwhile, the increase in the per capita daily domestic water consumption impeded the improvement of its carrying capacity, but the former was greater than the latter, and the overall performance of the WRCC showed a trend of improvement. In terms of the evaluation subsystems, the main reason was the increase in the regulation force. In addition, the C5 fluctuated greatly, and Bozhou City should earnestly implement the most stringent water resources system so that the utilization of their water resources can be kept in a reasonable range. The deterioration in the water resources carrying state of Bozhou City in 2019 was due to the combined effects of weakening support and regulation force and strengthening pressure force, with the per capita water resources C1 and the annual water production modulus C2 obstacle degree in the support force subsystem deteriorating from 0.9165 and 0.8936 in 2018 to 0.9602 and 0.9330 in 2019, respectively, the utilization ratio of water resources C5 in the regulation force subsystem deteriorating from 0.1381 in 2018 to 0.8603 in 2019, and the per capita daily domestic water consumption C8 in the pressure force subsystem deteriorating from 0.2934 in 2018 to 0.8636 in 2019.
- (4)
- The key obstacle factors affecting the enhancement in the WRCC in Suzhou City were C1, C2, C3, C7, and C11 in 2011–2015, and C1, C2, C3, C4, and C11 in 2016–2019. The water consumption ratio of the ecological environment C7 improved, while the vegetation coverage ratio C4 deteriorated, and the obstacle degree ranged between 0.6606–0.8174, keeping a high level. Therefore, the key obstacle factors hindering the improvement in the WRCC in Suzhou City were the per capita water resources C1, the annual water production modulus C2, the per capita water supply C3, the vegetation coverage ratio C4, and the population density C11, which showed that the water resources available was less while the population was more, and that the vegetation coverage was less, i.e., insufficient support force constraints on the improvement of the city’s WRCC. According to the related literature [51], the total water resources of Suzhou City were less, which led to its water resources carrying support force always being insufficient, which was consistent with the results of the analysis in this study. The obstacle degree of the utilization ratio of water resources C5, the per capita GDP C6, the water consumption ratio of the ecological environment C7, the water consumption per CNY 104 GDP C9, the water consumption per 104 yuan value-added by industry C10, and the farmland irrigation quota C13 in Suzhou City from 2011 to 2018 gradually decreased, i.e., these indexes improved, while the obstacle degree of the vegetation coverage ratio C4 and the urbanization ratio C12 gradually increased, i.e., these indexes worsened. In terms of the evaluation indexes, Suzhou City’s WRCC state developed into a better due to the overall reduction in the utilization ratio of water resources, the improvement in the economic development level, the increase in water consumption in the ecological environment year by year, and the reduction in the farmland irrigation quota. Although C4 and C12 were gradually deteriorating, and their obstacle degree deteriorated from 0.7031 and 0.1083 in 2011 to 0.7545 and 0.1279 in 2018, respectively the weight of C4 was only 0.028, and the multi-year average obstacle degree of C12 was 0.1199, which was not enough to cause a significant negative impact on the WRCC; therefore, under the dual positive and negative impacts in 2019, the reason for the deterioration in the WRCC in Suzhou City was similar to that of Bozhou City—mainly due to the weakening in the support force.
- (5)
- The key obstacle factors affecting the enhancement in the WRCC in Bengbu City were C1, C2, C4, C5, and C11 in 2011–2013 and 2015–2016, C1, C2, C3, C4, and C11 in 2014, C1, C2, C4, C7, and C11 in 2017–2018, and C1, C2, C4, C5, and C8 in 2019. The multi-year average obstacle degree of C5, C7, C8, and and C11 from 2011–2019 were 0.7742, 0.6582, 0.4800, and 0.8695, respectively, and C7 and C8 can be considered not to be the key obstacle factors; therefore, the per capita water resources C1, the annual water production modulus C2, the vegetation coverage ratio C4, the utilization ratio of water resources C5, and the population density C11 were the key obstacle factors restricting the enhancement in the WRCC of Bengbu City, in which the support force, regulation force, and pressure force subsystems were four (3/4 × 100% = 75%), one (1/3 × 100% = 33.3%), and one (1/6 × 100% = 16.7%), respectively; meanwhile, C1, as the first obstacle factor, appeared seven times (years) in nine years. Thus, the major reason for hindering the improvement in the WRCC of Huaibei City was an insufficient support force and a strong pressure force; meanwhile, the role of the regulation force was not obvious. The obstacles degree of the utilization ratio of water resources C5, the per capita GDP C6, the water consumption per CNY 104 GDP C9, the water consumption per 104 yuan value-added by industry C10, and the farmland irrigation quota C13 have gradually decreased in Bengbu City from 2011 to 2018. In terms of the evaluation indexes, these indexes have improved to promote the carrying capacity. Therefore, rationally controlling the degree in water resource utilization, promoting economic growth through market regulation, improving the efficiency of industrial water resource utilization, and rationally controlling the agricultural irrigation quota to improve the efficiency in agricultural water resource utilization were powerful measures to improve the severe situation of the WRCC in Bengbu City. The major reason for the deterioration in the WRCC in Bengbu City in 2019 was the weakening of the support force and the strengthening of the pressure force. The per capita water resources C1 and the annual water production modulus C2 in the support subsystem deteriorated, and these obstacle degrees increased from 0.8659 and 0.7711 to 0.9532 and 0.9325 in 2018, respectively. The per capita daily domestic water consumption C8 in the pressure force subsystem also deteriorated, and the obstacle degree increased from 0.4271 to 0.8757 in 2018.
- (6)
- The key obstacle factors affecting the enhancement in the WRCC in Fuyang City were C1, C2, C3, C4, and C11 in 2011–2012, C1, C2, C3, C7, and C11 in 2013, and C1, C2, C3, C4, and C11 in 2014–2019. The utilization ratio of water resources C5 has continued to evolve in a positive direction in 2011–2019, and decreased from 88.16% to 46.97%, and the corresponding obstacle degree decreased from 0.8661 to 0.3427, which was no longer the key obstacle factor. Therefore, the per capita water resources C1, the annual water production modulus C2, the per capita water supply C3, the vegetation coverage ratio C4, and the population density C11 were the key obstacle factors limiting the improvement in the WRCC in Fuyang City. The obstacle degree of the utilization ratio of water resources C5, the per capita GDP C6, the water consumption ratio of the ecological environment C7, the water consumption per CNY 104 GDP C9, the water consumption per 104 yuan value-added by industry C10, and the farmland irrigation quota C13 in Fuyang City from 2011 to 2018 gradually decreased, i.e., the indexes improved, while the obstacle degrees of C8 and C12 gradually increased, i.e., the indexes worsened. In terms of the evaluation indexes, the water resources carrying state of Fuyang City developed to a better due to the overall decrease in the utilization ratio of water resources, the increase in the level of economic development, the increase in water consumption of the ecological environment year by year, and the decrease in the farmland irrigation quota, which was similar to that of Suzhou City. C8 and C12 gradually deteriorated due to the weights of C8 and C12 only being 0.0396 and 0.0632; meanwhile, the multi-year average obstacle degrees of C8 and C12 were 0.3830 and 0.1204, respectively, which did not play a dominant role in the direction of the evolution of the WRCC being insufficient; therefore, the utilization ratio of water resources C5, the per capita GDP C6, the water consumption ratio of the ecological environment C7, the water consumption per CNY 104 GDP C9, the water consumption per 104 yuan value-added by industry C10, and the farmland irrigation quota C13 drove the change in the WRCC in Fuyang City, which was the main driving factor for the development of the carrying capacity. In terms of the evaluation subsystem, the reason for the good development of the WRCC in Fuyang City was the reduction in the water resources carrying pressure force and the increment of the regulation force. The major reason for the deterioration of Fuyang City’s WRCC state in 2019 was the weakening of the support force and regulation force. The per capita water resources C1 and the annual water production modulus C2 in the support force subsystem deteriorated, and the obstacle degree increased from 0.9273 and 0.8827 in 2018 to 0.9769 and 0.9336, respectively, while the utilization ratio of water resources C5 in the regulation force subsystem deteriorated, and the obstacle degree of it increased from 0.3427 in 2018 to 0.8715.
- (7)
- The key obstacle factors affecting the enhancement in the WRCC in Huainan City were C1, C2, C4, C5, and C10 in 2011, C1, C2, C4, C5, and C11 in 2012–2015 and 2019, and C1, C4, C5, C10, and C11 in 2016–2018. The annual water production modulus C2 continued to improve in 2011–2018, and the degree of obstacle decreased from 0.9075 to 0.1228, which can no longer constrain the carrying capacity leap, meaning that the key obstacle factors hindering the improvement in the WRCC in Huainan City were the per capita water resources C1, the vegetation coverage ratio C4, the utilization ratio of water resources C5, the water consumption per 104 yuan value-added by industry C10, and the population density C11, of which there were two indexes for the support force subsystem (2/4 × 100 = 50%), one index for the regulation force subsystem (1/3 × 100 = 33.3%), and two indexes for the pressure force subsystem (2/6 × 100 = 33.3%). In recent years, the situation of these three subsystems were more serious, which, together, caused the city’s water resources carrying capacity in the long term being in between the critically overloaded and overloaded states. Based on the year-by-year changes in the obstacle degree of the indexes to analyze the reasons for the changes in the carrying state, the obstacle degree of the per capita GDP C6, the water consumption ratio of the ecological environment C7, the water consumption per CNY 104 GDP C9, and the farmland irrigation quota C13 in Huainan City from 2011–2018 gradually decreased, which meant that these indexes improved, while the obstacle degree of the population density C11 gradually increased, which meant that the index worsened. It was found that on December 31, 2015, Shouxian County of Lu’an City was transferred to the jurisdiction of Huainan City, and its population density increased accordingly, and the diagnostic results of this city were in line with the reality. In terms of the evaluation indexes, the water resources carrying state of Huainan City has developed in a good direction due to the increase in the level of economic development, the increase in water consumption of the ecological environment year by year, a more coordinated relationship between economic development and water resource utilization, and the reduction in the farmland irrigation quota. The indexes of C7 and C13 have improved remarkably, decreasing to 0.5096 and 0.1403 from 0.8726 and 0.9002, respectively. Despite the fact that C11 has been progressively deteriorating, the weight of C11 is only 0.0792, which was not able to form a high pressure state, meaning that the WRCC of Huainan City was finally more inclined to the direction of improvement. In terms of the evaluation subsystem, the WRCC of Huainan City developed in the direction of improvement due to the pressure force decreasing and the regulation force increasing. The main reason for the deterioration in the WRCC of Huainan City in 2019 was the weakness of the support force and the regulation force and the increase in the pressure force. The per capita water resources C1 and the annual water production modulus C2 in the support force subsystem deteriorated, and these obstacle degrees increased to 0.9733 and 0.8944 from 0.8891 and 0.1228 in 2018, respectively. At the same time, the utilization ratio of water resources C5 in the regulation force subsystem deteriorated, and the obstacle degree of it increased to 0.9726 from 0.8658 in 2018.
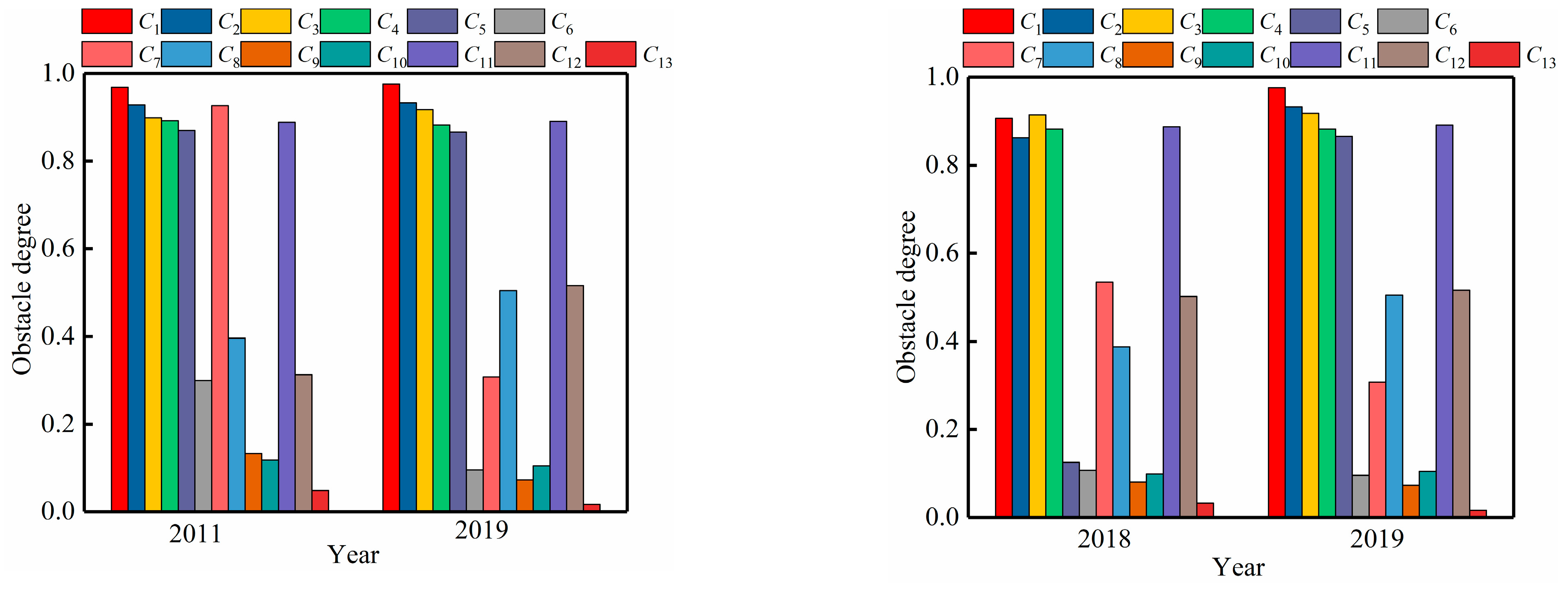
- (1)
- The key obstacle factors for Huaibei City in 2011 were the per capita water resources C1, the annual water production modulus C2, the per capita water supply C3, the vegetation coverage ratio C4, and the water consumption ratio of the ecological environment C7; however, those for both 2018 and 2019 were the per capita water resources C1, the annual water production modulus C2, the per capita water supply C3, the vegetation coverage ratio C4, and the population density C11, which showed that these obstacle factors continued to change over time, but in adjacent years tended to be similar.
- (2)
- In 2018, the key obstacle factors for Huaibei City and Bozhou City were the per capita water resources C1, the annual water production modulus C2, the per capita water supply C3, the vegetation coverage ratio C4, and the population density C11. Huainan City had the per capita water resources C1, he vegetation coverage ratio C4, the utilization ratio of water resources C5, the water consumption per 104 yuan of value-added by industry C10, and the population density C11. Referring to the geographical location and administrative zoning map of Huaibei Plain, Anhui Province, Huaibei City was adjacent to Bozhou City and had similarities in terms of its water resources, hydrological element distribution, and other aspects; however, Huaibei City and Huainan City were significantly different in spatial location and presented spatial differences in the obstacle factors of the WRCC.
- (3)
- It can be seen that the method constructed in this paper not only provides a new intelligent method for the diagnosis of obstacle factors, but also identifies the distribution characteristics and spatial–temporal scale change rules of the key obstacle factors, which will help water resource managers to accurately regulate all elements of the water resource system, to realize the water resources carrying state to the better, and to promote the sustainable utilization of water resources.
5. Conclusions
- (1)
- The WRCC of the Huaibei Plain varied around grade 2 from 2011–2019, and its insufficient support force was the main reason why the WRCC of the Huaibei Plain has been in between the critically overloaded and overloaded states for a long period of time; the water resources carrying state improved from 2011–2018 due to the gradual improvement in the per capita GDP and the water consumption ratio of the ecological environment, etc., i.e., the regulation force was enhanced, and the WRCC of the Huaibei Plain was on a trend of deterioration in 2019, with certain factors, such as low precipitation in that year, reduced water resources, and a higher degree of water resource utilization, being listed as important reasons. Spatially, the WRCC of Fuyang City and Huainan City in 2011–2019 was worse than the other four cities, which was mainly related to the regional water resources, population size, GDP, and farmland irrigation quota. The above results are in good agreement with official data sources and the literature. In addition, the factors affecting the water resources carrying state of the Huaibei Plain changed in 2019, and the method constructed in this paper can dynamically identify the changes in the WRCC, which shows that it is effective to determine the connection number components based on the mobility matrix, as well as to dynamically determine the difference degree coefficient using the semi-partial subtraction set pair potential and triangular fuzzy number, and that this method is sensitive to the response under the changing conditions, which contributes to the precise management of water resources.
- (2)
- The key obstacles factors affecting the enhancement in the WRCC in the Huaibei Plain were the per capita water resources C1, the annual water production modulus C2, the per capita water supply C3, the vegetation coverage ratio C4, the utilization ratio of water resources C5, the water consumption per 104 yuan value-added by industry C10, and the population density C11. These indexes are in urgent need of manual regulation. The method in this paper overcame the static bias in the difference degree coefficient and the shortcomings of the previous diagnosis method, and the diagnosis results of the key obstacle factors are consistent with the water resources condition of Huaibei Plain, which provides a new perspective for the diagnosis of the WRCC obstacle factors.
- (3)
- In time and space, there were differences and similarities in the key obstacle factors. The obstacle factors continued to change over time, but in adjacent years tended to show similarities, such as Huaibei City in 2018 and 2019. In addition, the key obstacle factors in adjacent regions generally exhibited spatial similarity, such as Huaibei City and Bozhou City in 2018, while regions with significantly different spatial locations generally appeared as having a spatial difference, such as Huaibei City and Huainan City in 2018, which is consistent with the distribution of regional water resources and hydrological elements. It is thus clear that the method of this paper not only provides a new intelligent method for the diagnosis of obstacle factors, but also analyzes and identifies the distribution characteristics and spatial–temporal scale change rules of the obstacle factors.
- (4)
- The quantitative diagnosis method of obstacle factors of the WRCC based on the CN and TOPSIS adopted the idea of evaluation–diagnosis–regulation, which can quantitatively express the distance between each evaluation index and optimal solution and provide the obstacle degree, with a strong interpretation of physical meaning, a sensitive response under changing conditions, and evaluation and diagnosis results that were accurate and reliable. It not only affords a new insight into water resource management, but also offers an impactful way to accurately evaluate the resource and environmental carrying capacity, diagnose the obstacle factors, and enrich the analysis theory and the method of uncertainty systems that integrate comprehensive evaluation obstacle factor diagnosis regulation. For example, the method constructed in this paper can be applied to the diagnosis and analysis of the ecological carrying capacity, the agricultural green development level, and the regional resource and environmental carrying capacity obstacle factors. It is worth emphasizing that, when applying the method, attention should be paid to the validity of the selection of the evaluation indexes and the rationality of the evaluation results. The research method is only feasible when the research results are consistent with the actual situation.
- (5)
- The scale of our study is not fine enough due to the limitations of the raw data. In the future, we can also define the study area unit at a smaller scale, for example, at the county administrative level or in a kilometer grid (1 km × 1 km), and we can use spatial data analysis tools to evaluate the regional water resources carrying capacity and identify obstacle factors in a more refined way. We could also interface with the managers responsible for the water resources carrying capacity authorities regarding the evaluation results with a view to obtaining their approval.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gulishengmu, A.; Yang, G.; Tian, L.; Pan, Y.; Huang, Z.; Xu, X.; Gao, Y.; Li, Y. Analysis of Water Resource Carrying Capacity and Obstacle Factors Based on GRA-TOPSIS Evaluation Method in Manas River Basin. Water 2023, 15, 236. [Google Scholar] [CrossRef]
- Jia, Y.; Wang, H. Study on Water Resource Carrying Capacity of Zhengzhou City Based on DPSIR Model. Int. J. Environ. Res. Public Health 2023, 20, 1394. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Song, S.; Li, F.; Yu, G.; He, G.; Cui, H.; Wang, R.; Sun, B.; Du, D.; Chen, G.; et al. Evaluating farmland ecosystem resilience and its obstacle factors in Ethiopia. Ecol. Indic. 2023, 146, 109900. [Google Scholar] [CrossRef]
- Yuan, K.; Hu, B.; Niu, T.; Zhu, B.; Zhang, L.; Guan, Y. Competitiveness Evaluation and Obstacle Factor Analysis of Urban Green and Low-Carbon Development in Beijing-Tianjin-Hebei Cities. Math. Probl. Eng. 2022, 2022, 5230314. [Google Scholar] [CrossRef]
- Zhu, J.; Li, X.; Zeng, X.; Zhong, K.; Xu, Y. Cultivated Land-Use Benefit Evaluation and Obstacle Factor Identification: Empirical Evidence from Northern Hubei, China. Land 2022, 11, 1386. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, Y.; Chen, H.; Zhu, L.; Wang, Y. Trend analysis and obstacle factor of inter provincial water resources carrying capacity in China: From the perspective of decoupling pressure and support capacity. Environ. Sci. Pollut. Res. 2022, 29, 31551–31566. [Google Scholar] [CrossRef]
- Meng, L.; Liu, Y.; Ma, W.; Wang, Q.; Mo, X.; Tian, J. Variable fuzzy evaluation model for water resources carrying capacity in the Tarim River Basin, China. Water Supply 2022, 22, 1445–1458. [Google Scholar] [CrossRef]
- Qin, J.; Niu, J.; Niu, W. Research on water resource carrying capacity of capital water conservation functional zone. Front. Environ. Sci. 2023, 10, 1108631. [Google Scholar] [CrossRef]
- Khorsandi, M.; Homayouni, S.; van Oel, P. The edge of the petri dish for a nation: Water resources carrying capacity assessment for Iran. Sci. Total Environ. 2022, 817, 153038. [Google Scholar] [CrossRef]
- Yan, B.; Xu, Y. Evaluation and prediction of water resources carrying capacity in Jiangsu Province, China. Water Policy 2022, 24, 324–344. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, C.; Hu, X.; Mei, H.; Hu, R. Evaluating water resource carrying capacity using the deep learning method: A case study of Yunnan, Southwest China. Environ. Sci. Pollut. Res. 2022, 29, 48812–48826. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Jiang, S.; Zhao, Y.; Li, H.H.; Zhu, Y.N.; Ling, M.H.; Qi, T.X.; He, G.H.; Yao, Y.; Wang, H. Comprehensive evaluation and scenario simulation of water resources carrying capacity: A case study in Xiong’an New Area, China. Ecol. Indic. 2023, 150, 110253. [Google Scholar] [CrossRef]
- Li, T.; Duan, Z.; He, H.; Song, H. Study on the Carrying Capacity and Change Trend of Groundwater Resources in Coal Mining Area: A Case Study of a Coal Mine in Northwest China. Water 2023, 15, 1551. [Google Scholar] [CrossRef]
- Ren, L.; Gao, J.; Song, S.; Li, Z.; Ni, J. Evaluation of Water Resources Carrying Capacity in Guiyang City. Water 2021, 13, 2155. [Google Scholar] [CrossRef]
- Yang, S.; Yang, T. Exploration of the dynamic water resource carrying capacity of the Keriya River Basin on the southern margin of the Taklimakan Desert, China. Reg. Sustain. 2021, 2, 73–82. [Google Scholar] [CrossRef]
- Wang, J.; Mu, X.; Chen, S.; Liu, W.; Wang, Z.; Dong, Z. Dynamic evaluation of water resources carrying capacity of the Dianchi Lake Basin in 2005–2015, based on DSPERM framework model and simulated annealing-projection pursuit model. Reg. Sustain. 2021, 2, 189–201. [Google Scholar] [CrossRef]
- Cao, W.; Deng, J.; Yang, Y.; Zeng, Y.; Liu, L. Water Carrying Capacity Evaluation Method Based on Cloud Model Theory and an Evidential Reasoning Approach. Mathematics 2022, 10, 266. [Google Scholar] [CrossRef]
- Jin, J.L.; Sheng, S.X.; Cui, Y.; Zhang, X.Y.; He, P.; Ning, S.W. Dynamic evaluation of water resources carrying capacity in the Yellow River diversion irrigation district based on semipartial subtraction set pair potential. J. Hydraul. Eng. 2021, 52, 507–520. (In Chinese) [Google Scholar] [CrossRef]
- Deng, L.; Yin, J.; Tian, J.; Li, Q.; Guo, S. Comprehensive Evaluation of Water Resources Carrying Capacity in the Han River Basin. Water 2021, 13, 249. [Google Scholar] [CrossRef]
- Li, Z.; Jin, J.; Cui, Y.; Zhang, L.; Wu, C.; Ning, S.; Zhou, Y. Dynamic evaluation of regional water resources carrying capacity based on set pair analysis and partial connection number. Water Supply 2022, 22, 2407–2423. [Google Scholar] [CrossRef]
- Zhou, R.; Jin, J.; Cui, Y.; Ning, S.; Zhou, L.; Zhang, L.; Wu, C.; Zhou, Y. Spatial Equilibrium Evaluation of Regional Water Resources Carrying Capacity Based on Dynamic Weight Method and Dagum Gini Coefficient. Front. Earth Sci. 2022, 9, 1–17. [Google Scholar] [CrossRef]
- Cui, Y.; Feng, P.; Jin, J.; Liu, L. Water Resources Carrying Capacity Evaluation and Diagnosis Based on Set Pair Analysis and Improved the Entropy Weight Method. Entropy 2018, 20, 359. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.; Zi, X.; Wang, S.; He, L. Evaluation and Optimization of Agricultural Water Resources Carrying Capacity in Haihe River Basin, China. Water 2019, 11, 999. [Google Scholar] [CrossRef]
- Xiang, W.; Yang, X.; Babuna, P.; Bian, D. Development, Application and Challenges of Set Pair Analysis in Environmental Science from 1989 to 2020: A Bibliometric Review. Sustainability 2022, 14, 153. [Google Scholar] [CrossRef]
- Cui, Y.; Zhou, Y.; Jin, J.; Wu, C.; Zhang, L.; Ning, S. Quantitative Evaluation and Diagnosis of Water Resources Carrying Capacity (WRCC) Based on Dynamic Difference Degree Coefficient in the Yellow River Irrigation District. Front. Earth Sci. 2022, 10, 816055. [Google Scholar] [CrossRef]
- Zhao, K.Q. Set Pair Analysis and Its Preliminary Application; Zhejiang Science and Technology Press: Hangzhou, China, 2000; pp. 11–24. [Google Scholar]
- Chen, M.; Ning, S.; Jin, J.; Cui, Y.; Wu, C.; Zhou, Y. Risk Assessment of Agricultural Drought Disaster on the Huaibei Plain of China Based on the Improved Connection Number and Entropy Information Diffusion Method. Water 2020, 12, 1089. [Google Scholar] [CrossRef]
- Wang, S.Y.; Dong, Z.C.; Zhang, L.; Jia, Q.W.; Xu, W.; Chen, Z.J. Ecological health evaluation of dike interference area based on average connection number and triangular fuzzy number. China Rural. Water Hydropower 2021, 10, 92–96, 104. (In Chinese) [Google Scholar]
- Sun, X.; Zhou, Z.; Wang, Y. Water resource carrying capacity and obstacle factors in the Yellow River basin based on the RBF neural network model. Environ. Sci. Pollut. Res. 2022, 30, 22743–22759. [Google Scholar] [CrossRef]
- Wang, D.; Li, Y.; Yang, X.; Zhang, Z.; Gao, S.; Zhou, Q.; Zhuo, Y.; Wen, X.; Guo, Z. Evaluating urban ecological civilization and its obstacle factors based on integrated model of PSR-EVW-TOPSIS: A case study of 13 cities in Jiangsu Province, China. Ecol. Indic. 2021, 133, 108431. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.; Wang, J.; Li, J.; Li, L. ExtendedTODIM-PROMETHEE IImethod with hesitant probabilistic information for solving potential risk evaluation problems of water resource carrying capacity. Expert Syst. 2021, 38, e12681. [Google Scholar] [CrossRef]
- Wang, W.; Jin, J.; Ding, J.; Li, Y. A new approach to water resources system assessment—Set pair analysis method. Sci. China Series E Technol. Sci. 2009, 52, 3017–3023. [Google Scholar] [CrossRef]
- Garg, H.; Kumar, K. A novel exponential distance and its based TOPSIS method for interval-valued intuitionistic fuzzy sets using connection number of SPA theory. Artif. Intell. Rev. Int. Sci. Eng. J. 2020, 53, 595–624. [Google Scholar] [CrossRef]
- Chen, S.Y. Theories and Methods of Variable Fuzzy Sets in Water Resources and Flood Control System; Dalian University of Technology Press: Dalian, China, 2005; pp. 3–20. [Google Scholar]
- Jin, J.L.; Wu, K.Y.; Wei, Y.M. Connection number based assessment model for watershed water security. J. Hydraul. Eng. 2008, 39, 401–409. (In Chinese) [Google Scholar] [CrossRef]
- Jin, J.-L.; Fu, J.; Wei, Y.-M.; Jiang, S.-M.; Zhou, Y.-L.; Wang, Y.-Z.; Wu, C.-G. Integrated risk assessment method of waterlog disaster in Huaihe River Basin of China. Nat. Hazards 2015, 75, 155–178. [Google Scholar] [CrossRef]
- Dingtian, Z.; Xiaoxi, Z. A Neural Network Forecasting Model of Beijing Environment Quality Based on Set Pare Analysis. Energy Procedia 2011, 5, 343–347. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, Y.; Xiong, P. Multiattribute Group Decision-Making Method Based on Quaternary Connection Number of Cloud Models. Math. Probl. Eng. 2022, 2022, 8101024. [Google Scholar] [CrossRef]
- Cheng, Q.S. Attribute recognition theoretical model with application. Acta Sci. Nat. Univ. Pekin. 1997, 33, 14–22. (In Chinese) [Google Scholar] [CrossRef]
- Jin, C.; Guan, Q.; Gong, L.; Zhou, Y.; Ji, Z. Evaluation of Regional Water Environmental Carrying Capacity and Diagnosis of Obstacle Factors Based on UMT Model. Water 2022, 14, 2621. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, S.; Xu, L.; Xu, H.; Guan, N. Resilience assessment and obstacle factor analysis of urban areas facing waterlogging disasters: A case study of Shanghai, China. Environ. Sci. Pollut. Res. 2023, 30, 65455–65469. [Google Scholar] [CrossRef]
- Zhang, K.; Shen, J.; He, R.; Fan, B.; Han, H. Dynamic Analysis of the Coupling Coordination Relationship between Urbanization and Water Resource Security and Its Obstacle Factor. Int. J. Environ. Res. Public Health 2019, 16, 4765. [Google Scholar] [CrossRef]
- Chen, M.; Wang, M.; Yin, H. Evaluation of sustainable urban land use based on weighted TOPSIS method: A case study of Chengdu City. IOP Conf. Series Earth Environ. Sci. 2019, 227, 062026. [Google Scholar] [CrossRef]
- Ou, Z.R.; Zhu, Q.K.; Sun, Y.Y. Regional ecological security and diagnosis of obstacle factors in underdeveloped regions: A case study in Yunnan Province, China. J. Mt. Sci. 2017, 14, 870–884. [Google Scholar] [CrossRef]
- Li, H.; Jin, J.L.; Wu, C.G.; Zhang, L.B. Dynamic evaluation and diagnostic analysis for water resources carrying capacity in Anhui Province based on connection number. South-to-North Water Transf. Water Sci. Technol. 2018, 16, 42–49. (In Chinese) [Google Scholar] [CrossRef]
- Lou, Y.Q.; Qiu, Q.T.; Zhang, M.T.; Feng, Z.L.; Dong, J. Spatial equilibrium evaluation of the water resources in Tai’an City based on the Lorenz Curve and Correlation Number. Water 2023, 15, 2617. [Google Scholar] [CrossRef]
- Kumar, K.; Garg, H. Connection number of set pair analysis based TOPSIS method on intuitionistic fuzzy sets and their application to decision making. Appl. Intell. 2018, 48, 2112–2119. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, H.M.; Xu, G.W.; Su, H.M. Fuzzy Comprehensive Evaluation of Water Resources Carrying Capacity in Suzhou City of Anhui Province. Adv. Mater. Res. 2012, 599, 686–689. [Google Scholar] [CrossRef]
- Wang, B. Comprehensive evaluation of water resources carrying capacity in Fuyang City. Harnessing Huaihe River 2013, 421, 9–11. (In Chinese) [Google Scholar]
- Bai, L. Comprehensive Evaluation and Trend Analysis of Regional Water Resources Carrying Capacity Based on Connection Number; Hefei University of Technology: Hefei, China, 2019. (In Chinese) [Google Scholar]
- Tang, Z.; Yang, T.Z. Comprehensive evaluation of water resources carrying capacity in Suzhou City based on AHP. Policy Res. Explor. 2018, 9, 78–79. (In Chinese) [Google Scholar]

| WRCC Subsystem System | Evaluation Index | Weight | Grade 1 (Loadable) | Grade 2 (Critically Overloaded) | Grade 3 (Overloaded) |
|---|---|---|---|---|---|
| Water resources carrying support force subsystem (B1) | C1—per capita water resources (m3/person) | 0.1332 | ≥1670 | 1670–1000 | <1000 |
| C2—annual water production modulus (104 m3/km2) | 0.1332 | ≥80 | 80–50 | <50 | |
| C3—per capita water supply (m3) | 0.1056 | ≥450 | 450–350 | <350 | |
| C4—vegetation coverage ratio (%) | 0.0280 | ≥40 | 40–25 | <25 | |
| Water resources carrying regulation force subsystem (B2) | C5—utilization ratio of water resources (%) | 0.0925 | ≤40 | 40–70 | >70 |
| C6—per capita GDP (yuan) | 0.0769 | ≥30,000 | 30,000–8000 | <8000 | |
| C7—water consumption ratio of the ecological environment (%) | 0.0305 | ≥5 | 5–1 | <1 | |
| Water resources carrying pressure force subsystem (B3) | C8—per capita daily domestic water consumption (L) | 0.0369 | ≤70 | 70–180 | >180 |
| C9—water consumption per CNY 104 GDP (m3) | 0.0792 | ≤100 | 100–400 | >400 | |
| C10—water consumption per 104 yuan of value-added by industry (m3) | 0.0596 | ≤50 | 50–200 | >200 | |
| C11—population density (person/km2) | 0.0792 | ≤200 | 200–500 | >500 | |
| C12—urbanization ratio (%) | 0.0632 | ≤50 | 50–80 | >80 | |
| C13—farmland irrigation quota (m3/hm2) | 0.0792 | ≤3750 | 3750–6000 | >6000 |
| District | Year | Connection Number Components of Index C4 | Connection Number Components of Index C6 | Connection Number Componentsof Index C8 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| vijk1 | vijk2 | vijk3 | vijk1 | vijk2 | vijk3 | vijk1 | vijk2 | vijk3 | ||
| Huainan City | 2011 | 0 | 0.426 | 0.574 | 0.503 | 0.497 | 0 | 0.263 | 0.500 | 0.238 |
| 2012 | 0 | 0.429 | 0.571 | 0.523 | 0.477 | 0 | 0.217 | 0.500 | 0.283 | |
| 2013 | 0 | 0.438 | 0.562 | 0.533 | 0.467 | 0 | 0.226 | 0.500 | 0.274 | |
| 2014 | 0 | 0.273 | 0.727 | 0.522 | 0.478 | 0 | 0.226 | 0.500 | 0.274 | |
| 2015 | 0 | 0.258 | 0.742 | 0.418 | 0.500 | 0.082 | 0.404 | 0.500 | 0.096 | |
| 2016 | 0 | 0.277 | 0.723 | 0.454 | 0.500 | 0.046 | 0.267 | 0.500 | 0.233 | |
| 2017 | 0 | 0.360 | 0.640 | 0.503 | 0.497 | 0 | 0.268 | 0.500 | 0.232 | |
| 2018 | 0 | 0.329 | 0.671 | 0.516 | 0.484 | 0 | 0.265 | 0.500 | 0.235 | |
| 2019 | 0 | 0.301 | 0.699 | 0.549 | 0.451 | 0 | 0.194 | 0.500 | 0.306 | |
| Year | Corrected Connection Number Components of Index C4 | Corrected Connection Number Components of Index C6 | Corrected Connection Number Components of Index C8 | |||||||
| 2011 | 0 | 0.451 | 0.549 | 0.502 | 0.498 | 0 | 0.276 | 0.469 | 0.255 | |
| 2012 | 0 | 0.452 | 0.548 | 0.515 | 0.485 | 0 | 0.238 | 0.469 | 0.293 | |
| 2013 | 0 | 0.459 | 0.541 | 0.522 | 0.478 | 0 | 0.246 | 0.469 | 0.285 | |
| 2014 | 0 | 0.338 | 0.662 | 0.515 | 0.485 | 0 | 0.246 | 0.469 | 0.285 | |
| 2015 | 0 | 0.325 | 0.675 | 0.408 | 0.481 | 0.111 | 0.395 | 0.479 | 0.126 | |
| 2016 | 0 | 0.340 | 0.660 | 0.445 | 0.488 | 0.067 | 0.279 | 0.469 | 0.252 | |
| 2017 | 0 | 0.404 | 0.596 | 0.502 | 0.498 | 0 | 0.280 | 0.469 | 0.251 | |
| 2018 | 0 | 0.381 | 0.619 | 0.511 | 0.489 | 0 | 0.278 | 0.469 | 0.253 | |
| 2019 | 0 | 0.360 | 0.640 | 0.533 | 0.467 | 0 | 0.219 | 0.470 | 0.311 | |
| District | Year | Connection Number Components | Level Eigenvalue Method | Attribute Identification Method | ||
|---|---|---|---|---|---|---|
| Huaibei City | 2011 | 0.201 | 0.391 | 0.409 | 2.208 | 3 |
| 2012 | 0.212 | 0.397 | 0.391 | 2.178 | 2 | |
| 2013 | 0.213 | 0.399 | 0.388 | 2.175 | 2 | |
| 2014 | 0.216 | 0.402 | 0.382 | 2.166 | 2 | |
| 2015 | 0.216 | 0.393 | 0.391 | 2.175 | 2 | |
| 2016 | 0.241 | 0.398 | 0.361 | 2.120 | 2 | |
| 2017 | 0.250 | 0.394 | 0.356 | 2.107 | 2 | |
| 2018 | 0.279 | 0.415 | 0.306 | 2.027 | 2 | |
| 2019 | 0.239 | 0.355 | 0.406 | 2.167 | 3 | |
| Bozhou City | 2011 | 0.179 | 0.410 | 0.411 | 2.232 | 3 |
| 2012 | 0.217 | 0.407 | 0.376 | 2.159 | 2 | |
| 2013 | 0.210 | 0.398 | 0.391 | 2.181 | 2 | |
| 2014 | 0.241 | 0.415 | 0.343 | 2.102 | 2 | |
| 2015 | 0.226 | 0.410 | 0.364 | 2.138 | 2 | |
| 2016 | 0.246 | 0.429 | 0.325 | 2.080 | 2 | |
| 2017 | 0.265 | 0.429 | 0.306 | 2.041 | 2 | |
| 2018 | 0.270 | 0.422 | 0.308 | 2.038 | 2 | |
| 2019 | 0.220 | 0.389 | 0.391 | 2.171 | 2 | |
| Suzhou City | 2011 | 0.225 | 0.404 | 0.371 | 2.145 | 2 |
| 2012 | 0.220 | 0.400 | 0.380 | 2.160 | 2 | |
| 2013 | 0.227 | 0.402 | 0.371 | 2.145 | 2 | |
| 2014 | 0.246 | 0.404 | 0.35 | 2.104 | 2 | |
| 2015 | 0.244 | 0.398 | 0.358 | 2.113 | 2 | |
| 2016 | 0.261 | 0.417 | 0.323 | 2.062 | 2 | |
| 2017 | 0.275 | 0.415 | 0.310 | 2.035 | 2 | |
| 2018 | 0.290 | 0.429 | 0.281 | 1.990 | 2 | |
| 2019 | 0.264 | 0.378 | 0.357 | 2.093 | 2 | |
| Bengbu City | 2011 | 0.187 | 0.465 | 0.347 | 2.160 | 2 |
| 2012 | 0.196 | 0.448 | 0.356 | 2.160 | 2 | |
| 2013 | 0.212 | 0.446 | 0.342 | 2.130 | 2 | |
| 2014 | 0.216 | 0.468 | 0.316 | 2.100 | 2 | |
| 2015 | 0.213 | 0.464 | 0.323 | 2.111 | 2 | |
| 2016 | 0.238 | 0.465 | 0.297 | 2.058 | 2 | |
| 2017 | 0.247 | 0.464 | 0.289 | 2.041 | 2 | |
| 2018 | 0.278 | 0.468 | 0.253 | 1.975 | 2 | |
| 2019 | 0.242 | 0.403 | 0.355 | 2.113 | 2 | |
| Fuyang City | 2011 | 0.144 | 0.399 | 0.457 | 2.312 | 3 |
| 2012 | 0.157 | 0.399 | 0.444 | 2.287 | 3 | |
| 2013 | 0.161 | 0.407 | 0.432 | 2.271 | 3 | |
| 2014 | 0.211 | 0.422 | 0.367 | 2.156 | 2 | |
| 2015 | 0.195 | 0.417 | 0.388 | 2.192 | 2 | |
| 2016 | 0.219 | 0.437 | 0.343 | 2.124 | 2 | |
| 2017 | 0.242 | 0.446 | 0.313 | 2.071 | 2 | |
| 2018 | 0.237 | 0.431 | 0.332 | 2.096 | 2 | |
| 2019 | 0.212 | 0.391 | 0.397 | 2.184 | 2 | |
| Huainan City | 2011 | 0.171 | 0.385 | 0.444 | 2.272 | 3 |
| 2012 | 0.16 | 0.366 | 0.474 | 2.314 | 3 | |
| 2013 | 0.178 | 0.375 | 0.447 | 2.269 | 3 | |
| 2014 | 0.181 | 0.413 | 0.406 | 2.225 | 3 | |
| 2015 | 0.178 | 0.402 | 0.419 | 2.241 | 3 | |
| 2016 | 0.243 | 0.417 | 0.340 | 2.097 | 2 | |
| 2017 | 0.267 | 0.422 | 0.310 | 2.043 | 2 | |
| 2018 | 0.276 | 0.425 | 0.298 | 2.022 | 2 | |
| 2019 | 0.205 | 0.375 | 0.420 | 2.215 | 3 | |
| District | Index | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
|---|---|---|---|---|---|---|---|---|---|---|
| Huaibei City | C1 | 0.9683 | 0.9558 | 0.9599 | 0.9529 | 0.9609 | 0.9465 | 0.9437 | 0.9064 | 0.9759 |
| C2 | 0.9286 | 0.9158 | 0.9193 | 0.9117 | 0.9195 | 0.9043 | 0.9005 | 0.8623 | 0.9328 | |
| C3 | 0.8991 | 0.9036 | 0.8985 | 0.9008 | 0.9061 | 0.9092 | 0.9120 | 0.9142 | 0.9176 | |
| C4 | 0.8919 | 0.8899 | 0.8809 | 0.8841 | 0.8814 | 0.8806 | 0.8840 | 0.8822 | 0.8825 | |
| C5 | 0.8702 | 0.8612 | 0.8639 | 0.8600 | 0.8618 | 0.5837 | 0.5072 | 0.1254 | 0.8661 | |
| C6 | 0.3001 | 0.1775 | 0.1342 | 0.1290 | 0.1296 | 0.1264 | 0.1134 | 0.1071 | 0.0963 | |
| C7 | 0.9268 | 0.9224 | 0.8764 | 0.8505 | 0.8334 | 0.6096 | 0.6392 | 0.5346 | 0.3081 | |
| C8 | 0.3964 | 0.3800 | 0.3821 | 0.3704 | 0.3724 | 0.3927 | 0.3943 | 0.3876 | 0.5048 | |
| C9 | 0.1334 | 0.1194 | 0.1128 | 0.1055 | 0.1017 | 0.0967 | 0.0858 | 0.0809 | 0.0734 | |
| C10 | 0.1186 | 0.1064 | 0.1080 | 0.1085 | 0.1092 | 0.1088 | 0.1008 | 0.0986 | 0.1053 | |
| C11 | 0.8885 | 0.8877 | 0.8862 | 0.8865 | 0.8870 | 0.8870 | 0.8871 | 0.8875 | 0.8911 | |
| C12 | 0.3135 | 0.3478 | 0.3756 | 0.4020 | 0.4208 | 0.4469 | 0.4744 | 0.5020 | 0.5162 | |
| C13 | 0.0490 | 0.0383 | 0.0441 | 0.0391 | 0.0386 | 0.0346 | 0.0339 | 0.0327 | 0.0161 | |
| Bozhou City | C1 | 0.9351 | 0.9269 | 0.9354 | 0.9115 | 0.9282 | 0.9139 | 0.9066 | 0.9165 | 0.9602 |
| C2 | 0.9161 | 0.9087 | 0.9150 | 0.8925 | 0.9072 | 0.8936 | 0.8856 | 0.8936 | 0.9330 | |
| C3 | 0.9204 | 0.9351 | 0.9287 | 0.9339 | 0.9283 | 0.9069 | 0.9095 | 0.9113 | 0.9102 | |
| C4 | 0.8864 | 0.8854 | 0.8832 | 0.8914 | 0.8885 | 0.8864 | 0.8871 | 0.8873 | 0.8881 | |
| C5 | 0.5184 | 0.2313 | 0.4506 | 0.1310 | 0.3396 | 0.1395 | 0.1298 | 0.1381 | 0.8603 | |
| C6 | 0.6648 | 0.6130 | 0.5745 | 0.5309 | 0.5057 | 0.4595 | 0.4135 | 0.3530 | 0.1335 | |
| C7 | 0.9167 | 0.9061 | 0.9011 | 0.8854 | 0.8908 | 0.6656 | 0.4288 | 0.3980 | 0.3920 | |
| C8 | 0.2794 | 0.2815 | 0.3017 | 0.3071 | 0.3083 | 0.3052 | 0.3012 | 0.2934 | 0.8636 | |
| C9 | 0.3514 | 0.2412 | 0.2447 | 0.1792 | 0.1803 | 0.1482 | 0.1335 | 0.1245 | 0.1023 | |
| C10 | 0.6069 | 0.5051 | 0.4685 | 0.3279 | 0.3150 | 0.3244 | 0.1623 | 0.1661 | 0.2676 | |
| C11 | 0.8795 | 0.8805 | 0.8829 | 0.8831 | 0.8832 | 0.8847 | 0.8851 | 0.8859 | 0.8706 | |
| C12 | 0.1043 | 0.1081 | 0.1112 | 0.1139 | 0.1166 | 0.1192 | 0.1222 | 0.1246 | 0.1269 | |
| C13 | 0.0782 | 0.0456 | 0.0325 | 0.0316 | 0.0446 | 0.0427 | 0.0333 | 0.0306 | 0.0252 | |
| Suzhou City | C1 | 0.9216 | 0.9288 | 0.9319 | 0.9263 | 0.9347 | 0.9188 | 0.9148 | 0.8732 | 0.9529 |
| C2 | 0.9078 | 0.9139 | 0.9161 | 0.9105 | 0.9174 | 0.9029 | 0.8982 | 0.8601 | 0.9312 | |
| C3 | 0.9266 | 0.9262 | 0.9236 | 0.9298 | 0.9337 | 0.9192 | 0.9229 | 0.9234 | 0.9212 | |
| C4 | 0.7031 | 0.6790 | 0.6606 | 0.8090 | 0.7847 | 0.8174 | 0.7273 | 0.7545 | 0.7766 | |
| C5 | 0.2102 | 0.3294 | 0.3795 | 0.1987 | 0.2868 | 0.1331 | 0.1256 | 0.0895 | 0.5376 | |
| C6 | 0.6042 | 0.5496 | 0.5058 | 0.4522 | 0.4127 | 0.3611 | 0.3057 | 0.2022 | 0.1302 | |
| C7 | 0.9641 | 0.9641 | 0.9315 | 0.9139 | 0.9112 | 0.7030 | 0.6265 | 0.5946 | 0.5069 | |
| C8 | 0.4062 | 0.3993 | 0.3937 | 0.3962 | 0.3986 | 0.3954 | 0.3894 | 0.3949 | 0.4892 | |
| C9 | 0.2582 | 0.2118 | 0.1778 | 0.1327 | 0.1235 | 0.1179 | 0.1098 | 0.1019 | 0.0906 | |
| C10 | 0.4314 | 0.4985 | 0.3842 | 0.3169 | 0.2764 | 0.2384 | 0.1369 | 0.1360 | 0.2243 | |
| C11 | 0.8739 | 0.8737 | 0.8727 | 0.8728 | 0.8735 | 0.8739 | 0.8740 | 0.8741 | 0.8661 | |
| C12 | 0.1083 | 0.1120 | 0.1150 | 0.1175 | 0.1201 | 0.1227 | 0.1256 | 0.1279 | 0.1301 | |
| C13 | 0.0313 | 0.0331 | 0.0322 | 0.0223 | 0.0273 | 0.0292 | 0.0250 | 0.0216 | 0.0065 | |
| Bengbu City | C1 | 0.8932 | 0.9212 | 0.9286 | 0.8968 | 0.8993 | 0.8967 | 0.8912 | 0.8659 | 0.9532 |
| C2 | 0.8856 | 0.9094 | 0.9154 | 0.8865 | 0.8883 | 0.8852 | 0.8788 | 0.7711 | 0.9325 | |
| C3 | 0.2997 | 0.4003 | 0.3136 | 0.8605 | 0.5403 | 0.1392 | 0.2927 | 0.4618 | 0.4031 | |
| C4 | 0.9055 | 0.9036 | 0.8832 | 0.8897 | 0.8871 | 0.8908 | 0.8907 | 0.8883 | 0.8893 | |
| C5 | 0.8605 | 0.8706 | 0.8757 | 0.5974 | 0.8597 | 0.8514 | 0.6353 | 0.2618 | 0.8851 | |
| C6 | 0.3516 | 0.2346 | 0.1375 | 0.1285 | 0.1220 | 0.1128 | 0.1006 | 0.0865 | 0.0474 | |
| C7 | 0.7086 | 0.6328 | 0.6522 | 0.6050 | 0.6187 | 0.7322 | 0.7640 | 0.7322 | 0.4779 | |
| C8 | 0.3981 | 0.4425 | 0.4400 | 0.4420 | 0.4403 | 0.4291 | 0.4255 | 0.4271 | 0.8757 | |
| C9 | 0.4114 | 0.3490 | 0.3129 | 0.1838 | 0.2055 | 0.1762 | 0.1359 | 0.1231 | 0.1116 | |
| C10 | 0.4483 | 0.2906 | 0.2018 | 0.1319 | 0.1281 | 0.1129 | 0.1244 | 0.1101 | 0.1218 | |
| C11 | 0.8693 | 0.8691 | 0.8689 | 0.8696 | 0.8704 | 0.8709 | 0.8711 | 0.8715 | 0.8651 | |
| C12 | 0.1348 | 0.1378 | 0.1401 | 0.1748 | 0.2191 | 0.2635 | 0.3041 | 0.3483 | 0.3772 | |
| C13 | 0.4724 | 0.4664 | 0.4620 | 0.1311 | 0.3044 | 0.3750 | 0.3077 | 0.2082 | 0.1215 | |
| Fuyang City | C1 | 0.9627 | 0.9565 | 0.9506 | 0.9259 | 0.9386 | 0.9205 | 0.9054 | 0.9273 | 0.9769 |
| C2 | 0.9231 | 0.9168 | 0.9108 | 0.8849 | 0.8971 | 0.8784 | 0.8618 | 0.8827 | 0.9336 | |
| C3 | 0.9225 | 0.9328 | 0.9284 | 0.9350 | 0.9280 | 0.9037 | 0.9045 | 0.9067 | 0.9066 | |
| C4 | 0.8912 | 0.8915 | 0.8856 | 0.8843 | 0.8830 | 0.8828 | 0.8860 | 0.8844 | 0.8841 | |
| C5 | 0.8661 | 0.8599 | 0.8456 | 0.2858 | 0.5313 | 0.2824 | 0.1331 | 0.3427 | 0.8715 | |
| C6 | 0.7198 | 0.6725 | 0.6357 | 0.5949 | 0.5732 | 0.5341 | 0.4866 | 0.4344 | 0.1345 | |
| C7 | 0.8908 | 0.8897 | 0.8875 | 0.8698 | 0.8707 | 0.7241 | 0.3889 | 0.3828 | 0.3688 | |
| C8 | 0.3322 | 0.3396 | 0.3510 | 0.3515 | 0.3581 | 0.3454 | 0.3401 | 0.3319 | 0.6973 | |
| C9 | 0.4277 | 0.3392 | 0.3263 | 0.2538 | 0.2582 | 0.2226 | 0.1824 | 0.1391 | 0.1062 | |
| C10 | 0.4714 | 0.4293 | 0.3702 | 0.2521 | 0.2058 | 0.1805 | 0.1923 | 0.1393 | 0.1952 | |
| C11 | 0.9179 | 0.9188 | 0.9208 | 0.9205 | 0.9192 | 0.9220 | 0.9233 | 0.9234 | 0.8917 | |
| C12 | 0.1088 | 0.1122 | 0.1150 | 0.1177 | 0.1203 | 0.1231 | 0.1260 | 0.1289 | 0.1313 | |
| C13 | 0.1182 | 0.0978 | 0.1023 | 0.0908 | 0.1024 | 0.1007 | 0.0929 | 0.0883 | 0.0774 | |
| Huainan City | C1 | 0.9565 | 0.9641 | 0.9646 | 0.9506 | 0.9328 | 0.9058 | 0.9013 | 0.8891 | 0.9733 |
| C2 | 0.9075 | 0.9154 | 0.9156 | 0.8999 | 0.8811 | 0.2253 | 0.1375 | 0.1228 | 0.8994 | |
| C3 | 0.0567 | 0.0662 | 0.0764 | 0.1000 | 0.4734 | 0.0945 | 0.0942 | 0.1023 | 0.1098 | |
| C4 | 0.8830 | 0.8823 | 0.8793 | 0.9291 | 0.9336 | 0.9280 | 0.9031 | 0.9126 | 0.9207 | |
| C5 | 0.9782 | 0.9979 | 0.9885 | 0.9206 | 0.8958 | 0.8755 | 0.8731 | 0.8658 | 0.9726 | |
| C6 | 0.1398 | 0.1331 | 0.1299 | 0.1334 | 0.2942 | 0.2350 | 0.1395 | 0.1353 | 0.1247 | |
| C7 | 0.8726 | 0.8602 | 0.8475 | 0.8120 | 0.7823 | 0.6690 | 0.5641 | 0.5415 | 0.5096 | |
| C8 | 0.4862 | 0.5370 | 0.5262 | 0.5269 | 0.3143 | 0.4814 | 0.4799 | 0.4835 | 0.5624 | |
| C9 | 0.5304 | 0.4671 | 0.4297 | 0.3975 | 0.3483 | 0.4706 | 0.4363 | 0.3914 | 0.3217 | |
| C10 | 0.9002 | 0.8783 | 0.8688 | 0.8733 | 0.8731 | 0.8721 | 0.6426 | 0.6942 | 0.8616 | |
| C11 | 0.6816 | 0.9029 | 0.9027 | 0.9027 | 0.9952 | 0.9988 | 0.9991 | 0.9991 | 0.9677 | |
| C12 | 0.4761 | 0.5055 | 0.5313 | 0.5537 | 0.4190 | 0.4454 | 0.4716 | 0.4836 | 0.5007 | |
| C13 | 0.8600 | 0.8599 | 0.5274 | 0.3921 | 0.0856 | 0.3871 | 0.3803 | 0.2596 | 0.1403 |
| District | Year | Item | The First Obstacle Factor | The Second Obstacle Factor | The Third Obstacle Factor | The Fourth Obstacle Factor | The Fifth Obstacle Factor |
|---|---|---|---|---|---|---|---|
| Huaibei City | 2011 | Index/obstacle degree | C1/0.9683 | C2/0.9286 | C7/0.9268 | C3/0.8991 | C4/0.8919 |
| 2012 | Index/obstacle degree | C1/0.9558 | C7/0.9224 | C2/0.9158 | C3/0.9036 | C4/0.8899 | |
| 2013 | Index/obstacle degree | C1/0.9599 | C2/0.9193 | C3/0.8985 | C11/0.8862 | C4/0.8809 | |
| 2014 | Index/obstacle degree | C1/0.9529 | C2/0.9117 | C3/0.9008 | C11/0.8865 | C4/0.8841 | |
| 2015 | Index/obstacle degree | C1/0.9606 | C2/0.9195 | C3/0.9061 | C11/0.8870 | C4/0.8806 | |
| 2016 | Index/obstacle degree | C1/0.9465 | C3/0.9092 | C2/0.9043 | C11/0.8870 | C4/0.8806 | |
| 2017 | Index/obstacle degree | C1/0.9437 | C3/0.9120 | C2/0.9005 | C11/0.8871 | C4/0.8840 | |
| 2018 | Index/obstacle degree | C3/0.9142 | C1/0.9064 | C11/0.8875 | C4/0.8822 | C2/0.8623 | |
| 2019 | Index/obstacle degree | C1/0.9759 | C2/0.9328 | C3/0.9176 | C11/0.8911 | C4/0.8825 | |
| Bozhou City | 2011 | Index/obstacle degree | C1/0.9351 | C3/0.9204 | C7/0.9167 | C2/0.9161 | C4/0.8864 |
| 2012 | Index/obstacle degree | C3/0.9351 | C1/0.9269 | C2/0.9087 | C7/0.9061 | C4/0.8854 | |
| 2013 | Index/obstacle degree | C1/0.9354 | C3/0.9287 | C2/0.9150 | C7/0.9011 | C4/0.8832 | |
| 2014 | Index/obstacle degree | C3/0.9339 | C1/0.9115 | C2/0.8925 | C4/0.8914 | C7/0.8854 | |
| 2015 | Index/obstacle degree | C3/0.9283 | C1/0.9282 | C2/0.9072 | C7/0.8908 | C4/0.8885 | |
| 2016 | Index/obstacle degree | C1/0.9139 | C3/0.9069 | C2/0.8936 | C4/0.8864 | C11/0.8847 | |
| 2017 | Index/obstacle degree | C3/0.9095 | C1/0.9066 | C4/0.8871 | C2/0.8856 | C11/0.8851 | |
| 2018 | Index/obstacle degree | C1/0.9165 | C3/0.9113 | C2/0.8936 | C4/0.8873 | C11/0.8859 | |
| 2019 | Index/obstacle degree | C1/0.9602 | C2/0.9330 | C3/0.9102 | C4/0.8881 | C11/0.8706 | |
| Suzhou City | 2011 | Index/obstacle degree | C7/0.9641 | C3/0.9266 | C1/0.9216 | C2/0.9078 | C11/0.8739 |
| 2012 | Index/obstacle degree | C7/0.9641 | C1/0.9288 | C3/0.9262 | C2/0.9139 | C11/0.8727 | |
| 2013 | Index/obstacle degree | C1/0.9319 | C7/0.9315 | C3/0.9236 | C2/0.9161 | C11/0.8727 | |
| 2014 | Index/obstacle degree | C3/0.9298 | C1/0.9263 | C7/0.9139 | C2/0.9105 | C11/0.8728 | |
| 2015 | Index/obstacle degree | C1/0.9347 | C3/0.9337 | C2/0.9174 | C7/0.9112 | C11/0.8735 | |
| 2016 | Index/obstacle degree | C3/0.9192 | C1/0.9188 | C2/0.9029 | C11/0.8739 | C4/0.8174 | |
| 2017 | Index/obstacle degree | C3/0.9229 | C1/0.9148 | C2/0.8982 | C11/0.8740 | C4/0.7273 | |
| 2018 | Index/obstacle degree | C3/0.9234 | C11/0.8741 | C1/0.8732 | C2/0.8601 | C4/0.7545 | |
| 2019 | Index/obstacle degree | C1/0.9529 | C2/0.9312 | C3/0.9212 | C11/0.8661 | C4/0.7766 | |
| Bengbu City | 2011 | Index/obstacle degree | C4/0.9055 | C1/0.8932 | C2/0.8856 | C11/0.8693 | C5/0.8605 |
| 2012 | Index/obstacle degree | C1/0.9212 | C2/0.9094 | C4/0.9036 | C5/0.8706 | C11/0.8691 | |
| 2013 | Index/obstacle degree | C1/0.9286 | C2/0.9154 | C4/0.8832 | C5/0.8757 | C11/0.8689 | |
| 2014 | Index/obstacle degree | C1/0.8968 | C4/0.8897 | C2/0.8865 | C11/0.8696 | C3/0.8605 | |
| 2015 | Index/obstacle degree | C1/0.8993 | C2/0.8883 | C4/0.8871 | C11/0.8704 | C5/0.8597 | |
| 2016 | Index/obstacle degree | C1/0.8967 | C4/0.8908 | C2/0.8852 | C11/0.8709 | C5/0.8514 | |
| 2017 | Index/obstacle degree | C1/0.8912 | C4/0.8907 | C2/0.8788 | C11/0.8711 | C7/0.7674 | |
| 2018 | Index/obstacle degree | C4/0.8883 | C11/0.8715 | C1/0.8659 | C2/0.7711 | C7/0.7322 | |
| 2019 | Index/obstacle degree | C1/0.9532 | C2/0.9325 | C4/0.8893 | C5/0.8851 | C8/0.8757 | |
| Fuyang City | 2011 | Index/obstacle degree | C1/0.9627 | C2/0.9231 | C3/0.9225 | C11/0.9179 | C4/0.8912 |
| 2012 | Index/obstacle degree | C1/0.9565 | C3/0.9328 | C11/0.9188 | C2/0.9168 | C4/0.8915 | |
| 2013 | Index/obstacle degree | C1/0.9506 | C3/0.9284 | C11/0.9208 | C2/0.9108 | C7/0.8875 | |
| 2014 | Index/obstacle degree | C3/0.9350 | C1/0.9259 | C11/0.9205 | C2/0.8849 | C4/0.8843 | |
| 2015 | Index/obstacle degree | C1/0.9386 | C3/0.9280 | C11/0.9192 | C2/0.8971 | C4/0.8830 | |
| 2016 | Index/obstacle degree | C11/0.9220 | C1/0.9205 | C3/0.9037 | C4/0.8828 | C2/0.8784 | |
| 2017 | Index/obstacle degree | C11/0.9233 | C1/0.9054 | C3/0.9045 | C4/0.8860 | C2/0.8618 | |
| 2018 | Index/obstacle degree | C1/0.9273 | C11/0.9234 | C3/0.9067 | C4/0.8844 | C2/0.8827 | |
| 2019 | Index/obstacle degree | C1/0.9769 | C2/0.9336 | C3/0.9066 | C11/0.8917 | C4/0.8841 | |
| Huainan City | 2011 | Index/obstacle degree | C5/0.9782 | C1/0.9565 | C2/0.9075 | C10/0.9002 | C4/0.8830 |
| 2012 | Index/obstacle degree | C5/0.9979 | C1/0.9641 | C2/0.9154 | C11/0.9029 | C4/0.8823 | |
| 2013 | Index/obstacle degree | C5/0.9885 | C1/0.9646 | C2/0.9156 | C11/0.9027 | C4/0.8793 | |
| 2014 | Index/obstacle degree | C1/0.9506 | C4/0.9291 | C5/0.9206 | C11/0.9027 | C2/0.8999 | |
| 2015 | Index/obstacle degree | C11/0.9952 | C4/0.9336 | C1/0.9328 | C5/0. 8958 | C2/0.8811 | |
| 2016 | Index/obstacle degree | C11/0.9988 | C4/0.9280 | C1/0.9058 | C5/0.8755 | C10/0.8721 | |
| 2017 | Index/obstacle degree | C11/0.9991 | C4/0.9031 | C1/0.9013 | C5/0.8731 | C10/0.6426 | |
| 2018 | Index/obstacle degree | C11/0.9991 | C4/0.9126 | C1/0.8891 | C5/0.8658 | C10/0.6942 | |
| 2019 | Index/obstacle degree | C1/0.9733 | C5/0.9726 | C11/0.9677 | C4/0.9207 | C2/0.8994 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Jiang, S.; Jin, J.; Shen, R.; Cui, Y. Quantitative Diagnosis of Water Resources Carrying Capacity Obstacle Factors Based on Connection Number and TOPSIS in Huaibei Plain. Water 2023, 15, 3217. https://doi.org/10.3390/w15183217
Li Z, Jiang S, Jin J, Shen R, Cui Y. Quantitative Diagnosis of Water Resources Carrying Capacity Obstacle Factors Based on Connection Number and TOPSIS in Huaibei Plain. Water. 2023; 15(18):3217. https://doi.org/10.3390/w15183217
Chicago/Turabian StyleLi, Zheng, Shangming Jiang, Juliang Jin, Rui Shen, and Yi Cui. 2023. "Quantitative Diagnosis of Water Resources Carrying Capacity Obstacle Factors Based on Connection Number and TOPSIS in Huaibei Plain" Water 15, no. 18: 3217. https://doi.org/10.3390/w15183217
APA StyleLi, Z., Jiang, S., Jin, J., Shen, R., & Cui, Y. (2023). Quantitative Diagnosis of Water Resources Carrying Capacity Obstacle Factors Based on Connection Number and TOPSIS in Huaibei Plain. Water, 15(18), 3217. https://doi.org/10.3390/w15183217






