A New Acidity-Based Approach for Estimating Total Dissolved Solids in Acidic Mining Influenced Water
Abstract
:1. Introduction
2. Methodology
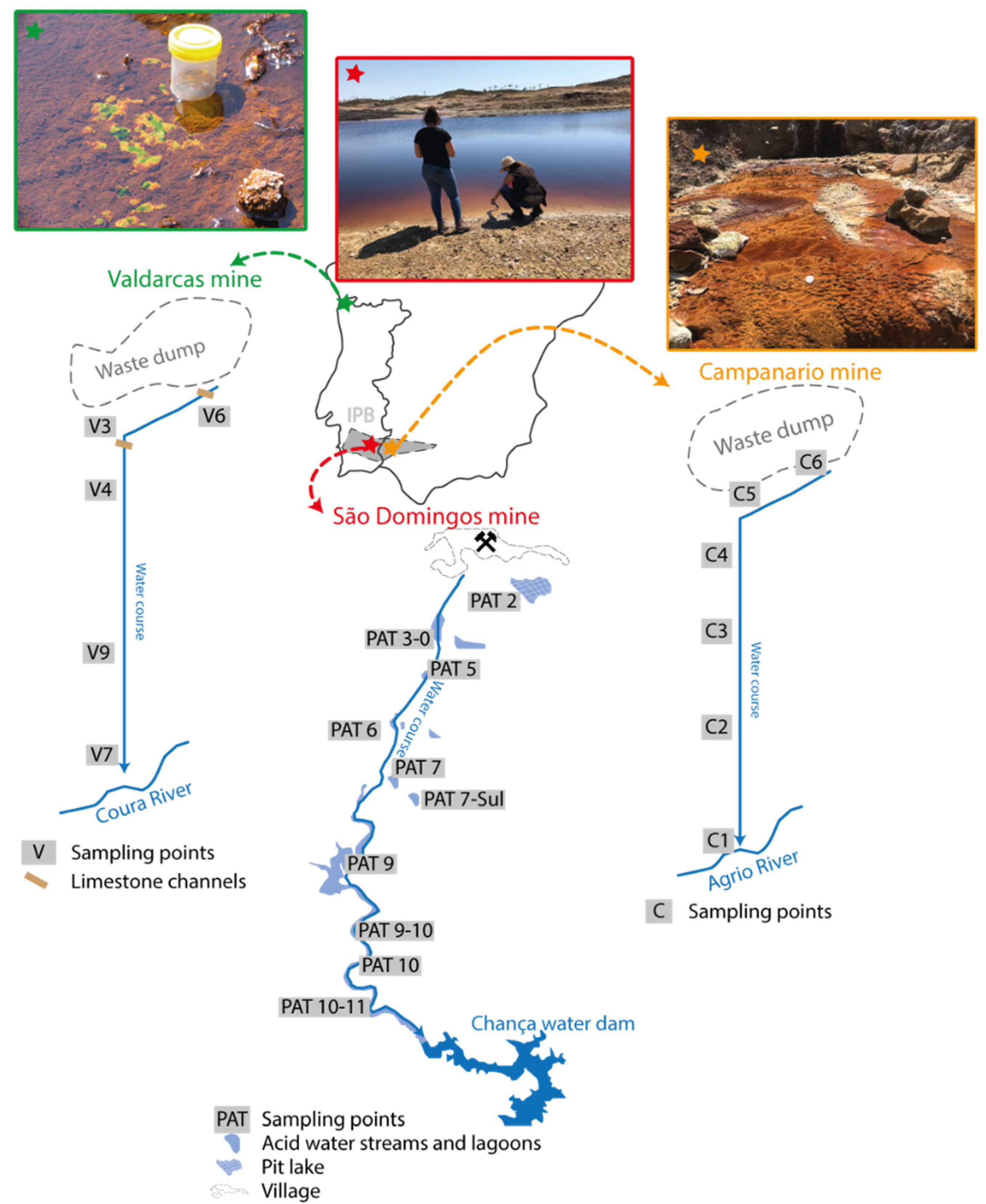
2.1. Study Areas
2.2. Water Sampling and Analysis
2.3. Statistical Treatment
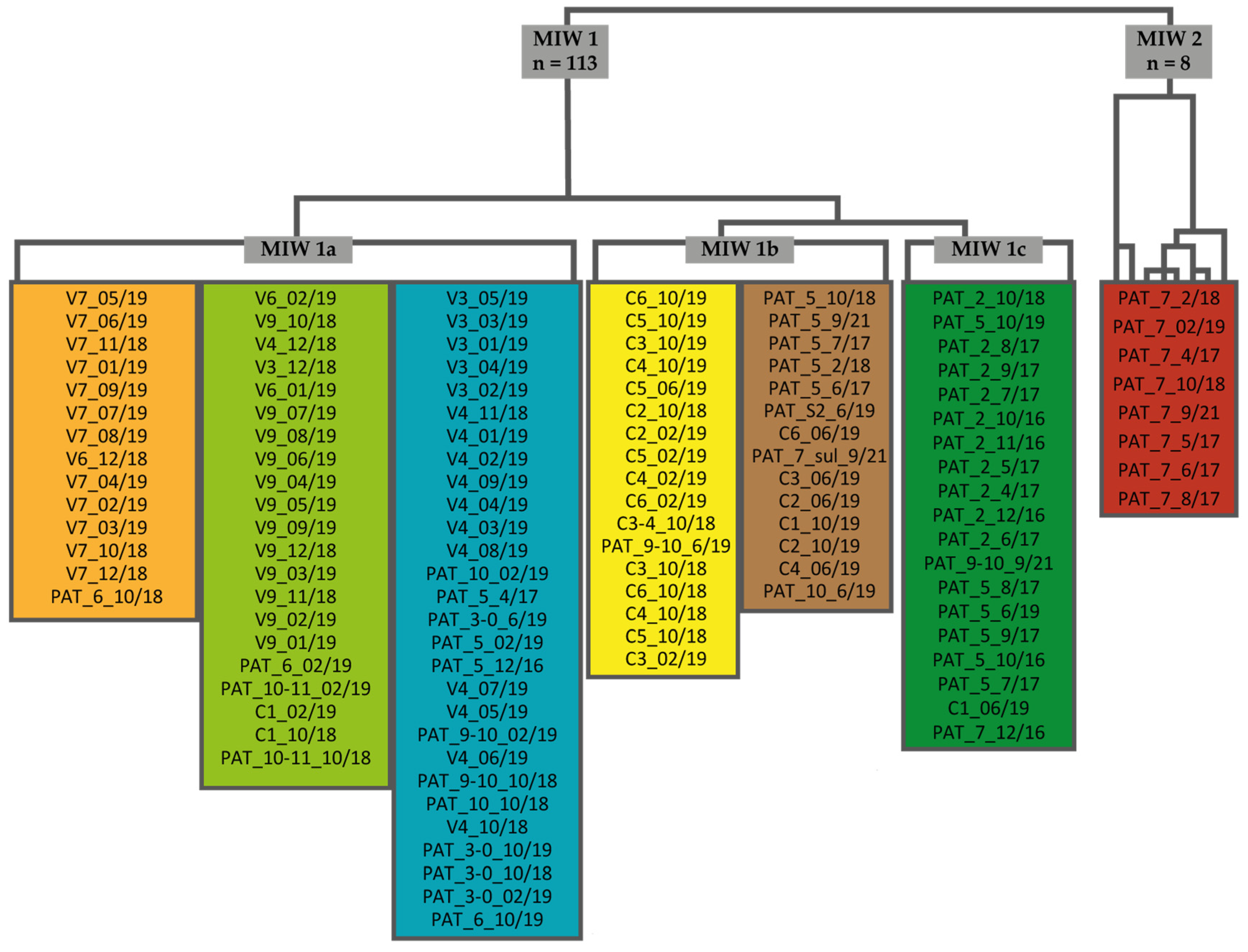
3. Results and Discussion
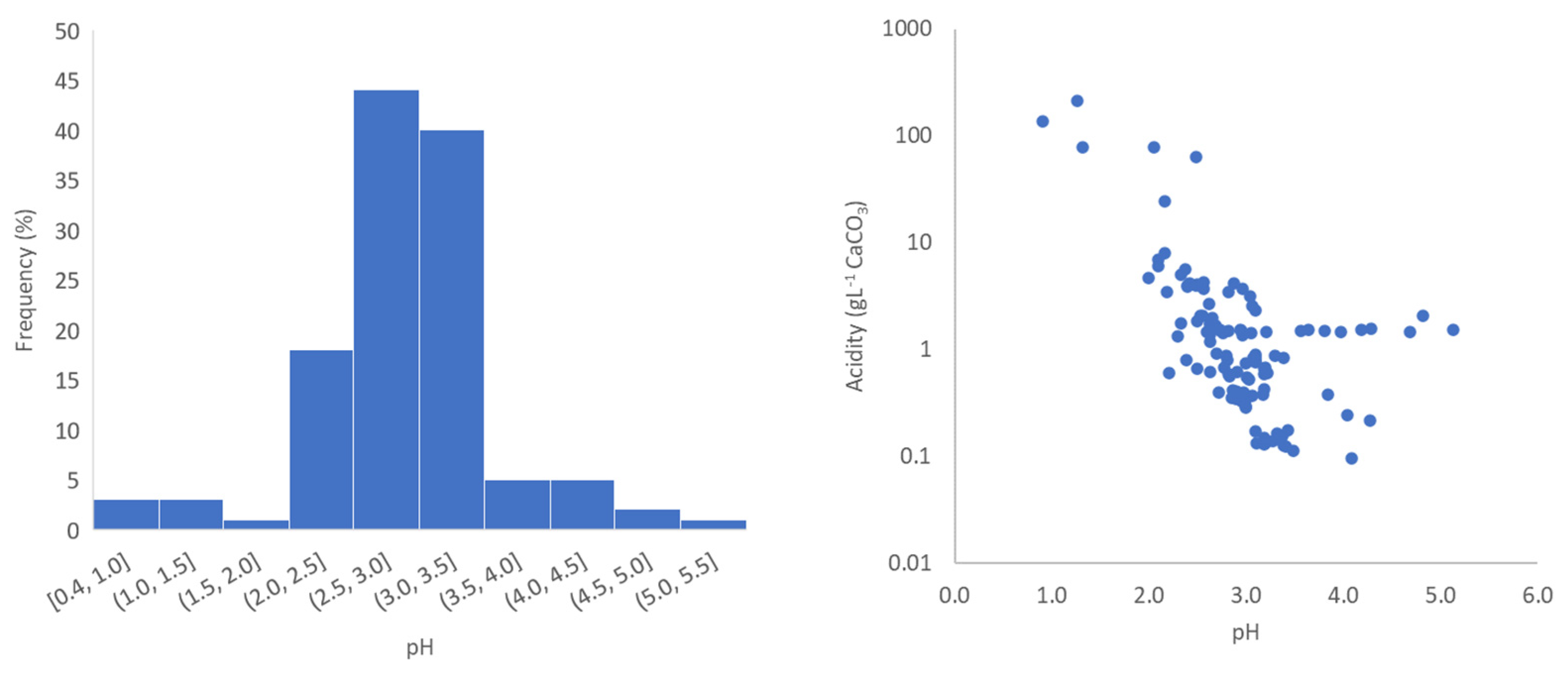
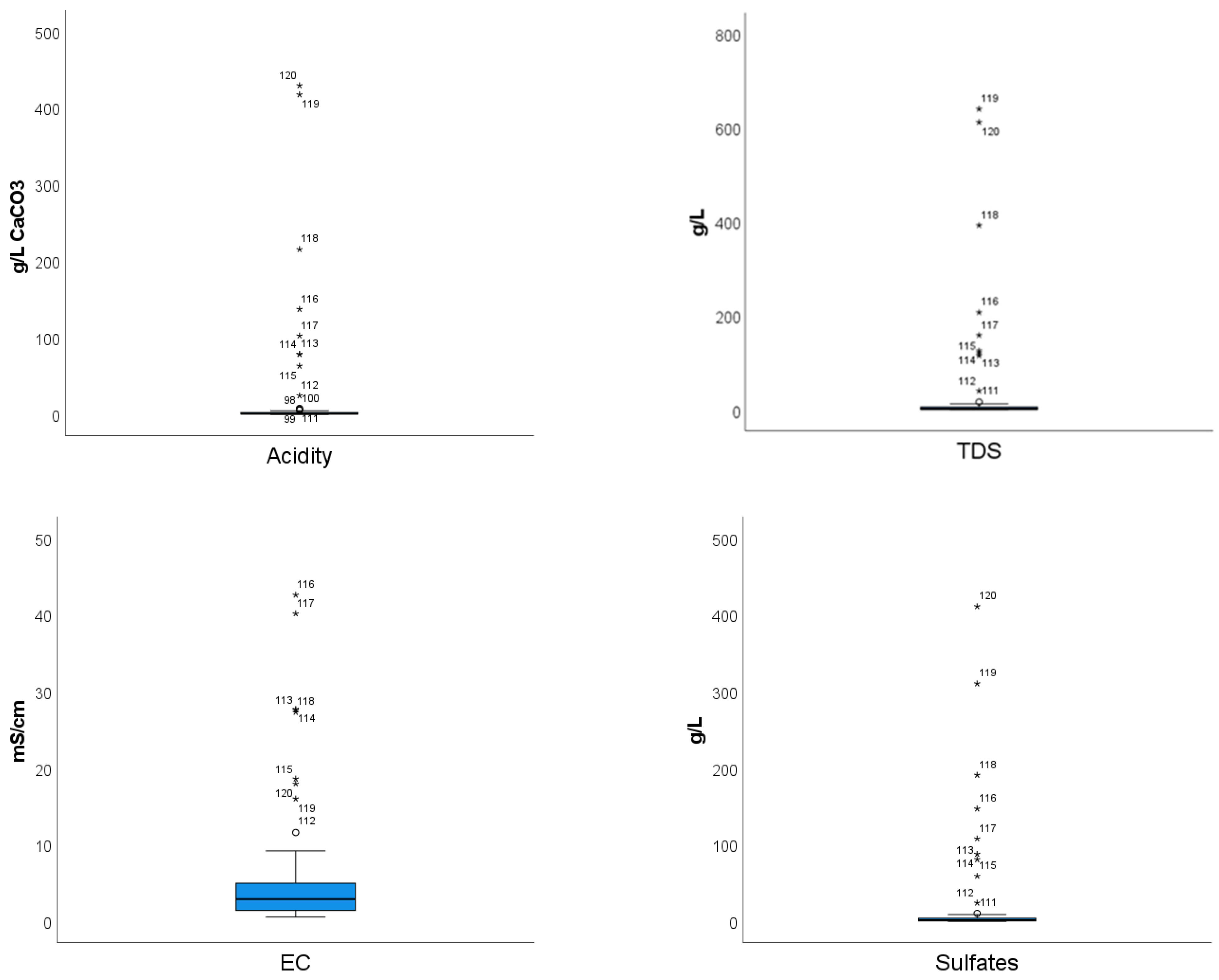
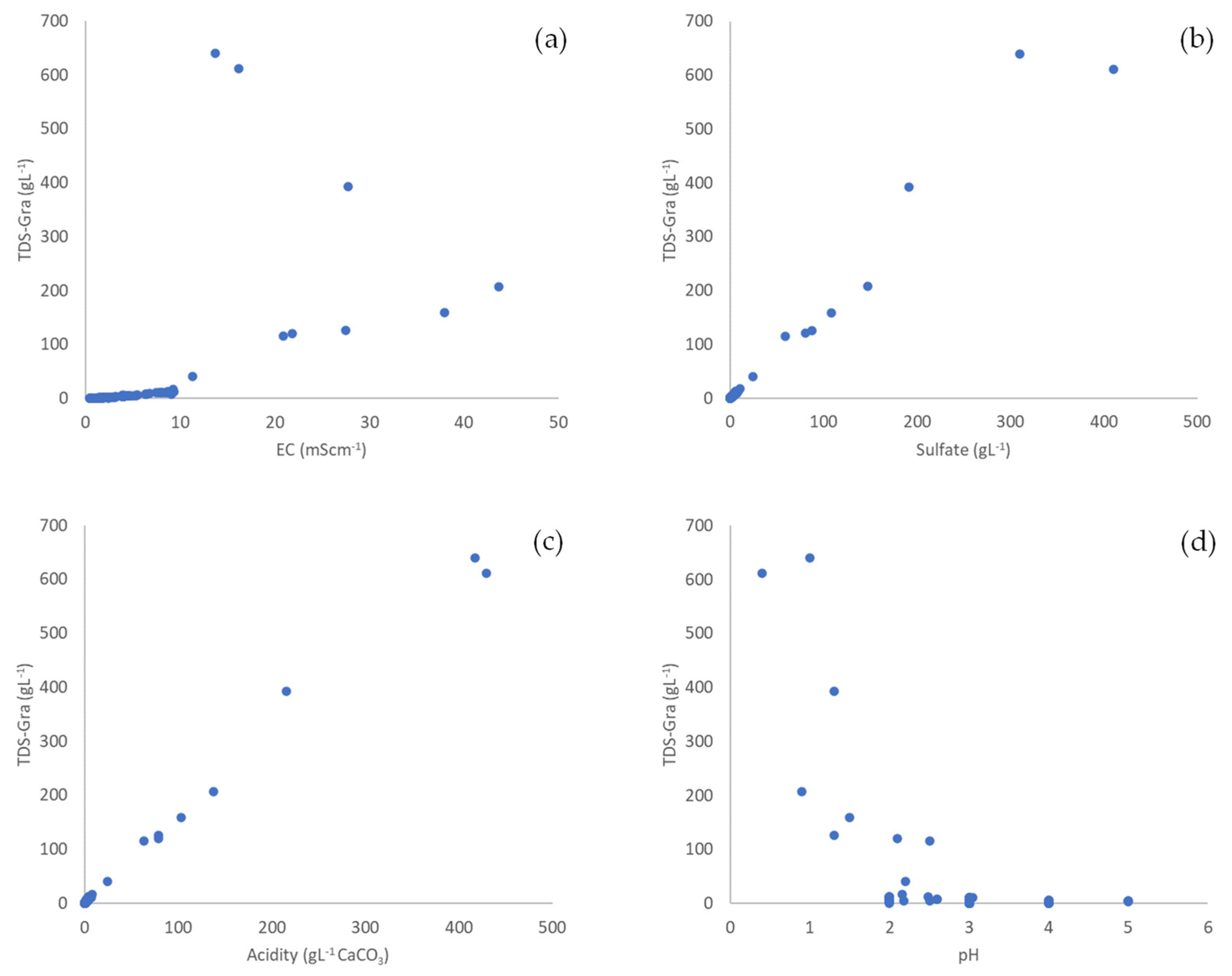
3.1. General Properties and Relationships in Mine Water
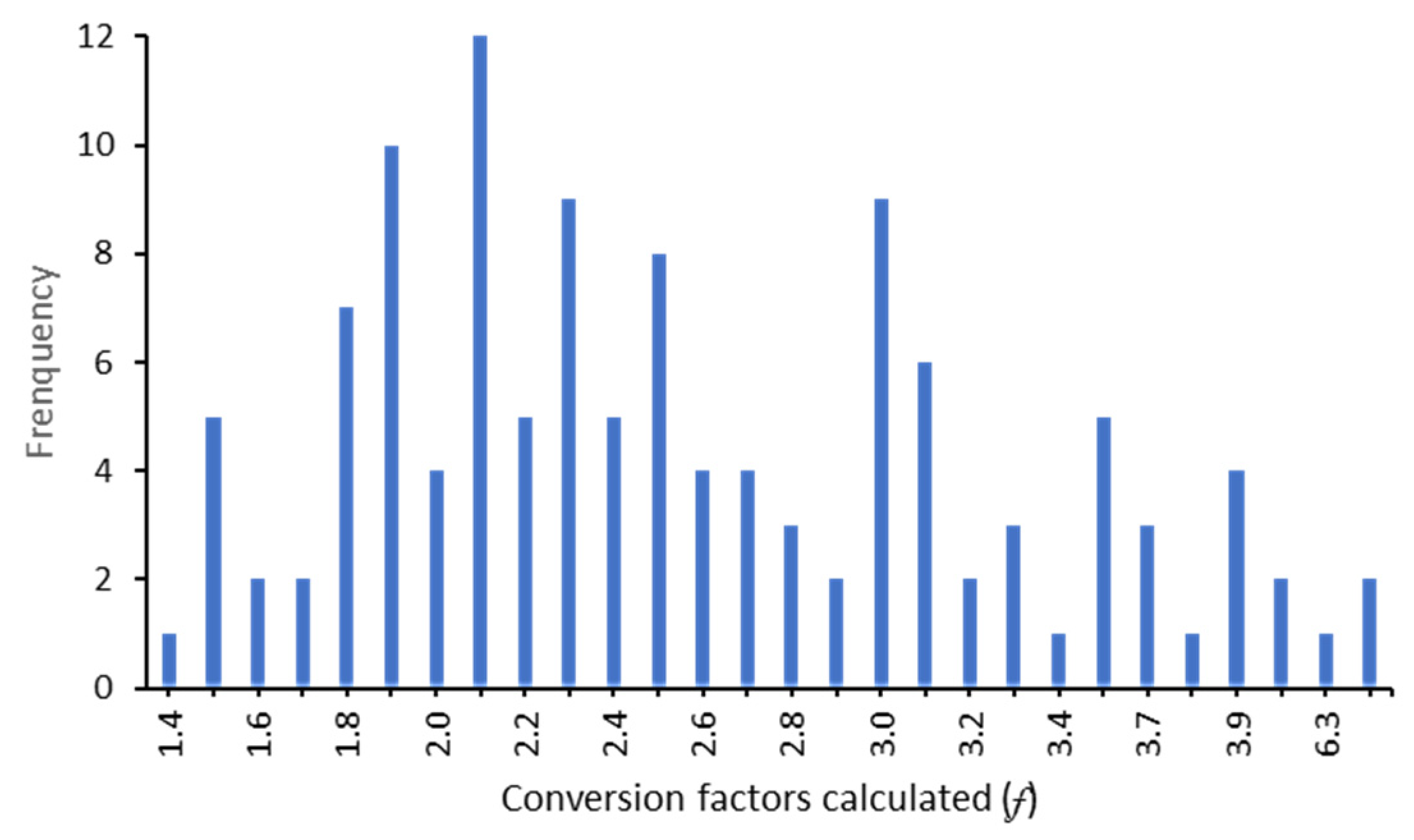
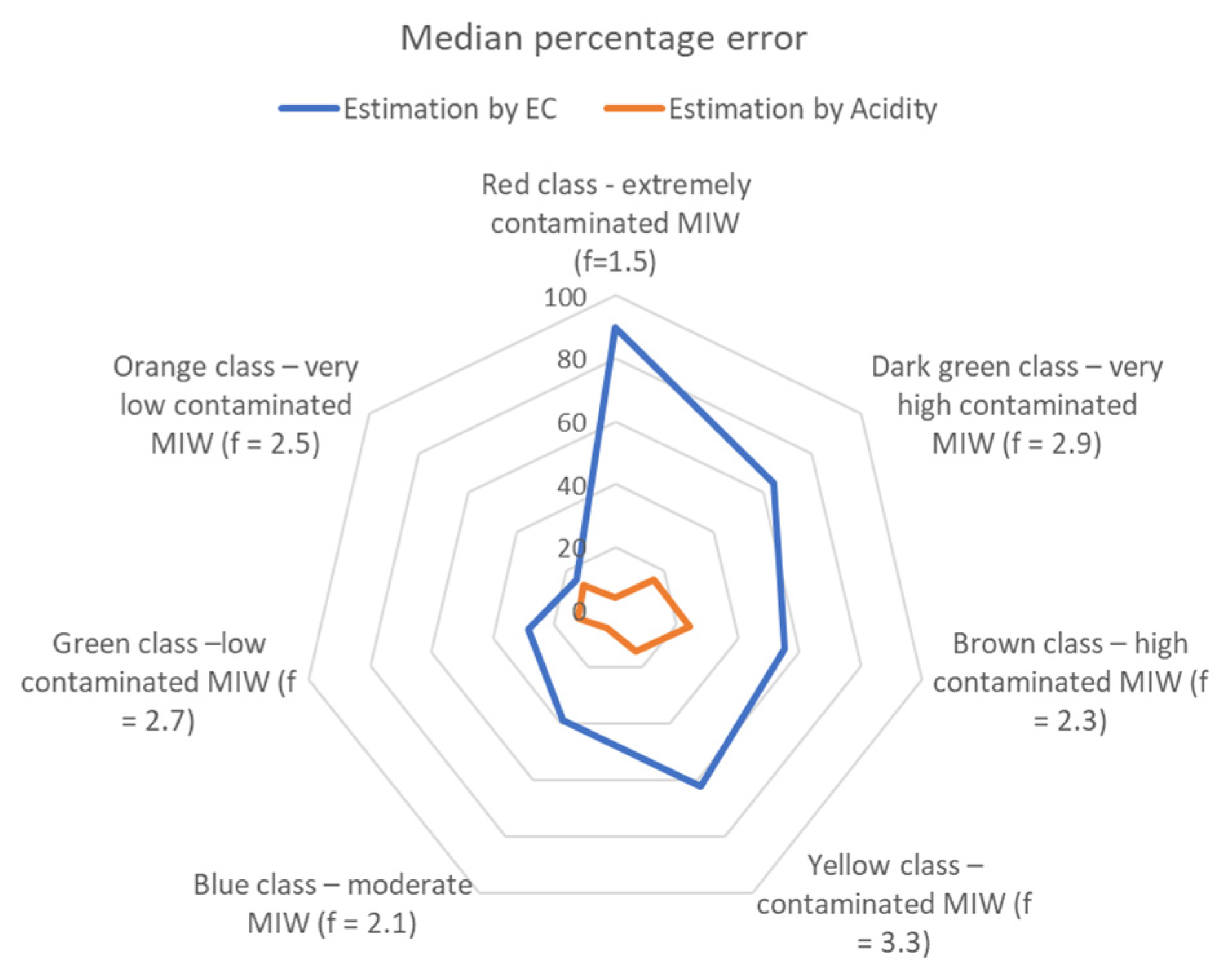
3.2. Conversion Factors
- 2.5 for very low MIW contamination, with very low sulfate (<0.250 gL−1) and acidity (<0.200 gL−1 of CaCO3);
- 2.7 for low MIW contamination, characterized by low sulfate (<0.800 gL−1) and acidity (<0.525 gL−1 of CaCO3);
- 2.1 for moderate MIW contamination, with sulfate concentration between 0.700 and 2.000 gL−1and acidity of 0.400 to 1.600 gL−1 of CaCO3;
- 3.3 for MIW contamination, with sulfate concentration range of 2.250 to 3.300 gL−1and acidity of 1.300 to 1.600 gL−1 of CaCO3;
- 2.3 for high MIW contamination, with high sulfate (2.250 to 5.200 gL−1) and acidity (1.400 to 4.300 gL−1 of CaCO3);
- 2.9 for very high MIW contamination, with sulfate concentration between 4.700 and 10.400 gL−1 and acidity of 2.000 to 8.000 gL−1 of CaCO3;
- and, for extreme MIW contamination, rich in sulfate (>24.000 gL−1) and very acidic (>24.400 gL−1 of CaCO3), the f is around 1.5.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Omer, N.H. Water quality parameters. In Water Quality—Science, Assessments and Policy; IntechOpen: London, UK, 2019; Volume 18, pp. 1–34. [Google Scholar]
- McNeil, V.H.; Cox, M.E. Relationship between conductivity and analysed composition in a large set of natural surface-water samples, Queensland, Australia. Environ. Geol. 2000, 39, 1325–1333. [Google Scholar] [CrossRef]
- Hubert, E.; Wolkersdorfer, C. Establishing a conversion factor between electrical conductivity and total dissolved solids in South African mine waters. Water SA 2015, 41, 490–500. [Google Scholar] [CrossRef]
- Rebello, L.R.B.; Siepman, T.; Drexler, S. Correlations between TDS and electrical conductivity for high-salinity for-mation brines characteristic of South Atlantic pre-salt basins. Water SA 2020, 46, 602–609. [Google Scholar]
- Hem, J.D. Study and Interpretation of the Chemical Characteristics of Natural Water; Department of the Interior, US Geological Survey: Reston, CA, USA, 1985; 2254, p. 263.
- APHA Standard Methods for the Examination of Water and Wastewater, 20th ed.; American Public Health Association, American Water Works Association, Water Environment Federation: Washington, DC, USA, 2012.
- Singh, T.; Kalra, Y.P. Specific conductance method for in situ estimation of total dissolved solids. J. Am. Water Work. Assoc. 1975, 67, 99–100. [Google Scholar] [CrossRef]
- Walton, N.R.G. Electrical Conductivity and Total Dissolved Solids—What is Their Precise Relationship? Desalination 1989, 72, 275–292. [Google Scholar] [CrossRef]
- Atekwana, E.A.; Atekwana, E.A.; Rowe, R.S.; Werkema, D.D., Jr.; Legall, F.D. The relationship of total dissolved solids measurements to bulk electrical conductivity in an aquifer contaminated with hydrocarbon. J. Appl. Geophys. 2004, 56, 281–294. [Google Scholar] [CrossRef]
- Marandi, A.; Polikarpus, M.; Jõeleht, A. A new approach for describing the relationship between electrical con-ductivity and major anion concentration in natural waters. Appl. Geochem. 2013, 38, 103–109. [Google Scholar] [CrossRef]
- Rusydi, A.F. Correlation between conductivity and total dissolved solid in various type of water: A review. IOP Conf. Ser. Earth Environ. Sci. 2018, 118, 012019. [Google Scholar] [CrossRef]
- Thirumalini, S.; Joseph, K. Correlation between Electrical Conductivity and Total Dissolved Solids in Natural Waters. Malays. J. Sci. 2009, 28, 55–61. [Google Scholar] [CrossRef]
- Weiner, E.R. Applications of Environmental Aquatic Chemistry—A Practical Guide; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Ali, N.S.; Mo, K.; Kim, M. A case study on the relationship between conductivity and dissolved solids to evaluate the potential for reuse of reclaimed industrial wastewater. KSCE J. Civ. Eng. 2012, 16, 708–713. [Google Scholar] [CrossRef]
- Taylor, M.; Elliott, H.A.; Navitsky, L.O. Relationship between total dissolved solids and electrical conductivity in Marcellus hydraulic fracturing fluids. Water Sci. Technol. 2018, 77, 1998–2004. [Google Scholar] [CrossRef] [PubMed]
- Wolkersdorfer, C. Mine Water Treatment—Active and Passive Methods; Springer: Berlin/Heidelberg, Germany, 2022; p. 328. ISBN 978-3-662-65770-6. [Google Scholar] [CrossRef]
- Nordstrom, D.K.; Alpers, C. Negative pH, efflorescent mineralogy, and consequences for environmental restoration at the Iron Mountain Superfund site, California. Proc. Natl. Acad. Sci. USA 1999, 96, 3455–3462. [Google Scholar] [CrossRef] [PubMed]
- Nordstrom, D.K. Mine Waters: Acidic to Circmneutral. Elements 2011, 7, 393–398. [Google Scholar] [CrossRef]
- Wolkersdorfer, C.; Nordstrom, D.K.; Beckie, R.D.; Cicerone, D.S.; Elliot, T.; Edraki, M.; Valente, T.; França, S.C.; Kumar, P.; Oyarzún Lucero, R.A.; et al. Guidance for the Integrated Use of Hydrological, Geochemical, and Isotopic Tools in Mining Operations. Mine Water Environ. 2020, 39, 204–228. [Google Scholar] [CrossRef]
- Fink, C.G. Chemical Composition versus Electrical Conductivity. Phys. Chem. 1917, 21, 32–36. [Google Scholar] [CrossRef]
- Appelo, C.; Postma, D. Geochemistry, Groundwater and Pollution, 2nd ed.; Balkema: Rotterdam, The Netherlands, 2005; p. 649. ISBN 04 1536 428 0. [Google Scholar] [CrossRef]
- Hedin, R.S.; Watzlaf, G.R. The effects of anoxic limestone drains on mine water chemistry. J. Am. Soc. Min. Reclam. 1994, 6, 185–194. [Google Scholar] [CrossRef]
- Langmuir, D. Aqueous Environmental Geochemistry; Prentice Hall: Upper Saddle River, NJ, USA, 1997; p. 600. ISBN 0-02-367412-1. [Google Scholar]
- Barriga, F.J.A.S. Metallogenesis in the Iberian Pyrite Belt. In Premesozoic Geology of Iberia; Dallmeyer, R.D., Martinez-Garcia, E., Eds.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1990; pp. 369–379. [Google Scholar] [CrossRef]
- Inverno, C.; Diez-Montes, A.; Rosa, C.; García-Crespo, J.; Matos, J.; García-Lobón, J.L.; Carvalho, J.; Bellido, F.; Caste-llo-Branco, J.M.; Ayala, C.; et al. Introduction and geological setting of the Iberian Pyrite Belt. In 3D, 4D and Predictive Modelling of Major Mineral Belts in Europe; Weihed, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 9, pp. 191–208. [Google Scholar] [CrossRef]
- Gomes, P.; Valente, T.M.; Pereira, P. Addressing quality and usability of surface water bodies in semi-arid regions with mining influences. Environ. Process. 2018, 5, 707–725. [Google Scholar] [CrossRef]
- Valente, T.M.; Gomes, C.L. Fuzzy modelling of acid mine drainage environments using geochemical, ecological and mineralogical indicators. Environ. Geol. 2009, 57, 653. [Google Scholar] [CrossRef]
- Valente, T.M.; Gomes, C.L. Occurrence, properties and pollution potential of environmental minerals in acid mine drainage. Sci. Total Environ. 2009, 407, 1135–1152. [Google Scholar] [CrossRef]
- Alves, R.C.; Valente, T.M.F.; Braga, M.A.; Gomes, C.L. Mineralogical composition and metals retention in the fine-fraction streambed precipitates of on AMD affected system. In Proceedings of the International Mine Water Association Congress-IMWA, Aachen, Germany, 4–11 September 2011; ISBN 9781618393050. [Google Scholar]
- Gomes, P.; Valente, T.; Geraldo, D.; Ribeiro, C. Photosynthetic pigments in acid mine drainage: Seasonal patterns and associations with stressful abiotic characteristics. Chemosphere 2020, 239, 124774. [Google Scholar] [CrossRef] [PubMed]
- Lobo, A.; Valente, T.; de la Torre, M.L.; Grande, J.A.; Santisteban, M.; Salmerón, I.; Sánchez Requena, J. Spatial behavior of acid mine drainage in a peculiar stream: Physical-chemical evolution from the source until the temporarily receptor in the Iberian Pyrite Belt. In Proceedings of the Energy and Environment Knowledge Week, Toledo, Spain, 30–31 October 2014; ISBN 978-84-697-1162-0. [Google Scholar]
- Egbueri, J.C. Groundwater quality assessment using pollution index of groundwater (PIG), ecological risk index (ERI) and hierarchical cluster analysis (HCA): A case study. Groundw. Sustain. Dev. 2020, 10, 100292. [Google Scholar] [CrossRef]
- Gomes, P.; Valente, T.; Albuquerque, T.; Henriques, R.; Flor-Arnau, N.; Pamplona, J.; Macías, F. Algae in acid mine drainage and relationships with pollutants in a degraded mining ecosystem. Minerals 2021, 11, 110. [Google Scholar] [CrossRef]
| pH | TDS–Gra (g L−1) | TDS–est (g L−1) | EC (mS cm−1) | Sulfate (g L−1) | Acidity (g L−1 of CaCO3) | |
|---|---|---|---|---|---|---|
| Minimum | 0.44 | 296 | 0.276 | 0.412 | 0.153 | 0.096 |
| Maximum | 4.82 | 640.086 | 20.850 | 43.710 | 41.0601 | 429.250 |
| Mean | 2.90 | 23.475 | 2.507 | 4.963 | 13.806 | 14.172 |
| Median | 2.92 | 2.414 | 1.413 | 3.052 | 1.389 | 1.180 |
| Standard deviation | 0.70 | 90.358 | 3.512 | 6.663 | 52.291 | 59.430 |
| pH | TDS | EC | Sulfate | Acidity | |
|---|---|---|---|---|---|
| pH | 1 | ||||
| TDS | −0.599 * | 1 | |||
| ρ < 0.001 | |||||
| EC | −0.652 * | 0.978 * | 1 | ||
| ρ < 0.001 | ρ < 0.001 | ||||
| Sulfate | −0.624 * | 0.981 * | 0.984 * | 1 | |
| ρ < 0.001 | ρ < 0.001 | ρ < 0.001 | |||
| Acidity | −0.637 * | 0.964 * | 0.971 * | 0.973 * | 1 |
| ρ < 0.001 | ρ < 0.001 | ρ < 0.001 | ρ < 0.001 |
| Orange Class f = 2.5 | ||||
|---|---|---|---|---|
| pH | CE | Sulfate | Acidity | |
| Median | 3 | 0.564 | 0.210 | 0.143 |
| Range | [3.0–4.0] | [0.412–0.872] | [0.153–0.247] | [0.096–0.173] |
| Green Class f = 2.7 | ||||
| pH | CE | Sulfate | Acidity | |
| Median | 3 | 1.302 | 0.553 | 0.325 |
| Range | [3.0–4.0] | [1.091–1.565] | [0.380–0.731] | [0.113–0.525] |
| Blue Class f = 2.1 | ||||
| pH | CE | Sulfate | Acidity | |
| Median | 3 | 2.236 | 1.034 | 0.754 |
| Range | [2.0–3.0] | [1.751–3.291] | [0.762–1.969] | [0.406–1.605] |
| Yellow Class f = 3.3 | ||||
| pH | CE | Sulfate | Acidity | |
| Median | 3 | 3.948 | 2.675 | 1.500 |
| Range | [3.0–5.0] | [3.848–4.189] | [2.255–3.265] | [1.360–1.560] |
| Brown Class f = 2.3 | ||||
| pH | CE | Sulfate | Acidity | |
| Median | 3 | 4.579 | 3.324 | 1.954 |
| Range | [2.0–5.0] | [3.856–6.330] | [2.244–5.152] | [1.405–4.305] |
| Dark green Class f = 2.9 | ||||
| pH | CE | Sulfate | Acidity | |
| Median | 2.3 | 8.306 | 6.158 | 4.128 |
| Range | [2.0–3.0] | [6.330–9.298] | [4.742–10.399] | [2.080–7.935] |
| Red Class f = 1.5 | ||||
| pH | CE | Sulfate | Acidity | |
| Median | 1.3 | 21.830 | 107.962 | 102.700 |
| Range | [0.4–2.5] | [11.320–43.710] | [24.075–410.601] | [24.438–429.250] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barroso, A.; Valente, T.; Marinho Reis, A.P.; Antunes, I.M.H.R. A New Acidity-Based Approach for Estimating Total Dissolved Solids in Acidic Mining Influenced Water. Water 2023, 15, 2995. https://doi.org/10.3390/w15162995
Barroso A, Valente T, Marinho Reis AP, Antunes IMHR. A New Acidity-Based Approach for Estimating Total Dissolved Solids in Acidic Mining Influenced Water. Water. 2023; 15(16):2995. https://doi.org/10.3390/w15162995
Chicago/Turabian StyleBarroso, Ana, Teresa Valente, Amélia Paula Marinho Reis, and Isabel Margarida H. R. Antunes. 2023. "A New Acidity-Based Approach for Estimating Total Dissolved Solids in Acidic Mining Influenced Water" Water 15, no. 16: 2995. https://doi.org/10.3390/w15162995
APA StyleBarroso, A., Valente, T., Marinho Reis, A. P., & Antunes, I. M. H. R. (2023). A New Acidity-Based Approach for Estimating Total Dissolved Solids in Acidic Mining Influenced Water. Water, 15(16), 2995. https://doi.org/10.3390/w15162995








