Stormwater Tree Pits for Decentralized Retention of Heavy Rainfall
Abstract
:1. Introduction
- A full reservoir ensures a maximum irrigation period but not the attenuation of the runoff peak.
- Excessively intensive irrigation inhibits root development and, in extreme cases, poses a risk of waterlogging.
- Water reaches the roots of young trees when irrigation is applied near the surface, but the storage potential is then limited to the root zone.
- Pollutant discharge, such as deicing salts and heavy metals that have leached from roof surfaces via rainfall, can negatively affect trees and thus should be prevented form entering the root zone untreated.
- Pollutant entry and retention in the soil or substrate as well as the potentially necessary pretreatment of inflowing runoff.
- Root expansion in stormwater tree pits.
- Suitable tree choice in terms of alternating dry and wet periods.
- The extent of waterlogging periods.
2. Materials and Methods
2.1. Study Site
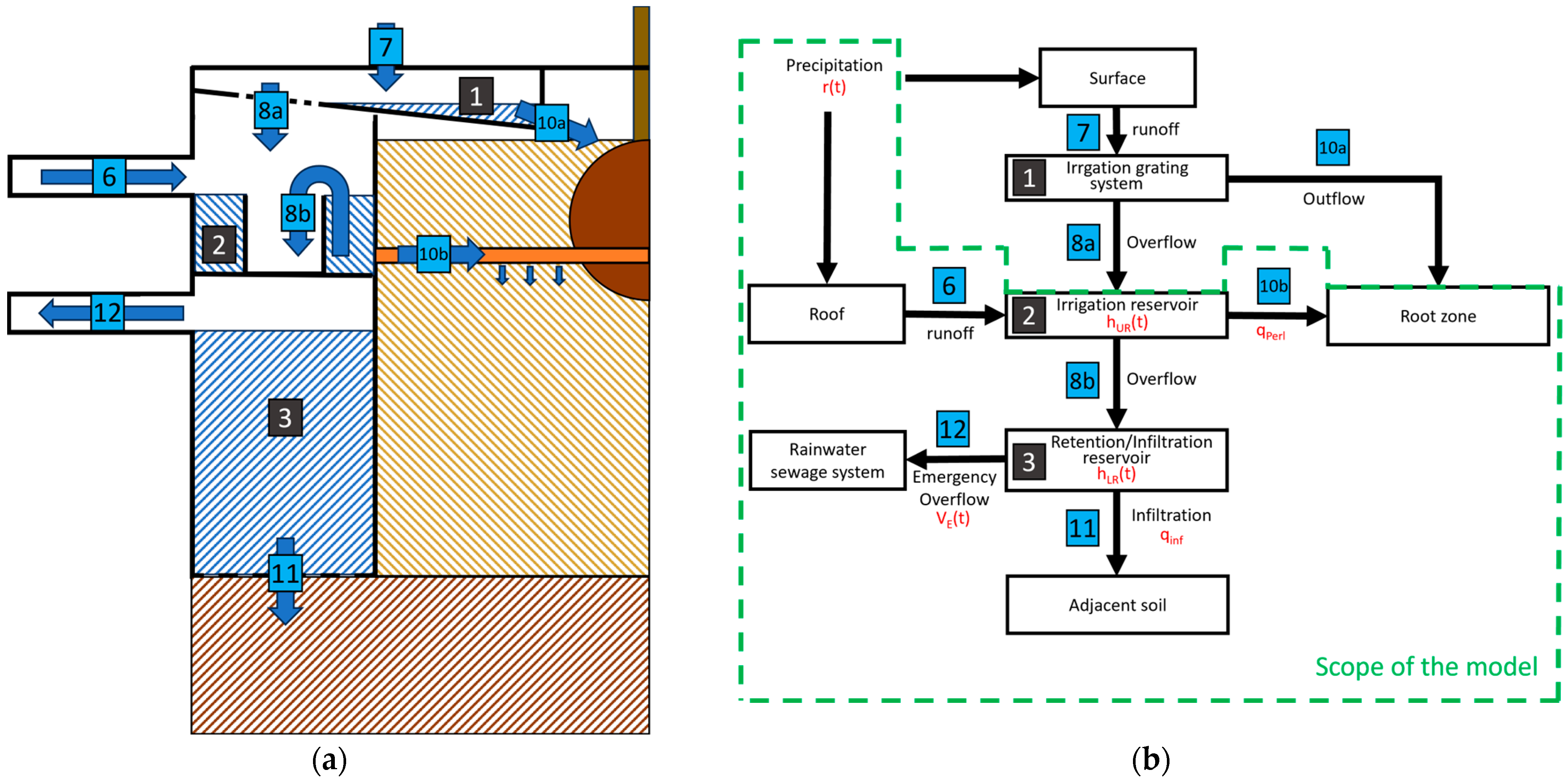
2.2. Design of ALVEUS Stormwater Tree Pit and Reference Tree Pits
2.3. Water Level Measurements and Soil Moisture Content
2.4. Meteorological Data
2.5. Water Distribution Model
- Perl hoses and infiltration: the exfiltration rate of the Perl hoses and the rate of infiltration into the lower soil are majorly influenced by the current water level in the respective reservoir.
- Perl hoses: the exfiltration rate of the Perl hoses is influenced by the growing season (roughly Mai–September in Germany) [12]
- Evaporation: the evaporation of water in the reservoirs is negligible.
- Irrigation grating system: the reservoir in the irrigation grating system was excluded from the model.
2.6. Retainable Heavy Rain Events
3. Results
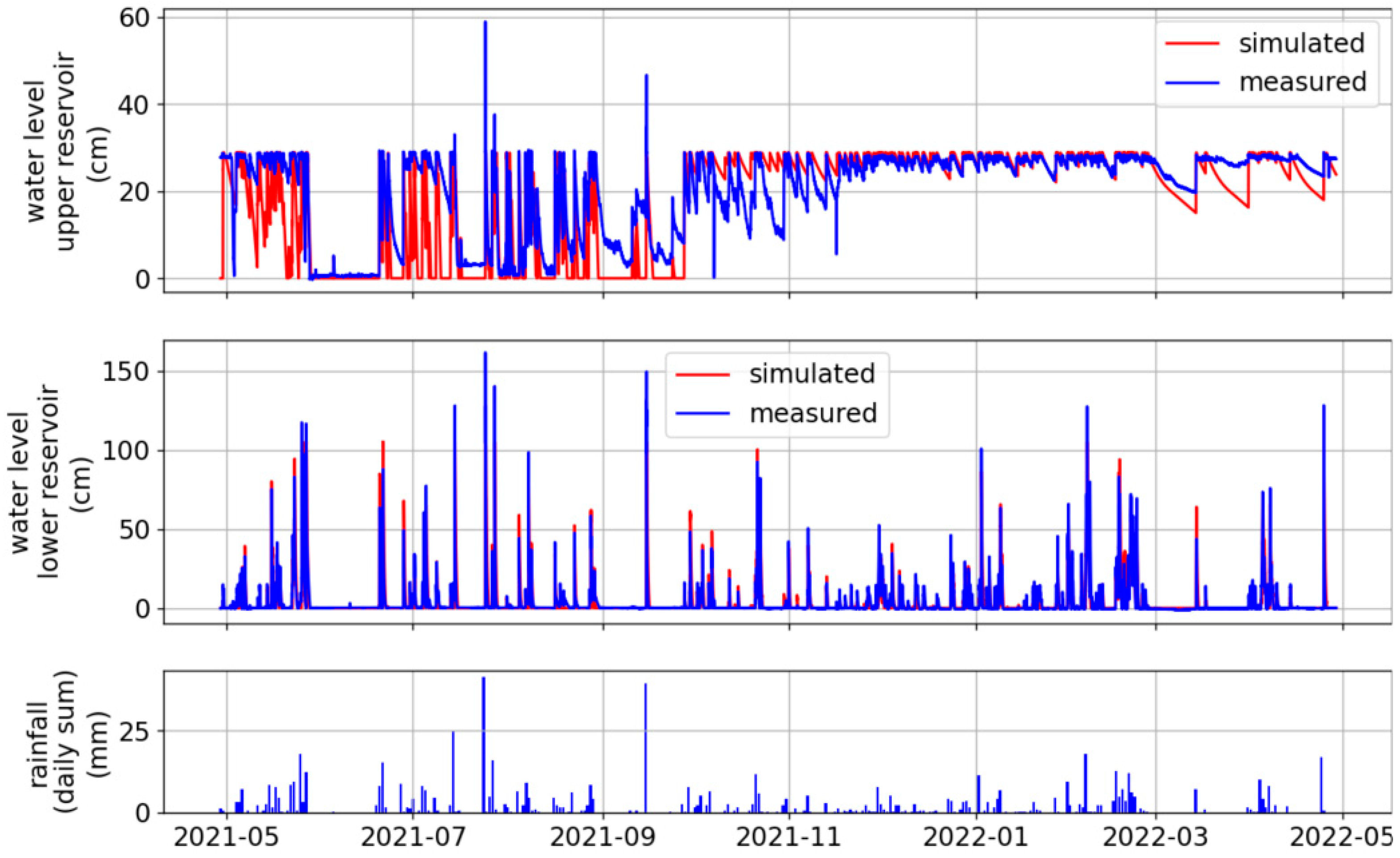
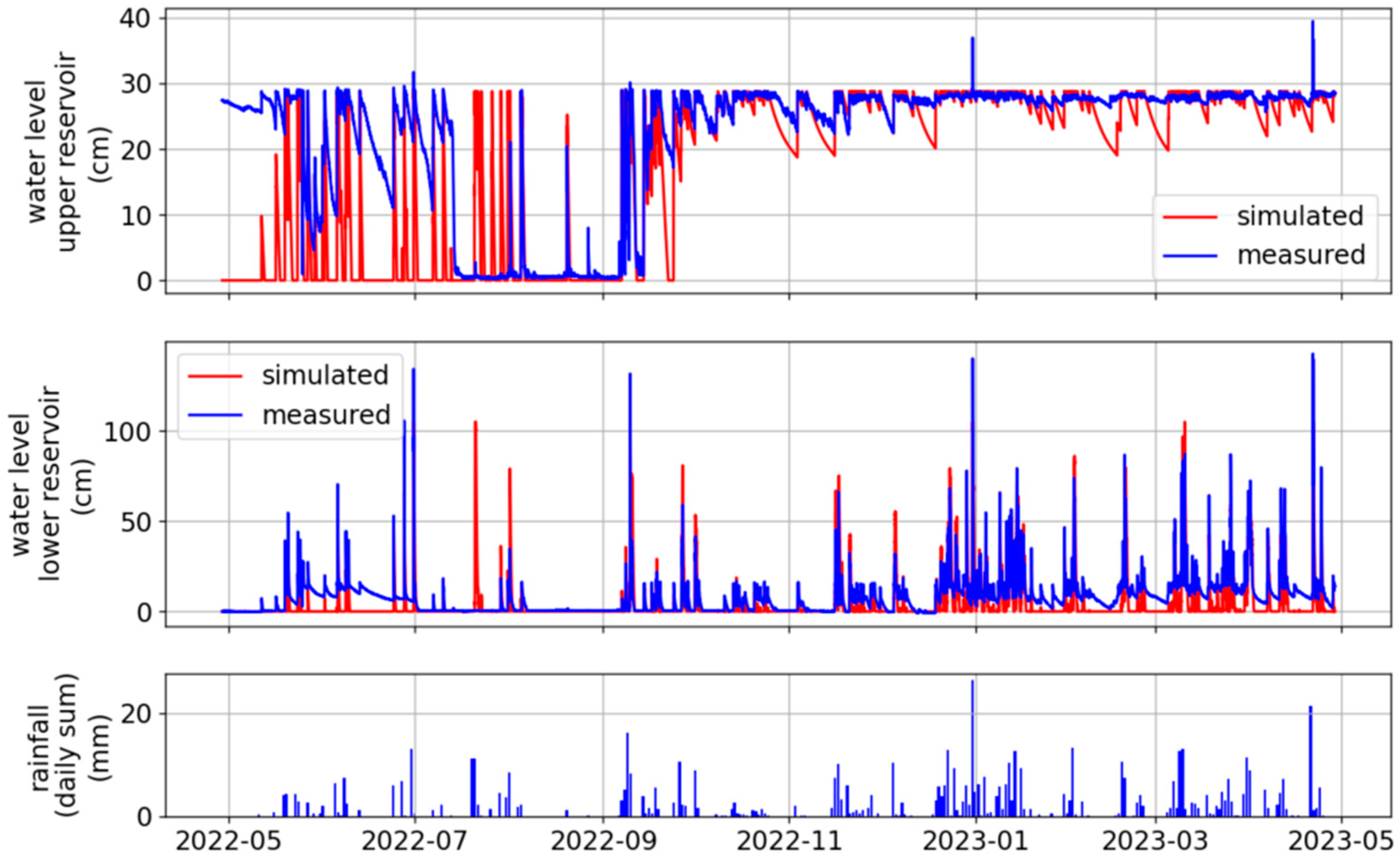
3.1. Water Level Measurements and Soil Moisture Content
3.2. Model Accuracy
3.3. Retainable Heavy Rain Events
3.4. Drought Mitigation
4. Discussion
4.1. Water Levels and Limits of the Model
4.2. Usage of Perl Hoses for Irrigation of Stormwater Tree Pits
4.3. Soil Moisture Content Probe Usage in Coarse-Grained Vegetation Substrates
4.4. Stormwater Tree Pits as Decentralized Storm Water Retention Tanks
4.5. Drought Mitigation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rahman, M.A.; Stratopoulos, L.M.F.; Moser-Reischl, A.; Zölch, T.; Häberle, K.H.; Rötzer, T.; Pretzsch, H.; Pauleit, S. Traits of trees for cooling urban heat islands: A meta-analysis. Build. Environ. 2020, 170, 106606. [Google Scholar] [CrossRef]
- Mullaney, J.; Lucke, T.; Trueman, S.J. A review of benefits and challenges in growing street trees in paved urban environments. Landsc. Urban Plan. 2015, 134, 157–166. [Google Scholar] [CrossRef]
- Kluge, B.; Pallasch, M.; Geisler, D.; Hübner, S. Straßenbäume und dezentrale Versickerung als Beitrag wassersensibler Stadtentwicklung—Teil 1. KA Korresp. Abwasser Abfall 2022, 69, 358–376. [Google Scholar] [CrossRef]
- Grey, V.; Livesley, S.J.; Fletcher, T.D.; Szota, C. Establishing Street trees in stormwater control measures can double tree growth when extended waterlogging is avoided. Landsc. Urban Plan. 2018, 178, 122–129. [Google Scholar] [CrossRef]
- Bartens, J.; Day, S.D.; Harris, J.R.; Wynn, T.M.; Dove, J.E. Transpiration and root development of urban trees in structural soil stormwater reservoirs. Environ. Manag. 2009, 44, 646–657. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Q.; McPherson, E.G. Performance of engineered soil and trees in a parking lot bioswale. Urban Water J. 2011, 8, 241–253. [Google Scholar] [CrossRef]
- Scharenbroch, B.C.; Morgenroth, J.; Maule, B. Tree Species Suitability to Bioswales and Impact on the Urban Water Budget. J. Environ. Qual. 2016, 45, 199–206. [Google Scholar] [CrossRef] [PubMed]
- Denman, L.; May, P.B.; Breen, P.F. An investigation of the potential to use street trees and their root zone soils to remove nitrogen from urban stormwater. Australas. J. Water Resour. 2006, 10, 303–311. [Google Scholar] [CrossRef]
- Climate-Data.org. Available online: https://de.climate-data.org/europa/deutschland/nordrhein-westfalen/coesfeld-890044/ (accessed on 15 June 2023).
- Granier, A.; Reichstein, M.; Bréda, N.; Janssens, I.A.; Falge, E.; Ciais, P.; Grünwald, T.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; et al. Evidence for soil water control on carbon and water dynamics in European forests during the extremely dry year: 2003. Agric. For. Meteorol. 2007, 143, 123–145. [Google Scholar] [CrossRef]
- dwd.de. Raster der Wiederkehrintervalle für Starkregen (Bemessungsniederschläge) in Deutschland (KOSTRA-DWD), Version 2020. Available online: https://www.dwd.de/DE/leistungen/kostra_dwd_rasterwerte/kostra_dwd_rasterwerte.html (accessed on 23 May 2023).
- dwd.de. Available online: https://www.dwd.de/DE/service/lexikon/Functions/glossar.html?lv2=102868&lv3=102890 (accessed on 3 June 2023).
- Granier, A.; Bréda, N.; Biron, P.; Villette, S. A lumped water balance model to evaluate duration and intensity of drought constraints in forest stands. Ecol. Model. 1999, 116, 269–283. [Google Scholar] [CrossRef]
- Black, T.A. Evapotranspiration from Douglas fir stands exposed to soil water deficits. Water Resour. Res. 1979, 15, 164–170. [Google Scholar] [CrossRef]
- Dunin, F.X.; Aston, A.R. The development and proving of models of large scale evapotranspiration: An Australian study. Agric. Water Manag. 1984, 8, 305–323. [Google Scholar] [CrossRef]
- Hunt, W.F.; Jarrett, A.R.; Smith, J.T.; Sharkey, L.J. Evaluating bioretention hydrology and nutrient removal at three field sites in North Carolina. J. Irrig. Drain. Eng 2006, 132, 600–608. [Google Scholar] [CrossRef]
- Li, H.; Sharkey, L.J.; Hunt, W.F.; Davis, A.P. Mitigation of impervious surface hydrology using bioretention in North Carolina and Maryland. J. Hydrol. Eng. 2009, 14, 407–415. [Google Scholar] [CrossRef]
- Page, J.L.; Winston, R.J.; Mayes, D.B.; Perrin, C.; Hunt, W.F. Retrofitting with innovative stormwater control measures: Hydrologic mitigation of impervious cover in the municipal right-of-way. J. Hydrol. 2015, 527, 923–932. [Google Scholar] [CrossRef]
- Deutsche Vereinigung für Wasserwirtschaft, Abwasser und Abfall e.V. DWA-A 117 Bemessung von Regenrückhalteräumen; Deutsche Vereinigung für Wasserwirtschaft, Abwasser und Abfall e.V.: Hennef, Germany, 2013. [Google Scholar]
- BlueGreenStreets. BlueGreenStreets als Multicodierte Strategie zur Klimafolgenanpassung—Wissenstand 2020, April 2020, Hamburg. Statusbericht im Rahmen der BMBF-Fördermaßnahme, Ressourceneffiziente Stadtquartiere für die Zukunft (RES:Z). Available online: https://repos.hcu-hamburg.de/handle/hcu/522 (accessed on 5 June 2023).






| Symbol | Title 2 | Value | Unit |
|---|---|---|---|
| Impervious connected area | 285 | m2 | |
| Connected area | 300 | m2 | |
| Base area of the infiltration reservoir (lower reservoir) | 2.30146 | m2 | |
| Base area of the irrigation reservoir (upper reservoir) | 1.141 | m2 | |
| Current day of date t | - | - | |
| Water level of the infiltration reservoir on date t | - | mm | |
| Water level of the infiltration reservoir on date t − 1 | - | mm | |
| Maximum water level of the infiltration reservoir | 1050 | mm | |
| Theoretical water level of the infiltration reservoir on date t | - | mm | |
| Water level of the irrigation reservoir on date t | - | mm | |
| Water level of the irrigation reservoir on date t − 1 | - | mm | |
| Maximum water level of the irrigation reservoir | 288 | mm | |
| Theoretical water level of the irrigation reservoir on date t | - | mm | |
| Current month of date t | - | - | |
| Static part of the infiltration rate of the lower soil | 0.1 | - | |
| Static part of the exfiltration rate of the Perl hoses | 0.3 | - | |
| Dynamic part of the infiltration rate of the lower soil | 0.9 | - | |
| Dynamic part of the exfiltration rate of the Perl hoses | 0.7 | - | |
| Maximum infiltration rate in the lower soil | 2 | mm × min−1 | |
| Maximum exfiltration rate of the Perl hoses | - | mm × min−1 | |
| Maximum exfiltration rate of the Perl hoses during growing season | 0.014 | mm × min−1 | |
| Maximum exfiltration rate of the Perl hoses outside of the growing season | 0.6 | mm × min−1 | |
| Rainfall that occurred in the period between t − 1 and t | - | mm | |
| Date | - | - | |
| Time resolution of the simulation/measurements | 5 | min | |
| Emergency overflow volume on date t | - | m3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siering, N.; Grüning, H. Stormwater Tree Pits for Decentralized Retention of Heavy Rainfall. Water 2023, 15, 2987. https://doi.org/10.3390/w15162987
Siering N, Grüning H. Stormwater Tree Pits for Decentralized Retention of Heavy Rainfall. Water. 2023; 15(16):2987. https://doi.org/10.3390/w15162987
Chicago/Turabian StyleSiering, Nils, and Helmut Grüning. 2023. "Stormwater Tree Pits for Decentralized Retention of Heavy Rainfall" Water 15, no. 16: 2987. https://doi.org/10.3390/w15162987






