Models and Interpretation Methods for Single-Hole Flowmeter Experiments
Abstract
:1. Introduction
2. Experiments and Interpretation Methods
2.1. Considered Experiments and Methods
- Single-pumping single-log experiments. The vertical flow rates and hydraulic heads are measured along the borehole while the flowmeter is lowered into the well during a single pumping test.
- Single-pumping double-log experiments. As before, the vertical flow rates and hydraulic heads are measured along the borehole during two log experiments that are conducted under the same pumping test.
- Multiple-pumping local-log experiments. A pumping test is performed for each conductive zone that needs to be characterized (except the upper one) with the logging tool localized above this zone.
2.2. Double Flowmeter Test with Transient Flow Rate (DFTTF)
2.3. Transient Flow Rate Flowmeter Test (TFFT)
- Model the data with variable pumping flow rate models, as described in Appendix C.1.
- Estimate the unknowns , , by inverting the data provided by the multi-aquifer model described in Appendix B using a numerical optimization method. More precisely, the Laplace transform of and are given in expressions (A15) and (A17) and numerically inverted with [37]’s algorithm.
3. Examples of Applications on Synthetic Cases
3.1. Considered Configurations
3.2. Single- and Double-Log Flowmeter Experiments
3.3. Series of Local Flowmeter Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Standard Models and Interpretation Methods
Appendix A.1. Single Flowmeter Test (SFT)
Appendix A.2. Double Flowmeter Test (DFT)
Appendix B. Multi-Aquifer Model
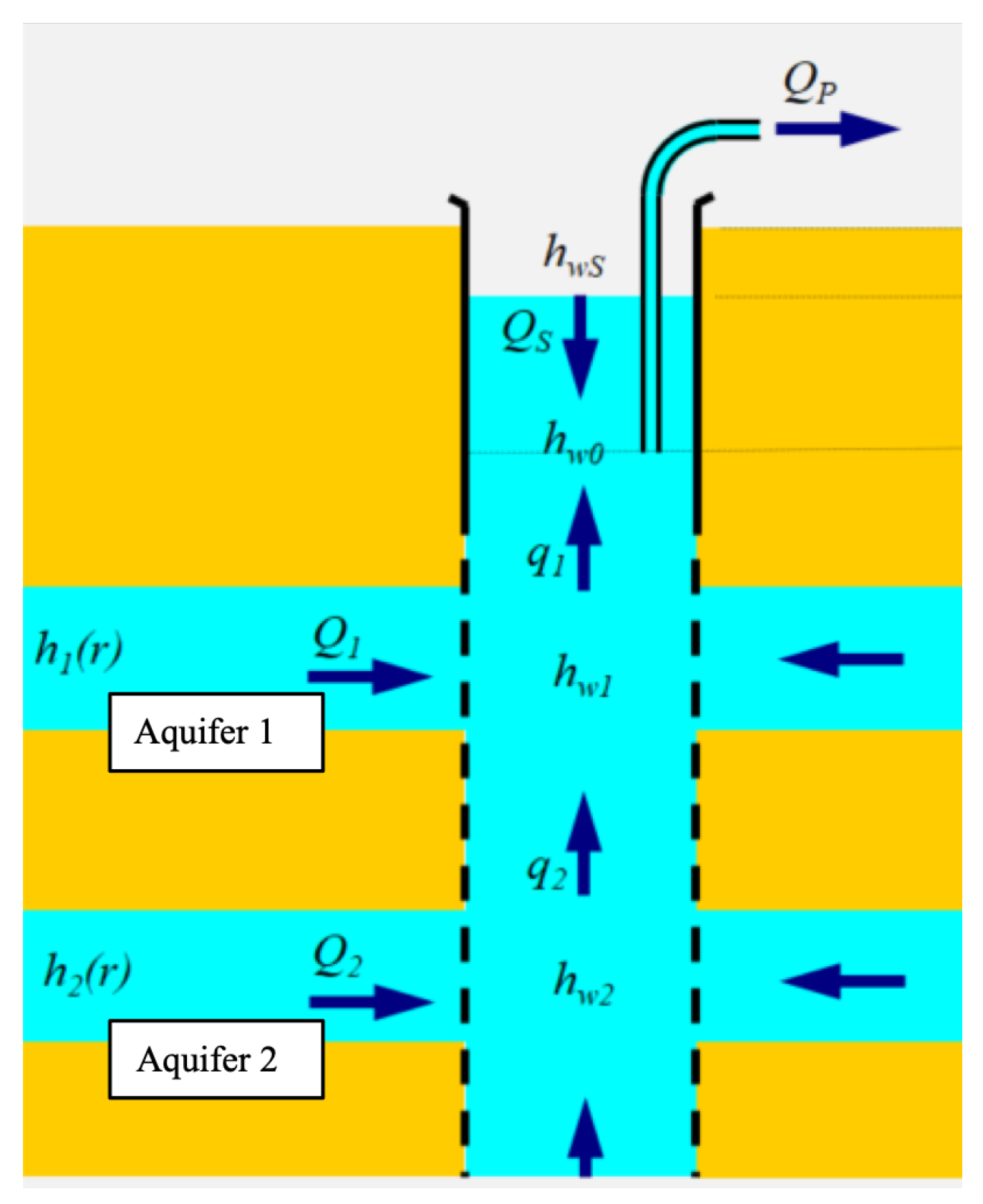
Appendix C. Models for Transient Parameters and Properties
Appendix C.1. Pumping Flow Rate Models
Appendix C.2. Couples of Equivalent Parameters (S si,σ i )
References
- Le Borgne, T.; Bour, O.; Riley, M.S.; Gouze, P.; Pezard, P.A.; Belghoul, A.; Lods, G.; Le Provost, R.; Greswell, R.B.; Ellis, P.A.; et al. Comparison of alternative methodologies for identifying and characterizing preferential flow paths in heterogeneous aquifers. J. Hydrol. 2007, 345, 134–148. [Google Scholar] [CrossRef]
- Moscoso Lembcke, L.G.; Roubinet, D.; Gidel, F.; Irving, J.; Pehme, P.; Parker, B.L. Analytical analysis of borehole experiments for the estimation of subsurface thermal properties. Adv. Water Resour. 2016, 91, 88–103. [Google Scholar] [CrossRef]
- Demirel, S.; Roubinet, D.; Irving, J.; Voytek, E. Characterizing Near-Surface Fractured-Rock Aquifers: Insights Provided by the Numerical Analysis of Electrical Resistivity Experiments. Water 2018, 10, 1117. [Google Scholar] [CrossRef]
- Klepikova, M.; Brixel, B.; Jalali, M. Transient hydraulic tomography approach to characterize main flowpaths and their connectivity in fractured media. Adv. Water Resour. 2020, 136, 103500. [Google Scholar] [CrossRef]
- Dorn, C.; Linde, N.; Le Borgne, T.; Bour, O.; de Dreuzy, J.R. Conditioning of stochastic 3-D fracture networks to hydrological and geophysical data. Adv. Water Resour. 2013, 62, 79–89. [Google Scholar] [CrossRef]
- Marinoni, M.; Delay, F.; Ackerer, P.; Riva, M.; Guadagnini, A. Identification of groundwater flow parameters using reciprocal data from hydraulic interference tests. J. Hydrol. 2016, 539, 88–101. [Google Scholar] [CrossRef]
- Somogyvari, M.; Jalali, M.; Parras, S.J.; Bayer, P. Synthetic fracture network characterization with transdimensional inversion. Water Resour. Res. 2017, 53, 5104–5123. [Google Scholar] [CrossRef]
- Zhou, Z.; Roubinet, D.; Tartakovsky, D.M. Thermal Experiments for Fractured Rock Characterization: Theoretical Analysis and Inverse Modeling. Water Resour. Res. 2021, 57, e2021WR030608. [Google Scholar] [CrossRef]
- Kruseman, G.P.; de Ridder, N.A. Analysis and Evaluation of Pumping Test Data; ILRI Publication, International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1990. [Google Scholar]
- Hemker, C. Transient well flow in vertically heterogeneous aquifers. J. Hydrol. 1999, 225, 1–18. [Google Scholar] [CrossRef]
- Le Borgne, T.; Bour, O.; de Dreuzy, J.R.; Davy, P.; Touchard, F. Equivalent mean flow models for fractured aquifers: Insights from a pumping tests scaling interpretation. Water Resour. Res. 2004, 40, W03512. [Google Scholar] [CrossRef]
- Zech, A.; Müller, S.; Mai, J.; Heße, F.; Attinger, S. Extending Theis’ solution: Using transient pumping tests to estimate parameters of aquifer heterogeneity. Water Resour. Res. 2016, 52, 6156–6170. [Google Scholar] [CrossRef]
- Paillet, F. Using Borehole Flow Logging to Optimize Hydraulic-Test Procedures In Heterogeneous Fractured Aquifers. Hydrogeol. J. 1995, 3, 4–20. [Google Scholar] [CrossRef]
- Roubinet, D.; Irving, J.; Day-Lewis, F.D. Development of a new semi-analytical model for cross-borehole flow experiments in fractured media. Adv. Water Resour. 2015, 76, 97–108. [Google Scholar] [CrossRef]
- Klepikova, M.; Brixel, B.; Roubinet, D. Analysis of thermal dilution experiments with distributed temperature sensing for fractured rock characterization. J. Hydrol. 2022, 610, 127874. [Google Scholar] [CrossRef]
- Hess, A. Identifying hydraulic conductive fractures with a slow-velocity heat-pulse flowmeter. Can. Geotech. J. 1986, 23, 69–78. [Google Scholar] [CrossRef]
- Young, S.C. Characterization of High-K Pathways by Borehole Flowmeter and Tracer Tests. Groundwater 1995, 33, 311–318. [Google Scholar] [CrossRef]
- Boman, G.; Molz, F.; Boone, K. Borehole flowmeter application in fluvial sediments: Methodology, results, and assessment. Groundwater 1997, 35, 443–450. [Google Scholar] [CrossRef]
- Read, T.; Bour, O.; Bense, V.; Le Borgne, T.; Goderniaux, P.; Klepikova, M.; Hochreutener, R.; Lavenant, N.; Boschero, V. Characterizing groundwater flow and heat transport in fractured rock using fiber-optic distributed temperature sensing. Geophys. Res. Lett. 2013, 40, 2055–2059. [Google Scholar] [CrossRef]
- Pehme, P.; Parker, B.; Cherry, J.; Molson, J.; Greenhouse, J. Enhanced detection of hydraulically active fractures by temperature profiling in lined heated bedrock boreholes. J. Hydrol. 2013, 484, 1–15. [Google Scholar] [CrossRef]
- Pehme, P.; Parker, B.L.; Cherry, J.A.; Blohm, D. Detailed measurement of the magnitude and orientation of thermal gradients in lined boreholes for characterizing groundwater flow in fractured rock. J. Hydrol. 2014, 513, 101–114. [Google Scholar] [CrossRef]
- Day-Lewis, F.D.; Johnson, C.D.; Paillet, F.L.; Halford, K.J. A computer program for Flow-Log Analysis of Single Holes (FLASH). Groundwater 2011, 49, 926–931. [Google Scholar] [CrossRef] [PubMed]
- Klepikova, M.V.; Le Borgne, T.; Bour, O.; de Dreuzy, J.R. Inverse modeling of flow tomography experiments in fractured media. Water Resour. Res. 2013, 49, 7255–7265. [Google Scholar] [CrossRef]
- Audouin, O.; Bodin, J.; Porel, G.; Bourbiaux, B. Flowpath structure in a limestone aquifer: Multi-borehole logging investigations at the hydrogeological experimental site of Poitiers, France. Hydrogeol. J. 2008, 16, 939–950. [Google Scholar] [CrossRef]
- Aliouache, M.; Wang, X.; Fischer, P.; Massonnat, G.; Jourde, H. An inverse approach integrating flowmeter and pumping test data for three-dimensional aquifer characterization. J. Hydrol. 2021, 603, 126939. [Google Scholar] [CrossRef]
- Paillet, F.L. Flow modeling and permeability estimation using borehole flow logs in heterogeneous fractured formations. Water Resour. Res. 1998, 34, 997–1010. [Google Scholar] [CrossRef]
- Lods, G.; Roubinet, D.; Matter, J.M.; Leprovost, R.; Gouze, P. Groundwater flow characterization of an ophiolitic hard-rock aquifer from cross-borehole multi-level hydraulic experiments. J. Hydrol. 2020, 589, 125152. [Google Scholar] [CrossRef]
- Morin, R.H.; Hess, A.E.; Paillet, F.L. Determining the Distribution of Hydraulic Conductivity in a Fractured Limestone Aquifer by Simultaneous Injection and Geophysical Logging. Groundwater 1988, 26, 587–595. [Google Scholar] [CrossRef]
- Molz, F.; Morin, R.; Hess, A.; Melville, J.; Guven, O. The Impeller Meter for measuring aquifer permeability variations: Evaluation and comparison with other tests. Water Resour. Res. 1989, 25, 1677–1683. [Google Scholar] [CrossRef]
- Kabala, Z. Measuring distribution of hydraulic conductivity and storativity by the double flowmeter test. Water Resour. Res. 1994, 30, 685–690. [Google Scholar] [CrossRef]
- Ruud, N.; Kabala, Z. Numerical Evaluation of Flowmeter Test Interpretation Methodologies. Water Resour. Res. 1996, 32, 845–852. [Google Scholar] [CrossRef]
- Ruud, N.; Kabala, Z. Numerical evaluation of the flowmeter test in a layered aquifer with a skin zone. J. Hydrol. 1997, 203, 101–108. [Google Scholar] [CrossRef]
- Riva, M.; Ackerer, P.; Guadagnini, A. Interpretation of flowmeter data in heterogeneous layered aquifers. J. Hydrol. 2012, 452–453, 76–82. [Google Scholar] [CrossRef]
- Aly, A.; Chen, H.; Lee, W. Development of a mathematical model for multilayer reservoirs with unequal initial pressures. In Situ 1996, 20, 61–92. [Google Scholar]
- Kabala, Z.; El-Sayegh, H. Transient flowmeter test: Semi-analytic crossflow model. Adv. Water Resour. 2002, 25, 103–121. [Google Scholar] [CrossRef]
- Bourdarot, G. Essais de Puits: Méthodes D’interprétation; Ed. Technip: Paris, France, 1996; p. 352. [Google Scholar]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transform. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Atkinson, L.C.; Gale, J.E.; Dudgeon, C.R. New Insight Into The Step-Drawdown Test In Fractured-Rock Aquifers. Hydrogeol. J. 1994, 2, 9–18. [Google Scholar] [CrossRef]
- Theis, C. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground water storage. Trans. Am. Geophys. Union 1935, 16, 519–524. [Google Scholar] [CrossRef]
- Hufschmied, P. Estimation of three-dimensional anisotropic hydraulic conductivity field by means of single well pumping tests combined with flowmeter measurements. Hydrogéol. B.R.G.M. Orléans Fr. 1986, 2, 163–174. [Google Scholar]
- Matthews, C.; Russel, D. Pressure buildup and flow tests in wells. SPE Am. Inst. Min. Met. Engrs. 1967, 1, 167. [Google Scholar]
- van Everdingen, A.; Hurst, W. The skin effect and its influence on the productive capacity of the well. Trans. Am. Inst. Mineral. Metall. Petrol. Eng. 1953, 198, 171–176. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Applied Mathematics Series; Dover Publications: Washington, DC, USA, 1972. [Google Scholar]

| Experiment Name | Collected Data | Interp. Methods |
|---|---|---|
| Single-pumping single-log | , | SFT |
| Single-pumping double-log | , | DFT, DFTTF |
| Multiple-pumping local-log | TFFT |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lods, G.; Roubinet, D. Models and Interpretation Methods for Single-Hole Flowmeter Experiments. Water 2023, 15, 2960. https://doi.org/10.3390/w15162960
Lods G, Roubinet D. Models and Interpretation Methods for Single-Hole Flowmeter Experiments. Water. 2023; 15(16):2960. https://doi.org/10.3390/w15162960
Chicago/Turabian StyleLods, Gerard, and Delphine Roubinet. 2023. "Models and Interpretation Methods for Single-Hole Flowmeter Experiments" Water 15, no. 16: 2960. https://doi.org/10.3390/w15162960
APA StyleLods, G., & Roubinet, D. (2023). Models and Interpretation Methods for Single-Hole Flowmeter Experiments. Water, 15(16), 2960. https://doi.org/10.3390/w15162960






