1. Introduction
A form of fluid known as a “nanofluid” has small particles scattered throughout a base fluid. Nanoscale particles typically have sizes of less than 100 nm. The base fluid becomes more thermally efficient when nanoparticles are added. In 1995, Choi and Eastman [
1] first proposed the concept of nanofluids, and the results of their experiments show that introducing nanoparticles into base fluids enhances the fluid’s capacity to offer heat conductivity. Medical areas, engineering detergent production, automotive cooling, nuclear reactor cooling fluid, and military applications are just a few of the different fields where nanofluids are used. Hybrid nanofluids are base fluids with two distinct nanoparticles that have been combined. The thermal efficiency of a hybrid nanofluid is higher than that of an ordinary nanofluid due to the combines two distinct nanoparticles with base fluid. Engineering, medical areas, nuclear reactor cooling, detergent production, automotive cooling, braking fluid, and military applications are just a few of the different fields where nanofluids are used. Three distinct nanoparticles together with a base fluid combine to form a ternary nanofluid. Ternary hybrid nanofluid has superior thermal efficiency and fluid flow motion than simple and hybrid nanofluid. Ternary nanofluids are used in industries, medical, and mechanical fields. Additionally, they are utilized as a coolant in automobiles, heat exchangers, and other automotive fields. Madhukesh et al. [
2] studied the movement of a hybrid nanofluid using Newtonian heating through a curved stretching sheet. Animasaun et al. [
3] explored the dynamics of a ternary-hybrid nanofluid on convectively heated surfaces by taking the impact of magnetic flux density and the presence of a heat source or sink into consideration. The findings reveal that convective heating and inclined magnetic fields have a significant positive influence on temperature distribution, and these outcomes have potential applications in enhancing heat transfer and managing thermal processes. Yaseen et al. [
4], investigated the bioconvection of a ternary nanofluid flow containing gyrotactic microbes, and the various factors considered, such as natural convection, heat source/sink, and radiation, while examining different shapes. Khan et al. [
5] studied the water-based ternary hybrid nanoparticles moving in a dependent-on-time mode over a rotating, porous stretching sphere. Ramesh et al. [
6] studied the thermal behavior of ternary nanofluids flow on the porous medium surface with a heat source/sink. Das et al. [
7] examined the theoretical modeling of a completely realized mixed convective flow of an ionic ternary hybrid nanofluid generated by electroosmosis and magnetohydrodynamics in an extended, vertical, non-conducting channel with linearly rising channel walls.
Pollutant concentration measures how much a hazardous chemical is present in a given volume of soil, water, air, or another medium. Nanoparticles have the potential to boost heat transfer and have many kinds of features in the removal of pollutants. A major problem that has influenced how individuals move about their everyday lives is pollution. Impurities seriously affect the health of animals, humans, plants, and living things. The heart, liver, kidneys, and respiratory systems are all negatively affected by pollution. In most cases, the main causes of air pollution in cities are heating systems in homes and automobile emissions. Pollution is only one of the industrial operations’ negative environmental consequences on the ecosystem. Even in tiny quantities, certain pollutants could have positive benefits. Sulfur dioxide, in small amounts, may promote plant development. Copper and zinc are vital elements in animal bodies. Some researchers have studied the contribution of external pollutant source factors on the concentration of pollutants. Makinde et al. [
8] investigated the system of equations regulating river pollution transfer using classical Lie points. Numerically examined the pollutant concentration dispersion in a 2D consolidated river model by Pengpop et al. [
9]. Chinyoka and Makinde [
10] explore the dynamics of polymeric pollutant dispersion in a rectangular channel, caused by an external source in a flowing Newtonian liquid, the numerical model provides insights into pollution scenarios resulting from an improper discharge of hydrocarbon products offering measurements for detecting contamination levels. The study initiated by Cintolesi et al. [
11] focuses on the interaction between inertial and thermal forces in urban canyons and their impact on turbulent characteristics and pollutant removal. Large-eddy simulations model the square canyons with different facade temperatures, while a street-level scalar source represents traffic emissions. Heated facades induce convective flows to create an energetic, turbulent region at the canyon-ambient interface, enhancing pollutant removal and reducing urban drag; heating the upwind facade strengthens the internal vortex and decreases overall pollutant concentration. Chinyoka and Makinde [
12] investigated the transient dispersion of a pollutant in a laminar channel flow using numerical methods, and the model considers density variation with pollutant concentration and provides insights into pollutant behavior aiding in understanding and addressing improper discharge incidents and evaluating decontamination measures for water bodies. Southerland et al. [
13] studied a neighborhood-scale analysis for determining the spread of air pollution health risks in cities with high-resolution data sets utilization in the bay area.
When introducing a heat source/sink parameter, the amount of heat distributed throughout the area may fluctuate. The heat source/sink parameter increases the thermal dispersion rate while decreasing the mass transfer rate. Nuclear reactors, semiconductors, and electronic materials are examples of real-world uses for the heat source/sink phenomenon. Gireesha et al. [
14] studied the effect of Biot number with an irregular heat source/sink and non-linear thermal radiation of nanofluids in the stretched surface. Khan et al. [
15] examined the water-based alumina nanofluid implanted in a porous media with buoyancy force that caused a two-dimensional stretched wall jet to transfer heat in fluid flow. Khan et al. [
16] studied the stability analysis and the movement of two distinct types of nanoparticles present in fluid across an extendable/shrinkable vertical surface produced by a micropolar fluid with an inconsistent heat source/sink. Kumar et al. [
17] studied the hybrid ferrofluid layer flow and heat transmission in the presence of radiation and erratic heat sources and sinks. Utilizing various nanofluids in three-dimensional motion across a Riga plate, a numerical analysis of the irregular heat source/sink qualities was conducted by Raghupati et al. [
18]. Khan et al. [
19] studied how a wall jet nanofluid moving under the influence of Lorentz forces was affected by activation energy, an irregular heat source/sink, thermophoretic particle deposition, and chemical reaction. Vijayalakshmi et al. [
20] studied the effect of the chemical reaction and nonuniform heat source/sink with a porous medium on Casson fluid in a vertical cone and flat plate.
The ability to transform fluid energy into motion energy is a characteristic of convergent channels. Pressure may be enhanced in divergent channels while velocity is raised in converging channels. Chemical, mechanical, biomechanical, civil, and environmental engineering are just a few practical applications in which fluid flow in a non-parallel channel is utilized. Convergent/divergent channels are used to produce wires, dynamics, heat exchangers, aeronautical, civil, biomechanical, pharmaceutical, biomedical devices, fiberglass, rocket engines, plastic sheets, and metal casting when a magnetic field is present. Blood movement through arteries and capillaries in the human body is an example of fluid flow in converging/diverging channels. The study of fluids over divergent/convergent channels has attracted the attention of many researchers. Rashid et al. [
21] examined the joule dissipation in the motion of water transporting zinc oxide across convergent and divergent channels with the impact of nanoparticles. Ramesh et al. [
22] studied the impact of the permeable medium and heat source/sink in convergent/divergent channels of ternary hybrid nanofluids. Khan et al. [
23] studied the MHD flow of a viscous fluid in a channel having irregular walls and the effect of mass and heat transport in a concentration and temperature profile. Mishra et al. [
24] examined the combined impact of joule heating, heat generation/absorption, and magnetohydrodynamic flow of nanofluids in stretching/shrinking, porous, divergent/convergent channels with a viscous dissipation and volume fraction. Based on ternary-nanoparticle efficiency for base fluid mixture along a convergent-divergent channel studied by Zahan et al. [
25]. Adnan et al. [
26] examined the influence of TR (thermal radiation) on the Jeffery-Hamel circulation as well as the motion of a viscous, incompressible liquid between two nonparallel plane walls. Saifi et al. [
27] developed an innovative mathematical method for assessing heat distributions in convergent-divergent channels between non-parallel planar walls in a Jeffery Hamel flow.
Based on the literature, no study examined the non-uniform heat source/sink and pollutant concentration impacts on the ternary-based nanofluid circulation across convergent/divergent channels. The current work has been studied by taking the above effects. Using suitable transformations, the governing equations are simplified to ODEs and solved numerically using the RKF-45 method. The significant dimensionless constraints are analyzed with the help of graphs.
2. Mathematical Formulation
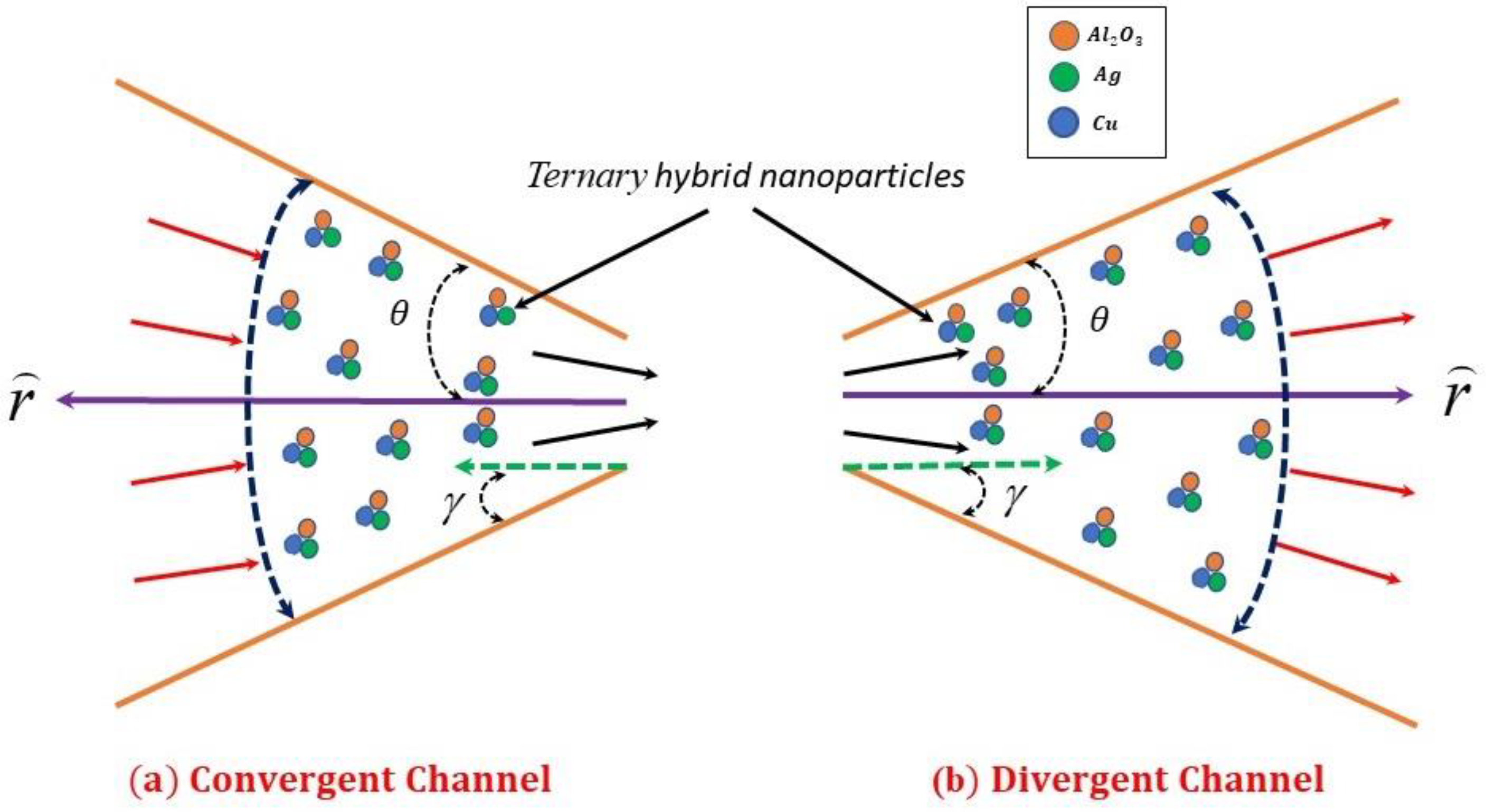
Consider a steady, incompressible, 2-dimensional flow and ternary nanofluid circulating between convergent/divergent channels with an angle
(see
Figure 1). Here
represents the uniform velocity in channels, and it depends on both
and
. The velocity profile is taken in the form of
. Temperature and concentration equations contain irregular heat source/sink and pollutant concentration discharge, and both depend on
and
.
The following are the equations that indicate the flow that was previously discussed (See [
22]):
with corresponding boundary conditions are,
In the temperature Equation (4),
represents the non-uniform heat source/sink, and modeled as, (see [
18])
The values of consequently and denotes the internal heat sink and internal heat source factors.
From the above-stated Equations (1)–(7), the expressions are listed below:
| : | Kinematic viscosity |
| : | Coefficient of mass diffusivity |
| : | External pollutant source variation parameter |
| : | Temperature dependent heat source/sink |
| : | Pressure |
| : | The space dependent heat source/sink |
| : | Specific heat |
| : | Thermal conductivity |
| : | Specific heat capacitance |
| : | Absolute viscosity |
| : | Density |
Furthermore, the rest of the mathematical symbols or notations used in the governing equations represent the thermophysical properties of the ternary nanofluids. Each symbol is namely defined as above, while the correlations of these thermophysical properties for ternary nanofluids are given below, (see [
7]):
Here,
—thermal conductivity,
—heat capacity,
—dynamic viscosity,
—density, and
—solid volume fraction of the nanoparticles. In the above expression, particularly the case
, it will reduce for hybrid nanofluid and
reduces to nanofluid expression,
denotes the expression to working base liquid. Moreover, the thermophysical experimental data of base/carrier liquid and the chosen nanoparticles are presented in
Table 1.
The term
that represents the external pollutant concentration in Equation (5), (see [
12])
To convert Equations (1)–(5) into non-dimensional form, introduced the following similarity variables, (see [
23])
For radial flow velocity profile can be represented in the form,
From the Equations (2) and (3) we can eliminate the pressure term by utilizing (10) and (11), we obtain,
and now Equations (4) and (5) are reduced to
The reduced boundary conditions are,
From the resultant equations, the important dimensionless constraints and its expressions are provided in
Table 2.
The important engineering coefficients are provided as follows:
Equation (16) reduces to the following form as follows:
4. Result and Discussion
The complete review of the outcomes of the numerical analysis is given in the present part. Graphs are used to illustrate the most important parameters and their effects on the corresponding profiles. This section also covers additional important components including skin friction, the Nusselt number, and the Sherwood number. This research also provides clarity on how ternary nanofluids in convergent and divergent channels, have a significant impact along with practical implications.
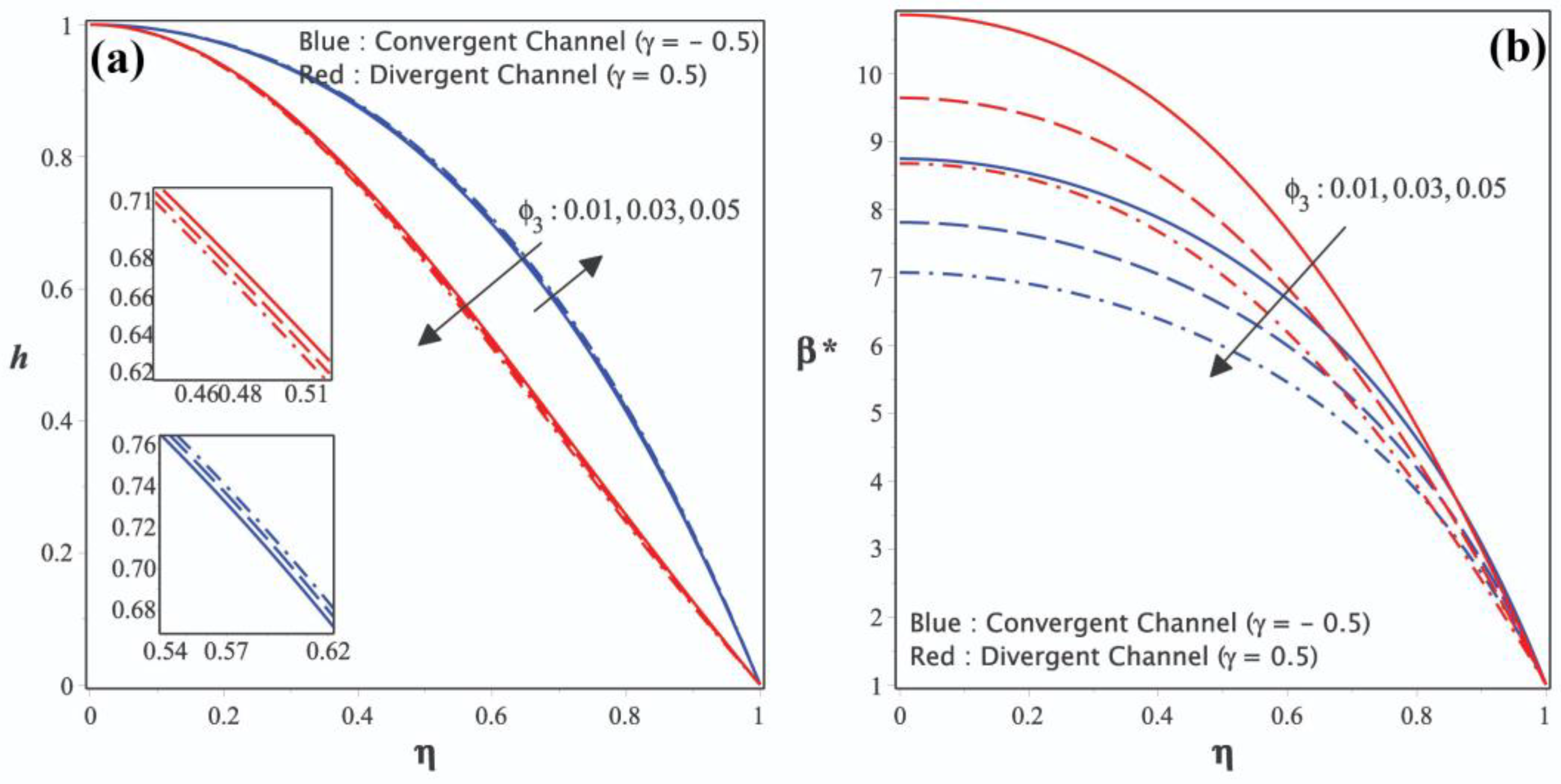
The impact of
on
and
profiles can be observed in
Figure 2a,b.
Figure 2a explains that increasing
will increase velocity
in convergent channels while decreasing in divergent channels. The behavior of the flow will be impacted by the presence of solid nanoparticles. The nanofluid will have a higher concentration as a result of the addition of nanoparticles, which will also strengthen the contact between the liquid and solid particles and improve velocity.
When there are solid particles present, the expanding process becomes difficult in a diverging channel, which reduces flow velocity. The enhancement in the values of
will decrease the concentration for both channel situations, as seen in
Figure 2b. This is because the solid particles act as conductive channels that carry heat throughout the fluid. As
increases, a narrower temperature distribution is produced because more solid particles contribute to overall thermal conductivity. The fact that the thermal distribution of the convergent channel is different from that of the divergent channel provides additional confirmation that the convergent form facilitates higher heat transfer. Fluid particles are brought in closer by the converging walls of the channel, which improves the transfer of heat energy. Thermal dispersion and an increased range of temperatures occur because of divergent channel shapes.
Figure 3 illustrates the impact of
on
for both convergent and divergent channel scenarios. Increasing in
will increases the
in both convergent and divergent channels. However, in this case of
the divergent channel exhibits a higher thermal dispersion than the converging channel. This is because the improved thermal distribution seen with higher
is caused by the fluid’s enhanced thermal conduction movement. Convective transfer of heat seems to be contributing more than other types of heat transmission when
values are higher. A more efficient exchange of thermal energy between the liquid and its surroundings is made possible by this increased convective heat transfer, leading to better thermal dispersion.
The impact of the space-dependent heat source/sink parameter on
is shown in
Figure 4a.
Figure 4a shows that, in the case of a convergent channel, an increase in the
(
) values improves the thermal distribution, whereas contrary behavior is shown in the situation of a divergent channel.
values represent the local heat production and absorption inside the liquid. Positive
values indicate that the fluid is producing heat, which raises the temperature, like how a negative value for
indicates the presence of heat causes a liquid to cool. Since the heat generated is partly confined in the convergent channel where the liquid is compressed, heat distribution is greatly improved. A decrease in temperature with rising values in the convergent channel can be attributed to heat being absorbed from the fluid. The temperature drops as a result of the fluid losing thermal energy due to the heat sink effect. The thermal energy within the fluid rises due to the generation of local heat, but as the fluid spreads in the diverging channel, the extra heat is diffused across a larger area. As a result, the rise in temperature becomes less substantial, which causes a fall in temperature. The distribution of temperature is evened as a result of the liquid’s thermal energy being drained by the heat sink effect. A more consistent temperature profile is produced as a result of heat absorption, which takes the place of temperature variations.
Figure 4b represents the impact of temperature-dependent heat source/sink (
) on
for both divergent/convergent channel. Negative values of
represents the temperature-dependent heat sink, and positive values of
represents the temperature-dependent heat source. The thermal distribution will drop in the convergent channel with increased values of the temperature-dependent heat source restriction, but increase in the divergent channel. The thermal distribution diminishes in the divergent channel but rises in the convergent channel due to the better temperature-dependent heat sink constraints.
indicates temperature is generated within the fluid as the temperature increases, and leads to the rise in temperature, while
indicates that temperature is transported by fluid as temperature improves, subsequently decreasing in thermal profile.
When , the fluid’s internal heat generation develops as the liquid’s temperature does. This additional heat increases the channel’s overall temperature distribution, resulting in a more stable temperature profile. As the fluid temperature increases, the amount of heat produced inside the fluid increases. However, the fluid gets squeezed in the convergent channel, which causes the additional heat to be more constrained and less distributed, leading to a decrease in temperature. As the temperature of the liquid improves when, the influence of the heat sink increases, increasing the heat absorption from the fluid. , the heat sink impact increases more efficient at storing thermal energy from heated locations as the temperature of the liquid increases. A more consistent temperature profile is produced as a result of this heat removal, which takes into account temperature variations in the convergent channel.
Figure 5a,b demonstrate the distribution of concentration profile for
and
. The concentration will drop as
and
values rise in a convergent channel, whereas the converse is true in a divergent channel. Both the external pollutant origin variation constraint and the local pollutant external source constraint pertain to fluctuations or external sources of contaminants injected into the liquid stream. An upsurge in these variables denotes a rise in pollutant intake or volatility, which raises concentration. When more pollutants are provided, or the diversity of pollutant sources develops, the overall concentration of pollutants in the liquid stream rises. The increase in concentration can be observed throughout as a result of the greater concentration being spread out across a larger volume in the diverging channel. When more pollutants are given, the fluid’s concentration of pollutants decreases. In the convergent channel, where the fluid gets squeezed, the concentration of the pollutant is less distributed and more constrained.
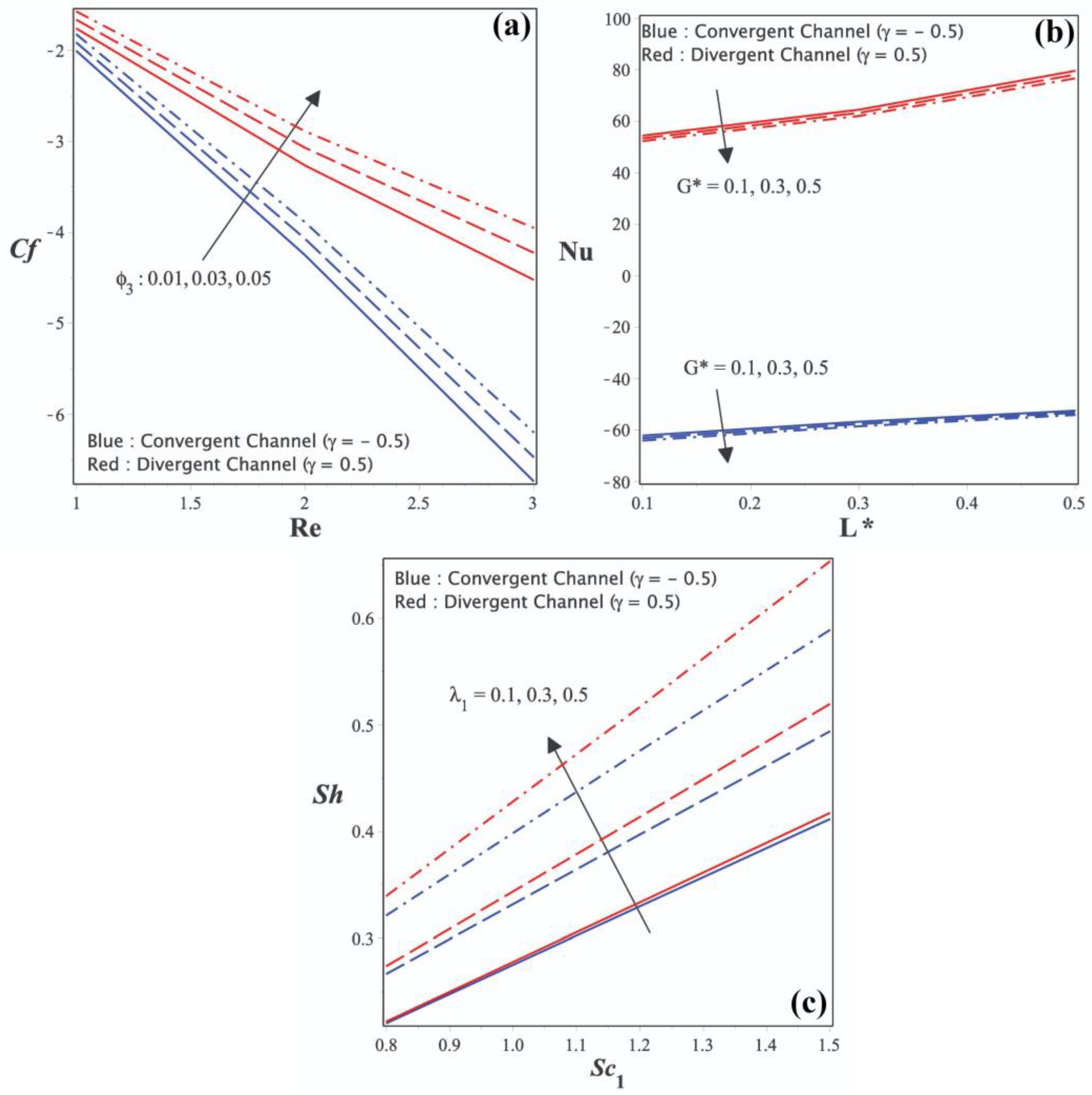
Figure 6a–c shows the engineering coefficients
,
, and
, on various non-dimensional parameters, respectively. The influence of skin friction over
for growth in the magnitude of
is shown in
Figure 6a. The addition of
and improved values of
will result in a surge at the surface drag force for the convergent and divergent channels. Additionally, divergent channels will have a greater surface drag force compared to convergent channels. Higher
values and an increase in the solid volume percentage will enhance the contact between liquid and solid nano-sized particles. The flow encounters a larger surface area in a divergent channel scenario than in a convergent channel situation. Therefore, there is more surface drag force in the case of a diverging channel.
Figure 6b represents the change in the thermal distribution rate on
for different values of
. The rate of heat transmission will decrease as these two parameters get higher. The graph also makes it very evident that
is more of a divergent channel case than a convergent channel scenario. When heat generation is more localized within the fluid and the parameters of heat transport change with temperature, thermal energy is diffused more slowly. The rate of heat dispersion decreases as a result. The fluid is compressed in the convergent channel, where the thermal energy is more concentrated, leading to a decreased rate of heat distribution. In the diverging channel, where the fluid expands, the thermal energy is distributed more uniformly, leading to a higher rate of heat dispersion.
The mass transfer rate on
for a rise in the value of the external pollution source variation parameter is shown in
Figure 6c. Increases in these two variables will speed up mass transport in the fluid flow. In addition, it has been discovered that divergent channels have a higher mass transfer rate than convergent channels. When the Schmidt number rises and the pollution input or variation from outside the fluid increases, the mass transfer inside the fluid becomes more effective. The rate of mass transfer consequently rises, indicating that contaminants move between locations faster. The fluid increases in the diverging channel, where there is more mixing and contact with the sources of pollution. As a result, mass transfer happens more quickly. The convergent channel, on the other hand, is subjected to greater compression, which minimizes the dissolution and contact between the liquid and the sources of pollution, resulting in a slower mass transmission rate.
5. Conclusions
The current work concentrates on the irregular heat source/sink impact and pollutant concentration in ternary nanofluid flow between convergent/divergent channels. The study’s principal findings are listed below.
For the convergent channel situation, the inclusion of values will improve the velocity profile, but the divergent channel exhibits the opposite characteristic.
The concentration profile in both channels will be improved by both and .
In the presence of the Eckert number, the heat spreading is more concentrated in divergent channels than convergent channels.
Convergent channels display a lower surface drag than divergent channels due to an increase in the solid volume percentage and Reynolds number.
When an external pollutant source parameter is present, the rate of mass transfer increases.
The domains of energy systems, environmental engineering, and thermal management systems can all benefit from the study’s conclusions. Information from pollutant concentration studies can assist environmental organizations, businesses, and governments in controlling and lowering pollution levels, which promotes sustainable development. In addition, the realistic behavior of these materials may differ owing to temperature-dependent changes, particle aggregation, and other phenomena not completely included in the model. The analysis may assume laminar flow conditions, ignoring turbulence, which is important in certain applications. Nonetheless, the results might improve heat management, minimize pollutant dispersion, and increase nanofluid circulation. The external pollutant source variation parameter affects the system’s behavior and pollution control performance. Increasing this parameter raises pollutant concentrations, influencing fluid flow patterns as well as heat and mass transfer rates. Reduced it leads to smoother flow and lower pollutant concentrations, making pollution management more achievable for lower pollutant loads.