Next Article in Journal
Computational Examination of Heat and Mass Transfer Induced by Ternary Nanofluid Flow across Convergent/Divergent Channels with Pollutant Concentration
Next Article in Special Issue
Enrichment Mechanism of Lithium in Geothermal Waters from a Bedrock Reservoir in Xiong’an New Area, China
Previous Article in Journal
Ice Phenology and Thickness Modelling for Lake Ice Climatology
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Water
Volume 15
Issue 16
10.3390/w15162953
water-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Seepage and Heat Transfer of Dominant Flow in Fractured Geothermal Reservoirs: A Review and Outlook

by
Zhiyan Liu
1,
Yanguang Liu
2,3,*,
Tingxin Li
2,3,* and
Meihua Wei
4,5,6,*
1
Merchant Marine College, Shanghai Maritime University, Shanghai 201306, China
2
Institute of Hydrogeology and Environmental Geology, Chinese Academy of Geological Sciences, Shijiazhuang 050061, China
3
Technology Innovation Center for Geothermal & Hot Dry Rock Exploration and Development, Ministry of Natural Resources, Shijiazhuang 050061, China
4
Shanxi Key Laboratory for Exploration and Exploitation of Geothermal Resources, Taiyuan 030024, China
5
School of Geophysics and Geomatics, China University of Geosciences, Wuhan 430074, China
6
Shanxi Geological Engineering Exploration Institute, Taiyuan 030024, China
*
Authors to whom correspondence should be addressed.
Water 2023, 15(16), 2953; https://doi.org/10.3390/w15162953
Submission received: 1 June 2023 / Revised: 12 August 2023 / Accepted: 15 August 2023 / Published: 16 August 2023
(This article belongs to the Special Issue Development and Utilization of Regional Geothermal Water Resources under the Carbon Neutral Situation)
Browse Figures
Versions Notes

Abstract

:
Deep geothermal reservoirs have great potential for exploitation and are characterized by high temperatures, high stress, and strong heterogeneity. However, these reservoirs contain widely and continuously distributed dominant flow channels with high permeability, predisposing these reservoirs to the formation of dominant flow, which notably decreases the efficiency of heat extraction. Focusing on the dominant flow in fractures, this study provides a definite concept, systematically reviews current studies, and puts forward suggestions for future research. It is expected that this study will serve as a reference for the sustainable, high-quality development of deep geothermal resources.

1. Introduction

With an increase in the exploitation depth, geothermal reservoirs with high temperatures, high stress, and strong heterogeneity have been found to generally host continuously distributed dominant flow channels with high permeability. Dominant flow channels refer to the channels with high permeability and continuous distribution in the fractures of highly heterogeneous geothermal reservoirs, and they can be as small as 10−3 m on a pore scale and can be up to 106 m on a regional scale [1,2]. During the cyclic production and reinjection of geothermal energy, low-temperature tailwater enters geothermal reservoirs and accumulates toward the dominant flow channels at a high flow velocity, forming dominant flow [3]. Dominant flow influences the distribution of the flow velocity of geothermal water in the heterogeneous geothermal reservoirs, thereby controlling the mass transport and heat transfer in fractures and reducing the temperature difference in geothermal reservoirs (Figure 1). The substantial drop in the temperature of a production well occurring during the geothermal production and reinjection is referred to as a “thermal breakthrough” (also known as “thermal short circuit”). A thermal breakthrough will reduce the heat-extraction efficiency and production lifespan of geothermal reservoirs and even necessitate the shutdown of geothermal wells, resulting in economic losses amounting to tens of millions of Yuan [4,5]. Dominant flow is generally believed to be the dominant factor inducing thermal breakthroughs. It has been observed in many geothermal fields, including Geyser, Miravalles, Prieto, and Xianxian in Hebei, thus having received wide attention [6,7,8,9,10].
This paper presents the definition of dominant flow in fractured geothermal reservoirs. It systematically summarizes and analyzes the research progress in the seepage and heat transfer of the dominant flow and offers suggestions for further research. The aim of this paper is to expedite the sustainable, high-quality exploration of deep geothermal resources and to improve and enrich the research system for the scientific exploration and development of the deep Earth of the country. This paper also serves the purpose of promoting the implementation of the national strategy named Deep Earth Exploration as a preliminary study.

2. Global Research Status at Home and Abroad and Analysis of Developmental Dynamics

2.1. Seepage and Heat-Transfer Mechanisms of Dominant Flow in Fractures of Geothermal Reservoirs

The presence of dominant flow is one of the most important characteristics of heterogeneous porous reservoirs. Accordingly, heterogeneous porous reservoirs yield completely different geothermal responses to the production–reinjection well system from homogeneous geothermal reservoirs even under the same reinjection conditions. Since deep geothermal reservoirs are highly heterogeneous in general, their seepage and heat-transfer processes cannot be characterized using homogeneous models or equivalent layered models [12]. Crooijmans et al. examined the seepage and heat-transfer processes of heterogeneous geothermal reservoirs under different geothermal production–reinjection schemes [13]. They proposed that the lifespan of geothermal well systems can only be accurately predicted using numerical models based on the heterogeneity of specific geothermal reservoirs. Ganguly et al. proposed that the heterogeneous geometry of the geothermal reservoirs significantly controls the anisotropy of the flow velocity and the nonlinear convective heat transfer [14]. Moreover, they developed an analytical model to characterize the transient temperature distribution and cold-front movement in geothermal reservoirs. Guo et al. found that high-permeability channels occur in heterogeneous geothermal reservoirs using a digital modeling method [15]. Furthermore, they pointed out that fluids accumulate and have a high flow velocity due to the heterogeneity of fracture apertures, resulting in a differential temperature drop in the rock matrix. The heterogeneity along the depth of geothermal reservoirs has a significant impact on the heat-extraction efficiency, and dominant flow is the main factor inducing thermal breakthroughs. Luo comparatively analyzed the influence of one and multiple dominant flow channels on the temperature field using an equivalent continuous model of discrete fractures [11]. He proposed that the inversion for dominant flow channels based on the breakthrough curves of conservative tracers is subjected to a multiplicity of solutions. Specifically, the concentration peak of the same tracer can be obtained through the fitting of two or three dominant flow channels (Figure 2). In this case, the effects of the heat transfer of the dominant flow on thermal breakthroughs may potentially be incorrectly evaluated. Many studies on the enhanced geothermal system (EGS) show that three parameters of a discrete fracture network, namely aperture, rock matrix permeability, and wellbore radius, serve as important factors affecting thermal breakthrough [16,17].
As indicated by Pandey et al. (2017), due to the rapid reactions of calcite, carbonate reservoirs are more significantly affected by heterogeneity than silicate reservoirs; accordingly, they show more complex seepage and heat-transfer processes [18]. The carbonate karst reservoirs in China enjoy considerable geothermal resources and are widely distributed in areas such as North China and northern Jiangsu, featuring high water yields and easy reinjection [9,19]. As shown by deep exploration in recent years, the karst geothermal reservoirs in the Jixianian Gaoyuzhuang Formation in North China have water yields of 25–110 m3/h and are characterized by high temperatures, high stress, and strong heterogeneity [8,20]. Under the action of compression and tectonism, deep karst geothermal reservoirs have spaces dominated by pores and fractures and generally have permeabilities of a few to tens of millidarcys, while parallel fractures with an aperture of 1 mm have permeabilities of hundreds of darcys [21,22,23]. Conservative tracer tests were conducted in typical geothermal fields in North China, such as Xiaotangshan in Beijing [24], Xiong’an New Area [25], Xianxian in Hebei [7,26], and Donglihu in Tianjin [27]. The test results showed that karst geothermal reservoirs in North China contain dominant flow, which is liable to decrease the heat-extraction efficiency and even induce thermal breakthroughs. As mentioned earlier, dominant flow channels were identified. However, there is a lack of research on the formation and evolutionary laws of the dominant flow, as well as its heat-transfer process. This makes it difficult to scientifically predict and prevent thermal breakthroughs in deep geothermal exploitation.

2.2. Indoor Experiments and On-Site Tests on Seepage and Heat Transfer in Fractures

A small proportion of geothermal energy is stored in geothermal fluids, while more than 90% of it is stored in the rock matrix. The thermal energy in the rock matrix of deep geothermal reservoirs can be cyclically extracted by reinjecting low-temperature tailwater into reservoirs. Therefore, the heat transfer between geothermal fluids and the rock matrix is a hot research topic in the field of geothermal exploitation [28,29,30]. Presently, indoor experiments, which primarily focus on cores or a single fracture, are designed to investigate the mechanical, hydraulic, or heat-transfer properties of rock fractures. In contrast, field tests primarily include hydraulic tests and tracer tests. For on-site research, tracer tests are cost-effective and can yield site parameters, thus offering certain information for the establishment of analytical or numerical models. The numerical models for seepage and heat transfer in geothermal reservoirs established based on experiments and tests can be used for the effective inversion of dynamic water and heat transport in geothermal reservoirs since they are adapted to various geological structures, nonlinear parameters, and complex boundary conditions.

2.2.1. Laboratory Experiments

In the early days, indoor experiments were mostly carried out based on fractures bounded by smooth, straight, parallel plates with certain apertures, forming Navier–Stokes equations and the famous cubic law. According to the cubic law, the volumetric flux of water through a fracture is proportional to the cube of its aperture. However, the simplification of actual rough fracture surfaces into parallel plates might introduce certain errors [31,32]. To more accurately reflect the practical engineering conditions, researchers carried out tests to simulate natural fractures and made various modifications to the cubic law. They found that the measured roughness provides a more practical approach for characterizing the roughness of fracture networks. Barton proposed the empirical criteria for determining the joint roughness coefficient (JRC) and joint shear strength, while many researchers determined the JRC values based on mechanical experiments of samples [33,34,35]. Sisavath et al. (2001) characterized the roughness of fractures using symmetrical sinusoidal curves, established the relationships between the average aperture, roughness, and hydraulic resistance coefficient of fractures, and verified the relationships by comparison with relevant model experiments [36]. To quantitatively characterize the fracture roughness, various methods for characterizing the roughness have been proposed, such as statistical parameters, the standard deviation of fracture apertures, and fractal dimension [37,38,39,40,41,42,43]. Accordingly, the effects of rough geometry on the flow and heat transfer have been effectively investigated. However, the seepage mechanisms are highly complex under the influence of the fracture geometry. Therefore, it is necessary to conduct in-depth research on the formation and evolutionary laws of dominant flow in the case of complex fracture geometries. Generally, laboratory experiments primarily focus on rock core samples or a single fracture, laying a solid foundation for research on the mechanical, hydraulic, or heat-transfer properties of rock fractures. However, their scales differ greatly from those of practical engineering.

2.2.2. Tracer Tests for Geothermal Production and Reinjection Projects

To reasonably characterize the seepage and heat transfer in geothermal reservoirs, reservoir information is frequently analyzed in combination with field tracer tests [8,44]. Tracers can be divided into two types based on their properties and functions, namely conservative tracers and active tracers (e.g., adsorption tracers and thermosensitive tracers; also known as reactive tracers). Conservative tracers, which are designed to analyze the flow connectivity and water residence time in geothermal reservoirs, have been widely applied [45,46,47,48,49,50,51,52,53,54]. Researchers previously assumed for a long time that the return rate of tracers is directly correlated with thermal breakthroughs. Later, after characterizing the heat transfer of the dominant flow channels using different types of tests (e.g., tracer tests, pressure transient tests, and nonisothermal injection tests), it was concluded that the rapid return of tracers does not necessarily imply a premature thermal breakthrough. Pruess and Bodvarsson (1984) held that the degree and time of the temperature drop in geothermal reservoirs depend not only on the duration of water transport between the reinjection and production wells (more specifically, the distribution of water residence time) but also on the heat transfer between the wells, as well as the average temperature and contact area of the flow channels [55]. However, the latter three characteristics can be scarcely reflected by conservative tracers.
As research deepens, active tracers have been used to obtain information about geothermal reservoirs. On the one hand, adsorption tracers are employed to identify the contact area of the geothermal reservoirs. Thermosensitive tracers, on the other hand, are used to indicate the temperature changes in tailwater’s flow channels since they undergo irreversible hydrolysis reactions with an increase in temperature. However, the indicative function and specific processes of active tracers should be utilized in combination with at least a reference (conservative tracer). In other words, the use of active tracer-based identification and quantification of reaction processes should be conducted based on the water-transport process revealed via using conservative tracers. Owing to the advantages of different tracers, active tracers (e.g., adsorption and thermosensitive tracers) are used in combination with conservative tracers, which are referred to as multitracer tests. By comparing the flux concentration vs. time curves (i.e., breakthrough curves) of active and conservative tracers, the expected information can be obtained from tracer tests. This concept can be illustrated by the schematic breakthrough curves for the simulated tracer tests after a pulse injection, as shown in Figure 3. In these curves, the time shift or the reduction in the peak area (tracer mass) indicates retardation or degradation, respectively. Therefore, the measured breakthrough curves can be inversely interpreted using analytical equations or numerical models to estimate the values of control parameters, such as the distribution coefficient of the sorption process, the decay rate of the sorption process, or the decay rate of the thermal degradation process.
Researchers revealed the contact area of geothermal reservoirs by combining conservative tracers with adsorption tracers. Their findings indicate that, given two different flow channels with the same water residence time, the channel with a higher ratio of contact area to rock matrix volume exhibited an earlier temperature drop in the rock matrix. This phenomenon can be contributed to the more effective heat transfer from hot rocks to cold water when the ratio of the contact area to rock matrix volume is increased. The average temperature of a flow channel does not affect the time at which the geothermal reservoir temperature drops. However, it does affect the decreased amplitude of the geothermal reservoir temperature. The estimated ratio of the contact area to rock matrix volume and the average temperature of a flow channel are complementary and can be jointly used to estimate the timing and magnitude of the temperature drop in geothermal reservoirs. Thermosensitive tracers can indicate changes in the temperature of the tailwater’s flow channel. These tracers, combined with the ratio of the contact area to rock matrix volume revealed by adsorption tracers, allow information such as the apertures of fractured rocks to be inferred. Accordingly, the distribution of seepage channels can be characterized, indicating the spatial distribution of the dominant flow. This can further constrain the numerical models of seepage and heat transfer, thus facilitating the accurate identification of dominant flow channels and enhancing the quantitative research on the controlling effects that the dominant flow has on the seepage and temperature fields [56,57,58,59,60,61,62,63,64]. Since the early 1990s, researchers have conducted a large number of indoor experiments and field tests of active tracers and have developed and tested multiple active tracers. Reimus et al. (2020) successfully estimated the seepage and heat-transfer characteristics of geothermal reservoirs using conservative tracers, thermal degradation tracers, and adsorption tracers [65]. They also discussed the uncertainties associated with combining multiple active tracers and the methods to reduce these uncertainties. Despite their advantages, active tracers are subjected to physical, chemical, and biological processes during transport compared to conservative tracers, which undergo a hydrodynamic transport process. To scientifically interpret the implications of the seepage and heat-transfer processes in the geothermal reservoirs based on tracer breakthrough curves, it is necessary to demonstrate the reaction rate between rocks and tracers through experiments prior to practical applications.
Fractures under experiments differ greatly from underground fractures in the order of magnitude. Therefore, the multiscale applications of microscopic mechanisms under experiments to macroscopic engineering are limited. However, such applications can be effectively achieved by combining indoor experiments and field tests. The areal contact rate-based correction method greatly simplifies the correction of the cubic law. Using this method, it is only necessary to understand the general contact of fractures while avoiding the difficulties of characterizing the distribution of bulges or fracture widths at each point on the fracture surface. In addition, this method also allows for measurements. For example, by applying adsorption tracers, the contact surfaces of fractures can be determined based on the absorption capacity of the tracer. By using the adsorption tracer technology to evaluate the contact area (also known as the effective heat-transfer area, which refers to the interface area between rock fractures and water) through indoor experiments and field tests, the multiscale seepage and heat-transfer mechanisms can be investigated by applying microscopic mechanisms to macroscopic engineering.
Therefore, the permeability coefficient field under the influence of THMC coupling during the reinjection of deep karst geothermal reservoirs is a dynamic evolution process. The effects of the seepage field on the evolution of seepage, heat transfer, and thermal diffusion, which are difficult to investigate, are highlighted in studies on the seepage and heat-transfer mechanisms in geothermal reservoir engineering. However, fractures under experiments differ greatly from underground fractures in the order of magnitude. As a result, it is difficult to achieve the multiscale applications of microscopic mechanisms to macroscopic engineering, posing constraints on the optimal design of the production–reinjection schemes in deep geothermal exploitation.

2.2.3. Numerical Simulations

Deep geothermal reservoirs are located in a high-temperature and high-pressure environment with the mutual coupling of the seepage field, temperature field, stress field, and chemical field. Therefore, this environment differs greatly from that with a normal temperature and pressure. The multifield coupling in geothermal reservoirs is subjected to spatiotemporal dynamic changes during geothermal production and reinjection, making the seepage and heat transfer of the dominant flow even more complex [65,66]. With the rapid advancement in computer science, software such as COMSOL Multiphysics 6.1, FEFLOW 7.2, TOUGHREACT v2.4, and FRACMAN v7.0 has seen significant development [9]. Consequently, numerical simulations have gradually become an indispensable tool in both scientific research and engineering applications [67]. To determine the accurate convective heat transfer in fractures, many researchers have investigated the multifield coupling in the field of geological engineering using methods such as analytical methods and numerical simulations based on experiments [4,68,69,70,71,72,73,74]. Using the 1D model of the convective heat transfer in fractures, Zhao et al. developed a method for calculating the temperature distribution in fractures based on the assumptions of the local thermal equilibrium and local nonthermal equilibrium [67]. As a result, they obtained significantly different coefficients for convective heat transfer under both assumptions. Liu et al. established an anisotropic heat-transfer model for low-temperature fractured rock masses [7]. Liu and Xiang proposed a time-domain semi-analytical method for calculating the seepage and heat transfer in fractured rock masses [75]. He et al. proposed an analytical method to calculate the convective heat transfer between fluids and rock fractures by combining experiments and numerical simulations [76]. Bai et al. calculated the temperature and pressure distribution in rock fractures during the seepage process and proposed a calculation method for characterizing the local heat-transfer coefficients (LHTCs) of fractures [77]. Sun et al. investigated the distribution patterns of the temperature, seepage, and stress fields within geothermal reservoirs [78]. According to their results, for areas with fully developed seepage heat transfer, the efficiency of local heat transfer in rock fractures does not vary significantly with an increase in the flow velocity but is closely related to the distribution of flow rates. Based on the simulation analysis using a discrete fracture network model, Chen et al. suggested that the permeability of the rock matrix has a significant effect on the seepage properties of fractures [79]. Moreover, when the permeability of the rock matrix is six orders of magnitude lower than that of the fractures, seepage will accumulate in the fractures, forming dominant flow. For karst geothermal reservoirs, their fractured rock matrix has high pore permeability, leading to a relatively high permeability caused by pores and fractures. Therefore, it is necessary to determine the boundary conditions for the formation of dominant flow. The permeability coefficient field, as a complex composite of pore and fracture geometries and the porosity of the rock matrix, is a dynamic evolutionary process under the action of coupled multiple fields (e.g., such as temperature, stress, hydraulic gradient, and water–rock reactions) and the disturbance of production and reinjection activities [78,79]. For instance, as indicated by the numerical simulation of the thermo–hydro–mechanical coupling process carried out by the enhanced geothermal system (EGS) project at Soultz-sous-Forets, the changes in the stress field have significant effects on the injection well zones, permeability, and porosity. The numerical and simulation results also indicate the variations in permeability will affect the overall temperature and pressure of a geothermal system. Given that the seepage field in geothermal reservoir engineering is a dynamic evolutionary process, the influencing mechanisms of the dynamic evolution of the heat transfer and thermal diffusion in the seepage field are a key research topic [80,81].
Numerical simulations, which are adapted to changeable geological structures, nonlinear parameters, and complex boundary conditions, have received growing attention and have gradually become the most powerful tool for the analysis of multiple physical field coupling in a geothermal system. There are two types of multifield coupling models for geothermal reservoirs with different geometries, namely continuous medium models for porous media and discrete fracture network models. Among them, discrete fracture network models mainly include the fracture network model and the dual-fracture model, with the latter being widely applied due to its simple conceptual model and a small number of parameters [82]. However, the dual-fracture model oversimplifies the structure of thermal reservoirs and suffers some defects in its hypotheses about representative elementary volume (REV) and water–rock interactions. To gain a better understanding of the seepage, heat-transfer, and deformation mechanisms of rock fractures, a method for simplifying discrete fractures into a stochastic continuous model has been proposed. This method is more suitable for fracture propagation. Moreover, it takes into account the permeability of the rock matrix and is suitable for large-scale modeling. However, since it is difficult for this method to obtain parameters of deep reservoirs, the inversion-derived spatial distribution of hydraulic conductivity coefficients of aquifers features a strong multiplicity of solutions, and constraints from more experiments and experimental parameters are required [16,17,80,81,82,83].

3. Existing Problems and Suggestions for Further Research

3.1. Existing Problems

Numerous researchers have conducted extensive studies on the seepage and heat-transfer processes of geothermal reservoirs, achieving fruitful results [84,85,86,87,88,89,90,91,92,93,94]. With an increase in the geothermal exploitation depth, geothermal reservoirs with high temperatures, high stress, and strong heterogeneity have emerged. In the process of the production and reinjection of deep geothermal reservoirs, dominant flow is likely to pose challenges with the technologies of geothermal reservoir engineering, such as reduced heat-extraction efficiency, shortened production lifespans, and even thermal breakthroughs.
Previous researchers have recognized the impacts of the dominant flow in deep geothermal reservoirs on the heat-extraction efficiency and the lifespan of geothermal production and reinjection systems. However, the challenges of reconstructing the in situ high-temperature, high-pressure environment in deep geothermal reservoirs in experimental settings have resulted in the undefined formation and evolutionary laws and heat-transfer mechanisms of the dominant flow within these reservoirs [95,96]. These complications are particularly evident under the influence of coupled multiple fields, such as high temperature, high stress, complex pore–fracture geometries, and perturbation caused by geothermal production and reinjection. Moreover, the fractures in experimental settings differ greatly from subsurface fractures in the order of magnitude, making it difficult to study the multiscale applications of the microscopic mechanisms to macroscopic engineering. In addition, the effects of the seepage and heat transfer of the dominant flow on the evolution of the temperature field of the fracture network in geothermal reservoirs are yet to be ascertained. All these restrict the efficient and sustainable development of deep geothermal resources.
(1)
The multifield coupling in geothermal reservoirs is a dynamic process in time and space during the operation of the geothermal production–reinjection system. Moreover, reconstructing the deep in situ high-temperature, high-pressure environment in experimental settings is challenging. All these lead to the unidentified formation and evolutionary laws of the dominant flow in deep geothermal reservoirs under coupled THMC fields. These laws include pore–fracture geometries, the spatial distribution of fracture networks, and the perturbation caused by geothermal production and reinjection.
(2)
The fractures in experimental settings differ greatly from subsurface fractures in the order of magnitude, making it difficult to study the multiscale applications of the microscopic mechanisms to macroscopic engineering. In addition, the effects of the seepage and heat transfer of the dominant flow on the evolution of the temperature field of the fracture network in geothermal reservoirs are yet to be ascertained. Accordingly, it is difficult to achieve the scientific design of the production–reinjection schemes for deep geothermal exploitation.

3.2. Suggestions for Further Research

Further research should focus on two critical scientific issues: (1) the first is to determine the formation and evolutionary mechanisms of the dominant flow in the fracture networks during the reinjection of deep karst geothermal reservoirs and to reveal the effects of THMC coupling on the permeability coefficient field of the fracture networks during geothermal reinjection; (2) the second is to achieve an accurate quantitative evaluation of the seepage and heat transfer of the dominant flow in the fracture networks during the reinjection of deep karst geothermal reservoirs and to reveal the evolutionary mechanisms of thermal convection and diffusion of the dominant flow in fractures under the influence of the seepage field.
To address the two critical scientific issues mentioned above, the following research should be conducted in the future:
(1)
The formation mode and heat-transfer process of the dominant flow in a single fracture
The authors of this study recommend extracting and reconstructing the 3D structures of fractures in in situ rocks using representative rock samples from karst geothermal reservoirs; conducting multitracer tests for the seepage and heat transfer in a single fracture under the in situ temperature and confining pressure using an independently developed displacement system for high-temperature and high-pressure flow reactions and heat transfer; investigating the seepage and heat transfer of a single fracture under different pore–fracture geometries, stresses, reinjection temperatures, and flow velocities; ascertaining the controlling factors and critical conditions for the formation of the dominant flow; and proposing criteria for identifying the dominant flow based on the dynamic distribution characteristics of local permeability coefficients of fractures under the influence of multifield coupling. The authors also suggest establishing a simplified continuous THMC coupling model of discrete fractures taking into account factors such as the chemical reactions between rocks and active tracers; proposing the constitutive equation reflecting tracer breakthrough curves and contact area; and further quantitatively evaluating the heat transfer of the dominant flow and its effects on the temperature evolution of geothermal reservoirs.
(2)
Evolutionary laws and accurate identification of the dominant flow in the fracture network of karst geothermal reservoirs
The authors of this study recommend building a numerical THMC coupling model of the fracture networks and conducting multitracer tests for reinjection based on geological information, such as the pore–fracture geometries and the distribution and developmental patterns of fractures in typical karst geothermal reservoirs. Furthermore, the authors suggest quantitatively evaluating parameters such as the geothermal reservoir connectivity and contact area based on the breakthrough curves obtained from multitracer tests; conducting simulative analyses of the effects of the changes in parameters (e.g., connectivity, contact rate, stress, reinjection temperature, and flow velocity) on the permeability coefficient field of fractures, and revealing the evolutionary laws of the seepage field in the fracture network of in situ geothermal reservoirs. They also recommend accurately identifying the distribution of the dominant flow channels in the fracture network of in situ karst geothermal reservoirs and quantitatively evaluating the evolution of the dominant flow in the fracture network by combining criteria for determining the dominant flow in a single fracture.
(3)
Heat transfer of the dominant flow in the fracture network of karst geothermal reservoirs and its quantitative evaluation
The authors of this study present the following recommendations: (i) constraining and correcting the numerical model of the fracture network using parameters obtained from multitracer breakthrough curves (e.g., water residence time, fracture aperture, and contact area); (ii) solving the thermal convection and diffusion equations of the dominant flow in fractures under the influence of the seepage field using the lattice Boltzmann method; (iii) investigating the distribution of the geothermal reservoir temperature field under the temporal and spatial coupling of multiple fields, including complex pore–fracture geometries and different production–reinjection schemes (e.g., well network layout, production and reinjection temperatures, and flow velocity); (iv) comprehensively analyzing the effects of the fracture geometries and hydraulic conditions on the heat transfer of the dominant flow; (v) calculating the parameters used to characterize the seepage and heat-transfer efficiency of the dominant flow in fractures; (vi) determining the critical parameters affecting the heat-transfer efficiency of the dominant flow in the fracture network; (vii) revealing the heat-transfer mechanisms of the dominant flow; and (viii) quantitatively evaluating the heat-transfer process of the dominant flow under multifield coupling conditions.
(4)
Effects of the dominant flow on the evolution of the temperature field in the fracture network of karst geothermal reservoirs and their optimal regulation
The authors of this study recommend analyzing the heat-transfer efficiency of the dominant flow and rock matrix in geothermal reservoirs; analyzing the influencing law of the dynamic heat transfer of the dominant flow on the evolution of the temperature field of geothermal reservoirs under different production–reinjection schemes by combining the ratio of the rock volume to contact area; clarifying the major factors controlling the temperature evolution of the fracture network in geothermal reservoirs; and determining the thresholds for thermal breakthroughs. Furthermore, they suggest establishing an index system for thermal sensitivity analysis based on a self-coded neural network of multilayer neurons; proposing a multiobjective optimization strategy for production–reinjection schemes while considering both the heat-extraction efficiency and production lifespan of geothermal reservoirs; and forming a regulation method for the balance between the heat-extraction efficiency and the production lifespan in deep geothermal exploitation.

4. Summary and Conclusions

This study reviews the research progress of the dominant flow in deep fractured geothermal reservoirs and presents a comparative analysis of the pros and cons of indoor experiments, field tests, and numerical simulations.
Dominant flow is liable to pose technical challenges to geothermal reservoir engineering during the production and reinjection of deep geothermal reservoirs. These challenges include a reduced heat-extraction efficiency, shortened production lifespans, and even thermal breakthroughs. To deal with these challenges, this study proposes conducting research on the seepage laws and heat-transfer mechanisms of the dominant flow in deep fractured geothermal reservoirs using multitracer techniques and a combination of indoor experiments, field tests, and numerical simulations. This study will play an important role in the sustainable and high-quality development of the exploitation of deep geothermal resources.

Author Contributions

Conceptualization, Z.L. and Y.L.; methodology, T.L.; formal analysis, M.W.; writing—original draft preparation, Z.L. and T.L.; writing—review and editing, Y.L. and Z.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Nature Science Foundation of China (Grant Nos. 42272350), the National Key R&D Program of China (Grant Nos. 2021YFB1507402), the Foundation of Shanxi Key Laboratory for Exploration and Exploitation of Geothermal Resources (Grant Nos. SX202202).

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Velez, M.I.; Blessent, D.; Cordoba, S.; Lopez-Sanchez, J.; Raymond, J. Geothermal potential assessment of the Nevado del Ruiz volcano based on rock thermal conductivity measurements and numerical modeling of heat transfer. J. S. Am. Earth Sci. 2018, 81, 153–164. [Google Scholar] [CrossRef]
  2. Liu, Y.G.; Huang, Z.L.; Wang, Y.; Wang, W.L.; Wang, J.G. Thermo-hydro-mechanical Coupling Processes in Carbonate Geothermal Reservoirs and Their Numerical Simulation. Lithosphere 2022, 18, 1–18. [Google Scholar] [CrossRef]
  3. Matsumoto, M. A single-phase reservoir simulation method based on a roughly distributed and highly permeable fracture network model with applications to production and reinjection problems. Geothermics 2020, 84, 15. [Google Scholar] [CrossRef]
  4. Asai, P.; Panja, P.; McLennan, J.; Moore, J. Efficient workflow for simulation of multifractured enhanced geothermal systems (EGS). Renew. Energy 2019, 131, 763–777. [Google Scholar] [CrossRef]
  5. Reimus, P.; Marina, O.; Norskog, K.; Caporuscio, F.; Perkins, G.; Sams, S. Results and interpretation of a 2016 tracer test at the Lightning Dock Geothermal Facility and planning for a reactive tracer test in 2017. In Confidential New Mexico Small Business Assistance Report Provided to Participating Companies; Los Alamos National Laboratory: Los Alamos, NM, USA, 2016. [Google Scholar]
  6. Beall, J.J. R-13 tracing of injection in the Geysers. Geotherm. Resour. Counc. Trans. 1994, 18, 151–159. [Google Scholar]
  7. Liu, Y.G.; Liu, G.H.; Zhao, Z.H.; Zhang, H.L. Theoretical model of geothermal tail water reinjection based on an equivalent flow channel model: A case study in Xianxian, North China Plain. Energy Explor. Exploit. 2019, 37, 849–864. [Google Scholar]
  8. Cao, V.; Schaffer, M.; Taherdangkoo, R.; Licha, T. Solute Reactive Tracers for Hydrogeological Applications: A Short Review and Future Prospects. Water 2020, 12, 653. [Google Scholar] [CrossRef]
  9. Liu, Y.; Long, X.; Liu, F. Tracer test and design optimization of doublet system of carbonate geothermal reservoirs. Geothermics 2022, 105, 102533. [Google Scholar] [CrossRef]
  10. Liu, Y.; Guo, L.; Wang, Y.; Liao, Y.; Zhao, G. Numerical simulation and design optimization of large-scale geothermal production based on a multi-well layout in Xianxian geothermal field. Lithosphere 2022, 20, 2929551. [Google Scholar] [CrossRef]
  11. Luo, S. Numerical Analysis of Coupled Fluid Flow and Heat Transfer at Multiple Scales in Deep Geothermal Systems. Ph.D. Thesis, Tsinghua University, Beijing, China, 2018. [Google Scholar]
  12. Radilla, G.; Sausse, J.; Sanjuan, B.; Fourar, M. Interpreting tracer tests in the enhanced geothermal system (EGS) of Soultz-sous-Forêts using the equivalent stratified medium approach. Geothermics 2012, 44, 43–51. [Google Scholar] [CrossRef]
  13. Crooijmans, R.A.; Willems, C.J.L.; Nick, H.M.; Bruhn, D.F. The influence of facies heterogeneity on the doublet performance in low-enthalpy geothermal sedimentary reservoirs. Geothermics 2016, 64, 209–219. [Google Scholar] [CrossRef]
  14. Ganguly, S.; Kumar, M.S.M.; Date, A.; Akbarzadeh, A. Numerical modeling and analytical validation for transient temperature distribution in a heterogeneous geothermal reservoirs due to cold-water reinjection. Proc. World Geotherm. Congr. 2015, 4, 19–25. [Google Scholar]
  15. Guo, B.; Fu, P.; Hao, Y.; Peters, C.A.; Carrigan, C.R. Thermal drawdown-induced flow channeling in a single fracture in EGS. Geothermics 2016, 61, 46–62. [Google Scholar] [CrossRef]
  16. Mahmoodpour, S.; Singh, M.; Bär, K.; Sass, I. Thermo-hydro-mechanical modeling of a enhanced geothermal system in a fractured reservoir using co2 as heat transmission fluid—A sensitivity investigation. Geophysics 2021, 254, 124266. [Google Scholar]
  17. Mahmoodpour, S.; Singh, M.; Turan, A.; Bär, K.; Sass, I. Simulations and global sensitivity analysis of the thermo-hydraulic-mechanical processes in a fractured geothermal reservoir. Energy 2022, 247, 123511. [Google Scholar] [CrossRef]
  18. Pandey, S.N.; Chaudhuri, A. The effect of heterogeneity on heat extraction and transmissivity evolution in a carbonate reservoir: A thermo-hydro-chemical study. Geothermics 2017, 69, 45–54. [Google Scholar] [CrossRef]
  19. Wang, Y.; Liu, Y.; Bian, K.; Zhang, H.; Wang, X.; Zhang, H.; Wang, W. Influence of low temperature tail water reinjection on seepage and heat transfer of carbonate reservoirs. Energy Explor. Exploit. 2021, 39, 2062–2079. [Google Scholar] [CrossRef]
  20. Wang, G.; Zhang, W.; Lin, W.; Liu, F.; Zhu, X.; Liu, Y.; Li, J. Research on formation mode and development potential of geothermal resources in Beijing-Tianjin-Hebei region. Geol. China 2017, 44, 1074–1085. [Google Scholar]
  21. Ciriaco, A.; Zarrouk, S.J.; Zakeri, G. Geothermal resource and reserve assessment methodology: Overview, analysis and future directions. Renew. Sustain. Energy Rev. 2019, 119, 3. [Google Scholar] [CrossRef]
  22. Liu, Y.; Wang, G.; Guo, X.; Hu, J.; Wang, J.; Wang, X.; Zhao, G. A Joint Method Based on Geochemistry and Magnetotelluric Sounding for Exploring Geothermal Resources in Sedimentary Basins and Its Application. Water 2022, 14, 3299. [Google Scholar] [CrossRef]
  23. Ma, F.; Wang, G.; Zhang, W.; Zhu, X.; Zhang, H.; Yue, G. Structure of geothermal reservoirs and resource potential in the Rongcheng geothermal field in Xiong’an New Area. Acta Geol. Sin. 2020, 94, 1981–1990. [Google Scholar]
  24. Yang, Y.; Ding, G.; Xu, W.; Li, H.; Lu, H.; Wang, Y.; Zhang, J.; Wang, Y. Tracer test and geothermal resource quantity evaluation based on dynamic data in the Xiaotangshan area of Beijing. Hydrogeol. Eng. Geol. 2020, 47, 196–200. [Google Scholar]
  25. Wang, S.; Liu, J.; Lin, P.; Li, H.; Yin, M.; Pang, J.; Sun, C.; Gao, X. A study of reinjection experiment and tracer test in a karst geothermal reservoir. Hydrogeol. Eng. Geol. 2013, 40, 129–133. [Google Scholar]
  26. Wang, Y.; Liu, Y.; Bian, K.; Zhang, H.; Qin, S.; Wang, X. Seepage-heat transfer coupling process of low temperature return water injected into geothermal reservoir in carbonate rocks in Xian County, China. J. Groundw. Sci. Eng. 2020, 8, 305–314. [Google Scholar]
  27. Zeng, M.; Ruan, C.; Tian, G.; Zhao, Y.; Tian, G. Connect test between karst cranny reservoir pumping well and injection well. Geol. Prospect. 2008, 44, 105–109. [Google Scholar]
  28. Zhou, L.; Zhu, Z.; Xie, X.; Hu, Y. Coupled thermal–hydraulic–mechanical model for an enhanced geothermal system and numerical analysis of its heat mining performance. Renew. Energy 2022, 181, 1440–1458. [Google Scholar] [CrossRef]
  29. Kamila, Z.; Kaya, E.; Zarrouk, S.J. Reinjection in geothermal fields: An updated worldwide review 2020. Geothermics 2020, 89, 1–5. [Google Scholar] [CrossRef]
  30. Long, X.; Zhang, K.; Yuan, R.; Zhang, L.; Liu, Z. Hydrogeochemical and Isotopic Constraints on the Pattern of a Deep Circulation Groundwater Flow System. Energies 2019, 12, 404. [Google Scholar] [CrossRef]
  31. Snow, D.T. A Parallel Plate Model of Fractured Permeable Media. Ph.D. Thesis, University of California, Riverside, CA, USA, 1965. [Google Scholar]
  32. Andrade, J.J.S.; Henrique, E.A.A.; Almeida, M.P.; Costa, M.H.A.S. Heat transport through rough channels. Phys. A Stat. Mech. Its Appl. 2004, 339, 296–310. [Google Scholar] [CrossRef]
  33. Sanei, M.; Faramarzi, L.; Fahimifar, A.; Goli, S.; Rahmati, A. Shear strength of discontinuities in sedimentary rock masses based on direct shear tests. Int. J. Rock Mech. Min. Sci. 2015, 75, 119–131. [Google Scholar] [CrossRef]
  34. Xie, H.; Chen, Z. Fractal Geometry and Fracture of Rock. Acta Mech. Sin. 1988, 4, 255–264. [Google Scholar]
  35. Duan, Z.; Li, F.; Gong, L.; Yang, Y.; Li, X. Geo-thermal development well spacing patterns based onhydrothermal coupled modeling in oil-gas bearing areas. Nat. Gas Ind. 2020, 40, 156–162. [Google Scholar]
  36. Sisavath, S.; Jing, X.; Zimmerman, R.W. Creeping flow through a pipe of varying radius. Phys. Fluids 2001, 13, 2762–2772. [Google Scholar] [CrossRef]
  37. Cheng, L.; Luo, Z.; Xie, Y.; Zhao, L.; Wu, L. Numerical simulation and analysis of damage evolution and fracture activation in enhanced tight oil recovery using a THMD coupled model. Comput. Geotech. 2023, 155, 105244. [Google Scholar] [CrossRef]
  38. Ibemesi, P.; Benson, P. Effect of Pressure and Stress Cycles on Fluid Flow in Hydraulically Fractured, Low-Porosity, Anisotropic Sandstone. Rock Mech. Rock Eng. 2022, 56, 19–34. [Google Scholar] [CrossRef]
  39. Li, S.; Zhang, D. Three-Dimensional Thermoporoelastic Modeling of Hydrofracturing and Fluid Circulation in Hot Dry Rock. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025673. [Google Scholar] [CrossRef]
  40. Zheng, C.; Wang, D.; Shen, B.; Wang, Q.; Liu, X.; Sun, D.; Yu, B.; Zhou, F.; Zhang, J. An experimental study of the temporary plugging mechanisms of rough fractures in hot dry rocks under a high temperature. Powder Technol. 2023, 427, 118687. [Google Scholar] [CrossRef]
  41. Richter, S.; Lubashevsky, K.; Randow, J.; Henker, S.; Bucher, A. Global Sensitivity Analysis and Uncertainty Quantification for Design Parameters of Shallow Geothermal Systems. Geotherm. Energy 2023. [Google Scholar] [CrossRef]
  42. Xie, H.; Lu, J.; Li, C.; Li, M.; Gao, M. Experimental study on the mechanical and failure behaviors of deep rock subjected to true triaxial stress: A review. Int. J. Min. Sci. Technol. 2022, 32, 915–950. [Google Scholar] [CrossRef]
  43. Zhou, Z.; Mikada, H.; Takekawa, J.; Xu, S. Numerical Simulation of Hydraulic Fracturing in Enhanced Geothermal Systems Considering Thermal Stress Cracks. Pure Appl. Geophys. 2022, 179, 1775–1804. [Google Scholar] [CrossRef]
  44. Knapp, J.L.A.; González-Pinzón, R.; Drummond, J.D.; Larsen, L.G.; Cirpka, O.A.; Harvey, J.W. Tracer-based characterization of hyporheic exchange and benthic biolayers in streams. Water Resour. Res. 2017, 53, 1575–1594. [Google Scholar] [CrossRef]
  45. Fouillac, C.; Sauty, J.P.; Vuataz, F.D. Use of Tracers in the Geothermal Industry-Tracer Flow Equations in Porous Media. In Geothermal Reservoir Engineering; Springer: Dordrecht, The Netherlands, 1988. [Google Scholar]
  46. Rose, P.E.; Clausen, S. The Use of Amino G as a Thermally Reactive Tracer for Geothermal Applications. In Proceedings of the 39th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 24–26 February 2014; pp. 1–5. [Google Scholar]
  47. Asadollahi, P. Stability Analysis of a Single Three Dimensional Rock Block: Effect of Dilatancy and High-Velocity Water Jet Impact; University of Texas at Austin: Austin, TX, USA, 2009. [Google Scholar]
  48. Heinze, T.; Hamidi, S.; Galvan, B. A dynamic heat transfer coefficient between fractured rock and flowing fluid. Geothermics 2017, 65, 10–16. [Google Scholar] [CrossRef]
  49. Ayling, B.F.; Hogarth, R.A.; Rose, P.E. Tracer testing at the Habanero EGS site, central Australia. Geothermics 2016, 63, 15–26. [Google Scholar] [CrossRef]
  50. Liu, J. The status geothermal reinjection. Hydrogeol. Eng. Geol. 2003, 3, 100–104. [Google Scholar]
  51. Liu, H.; He, H.; Du, L.; Zhao, L.; Qiao, Y.; Nie, F. Study on the influencing factors of the seepage law of reinjection water in carbonate fractured geothermal reservoir. Sci. Technol. Eng. 2020, 20, 14505–14511. [Google Scholar]
  52. Li, T.; Cai, Y.; Liu, Y.; Liu, G.; Zhang, H.; Qin, X. Tracer test and simulation of thermal energy storage in carbonate rocks ofthe Xian County geothermal field. Earth Sci. Front. 2020, 27, 152–158. [Google Scholar]
  53. Ganguly, S.; Kumar, M.S.M. Analytical solutions for movement of cold water thermal front in a heterogeneous geothermal reservoirs. Appl. Math. Model. 2014, 38, 451–463. [Google Scholar] [CrossRef]
  54. Delbar, A.; Chapuis, R.P. Tracer movements in a straight uniform flow: New equations for the advective part considering the distortion of flow lines around the well. J. Contam. Hydrol. 2021, 239, 5. [Google Scholar] [CrossRef]
  55. Pruess, K.; Bodvarsson, G.S. Thermal effects of reinjection in geothermal reservoirs with major vertical fractures. J. Pet. Technol. 1984, 36, 1567–1578. [Google Scholar] [CrossRef]
  56. Nottebohm, M.; Licha, T.; Sauter, M. Tracer design for tracking thermal fronts in geothermal reservoirs. Geothermics 2012, 43, 37–44. [Google Scholar] [CrossRef]
  57. Leecaster, K.; Ayling, B.; Moffitt, G.; Rose, P. Use of safranin T as a reactive tracer for geothermal reservoir characterization. In Proceedings of the 37th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 30 January–1 February 2012. [Google Scholar]
  58. Maier, F.; Schaffer, M.; Licha, T. Determination of temperatures and cooled fractions by means of hydrolyzable thermo-sensitive tracers. Geothermics 2015, 58, 87–93. [Google Scholar] [CrossRef]
  59. Hawkins, A.J.; Fox, D.B.; Becker, M.W.; Tester, J.W. Measurement and simulation of heat exchange in fractured bedrock using inert and thermally degrading tracers. Water Resour. Res. 2017, 53, 1210–1230. [Google Scholar] [CrossRef]
  60. Rose, P.; Clausen, S. The use of amino-substituted naphthalene sulfonates as tracers in geothermal reservoirs. In Proceedings of the 42nd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 13–15 February 2017; Volume 42, pp. 1–7. [Google Scholar]
  61. Schaffer, M.; Idzik, K.R.; Wilke, M.; Licha, T. Amides as thermo-sensitive tracers for investigating the thermal state of geothermal reservoirs. Geothermics 2016, 64, 180–186. [Google Scholar] [CrossRef]
  62. Bottacin-Busolin, A.; Dallan, E.; Marion, A. STIR-RST: A Software Tool for Reactive Smart Tracer Studies. Environ. Model. Softw. 2020, 135, 10. [Google Scholar] [CrossRef]
  63. Samal, S.K.; Moharana, M.K. Numerical Assessment of Nanofluids in Recharging Microchannel: Thermo-Hydrodynamic and Entropy Generation Analysis. J. Therm. Sci. 2021, 13, 1–15. [Google Scholar] [CrossRef]
  64. Wang, G.; Lin, W.; Liu, F.; Gan, H.; Wang, S.; Yue, G.; Long, X.; Liu, Y. Theory and survey practice of deep heat accumulation in geothermal system and exploration practice. Acta Geol. Sin. 2023, 97, 639–660. [Google Scholar]
  65. Reimus, P.; Caporuscio, F.; Marina, O.; Janney, D. Field demonstration of the combined use of thermally-degrading and cation-exchanging tracers to predict thermal drawdown in a geothermal reservoir. Geothermics 2020, 83, 5. [Google Scholar] [CrossRef]
  66. Seyedrahimi-Niaraq, M.; Ardejani, F.D.; Noorollahi, Y.; Porkhial, S.; Itoi, R.; Nasrabadi, S.J. A three-dimensional numerical model to simulate Iranian NW Sabalan geothermal system. Geothermics 2019, 77, 42–61. [Google Scholar] [CrossRef]
  67. Zhao, Z.; Liu, G.; Tan, X.; Zhang, P. Theoretical model of geothermal tail water reinjection based on the equivalent seepage channel model. Hydrogeol. Eng. Geol. 2017, 44, 158–164. [Google Scholar]
  68. Long, J.C.S.; Gilmour, P.; Witherspoon, P.A. A model for steady f1uid in random three-dimensional networks of Disc-shaped fractures. Water Resour. Res. 1985, 21, 1105–1115. [Google Scholar] [CrossRef]
  69. Shao, H.; Wang, W.; Bauer, S. Thermo-Hydro-Mechanical Chemical Processes in Fractured Porous Media: Modelling and Benchmarking; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
  70. Liu, B.; Wang, M.; Zhang, M.; Li, W. Dispersivity Experimental Investigation Based on Fracture Network Pipe Model. J. Jilin Univ. (Earth Sci. Ed.) 2016, 46, 230–239. [Google Scholar]
  71. Ma, Y.; Zhang, Y.; Yu, Z.; Huang, Y.; Chi, Z. Heat transfer by water flowing through rough fractures and distribution of local heat transfer coefficient along the flow direction. 14at transfer coefficient along the flow direction. Int. J. Heat Mass Transf. 2018, 119, 139–147. [Google Scholar] [CrossRef]
  72. Long, X.; Xie, H.; Deng, X.; Wen, X.; Ou, J.; Ou, R.; Wang, J.; Liu, F. Geological and Geochemical Characteristics of the Geothermal Resources in Rucheng. China. Lithosphere 2021, 2021, 1357568. [Google Scholar] [CrossRef]
  73. Jin, P.; Hu, Y.; Shao, J.; Zhao, G.; Zhu, X.; Li, C. Influence of different thermal cycling treatments on the physical, mechanical and transport properties of granite. Geothermics 2019, 78, 118–128. [Google Scholar] [CrossRef]
  74. Chen, Y.; Zhao, Z.; Peng, H. Convective heat transfer of water flow in intersected rock fractures for enhanced geothermal extraction. J. Rock Mech. Geotech. Eng. 2021, 14, 108–122. [Google Scholar] [CrossRef]
  75. Liu, D.; Xiang, Y. Temporal semi-analytical method for water flow and heat transfer in fractured rocks. J. Cent. South Univ. (Sci. Technol.) 2020, 51, 523–531. [Google Scholar]
  76. He, Y.; Bai, B.; Hu, S.; Li, X. Effects of surface roughness on the heat transfer characteristics of water flow through a single granite fracture. Comput. Geotech. 2016, 80, 312–321. [Google Scholar] [CrossRef]
  77. Bai, B.; He, Y.; Li, X.; Huang, X.; Zhu, J. Experimental and analytical study of the overall heat transfer coefficient of water flowing through a single fracture in a granite core. Appl. Therm. Eng. 2017, 116, 79–90. [Google Scholar] [CrossRef]
  78. Sun, Z.; Xu, Y.; Lv, S.; Xu, Y.; Sun, Q.; Cai, M.; Yao, J. A thermo-hydro-mechanical coupling model for numerical simulation of enhanced geothermal systems. J. China Univ. Pet. (Ed. Nat. Sci.) 2016, 40, 109–417. [Google Scholar]
  79. Chen, B.; Song, E.; Cheng, X. A numerical method for discrete fracture network model for flow and heat transfer in tuwo-dimensional fractured rocks. Chin. J. Rock Mech. Eng. 2014, 33, 43–51. [Google Scholar]
  80. Mahmoodpour, S.; Singh, M.; Mahyapour, R.; Tangirala, S.K.; Bär, K.; Sass, I. Numerical Simulation of Thermo-Hydro-Mechanical Processes at Soultz-sous-Forêts. Energies 2022, 15, 9285. [Google Scholar] [CrossRef]
  81. Mahmoodpour, S.; Singh, M.; Turan, A.; Bär, K.; Sass, I. Hydro-thermal modeling for geothermal energy extraction from soultz-sous-Forêts, France. Geosciences 2021, 11, 464. [Google Scholar] [CrossRef]
  82. Xia, Y.; Plummer, M.; Mattson, E.; Podgorney, R.; Ghassemi, A. Design, modeling, and evaluation of a doublet heat extraction model in enhanced geothermal systems. Renew. Energy 2017, 105, 232–247. [Google Scholar] [CrossRef]
  83. Reimus, P.; Dean, C.; Newell, D. Evaluation of a cation-exchanging tracer to interrogate fracture surface area in enhanced geothermal systems. Geothermics 2018, 71, 12–23. [Google Scholar] [CrossRef]
  84. Reimus, P.W.; Pohll, G.; Mihevc, T.; Chapman, J.; Papelis, L.; Lyles, B.; Kosinski, S.; Niswonger, R.; Sanders, P. Testing and parameterizing aconceptual model for radionuclide transport in a fractured granite using multiple tracers in a forced-gradient test. Water Resour. Res. 2003, 39, 1350. [Google Scholar] [CrossRef]
  85. Wang, G.; Lin, W. Main hydro- geothermal systems and their genetic models in China. Acta Geol. Sin. 2020, 94, 1923–1937. [Google Scholar]
  86. Hoteit, H.; He, X.; Yan, B.; Vahrenkam, V. Optimization and uncertainty quantification model for time-continuous geothermal energy extraction undergoing re-injection. Geophysics 2021, 12, 1–44. [Google Scholar]
  87. Parini, M.; Acuna, J.A.; Laudiano, M. Reinjected water return at Miravalles geothermal reservoirs, Costa Rica: Numerical modelling and observations. In Proceedings of the 21st Workshopon Geothermal reservoirs Engineering, Stanford, CA, USA, 17–27 January 1997; Volume 22, pp. 127–134. [Google Scholar]
  88. Robinson, B.A.; Tester, J.W. Kinetics of alkaline hydrolysis of organic esters and amides in neutrally-buffered solution. Int. J. Chem. Kinet. 1990, 22, 431–448. [Google Scholar] [CrossRef]
  89. Yazdi, M.R.; Mohebbi, A. Comparison of dissolution in a calcite fracture by isothermal and non-isothermal models. Comput. Geosci. 2022, 26, 401–421. [Google Scholar] [CrossRef]
  90. Zhao, Z. On the heat transfer coefcient between rock fracture walls and flowing fluid. Comput. Geotech. 2014, 59, 105–111. [Google Scholar] [CrossRef]
  91. Batchelor, A. Reservoir behaviour in a stimulated hot dry rock system. In Proceedings of the Eleventh Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 21–23 January 1986; Volume 21–23, pp. 35–41. [Google Scholar]
  92. Du, Y.; Guan, L. Interwell Tracer Tests: Lessons Learned From Past Field Studies. In Proceedings of the SPE Asia Pacific Oil & Gas Conference and Exhibtion, Jakharta, Indonesia, 5–7 April 2005; Volume 5, pp. 1–9. [Google Scholar]
  93. Liu, Y.; Zhu, X.; Wang, G. A review of fluid flow and heat transfer in the CO2-EGS. J. Groundw. Sci. Eng. 2015, 3, 170–175. [Google Scholar] [CrossRef]
  94. Ke, Z.; Feng, B.; Liu, Y.; Cui, Z.; Liu, X. Dissolution and sedimentation patterns of typical minerals in artificial reservoirs under different environment. Unconv. Resour. 2022, 2, 60–71. [Google Scholar] [CrossRef]
  95. Liu, Y.; Lu, C.; Zhu, X.; Wang, G. Reconstruction of deep fluid chemical constituents for estimation of geothermal reservoir temperature using chemical geothermometers. J. Groundw. Sci. Eng. 2017, 5, 87–95. [Google Scholar] [CrossRef]
  96. Long, X.; Wang, G.; Lin, W.; Wang, J.; He, Z.; Ma, J.; Yin, X. Locating geothermal resources using seismic exploration in Xian county, China. Geothermics 2023, 112, 102747. [Google Scholar] [CrossRef]
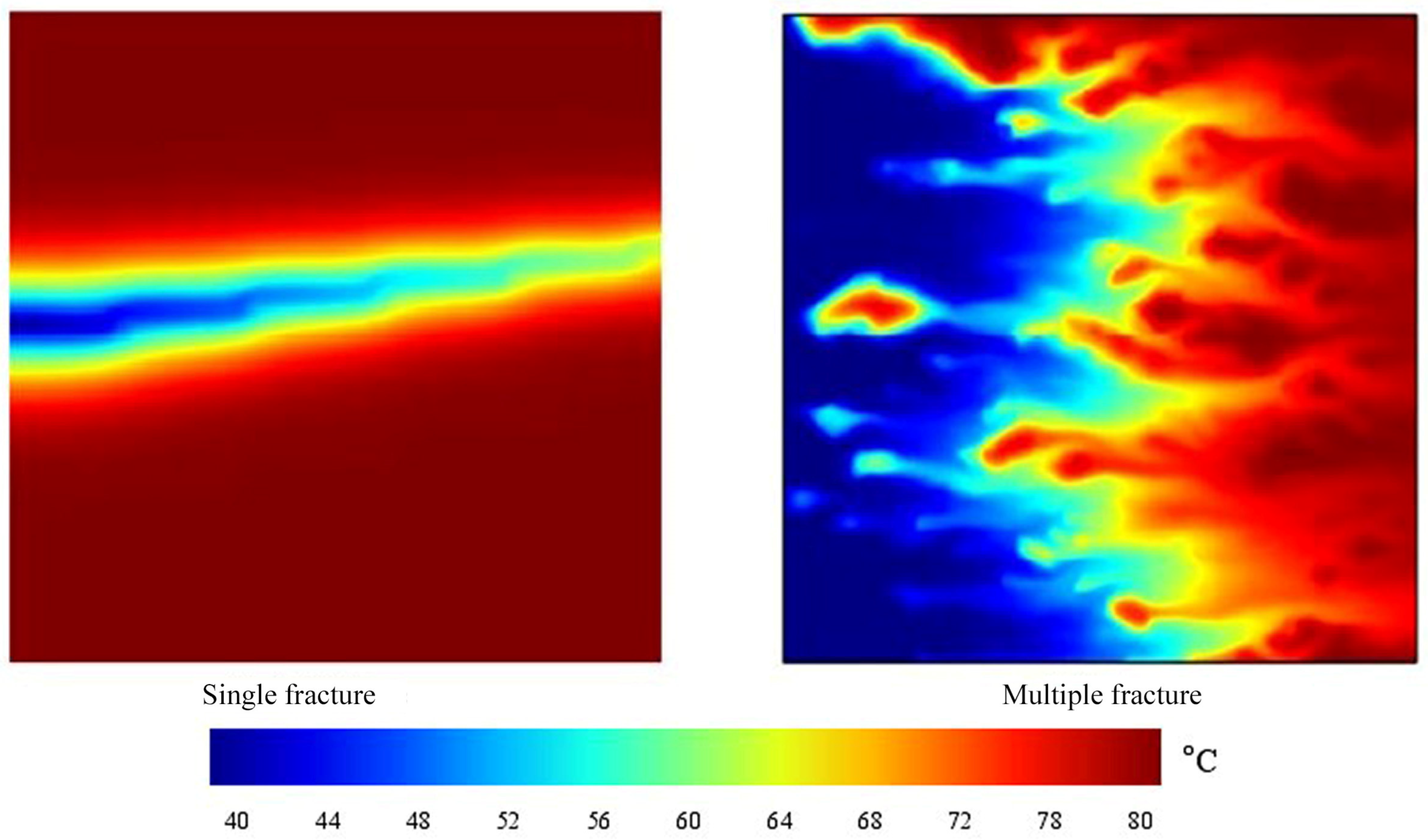
Water 15 02953 g001
Figure 1. Influence of dominant flow channels on the evolution of temperature field [11].
Figure 1. Influence of dominant flow channels on the evolution of temperature field [11].
Water 15 02953 g001
Water 15 02953 g002
Figure 2. Tracer breakthrough curves can be obtained through the fitting of multiple dominant flow channels (left); two and three dominant flow channels can be obtained through the fitting of tracer breakthrough curves (right) [11].
Figure 2. Tracer breakthrough curves can be obtained through the fitting of multiple dominant flow channels (left); two and three dominant flow channels can be obtained through the fitting of tracer breakthrough curves (right) [11].
Water 15 02953 g002
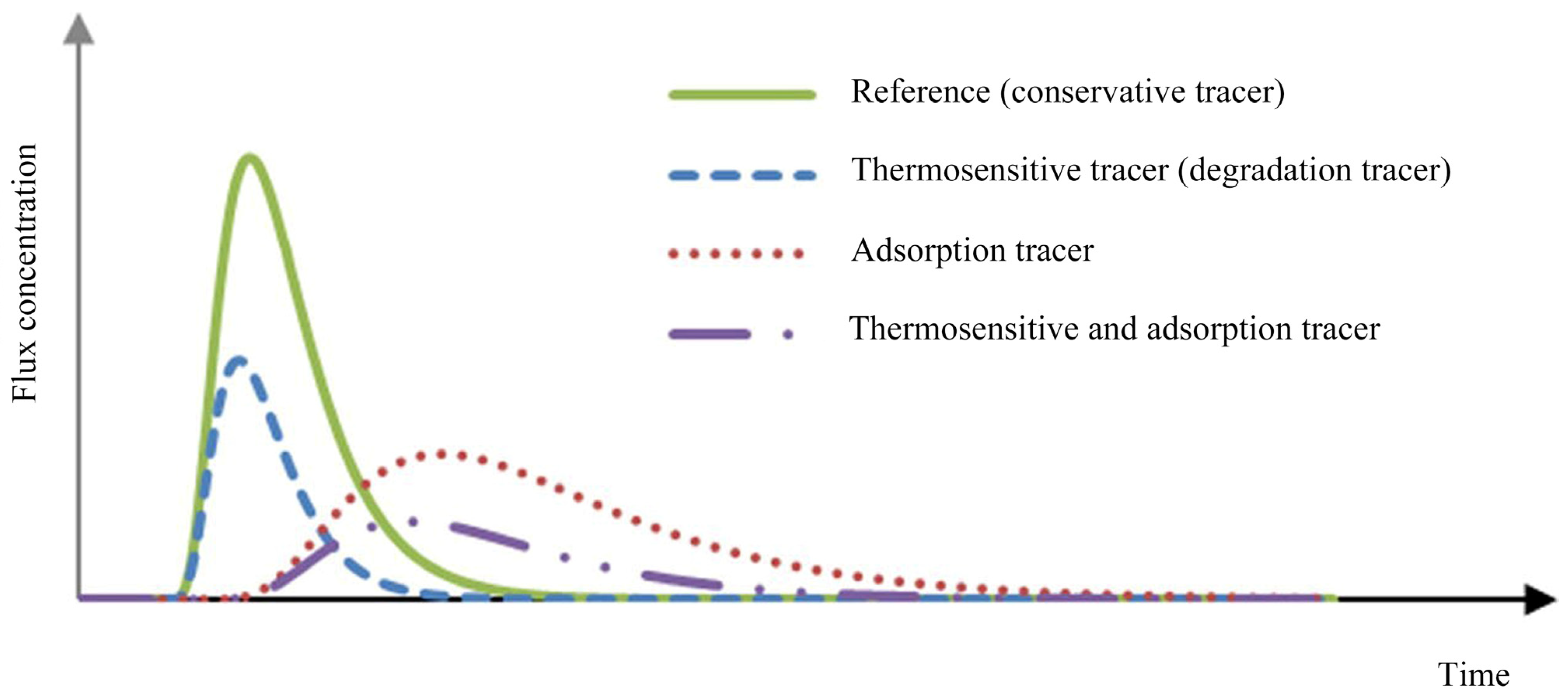
Water 15 02953 g003
Figure 3. Schematic breakthrough curves for conservative and active tracers after a pulse injection [8].
Figure 3. Schematic breakthrough curves for conservative and active tracers after a pulse injection [8].
Water 15 02953 g003
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Liu, Z.; Liu, Y.; Li, T.; Wei, M. Seepage and Heat Transfer of Dominant Flow in Fractured Geothermal Reservoirs: A Review and Outlook. Water 2023, 15, 2953. https://doi.org/10.3390/w15162953

AMA Style

Liu Z, Liu Y, Li T, Wei M. Seepage and Heat Transfer of Dominant Flow in Fractured Geothermal Reservoirs: A Review and Outlook. Water. 2023; 15(16):2953. https://doi.org/10.3390/w15162953

Chicago/Turabian Style

Liu, Zhiyan, Yanguang Liu, Tingxin Li, and Meihua Wei. 2023. "Seepage and Heat Transfer of Dominant Flow in Fractured Geothermal Reservoirs: A Review and Outlook" Water 15, no. 16: 2953. https://doi.org/10.3390/w15162953

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop