Characterization of the Erosion Basin Shaped by the Jet Flow of Sky-Jump Spillways
Abstract
:1. Introduction
2. Materials and Methods
2.1. General Approach
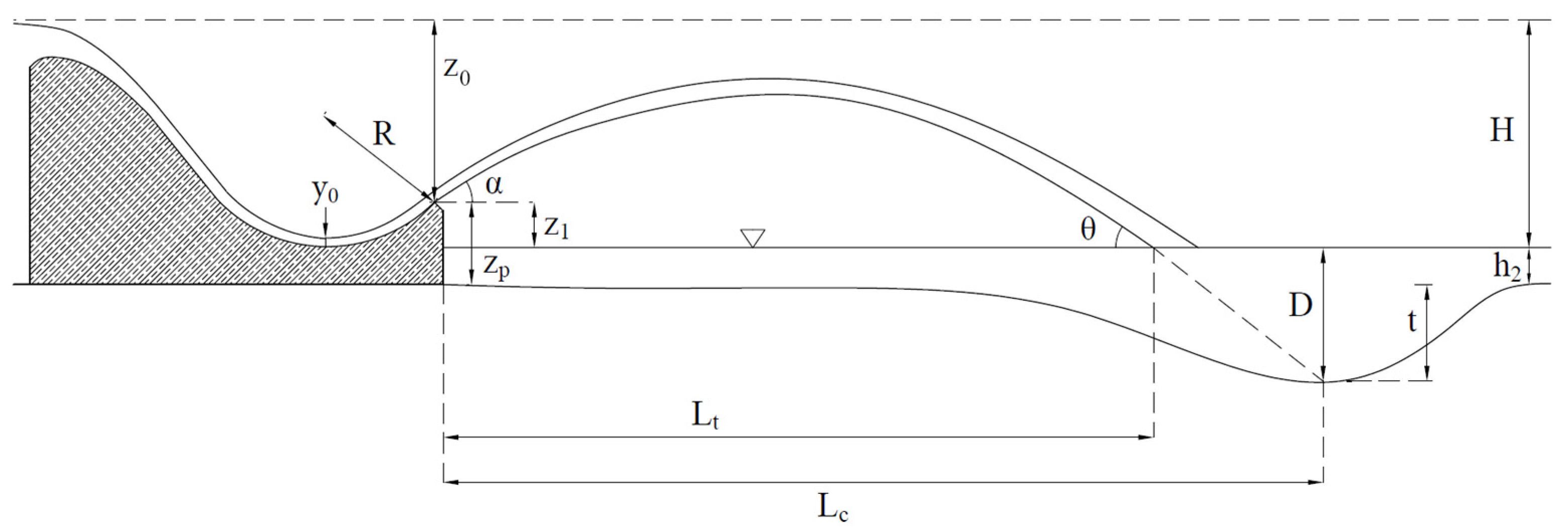
2.2. Relevant Parameters
2.3. Physical Modeling
2.3.1. Experimental Set-Up
2.3.2. Test Procedure
2.3.3. Test Program
3. Results and Discussion
3.1. Erosion Depth
3.1.1. Estimation of Erosion Depth
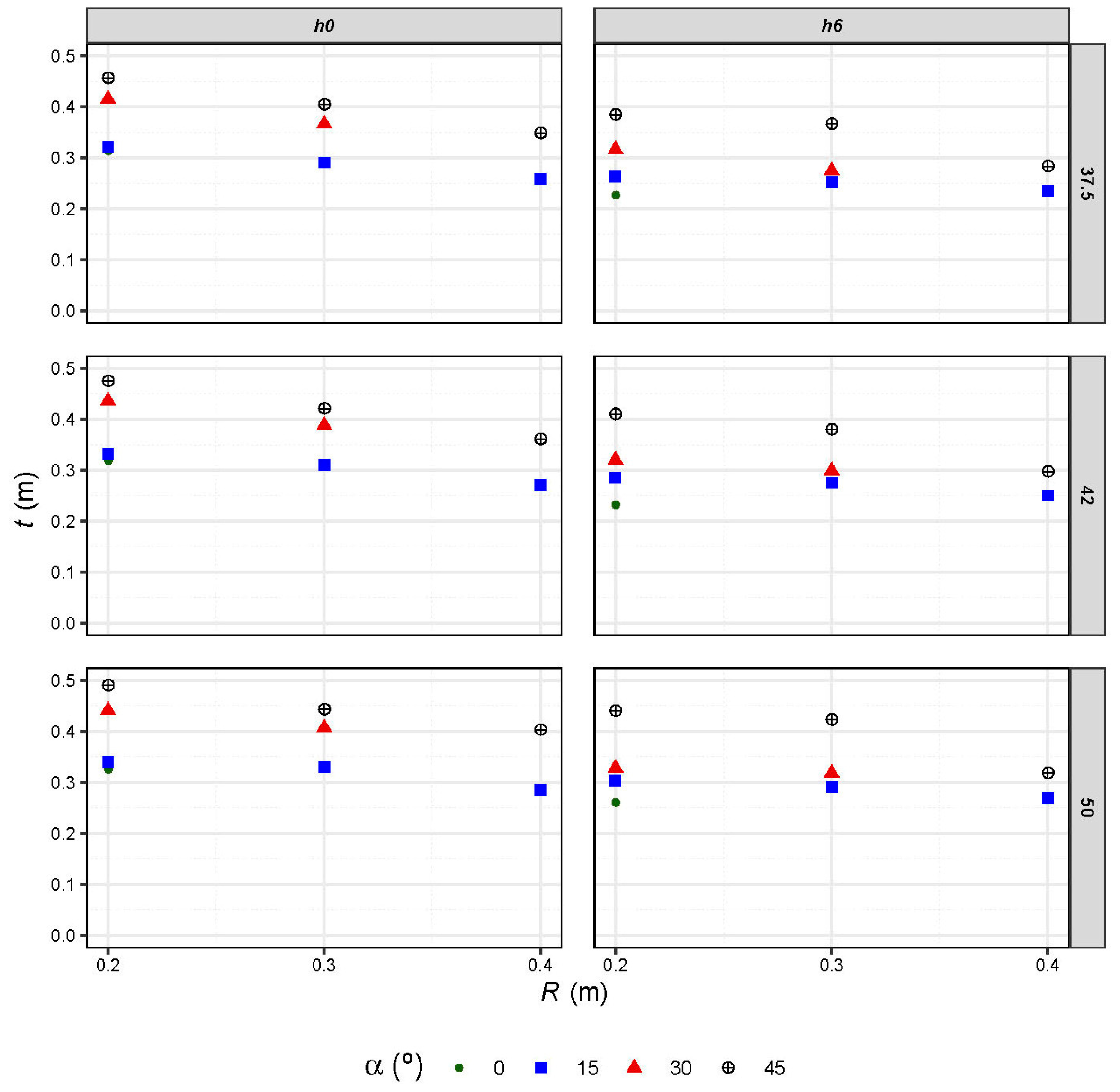
3.1.2. Influence of the Flip Bucket Radius
3.1.3. Influence of the Flip Angle
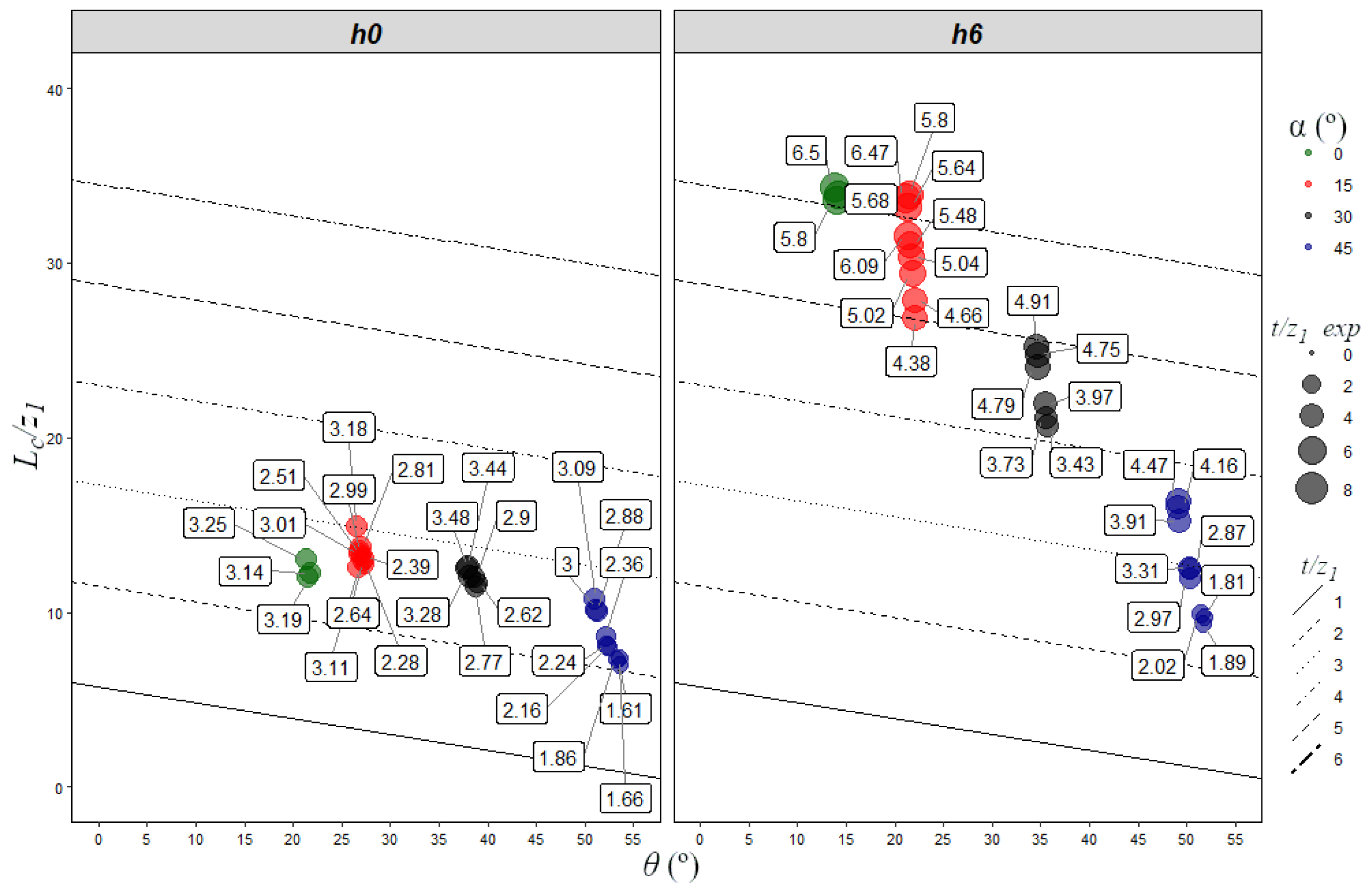
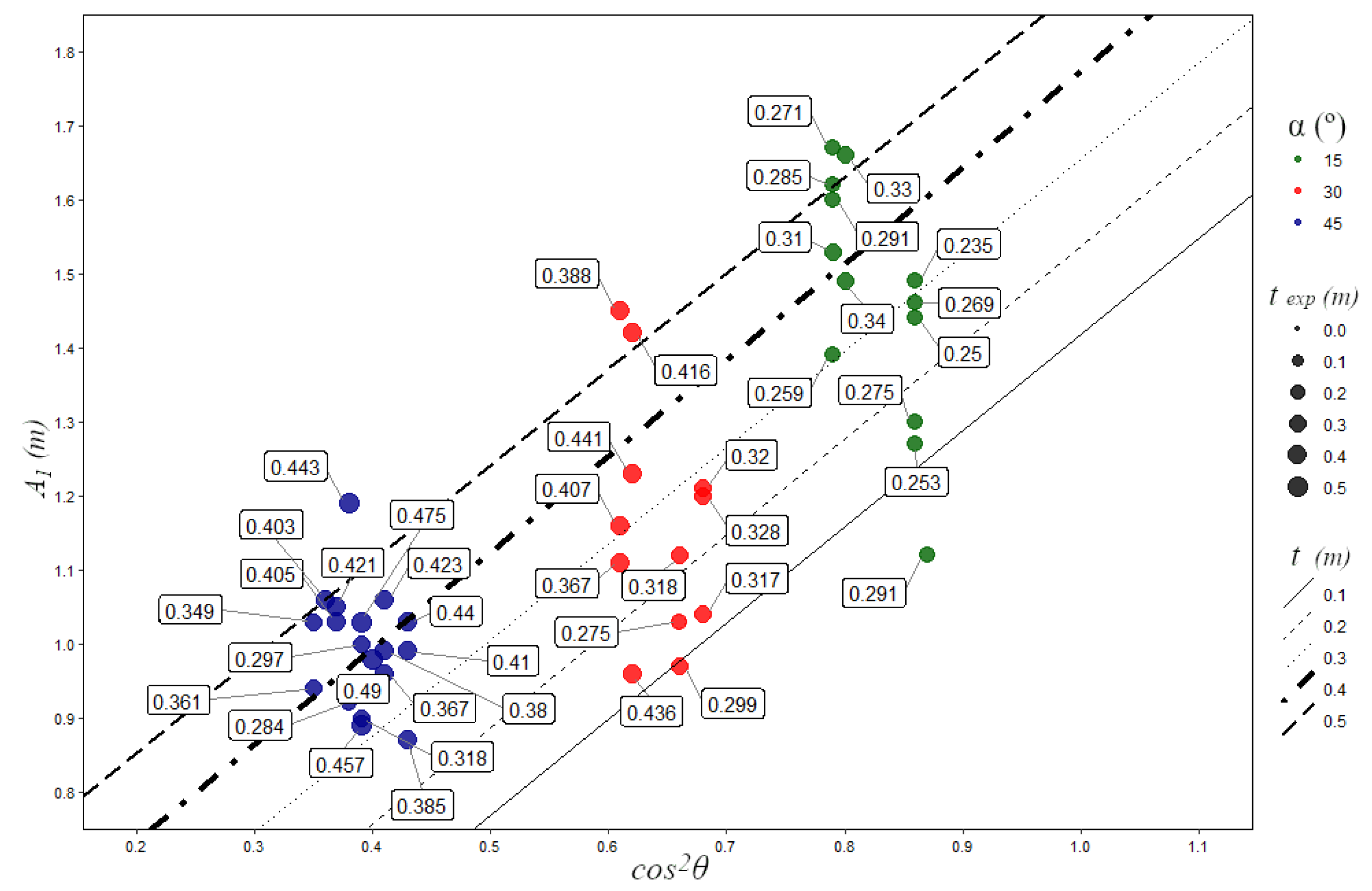
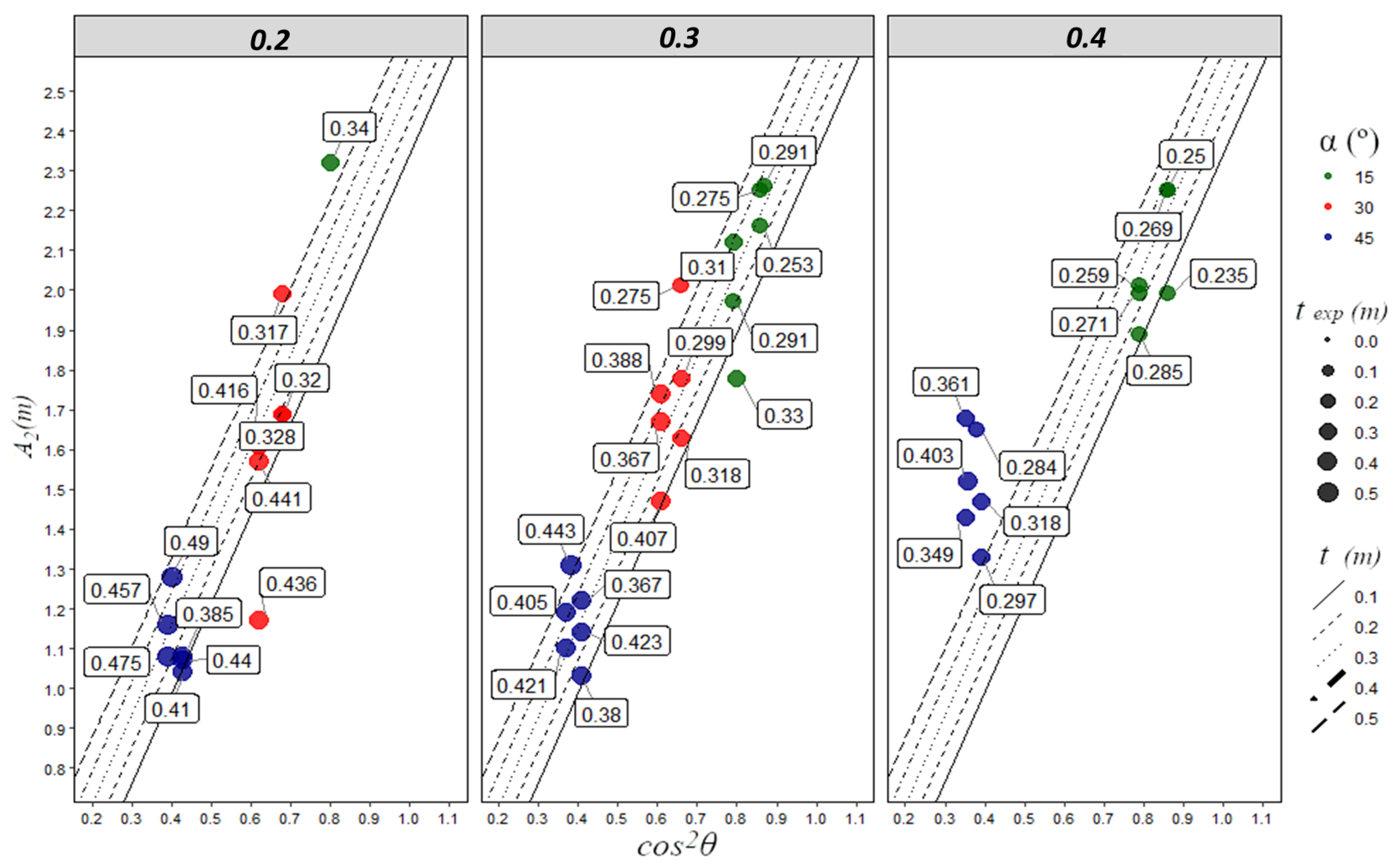
3.2. Position of the Point of Maximum Erosion Depth
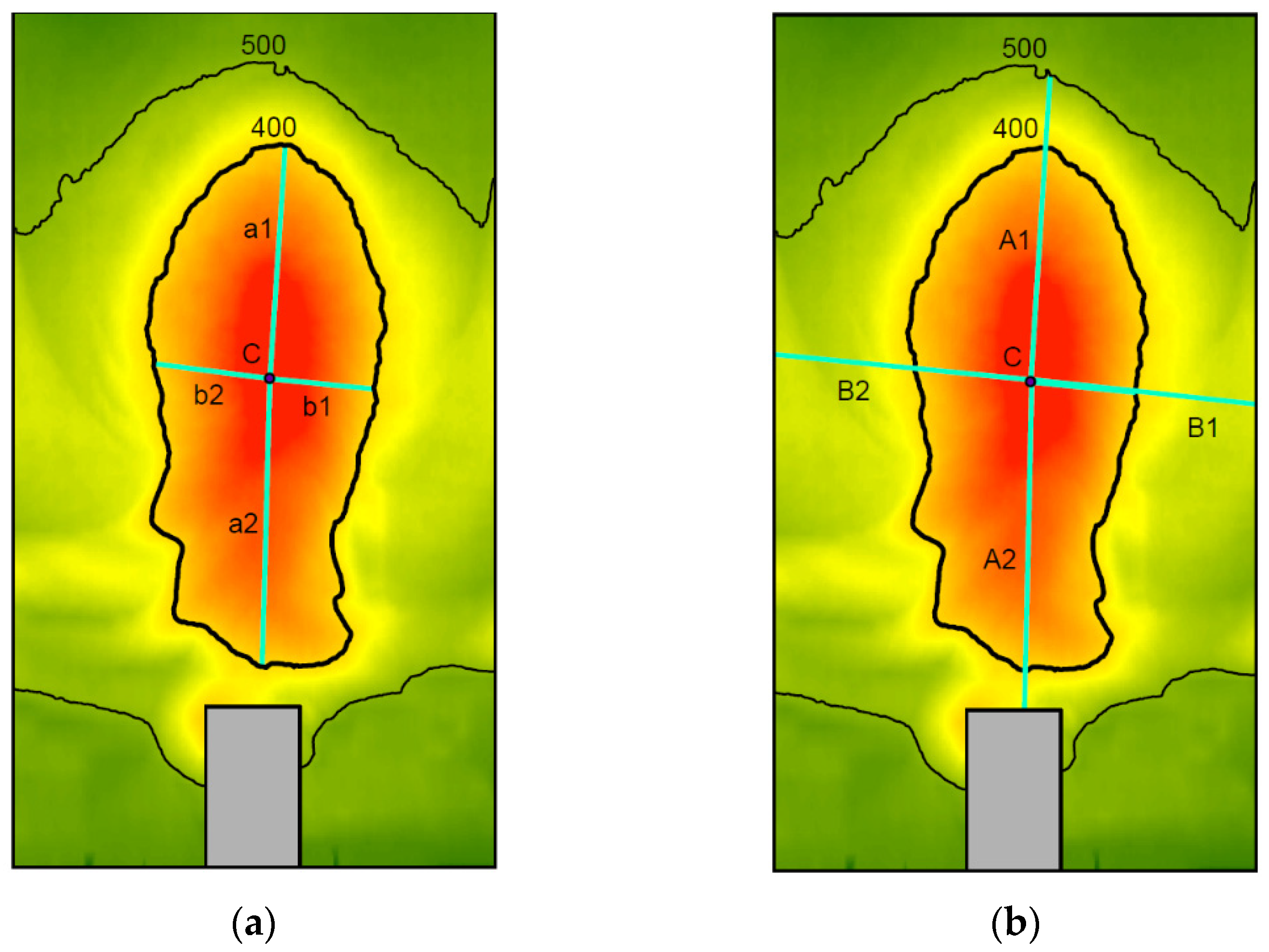
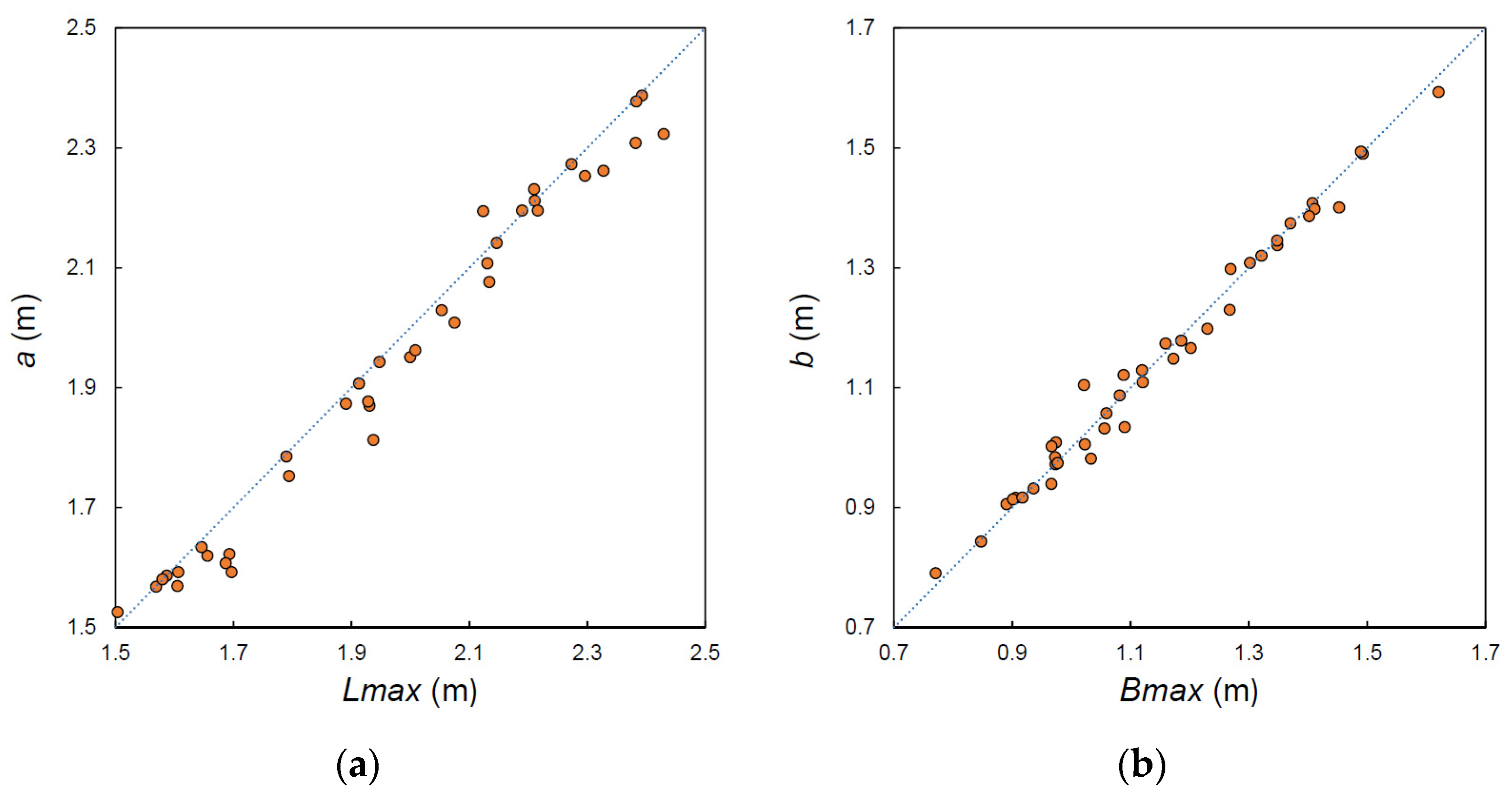
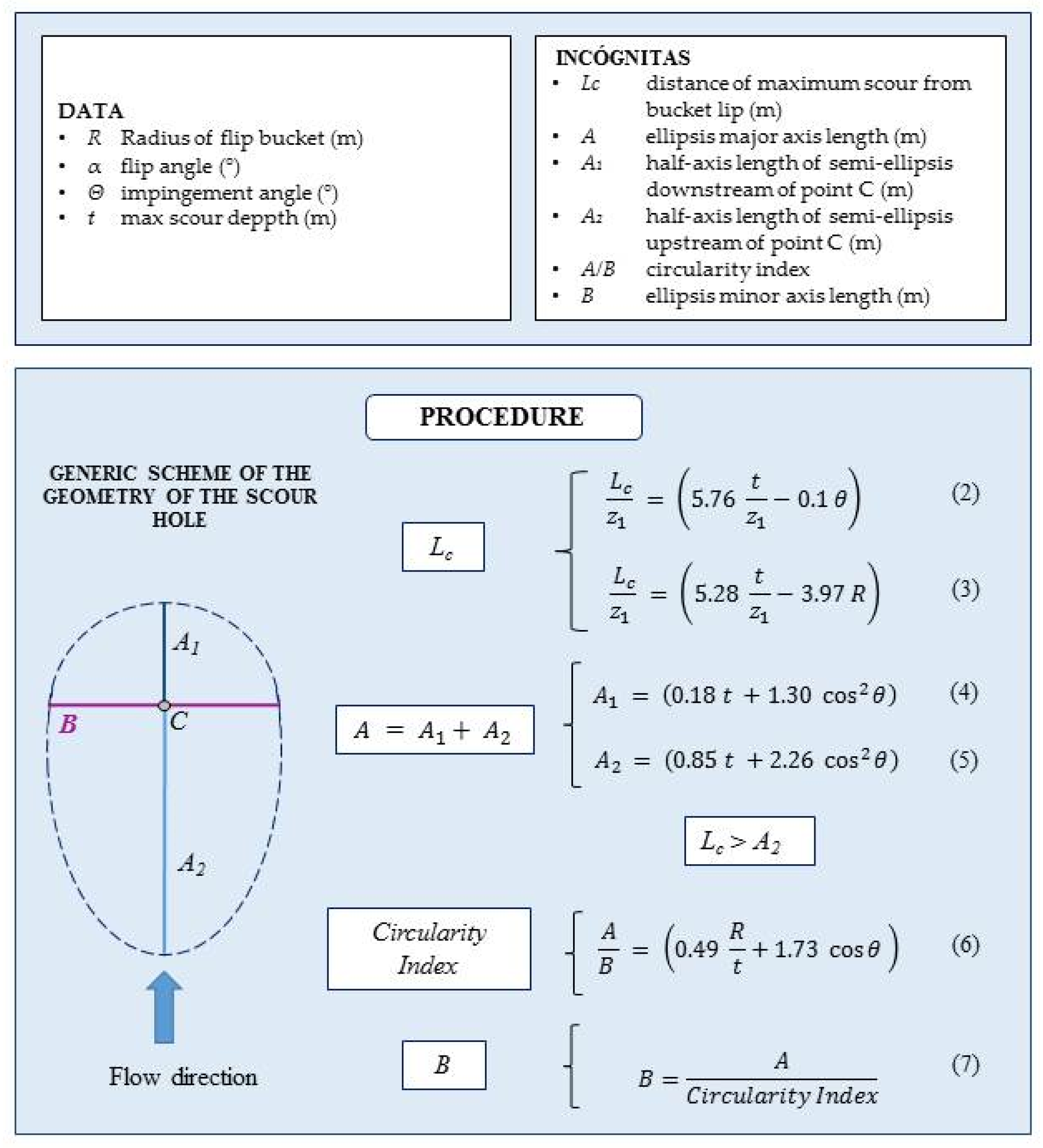
3.3. Length of the Erosion Basin
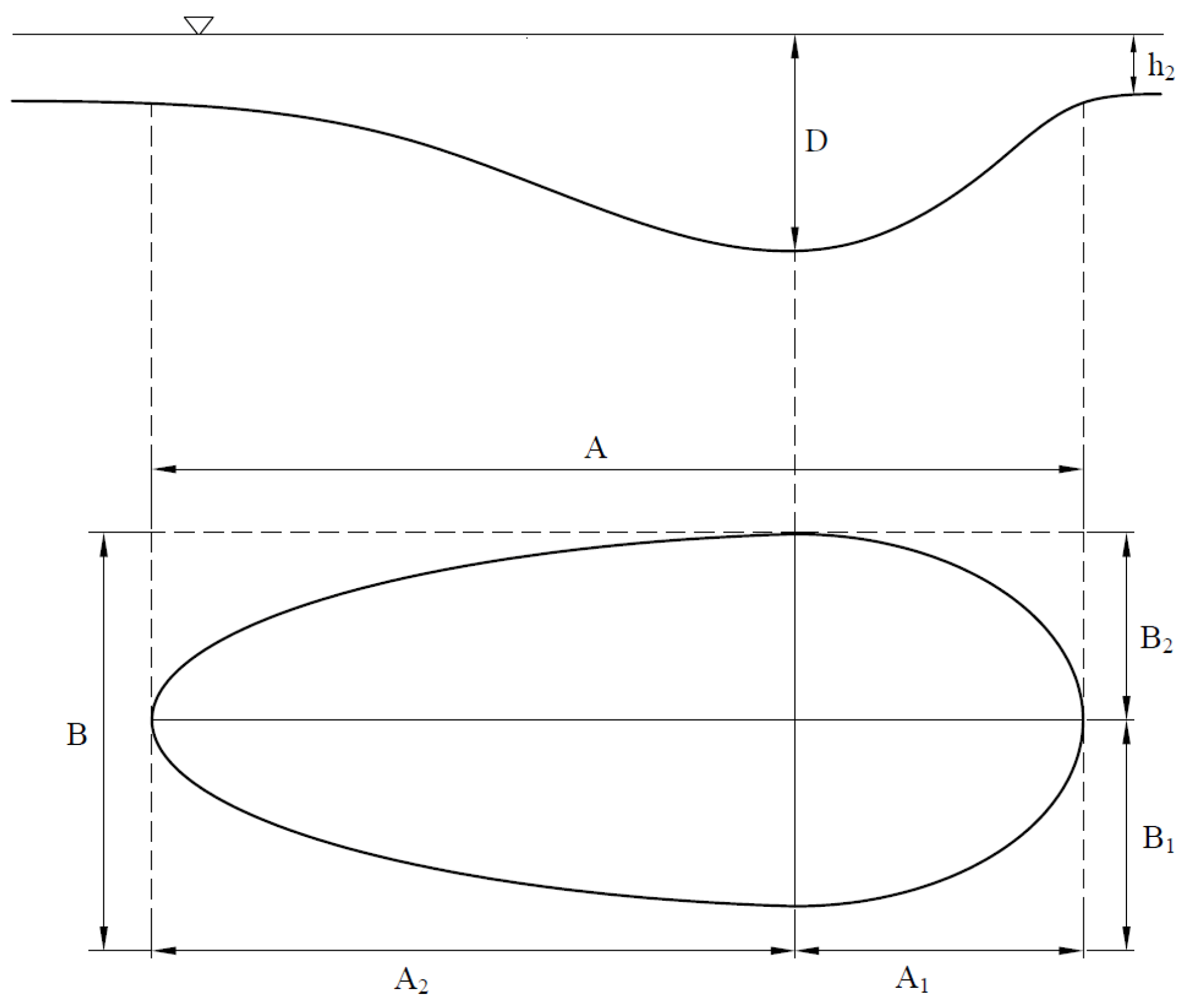
3.4. Erosion Basin Shape
3.5. Procedure for Estimating the Location, the Size, and the Shape of the Erosion Basin
3.6. Limitations of the Present Study
- -
- The height of the spillway is constant, so it has not allowed us to obtain a formula in order to estimate the depth of erosion depending on the flow and the geometric characteristics of the spillway; one of the formulas provided by any other author can be used for this purpose;
- -
- The spillway width is constant, so it has not allowed us to provide a direct formula for the estimation of the total width of the limit scour hole;
- -
- A wider test channel would reduce the effect of the walls, which are most likely the reason for the deviations observed in the limit scour hole.
4. Conclusions
- -
- Increasing the radius of the flip bucket allows a reduction in the depth of the scour hole. Although the cost of the structure is higher for a greater radius, this extra cost might in some cases be justified for the extra safety level achieved.
- -
- The greater the flip angle is, in the range of tested angles, 15° to 45°, the greater the depth of erosion is.
- -
- Scour hole is longer in the riverbed direction and less deep for low flip angles.
- -
- For the length of flip bucket tested, the scour hole is quasi-circular for a flip angle of 45° and more elongated for lower angles. However, the influence of the lip length is evident, so a different shape should be expected for different lip lengths.
- -
- The plan position of the point where the depth erosion is maximum moves away from the flip bucket with increasing flip angles between 0° and 30°. However, it is nearer the structure for a flip angle of 45°. Two opposite effects might explain this fact: increasing the angle increases the launch scope, up to 45°, but a greater angle of incidence makes the erosion more vertical, so the scour hole develops less in the direction of the riverbed and more in depth.
- -
- Empirical formulas were derived from the experimental data to estimate the position, size and shape of the scour hole. However, it should be noted that a different width, and so shape, should be expected for different lengths of the flip bucket lip, which is a parameter not considered in this experimental research. More tests are needed with different lip lengths.
- -
- A methodology is proposed, using the above mentioned formulas, to estimate position, size, and shape of the scour hole, which was fitted to a combination of two semi-ellipses.
- -
- The proposed methodology was used with success to determine whether the scour hole is likely to affect the flip bucket structure, comparing the length of the scour hole upstream of the point where the depth is maximum with the distance from that point to the flip bucket. If the scour hole overlaps with the structure, affection is likely to occur.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A | total length of the limit scour hole in the river longitudinal direction |
| A/B | circularity index |
| A1 | semi-axis length in the direction of flow from the maximum scour point to the furthest downstream point |
| A2 | semi-axis length in the direction of flow from the maximum scour point to the furthest upstream point |
| AR | absolute error |
| B | total width of the limit scour hole |
| B1 | semi-axis length in the transverse direction to the flow from the maximum scour point towards the furthest point towards the hydraulic right |
| B2 | semi-axis length in the transverse direction to the flow from the maximum scour point towards the furthest point towards the hydraulic left |
| D | total scour depth |
| Dexp | experimental total scour depth |
| Dcal | calculated total scour depth |
| d50 | grain diameter at 50% of weight |
| d90 | grain diameter at 90% of weight |
| H | total head (distance between upstream and downstream water level) |
| h2 | tailwater depth (downstream water level) |
| Lc | distance of maximum scour from bucket lip |
| MAE | mean absolute error |
| MRE | mean relative error |
| Q | flow rate |
| q | unit flow rate |
| R | radius of flip bucket |
| RE | relative error |
| T | scour depth |
| z1 | distance from the flip bucket’s lip to the downstream water level |
| zo | distance between flip bucket’s lip and upstream water level |
| zp | distance from the flip bucket’s lip to the ground |
| α | flip angle |
| θ | impingement jet angle |
References
- Pfister, M.; Schleiss, A.J. Ski Jumps, Jets and Plunge Pools. In Energy Dissipation in Hydraulic Structures; Chanson, H., Ed.; IAHR Monograph; CRC Press, Taylor & Francis Group: Leiden, The Netherlands, 2015. [Google Scholar]
- Schoklitsch, A. Kolkbildung Unter Ueberfallstrahlen; Berlin, Germany Verlag Nicht Ermittelbar; 1932. [Google Scholar]
- Veronese, A. Erosioni di Fondo a Valle di Uno Scarico. Annale dei Lavori Publici 1937, 75, 717-176. [Google Scholar]
- United States Bureau of Reclamation. Design of Small Dams; US Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1987.
- Yildiz, D.; Üzücek, E. Prediction of scour depth from free falling flip bucket jets. Int. Water Power Dam Constr. 1994, 46, 50–56. [Google Scholar]
- Chanson, H.; Gonzalez, C.A. Physical modelling and scale effects of air-water flows on stepped spillways. J. Zhejiang Univ.-Sci. 2005, 6, 243–250. [Google Scholar]
- Jian-ming, Y.; Jian-hua, W. Numerical simulation of scouring process under spillway. J. Hydrodyn. 2001, 4, 55–59. [Google Scholar]
- Heller, V.; Hager, W.H.; Minor, H. Ski jump hydraulics. J. Hydraul. Eng. 2005, 131, 347–355. [Google Scholar]
- Schmocker, L.; Pfister, M.; Hager, W.H. Aeration characteristics of ski jump jets. J. Hydraul. Eng. 2008, 134, 90–97. [Google Scholar] [CrossRef]
- Azmathullah, H.M.; Deo, M.C.; Deolalikar, P.B. Neural networks for estimation of scour downstream of a ski-jump bucket. J. Hydraul. Eng. 2005, 131, 898–908. [Google Scholar]
- Lee, T.L. Neural network modeling for estimation of scour depth around bridge piers. J. Hydrodyn. 2007, 19, 378–386. [Google Scholar] [CrossRef]
- Damle, P.M.; Venkatraman, C.P.; Desai, S.C. Evaluation of Scour Below Ski-Jump Buckets of Spillways; CWPRS Golden Jubilee Symposia, 1966; Available online: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=Evaluation+of+Scour+Below+Ski-Jump+Buckets+of+Spillways&btnG= (accessed on 12 June 2023).
- Rubinstein, G.L. Laboratory investigation of local erosion on channel beds below high overflow dams. In Transactions of Coordination Conferences on Hydraulic Engineering. 1ss. VII, Conference on Hydraulics of High Head Water Discharge Structures; Gosenergoizdat: Moscow, Russia, 1963. [Google Scholar]
- Yuditskii, G.A. Experimental Prediction of Rock Bed Scour Below a Ski-Jump Spillway Dam; 81–90. Jerusalem: IPST. Trans. Vedeneev All-Union Scientific Research Institute of Hydraulic Engineering, 1971; Available online: https://scholar.google.com.hk/scholar?hl=zh-CN&as_sdt=0%2C5&q=Experimental+Prediction+of+Rock+Bed+Scour+Below+a+Ski-Jump+Spillway+Dam&btnG= (accessed on 12 June 2023).
- Mirtskhulava, T. Mechanism and computation of local and general scour in non-cohesive, cohesive soils and rock beds. In Proceedings of the 12th Congress of the IAHR, Fort Collins, CO, USA, 11–14 September 1967; Volume 3, pp. 169–176. [Google Scholar]
- Zvorykin, K.A.; Kouznetsov, N.V.; Akhmedov, T.K. Scour of Rock bed by a jet spilling from a deflecting bucket of an overflow dam. In Proceedings of the 16th IAHR Congress, São Paulo, Brazil, 27 July–1 August 1975; Volume 2. [Google Scholar]
- Doddiah, D.; Albertson, M.L.; Thomas, R. Scour from jet. In Proceedings of the 5th IAHR Congress, Minneapolis, MN, USA, 1–4 September 1953. [Google Scholar]
- Ervine, D.A. The entrainment of air in water. Water Power Dam Constr. 1976, 28, 27–30. [Google Scholar]
- Canepa, S.; Hager, W.H. Effect of jet air content on plunge pool scour. J. Hydraul. Eng. 2003, 129, 358–365. [Google Scholar]
- Pagliara, S.; Hager, W.H.; Minor, H. Hydraulics of plane plunge pool scour. J. Hydraul. Eng. 2006, 132, 450–461. [Google Scholar] [CrossRef]
- Castillo, L.G.; Carrillo, J.M.; Blázquez, A. Plunge pool dynamic pressures: A temporal analysis in the nappe flow case. J. Hydraul. Res. 2015, 53, 101–118. [Google Scholar] [CrossRef]
- Castillo, L.G.; Carrillo, J.M. Scour, velocities and pressures evaluations produced by spillway and outlets of dam. Water 2016, 8, 68. [Google Scholar] [CrossRef] [Green Version]
- Mason, P.J. Scour Downstream of Energy Dissipating Spillways. In Thesis Submitted for the Degree of Master of Philosophy; Department of Civil Engineering, City University: London, UK, 1983. [Google Scholar]
- Chee, S.P.; Kung, T. Stable profiles of plunge basins. J. Am. Water Resour. Assoc. 1971, 7, 303–308. [Google Scholar] [CrossRef]
- Pagliara, S.; Dipankar, R.; Palermo, M. 3D plunge pool scour with protection measures. J. Hydro-Environ. Res. 2010, 4, 225–233. [Google Scholar] [CrossRef]
- Pagliara, S.; Dipankar, R.; Palermo, M. Scour due to crossing jets at fixed vertical angle. J. Irrig. Drain. Eng. 2011, 137, 49–55. [Google Scholar] [CrossRef]
- Azmathullah, H.M.; Ghani, A.A.B.; Zakaria, N.A. Prediction of scour below flip bucket using soft computing techniques. In Proceedings of the 12th International Conference on enhancement and promotional methods in engineering and science, Hong Kong, China, 30 November–3 December 2009. [Google Scholar]
- Sammen, S.S.; Ghorbani, M.A.; Malik, A.; Tikhamarine, Y.; Amirrahmani, M.; Al-Ansari, N.; Chau, K.W. Enhanced artificial neural network with Harris hawks optimization for predicting scour depth downstream of ski-jump spillway. Appl. Sci. 2020, 10, 5160. [Google Scholar] [CrossRef]
- Castillo, L.G.; Carrillo, J.M. Comparison of methods to estimate the scour downstream of a ski jump. Int. J. Multiph. Flow 2017, 92, 171–180. [Google Scholar] [CrossRef]
- INCYTH-LHA. Estudio Sobre Modelo de Aliviadero de la Presa Casa de Piedra, Informe Final; Laboratorio de Hidráulica Instituto Nacional del Agua: Ezeiza, Argentina, 1982.
- Eggenberger, W. Die Kolkbildung Bei Einem Uberstromen und Bei Der Kombination Uberstromen-Unterstromen. Ph.D. Thesis, ETH Zürich, Zurich, Switzerland, 1994. [Google Scholar]
- Hartung, W. Die Kolkbildung hinter überstromten wehren im hindblick auf eine beweglich sturzbettgestaltung. Die Wasser Wirtshaft 1959, 49, 309–313. [Google Scholar]
- Franke, P.G. Uber kalkbildung und kolkformen. Oesterreichische Wasserwirschaft 1960, 1, 11–16. [Google Scholar]
- Martins, R. Contribution to the knowledge on the scour action of free jets on rocky river-beds. 11th Inter. Comm. Large Dams Trans. 1973, 44, 799–814. [Google Scholar]
- Martins, R. Scouring of rocky riverbeds by free-jet spillways. Int. Water Power Dam. Constr. 1975, 27, 152–153. [Google Scholar]
- Taraimovich, I.I. Deformations of channels below high-head spillways on rock foundations. Hydrotech. Constr. 1978, 12, 917–923. [Google Scholar] [CrossRef]
- Machado, L.I. O Sistema de Dissipacao de Energia Proposto para a Barragem de Xingo; Transactions of the International Symposium on the Layout of Dams in Narrow Gorges ICOLD: Rio de Janeiro, Brazil, 1982. [Google Scholar]
- SOFRELEC. Kamdadji Dam, Niger, 3rd Phase Design Report; Societé FranGaise d’Etudes et de Realisation d’Equipement Electriques: Paris, France, 1980. [Google Scholar]
- Kotoulas, D. Das Kolkproblem unter Besonderer Berücksichtigung der Faktoren Zeit und Geschiebemischung im Rahmen der Wildbachverbauung. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 1967. [Google Scholar]
- Chee, S.P.; Padiyar, P.V. Erosion at the base of flip buckets. Eng. J. 1969, 52, 22–24. [Google Scholar]
- Bisaz, E.; Tschopp, J. Profundidad de erosión al pie de un vertedero para la aplicación de corrección de arroyos en quebradas empinadas. In Proceedings of the Fifth Congreso Latinoamericano de Hidraulica, Lima (IAHR), Peru, 23–28 October 1972. [Google Scholar]
- Jaeger, C. Engineering Fluid Mechanics; Blackie and Sons Ltd.: London, UK, 1956. [Google Scholar]
- Mason, P.J.; Arumugam, K. Free jet scour below dams and flip buckets. J. Hydraul. Eng. 1985, 111, 220–235. [Google Scholar] [CrossRef]
- Ghodsian, M.; Mehraein, M.; Ranjbar, H.R. Local scour due to free fall jets in non-uniform sediment. Sci. Iran. 2012, 19, 1437–1444. [Google Scholar] [CrossRef] [Green Version]
- Kumar, C.; Sreeja, P. Evaluation of selected equations for predicting scour at downstream of ski-jump spillway using laboratory and field data. Eng. Geol. 2012, 129, 98–103. [Google Scholar] [CrossRef]
- Peterka, A.J. Hydraulic Design of Stilling Basins and Energy Dissipators; No. 25; US Department of the Interior, Bureau of Reclamation: Washington, DC, USA, 1964.
- Gunko, F.G.; Burkov, A.F.; Isachenko, N.B.; Rubinstein, G.L.; Soloviova, G.L.; Yuditsky, G.A. Research on the Hydraulic Regime and Local Scour of River Bed below Spillways of High Head Dams. In Proceedings of the 11th IAHR Conference, Leningrad, Russia, 6–11 September 1965. [Google Scholar]
- Rajan, B.H.; Rao, K.N. Design of trajectory buckets. Water Energy Int. 1980, 37, 63–76. [Google Scholar]
- Pellegrino, R.; Toledo, M.Á.; Aragoncillo, V. Discharge Flow Rate for the Initiation of Jet Flow in Sky-Jump Spillways. Water 2020, 12, 1814. [Google Scholar] [CrossRef]
- Breusers HN, C.; Nicollet, G.; Shen, H.W. Local scour around cylindrical piers. J. Hydraul. Res. 1977, 15, 211–252. [Google Scholar] [CrossRef]
- Whittaker, J. Scour Related to Energy Dissipators for Head Structure; N.73 Mitteilungel der Versuchsanstalt fur Wasserbau, Hydrologie und Glaziologie, Zurich; 1984; Available online: https://ethz.ch/content/dam/ethz/special-interest/baug/vaw/vaw-dam/documents/das-institut/mitteilungen/1980-1989/073.pdf (accessed on 12 June 2023).
- Hakanson, L. A Manual of Lake Morphomrtry; Springer: New York, NY, USA, 1981. [Google Scholar]















| Authors | Erosion Depth (m) | |
|---|---|---|
| Veronese B | [3] | |
| Damle A | [12] | |
| Damle B | [12] | |
| Damle C | [12] | |
| INCYTH | [30] | |
| Schoklitsch | [2] | |
| Veronese A | [3] | |
| Eggenberger | [31] | |
| Hartung | [32] | |
| Franke | [33] | |
| Mikhalev | [23] | |
| Mirtskhulava | [15] | |
| Chee and Kung | [24] | |
| Yildiz and Üzücek | [5] | |
| Martins A | [34] | |
| Chian Min Wu | [23] | |
| Martins B | [35] | |
| Taraimovich | [36] | |
| Machado B | [37] | |
| SOFRELEC | [38] | |
| Kotoulas | [39] | |
| Chee and Padyar | [40] | |
| Bisaz and Tschopp | [41] | |
| Chee and Kung | [24] | |
| Machado A | [37] | |
| Jaeger | [42] | |
| Rubinstein | [13] | |
| Mason and Arumugam | [43] | |
| Ghodsian et al. | [44] | |
| Flip Bucket | A1 | A2 | A3 | A4 | B2 | B3 | B4 | C2 | C4 |
|---|---|---|---|---|---|---|---|---|---|
| R (m) | 0.20 | 0.20 | 0.20 | 0.20 | 0.30 | 0.30 | 0.30 | 0.40 | 0.40 |
| α (°) | 0 | 15 | 30 | 45 | 15 | 30 | 45 | 15 | 45 |
| h2 (m) | 0.00 0.06 | 0.00 0.06 | 0.00 0.06 | 0.00 0.06 | 0.00 0.06 | 0.00 0.06 | 0.00 0.06 | 0.00 0.06 | 0.00 0.06 |
| Q (L/s) | 37.50 42.00 50.00 | 37.50 42.00 50.00 | 37.50 42.00 50.00 | 37.50 42.00 50.00 | 37.50 42.00 50.00 | 37.50 42.00 50.00 | 37.50 42.00 50.00 | 37.50 42.00 50.00 | 37.50 42.00 50.00 |
| Author | MAE (m) | MRE | MAEs (m) | MREs | |
|---|---|---|---|---|---|
| Veronese B | [3] | 0.159 | 0.47 | 0.116 | 0.32 |
| Damle A | [12] | 0.188 | 0.50 | 0.230 | 0.56 |
| Damle B | [12] | 0.218 | 0.58 | 0.259 | 0.63 |
| Damle C | [12] | 0.268 | 0.72 | 0.308 | 0.75 |
| INCYTH | [30] | 0.072 | 0.22 | 0.054 | 0.14 |
| Chian Min Wu | [23] | 0.050 | 0.13 | 0.069 | 0.16 |
| Martins B | [35] | 0.053 | 0.15 | 0.055 | 0.13 |
| Taraimovich | [36] | 0.238 | 0.64 | 0.277 | 0.68 |
| Machado B | [37] | 0.528 | 1.50 | 0.479 | 1.23 |
| SOFRELEC | [38] | 0.214 | 0.62 | 0.174 | 0.46 |
| Schoklitsch | [2] | 0.734 | 2.07 | 0.686 | 1.75 |
| Veronese A | [3] | 0.878 | 2.47 | 0.827 | 2.11 |
| Eggenberger | [31] | 0.090 | 0.23 | 0.132 | 0.31 |
| Hartung | [32] | 0.100 | 0.26 | 0.141 | 0.33 |
| Franke | [33] | 0.184 | 0.49 | 0.225 | 0.55 |
| Kotoulas | [39] | 0.237 | 0.64 | 0.275 | 0.67 |
| Chee-Padiyar | [40] | 0.340 | 0.97 | 0.297 | 0.77 |
| Bisaz-Tschopp | [41] | 0.443 | 1.26 | 0.396 | 1.02 |
| Chee-Kung | [24] | 0.477 | 1.350 | 0.432 | 1.11 |
| Machado A | [37] | 0.234 | 0.68 | 0.188 | 0.50 |
| Jaeger | [42] | 0.461 | 1.299 | 0.430 | 1.099 |
| Rubinstein | [13] | 0.283 | 0.765 | 0.313 | 0.756 |
| Martins A | [34] | 0.293 | 0.791 | 0.282 | 0.680 |
| Mason-Arumugam | [43] | 0.216 | 0.620 | 0.176 | 0.451 |
| Ghodsian | [44] | 0.336 | 0.952 | 0.296 | 0.739 |
| Mikhalev | [23] | 0.087 | 0.253 | 0.185 | 0.464 |
| Mirtskulava | [15] | 1.687 | 4.628 | 1.493 | 3.758 |
| Cheen-Kung | [24] | 0.418 | 1.151 | 0.369 | 0.937 |
| Yildiz and Üzücek | [5] | 0.083 | 0.237 | 0.145 | 0.349 |
| (a) (h2 = 0.0 m) | ||||||
| Practice | Q (l/s) | α (°) | R (m) | t (m) | AR (m) | RE |
| A2_h0_17 | 37.5 | 15 | 0.2 | 0.321 | 0.062 | 0.24 |
| B2_h0_17 | 37.5 | 15 | 0.3 | 0.291 | 0.032 | 0.12 |
| C2_h0_17 | 37.5 | 15 | 0.4 | 0.259 | - | - |
| A2_h0_18 | 42.0 | 15 | 0.2 | 0.332 | 0.061 | 0.23 |
| B2_h0_18 | 42.0 | 15 | 0.3 | 0.310 | 0.039 | 0.14 |
| C2_h0_18 | 42.0 | 15 | 0.4 | 0.271 | - | - |
| A2_h0_20 | 50.0 | 15 | 0.2 | 0.34 | 0.055 | 0.19 |
| B2_h0_20 | 50.0 | 15 | 0.3 | 0.329 | 0.044 | 0.16 |
| C2_h0_20 | 50.0 | 15 | 0.4 | 0.285 | - | - |
| (b) (h2 = 0.0 m) | ||||||
| Practice | Q (l/s) | α (°) | R (m) | t (m) | AR (m) | RE |
| A3_h0_17 | 37.5 | 30 | 0.2 | 0.416 | 0.049 | 0.13 |
| B3_h0_17 | 37.5 | 30 | 0.3 | 0.367 | - | - |
| C3_h0_17 | 37.5 | 30 | 0.4 | - | - | - |
| A3_h0_18 | 42.0 | 30 | 0.2 | 0.436 | 0.048 | 0.12 |
| B3_h0_18 | 42.0 | 30 | 0.3 | 0.388 | - | |
| C3_h0_18 | 42.0 | 30 | 0.4 | - | - | - |
| A3_h0_20 | 50.0 | 30 | 0.2 | 0.441 | 0.034 | 0.08 |
| B3_h0_20 | 50.0 | 30 | 0.3 | 0.407 | - | - |
| C3_h0_20 | 50.0 | 30 | 0.4 | - | - | - |
| (c) (h2 = 0.0 m) | ||||||
| Practice | Q (l/s) | α (°) | R (m) | t (m) | AR (m) | RE |
| A4_h0_17 | 37.5 | 45 | 0.2 | 0.457 | 0.108 | 0.31 |
| B4_h0_17 | 37.5 | 45 | 0.3 | 0.405 | 0.056 | 0.16 |
| C4_h0_17 | 37.5 | 45 | 0.4 | 0.349 | - | - |
| A4_h0_18 | 42.0 | 45 | 0.2 | 0.475 | 0.114 | 0.32 |
| B4_h0_18 | 42.0 | 45 | 0.3 | 0.421 | 0.060 | 0.17 |
| C4_h0_18 | 42.0 | 45 | 0.4 | 0.361 | - | - |
| A4_h0_20 | 50.0 | 45 | 0.2 | 0.490 | 0.087 | 0.22 |
| B4_h0_20 | 50.0 | 45 | 0.3 | 0.443 | 0.040 | 0.10 |
| C4_h0_20 | 50.0 | 45 | 0.4 | 0.403 | - | - |
| (d) (h2 = 0.06 m) | ||||||
| Practice | Q (l/s) | α (°) | R (m) | t (m) | AR (m) | RE |
| A2_h6_17 | 37.5 | 15 | 0.2 | 0.264 | 0.029 | 0.12 |
| B2_h6_17 | 37.5 | 15 | 0.3 | 0.253 | 0.018 | 0.08 |
| C2_h6_17 | 37.5 | 15 | 0.4 | 0.235 | - | - |
| A2_h6_18 | 42.0 | 15 | 0.2 | 0.285 | 0.035 | 0.14 |
| B2_h6_18 | 42.0 | 15 | 0.3 | 0.275 | 0.025 | 0.10 |
| C2_h6_18 | 42.0 | 15 | 0.4 | 0.250 | - | - |
| A2_h6_20 | 50.0 | 15 | 0.2 | 0.303 | 0.034 | 0.13 |
| B2_h6_20 | 50.0 | 15 | 0.3 | 0.291 | 0.022 | 0.08 |
| C2_h6_20 | 50.0 | 15 | 0.4 | 0.269 | - | - |
| (e) (h2 = 0.06 m) | ||||||
| Practice | Q (l/s) | α (°) | R (m) | t (m) | AR (m) | RE |
| A3_h6_17 | 37.5 | 30 | 0.2 | 0.317 | 0.042 | 0.15 |
| B3_h6_17 | 37.5 | 30 | 0.3 | 0.275 | - | - |
| C3_h6_17 | 37.5 | 30 | 0.4 | - | - | - |
| A3_h6_18 | 42.0 | 30 | 0.2 | 0.320 | 0.021 | 0.07 |
| B3_h6_18 | 42.0 | 30 | 0.3 | 0.299 | - | |
| C3_h6_18 | 42.0 | 30 | 0.4 | - | - | - |
| A3_h6_20 | 50.0 | 30 | 0.2 | 0.328 | 0.01 | 0.03 |
| B3_h6_20 | 50.0 | 30 | 0.3 | 0.318 | - | - |
| C3_h6_20 | 50.0 | 30 | 0.4 | - | - | - |
| (f) (h2 = 0.06 m) | ||||||
| Practice | Q (l/s) | α (°) | R (m) | t (m) | AR (m) | RE |
| A4_h6_17 | 37.5 | 45 | 0.2 | 0.385 | 0.101 | 0.36 |
| B4_h6_17 | 37.5 | 45 | 0.3 | 0.367 | 0.083 | 0.29 |
| C4_h6_17 | 37.5 | 45 | 0.4 | 0.284 | - | |
| A4_h6_18 | 42.0 | 45 | 0.2 | 0.410 | 0.113 | 0.38 |
| B4_h6_18 | 42.0 | 45 | 0.3 | 0.380 | 0.083 | 0.28 |
| C4_h6_18 | 42.0 | 45 | 0.4 | 0.297 | - | - |
| A4_h6_20 | 50.0 | 45 | 0.2 | 0.440 | 0.122 | 0.38 |
| B4_h6_20 | 50.0 | 45 | 0.3 | 0.423 | 0.105 | 0.33 |
| C4_h6_20 | 50.0 | 45 | 0.4 | 0.318 | - | - |
| (g) (h2 = 0.00 m) | ||||||
| Practice | Q (l/s) | α (°) | R (m) | t (m) | AR (m) | RE |
| A2_h0_17 | 37.5 | 15 | 0.2 | 0.321 | 0.136 | 0.30 |
| B2_h0_17 | 37.5 | 30 | 0.2 | 0.416 | 0.041 | 0.09 |
| C2_h0_17 | 37.5 | 45 | 0.2 | 0.457 | - | - |
| A2_h0_18 | 42.0 | 15 | 0.2 | 0.332 | 0.143 | 0.30 |
| B2_h0_18 | 42.0 | 30 | 0.2 | 0.436 | 0.039 | 0.08 |
| C2_h0_18 | 42.0 | 45 | 0.2 | 0.475 | - | - |
| A2_h0_20 | 50.0 | 15 | 0.2 | 0.340 | 0.150 | 0.31 |
| B2_h0_20 | 50.0 | 30 | 0.2 | 0.441 | 0.049 | 0.10 |
| C2_h0_20 | 50.0 | 45 | 0.2 | 0.490 | - | - |
| (h) (h2 = 0.0 m) | ||||||
| Practice | Q (l/s) | α (°) | R (m) | t (m) | AR (m) | RE |
| A3_h0_17 | 37.5 | 15 | 0.3 | 0.291 | 0.114 | 0.28 |
| B3_h0_17 | 37.5 | 30 | 0.3 | 0.367 | 0.038 | 0.09 |
| C3_h0_17 | 37.5 | 45 | 0.3 | 0.405 | - | - |
| A3_h0_18 | 42.0 | 15 | 0.3 | 0.310 | 0.111 | 0.26 |
| B3_h0_18 | 42.0 | 30 | 0.3 | 0.388 | 0.033 | 0.08 |
| C3_h0_18 | 42.0 | 45 | 0.3 | 0.421 | - | - |
| A3_h0_20 | 50.0 | 15 | 0.3 | 0.330 | 0.113 | 0.26 |
| B3_h0_20 | 50.0 | 30 | 0.3 | 0.407 | 0.036 | 0.08 |
| C3_h0_20 | 50.0 | 45 | 0.3 | 0.443 | - | - |
| (i) (h2 = 0.0 m) | ||||||
| Practice | Q (l/s) | α (°) | R (m) | t (m) | AR (m) | RE |
| A4_h0_17 | 37.5 | 15 | 0.4 | 0.259 | 0.09 | 0.26 |
| B4_h0_17 | 37.5 | 30 | 0.4 | - | - | - |
| C4_h0_17 | 37.5 | 45 | 0.4 | 0.349 | - | - |
| A4_h0_18 | 42.0 | 15 | 0.4 | 0.271 | 0.09 | 0.25 |
| B4_h0_18 | 42.0 | 30 | 0.4 | - | - | - |
| C4_h0_18 | 42.0 | 45 | 0.4 | 0.361 | - | - |
| A4_h0_20 | 50.0 | 15 | 0.4 | 0.285 | 0.118 | 0.29 |
| B4_h0_20 | 50.0 | 30 | 0.4 | - | - | - |
| C4_h0_20 | 50.0 | 45 | 0.4 | 0.403 | - | - |
| (jl) (h2 = 0.06 m) | ||||||
| Practice | Q (l/s) | α (°) | R (m) | t (m) | AR (m) | RE |
| A2_h6_17 | 37.5 | 15 | 0.2 | 0.264 | 0.121 | 0.31 |
| B2_h6_17 | 37.5 | 30 | 0.2 | 0.317 | 0.068 | 0.18 |
| C2_h6_17 | 37.5 | 45 | 0.2 | 0.385 | - | - |
| A2_h6_18 | 42.0 | 15 | 0.2 | 0.285 | 0.125 | 0.30 |
| B2_h6_18 | 42.0 | 30 | 0.2 | 0.320 | 0.09 | 0.22 |
| C2_h6_18 | 42.0 | 45 | 0.2 | 0.410 | - | - |
| A2_h6_20 | 50.0 | 15 | 0.2 | 0.303 | 0.137 | 0.31 |
| B2_h6_20 | 50.0 | 30 | 0.2 | 0.328 | 0.112 | 0.25 |
| C2_h6_20 | 50.0 | 45 | 0.2 | 0.440 | - | - |
| (k) (h2 = 0.06 m) | ||||||
| Practice | Q (l/s) | α (°) | R (m) | t (m) | AR (m) | RE |
| A3_h6_17 | 37.5 | 15 | 0.3 | 0.253 | 0.114 | 0.31 |
| B3_h6_17 | 37.5 | 30 | 0.3 | 0.275 | 0.092 | 0.25 |
| C3_h6_17 | 37.5 | 45 | 0.3 | 0.367 | - | - |
| A3_h6_18 | 42.0 | 15 | 0.3 | 0.275 | 0.105 | 0.28 |
| B3_h6_18 | 42.0 | 30 | 0.3 | 0.299 | 0.081 | 0.21 |
| C3_h6_18 | 42.0 | 45 | 0.3 | 0.380 | ||
| A3_h6_20 | 50.0 | 15 | 0.3 | 0.291 | 0.132 | 0.31 |
| B3_h6_20 | 50.0 | 30 | 0.3 | 0.318 | 0.105 | 0.25 |
| C3_h6_20 | 50.0 | 45 | 0.3 | 0.423 | - | - |
| (l) (h2 = 0.06 m) | ||||||
| Practice | Q (l/s) | α (°) | R (m) | t (m) | AR (m) | RE |
| A4_h6_17 | 37.5 | 15 | 0.4 | 0.235 | 0.049 | 0.17 |
| B4_h6_17 | 37.5 | 30 | 0.4 | - | - | - |
| C4_h6_17 | 37.5 | 45 | 0.4 | 0.284 | - | - |
| A4_h6_18 | 42.0 | 15 | 0.4 | 0.250 | 0.047 | 0.16 |
| B4_h6_18 | 42.0 | 30 | 0.4 | - | - | - |
| C4_h6_18 | 42.0 | 45 | 0.4 | 0.297 | - | - |
| A4_h6_20 | 50.0 | 15 | 0.4 | 0.269 | 0.049 | 0.15 |
| B4_h6_20 | 50.0 | 30 | 0.4 | - | - | - |
| C4_h6_20 | 50.0 | 45 | 0.4 | 0.318 | - | - |
| (a) | |||||
| Practice | A1 extr | A1 exp | AE (m) | RE | |
| A4_h0_17 | 0.891 | 0.895 | 0.004 | 0.005 | |
| A4_h0_18 | 1.035 | 1.027 | 0.008 | 0.007 | |
| A4_h0_18 | 0.983 | 0.974 | 0.008 | 0.009 | |
| A4_h6_17 | 0.873 | 1.085 | 0.211 | 0.195 | |
| A4_h6_18 | 0.991 | 0.916 | 0.075 | 0.082 | |
| A4_h6_20 | 1.027 | 1.035 | 0.007 | 0.007 | |
| B3_h0_20 | 1.158 | 1.210 | 0.051 | 0.042 | |
| B3_h6_17 | 1.026 | 0.982 | 0.044 | 0.045 | |
| B4_h6_18 | 0.989 | 1.052 | 0.063 | 0.060 | |
| B4_h6_20 | 1.062 | 1.095 | 0.032 | 0.029 | |
| C4_h0_17 | 1.032 | 1.001 | 0.031 | 0.031 | |
| C4_h0_20 | 1.058 | 1.120 | 0.062 | 0.056 | |
| C4_h6_17 | 0.920 | 0.878 | 0.042 | 0.048 | |
| C4_h6_20 | 0.901 | 0.931 | 0.030 | 0.033 | |
| MAEv | 0.048 | ||||
| MREv | 0.046 | ||||
| (b) | |||||
| Practice | A2 extr | A2 exp | AE (m) | RE | |
| A4_h0_17 | 1.163 | 1.244 | 0.081 | 0.065 | |
| A4_h0_18 | 1.075 | 1.114 | 0.038 | 0.034 | |
| A4_h0_18 | 1.285 | 1.516 | 0.231 | 0.152 | |
| A4_h6_17 | 1.082 | 1.137 | 0.056 | 0.049 | |
| A4_h6_18 | 1.042 | 1.280 | 0.238 | 0.186 | |
| A4_h6_20 | 1.067 | 1.189 | 0.122 | 0.102 | |
| B3_h0_20 | 1.468 | 1.519 | 0.051 | 0.034 | |
| B3_h6_17 | 2.008 | 1.525 | 0.483 | 0.316 | |
| B4_h6_18 | 1.027 | 0.997 | 0.030 | 0.030 | |
| B4_h6_20 | 1.137 | 1.764 | 0.627 | 0.356 | |
| C4_h0_17 | 1.426 | 1.245 | 0.181 | 0.145 | |
| C4_h0_20 | 1.518 | 1.559 | 0.042 | 0.027 | |
| C4_h6_17 | 1.650 | 1.517 | 0.133 | 0.088 | |
| C4_h6_20 | 1.468 | 1.200 | 0.269 | 0.224 | |
| MAEv | 0.184 | ||||
| MREv | 0.129 | ||||
| (c) | |||||
| Practice | B1 extr | B1 exp | AE (m) | RE | |
| A4_h0_17 | 0.787 | 0.795 | 0.009 | 0.011 | |
| A4_h0_18 | 0.810 | 0.830 | 0.020 | 0.024 | |
| A4_h0_18 | 0.915 | 0.813 | 0.102 | 0.125 | |
| A4_h6_17 | 0.725 | 0.753 | 0.027 | 0.036 | |
| A4_h6_18 | 0.914 | 0.844 | 0.070 | 0.083 | |
| A4_h6_20 | 0.930 | 0.884 | 0.046 | 0.052 | |
| B3_h0_20 | 0.930 | 1.256 | 0.326 | 0.259 | |
| B3_h6_17 | 0.752 | 0.846 | 0.094 | 0.111 | |
| B4_h6_18 | 0.736 | 0.734 | 0.003 | 0.004 | |
| B4_h6_20 | 0.861 | 0.837 | 0.023 | 0.028 | |
| C4_h0_17 | 1.033 | 1.087 | 0.054 | 0.050 | |
| C4_h0_20 | 0.768 | 0.809 | 0.041 | 0.051 | |
| C4_h6_17 | 0.579 | 0.694 | 0.115 | 0.166 | |
| C4_h6_20 | 0.752 | 1.110 | 0.358 | 0.322 | |
| MAEv | 0.092 | ||||
| MREv | 0.094 | ||||
| (d) | |||||
| Practice | B2 extr | B2 exp | AE (m) | RE | |
| A4_h0_17 | 0.900 | 0.979 | 0.079 | 0.080 | |
| A4_h0_18 | 0.989 | 1.147 | 0.159 | 0.139 | |
| A4_h0_18 | 0.999 | 1.113 | 0.114 | 0.103 | |
| A4_h6_17 | 0.877 | 1.085 | 0.208 | 0.191 | |
| A4_h6_18 | 0.892 | 1.136 | 0.244 | 0.215 | |
| A4_h6_20 | 0.910 | 0.993 | 0.083 | 0.083 | |
| B3_h0_20 | 0.794 | 0.921 | 0.127 | 0.138 | |
| B3_h6_17 | 0.765 | 0.991 | 0.226 | 0.228 | |
| B4_h6_18 | 0.772 | 1.043 | 0.271 | 0.260 | |
| B4_h6_20 | 0.967 | 1.206 | 0.239 | 0.198 | |
| C4_h0_17 | 0.708 | 0.813 | 0.105 | 0.129 | |
| C4_h0_20 | 1.221 | 1.343 | 0.123 | 0.091 | |
| C4_h6_17 | 0.744 | 0.920 | 0.175 | 0.191 | |
| C4_h6_20 | 0.652 | 0.712 | 0.060 | 0.084 | |
| MAEv | 0.158 | ||||
| MREv | 0.152 | ||||
| Parameter | Lc(θ) (m) | Lc(R) (m) | A1 (m) | A2(m) (m) | A(m) (m) | A/B | B(m) (m) |
|---|---|---|---|---|---|---|---|
| MAEv (m) | 0.19 | 0.26 | 0.126 | 0.12 | 0.19 | 0.15 | 0.15 |
| MREv (%) | 12.76 | 17.44 | 10.70 | 8.40 | 7.40 | 8.70 | 9.90 |
| Validation Test | t (m) | cos2θ | A2_exp (m) | A2_cal (m) | Lc exp (m) | Lc (θ) (m) | Lc (R) (m) | Reached Trampoline | A2_cal > |
|---|---|---|---|---|---|---|---|---|---|
| A3_h0_20 | 0.441 | 0.62 | 1.568 | 1.785 | 1.594 | 2.061 | 2.228 | no | no |
| A3_h6_18 | 0.320 | 0.68 | 1.694 | 1.800 | 1.607 | 1.612 | 1.637 | yes | yes |
| A4_h0_17 | 0.457 | 0.39 | 1.163 | 1.271 | 1.596 | 1.819 | 2.287 | yes | no |
| A4_h6_18 | 0.410 | 0.43 | 1.042 | 1.314 | 1.572 | 1.877 | 2.087 | no | no |
| B2_h0_17 | 0.291 | 0.79 | 1.970 | 2.037 | 1.429 | 1.377 | 1.405 | yes | yes |
| B2_h6_20 | 0.291 | 0.87 | 2.262 | 2.202 | 1.704 | 1.568 | 1.477 | yes | yes |
| B3_h0_17 | 0.367 | 0.61 | 1.666 | 1.681 | 1.641 | 1.569 | 1.771 | yes | = |
| B3_h6_20 | 0.318 | 0.66 | 1.627 | 1.769 | 1.756 | 1.548 | 1.584 | yes | yes |
| B4_h0_18 | 0.421 | 0.37 | 1.098 | 1.202 | 1.514 | 1.443 | 1.999 | yes | no |
| B4_h6_17 | 0.367 | 0.41 | 1.216 | 1.228 | 1.594 | 1.469 | 1.786 | no | no |
| C2_h0_20 | 0.285 | 0.79 | 1.885 | 2.033 | 1.507 | 1.334 | 1.324 | yes | yes |
| C2_h6_18 | 0.250 | 0.86 | 2.246 | 2.154 | 1.497 | 1.322 | 1.235 | yes | yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pellegrino, R.; Toledo, M.Á. Characterization of the Erosion Basin Shaped by the Jet Flow of Sky-Jump Spillways. Water 2023, 15, 2930. https://doi.org/10.3390/w15162930
Pellegrino R, Toledo MÁ. Characterization of the Erosion Basin Shaped by the Jet Flow of Sky-Jump Spillways. Water. 2023; 15(16):2930. https://doi.org/10.3390/w15162930
Chicago/Turabian StylePellegrino, Raffaella, and Miguel Á. Toledo. 2023. "Characterization of the Erosion Basin Shaped by the Jet Flow of Sky-Jump Spillways" Water 15, no. 16: 2930. https://doi.org/10.3390/w15162930






