Ascertainment of Hydropower Potential Sites Using Location Search Algorithm in Hunza River Basin, Pakistan
Abstract
1. Introduction
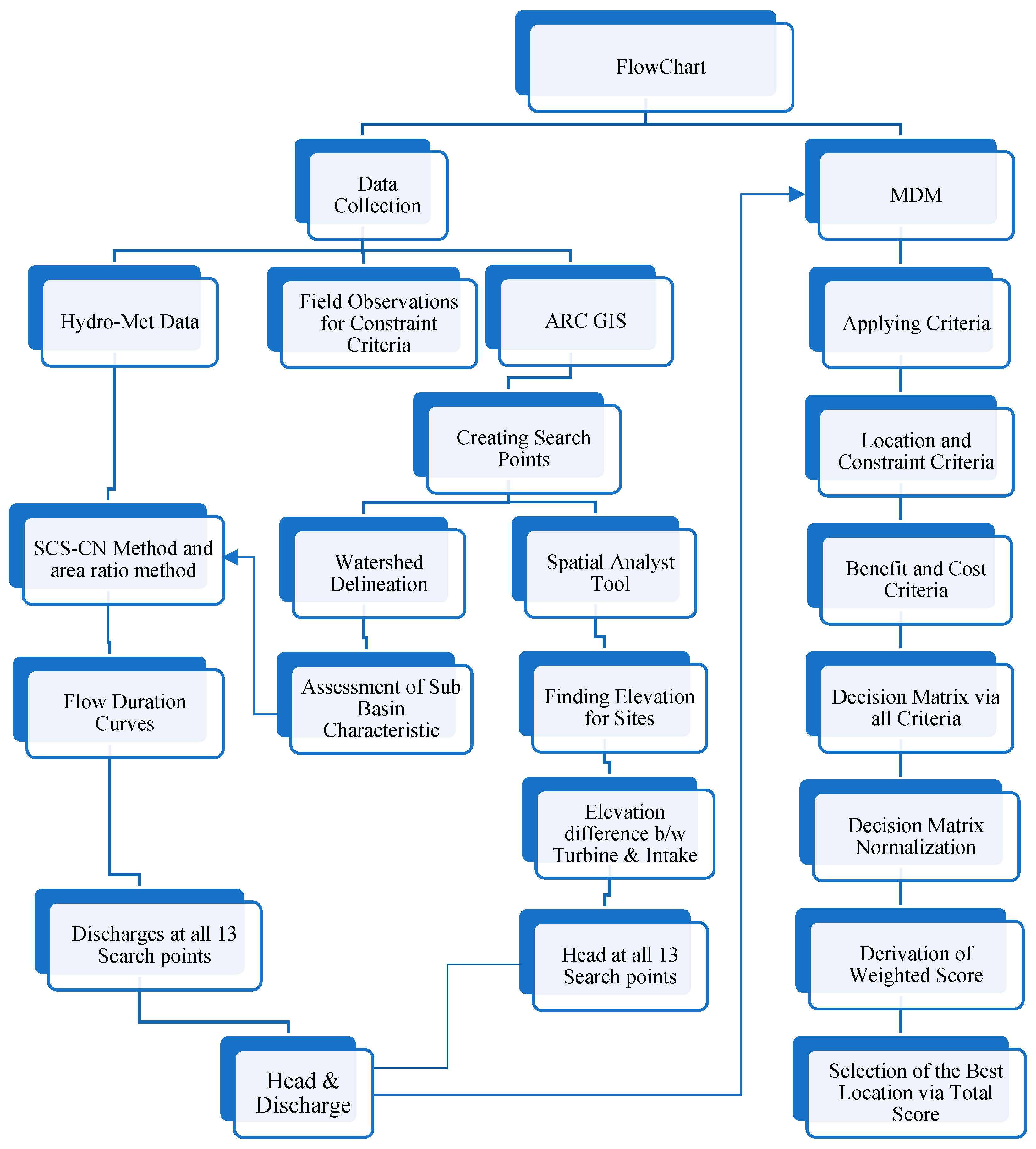
2. Materials and Methods
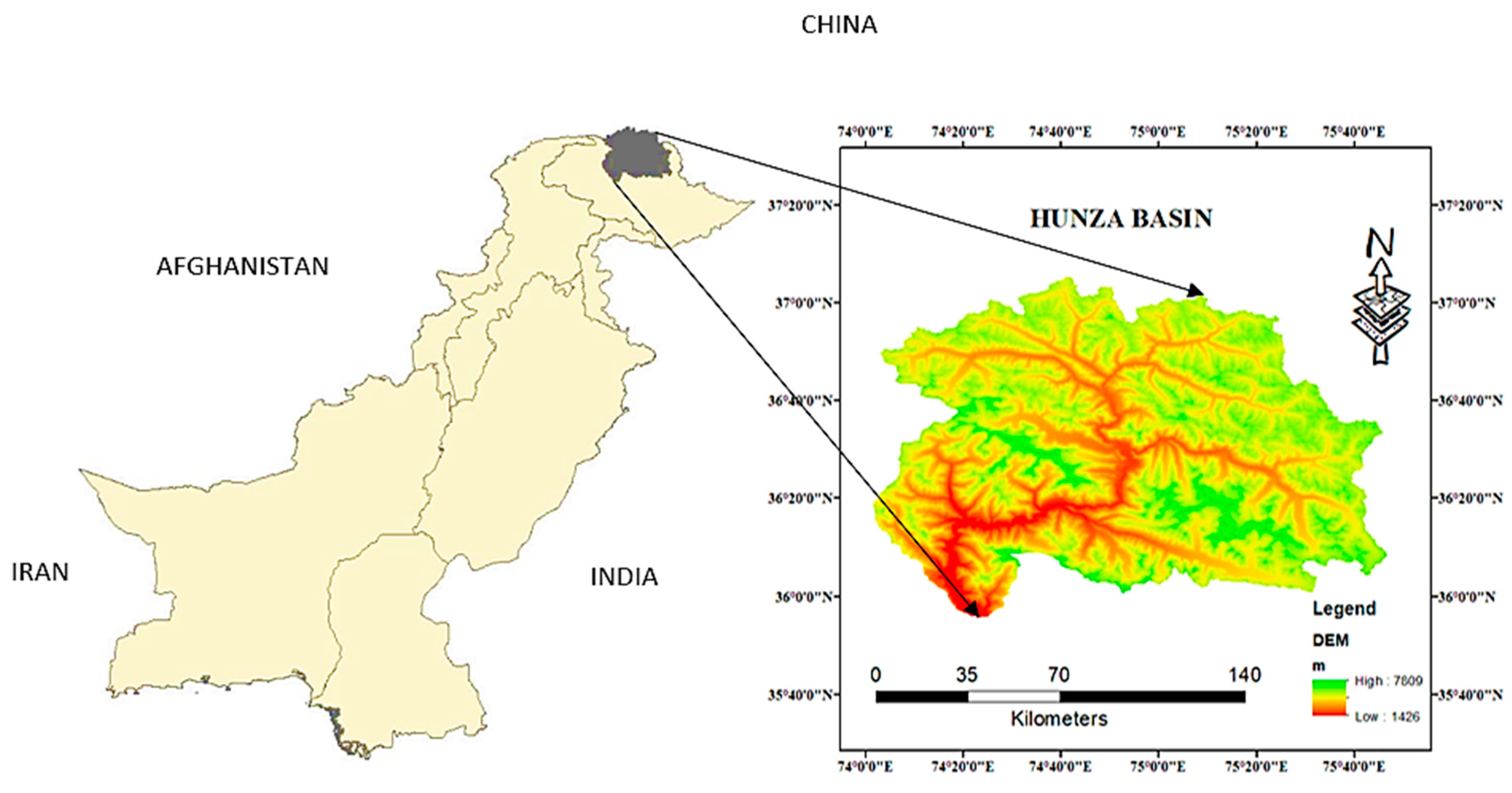
2.1. Study Area
2.2. Multi-Criteria Decision Making (MDM)
- Step 1:
- Selection of Criteria.
- Step 2:
- Estimation of Location Criteria.
- (a)
- Head Determination at Proposed Sites
- (b)
- Estimation of Flow Duration Curve at Ungauged Sites
- Step 3:
- Normalization of location and constraint criteria.
- Step 4:
- Assigning the weights to individual criterion.
- Step 5:
- Final Ranking of suitable sites based on the weighted average score.
- Step 6:
- Estimation of hydropower potential and plant factor.
3. Results
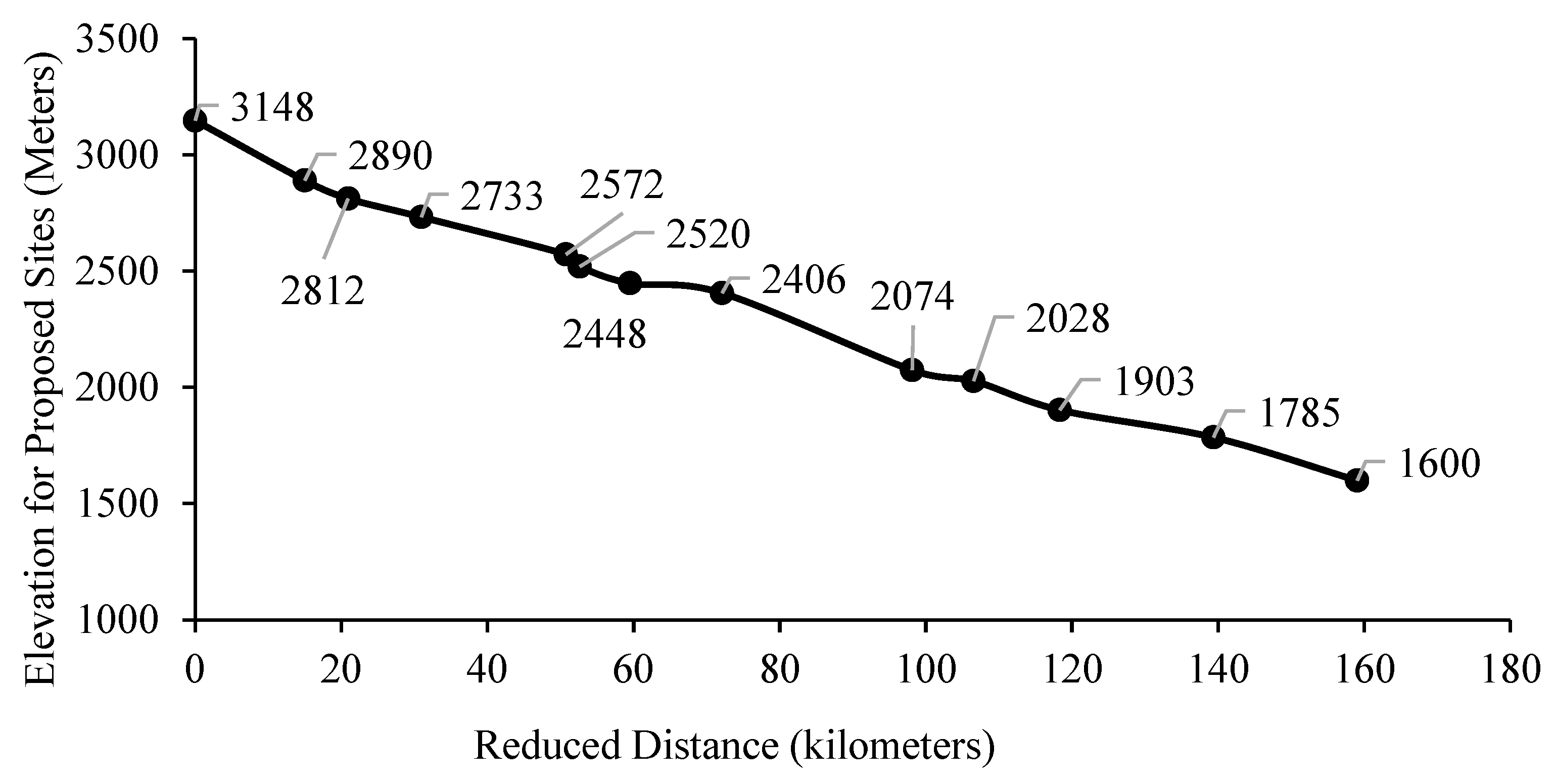
3.1. Head Determination
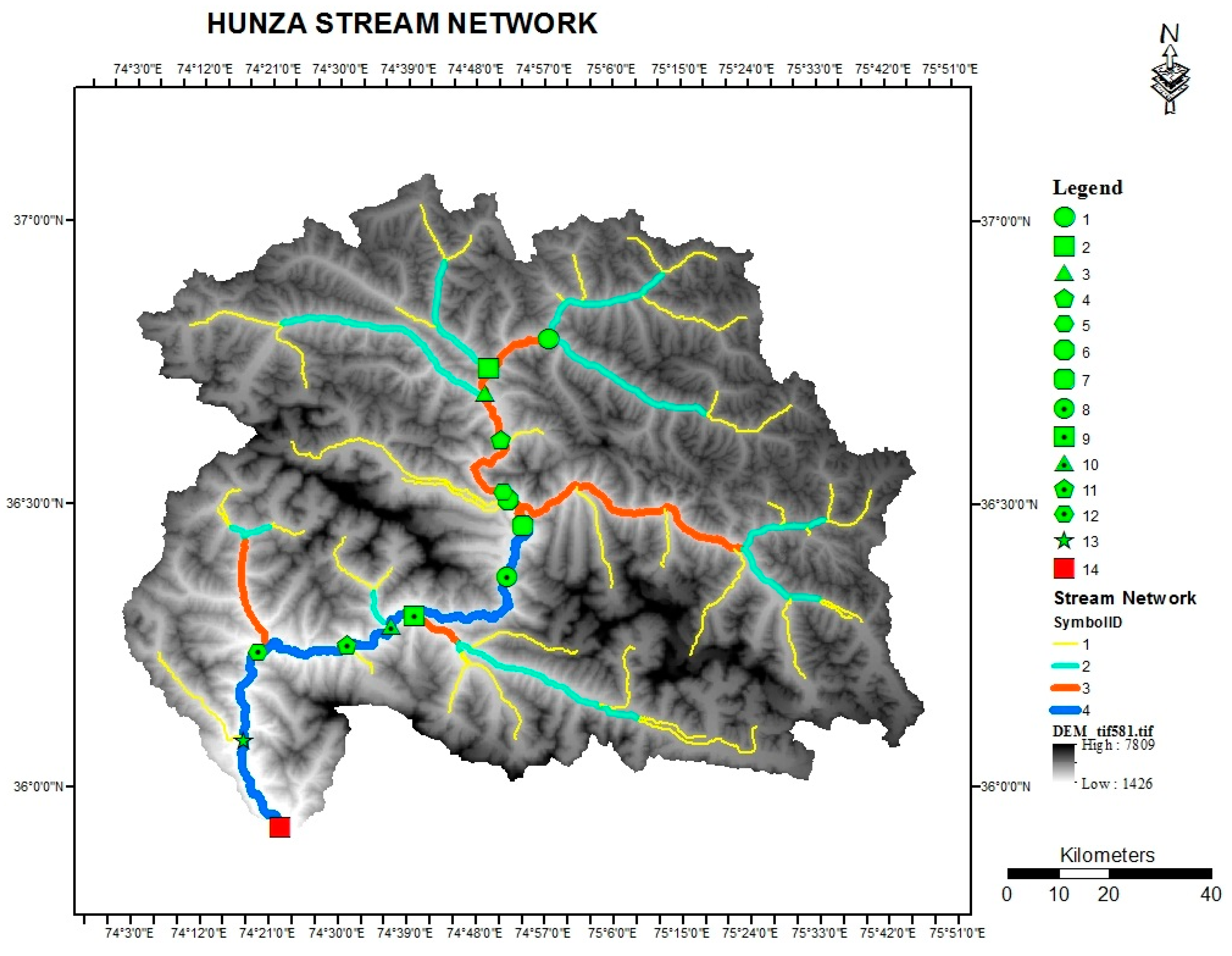
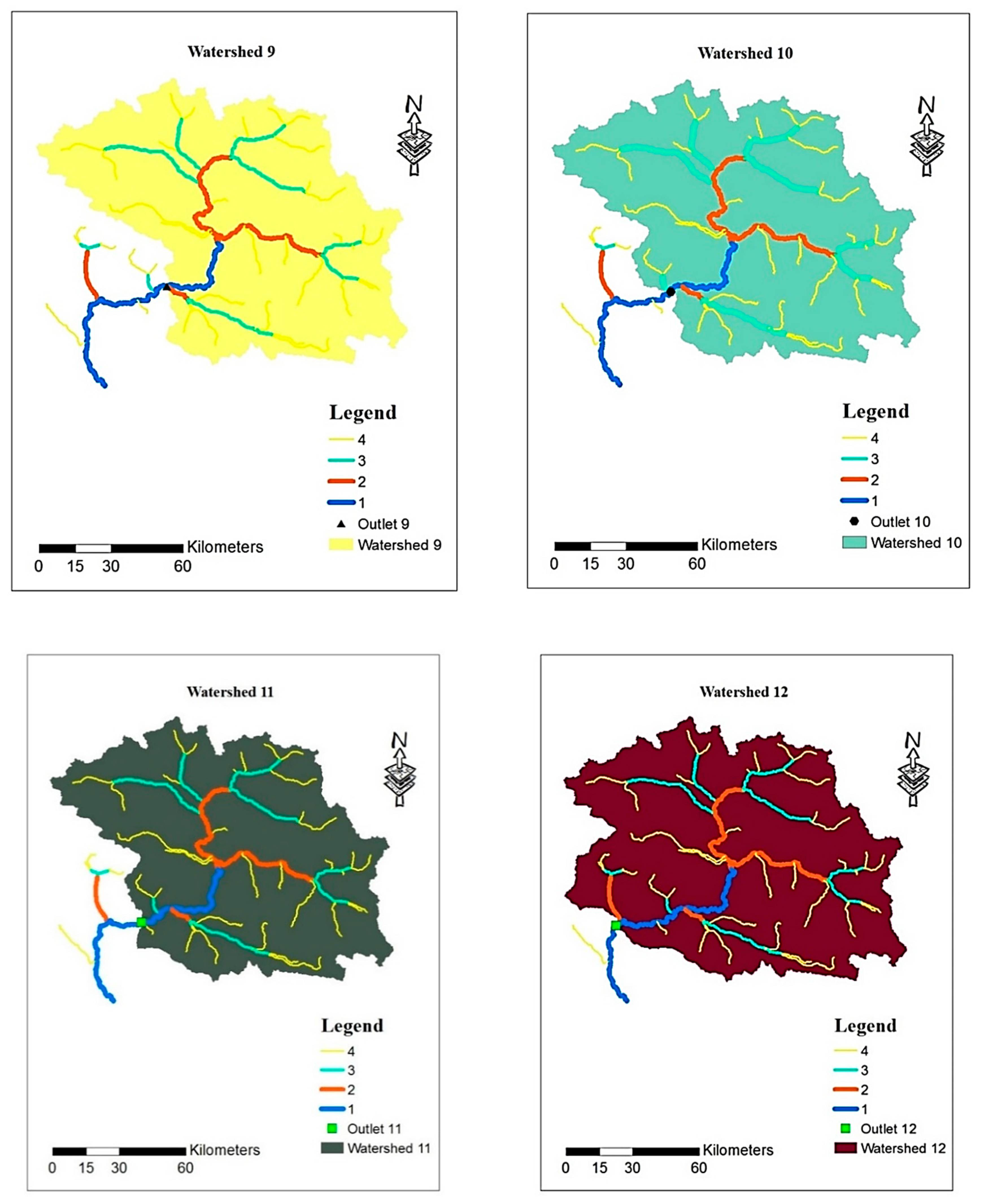
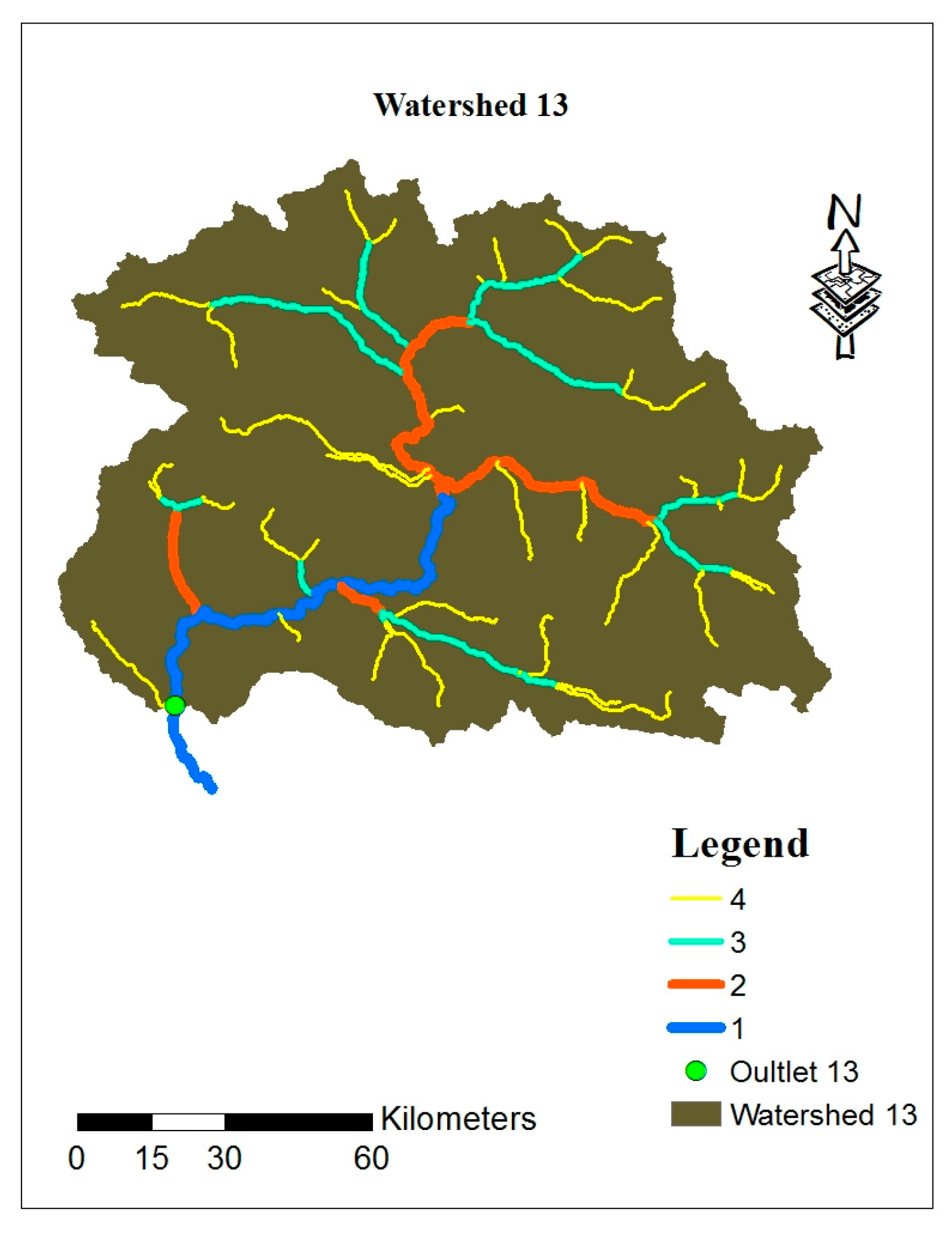
3.2. Watershed Delineation for All Sites
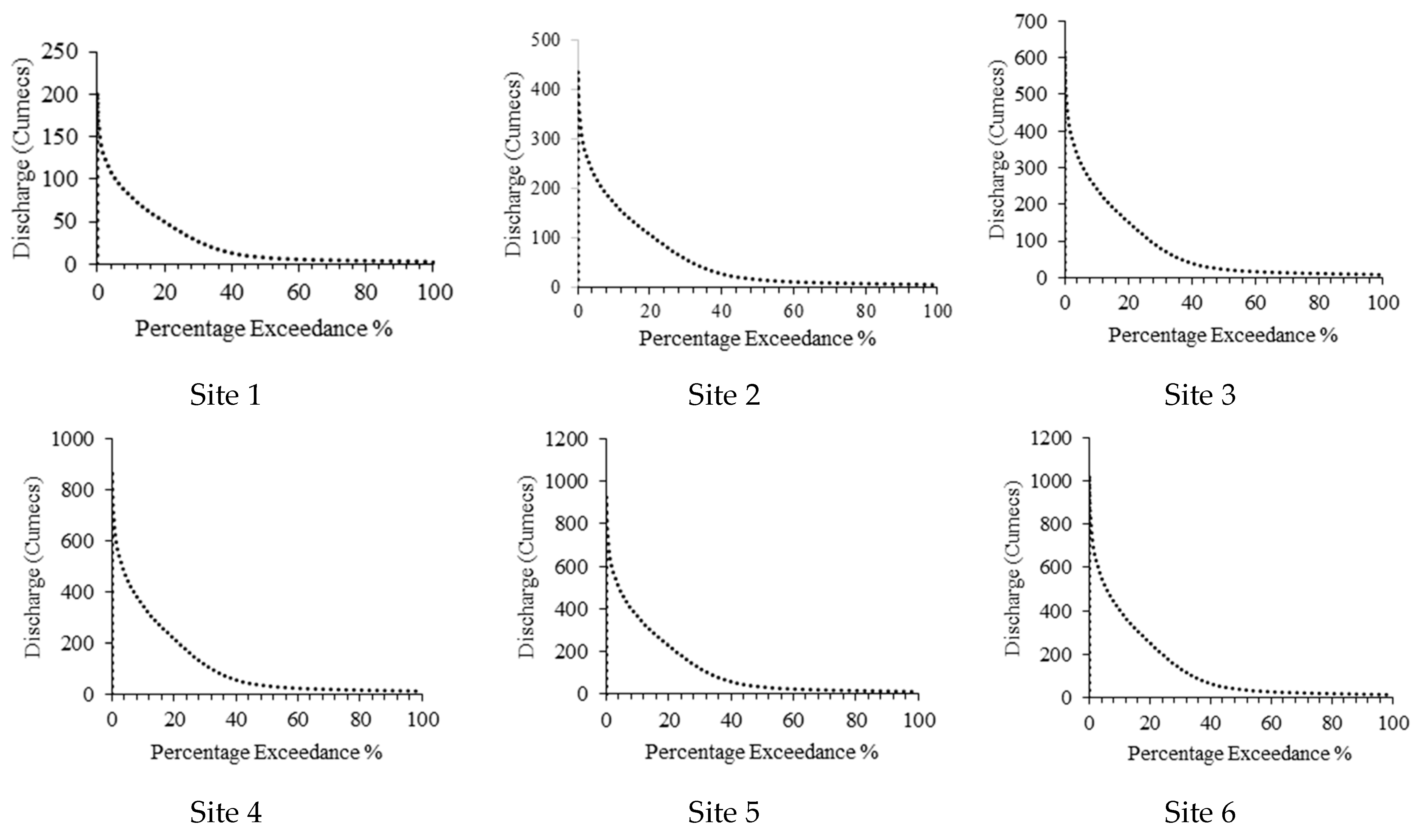
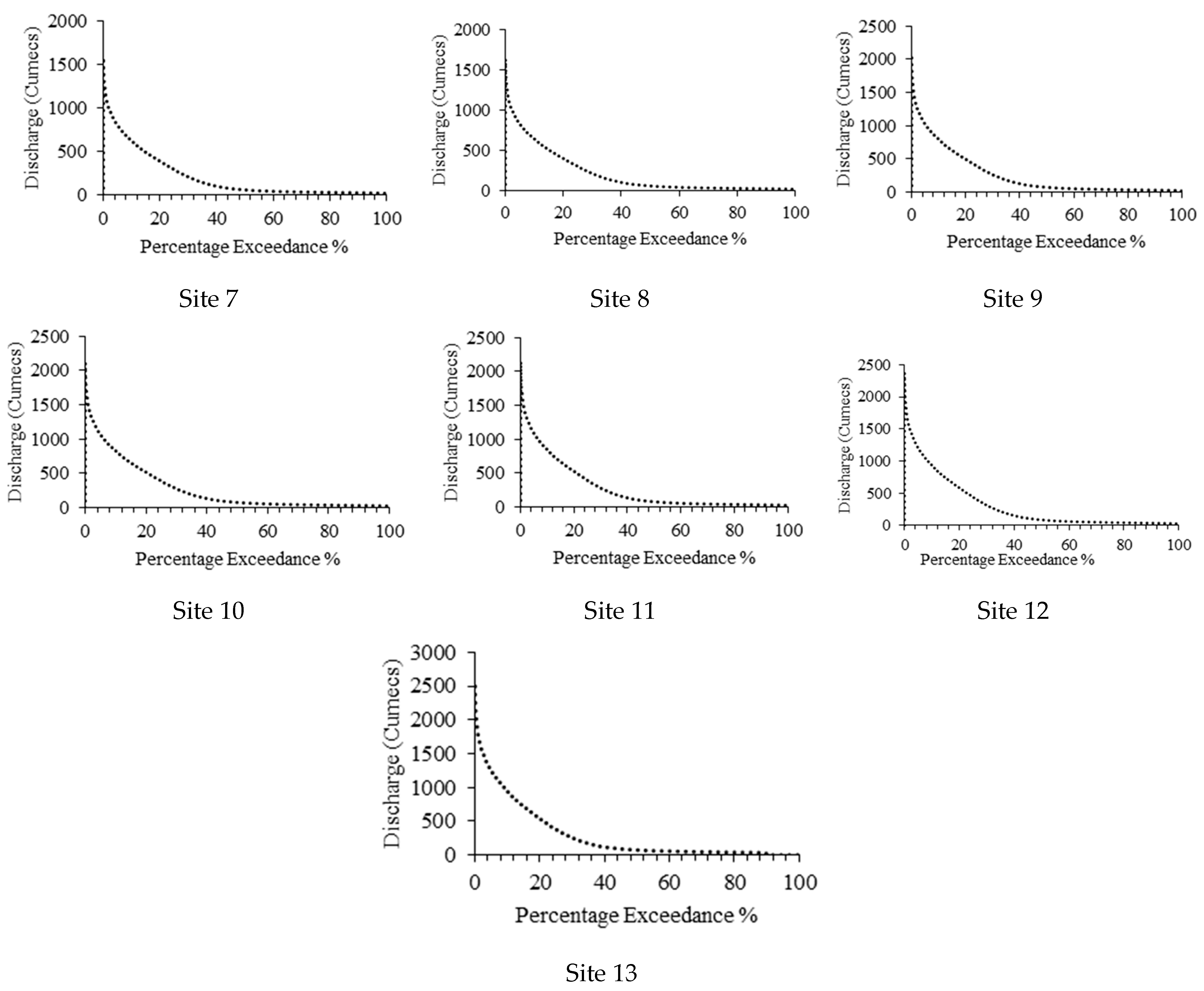
3.3. Estimation of Flow Duration Curve at Each Site
3.4. Hydropower Potential
3.5. Selection of Suitable Sites Using MDM Method
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bartle, A. Hydropower potential and development activities. Energy Policy 2002, 30, 1231–1239. [Google Scholar] [CrossRef]
- World Energy Council, World Energy Resources Hydropower. 2016. Available online: https://www.worldenergy.org/assets/images/imported/2016/10/World-Energy-Resources-Full-report-2016.10.03.pdf (accessed on 1 May 2023).
- UNCC. How Hydropower Can Help Climate Action. 2018. Available online: https://unfccc.int/news/how-hydropower-can-help-climate-action (accessed on 1 May 2023).
- Tahir, A.A.; Chevallier, P.; Arnaud, Y.; Neppel, L.; Ahmad, B. Modeling snowmelt-runoff under climate scenarios in the Hunza River basin, Karakoram Range, Northern Pakistan. J. Hydrol. 2011, 409, 104–117. [Google Scholar] [CrossRef]
- Mirjat, N.H.; Uqaili, M.A.; Harijan, K.; Das Valasai, G.; Shaikh, F.; Waris, M. A review of energy and power planning and policies of Pakistan. Renew. Sustain. Energy Rev. 2017, 79, 110–127. [Google Scholar] [CrossRef]
- Siddiqi, A.; Wescoat, J.L.; Humair, S.; Afridi, K. An empirical analysis of the hydropower portfolio in Pakistan. Energy Policy 2012, 50, 228–241. [Google Scholar] [CrossRef]
- Dudhani, S.; Sinha, A.; Inamdar, S. Assessment of small hydropower potential using remote sensing data for sustainable development in India. Energy Policy 2006, 34, 3195–3205. [Google Scholar] [CrossRef]
- Rojanamon, P.; Chaisomphob, T.; Bureekul, T. Application of geographical information system to site selection of small run-of-river hydropower project by considering engineering/economic/environmental criteria and social impact. Renew. Sustain. Energy Rev. 2009, 13, 2336–2348. [Google Scholar] [CrossRef]
- Kusre, B.; Baruah, D.; Bordoloi, P.; Patra, S. Assessment of hydropower potential using GIS and hydrological modeling technique in Kopili River basin in Assam (India). Appl. Energy 2010, 87, 298–309. [Google Scholar] [CrossRef]
- Larentis, D.G.; Collischonn, W.; Olivera, F.; Tucci, C.E. Gis-based procedures for hydropower potential spotting. Energy 2010, 35, 4237–4243. [Google Scholar] [CrossRef]
- Yi, C.-S.; Lee, J.-H.; Shim, M.-P. Site location analysis for small hydropower using geo-spatial information system. Renew. Energy 2010, 35, 852–861. [Google Scholar] [CrossRef]
- Cuya, D.G.P.; Brandimarte, L.; Popescu, I.; Alterach, J.; Peviani, M. A GIS-based assessment of maximum potential hydropower production in La Plata basin under global changes. Renew. Energy 2013, 50, 103–114. [Google Scholar] [CrossRef]
- Akbar, H.; Gheewala, S.H. Impact of Climate and Land Use Changes on flowrate in the Kunhar River Basin, Pakistan, for the Period (1992–2014). Arab. J. Geosci. 2021, 14, 707. [Google Scholar] [CrossRef]
- Alashan, S.; Şen, Z.; Toprak, Z.F. Hydroelectric Energy Potential of Turkey: A Refined Calculation Method. Arab. J. Sci. Eng. 2016, 41, 1511–1520. [Google Scholar] [CrossRef]
- Zaidi, A.Z.; Khan, M. Identifying high potential locations for run-of-the-river hydroelectric power plants using GIS and digital elevation models. Renew. Sustain. Energy Rev. 2018, 89, 106–116. [Google Scholar] [CrossRef]
- Bayazıt, Y.; Bakış, R.; Koç, C. An investigation of small-scale hydropower plants using the geographic information system. Renew. Sustain. Energy Rev. 2017, 67, 289–294. [Google Scholar] [CrossRef]
- Belmonte, S.; Núñez, V.; Viramonte, J.; Franco, J. Potential renewable energy resources of the Lerma Valley, Salta, Argentina for its strategic territorial planning. Renew. Sustain. Energy Rev. 2009, 13, 1475–1484. [Google Scholar] [CrossRef]
- Punys, P.; Dumbrauskas, A.; Kvaraciejus, A.; Vyciene, G. Tools for Small Hydropower Plant Resource Planning and Development: A Review of Technology and Applications. Energies 2011, 4, 1258–1277. [Google Scholar] [CrossRef]
- Tecle, A.; Fogel, M.; Duckstein, L. Multicriterion Selection of Wastewater Management Alternatives. J. Water Resour. Plan. Manag. 1988, 114, 383–398. [Google Scholar] [CrossRef]
- Weng, S.; Huang, G.; Li, Y. An integrated scenario-based multi-criteria decision support system for water resources management and planning—A case study in the Haihe River Basin. Expert Syst. Appl. 2010, 37, 8242–8254. [Google Scholar] [CrossRef]
- Atieh, M.; Gharabaghi, B.; Rudra, R. Entropy-based neural networks model for flow duration curves at ungauged sites. J. Hydrol. 2015, 529, 1007–1020. [Google Scholar] [CrossRef]
- Gazendam, E.; Gharabaghi, B.; McBean, E.; Whiteley, H.; Kostaschuk, R. Ranking of Waterways Susceptible to Adverse Stormwater Effects. Can. Water Resour. J. 2009, 34, 205–228. [Google Scholar] [CrossRef]
- Kodikara, P.; Perera, B.; Kularathna, M. Stakeholder preference elicitation and modelling in multi-criteria decision analysis—A case study on urban water supply. Eur. J. Oper. Res. 2010, 206, 209–220. [Google Scholar] [CrossRef]
- Noori, A.; Bonakdari, H.; Morovati, K.; Gharabaghi, B. The optimal dam site selection using a group decision-making method through fuzzy TOPSIS model. Environ. Syst. Decis. 2018, 38, 471–488. [Google Scholar] [CrossRef]
- Lai, V.; Huang, Y.F.; Koo, C.H.; Ahmed, A.N.; El-Shafie, A. A Review of Reservoir Operation Optimisations: From Traditional Models to Metaheuristic Algorithms. Arch. Comput. Methods Eng. 2022, 29, 3435–3457. [Google Scholar] [CrossRef] [PubMed]
- Sustainable Development Goals. 2022. Available online: https://www.un.org/sustainabledevelopment/energy/ (accessed on 1 May 2023).
- Jasso, A.T. Evaluation of Small Hydro Power Potential in Three River Basins of Mexico; Mexican Institute of Water Technology (IMTA): Jiutepec, Mexico, 2009; pp. 1–14. [Google Scholar]
- Wali, U.G. Estimating Hydropower Potential of an Ungauged Stream. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 592–600. [Google Scholar]
- Ajmal, M.; Kim, T.-W.; Ahn, J.-H. Stability assessment of the curve number methodology used to estimate excess rainfall in forest-dominated watersheds. Arab. J. Geosci. 2016, 9, 402. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D.; Dercas, N.; Londra, P.A. Investigation of the direct runoff generation mechanism for the analysis of the SCS-CN method applicability to a partial area experimental watershed. Hydrol. Earth Syst. Sci. 2009, 13, 605–615. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D. SCS-CN parameter determination using rainfall-runoff data in heterogeneous watersheds—The two-CN system approach. Hydrol. Earth Syst. Sci. 2012, 16, 1001–1015. [Google Scholar] [CrossRef]
- Gianfagna, C.C.; Johnson, C.E.; Chandler, D.G.; Hofmann, C. Watershed area ratio accurately predicts daily streamflow in nested catchments in the Catskills, New York. J. Hydrol. Reg. Stud. 2015, 4, 583–594. [Google Scholar] [CrossRef]
- Ergen, K.; Kentel, E. An integrated map correlation method and multiple-source sites drainage-area ratio method for estimating streamflows at ungauged catchments: A case study of the Western Black Sea Region, Turkey. J. Environ. Manag. 2016, 166, 309–320. [Google Scholar] [CrossRef]
- Farmer, W.H.; Vogel, R.M. Performance-weighted methods for estimating monthly streamflow at ungauged sites. J. Hydrol. 2013, 477, 240–250. [Google Scholar] [CrossRef]
- Shu, C.; Ouarda, T.B.M.J. Improved methods for daily streamflow estimates at ungauged sites. Water Resour. Res. 2012, 48, 1–15. [Google Scholar] [CrossRef]
- Roszkowska, E.; Białymstoku, U.W. Rank Ordering Criteria Weighting Methods—A Comparative Overview. Optimum. Econ. Stud. 2013, 5, 14–33. [Google Scholar] [CrossRef]
- Khan, M.; Zaidi, A.Z. Run-of-River Hydropower Potential of Kunhar River, Pakistan. Pak. J. Meteorol. 2015, 12, 25–32. [Google Scholar]
- Cai, X.; Ye, F.; Gholinia, F. Application of artificial neural network and Soil and Water Assessment Tools in evaluating power generation of small hydropower stations. Energy Rep. 2020, 6, 2106–2118. [Google Scholar] [CrossRef]


| Criterion | Location Criteria | Constraint Criteria | ||||
|---|---|---|---|---|---|---|
| (Power) | (Environmental) | |||||
| Definition | Head | Discharge | Site Access | Agriculture Area | Residential Area | Interaction with other HPP * |
| Benefit or Cost aspect | Benefit | Benefit | Benefit | Cost | Cost | Cost |
| Benefit Criteria | Values | Cost Criteria |
|---|---|---|
| 00 | ||
| Very Low | 01 | Very High |
| Low | 03 | High |
| Average | 05 | Average |
| High | 07 | Low |
| Very High | 09 | Very Low |
| 10 |
| Site No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Head (m) | 80.79 | 75.23 | 38.41 | 94.5 | 117.0 | 80.48 | 46.34 | 0.91 | 30.18 | 21.0 | 29.80 | 28.0 | 81.70 |
| Site No. | Q50 (Cumecs) | H (meters) | g (m/s2) | η | Density (kg/m3) | P (MW) |
|---|---|---|---|---|---|---|
| 1 | 7.512 | 80.79 | 9.81 | 0.81 | 1000 | 04.82 |
| 2 | 16.210 | 75.23 | 9.81 | 0.81 | 1000 | 09.69 |
| 3 | 22.967 | 38.41 | 9.81 | 0.81 | 1000 | 07.01 |
| 4 | 32.566 | 94.50 | 9.81 | 0.81 | 1000 | 24.45 |
| 5 | 34.409 | 117.0 | 9.81 | 0.81 | 1000 | 31.99 |
| 6 | 38.124 | 80.48 | 9.81 | 0.81 | 1000 | 24.38 |
| 7 | 58.687 | 46.34 | 9.81 | 0.81 | 1000 | 21.61 |
| 8 | 60.648 | 0.91 | 9.81 | 0.81 | 1000 | 0.44 |
| 9 | 75.091 | 30.18 | 9.81 | 0.81 | 1000 | 18.00 |
| 10 | 78.383 | 21.0 | 9.81 | 0.81 | 1000 | 13.08 |
| 11 | 79.804 | 29.80 | 9.81 | 0.81 | 1000 | 18.90 |
| 12 | 88.079 | 28.0 | 9.81 | 0.81 | 1000 | 19.60 |
| 13 | 92.805 | 81.70 | 9.81 | 0.81 | 1000 | 60.25 |
| Site No. | Power (MW) | Site Access | Agriculture Area | Residential Area | Interaction with Other HPP |
|---|---|---|---|---|---|
| 1 | 04.82 | 5 | 9 | 9 | 9 |
| 2 | 09.69 | 7 | 9 | 9 | 9 |
| 3 | 07.01 | 5 | 9 | 9 | 9 |
| 4 | 24.45 | 7 | 3 | 3 | 9 |
| 5 | 31.99 | 7 | 9 | 9 | 9 |
| 6 | 24.38 | 7 | 9 | 9 | 9 |
| 7 | 21.61 | 5 | 5 | 3 | 9 |
| 8 | 0.44 | 7 | 5 | 3 | 9 |
| 9 | 18.00 | 7 | 3 | 3 | 9 |
| 10 | 13.08 | 7 | 3 | 3 | 9 |
| 11 | 18.90 | 5 | 5 | 5 | 9 |
| 12 | 19.60 | 7 | 5 | 3 | 9 |
| 13 | 60.25 | 7 | 5 | 3 | 9 |
| Site No. | Power (MW) | Site Access | Agriculture Area | Residential Area | Interaction with Other HPP |
|---|---|---|---|---|---|
| 1 | 0.080 | 1.0 | 0.33 | 0.33 | 1.0 |
| 2 | 0.161 | 1.0 | 0.33 | 0.33 | 1.0 |
| 3 | 0.116 | 1.0 | 0.33 | 0.33 | 1.0 |
| 4 | 0.406 | 1.0 | 1.0 | 1.0 | 1.0 |
| 5 | 0.531 | 1.0 | 0.33 | 0.33 | 1.0 |
| 6 | 0.405 | 1.0 | 0.33 | 0.33 | 1.0 |
| 7 | 0.359 | 1.0 | 0.60 | 1.0 | 1.0 |
| 8 | 0.007 | 1.0 | 0.60 | 1.0 | 1.0 |
| 9 | 0.299 | 1.0 | 1.0 | 1.0 | 1.0 |
| 10 | 0.217 | 1.0 | 1.0 | 1.0 | 1.0 |
| 11 | 0.314 | 1.0 | 0.60 | 0.60 | 1.0 |
| 12 | 0.325 | 1.0 | 0.60 | 1.0 | 1.0 |
| 13 | 1.0 | 1.0 | 0.60 | 1.0 | 1.0 |
| Criterion | Preference | Relative Weight |
|---|---|---|
| Power | 1 | 0.333 |
| Site Access | 2 | 0.267 |
| Agriculture Area | 3 | 0.200 |
| Residential Area | 4 | 0.133 |
| Interaction with other HPP | 5 | 0.067 |
| Site No. | Results Obtained by Multiplying Criteria with Relative Weights | Sum of All Criteria Weightage | ||||
|---|---|---|---|---|---|---|
| Power | Site Access | Agriculture Area | Residential Area | Interaction with Other HPP | ||
| 1 | 0.0173 | 0.2667 | 0.0667 | 0.0444 | 0.0667 | 0.4618 |
| 2 | 0.0348 | 0.2667 | 0.0667 | 0.0444 | 0.0667 | 0.4793 |
| 3 | 0.0251 | 0.2667 | 0.0667 | 0.0444 | 0.0667 | 0.4696 |
| 4 | 0.0877 | 0.2667 | 0.20 | 0.1333 | 0.0667 | 0.7544 |
| 5 | 0.1148 | 0.2667 | 0.0667 | 0.0444 | 0.0667 | 0.5593 |
| 6 | 0.0875 | 0.2667 | 0.0667 | 0.0444 | 0.0667 | 0.5319 |
| 7 | 0.0775 | 0.2667 | 0.120 | 0.1333 | 0.0667 | 0.6642 |
| 8 | 0.0016 | 0.2667 | 0.120 | 0.1333 | 0.0667 | 0.5883 |
| 9 | 0.0646 | 0.2667 | 0.20 | 0.1333 | 0.0667 | 0.7313 |
| 10 | 0.0469 | 0.2667 | 0.20 | 0.1333 | 0.0667 | 0.7136 |
| 11 | 0.0678 | 0.2667 | 0.120 | 0.0799 | 0.0667 | 0.6012 |
| 12 | 0.0703 | 0.2667 | 0.120 | 0.1333 | 0.0667 | 0.6570 |
| 13 | 0.2162 | 0.2667 | 0.120 | 0.1333 | 0.0667 | 0.8029 |
| Site No. | Longitude | Latitude | Sum of All Criteria Weightage (from Table 8) | Final Rankings |
|---|---|---|---|---|
| 1 | 74.95 E | 36.79 N | 0.4618 | 13 |
| 2 | 74.82 E | 36.74 N | 0.4793 | 11 |
| 3 | 74.81 E | 36.69 N | 0.4696 | 12 |
| 4 | 74.85 E | 36.61 N | 0.7544 | 2 |
| 5 | 74.86 E | 36.52 N | 0.5593 | 9 |
| 6 | 74.87 E | 36.51 N | 0.5319 | 10 |
| 7 | 74.90 E | 36.46 N | 0.6642 | 5 |
| 8 | 74.86 E | 36.37 N | 0.5883 | 8 |
| 9 | 74.66 E | 36.30 N | 0.7313 | 3 |
| 10 | 74.61 E | 36.28 N | 0.7136 | 4 |
| 11 | 74.35 E | 36.25 N | 0.6012 | 7 |
| 12 | 74.35 E | 36.25 N | 0.6570 | 6 |
| 13 | 74.29 E | 36.08 N | 0.8029 | 1 |
| Site No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Power (MW) | 4.82 | 9.69 | 7.01 | 24.45 | 31.99 | 24.38 | 21.61 | 0.44 | 18.00 | 13.08 | 18.90 | 19.60 | 60.25 |
| Energy (GWh) | 31.41 | 63.13 | 45.66 | 159.3 | 208.4 | 158.9 | 140.8 | 02.85 | 117.3 | 85.22 | 123.1 | 127.7 | 392.6 |
| Plant factor (%) | 74.39 | 74.37 | 74.39 | 74.39 | 74.39 | 74.39 | 74.39 | 74.39 | 74.39 | 74.39 | 74.39 | 74.39 | 74.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Butt, A.Q.; Shangguan, D.; Waseem, M.; Haq, F.u.; Ding, Y.; Mukhtar, M.A.; Afzal, M.; Muhammad, A. Ascertainment of Hydropower Potential Sites Using Location Search Algorithm in Hunza River Basin, Pakistan. Water 2023, 15, 2929. https://doi.org/10.3390/w15162929
Butt AQ, Shangguan D, Waseem M, Haq Fu, Ding Y, Mukhtar MA, Afzal M, Muhammad A. Ascertainment of Hydropower Potential Sites Using Location Search Algorithm in Hunza River Basin, Pakistan. Water. 2023; 15(16):2929. https://doi.org/10.3390/w15162929
Chicago/Turabian StyleButt, Asim Qayyum, Donghui Shangguan, Muhammad Waseem, Faraz ul Haq, Yongjian Ding, Muhammad Ahsan Mukhtar, Muhammad Afzal, and Ali Muhammad. 2023. "Ascertainment of Hydropower Potential Sites Using Location Search Algorithm in Hunza River Basin, Pakistan" Water 15, no. 16: 2929. https://doi.org/10.3390/w15162929
APA StyleButt, A. Q., Shangguan, D., Waseem, M., Haq, F. u., Ding, Y., Mukhtar, M. A., Afzal, M., & Muhammad, A. (2023). Ascertainment of Hydropower Potential Sites Using Location Search Algorithm in Hunza River Basin, Pakistan. Water, 15(16), 2929. https://doi.org/10.3390/w15162929










