1. Introduction
Water, along with its importance for life on the planet, faces intense harvesting, impoundments, pollution, and contamination problems, among others, making the future of this resource insecure and uncertain, especially when considering it from the perspective of climate change [
1]. Freshwater ecosystems are threatened by various widespread stressors, such as eutrophication and contamination, that are aggravated by the climate crisis as well as practices such as water harvesting and impoundments [
2]. Wetlands, lakes, and temporal waterbodies are rapidly disappearing, So essential and meaningful coordination in water management is required and must be directed towards precise goals. Water managers must therefore act proactively to avoid further losses and cooperate/mobilize more stakeholders and end users.
Water resources management (WRM) is not simply an optimization problem; it requires a systemic approach that implies the involvement of interacting entities, intricate dynamics, and multifaceted elements. Typically, WRM involves many criteria, multiple purposes, many stakeholders, and both structural and not structural measures, among others [
3]. The WRM was therefore introduced as an approach where all the system “poles”, meaning resources, environment, and consumers, are harmonically addressed to provide immediate solutions while also sustainably safeguarding the future [
4]. Originally, the WRM approach had a typical sub-sectoral approach, dealing mostly with water supply, sanitation, irrigation, and hydropower generation [
5]. Therefore, the problem could be reduced to a monocriterion optimization problem based on the axiomatic consideration that the “needs” must be covered. There was often a lack of coordination between sectors, and the environmental requirements were either ignored, or some simple constraints were added within the mathematical formulation.
After 2000, the WRM gradually transformed into Integrated Water Resource Management (IWRM), which is a more environmental approach. Its three major pillars are ensuring equitable access to water resources, enhancing environmental sustainability, and promoting economic efficiency of the resource (including allocations). The notion of IWRM entails an endeavor to comprehensively address and harmonize various technical and social aspects of water utilization and governance. Inevitably, it entails the involvement of stakeholders in some capacity [
6]. During the last two decades, stakeholder engagement has received increasing amounts of research attention for designing and implementing solutions to tackle water challenges. The IWRM has introduced stakeholder engagement and adaptivity (among other associated practices) as schemes for novel paradigm management. Nonetheless, the successful implementation of such practices remains a formidable challenge [
7]. The participatory approaches, which have the goal of engaging (in an institutionalized approach) the stakeholders, aim to foster a sense of ownership from the design process through the implementation of measures, but has not yet (theoretically) yielded the expected reforms in water management [
8]. The importance of “hearing the local voices” is reflected in resolutions from organizations like the World Bank, the UN, and the OECD, or the European Commission (aligned with the Europe 2020 strategy). Good water governance and IWRM are intertwined with stakeholder engagement [
9].
Nowadays, new concepts and challenges are incorporated in the IWRM as the adaptation to the Water–Energy–Food–Environment (WEFE) nexus, the extreme phenomena, public participation, and globalization, among others. The largest water-related policy that exists at this time in Europe is the revised 20+ version of the Water Framework Directive (WFD) (2000/60/EC), which introduces a framework for a “basin approach” that also embeds the concept of IWRM paradigm. But even the WFD has raised skepticism due to several issues that may occur trying to reach good status in EU waterbodies since stakeholder engagement is low, and, in most countries, there is a top-down procedure in decision making that usually adopts horizontal measures. The complexity that is inherent within catchments (i.e., covering needs, conflicting water uses, ecological services, and uninterrupted provision) presents a significant barrier to the implementation of the mitigation measures in water uses planning (as in WFD RBMPs), where assessments tend to focus, mainly, on human needs, and therefore fail to recognize the water resource’s sustainability. This highlights the need for knowledge improvement through common technical language to ensure common understanding.
Multicriteria decision making (MCDM) is a valuable tool in water resources management problems since it can incorporate complex and often conflicting goals and objectives and multiple-stakeholders. The MCDM techniques can help decision makers systematically evaluate and rank different options based on multiple criteria, such as cost-effectiveness, environmental impact, social acceptability, and technical feasibility. By considering multiple criteria, MCDM can help decision makers make more informed and transparent decisions since the weights and scores of some criteria can be assessed by using the participation of the stakeholders. The mapping of regional/local stakeholder communities is equally important to establish a common technical language, with attention paid to ensuring inclusiveness and assuring that the needs and roles of stakeholders are recognized. However, there are problematics and challenges which must be addressed, including the qualitative evaluation of the criteria, the existence of multiple stakeholders, the different nature of the criteria, and the inherent uncertainty of the multicriteria problem, among others. There are several “schools” of multicriteria analyses; of them, the distance methods are used frequently since these methods can be understandable to the analyst and have a medium degree of difficulty. These approaches identify ideal and anti-ideal points which are fictitious alternatives in the edges of the decision spaces. They then distinguish the alternatives that are nearest to the ideal and furthest from the anti-ideal [
10].
Due to the fact that, by using the fuzziness, uncertainty can be incorporated in the models, and, furthermore, since the fuzzy logic simulates the human reasoning, fuzziness is widely used in multicriteria analysis. In brief, fuzzy set theory [
11] generalizes the classical or crisp sense, according to Zimmerman [
12] and Kafas [
13], into the fuzziness sense that is involved in human language, that is, in human judgment, evaluation, and decisions, although this is not an exclusive list of linguistic social terms. Fuzziness can express the linguistic variables whose values are words or sentences in a natural or artificial language [
14]. Apart from these, fuzziness can enable us to express the grey zone of decisions and, furthermore, can provide understandable ways to aggregate different information. Fuzziness, based on the ability to imitate the process of thinking, can generate understandable solutions without ambiguous considerations, like the choice of weights or the aggregation method of objective functions, among others [
15,
16,
17].
After the invention of the intuitionistic fuzzy (IF) set and IF numbers [
18,
19], the expressions used to describe fuzzy sets were totally changed. A fuzzy set uses only a membership function to indicate the degree of belongingness that a member has in the considered set. The degree of non-belongingness is automatically determined as the complement by using the widely used fuzzy complement [
20]. The intuitionistic fuzzy sets overcome this restriction. The inherent uncertainty of many real-world problems can be robustly incorporated by using an intuitionistic fuzzy set (IFS) [
18], which is an extension of an ordinary fuzzy set (FS) [
11]. The main difference between an IFS and an FS is the representation of hesitancy. More specifically, by using fuzzy sets, the decision can be obtained based on the satisfaction (or dissatisfaction) degree to an alternative by using the membership function and its compliment. However, in the case where the decision maker (DM) uses the IFS, a further hesitation degree can be provided to an alternative that is equal to the difference between the unit and the sum of the membership degree and the non-membership degree. Consequently, the opinion of the DMs can be reflected more comprehensively [
21]. In recent years, the field of intuitionistic fuzzy multicriteria methods has exhibited significant potential, as evidenced by its growing prominence, particularly since the year 2009 [
22]. The use of an intuitionistic fuzzy set has a great importance in this research since it enables us to use the stakeholder’s opinion and then quantify the information.
Linking the above, regarding stakeholder participation within IWRM with the aid of IFS, the focus lies on the spatial scale of the application since some catchments are more vulnerable than others. Remote areas are generally characterized by low income (the Thrace region is one of the poorest regions in EU) and a lack of river stewardship, non-government organization (NGO) participation, and environmental awareness, factors that are crucial to create stakeholder engagement in decision making. Meanwhile, water shortage, especially in times of climate crisis, usually becomes the main issue, and other problems are neglected. This made our effort larger but more valuable. The eye4water project [
23] has invested in seminars/workshops, living labs, newsletters, data and findings presented in open publications, and citizens-to-researchers interactions in a “cluster” type to foster regional water governance, enhance the sustainability of monitoring networks, and create stronger bonds with the society. Through its consulting role, eye4water wishes to support decision making and strategic planning by taking into account the stakeholders’ opinions on pressures and possible solutions, assisting ultimately in two remote rural river basins (Laspias and Lissos) to create resilience and mitigate risk. By activating many forms of two-way communication among participants and utilizing institutional support in the form of facilitation and coordination, the aim of good water governance processes was served.
The aim of this study is to incorporate stakeholders’ opinions to assist operationalization and decision making for participatory integrated water resources management in the remote, rural Laspias river basin. Such a method can address complex issues and provide the basis for mitigation measures hierarchy. Stakeholder groups were identified for collaboration in the form of co-management-based governance arrangement. To this aim, semi-structured interviews were held in key areas within the basin. Intuitionistic fuzzy set was used to incorporate the opinions of the stakeholders concerning the weights and the evaluation of criteria. Next, an intuitionistic distance-based method was applied in order to rank several alternatives under multiple criteria.
3. Results and Discussion
The applied method managed to gather valuable responses in a wide variety of questions posed in our attempt to address holistically the known issues related to the water management and measures planning in such a remote and heavily pressured river basin. The inclusiveness of stakeholders from all groups meant that their voices were heard and their opinions on the needs and problems were expressed, offering us the ability to order them hierarchically, assisting the decision makers. Furthermore, the objectivity and transparency of this method is a tool for conflict resolution.
Moving on to the actual findings that originated from the semi-structured interviews, the stakeholder group that is dependent on water, i.e., farmers, recognize the problem of river quantity and quality and are interested in finding solutions that will allow them to maintain their business operations.
The biggest concern for most stakeholders seem to be related to the quality of the water of the Laspias river, especially in drought periods. However, in the region of Dekarcho, the farmers also emphasize the water irrigation quantities. A significant percentage (≈78%) of the respondents believe that the Laspias river definitely needs some intervention, approximately 19% believe that some intervention may be necessary, while only one respondent (≈2.5%) believed that no intervention was necessary. Regarding groundwater, the corresponding percentages are ≈66% (27/41), ≈22% (9/41), and 5/41 (≈12%), respectively. The development of an irrigation network that will be based on the drilling of new municipal/public wells is advanced by the stakeholders (mainly farmers) as one of the best alternatives to deal with the water shortage in the area which is not affected by the Laspias River. It is also worth mentioned that approximately 53% of the respondents believe that irrigation can contribute to the economic development of the region in the future, while a significant percentage (≈34%) does not know what such an ecosystem service of the Laspias river could be.
Also of interest are the answers to the questions about what criteria farmers use to choose the type of crop they plant. The sample size in this question is n = 29 (crowd of farmers). According to the responses, economic efficiency is the most popular answer, followed by human productivity, defined as the ratio of the production divided by human work (in hours). Dryland or thirsty crops are not a selection criterion, except in the area around the settlement of Abdira, where most of the crops are dryland cotton due to the presence of the Abdira swell. Resistant crops, perennial, annual, or seasonal crops, and traditional crops are also not a selection criterion if the criteria of economic efficiency and lower employment are not met. Furthermore, the cultivators placed greater emphasis on the economic criterion, but also placed great importance on the environment (
Figure 5).
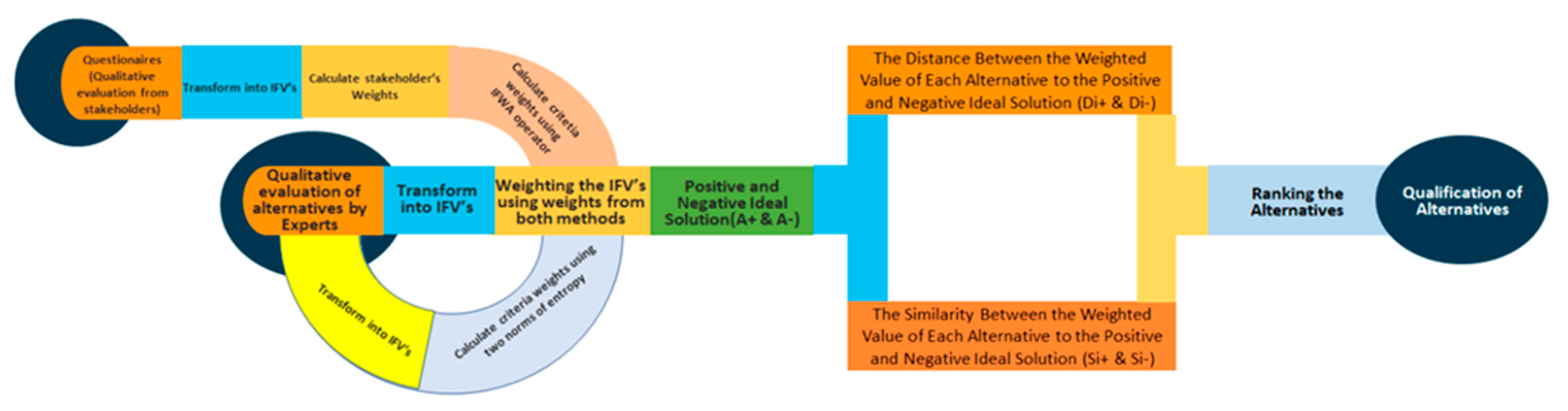
As aforementioned, the following steps are used in order to achieve the multicriteria ranking under multiple stakeholders:
Step 1. Determine the weights of each participant. The importance of each participant was calculated with respect to the scale proposed by [
37], that is, by considering the educational level and experience. Then, the weight of each participant can be obtained as a crisp value by using Equation (15) [
41].
For instance, based on the answers, the first stakeholder was proficient (Pt), with μ = 0.5, v = 0.45, and π = 0.05, and therefore his weight:
The denominator of this equation is estimated by summing all 43 numerators of the participants.
A total of 43 questionnaires was completed; of the total participants, 29 of them were farmers, and the rest were experts or administrative officers.
Step 2. Aggregate all information based on the participants by using the IFWA operator (Equation (14)). In this application, these steps concern mainly the weights of the criteria. As aforementioned, in this application, participants had different levels of practice and education, so the value
λ takes different values. The final criteria’s weights, derived as fuzzy intuitionistic information, are presented in
Table 1.
From the results, it is found that stakeholders put great importance on the environmental criterion and less on criteria involving various technical projects. However, the economical aspect seems as the most important criterion.
There might be some threads to validity for the faultless and reproducible methodology in acquiring stakeholders’ opinion, and for the methodology used for translating qualitative and quantitative information. However, the societal needs, values, and aspirations were expressed and could be integrated into planning. The findings could be dependent on prior training and knowledge but also reflect the participants’ social, political and cultural individual backgrounds. The stakeholder’s opinion might not be the most solid from a scientific point of view, but balancing of priorities and competing demands in an assimilable way by policy makers is exactly what is needed for operationalization of the basin.
Step 3. Construct an intuitionistic fuzzy decision matrix for each criterion (C
i) and alternative A
j by transforming the opinions of experts into Intuitionistic Fuzzy Values using (Equation (16)) (
Table 2).
Step 4. Construct aggregated weighted intuitionistic fuzzy decision matrix for each criterion based on the alternative Aj and the corresponding weight using Equation (4).
Hence, the aggregated weighted intuitionistic fuzzy decision matrix is presented in
Table 3 using Equation (17).
Step 5. Determine intuitionistic fuzzy positive ideal (A*) and intuitionistic fuzzy negative ideal (A
−) solutions. Let only the benefit criteria exist (
Table 4).
Step 6. Calculate for each alternative the similarity from both the ideal and anti-ideal solutions.
The similarity measures, and , for each alternative from the intuitionistic fuzzy positive ideal and intuitionistic fuzzy negative ideal solutions are calculated with respect to criterion Ci by using the Equations (18) and (19). Finally, a simple weighted model is used to assess the similarity measures over all criteria.
Step 7. Calculate the relative closeness coefficient to the intuitionistic fuzzy positive ideal solution.
The relative closeness coefficient of an alternative A
j with respect to the intuitionistic fuzzy ideal solution A* is defined as follows:
Step 8. Rank the alternatives in descending order. The final results are presented in
Table 5.
In addition, two main methods are examined. The first one is based on the concept of entropy (
Appendix A). It differs from the proposed method since the concept of entropy is used instead of the IFWA operator in order to assess the weights of criteria. In this case, a main disadvantage is produced, which is that the questionnaires regarding the weight’s importance will not be considered. The method emphasized the criteria with low hesitancy; finally, the A
4 alternative is selected.
The second examined method is the method in [
41]. The main difference between the proposed method and that one is that the Euclidean distance is used during the implementation of the TOPSIS method. The results are presented in
Table 6.
Regarding the two TOPSIS methods, they have little deviation in the results; however, the results based on the similarity measure are slightly preferred due to the fact that this measure leads to more balanced (centripetal) solutions, and, furthermore, it overcomes drawbacks, such as the “the division by zero problem”. Hence, the reuse of wastewater (A1), strict implementation of the pollution pricing policy (A13), and the monitoring of system pollutants (A14) are selected most often. In addition, by using the widely used TOPSIS, the alternative A4 has a lower rank.
The main difference is that the similarity-based TOPSIS puts emphasis on the alternative of creating a central irrigation network (fourth choice). In fact, this choice restores the water regime situation before the great river infrastructure. It is very encouraging that the alternative of doing nothing is last in preference among all the methods. It should be noted that these three first alternatives (strict implementation of the pollution pricing policy (A13), monitoring of system pollutants (A14), and wastewater reuse (A1) can be characterized as eco-friendly. The final ranking could be characterized rather as rational and balanced. Therefore, the similarity measures that are used have a theoretical sound foundation and lead to balanced solutions. Therefore, this research provides a series of acceptable measures that lead to the hierarchy of problems as were recognized by the stakeholders.
Consequently, the use of the IFWA operator to combine the aspects of the weight and the intuitionistic fuzzy similarity-based TOPSIS method is selected because of its balanced outcomes. The benefits of this method, i.e., transparency and objectivity, can assist WFD application in the RBMPs program of measures consultation. In particular, given the delay in decision making and mitigation measures planning, it can assist the actual dual nature of WFD (humans and the environment) by providing the means to determine hierarchy, given the cost, time, and water scarcity/deficiency.
It is worth mentioning that, regarding the alternative A
4 (which is ranked first when the entropy method is applied), a previous study [
45], has substantiated that it is possible to transfer water from the Nestos river and create a large and organized irrigation network that will meet the water needs of the wider area and simultaneously have environmental benefits. According to the same study, the annual volume of the Nestos river is approximately estimated at 788 × 10
6 m
3, exceeding the beneficial volume of the main (from a reservoir system) reservoir of Thesauros, which is 570 × 10
6 m
3. It should be pointed out that only 3000 ha of the land located between the Nestos river and the Laspias river are irrigated by the water of the Nestos river, 16,000 ha in the prefecture of Kavala, to the west of Nestos river, are irrigated by that river. Irrigation of the hectares of the area under consideration is mainly carried out with a system of open canals. Thus, in a way, the natural recharge of the aquifers, which was contributed to by the Nestos Delta, has been artificially compensated for since 1955, when the Nestos river was regulated and many structures were built.
4. Conclusions
The methodological approach designed for this study, based on the principles of participatory approach and intuitionistic fuzzy approach, have proven to be useful for addressing complex problems related to water quality, quantity, and uses while setting the hierarchy for catchment operationalization concerning the measures’ planning. During the process of this study, the scientific team managed to empower local people, including traditionally disadvantaged groups, especially in such a remote area. This ultimately created greater effectiveness in suggestions that were more participatory for operationalized water management. The mathematical “enablers” achieved were able to encompass a multi-stakeholder collaboration and create an operational model applicable for all river basins.
This work presents a multicriteria group decision making model to rank several water resource measures against the water crisis using intuitionistic fuzzy TOPSIS and emphasizing the integration of local experience and knowledge. The use of the intuitionistic fuzzy sets is a suitable way to deal with uncertainty, especially in cases that include qualitative information. This fact enables us to incorporate group decision making methodologies during the decision phase. Hence, the IFWA (intuitionistic fuzzy weighted averaging) operator was implemented to aggregate opinions of decision makers. The intuitionistic fuzzy TOPSIS method is used by choosing suitable similarity measures. Hence, a complicated solution can be modulated that consists of the reuse of wastewater (A
1), strict implementation of the pollution pricing policy (A
13), monitoring of system pollutants (A
14), and the creation of a central irrigation network or the modernization of the existing one (A
4). The methodology was compared with the intuitionistic TOPSIS based on the Euclidean distance measure [
41]. Furthermore, the methodology was applied using weights derived by the entropy measures.
An interesting point is that, according to Greek conditions, there are a variety of basins and hydrological regimes, and, hence, the results cannot be generalized or duplicated in all basins as the ranking of the alternatives could be different. However, the proposed methodology is actually a tool that can make sure that all voices are heard as well as an objective method that can surpass conflicts through a common “technical” language that has multiple applications for planning depending on the questions posed, thereby assisting in strategic water resources management.