Enhancing Urban Surface Runoff Conveying System Dimensions through Optimization Using the Non-Dominated Sorting Differential Evolution (NSDE) Metaheuristic Algorithm
Abstract
1. Introduction
2. Materials and Methods
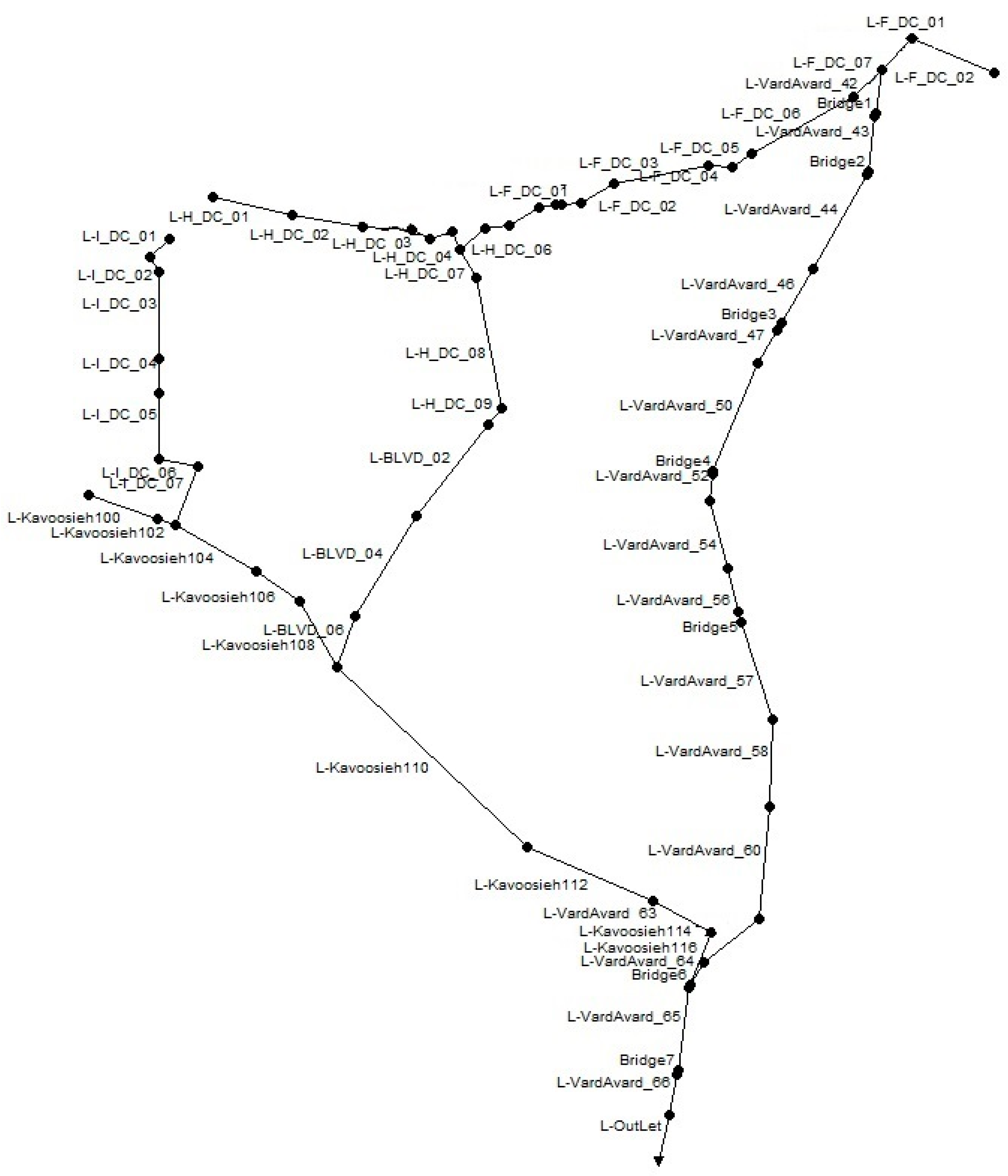
2.1. Study Area and Dataset
2.2. Methodology
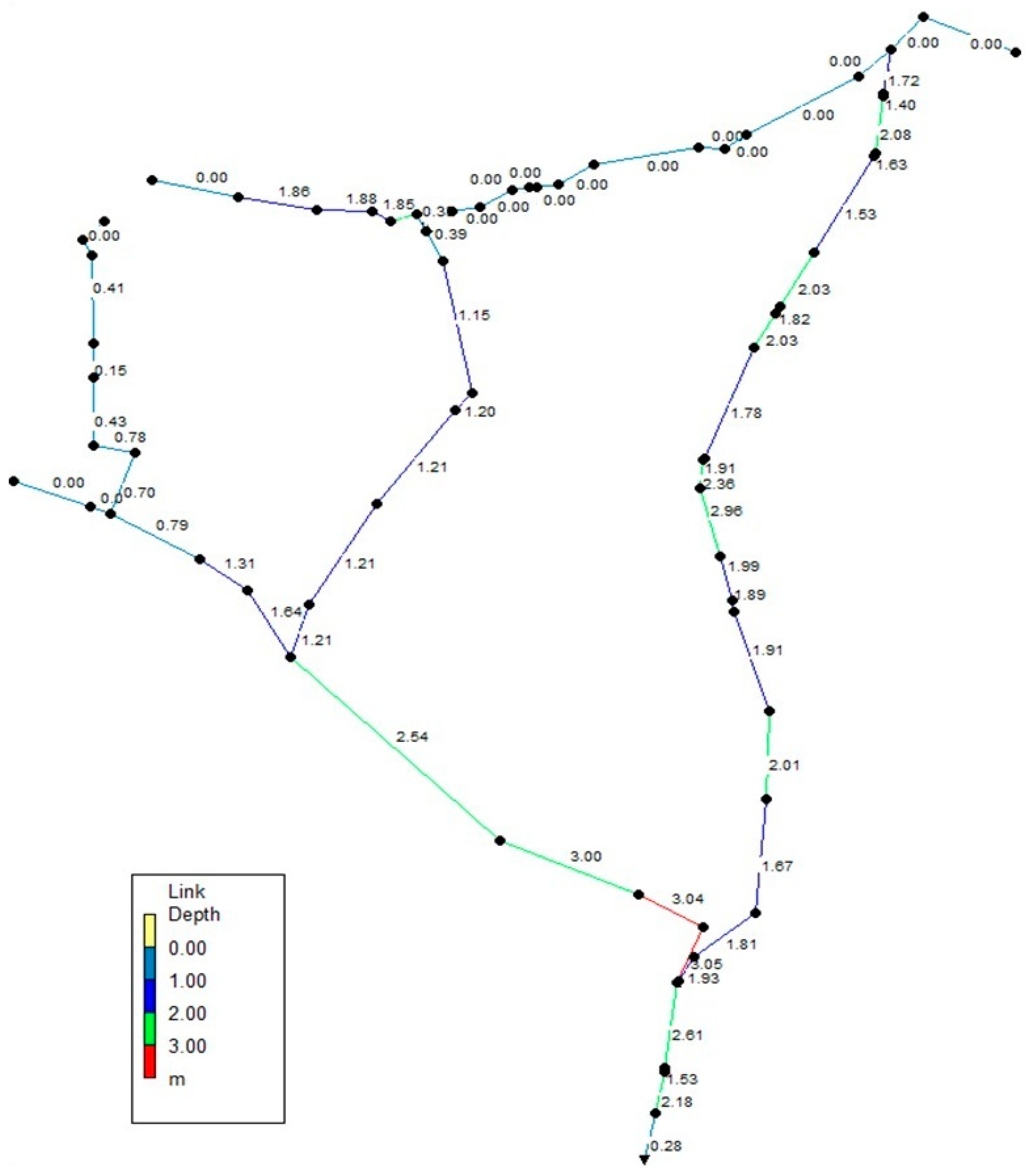
2.2.1. The Hydraulic Simulations
- Ability to analyze flow in separate and combined sewer networks.
- Ability to analyze one-dimensional flow in both steady and unsteady states.
- Capability to model various channels and pipes with different cross-sectional shapes.
- Capability to model different hydraulic structures.
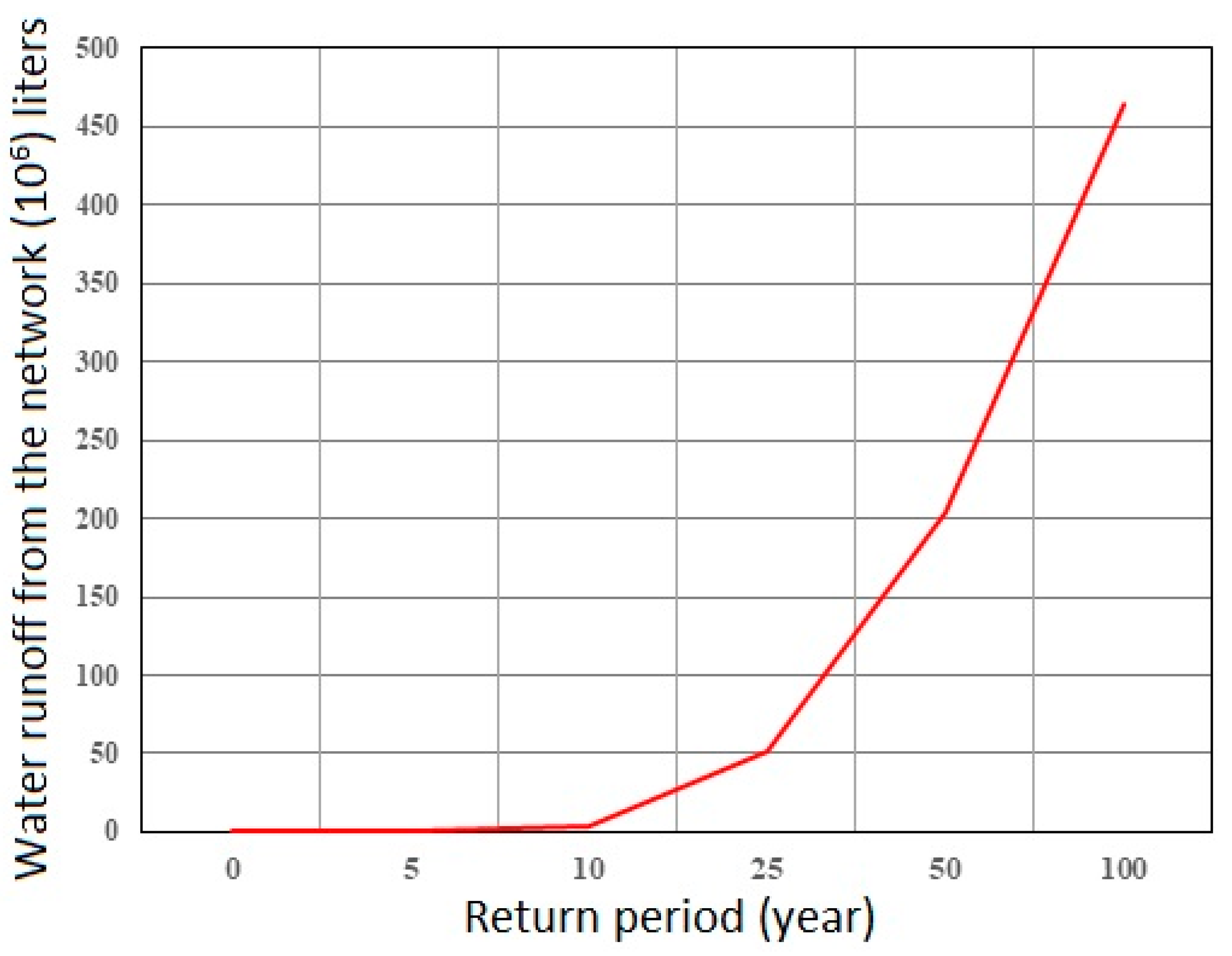
- Ability to estimate flow volume and duration of runoff from the network.
- Capability to simulate flow in free and pressurized stormwater systems.
- Capability to simulate complex networks, including networks with parallel, series, and looped pipe or channel arrangements.
2.2.2. The Optimizations
| Algorithm 1 A summary view of the process by optimization algorithm |
| Begin Set Npop = 100 MaxIter: Maximum number of Iteration Initialize a random population Xgi ∀I, i = 1, …, Npop Evaluate f (xig) ∀i, i = 1, …, Npop for iter = 1 to MaxIter do for i = 1 to Npop x = pop (i).Position; A = randperm(nPop) XBestPosition = pop (XBestRank).Position; XBestCost = CostFunction(XBestPosition); XWorstPosition = pop (XWorstRank).Position; XWorstCost = CostFunction(XWorstPosition); XBetterPosition = pop (XBetterRank).Position; XBetterCost = CostFunction(XBetterPosition); # Mutation operator XavgPosition = 1/3 ×(XBestPosition + XWorstPosition + XBetterPosition); XavgCost = CostFunction XavgPosition); F = unifrnd(0.1,0.8);%Pmax and Pmin recommended to be 1 and 0.1, respectively if rand < Pmax + (Pmax-Pmin) × e(it/MaxIt) y1Position = pop(1).Position + F × (pop(2).Position − pop(3).Position) + F × (pop(4).Position − pop(5).Position); y2Position = XBestPosition + F × (pop(1).Position − pop(2).Position) + F × (pop(3).Position − pop(4).Position); y3Position = pop(i).Position + F × (XBestPosition -pop(i).Position) + F × (pop(1).Position − pop(2).Position); else y1Position = XavgPosition + F1 × (XBestPosition − XBetterPosition) + F2 × (XBestPosition − XWorstPosition) + [(F1 + F2)/2] × (XBestPosition − XWorstPosition); y2Position = XavgPosition + (P2-P1) × (XBestPosition − XWorstPosition) + (P3-P2) × (XBestPosition − XWorstPosition) + (P1-P3) × (XBestPosition − XWorstPosition); y3Position = XBestPosition + F1 × (XBestPosition − XBetterPosition) + F2 × (XBestPosition − XWorstPosition); end if rand < 0.5 σ = [2×rand](1/η + 1) − 1; else σ = 1 [2-2×rand](1/η + 1); end %where σ is polynomial mutation, η is a distribution index, Ub and Lb are the lower and upper bounds of decision variable, # Crossover operator z = zeros(size(x)); j0 = randi([1 numel(x)]); for j = 1:numel(x) if j = j0 || rand <= PCR z(j) = y1Position (j) + σ × (Ub-Lb); elseif rand < 0.5 z(j) = y2Position (j); elseif rand >0.5 or rand < 0.75 z(j) = y3Position (j); else z(j) = xPosition (j); end % Apply Variable Limits z = max(z, Lb); z = min(z, Ub); NEWiPosition = z; NEWiCost = CostFunction(NEWiPosition); end |
2.3. Formulation of the Optimizations
2.4. Encoding
2.5. Model Establishment
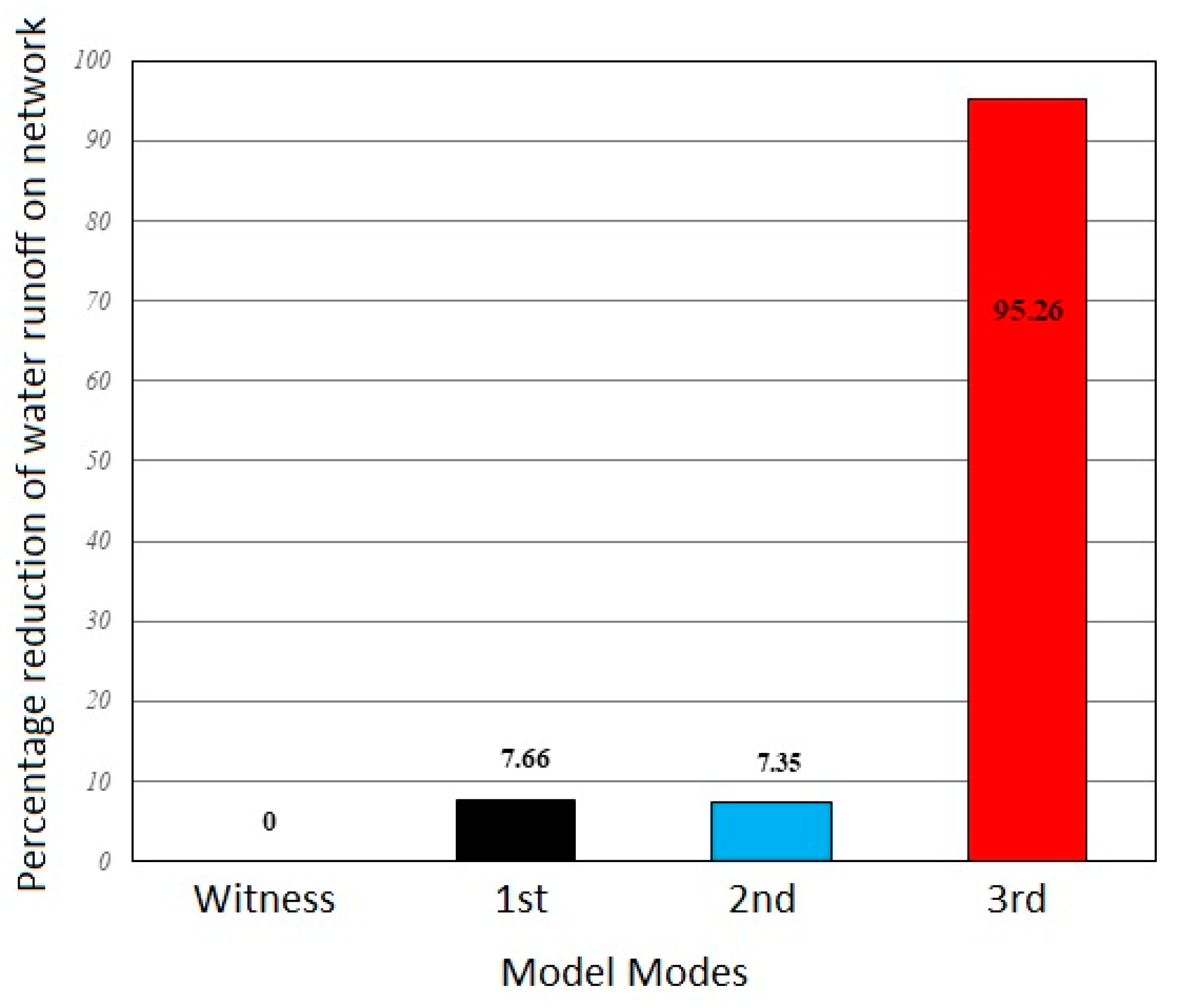
3. Results
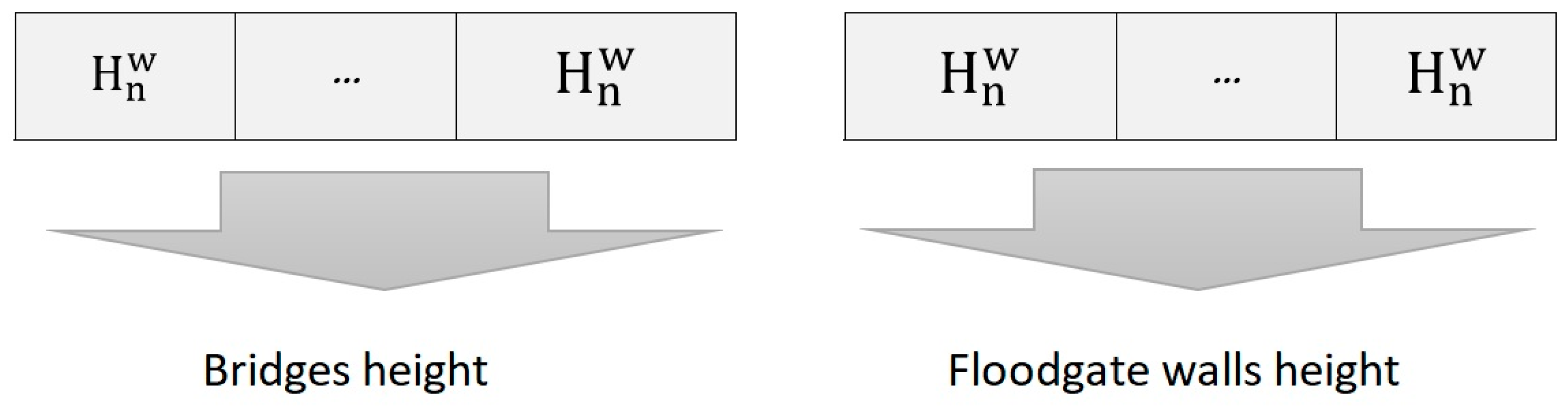
- The amount of height increase for the flood walls is defined for 16 intervals. In this variable, the corresponding channel is divided into 16 unequal parts, and the criterion is the increase in height in critical walls that may result in the overflow of the stormwater due to their low height. Increasing the height of these walls prevents water from escaping the network or minimizes its quantity (16 decision variables).
- The acceptable increase in channel width based on the required capacity for width expansion (16 decision variables).
- The increase in dimensions of cross-sectional structures or bridges (seven decision variables). In this case, based on field observations and comparing bridges that have the potential for modification, they are considered decision variables. Sometimes, the low height of the bridges increases the likelihood of water overflow from the channel and creating space for height variations in these cross-sectional structures or culverts, considering the necessary costs, can be a good option for reducing damages and the volume of water escaping from the corresponding channel.
- Since in some cases, the width of the bridges is smaller than the channel width, widening the bridges is considered a decision variable based on the maximum required capacity for expansion (seven decision variables).
- Scenario one considers only the increase in height and widening of bridges and cross-sectional structures along the selected channel path. The number of decision variables for this scenario is 14.
- Scenario two is the case where the increase in wall height and the widening of channels and bridges are considered at different intervals for the Chitgar River basin channel. Hence, the number of decision variables for this scenario is 32.
- Scenario three includes both previous scenarios, i.e., the increase in height for bridges and cross-sectional structures, wall height, and the widening of channels and bridges. The number of decision variables in scenario three is 46 (Table 3).
4. Discussion
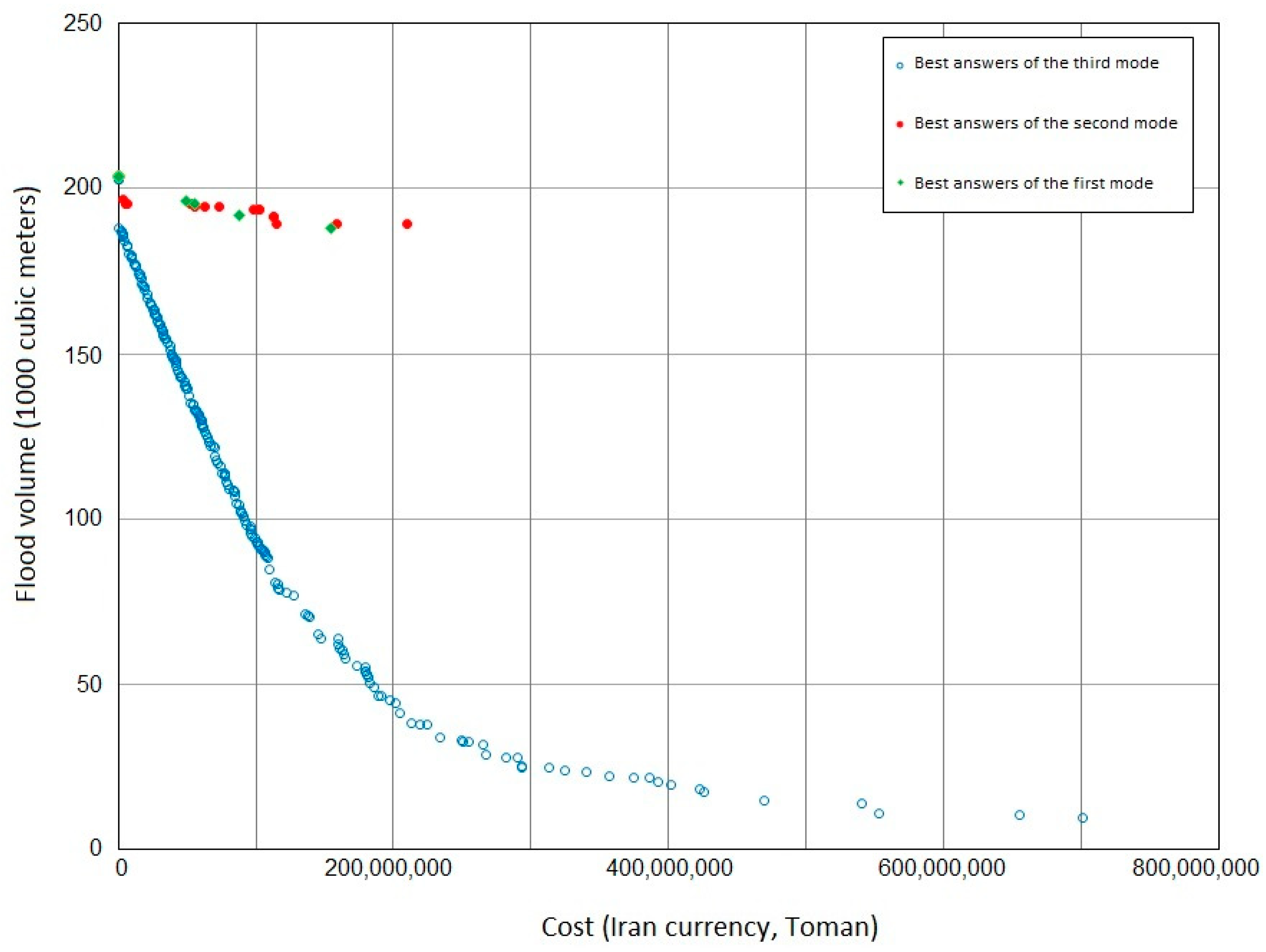
- Determining the final point based on the expected reduction in the flood volume in the study area.
- Determining the final point based on considering each of the first, second, and third scenarios, where changes are possible (generally based on the available resources of the municipality or relevant organizations for improvement in the objective function).
- Determining the final point based on a location on the curve that has an acceptable reduction in the flood volume, with a proportional decrease in the associated cost compared to the general state, and the potential for better cost-effective defense.
- Determining the final point based on the maximum approved budget for the Tehran urban stormwater management project.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NSDE | Non-dominated Sorting Differential Evolution |
| SVMM | Storm Water Management Model |
| RCS | Runoff Conveying System |
| MCS | Monte Carlo simulation |
| PSO | Particle Swarm Optimization |
| USDS | Urban Stormwater Drainage System |
| NSHS | Non-dominated Sorting Harmony Search |
| EPA | Environmental Protection Agency (US) |
| BMPs | Best Management Practices |
| SCS | Soil Conservation Service |
| DE | Differential Evolution algorithm |
| IDF | Intensity–Duration–Frequency |
| NRCS | National Resources Conservation Service |
References
- Ahmad, S.; Jia, H.; Chen, Z.; Li, Q.; Xu, C. Water-energy nexus and energy efficiency: A systematic analysis of urban water systems. Renew. Sustain. Energy Rev. 2020, 134, 110381. [Google Scholar] [CrossRef]
- Newman, J.P.; Dandy, G.C.; Maier, H.R. Multiobjective optimization of cluster-scale urban water systems investigating alternative water sources and level of decentralization. Water Resour. Res. 2014, 50, 7915–7938. [Google Scholar] [CrossRef]
- Sarbu, I. Optimization of urban water distribution networks using deterministic and heuristic techniques: Comprehensive review. J. Pipeline Syst. Eng. Pract. 2021, 12, 03121001. [Google Scholar] [CrossRef]
- Yin, D.; Xu, T.; Li, K.; Leng, L.; Jia, H.; Sun, Z. Comprehensive modelling and cost-benefit optimization for joint regulation of algae in urban water system. Environ. Poll. 2022, 296, 118743. [Google Scholar] [CrossRef] [PubMed]
- Bach, P.M.; Rauch, W.; Mikkelsen, P.S.; McCarthy, D.T.; Deletic, A. A critical review of integrated urban water modelling—Urban drainage and beyond. Environ. Model. Softw. 2014, 54, 88–107. [Google Scholar] [CrossRef]
- Dogani, A.; Dourandish, A.; Ghorbani, M.; Shahbazbegian, M.R. A hybrid meta-heuristic for a bi-objective stochastic optimization of urban water supply system. IEEE Access 2020, 8, 135829–135843. [Google Scholar] [CrossRef]
- Oraei Zare, S.; Saghafian, B.; Shamsai, A. Multi-objective optimization for combined quality–quantity urban runoff control. Hydrol. Earth Syst. Sci. 2012, 16, 4531–4542. [Google Scholar] [CrossRef]
- Azari, B.; Tabesh, M. Urban storm water drainage system optimization using a sustainability index and LID/BMPs. Sustain. Cities Soc. 2022, 76, 103500. [Google Scholar] [CrossRef]
- Yao, L.; Wei, W.E.I.; Yu, Y.; Xiao, J.; Chen, L. Rainfall-runoff risk characteristics of urban function zones in Beijing using the SCS-CN model. J. Geograph. Sci. 2018, 28, 656–668. [Google Scholar] [CrossRef]
- Chen, Y.; Samuelson, H.W.; Tong, Z. Integrated design workflow and a new tool for urban rainwater management. J. Environ. Manag. 2016, 180, 45–51. [Google Scholar] [CrossRef]
- Meilvang, M.L. From rain as risk to rain as resource: Professional and organizational changes in urban rainwater management. Curr. Soc. 2021, 69, 1034–1050. [Google Scholar] [CrossRef]
- Schuetze, T.; Chelleri, L. Integrating decentralized rainwater management in urban planning and design: Flood resilient and sustainable water management using the example of coastal cities in the Netherlands and Taiwan. Water 2013, 5, 593–616. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.; Hwang, S.; Kang, J. Urban flood adaptation and optimization for net-zero: Case study of Dongjak-gu, Seoul. J. Hydrol. Region. Stud. 2022, 41, 101110. [Google Scholar] [CrossRef]
- Baek, S.S.; Choi, D.H.; Jung, J.W.; Lee, H.J.; Lee, H.; Yoon, K.S.; Cho, K.H. Optimizing low impact development (LID) for stormwater runoff treatment in urban area, Korea: Experimental and modeling approach. Water Res. 2015, 86, 122–131. [Google Scholar] [CrossRef]
- Saraswat, C.; Kumar, P.; Mishra, B.K. Assessment of stormwater runoff management practices and governance under climate change and urbanization: An analysis of Bangkok, Hanoi and Tokyo. Environ. Sci. Policy 2016, 64, 101–117. [Google Scholar] [CrossRef]
- Jia, H.; Yao, H.; Yu, S.L. Advances in LID BMPs research and practice for urban runoff control in China. Front. Environ. Sci. Eng. 2013, 7, 709–720. [Google Scholar] [CrossRef]
- Ekka, S.A.; Rujner, H.; Leonhardt, G.; Blecken, G.T.; Viklander, M.; Hunt, W.F. Next generation swale design for stormwater runoff treatment: A comprehensive approach. J. Environ. Manag. 2021, 279, 111756. [Google Scholar] [CrossRef]
- Xu, D.; Lee, L.Y.; Lim, F.Y.; Lyu, Z.; Zhu, H.; Ong, S.L.; Hu, J. Water treatment residual: A critical review of its applications on pollutant removal from stormwater runoff and future perspectives. J. Environ. Manag. 2020, 259, 109649. [Google Scholar] [CrossRef]
- Sharma, R.; Vymazal, J.; Malaviya, P. Application of floating treatment wetlands for stormwater runoff: A critical review of the recent developments with emphasis on heavy metals and nutrient removal. Sci. Total Environ. 2021, 777, 146044. [Google Scholar] [CrossRef]
- Kayhanian, M.; Li, H.; Harvey, J.T.; Liang, X. Application of permeable pavements in highways for stormwater runoff management and pollution prevention: California research experiences. Int. J. Transport. Sci. Technol. 2019, 8, 358–372. [Google Scholar] [CrossRef]
- Tsihrintzis, V.A.; Hamid, R. Modeling and management of urban stormwater runoff quality: A review. Water Resour. Manag. 1997, 11, 136–164. [Google Scholar] [CrossRef]
- Huang, C.L.; Hsu, N.S.; Wei, C.C.; Luo, W.J. Optimal spatial design of capacity and quantity of rainwater harvesting systems for urban flood mitigation. Water 2015, 7, 5173–5202. [Google Scholar] [CrossRef]
- Hsieh, C.H.; Davis, A.P. Evaluation and optimization of bioretention media for treatment of urban storm water runoff. J. Environ. Eng. 2005, 131, 1521–1531. [Google Scholar] [CrossRef]
- Sharifan, R.A.; Roshan, A.; Aflatoni, M.; Jahedi, A.; Zolghadr, M. Uncertainty and sensitivity analysis of SWMM model in computation of manhole water depth and subcatchment peak flood. Proc. Soc. Behav. Sci. 2005, 21, 39–44. [Google Scholar] [CrossRef]
- Caradot, N.; Granger, D.; Chapgier, J.; Cherqui, F.; Chocat, B. Urban flood risk assessment using sewer flooding databases. Water Sci. Technol. 2011, 64, 832–840. [Google Scholar] [CrossRef]
- Yazdi, J.; Lee, E.H.; Kim, J.H. Stochastic multiobjective optimization model for urban drainage network rehabilitation. J. Water Resour. Plan. Manag. 2014, 141, 04014091. [Google Scholar] [CrossRef]
- Obaid, H.A.; Shamsuddin, S.; Basim, K.N.; Shreeshivadasan, C. Modeling sewer overflow of a city with a large floating population. Hydrol. Curr. Res. 2014, 5, 1. [Google Scholar]
- Li, C.; Wang, W.; Xiong, J.; Chen, P. Sensitivity analysis for urban drainage modeling using mutual information. Entropy 2014, 16, 5738–5752. [Google Scholar] [CrossRef]
- Yazdi, J.; Sadollah, A.; Lee, E.H.; Yoo, D.G.; Kim, J.H. Application of multi-objective evolutionary algorithms for the rehabilitation of storm sewer pipe networks. J. Flood Risk Manag. 2015, 10, 326–338. [Google Scholar] [CrossRef]
- Yazdi, J.; Yoo, D.G.; Kim, J.H. Comparative study of multi-objective evolutionary algorithms for hydraulic rehabilitation of urban drainage networks. Urban Water J. 2017, 14, 483–492. [Google Scholar] [CrossRef]
- Hooshyaripor, F.; Yazdi, J. A new methodology for surcharge risk management in urban areas (case study: Gonbad-e-Kavus city). Water Sci. Technol. 2017, 75, 823–832. [Google Scholar] [CrossRef] [PubMed]
- Housh, M. Non-probabilistic robust optimization approach for flood control system design. Environ. Model. Soft. 2017, 95, 48–60. [Google Scholar] [CrossRef]
- Khaleghi, E.; Sadoddin, A.; Najafinejad, A.; Bahremand, A. Flood hydrograph simulation using the SWMM model: A semiarid zone watershed case study, Shiraz Khoshk River, Iran. Nat. Resour. Model. 2020, 33, e12269. [Google Scholar] [CrossRef]
- Basnet, K.; Khadka, S.; Shrestha, K.K. Sustainable Urban Storm Water Drainage Design using SWMM: A Case Study of Lamachaur, Pokhara, Nepal. Res. Inv. Int. J. Eng. Sci. 2020, 10, 1–12. [Google Scholar]
- Annisa, N.; Prasetia, H.; Sholihah, Q. Potential of carbonized rice husk as a filter media rain garden to decrease the turbidity of water and Coli bacteria in the Stormwater Runoff. a review of current research. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1011, 012013. [Google Scholar] [CrossRef]
- Wang, J.; Meng, Q.; Zou, Y.; Qi, Q.; Tan, K.; Santamouris, M.; He, B.J. Performance synergism of pervious pavement on stormwater management and urban heat island mitigation: A review of its benefits, key parameters, and co-benefits approach. Water Res. 2022, 221, 118755. [Google Scholar] [CrossRef] [PubMed]
- McDonald, W. Drones in urban stormwater management: A review and future perspectives. Urban Water J. 2019, 16, 505–518. [Google Scholar] [CrossRef]
- Wang, S.; Ma, Y.; Zhang, X.; Shen, Z. Transport and sources of nitrogen in stormwater runoff at the urban catchment scale. Sci. Total Environ. 2022, 806, 150281. [Google Scholar] [CrossRef]
- Tuomela, C.; Sillanpää, N.; Koivusalo, H. Assessment of stormwater pollutant loads and source area contributions with storm water management model (SWMM). J. Environ. Manag. 2019, 233, 719–727. [Google Scholar] [CrossRef] [PubMed]
- Panos, C.L.; Wolfand, J.M.; Hogue, T.S. SWMM sensitivity to LID siting and routing parameters: Implications for stormwater regulatory compliance. JAWRA J. Am. Water Resour. Assoc. 2020, 56, 790–809. [Google Scholar] [CrossRef]
- Liu, G.; Qin, H.; Tian, R.; Tang, L.; Li, J. Non-dominated sorting culture differential evolution algorithm for multi-objective optimal operation of Wind-Solar-Hydro complementary power generation system. Glob. Energy Intercon. 2019, 2, 368–374. [Google Scholar] [CrossRef]
- Heydari Mofrad, H.; Yazdi, J. An enhanced multi-objective evolutionary algorithm for the rehabilitation of urban drainage systems. Eng. Optimiz. 2022, 54, 349–367. [Google Scholar] [CrossRef]
- Tabarzadi, A.; Jourgholami, M.; Moghaddam Nia, A.; Majnounian Garagiz, B.; Attarod, P. Evaluation of the effect of forest cover on quantitative and qualitative runoff parameters in Chitgar Forest Park Watershed, Tehran. J. Range Watershed Manag. 2019, 71, 997–1011. [Google Scholar]
- Estalaki, S.M.; Kerachian, R.L.; Nikoo, M.R. Developing water quality management policies for the Chitgar urban lake: Application of fuzzy social choice and evidential reasoning methods. Environ. Earth Sci. 2016, 75, 1–16. [Google Scholar] [CrossRef]
- Rossman, L. Storm Water Management Model User’s Manual: Version 5.0, EPA/600/R-05/040; National Risk Management Research Laboratory: Cincinnati, OH, USA, 2008. [Google Scholar]
- Gironás, J.; Roesner, L.A.; Rossman, L.A.; Davis, J. A new applications manual for the Storm Water Management Model (SWMM). Environ. Model. Soft. 2010, 25, 813–814. [Google Scholar] [CrossRef]
- Jang, S.; Cho, M.; Yoon, J.; Yoon, Y.; Kim, S.; Kim, G.; Aksoy, H. Using SWMM as a tool for hydrologic impact assessment. Desalination 2007, 212, 344–356. [Google Scholar] [CrossRef]
- Abi Aad, M.P.; Suidan, M.T.; Shuster, W.D. Modeling techniques of best management practices: Rain barrels and rain gardens using EPA SWMM-5. J. Hydrol. Eng. 2010, 15, 434–443. [Google Scholar] [CrossRef]
- Babaei, S.; Ghazavi, R.; Erfanian, M. Urban flood simulation and prioritization of critical urban sub-catchments using SWMM model and PROMETHEE II approach. Phy. Chem. Earth Parts A/B/C 2018, 105, 3–11. [Google Scholar] [CrossRef]
- MGCE. Tehran Stormwater Management Master Plan, Vol 2, Part 3: Urban Food Hydrology & Sediment Load; Mahab Ghods Consultant Engineers, Technical and Development Deputy of Tehran Municipality: Tehran, Iran, 2011. [Google Scholar]
- MGCE. Tehran Stormwater Management Master Plan, Vol 2: Basic Studies, Part 1: Meteorology; Mahab Ghods Consultant Engineers, Technical and Development Deputy of Tehran Municipality: Tehran, Iran, 2011. [Google Scholar]
- USACE. Hydrologic Modelling System HEC-HMS, Quick Start Guide, Version 4.0; Institute for Water Resources Hydrologic Engineering Center: Davis, CA, USA, 2008. [Google Scholar]
- Yazdi, J.; Mohammadiun, S.; Sadiq, R.; Neyshabouri, S.S.; Gharahbagh, A.A. Assessment of different MOEAs for rehabilitation evaluation of Urban Stormwater Drainage Systems–Case study: Eastern catchment of Tehran. J. Hydro-Environ. Res. 2018, 21, 76–85. [Google Scholar] [CrossRef]
- Lord, S.A.; Ghasabsaraei, M.H.; Movahedinia, M.; Shahdany, S.M.H.; Roozbahani, A. Redesign of stormwater collection canal based on flood exceedance probability using the ant colony optimization: Study area of eastern Tehran metropolis. Water Sci. Technol. 2021, 84, 820–839. [Google Scholar] [CrossRef]
- Yazdi, J.; Khazaei, P. Copula-based performance assessment of online and offline detention ponds for urban stormwater management. J. Hydrol. Eng. 2019, 24, 04019025. [Google Scholar] [CrossRef]
- Shariat, R.; Roozbahani, A.; Ebrahimian, A. Risk analysis of urban stormwater infrastructure systems using fuzzy spatial multi-criteria decision making. Sci. Total Environ. 2019, 647, 1468–1477. [Google Scholar] [CrossRef] [PubMed]
- Mani, M.; Bozorg-Haddad, O.; Loáiciga, H.A. A new framework for the optimal management of urban runoff with low-impact development stormwater control measures considering service-performance reduction. J. HydroInform. 2019, 21, 727–744. [Google Scholar] [CrossRef]
- Azadi, A.; Esmatkhah Irani, A.; Azarafza, M.; Hajialilue Bonab, M.; Sarand, F.B.; Derakhshani, R. Coupled numerical and analytical stability analysis charts for an earth-fill dam under rapid drawdown conditions. Appl. Sci. 2022, 12, 4550. [Google Scholar] [CrossRef]
- Rahnama-Rad, J.; Bavali, M.Y.; Derakhshani, R. Optimization of hydraulic parameters of Iranshahr alluvial aquifer. Am. J. Environ. Sci. 2010, 6, 477–483. [Google Scholar] [CrossRef][Green Version]





| No. | Parameter | Value |
|---|---|---|
| 1 | Population Size | 100 |
| 2 | Mutation Rate | 0.5 |
| 3 | Crossover Rate | 0.9 |
| 4 | Scaling Factor | 0.8 |
| 5 | Maximum Generations | 200 |
| 6 | Termination Criteria | Convergence or Maximum Generations Reached |
| Height (m) | Return Periods (Years) | ||||||
|---|---|---|---|---|---|---|---|
| 2 | 5 | 10 | 20 | 25 | 50 | 100 | |
| 900 | 99 | 127 | 148 | 169 | 176 | 197 | 218 |
| 1000 | 108 | 138 | 161 | 184 | 191 | 214 | 236 |
| 1100 | 117 | 149 | 174 | 198 | 206 | 231 | 255 |
| 1200 | 125 | 160 | 187 | 213 | 221 | 248 | 274 |
| 1300 | 134 | 171 | 199 | 228 | 237 | 265 | 293 |
| 1400 | 143 | 182 | 212 | 242 | 252 | 282 | 312 |
| 1500 | 151 | 193 | 225 | 257 | 267 | 299 | 331 |
| 1600 | 160 | 204 | 238 | 272 | 283 | 316 | 350 |
| 1700 | 168 | 215 | 251 | 286 | 298 | 333 | 369 |
| 1800 | 177 | 226 | 264 | 301 | 313 | 350 | 388 |
| 1900 | 186 | 238 | 277 | 316 | 328 | 368 | 407 |
| 2000 | 194 | 249 | 290 | 330 | 344 | 385 | 426 |
| 2100 | 203 | 260 | 302 | 345 | 359 | 402 | 445 |
| 2200 | 212 | 271 | 315 | 360 | 374 | 419 | 463 |
| 2300 | 220 | 182 | 328 | 375 | 389 | 436 | 482 |
| 2400 | 229 | 293 | 341 | 389 | 405 | 453 | 501 |
| 2500 | 238 | 304 | 354 | 404 | 420 | 470 | 520 |
| Case | Number of Channels | Number of Bridges | Number of Decision Variables |
|---|---|---|---|
| 1 | - | 14 | 14 |
| 2 | 32 | - | 32 |
| 3 | 32 | 14 | 46 |
| No | Variable | Value (m) | No | Variable | Value (m) | No | Variable | Value (m) |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.84 | 17 | 0.10 | 33 | 0.16 | |||
| 2 | 0.00 | 18 | 0.18 | 34 | 0.69 | |||
| 3 | 0.11 | 19 | 0.13 | 35 | 0.12 | |||
| 4 | 0.08 | 20 | 0.10 | 36 | 0.11 | |||
| 5 | 0.13 | 21 | 0.48 | 37 | 0.00 | |||
| 6 | 1.40 | 22 | 1.13 | 38 | 0.39 | |||
| 7 | 0.45 | 23 | 0.11 | 39 | 0.11 | |||
| 8 | 0.29 | 24 | 0.00 | 40 | 0.04 | |||
| 9 | 0.07 | 25 | 0.11 | 41 | 0.11 | |||
| 10 | 0.08 | 26 | 0.12 | 42 | 1.71 | |||
| 11 | 0.48 | 27 | 0.00 | 43 | 0.12 | |||
| 12 | 0.57 | 28 | 0.10 | 44 | 0.14 | |||
| 13 | 0.11 | 29 | 0.11 | 45 | 1.56 | |||
| 14 | 0.02 | 30 | 0.16 | 46 | 0.09 | |||
| 15 | 0 | 31 | 0.59 | |||||
| 16 | 0.22 | 32 | 0 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cemiloglu, A.; Zhu, L.; Chen, B.; Lu, L.; Nanehkaran, Y.A. Enhancing Urban Surface Runoff Conveying System Dimensions through Optimization Using the Non-Dominated Sorting Differential Evolution (NSDE) Metaheuristic Algorithm. Water 2023, 15, 2927. https://doi.org/10.3390/w15162927
Cemiloglu A, Zhu L, Chen B, Lu L, Nanehkaran YA. Enhancing Urban Surface Runoff Conveying System Dimensions through Optimization Using the Non-Dominated Sorting Differential Evolution (NSDE) Metaheuristic Algorithm. Water. 2023; 15(16):2927. https://doi.org/10.3390/w15162927
Chicago/Turabian StyleCemiloglu, Ahmed, Licai Zhu, Biyun Chen, Li Lu, and Yaser A. Nanehkaran. 2023. "Enhancing Urban Surface Runoff Conveying System Dimensions through Optimization Using the Non-Dominated Sorting Differential Evolution (NSDE) Metaheuristic Algorithm" Water 15, no. 16: 2927. https://doi.org/10.3390/w15162927
APA StyleCemiloglu, A., Zhu, L., Chen, B., Lu, L., & Nanehkaran, Y. A. (2023). Enhancing Urban Surface Runoff Conveying System Dimensions through Optimization Using the Non-Dominated Sorting Differential Evolution (NSDE) Metaheuristic Algorithm. Water, 15(16), 2927. https://doi.org/10.3390/w15162927








