An Improved ResNet-Based Algorithm for Crack Detection of Concrete Dams Using Dynamic Knowledge Distillation

Abstract

Crack detection is an important component of dam safety monitoring. Detection methods based on deep convolutional neural networks (DCNNs) are widely used for their high efficiency and safety. Most existing DCNNs with high accuracy are too complex for users to deploy for real-time detection. However, compressing models face the dilemma of sacrificing detection accuracy. To solve this dilemma, an improved residual neural network (ResNet)-based algorithm for concrete dam crack detection using dynamic knowledge distillation is proposed in this paper in order to obtain higher accuracy for small models. To see how well distillation works, preliminary experiments were carried out on mini-ImageNet. ResNet18 was trained by adding additional tasks to match soft targets generated by ResNet50 under dynamic high temperatures. Furthermore, these pre-trained teacher and student models were transferred to experiments on concrete crack detection. The results showed that the accuracy of the improved algorithm was up to 99.85%, an increase of 4.92%.

1. Introduction

Concrete structures are widely used in the construction of dams because of their high compressive strength. Under the influence of external forces [1] such as cyclic loads, temperature changes, and destructive earthquakes during long-term service, their surfaces are prone to cracks. In addition, cavitation [2,3,4,5] plays a significant role in dam damage. The development of cracks will destroy the integrity of concrete structures, which will cause leakage problems and affect the overall strength and stability of structures. Even worse, dams will end up in catastrophic accidents such as collapses and dam breaks. Therefore, crack detection is essential for the safety inspection of concrete dams to detect faults and repair them in a timely manner.

Historically, crack detection in concrete dams mainly depended on manual inspection. However, the results of manual detection are highly subjective, time-consuming, and laborious in the case of extensive fracture data. In addition, reservoir dams are primarily built in mountainous or hilly areas with complex terrain conditions, resulting in poor efficiency and safety in the detection process, especially in harsh environmental conditions such as underwater, where localization is even more prominent. In order to reduce the limitations of naked-eye observation and improve detection accuracy and efficiency, automatic detection technologies have emerged, such as vibrating wire sensors, fiber grating sensors, acoustic emission equipment, etc. However, these detection methods must determine where cracks are in advance, and their detection area is significantly small. In recent years, with the improvement of computer equipment performance and the rapid development of computer vision technology, crack detection methods based on artificial intelligence and deep learning have ushered in a tumultuous period of growth. Crack images of concrete structures are collected by image acquisition systems such as unmanned aerial vehicles (UAV) [6] and underwater detection robots and then processed by digital image processing techniques [7] or deep learning methods to classify and identify whether there are cracks in these images. Among them, image classification methods based on deep convolutional neural networks (DCNNs) are superior to digital image processing methods that rely on manual intervention and discrimination because they automatically extract image features. They have brought a series of breakthroughs in image classification and are widely used in crack detection.

Because of the complexity of computing, memory, and storage requirements, the training phase of the networks is performed on CPU or GPU clusters in a distributed computing environment. These networks, however, typically involve large models with numerous parameters. Once trained, a challenging aspect is the deployment of the trained models on resource-constrained inference systems such as portable devices, including underwater detection robots, as mentioned above, or sensor networks, and on applications in which real-time predictions are required. Performing inference on edge devices comes with severe memory, computing, and power constraints. We hope to deploy deep neural networks for real-time operations, which have more stringent requirements for latency and computing resources. We need to use smaller models to extract structures from less abundant data sets without losing accuracy.

Quantization using low-precision numerics [8,9,10] and model compression [11] have emerged as popular solutions for resource-constrained deployment scenarios. With quantization, a low-precision version of the network model is generated and deployed on the device. Operating in lower precision mode reduces computation, data movement, and storage requirements. However, the majority of existing works in low-precision DCNNs sacrifice accuracy over the baseline full-precision networks [12]. Therefore, we propose an improved DCNN crack detection algorithm using knowledge distillation. A smaller, low-memory footprint network is trained to mimic the behavior of the original complex network, “transferring” knowledge from the complex network to the smaller network, compressing the model without reducing accuracy, and allowing the smaller network to achieve accuracy equivalent to or slightly better than the original complex model.

The knowledge distillation system consists of a teacher network (large model) and a student network (small model). The category probability generated by the teacher model under high temperature is used as the “soft target” for training the student model, and knowledge is transferred from the large model in the training stage to the small model that is more suitable for deployment to obtain more accurate crack detection results on the small model [13,14]. It is necessary to select appropriate teacher networks and student networks for crack detection to ensure the benchmark accuracy of the knowledge distillation system. Common neural networks for crack detection include LeNet [15], AlexNet [16], VGG-Net [17], etc. These DCNNs improve model accuracy by increasing the depth of networks. However, as network layers continue to rise, training accuracy and testing accuracy rapidly decline when network layers increase to a certain number, indicating that the deeper these networks continue to grow, the more activation functions are introduced and the more discretely data are mapped, making it difficult to return to the origin space (also known as identity transformation), which means that DCNNs have a degradation problem. Therefore, residual neural networks (ResNet) are introduced as the basic framework of the improved crack detection algorithm. By adding a short-cut connection (also known as a residual connection) to nonlinear convolution layers, ResNet improves the efficiency of information dissemination and solves the problem of degradation. With ResNet50 used as the teacher model and ResNet18 used as the student model, knowledge distillation is performed to ensure basic accuracy.

On the other hand, scholars have continuously improved DCNNs used in crack detection, but they are all oriented toward enhancing their accuracy. Although the accuracy of these models has improved, there is still a large gap between the accuracy of training sets and validation sets, indicating that there is still considerable room for improvement in the generalization ability of networks. The improved algorithm has better model generalization ability, which is also a contribution to this paper.

In addition, the most critical parameter in knowledge distillation systems is distillation temperature [18,19,20,21,22]. However, current work generally uses fixed temperature parameters, which are usually set to 4. Although some research and experiments have verified this empirical value, it does not apply to all knowledge distillation tasks and models. For specific tasks, if one wants to match the soft targets of the teacher model and the student models’ soft targets under the optimal temperature parameters, an exhausting search method is required, which poses a great challenge to computing resources and efficiency. In this context, we propose a dynamic temperature search method for knowledge distillation, adding an adversarial dynamic temperature module. As the main contribution of this paper, the proposed method makes it possible for the network to adjust temperature parameters by itself, and in each epoch of training, a suitable temperature can be found for distillation.

It is worth noting that the initial training samples of this algorithm were not concrete crack datasets because this type of dataset has a relatively small size and a single type, which are sometimes not easy to obtain. Applying this algorithm directly to concrete crack datasets for classification cannot guarantee a satisfactory training result. Therefore, preliminary experiments were carried out on mini-ImageNet and then transferred their training results to experiments on concrete crack detection to ensure more accurate detection of concrete cracks. Through experiments, the contribution of transfer learning (pretraining) to the improvement of model accuracy was proven.

This paper is organized as follows: Section 2 explains the proposed methodology, including knowledge distillation and transfer learning; Section 3 illustrates preliminary experiments conducted on mini-ImageNet and discusses the findings; Section 4 transfers the improved algorithm pre-trained in Section 3 to crack detection and discusses the results; and Section 5 applies the improved algorithm to the crack detection task of HKC Dam. Finally, Section 6 discusses the main conclusions.

2. Methodology

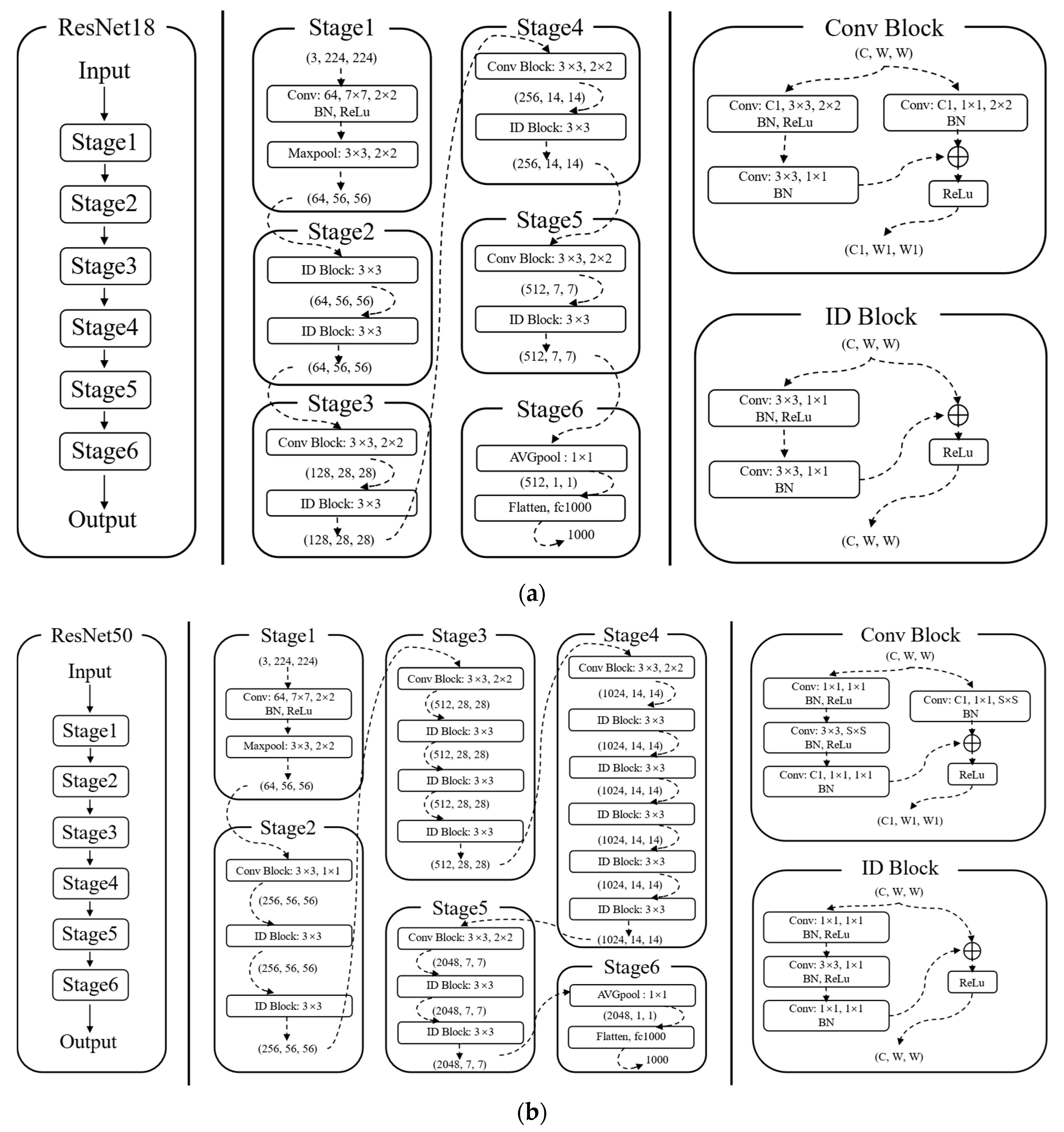
2.1. ResNet-Based Dynamic Knowledge Distillation Architecture

Large DCNNs have achieved remarkable success with good performance, especially in cases with large-scale data, because the over-parameterization improves the generalization performance when new data are considered [23,24,25,26]. With the significant breakthrough of DCNNs in image classification, much research has emerged that applies them to crack detection. However, deploying deep models on mobile devices and embedded systems is a great challenge due to the devices’ limited computational capacity and memory. Model compression [11] was proposed to address this issue by transferring the information from a large model or an ensemble of models into training a small model without a significant drop in accuracy. The improved algorithm using dynamic knowledge distillation proposed in this paper regards large models as “teachers” and small models as “students”. In this algorithm, a small student model is generally supervised by a large teacher model [27,28,29], and a temperature parameter [28] is introduced into the softmax function. Taking the probability distribution generated by the teacher model as “soft targets” for training the student model, it can be softened by adjusting the temperature. Soft targets usually have high entropy, providing much more information for each training case than hard targets, and the gradient variance between training cases is much smaller. If the student model is trained at the same temperature, it can learn such knowledge from the teacher model, achieving competitive and even superior performance.

A knowledge distillation system is composed of three key components: teacher-student architecture, knowledge, and distillation loss. A general framework for knowledge distillation is shown in Figure 1.

As seen in Figure 1, in the process of knowledge distillation, a teacher model with a complex network structure needs to be trained on datasets at a high temperature in advance. Thereafter, a simplified student network must be guided to carry out the same task at the same temperature and at a low temperature for model migration. Neural networks typically use a converted softmax output layer to generate class probabilities. The difference among probability distributions is significantly small. Generally, softmax classifiers use an exponential function to amplify the gap between logits. After standardizing these logits, it will output a one-hot vector, which is also called a hard target. One variable of the one-hot vector equals 1, indicating that the input data belongs to a specific class, while the other variables are all 0, containing too little information, which is not conducive to the optimization of the network. Knowledge distillation provides a generalized softmax function to soften the output:

$$q_i=\frac{exp(z_i/T)}{{\sum }_1^{N}exp(z_i/T)}$$

(1)

where $z_i$ represents logits generated by networks, $q_i$ is a soft target, and T is a temperature usually set to 1. Using a higher T will produce a softer probability distribution over classes.

The temperature represents the softening degree of targets. When T approaches 0, the softmax function is still the standard softmax function and will still output a one-hot vector without the softening effect. When T approaches infinity, the output of the softmax function will be very soft, and more adequate information can be obtained from soft targets. Therefore, when training the teacher network, a higher T was set to make the output of softmax sufficiently soft target, and the output of the student network at the same temperature would be close to the teacher model. Finally, we trained the student network again at the normal temperature (T = 1) to output hard targets.

2.1.1. Selection of Appropriate Teacher and Student Models

DCNNs are continuously optimized by various means to improve detection accuracy, most of which are to deepen the networks. In a network without residual blocks, the deeper the network is, the stronger its learning ability should become. However, in practice, features learned from input data are often far from those we need because of gradient disappearance or explosion. The network needs to be improved to make it, once deepened, still extract more valuable features for training that are not worse than the shallower networks.

In this paper, two residual neural networks [30] with different depths were introduced as the teacher model and student model for knowledge distillation to solve the problem that the classification effect of convolutional neural networks deteriorates with the increase of depth and ensure the benchmark accuracy of subsequent experiments.

Taking a two-layer neural network as an example, as shown in Figure 2, the left part of the figure is an ordinary neural network, while the right one is a residual neural network. The main path of a common neural network is to input an x into the network. After two weight layers and one ReLU nonlinear activation, F(x) is outputted. Thereafter, F(x) is used as a new input to experience the next ReLU nonlinear activation. The difference between an ordinary neural network and a residual neural network is that there is an additional shortcut connection in the latter one. The input x of the residual neural network enters the deeper layer along with the output F(x) of its last layer, which acts together on the subsequent ReLU nonlinear activation function, forming a residual block. The curved arrow in Figure 2 is a “shortcut”, which means that the input x should not only go through the main path of the ordinary neural network but also affect the deeper network with the output F(x). A convolutional neural network with such shortcut connections is a residual block, and several residual blocks constitute ResNet.

The structures of ResNet18 and ResNet50 are shown in Figure 3. They are divided into six stages. The first stage is convolution and maximum pooling once data are input. Data are convolved with residual blocks from the second to the fifth stage. Each stage has two different basic residual blocks: the Conv Block and the Identity Block (ID Block). The data are convolved three times in each residual block. Conv Blocks’ function is to change the dimension of the network, so the input and output dimensions of these blocks are different and cannot be connected in series. In contrast, ID Blocks’ input and output dimensions are the same, so they can be concatenated to deepen the network. In the sixth stage, data are pooled globally and flattened, and then data can be classified. The structure of ResNet18 is quite similar to that of ResNet50. The only difference is that the number of residual blocks differs from [2, 2, 2, 2] to [3, 4, 6, 3].

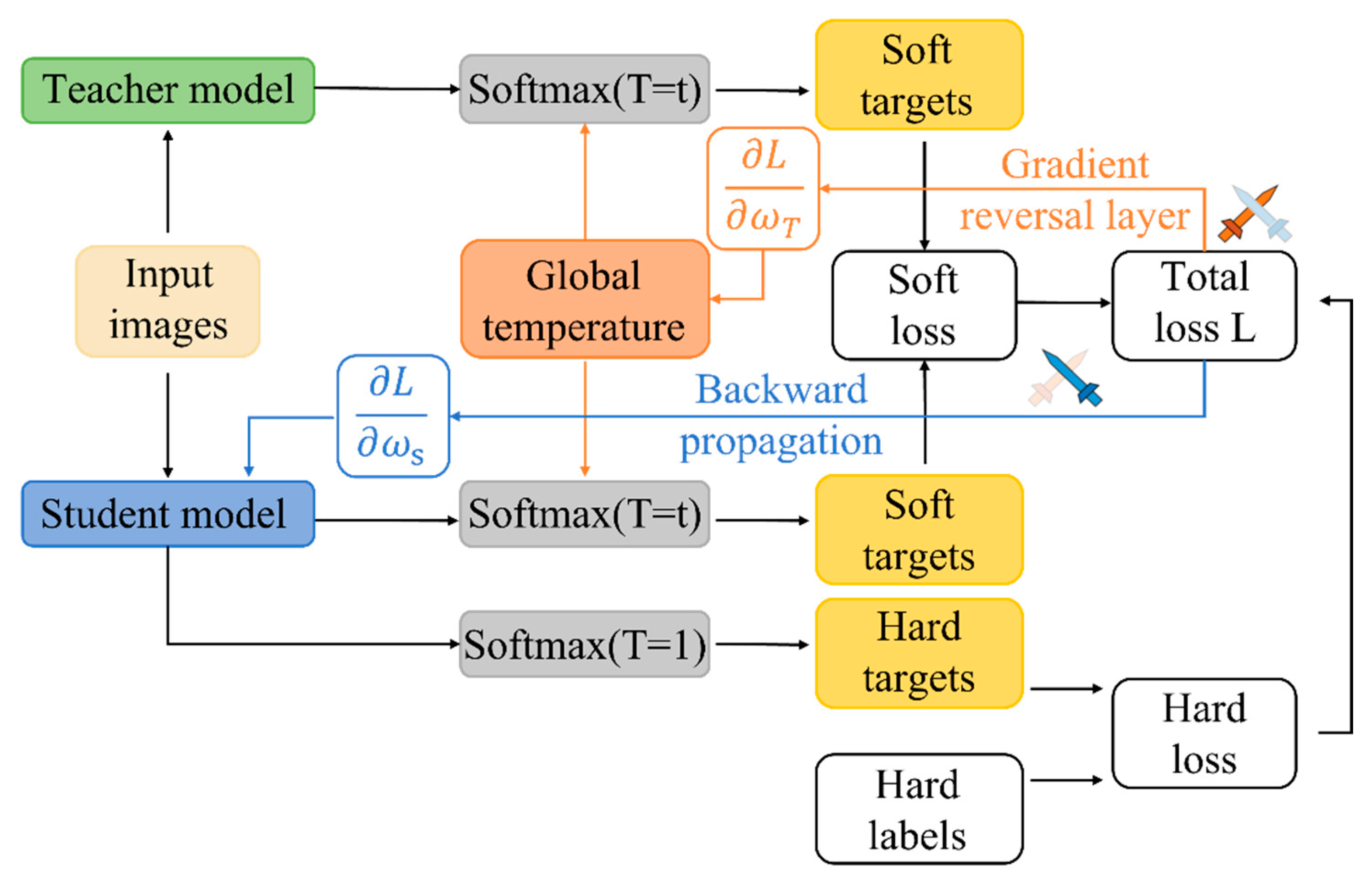
2.1.2. Distillation Loss Function

Knowledge distillation aims to minimize the difference between the output of the student network and that of the teacher network. A distillation loss function can quantify this objective. As shown in Figure 1, the loss function in the distillation process consists of distillation loss (soft loss) and student loss (hard loss).

When the correct labels are known for all or some of the datasets, this method can be significantly improved by training the distilled model (the student model) to produce the correct labels. One way to achieve this is to use the correct labels to modify the soft targets, but we found that a better way is to simply use a weighted average of two different objective functions.

$$L=\mathsf{\alpha }{L}_{\mathrm{soft}}+(1-\mathsf{\alpha })L_{\mathrm{hard}}$$

(2)

here, $L_{\mathrm{soft}}$ is the first objective function, representing the cross entropy with the soft targets, and this cross-entropy is computed using the same high temperature in the softmax of the distilled model as was used for generating the soft targets from the cumbersome teacher model. The formula is as follows:

$$L_{\mathrm{soft}}=-{\sum }_1^N{t}_i^{T}log\left(s_i^T\right)$$

(3)

where N represents the total number of labels/classes, and $t_i^T$ and $s_i^T$ are soft targets of the teacher and student models in class i when the temperature is T. The formulae to calculate $t_i^T$ and $s_i^T$ are as follows:

$$t_i^T=\frac{exp(u_i/T)}{{\sum }_1^{N}exp(u_i/T)}$$

(4)

$$s_i^T=\frac{exp(v_i/T)}{{\sum }_1^{N}exp(v_i/T)}$$

(5)

where $u_i$ and $v_i$ represent the logits of teacher and student networks, respectively.

The second objective function is $L_{\mathrm{hard}}$. It represents the cross-entropy with the correct labels (hard labels). It is computed using exactly the same logits in the softmax function of the distilled model, but at a temperature of 1:

$$L_{\mathrm{hard}}=-{\sum }_1^N{c}_i\frac{v_i}{{\sum }_1^{N}exp\left(v_i\right)}$$

(6)

where $c_i$ represents the correct label on class j. In $c_i\in \left\{\mathrm{0,1}\right\}$ 1 is the positive label and 0 is the negative one.

Since the magnitudes of the gradients produced by the soft targets scale as 1/T², it is essential to multiply them by T² when considering soft loss. This ensures that the relative contributions of the hard and soft targets remain roughly unchanged if the temperature used for distillation is changed while experimenting with meta-parameters.

2.1.3. Dynamic Temperature for Knowledge Distillation

For a knowledge distillation system, the temperature parameter controls the smoothness of two prediction results and determines the distance between two probability distributions. The higher the temperature is, the smoother the probability distribution will be; otherwise, the closer the temperature is to zero, the sharper the probability distribution will be. At the same time, temperature affects how difficult it is for the student model to mimic the teacher model during the distillation process. Different distillation results will be produced at different temperatures. The common method in existing work is to use a fixed temperature parameter, generally set to 4.

However, the optimal temperature parameter for different distillation systems for various tasks is not necessarily equal to 4. Suppose we want to find the optimal temperature parameter for a specific task. In that case, we need to perform an exhaustive search, which will result in a large amount of computation, and the entire training process is very inefficient. At the same time, maintaining a static and fixed temperature parameter is not the best choice for student models. Based on curriculum learning [31], humans learn from simplicity to difficulty in the learning process. We also hope to form a step-by-step distillation difficulty model for the student during the distillation process.

Therefore, we propose to dynamically adjust the temperature during the training process by adding an antagonistic dynamic temperature module, making it possible for the network to automatically select a suitable temperature for distillation in each training epoch. After adding the dynamic temperature module, the overall architecture of knowledge distillation is shown in Figure 4.

As shown in Figure 4, a dynamic temperature parameter is implemented through a nonparametric gradient reverse layer (GRL) to satisfy the need for confrontation: inserting a GRL between the softmax layer and the learnable temperature module and using the GRL to reverse the gradient of the learnable temperature parameter to amplify the distillation loss between the student and teacher model when the student network is trained to minimize distillation loss. The effect of confrontation can be achieved very directly in this case. The inverse gradient’s weight rises with training progress, thereby increasing the learning difficulty.

After adding the dynamic temperature module, the target function of distillation loss is modified as follows:

$$\underset{{\omega }_s}{\min }\underset{{\omega }_T}{\max }L=\underset{{\omega }_s}{\min }\underset{{\omega }_T}{\max }\sum _{x\in D}\mathsf{\alpha }{L}_{\mathrm{soft}}\left(f^t\left(x;{\omega }_t\right),f^s\left(x;{\omega }_s\right),{\omega }_T\right)+(1-\mathsf{\alpha })L_{\mathrm{hard}}\left(f^s\left(x;{\omega }_s\right),y\right)$$

(7)

The formula above can be solved by alternating algorithms: fixing one set of variables, solving another set of variables, and alternating between solving subproblems related to these two variables. The relevant pseudocode is shown in Algorithm 1.

Algorithm 1: Implementation of Dynamic Distillation

Input: Training dataset D; Total training epoch M; Pre-trained Teacher ${\omega }_t$; Learnable Temperature Module ${\omega }_T$

Output: Distilled Student ${\omega }_s$

Initialize: Epoch m = 1; Randomly initialize: ${\omega }_T$, ${\omega }_s$

while m ≤ M do

for batch x in D do

Forward propagation through ${\omega }_t$ and ${\omega }_s$ to obtain predictions $f^t\left(x;{\omega }_t\right),f^s\left(x;{\omega }_s\right)$

Obtain temperature T by ${\omega }_T$

Calculate the loss L and update ${\omega }_s$ and ${\omega }_T$ by backward propagation

end for

m = m + 1;

end while

In the dynamic temperature module, we use a global temperature, adapting the same temperature to all instances to be predicted. This efficient version does not incur additional computational costs for the distillation process because it involves only one learnable parameter.

2.2. Transfer Learning

In some deep learning scenarios, the cost of directly training the target task is too high, and the dataset provided by the target task is too small to support deep learning and achieve good results. For example, there had not yet been a set of crack images with rich samples for non-destructive crack detection of concrete structures, the research object of this chapter. Therefore, we expected that the model trained in advance on the task with sufficient samples could be directly applied to the new target task.

Transfer learning [32,33] is an effective method to solve training tasks without rich samples in computer vision. The training set and the test set do not need to meet the assumption of independent and identical distribution, so they can extract the common or essential features between two different but correlational tasks and use the common features to realize the mutual transfer of learning ability between these two tasks. The network in the target task also does not need to start training from scratch but extracts high-dimensional semantic features to complete the target task based on the common features mined in the source task. This shortens the training time and achieves considerable performance even with a small amount of data in the target task because it does not need a large number of training data to obtain features. In short, transfer learning can obtain common invariants from the source task and transfer them to the target task.

Transfer learning can be divided into sample transfer, feature transfer, and parameter/model transfer according to different learning objects [34]. The crack detection algorithm established in this paper mainly includes a backbone coding module and a classification module. The backbone coding module is primarily composed of multiple convolutional and pooling layers for feature coding. The classification module mainly consists of numerous fully connected layers whose primary function is to output the probability distribution of each category to achieve final results. The shallow convolutional layers near the input layer in the backbone coding module are suitable for extracting common features. In contrast, the deeper convolutional and classification layers are ideal for mining specific personality features. When the pre-trained network of the source task is transferred to the target task, the weight and bias parameters of the classification module need to be removed and redesigned to suit the target task. Therefore, the parameter/model transfer method was used in this chapter. Firstly, an improved image classification model on mini-ImageNet with excellent performance was trained. Secondly, its structure and parameters were frozen for invocation as the backbone coding module for feature extraction in the target task of crack detection. Thirdly, some important hyperparameters were fine-tuned, and the structure of the fully connected layer was modified to a two-classifier for crack detection. Thus, the multi-classification problem of mini-ImageNet was changed to the two-classification problem of crack detection, as shown in Figure 5. In other words, it was not necessary to start training the improved network used for crack detection from scratch but only to iterate and update parts of the parameters, which significantly reduced the training workload and shortened the training time.

3. Preliminary Experiments on Mini-ImageNet

ImageNet [35] is one of the most influential image recognition datasets in the world at present, with a total of 1,431,167 images in 1000 categories and their corresponding labels. Based on its large samples and diversity, ImageNet is the most popular dataset for pre-training various neural networks. The parameters are reliable and versatile after pre-training. However, training neural networks on ImageNet must consume a large amount of computing resources. Sixty thousand pictures (including 100 categories and 600 samples for each category) were extracted from ImageNet as the pretraining dataset of residual neural networks to save training time in this chapter.

3.1. Training Tricks

In deep learning, the learning rate is a vital hyperparameter that controls optimization algorithms’ convergence speed. A high learning rate can lead to rapid convergence and cause the optimization algorithm to oscillate or converge to a suboptimal solution. A low learning rate, on the other hand, can ensure that the optimization algorithm converges to a good solution, but its convergence speed may be slow.

There are two strategies to solve this dilemma. The first strategy is to warm up the learning rate [36]. The parameters of ResNet18 and ResNet50 are randomly initialized at the initial stage of training. During this stage, if a relatively high learning rate is selected, it may cause oscillations in the networks. Warming up the learning rate can make the learning rate in the first few epochs of training relatively small. The networks can slowly become stable with a lower learning rate in the warm-up stage. When these two networks are relatively stable, the pre-set learning rate can be used for training. This strategy makes the convergence speed of the networks faster and their training effects better. In this paper, the steps of the warm-up stage were set to 1.

Another helpful trick is the decay strategy of the learning rate. The decay strategy used in this paper was cosine annealing [37,38]. When using gradient descent algorithms to optimize objective functions, the closer networks get to the global minimum loss, the smaller the learning rate should become to avoid networks missing this point. The cosine annealing decay strategy can reduce the learning rate through the cosine function. With the increase in input to the cosine function, the cosine value first slowly decreases, then accelerates to decline, and then slowly decreases again. This gradual decrease in learning rate helps to avoid overshooting the optimal solution and ensure that the optimization algorithm converges to a reasonable solution smoothly and stably.

3.2. Some Findings

To see how well distillation works, we trained two residual neural networks with different depths on mini-ImageNet, a large dataset with 60,000 samples. The accuracy of the teacher network ResNet50 was 81.79%, while the accuracy of the student network ResNet18 without knowledge distillation was 79.41%. However, if the smaller network was trained by adding the additional task of matching the soft targets produced by the large network at a higher temperature, empirically taking T = 4 and α = 0.6 as an example, its accuracy reached 82.33%. It shows that soft targets can transfer a great deal of knowledge to the distilled model, including how to generalize what is learned from translated training data, even though the transfer set does not contain any translations.

Table 1. Results of ablation experiments.

Model	T	Epoch 1	Train Acc 2 (%)	Hard Loss (%)	Best Acc 2 (%)	Val 3 Loss (%)
Student ResNet18	-	96	93.44	0.26	79.41	0.86
Teacher ResNet50	-	99	94.40	0.22	81.79	0.76
KD 4	2	97	93.05	0.10	81.61	0.79
KD	3	93	92.53	0.11	81.95	0.78
KD	4	97	92.49	0.11	82.33	0.78
KD	5	94	91.99	0.12	82.04	0.77
KD(DT 5)	-	99	92.34	0.11	82.52	0.77

Note(s): ¹ Epoch represents the number of training epochs with the highest accuracy. ² Acc is the abbreviation for accuracy. ³ Val is the abbreviation for validation. ⁴ KD is the abbreviation for knowledge distillation, representing the distilled student network ResNet18. ⁵ DT is the abbreviation for dynamic temperature.

shows the results of ablation experiments at different distillation temperatures.

In addition, we find that knowledge distillation can also improve generalization by narrowing the gap between training and validation accuracy compared to that of the original student model and even the teacher model. For instance, the training accuracy and the validation accuracy of ResNet18 were 93.44% and 79.41%, which differed by 14.03%, and those of ResNet50 were 94.40% and 81.79%, which differed by 12.61%, while those of distilled (T = 4, α = 0.6) ResNet18 were 92.49% and 82.33%, which differed by 10.16%. This is solid and decisive proof that the generalization ability of the improved algorithm is enhanced through knowledge distillation, which provides excellent support for transferring this algorithm to train crack datasets in the following experiments.

Furthermore, based on the empirical fixed temperature of 4, we set the variation range of dynamic temperature to [3, 5] and found that the model’s accuracy using dynamic temperature parameters reached 82.52%. The final distillation temperature approached 3.95. Compared with the results of distillation systems under fixed temperature parameters, the distillation effect was significantly improved with a dynamic temperature module. The network itself can adjust the distillation temperature without repeating exhausting experiments to find the optimal fixed temperature or simply taking an empirical one. In the next experiment, we apply dynamic temperature to crack detection.

4. Experiments on Concrete Crack Detection

As mentioned above, the improved algorithm has achieved a more accurate image classification performance on mini-ImageNet. The next step is to transfer its training results to practice on crack datasets. The work to be carried out includes establishing crack datasets of concrete structures and transfer learning.

4.1. Concrete Crack Datasets

The original dataset [39,40] comprises 458 high-resolution images (4032 × 3024 pixels) of concrete cracks. Due to the limited number of samples, these images were cropped to generate 20,000 positive samples with cracks and 20,000 negative samples without cracks. Each sample is a 224 × 224 RGB image; thus, a dataset [41] of concrete cracks was established.

These images were randomly put into the training set and the validation set at a ratio of 8:2. There are two folders under the training set and the validation set: one for collecting positive samples and the other for collecting negative samples, respectively. Some samples with and without cracks are shown in Figure 6. It can be seen that the crack dataset established in this paper contains cracks of various shapes and widths and has good randomness and richness.

4.2. Results

Taking the pre-trained network as the starting point and changing its fully connected layer, the multi-classification problem on mini-ImageNet was modified to a two-classification problem of concrete cracks (with or without cracks). Image enhancement measures such as random rotation and horizontal and vertical flipping were also taken to improve model generalization. In addition, the normalization of each channel was conducive to the training of networks, thus further enhancing the accuracy of the crack detection model. The network was trained for a total of 10 epochs. The performance of the improved algorithm on crack detection can be evaluated by the accuracy and loss of the training set and the validation set during each epoch of training, as shown in Figure 7.

It can be seen from Figure 7 that the improved ResNet-based algorithm using knowledge distillation performed exceptionally well on crack detection at the right beginning, taking the accuracy and loss of the validation set as the evaluation criteria. The high accuracy of the first epoch is the result of pre-training on mini-ImageNet and transfer learning. With the increase in training epochs, the improved algorithm performed better and better. When training to the eighth epoch, the algorithm achieved the best performance. Comparing the performance of ResNet18, ResNet50, and distilled ResNet18 on the task of crack detection, the detection ability of the teacher model is generally better than that of the student model. Additionally, the feature extraction ability of the distilled student model is enhanced, so its accuracy is higher than that of the original model, even exceeding that of the teacher model. Taking the optimal results as an example, the accuracy of the improved algorithm based on knowledge distillation applied to the crack detection of concrete structures was as high as 99.85%. Compared with the original algorithm, the accuracy was increased by 3.78%. With six images randomly selected from the crack dataset, correct detection results were obtained, taking the trained model of this epoch as the ultimate one for detection, as shown in Figure 8.

Meanwhile, we also carried out ablation experiments from different angles. For example, we compared the crack detection results of student and teacher networks with and without pretraining, respectively, as well as other improved methods of ResNets other than knowledge distillation, such as the insertion of convolutional block attention module (CBAM) and some other DCNNs applied to crack detection, such as AlexNet and VGG-Net. The results are shown in

Table 2. Crack detection results for different networks.

Model	ResNet18 *		ResNet50 *		KD	CBAM	AlexNet	VGG-Net
Best Acc	94.93	96.07	95.56	98.62	99.85	98.80	97.02	94.93
		(+1.14)	(+0.63)	(+3.69)	(+4.92)	(+3.87)	(+2.09)	(+0.00)
			(−0.51)	(+2.55)	(+3.78)	(+2.73)	(+0.95)	(−1.14)

Note(s): * The student and teacher models have two columns of data, which are the crack detection results of pre-trained models and those without pretraining. The values in parentheses in the second row are the degrees of improvement compared to the accuracy of the student model without pre-training, and the values in parentheses in the third row are the degrees of improvement compared to that of the pre-trained student model.

.

From Table 2, it can be seen that the improved pre-trained network based on dynamic knowledge distillation presented an improvement of 4.92% in accuracy compared to the original student network without pretraining. The accuracy was 1.05% higher than that of networks with CBAM. Compared with other DCNNs, such as AlexNet and VGG-Net, the accuracy was improved by 2.83% and 4.92%, respectively. This algorithm is well prepared for application to crack detection in concrete dams. In the subsequent case study, we take the HKC Dam as an example to conduct crack detection on the concrete structures of its spillway.

5. Case Study

Long-term and periodic changes in water pressure and temperature, structural settlement, geological disasters, and other factors can easily lead to the evolution of small cracks in concrete dams into more severe damage. Timely crack detection is necessary to ensure the safety and stability of concrete dams. Furthermore, accurately identifying whether there are cracks in a specific area of a dam is an essential requirement for crack detection. Since the evolution of cracks in concrete dams is quite a slow process, lasting for several years to several decades, few crack images are available in the short term. It is necessary to conduct research on crack detection in the case of a small number of samples. Taking the HKC Dam as an example, the improved ResNet-based algorithm using knowledge distillation mentioned above in this paper and already trained on crack datasets was applied to identify the cracks in the concrete dam.

5.1. Case Description—HKC Dam

HKC Dam is located at the exit of the Qin River’s last section, the Yellow River’s primary tributary. The basin area controlled by the reservoir is 9223 km², accounting for 68.2% of the basin area of the Qin River. The design flood control standard has a 500-year return period, and the check standard has a 2000-year return period. With a total storage capacity of 317 million cubic meters, the dam is a hydraulic project focusing on flood control, water supply, and the comprehensive utilization of irrigation and power generation. The main structures include a concrete face rockfill dam, spillway, and power generation system, as shown in Figure 9. We used UAVs to acquire images of the dam, and it was found that the spillway of the dam had many cracks due to long-term operation, as shown in Figure 10.

5.2. Application to HKC Dam

When applying the improved ResNet-based algorithm to crack detection at HKC Dam, the first step was to divide crack images into several blocks, the size of which is determined by that of the crack images in the above chapter (224 × 224 pixels). Thereafter, we classified each block using the previously trained model, resulting in an accuracy rate of 98.39%. A threshold segmentation method, a kind of digital image processing technique, was also used to detect cracks for comparison. The results of these two methods are shown in

Table 3. Crack detection results for HKC Dam.

Original Images	Original Feature Maps	Segmented Images	Detection Results
			positive
			positive
			positive
			negative

.

Taking the four samples shown in Table 3 as an example, it was determined that they were all samples with cracks using the threshold segmentation method, but there was one without cracks. The improved ResNet-based algorithm using knowledge distillation still had good performance in the case of crack detection in concrete dams. It should be noted that the above algorithm cannot directly extract cracks from the image at the pixel level. This crack detection algorithm based on deep learning still needs to be combined with image segmentation technology to complete the pixel-level extraction of cracks. However, compared with the traditional digital image processing techniques, the improved algorithm proposed in this paper does not require any pre-processing of the original images, such as manually filtering background and noise in images. As long as all the samples are classified according to their categories, the algorithm can perform well in crack detection, which proves that it has a certain progressiveness.

6. Discussion

In this paper, we present an improved ResNet-based algorithm for crack detection in concrete dams using dynamic knowledge distillation. The improved algorithm eliminates the incompatibility of high accuracy and model compression of DCNNs applied to crack detection tasks, such as AlexNet, VGG-Net, ResNet50, and other improved versions using CBAM, enabling student models to have superior crack recognition capabilities compared to their teacher and facilitating their deployment on devices with limited resources.

Meanwhile, our method has abolished the practice of using fixed distillation temperatures in previous knowledge distillation systems and proposes to dynamically adjust the temperature during the training process by adding an antagonistic dynamic temperature module, making it possible for the network to select a suitable temperature for distillation automatically in each training epoch. This measure also greatly benefits the improvement of model accuracy.

Besides, we used transfer learning to solve the problem of insufficient samples in the crack detection task. Preliminary experiments were carried out on mini-ImageNet, and the pre-trained model was transferred to the target task. Through experiments, we have come to the following conclusions:

• Preliminary experiments on mini-ImageNet prove soft targets can transfer a great deal of knowledge to the distilled model. If the smaller network is trained by adding the additional task of matching the soft targets produced by the large network at a higher temperature (T = 4), its accuracy will increase from 79.41% to 82.33%. We also find that knowledge distillation can improve generalization by narrowing the gap between training and validation accuracy compared to the original student model (from 14.03% to 10.16%) and even the teacher model (from 12.61% to 10.16%). In addition, the distillation effect is further improved with a dynamic temperature module (from 82.33% to 82.52%), compared with the results of distillation systems under fixed temperature parameters. The final distillation temperature approaches 3.95, which is different from the empiric value of 4, which confirms our previous conjecture.
• Experiments on concrete crack detection prove the improved pre-trained network based on dynamic knowledge distillation has an improvement of 4.92% compared to the original student network without pretraining, with an accuracy of 99.85%. The accuracy is 1.05% higher than that of networks with CBAM. Compared with other DCNNs, such as AlexNet and VGG, the accuracy is improved by 2.83% and 4.92%, respectively. Experimental results demonstrate that the proposed dynamic distillation and transfer learning are highly beneficial for crack detection tasks and can satisfy the dual requirements of high accuracy and model compression. It is particularly true for tasks with insufficient samples, such as the application of HKC Dam.
• When common feature encoders obtained from concrete cracks with rich features were applied to crack detection in HKC Dam through transfer learning, its accuracy reached 98.39%, making it easy to draw sweeping conclusions: dynamic distillation and transfer learning can help networks improve the ability to extract common features such as texture and contour of cracks and alleviate the overfitting problem of datasets involving unrich samples.