Flushing Efficiency of Run-of-River Hydropower Plants: Novel Approaches Based on Physical Laboratory Experiments
Abstract
:1. Introduction
2. Materials and Methods
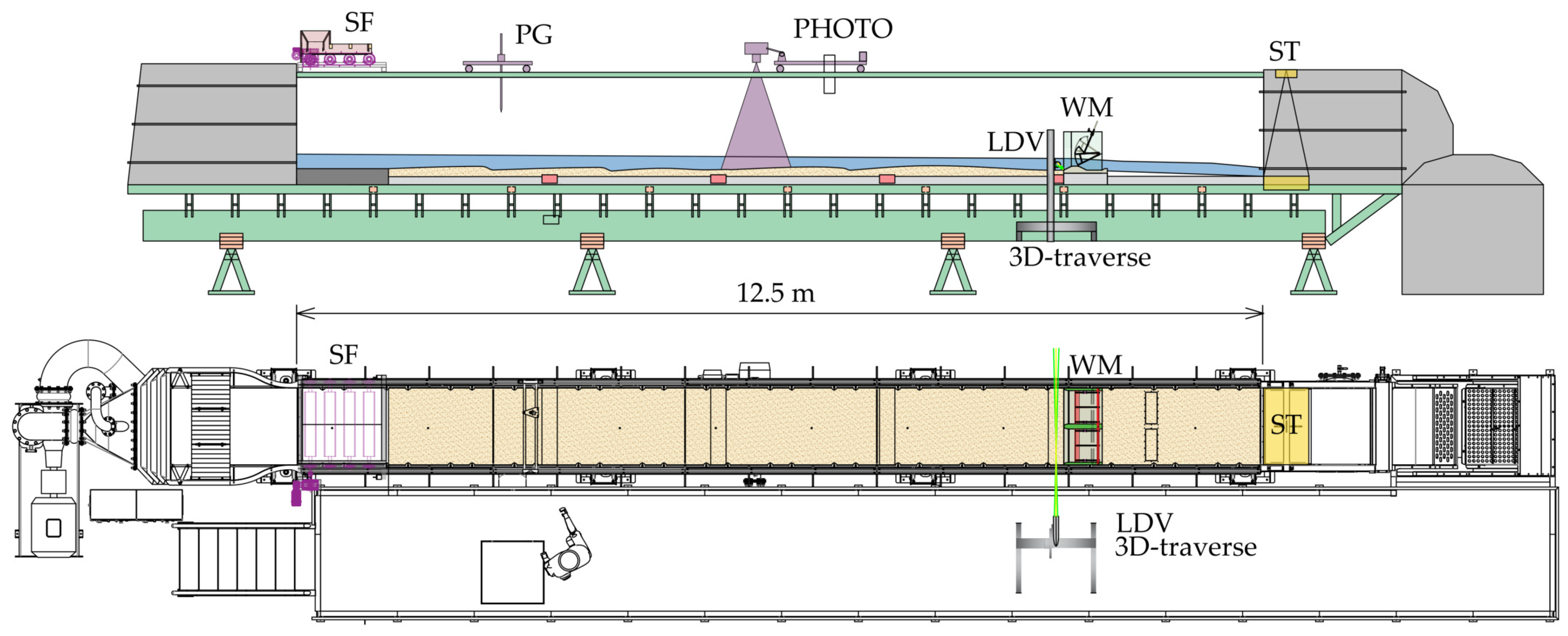
2.1. Sediment Flume and Model Scaling
2.2. Laser Doppler Velocimetry (LDV)
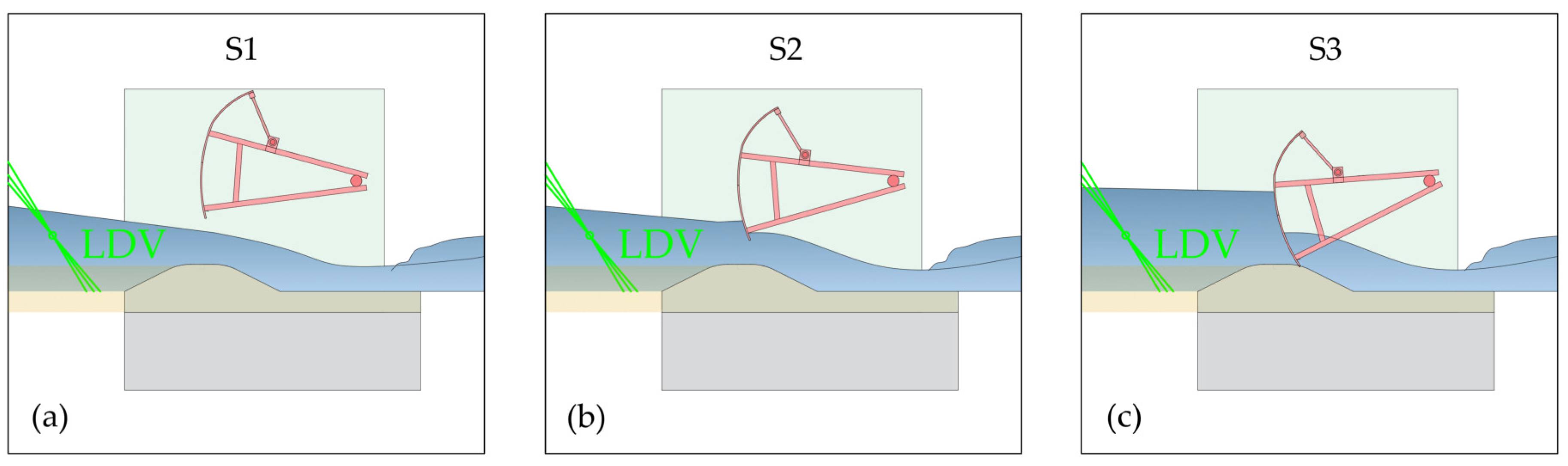
2.3. Experimental Procedure and Conditions
3. Results
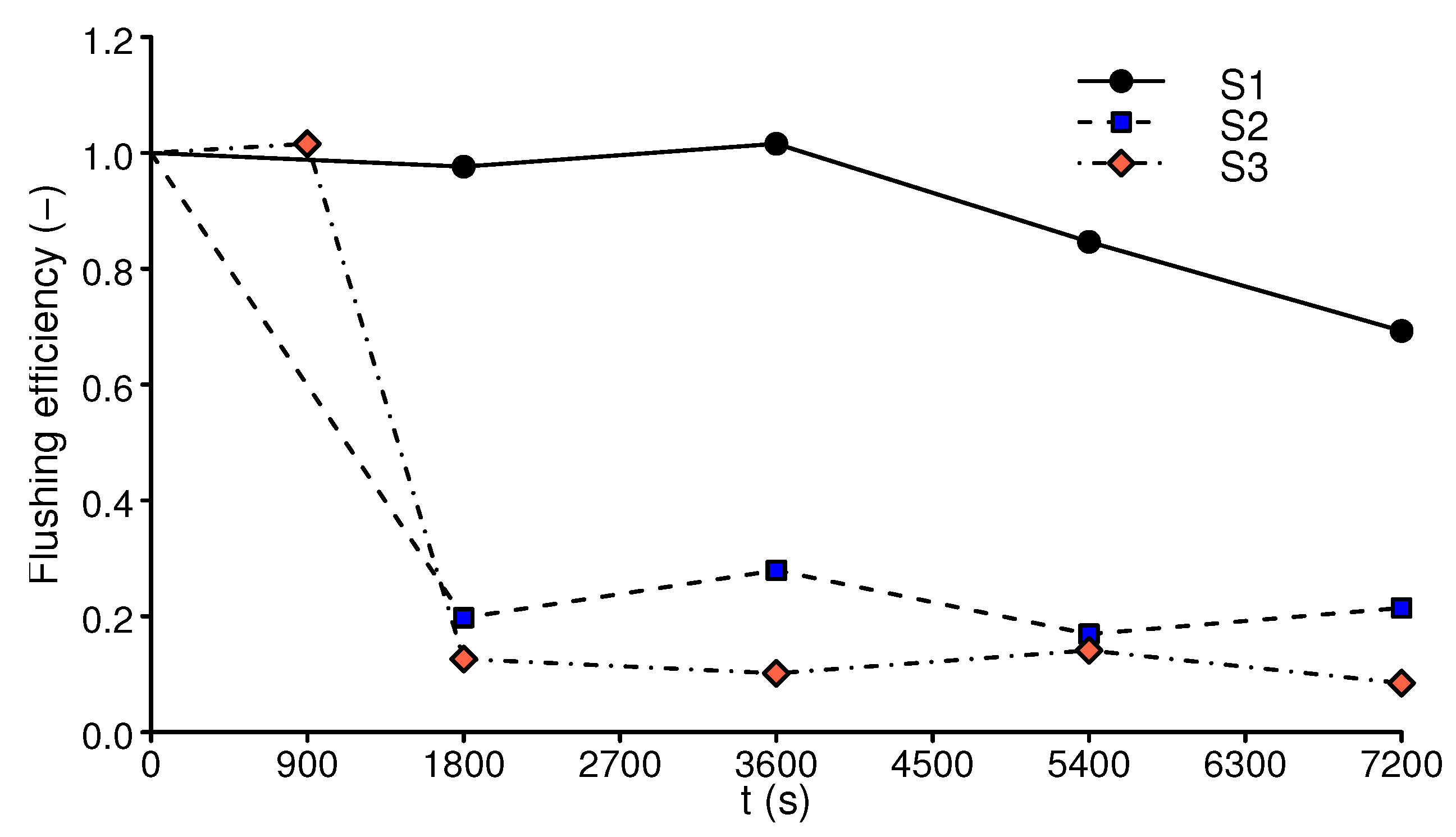
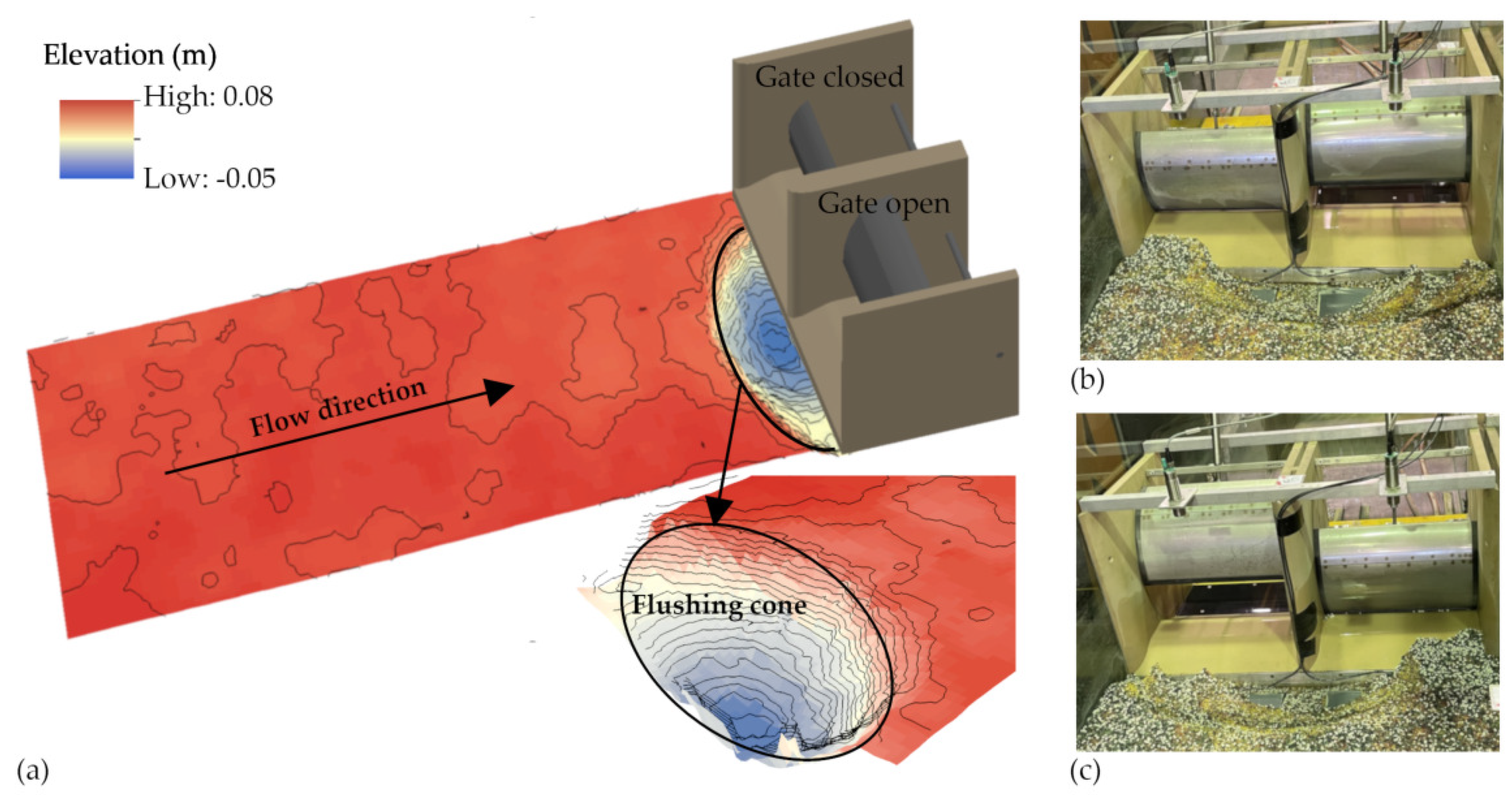
3.1. Flushing Efficiency and Morphological Effects
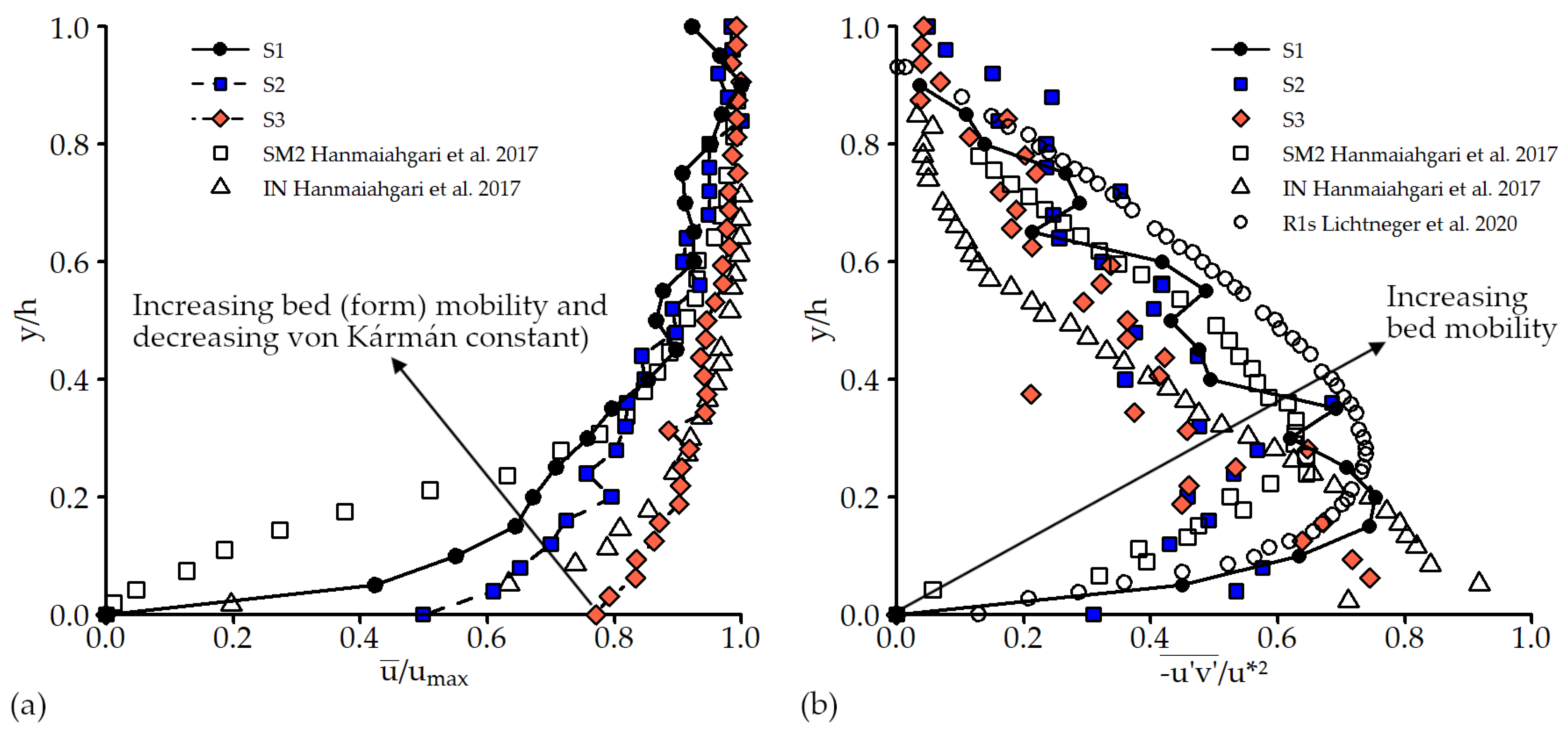
3.2. Velocity Profiles and Reynolds Stress from LDV
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DEM | digital elevation model |
| HPP | hydropower plant |
| HQ | annual flood flow |
| LDV | laser doppler velocimetry |
| LFFFO | low-flood-flow flushing operations |
| PG | point gauge |
| PHOTO | camera system for photogrammetry |
| Q | flow rate |
| RoR | run-of-river |
| SIC | constant sediment input |
| ST | sediment trap |
| WM | weir model |
Notations
| areal scale | |
| maximum grain diameter | |
| mean grain diameter | |
| Shields number | |
| Froude number | |
| h | water depth |
| geometric length scale | |
| Von Kármán constant | |
| kinematic viscosity | |
| scale ratio for flow rate | |
| Reynolds stress | |
| particle Reynolds number | |
| water density | |
| sediment density | |
| hydraulic timescale | |
| sediment timescale | |
| reference shear stress | |
| u | measured longitudinal velocity |
| time-averaged longitudinal velocity | |
| turbulent longitudinal velocity fluctuation | |
| maximum longitudinal velocity | |
| friction velocity | |
| v | measured vertical velocity |
| velocity scale | |
| time-averaged vertical velocity | |
| turbulent vertical velocity fluctuation |
References
- Grill, G.; Lehner, B.; Thieme, M.; Geenen, B.; Tickner, D.; Antonelli, F.; Babu, S.; Borrelli, P.; Cheng, L.; Crochetiere, H.; et al. Mapping the world’s free-flowing rivers. Nature 2019, 569, 215–221. [Google Scholar] [CrossRef] [PubMed]
- Sindelar, C.; Gold, T.; Reiterer, K.; Hauer, C.; Habersack, H. Experimental Study at the Reservoir Head of Run-of-River Hydropower Plants in Gravel Bed Rivers. Part I: Delta Formation at Operation Level. Water 2020, 12, 2035. [Google Scholar] [CrossRef]
- Reiterer, K.; Gold, T.; Habersack, H.; Hauer, C.; Sindelar, C. Experimental Study at the Reservoir Head of Run-of-River Hydropower Plants in Gravel Bed Rivers. Part II: Effects of Reservoir Flushing on Delta Degradation. Water 2020, 12, 38. [Google Scholar] [CrossRef]
- Gold, T.; Reiterer, K.; Hauer, C.; Habersack, H.; Sindelar, C. The effect of reservoir flushing on existing headwater delta formations of run-of-river hydropower plants—Experimental studies with nonuniform sediments. In Proceedings of the 6th IAHR Europe Congress, Warsaw, Poland, 15–18 February 2021; pp. 603–604. [Google Scholar]
- Habersack, H.; Hein, T.; Stanica, A.; Liska, I.; Mair, R.; Jäger, E.; Hauer, C.; Bradley, C. Challenges of river basin management: Current status of, and prospects for, the River Danube from a river engineering perspective. Sci. Total Environ. 2016, 543, 828–845. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sindelar, C.; Schobesberger, J.; Habersack, H. Effects of weir height and reservoir widening on sediment continuity at run-of-river hydropower plants in gravel bed rivers. Geomorphology 2017, 291, 106–115. [Google Scholar] [CrossRef]
- Kondolf, G.M.; Gao, Y.; Annandale, G.W.; Morris, G.L.; Jiang, E.; Zhang, J.; Cao, Y.; Carling, P.; Fu, K.; Guo, Q.; et al. Sustainable sediment management in reservoirs and regulated rivers: Experiences from five continents. Earth’s Future 2014, 2, 256–280. [Google Scholar] [CrossRef]
- Reisenbüchler, M.; Bui, M.; Skublics, D.; Rutschmann, P. Sediment Management at Run-of-River Reservoirs Using Numerical Modelling. Water 2020, 12, 249. [Google Scholar] [CrossRef] [Green Version]
- Gold, T.; Reiterer, K. Untersuchung der Sedimenttransportprozesse bei der Stauraumver- und Entlandung von Flusskraftwerken anhand hydraulischer Modellversuche mit Heterogenen Sedimenten. Master’s Thesis, Institute of Hydraulic Engineering and River Research (IWA), University of Natural Resources and Life Sciences, Vienna, Austria, 2020; p. 207. [Google Scholar]
- Hanmaiahgari, P.R.; Roussinova, V.; Balachandar, R. Turbulence characteristics of flow in an open channel with temporally varying mobile bedforms. J. Hydrol. Hydromech. 2017, 65, 35–48. [Google Scholar] [CrossRef] [Green Version]
- Lichtneger, P.; Sindelar, C.; Schobesberger, J.; Hauer, C.; Habersack, H. Experimental investigation on local shear stress and turbulence intensities over a rough non-uniform bed with and without sediment using 2D particle image velocimetry. Int. J. Sediment Res. 2020, 35, 193–202. [Google Scholar] [CrossRef]
- Bennett, S.J.; Bridge, J.S.; Best, J.L. Fluid and sediment dynamics of upper stage plane beds. J. Geophys. Res. Oceans 1998, 103, 1239–1274. [Google Scholar] [CrossRef]
- Nikora, V.; Goring, D. Flow Turbulence over Fixed and Weakly Mobile Gravel Beds. J. Hydraul. Eng. 2000, 126, 679–690. [Google Scholar] [CrossRef]
- Shields, A.M. Anwendung der Aehnlichkeitsmechanik und der Turbulenzforschung auf die Geschiebebewegung. Ph.D. Thesis, Technical University Berlin, Berlin, Germany, 1936. [Google Scholar]
- Kobus, H. Wasserbauliches Versuchswesen. In VWK; Paul Parey: Hamburg/Berlin, Germany, 1984; Volume 39. [Google Scholar]
- Ruck, B. Laser Doppler Anemometry—A non-intrusive optical measuring technique for fluid velocity. Part. Part. Syst. Charact. 1987, 4, 26–37. [Google Scholar] [CrossRef]
- Faruque, M.A.A.; Balachandar, R. Roughness effects on turbulence characteristics in an open channel flow. Can. J. Civ. Eng. 2010, 37, 1600–1612. [Google Scholar] [CrossRef] [Green Version]
- Cameron, S.M.; Nikora, V.I.; Witz, M.J. Entrainment of sediment particles by very large-scale motions. J. Fluid Mech. 2020, 888, A7. [Google Scholar] [CrossRef]
- Nikora, V. Flow turbulence over mobile gravel-bed: Spectral scaling and coherent structures. Acta Geophys. Pol. 2005, 53, 539–552. [Google Scholar]
- Schobesberger, J.; Gold, T.; Reiterer, K.; Worf, D.; Lichtneger, P.; Hauer, C.; Habersack, H.; Sindelar, C. Coherent Structures, Sediment entrainment and varying Shields numbers below threshold conditions of motion. In Proceedings of the 39th IAHR World Congress, Granada, Spain, 19–24 June 2022; pp. 503–509. [Google Scholar] [CrossRef]
- Vowinckel, B.; Jain, R.; Kempe, T.; Fröhlich, J. Entrainment of single particles in a turbulent open-channel flow: A numerical study. J. Hydraul. Res. 2016, 54, 158–171. [Google Scholar] [CrossRef]
- Harb, G.; Badura, H.; Schneider, J.; Zenz, G. Verlandungsproblematik bei Wasserkraftanlagen mit niedrigen Fallhöhen. Österreichische Wasser- und Abfallwirtschaft 2015, 67, 315–324. [Google Scholar] [CrossRef]
- Mao, L. The effect of hydrographs on bed load transport and bed sediment spatial arrangement. J. Geophys. Res. Earth Surf. 2012, 117, F03024. [Google Scholar] [CrossRef] [Green Version]


| 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|
| 1:20 | (1:20) | (1:20) | (1:20) | (1:20) |
| Scenario | Gate Position | Duration (s) | SIC 1 (kgh) | Q (ms) |
|---|---|---|---|---|
| S1 | Both open | 4 × 1800 | 60 | 0.07 |
| S2 | Both slightly submerged | 4 × 1800 | 60 | 0.07 |
| S3 | One closed, one open | 2 × 900 and 3 × 1800 | 60 | 0.07 |
| Scenario | h1 (m) | 1 (ms) | 1 (Nm) | Sediment Output 2 (kgh) | Flushing Efficiency |
|---|---|---|---|---|---|
| S1 | 0.105 | 0.78 | 3.8 | 54 | 0.90 |
| S2 | 0.130 | 0.57 | 1.8 | 13 | 0.22 |
| S3 | 0.165 | 0.56 | 0.8 | 12 | 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gold, T.; Reiterer, K.; Hauer, C.; Habersack, H.; Sindelar, C. Flushing Efficiency of Run-of-River Hydropower Plants: Novel Approaches Based on Physical Laboratory Experiments. Water 2023, 15, 2657. https://doi.org/10.3390/w15142657
Gold T, Reiterer K, Hauer C, Habersack H, Sindelar C. Flushing Efficiency of Run-of-River Hydropower Plants: Novel Approaches Based on Physical Laboratory Experiments. Water. 2023; 15(14):2657. https://doi.org/10.3390/w15142657
Chicago/Turabian StyleGold, Thomas, Kevin Reiterer, Christoph Hauer, Helmut Habersack, and Christine Sindelar. 2023. "Flushing Efficiency of Run-of-River Hydropower Plants: Novel Approaches Based on Physical Laboratory Experiments" Water 15, no. 14: 2657. https://doi.org/10.3390/w15142657
APA StyleGold, T., Reiterer, K., Hauer, C., Habersack, H., & Sindelar, C. (2023). Flushing Efficiency of Run-of-River Hydropower Plants: Novel Approaches Based on Physical Laboratory Experiments. Water, 15(14), 2657. https://doi.org/10.3390/w15142657








