Research and Application of the Calculation Method of River Roughness Coefficient with Vegetation
Abstract
:1. Introduction
2. Methods and Materials
2.1. Calculation Method of Roughness Coefficient with Vegetation
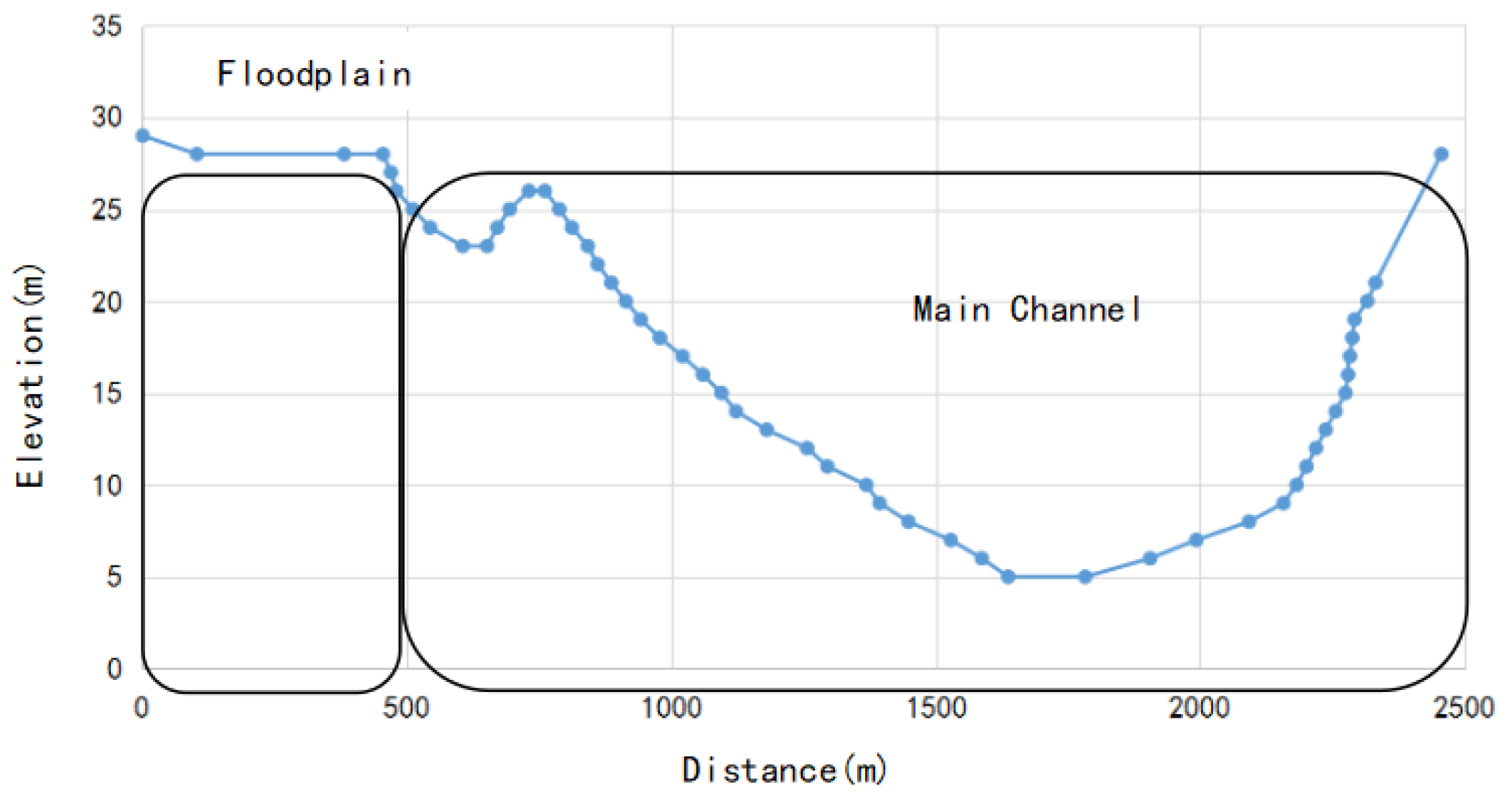
2.2. Materials
3. Results
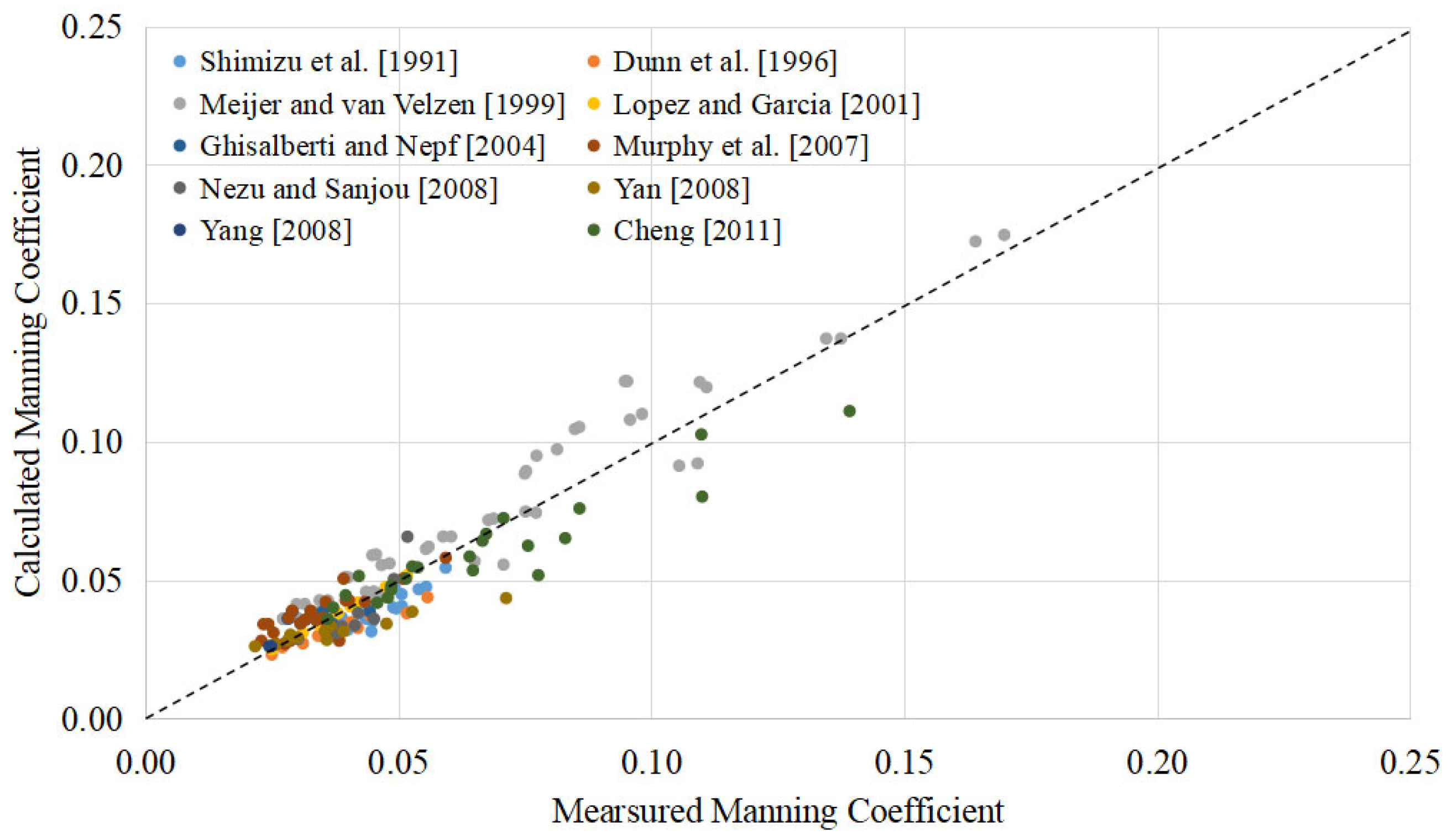
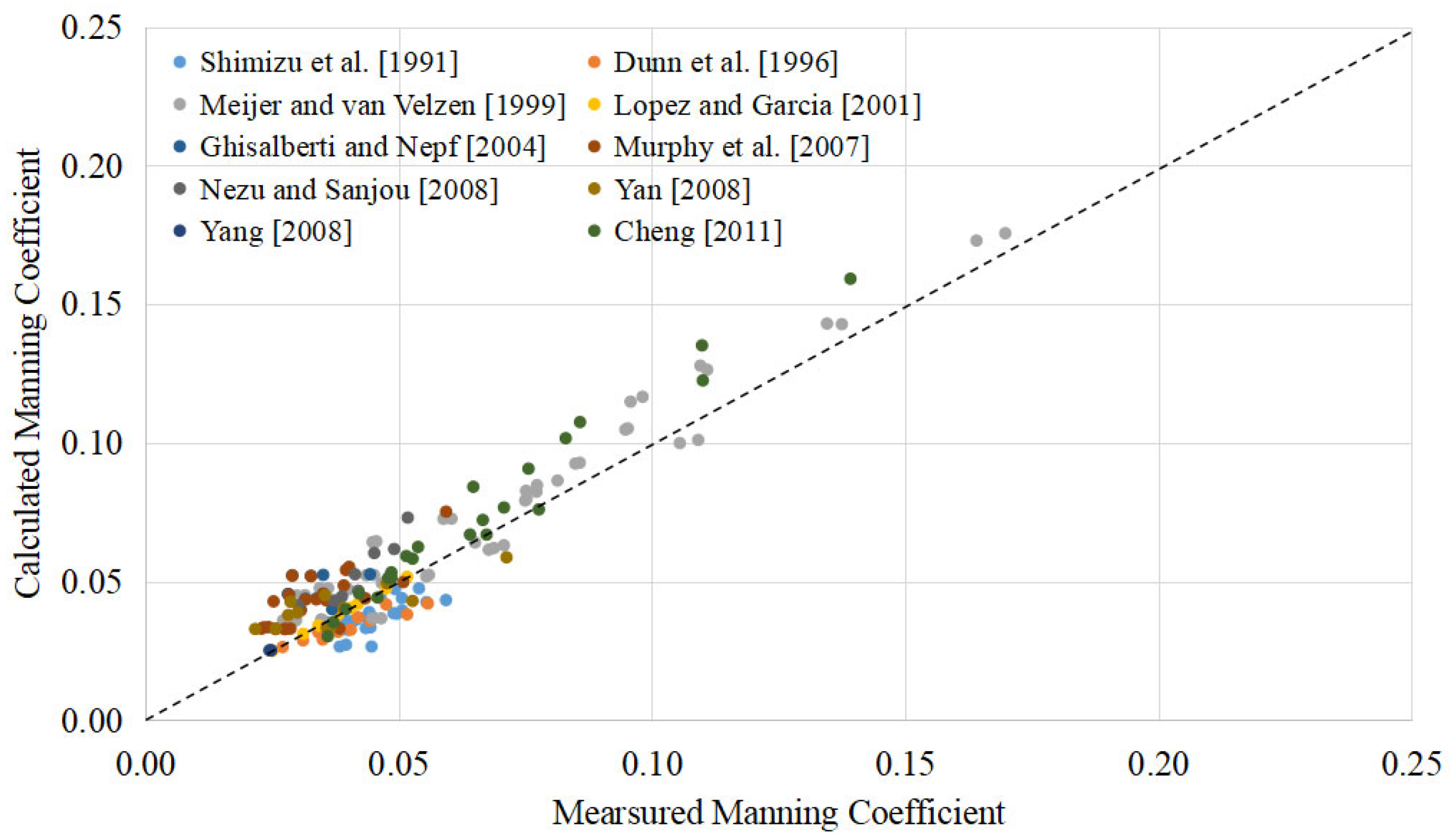
3.1. Model Validation
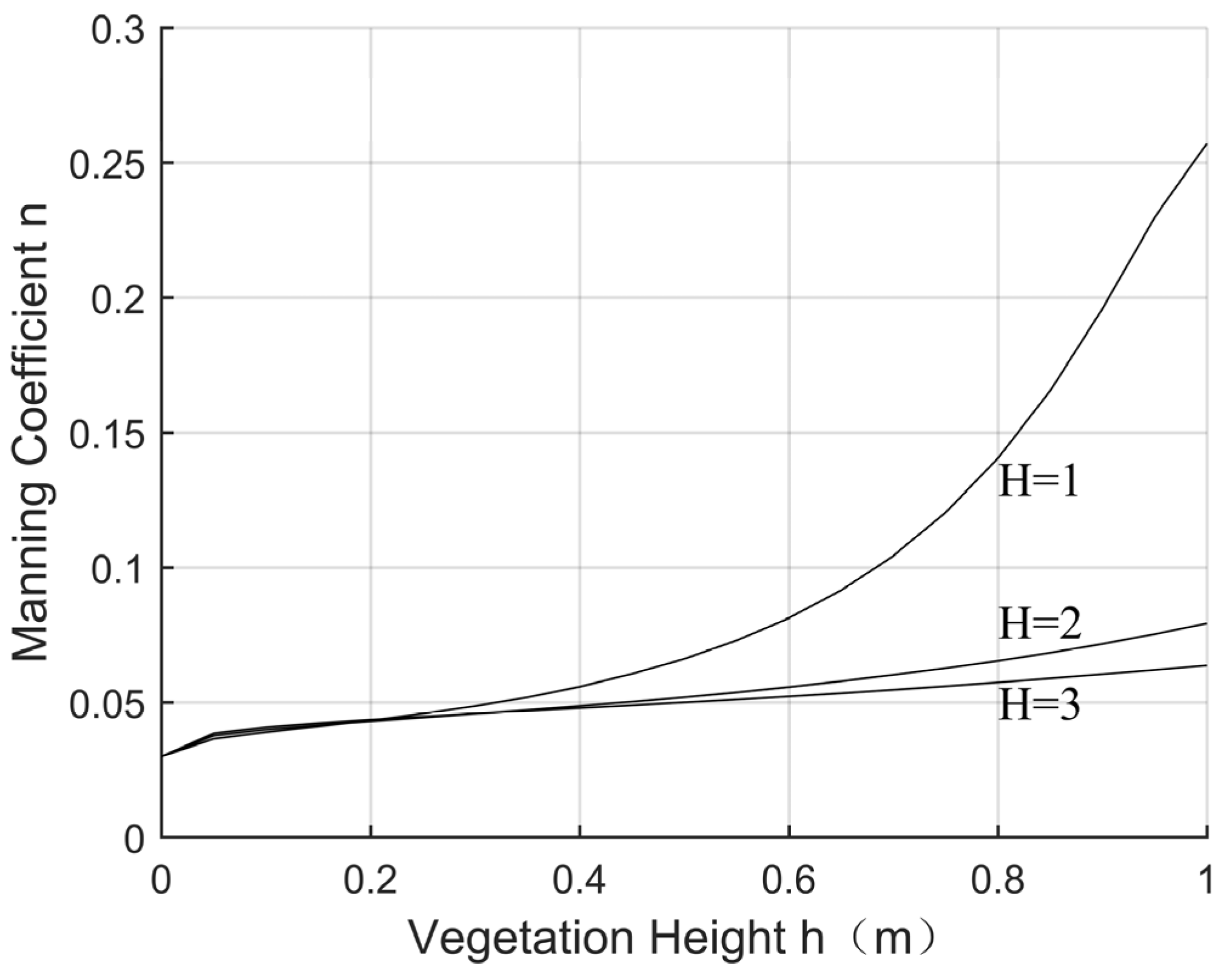
3.2. Variation of Roughness Coefficient
- (1)
- Emerged vegetation flow
- (2)
- Submerged vegetation flow
4. Practical Applications
4.1. Emerged Vegetation Flow
4.2. Submerged Vegetation Flow
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Costanza, R.; d’Arge, R.; de Groot, R.; Farber, S.; Grasso, M.; Hannon, B.; Limburg, K.; Naeem, S.; O’Neill, R.V.; Paruelo, J.; et al. The value of the world’s ecosystem services and natural capital. Nature 1997, 387, 253–260. [Google Scholar] [CrossRef]
- Nepf Heidi, M. Flow and Transport in Regions with Aquatic Vegetation. Annu. Rev. Fluid Mech. 2012, 44, 123–142. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Shan, Y. Impact of an emergent model vegetation patch on flow adjustment and velocity. Proc. Inst. Civ. Eng.-Water Manag. 2022, 175, 55–66. [Google Scholar] [CrossRef]
- Liu, C.; Yan, C.; Sun, S.; Lei, J.; Nepf, H.; Shan, Y. Velocity, turbulence, and sediment deposition in a channel partially filled with a Phragmites australis canopy. Water Resour. Res. 2022, 58, e2022WR032381. [Google Scholar] [CrossRef]
- Nicosia, A.; Ferro, V. Flow resistance due to shrubs and woody vegetation. Flow Meas. Instrum. 2023, 89, 102308. [Google Scholar] [CrossRef]
- Lauria, A. Flow Resistance in Open Channel due to Vegetation at Reach Scale: A Review. Water 2021, 13, 116. [Google Scholar]
- Ikhsan, C.; Permana, A.S.; Negara, A.S. Armor layer uniformity and thickness in stationary conditions with steady uniform flow. Civ. Eng. J. 2022, 8, 1086–1099. [Google Scholar] [CrossRef]
- Ree, W. Hydraulic characteristics of vegetation for vegetated waterways. Agric. Eng. 1949, 30, 184–189. [Google Scholar]
- Kouwen, N.; Unny, T.; Hill, H.M. Flow retardance in vegetated channels. J. Hydraul. Div. ASCE 1969, 95, 329–342. [Google Scholar] [CrossRef]
- Kouwen, N.; Unny, T.E. Flexible roughness in open channels. J. Hydraul. Div. ASCE 1973, 99, 713–728. [Google Scholar] [CrossRef]
- Järvelä, J. Flow resistance of flexible and stiff vegetation: A flume study with natural plants. J. Hydrol. 2002, 269, 44–54. [Google Scholar] [CrossRef]
- Stone, B.M.; Shen, H.T. Hydraulic resistance of flow in channels with cylindrical roughness. J. Hydraul. Eng. 2002, 128, 500–506. [Google Scholar] [CrossRef]
- Tanino, Y.; Nepf, H.M. Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraul. Eng. 2008, 134, 34–41. [Google Scholar] [CrossRef]
- Yang, W.; Choi, S. A two-layer approach for depth-limited open-channel flows with submerged vegetation. J. Hydraul. Res. 2010, 48, 466–475. [Google Scholar] [CrossRef]
- Li, S.; Shi, H.; Xiong, Z.; Huai, W.; Cheng, N. New formulation for the effective relative roughness height of open channel flows with submerged vegetation. Adv. Water Resour. 2015, 86, 46–57. [Google Scholar] [CrossRef]
- Cheng, N.S. Representative roughness height of submerged vegetation. Water Resour. Res. 2011, 47, 427–438. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Z. Evaluating riparian vegetation roughness computation methods integrated within HEC-RAS. J. Hydraul. Eng. 2019, 145, 04019020. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, C.; Nepf, H. Flow adjustment at the leading edge of a submerged aquatic canopy. Water Resour. Res. 2013, 49, 5537–5551. [Google Scholar] [CrossRef]
- Shimizu, Y.; Tsujimoto, T.; Nakagawa, H.; Kitamura, T. Experimental study on flow over rigid vegetation simulated by cylinders with equi-spacing. Proc. Jpn. Soc. Civ. Eng. 1991, 438, 31–40. (In Japanese) [Google Scholar] [CrossRef] [Green Version]
- Dunn, C.J.; López, F.; García, M.H. Mean Flow and Turbulence in a Laboratory Channel with Simulated Vegetation; Hydrosystems Laboratory, Department of Civil Engineering, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 1996. [Google Scholar]
- Meijer, D.G.; Van Velzen, E.H. Prototype-scale flume experiments on hydraulic roughness of submerged vegetation. In Proceedings of the 28th International IAHR Conference, Graz, Austria, 22–27 August 1999. [Google Scholar]
- Lopez, F.; Garcia, M.H. Mean flow and turbulence structure of open-channel flow through non-emergent vegetation. J. Hydrol. Eng. 2001, 127, 392–402. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H.M. The limited growth of vegetated shear layers. Water Resour. Res. 2004, 40, 196–212. [Google Scholar] [CrossRef]
- Murphy, E.; Ghisalberti, M.; Nepf, H. Model and laboratory study of dispersion in flows with submerged vegetation. Water Resour. Res. 2007, 43, 687–696. [Google Scholar] [CrossRef]
- Nezu, I.; Sanjou, M. Turbulence structure and coherent motion in vegetated canopy open-channel flows. J. Hydro-Environ. Res. 2008, 2, 62–90. [Google Scholar] [CrossRef]
- Yan, J. Experimental Study of Flow Resistance and Turbulence Characteristics of Open Channel Flow with Vegetation. Ph.D. Thesis, Hohai University, Nanjing, China, 2008. [Google Scholar]
- Yang, W. Experimental Study of Turbulent Open-Channel Flows with Submerged Vegetation. Ph.D. Thesis, Yonsei University, Seoul, Republic of Korea, 2008. [Google Scholar]
- Gao, X.; Lu, J.; Sun, B.; Liu, Y. Experimental study on equivalent bed resistance of river containing vegetation. J. Hydraul. Eng. 2021, 52, 1024–1035. (In Chinese) [Google Scholar]
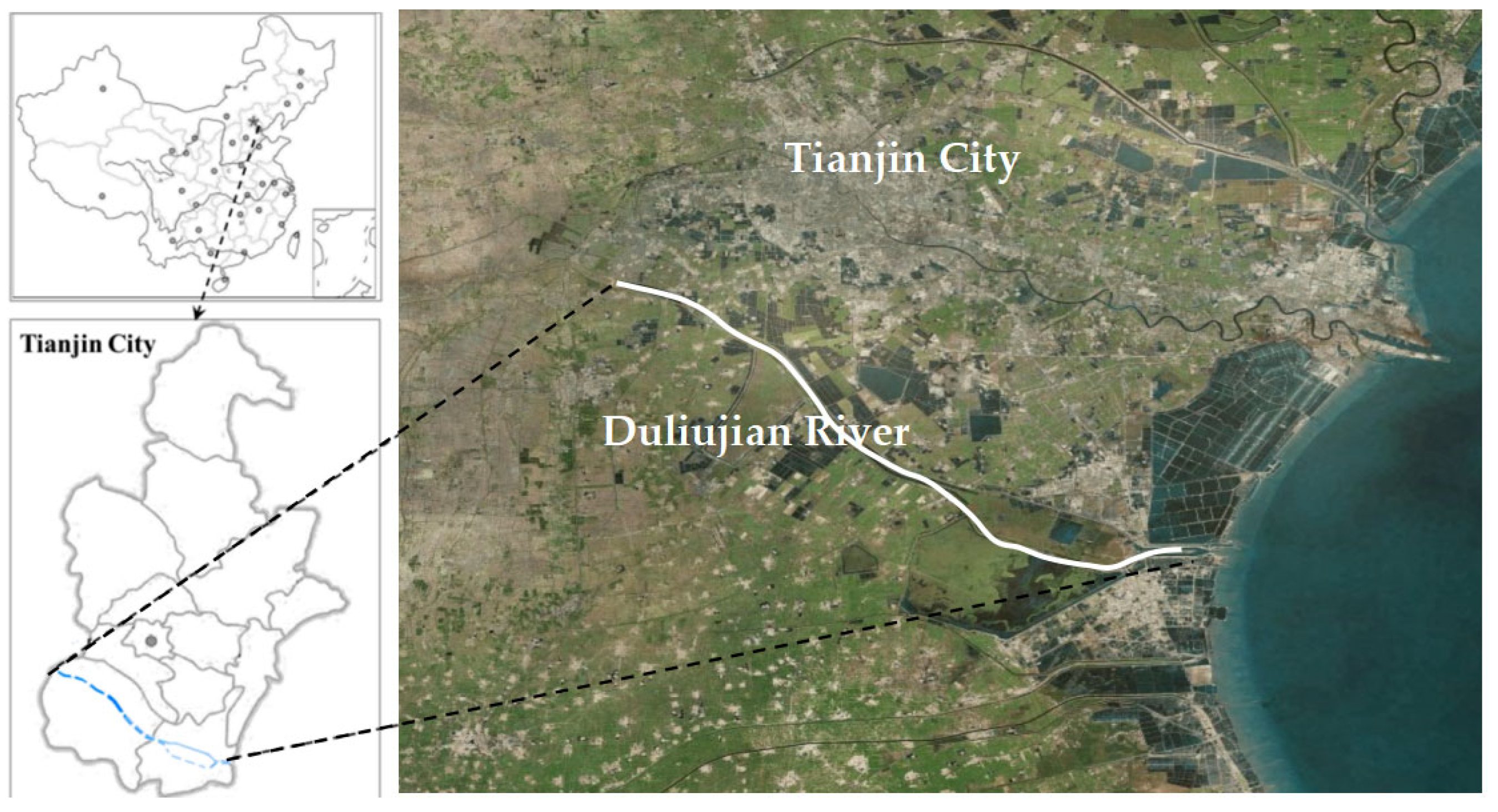
- Sun, X.; Zhang, H.; Zhong, M.; Wang, Z.; Liang, X.; Huang, T.; Huang, H. Analyses on the Temporal and Spatial Characteristics of Water Quality in a Seagoing River Using Multivariate Statistical Techniques: A Case Study in the Duliujian River, China. Int. J. Environ. Res. Public Health 2019, 16, 1020. [Google Scholar] [CrossRef] [Green Version]
- Chai, Y.; Yang, Y.; Deng, J.; Sun, Z.; Li, Y.; Zhu, L. Evolution characteristics and drivers of the water level at an identical discharge in the Jingjiang reaches of the Yangtze River. J. Geogr. Sci. 2020, 30, 1633–1648. [Google Scholar] [CrossRef]
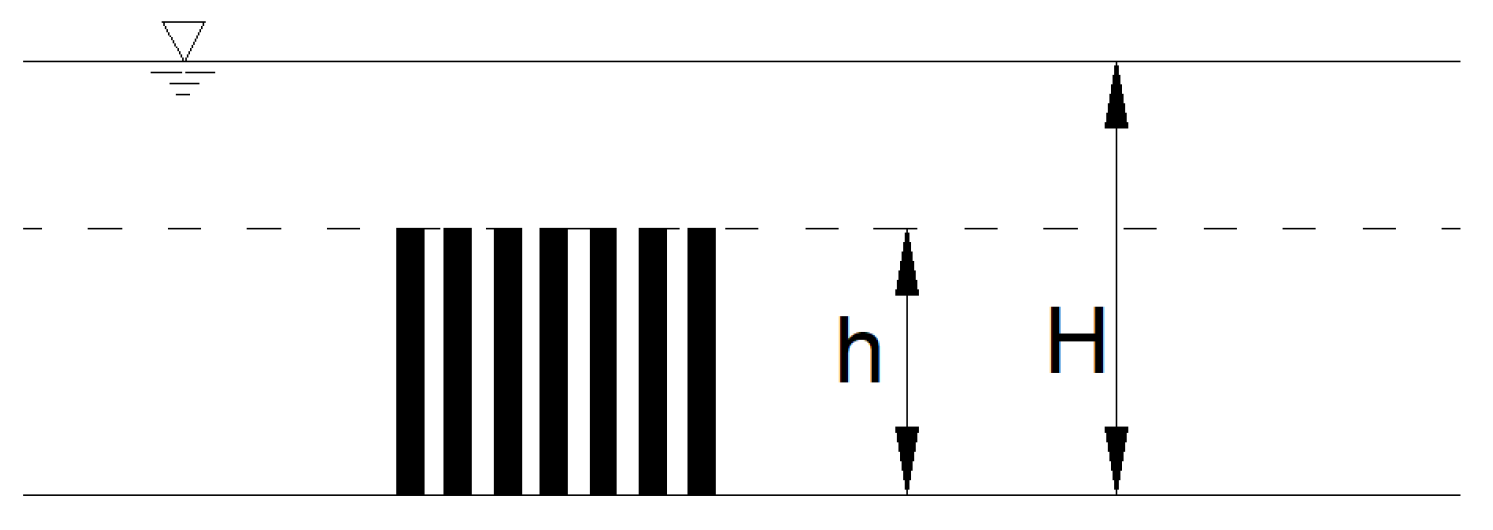





| Researcher | Vegetation Diameter (mm) | Vegetation Height (m) | Volume Fraction (%) | Vegetation Shape | Pattern | Number of Runs |
|---|---|---|---|---|---|---|
| Shimizu et al. [19] | 1–1.5 | 0.041–0.046 | 0.44–0.79 | Cylinder | Linear | 28 |
| Dunn et al. [20] | 6.35 | 0.118 | 0.14–1.23 | Cylinder | Staggered | 12 |
| Meijer and van Velzen [21] | 8 | 0.45–1.5 | 0.32–1.29 | Cylinder | Staggered | 48 |
| Lopez and Garcia [22] | 6.4 | 0.12 | 0.55–1.24 | Cylinder | Staggered | 8 |
| Ghisalberti and Nepf [23] | 6.4 | 0.138 | 1.26–4.02 | Cylinder | Staggered | 11 |
| Murphy et al. [24] | 6.4 | 0.07–0.14 | 1.18–3.77 | Cylinder | Random | 24 |
| Nezu and Sanjou [25] | 8 | 0.05 | Flat strip | Linear | 9 | |
| Yan [26] | 6 | 0.06 | 1.41–5.66 | Cylinder | Linear | 12 |
| Yang [27] | 2 | 0.035 | 0.44 | Cylinder | Staggered | 2 |
| Cheng [16] | 3.2–8.3 | 0.1 | 0.41–11.9 | Cylinder | Staggered | 23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Zhou, J.; Chen, Q. Research and Application of the Calculation Method of River Roughness Coefficient with Vegetation. Water 2023, 15, 2638. https://doi.org/10.3390/w15142638
Chen Z, Zhou J, Chen Q. Research and Application of the Calculation Method of River Roughness Coefficient with Vegetation. Water. 2023; 15(14):2638. https://doi.org/10.3390/w15142638
Chicago/Turabian StyleChen, Zhengbing, Jianyin Zhou, and Qianhai Chen. 2023. "Research and Application of the Calculation Method of River Roughness Coefficient with Vegetation" Water 15, no. 14: 2638. https://doi.org/10.3390/w15142638






