The Displacement of the Resident Wetting Fluid by the Invading Wetting Fluid in Porous Media Using Direct Numerical Simulation

Abstract

Understanding the displacement of the resident wetting fluid in porous media is crucial to the remediation strategy. When pollutants or nutrients are dissolved in the surface wetting fluid and enter the unsaturated zone, the resident wetting fluid in the porous system may remain or be easily flushed out and finally arrive in the groundwater. The fate and transport of the resident wetting fluid determine the policy priorities on soil or groundwater. In this study, the displacement of the resident wetting fluid by the invading wetting fluid in porous media was simulated using direct numerical simulation (DNS). Based on the simulations of the displacements in porous media, the effect of the non-wetting fluid on the displacement was evaluated by observation and quantification, which were difficult to achieve in laboratory experiments. The result can also explain the unknown phenomenon in previous column experiments, namely that the old water is continuously released from the unsaturated porous media even after a long period of flushing with the new water. The effects of the interfacial tension, contact angle, and injection rate, which affected the immiscible fluid–fluid flow pattern, were also evaluated. Since pollutants dissolved in the wetting fluid could change the physical properties of the wetting fluid, the interfacial tensions of the resident wetting fluid and the invading wetting fluid were set separately in the simulation. Moreover, our simulation demonstrated that the consecutive drainage–imbibition cycles could improve the displacement of the resident wetting fluid in porous media. The successful simulation in this study implied that this method can be applied to predict other immiscible fluid–fluid flow in natural or industrial processes.

1. Introduction

Multiphase flow in porous media plays a key role in natural or industrial processes, including transporting pollutants or nutrients in soils, geologic carbon sequestration, groundwater remediation, and enhanced oil recovery [1,2,3,4]. The vadose zone, or so-called unsaturated zone, is the interface connecting land surface and groundwater. When pollutants or nutrients released from the surface enter the vadose zone, they may remain in the vadose zone or be flushed out by the following invading water and enter the groundwater. Whether the pollutants or nutrients stay in the vadose zone or finally enter groundwater determines the government’s pollution remediation strategy on soil or groundwater. Therefore, understanding the displacement efficiency of the resident wetting fluid in porous media by the following invading wetting fluid helps decide the policy priorities. For example, in the porous system, the transport and retention behaviors of per- and poly-fluoroalkyl substances (so-called “PFAS”), a family of persistent organic pollutants [5], are widely investigated [6,7,8,9].

The displacement efficiency of the resident wetting fluid in porous media is influenced by many factors, including pore geometry, the presence of the non-wetting fluid, interfacial tension, the contact angle, the injection rate, and consecutive drainage and imbibition cycles. These factors cause uncertainty in estimating the fate of pollutants.

“Trapped air” (the non-wetting fluid) has been proven to affect the flow pattern of the wetting fluid in porous media during infiltration [10,11]. Understanding the interplay between “old water” (the resident wetting fluid) and “new water” (the invading wetting fluid) in porous media with “air” (the non-wetting fluid) helps evaluate the displacement efficiency of old water. Gouet-Kaplan and Berkowitz (2011) [12] used a 2D glass micromodel and image analysis to observe the dynamics of old-new water exchange. Gouet-Kaplan et al. (2012) [13] used conservative tracers to monitor the solute transport in column experiments. Although the experiments mentioned above [12,13] were carried out under partially saturated conditions, the effect of “air” on the old-new water interplay was not fully discussed. How the old water was trapped in the system and why the old water was unceasingly monitored in the outflow even over a long-time scale [13] were never elucidated.

Interfacial tension is the adhesive force between two substances. The displacement efficiency of the resident wetting fluid in porous media will vary with surface tension (the interfacial tension of the “air–water” interface) because this property affects the flow behavior of fluids. In a natural system, pollutants or nutrients dissolved in water can change the surface tension of the solution. For example, inorganic salts, such as NaCl and CaCl₂, would increase the surface tension [14], while some miscible pollutants, such as amines, alcohols, and other organic compounds, would reduce the surface tension of water [15].

Wettability is the ability of a liquid to adhere to a solid surface, and different porous materials have different wettability. The wettability can be expressed by measuring the contact angle between the liquid and the solid. A contact angle greater than 90° indicates a hydrophobic surface, while a contact angle less than 90° indicates a hydrophilic surface. Decreasing the contact angle increases the capillary pressure, the pressure difference across the interface between two immiscible fluids in porous media, which means that the wetting fluid will displace more of the non-wetting fluid. Therefore, the flow pattern and distribution of the resident wetting fluid in porous media will change with the contact angle.

The injection rate of the invading wetting fluid influences the displacement efficiency of the resident wetting fluid in porous media. Theoretically, a higher injection rate of the invading wetting fluid has a stronger driving force to flush out the resident wetting fluid as well as the non-wetting fluid in porous media. However, a higher injection rate may result in preferential flow in porous media so that the invading wetting fluid flows out quickly through the preferential pathway and has less opportunity to mix with the resident wetting fluid in porous media and displace it. Thus, not simply the injection rate, but whether the resident wetting fluid can mix with the invading wetting fluid is what completely determines the displacement efficiency.

“Imbibition” means increasing the saturation of the wetting fluid and decreasing the saturation of the non-wetting fluid, while “drainage” means decreasing the saturation of the wetting fluid and increasing the saturation of the non-wetting fluid. The cycle of imbibition and drainage occurs repetitively in the nature system’s unsaturated zone. Li et al. (2013) [16] conducted a series of column experiments to study the saturation–capillary pressure relation under consecutive drainage–imbibition cycles. During consecutive imbibition–drainage cycles, the saturation of the non-wetting phase (S_nw) varied in the stable and unstable states. The results revealed that the stability of trapped air in the porous medium was affected by the consecutive drainage–imbibition cycles. Tavangarrad et al. (2019) [17] evaluated the effect of multiple imbibition–drainage cycles on capillary pressure–saturation curves of thin hydrophilic fibrous layers. The result showed that if a sample was wetted in the first imbibition–drainage cycle, the capillary phenomenon would be more obvious in the next cycles. The discussion mentioned above infers that the drainage–imbibition cycles influence the two immiscible fluid–fluid flows in porous media and the displacement of the resident wetting fluid.

Several laboratory methods, such as the 2D glass micromodel [12] and the Dacry-scale column experiment [13], have been developed to study the displacement and mixing of the resident wetting fluid by the invading wetting fluid in porous media. For instance, Gouet-Kaplan and Berkowitz (2011) [12] applied dyes in the 2D glass micromodel to observe the interplay between old water and new water. Although the saturations of water can be quantified by volumetric fractions, the concentrations of water, especially the partially mixing zone, cannot be accurately quantified.

Visualizing and quantifying the interplay between the resident wetting fluid and the invading wetting fluid in porous media are useful to study the displacement efficiency of the resident wetting fluid and to evaluate related influencing factors. However, measuring the local concentration of the solute in porous media is always challenging. Although techniques based on Beer’s Law have been developed and applied to column experiments [18,19], these measurements of local concentrations are the average values over several pore sizes. They cannot meet the detection requirements for pore-scale research. Only a few experimental methods using the fluorescent tracer can precisely measure the local concentration in pores [20]. However, fluorescence analysis requires advanced skills and is not yet widely applied to pore-scale research.

Unlike traditional laboratory experiments, the computational method is a useful tool to simulate the multiphase flow in porous media for investigating the displacement efficiency of the resident wetting fluid. The simulation can provide quantified information that is difficult to measure or completely acquire in laboratory experiments. With recent advances in computational resources, several approaches, including smoothed particle hydrodynamics (SPH) [21,22,23], the lattice Boltzmann method (LBM) [24,25,26], and direct numerical simulation (DNS) [27,28], have been developed to simulate the multiphase flows in pore-scale systems.

Smoothed particle hydrodynamics (SPH) is a mesh-free Lagrangian method [21,28]. SPH regards a continuous fluid as an interacting particle group that carries various physical quantities. By solving the particle group’s dynamic equation and recording the movement of each particle, the mechanical behavior of the whole system will be obtained. The Lattice Boltzmann method (LBM), which is intrinsically a mesoscopic method to simulate fluid flows, is considered an alternative to traditional computational fluid dynamics (CFD) [28]. Unlike traditional CFD that solves macroscopic conservative equations (Navier–Stokes equations), the fluid in LBM is regarded as a discrete system composed of large numbers of particles. The behavior of these particles is described based on mesoscopic kinetic equations and then is converted to the macroscopic properties of the fluids.

In contrast to the SPH or LBM methods, direct numerical simulation (DNS) straightforwardly solves Navier–Stokes equations to obtain the instantaneous fluid physical quantities at a specific time position. DNS coupling with interface tracking and capturing approaches can truly simulate high density and high viscosity ratios of two immiscible fluids in porous media, which is always challenging in simulations [27,29]. Since the DNS method is based on conservation principles, and the simulations faithfully describe the two-phase flow and successfully capture the deformation of the fluid–fluid interface in porous media, we applied DNS coupled with the VOF method, whose model parameters were physical properties of the fluids, for the following research.

The aim of this study was to provide simulation-based evidence that supports and validates previous experimental observations. Additionally, the study sought to elucidate the potential mechanism by which the non-wetting fluid affected the separation of the resident and invading wetting fluid. With DNS, the displacements of the resident wetting fluid (w₁) by the invading wetting fluid (w₂) in porous media under different conditions were simulated. The effects of the non-wetting fluid (nw), interfacial tension (σ_w1nw), contact angle (θ), injection rate, and drainage–imbibition cycles on the displacements were evaluated by observing and quantifying the simulation results. Furthermore, the implications and significance of these simulation results for research and applications in the environmental field were discussed in the following sections.

2. Methodology

All CFD simulations in this study were performed using the finite volume method via OpenFOAM software (OpenFOAM v9) [30]. The workflow diagram of OpenFOAM was referred to as Figure A1 (Appendix A). The Navier–Stokes equations were solved by direct numerical simulation (DNS). The volume of fluid (VOF) method [31] was applied to capture the immiscible fluid–fluid interface.

2.1. Navier-Stokes Equations

The two-phase flow system studied in this article was assumed to be isothermal. Both the wetting phase and the non-wetting phase were considered incompressible. Therefore, the two-phase flow was governed by Navier–Stokes equations, of which the continuity equation (Equation (1)) and momentum equation (Equation (2)) were:

$$\nabla \cdot u=0$$

(1)

and

$$\frac{\partial \rho \mu }{\partial t}+\nabla \cdot \left(\rho uu\right)=-\nabla p+\nabla \cdot \left[\mu \left(\nabla u+\nabla u^T\right)\right]+F_s$$

(2)

where u, ρ, μ, p, and F_s denoted velocity, density, viscosity, pressure, and surface force, respectively.

2.2. Volume of Fluid (VOF) Method

The VOF method was a surface-tracking approach in CFD for tracking the motion of an immiscible fluid–fluid interface applied in Eulerian mesh [31]. In a two-phase flow system, each phase was represented by its volume fraction α (α = 1 referred to as fully occupied by the wetting phase, while α = 0 referred to as fully occupied by the non-wetting phase), and the interface grid cells were represented by the intermediate values of α (0 < α < 1). Moreover, the density (ρ) and viscosity (μ) varied in space and time were expressed as follows:

$$\left\{\begin{array}{c}\rho =\alpha {\rho }_w+(1-\alpha ){\rho }_{nw}\\ \mu =\alpha {\mu }_w+(1-\alpha ){\mu }_{nw}\end{array}\right.$$

(3)

where the subscripts “w” denoted the wetting phase and “nw” denoted the non-wetting phase. The volume fraction α was obtained by solving a simple advection equation (Equation (4)) as follows:

$$\frac{\partial \alpha }{\partial t}+\nabla \cdot \left(\alpha u\right)+\nabla \cdot \left(\alpha \left(1-\alpha \right)u_r\right)=0$$

(4)

where u_r was the relative velocity between two phases.

Additionally, the surface force (F_s) imposed on the interface and changing with volume fraction was expressed as F_s = σk∇α, where σ is the interfacial tension and k is the curvature of the interface. The curvature of the interface k, defined as the divergence of a unit normal vector $\widehat{n}$, was expressed as $\kappa =-\nabla \cdot \widehat{n}=-\nabla \cdot \left(\frac{\nabla \alpha }{‖\nabla \alpha ‖}\right)$. The wettability was expressed by the static contact angle (θ) following the equation $\widehat{n}={\widehat{n}}_{w}cos\theta +{\widehat{t}}_{w}cos\theta$, where ${\widehat{n}}_w$ and ${\widehat{t}}_w$ were the unit normal vector to the solid and the unit tangent vector to the solid, respectively [28,32,33].

In this study, OpenFOAM’s solver interMixingFoam, which was developed for 3 incompressible fluids of which 2 were miscible, was selected to implement the computation. The interMixingFoam solver was developed based on the interFoam solver (for 2 incompressible and immiscible fluids). The performance of the interFoam solver using the VOF approach based on OpenFOAM was evaluated by Deshpande et al. in 2012 [34], and the result indicated that the algorithm of the solver ensured a consistent formulation of pressure and interfacial tension. As for the mixing of the two miscible fluids, the resident wetting fluid (w₁) and the invading wetting fluid (w₂), the process was regarded as a solute transport phenomenon and described as the following advection–diffusion equation:

$$\frac{\partial C}{\partial t}+u\cdot \nabla C-\nabla \cdot \left(D_m\nabla C\right)=0$$

(5)

where C is the concentration of w₁ (or w₂) and D_m is the diffusivity.

2.3. Numerical Domain, Boundary, and Initial Conditions

All the numerical domains were two-dimensional (2D) square geometries (7.5 mm × 7.5 mm) containing N cylindrical grains (solid obstacles) with radii of R. Six micromodels (Appendix A Figure A2 were used in this study. Micromodel 1, Micromodel 2, and Micromodel 3 had the same grain size and porosity, but they were different in the spatial distribution of the grain. Micromodel 4 and Micromodel 5 had similar porosity to Micromodel 1 (Micromodel 2, Micromodel 3), but had different grain sizes and pore throats, which would result in different capillary pressure. Micromodel 6 had the same grain size as Micromodel 1 (Micromodel 2, Micromodel 3), but had larger porosity. The porosities of Micromodel 1 (the same as Micromodel 2 and Micromodel 3), Micromodel 4, Micromodel 5, and Micromodel 6 were 49.73% (N = 36, R = 5 × 10⁻⁴ m), 48.39% (N = 64, R = 3.8 × 10⁻⁴ m), 49.73% (N = 25, R = 6 × 10⁻⁴ m), and 65.09% (N = 25, R = 5 × 10⁻⁴ m), respectively.

All the domains were meshed by OpenFOAM’s mesh generators, blockMesh and snappyHexMesh. The mesh generation process was described as follows: (1) The blockMesh generated structured hexahedral meshes as the background mesh; (2) the snappyHexMesh generated high-quality hexahedral and split-hexahedral meshes near the surface of the geometry. To ensure the accuracy of the simulations while saving computational resources, the mesh discretization in this study was based on the evaluation results of Ferrari and Lunati (2013) [27]. Ferrari and Lunati (2013) [27] used DNS coupled with the VOF method via OpenFOAM to simulate the immiscible fluid–fluid flow in a porous system similar to the pore structures adopted in this study (a 2D domain containing cylindrical obstacles). Five different discretization levels, defined by d/Δx (where d represents the mean pore diameter and Δx represents the typical cell size), including d/Δx = 8, 12, 15, 24, and 48, were tested to assess the effect of discretization on the simulation. The result showed that the difference between d/Δx = 8 and the finest mesh d/Δx = 48) was approximately 15%, while the relative errors of the others (d/Δx = 12, 15, 24) were all within 10%. In this study, d/Δx ≈ 12 was selected to construct the mesh. The total number of mesh cells for Micromodel 1, Micromodel 2, Micromodel 3, Micromodel 4, Micromodel 5, and Micromodel 6 were 38,780, 38,673, 38,769, 48,284, 33,877, and 33,371, respectively.

The left boundary was set up as an inlet with constant velocity and the right boundary was set up as an outlet with constant pressure zero. The solid phase, including top and bottom boundaries, and solid obstacles, were set up as “no-slip” conditions. In this study, a series of simulations of the displacement of w₁ by w₂ in porous media with or without nw were implemented. All the properties for simulations are listed in

Table 1. Properties of the fluids used in the simulations.

Parameter	Value	Unit
density, ρw1	1000	kg/m3
density, ρw2	1000	kg/m3
density, ρnw	1	kg/m3
kinetic viscosity, νw1	10−6	m2/s
kinetic viscosity, νw2	10−6	m2/s
kinetic viscosity, νnw	1.48 × 10−5	m2/s
interfacial tension, σw1nw	0.0707	kg/s2
interfacial tension, σw2nw	0.0707	kg/s2
Diffusivity, Dw1w2	3 × 10−9	-
contact angle, θ	45	° (degree)

.

To evaluate the effect of the non-wetting phase (Section 3.1), Micromodel 1 under different conditions, with and without nw, was simulated for comparison. Initially, the system was assumed to be filled with w₁. As for the condition without nw, w₂ was directly injected into the system at a constant rate (0.05 m/s). As for the condition with nw, nw was first injected into the system at a constant rate (0.05 m/s). After dynamic balance, w₂ was injected into the system at a constant rate (0.05 m/s), and monitoring of the displacement started.

To evaluate the effects of interfacial tension (σ_w1nw) and contact angle (θ) (Section 3.2), three micromodels (Micromodel 1, Micromodel 2, and Micromodel 3) with little difference in the spatial distribution of the grain were adopted to avoid an extremely abnormal result causing misinterpretation. All the simulations were assumed under the condition with nw. At first, nw was injected into the system, which was assumed to be initially filled with w₁, at a constant rate (0.05 m/s). After dynamic balance, w₂ was injected into the system at a constant rate (0.05 m/s), and monitoring of the displacement started. During the injection process of nw, all the parameters for simulation were the same as in Table 1 to ensure that the initial conditions for all cases were identical. When w₂ started entering the system, the parameters, interfacial tension (σ_w1nw), or contact angle (θ) were changed for comparison.

To evaluate the effect of the injection rate (Section 3.3), Micromodel 2 was simulated at different injection rates of w₂ for comparison under the condition with nw. At first, nw was injected into the system, which was assumed to be initially filled with w₁, at a constant rate (0.05 m/s). After dynamic balance, w₂ was injected into the system at a constant rate and monitoring of the displacement started. As for the high injection rate condition, the rate was 0.05 m/s for 0.2 s, while for the low injection rate condition, the rate was 0.01 m/s for 1 s.

To evaluate the effect of drainage–wetting cycles (Section 3.4), the micromodels (Micromodel 1~Micromodel 6) were simulated by injecting two cycles of nw followed by w₂ into the system. Initially, the system was assumed to be filled with w₁. Then nw, w₂, nw, and w₂ were sequentially injected into the system at a constant rate (0.05 m/s) for 0.15 s.

2.4. Quantification of Fluid Saturations

Based on the simulations mentioned in Section 2.3, all the computed results, including α_w1, α_w2, and α_nw, were recorded. To further investigate the displacement efficiency, the fluid saturations were quantified using the data extracted from the simulation results at each time step. The fluid saturations (S) were calculated as follows:

$$S_{w1}=\frac{\sum _{i=1}^n{\alpha }_{w1}}{\sum _{i=1}^n\left({\alpha }_{w1}+{\alpha }_{w2}+{\alpha }_{nw}\right)}$$

(6)

$$S_{w2}=\frac{\sum _{i=1}^n{\alpha }_{w2}}{\sum _{i=1}^n\left({\alpha }_{w1}+{\alpha }_{w2}+{\alpha }_{nw}\right)}$$

(7)

$$S_{nw}=\frac{\sum _{i=1}^n{\alpha }_{nw}}{\sum _{i=1}^n\left({\alpha }_{w1}+{\alpha }_{w2}+{\alpha }_{nw}\right)}$$

(8)

where n was the total number of cells in the simulation. All the saturation data, including S_w1, S_w2, and S_nw, mentioned in this study were quantified using the central area (the quadrilateral region was formed by the four centers of circles in four corners, such as the yellow quadrilateral in Figure 1). In addition, the normalized concentration (C/C₀) represented in Figure 2 was defined as the following equation:

$$\frac{C}{C_0}=\frac{\sum _{i=1}^n{\left({\alpha }_{w1}\right)}_{t=i}}{\sum _{i=1}^n{\left({\alpha }_{w1}\right)}_{t=0}}$$

(9)

3. Results and Discussions

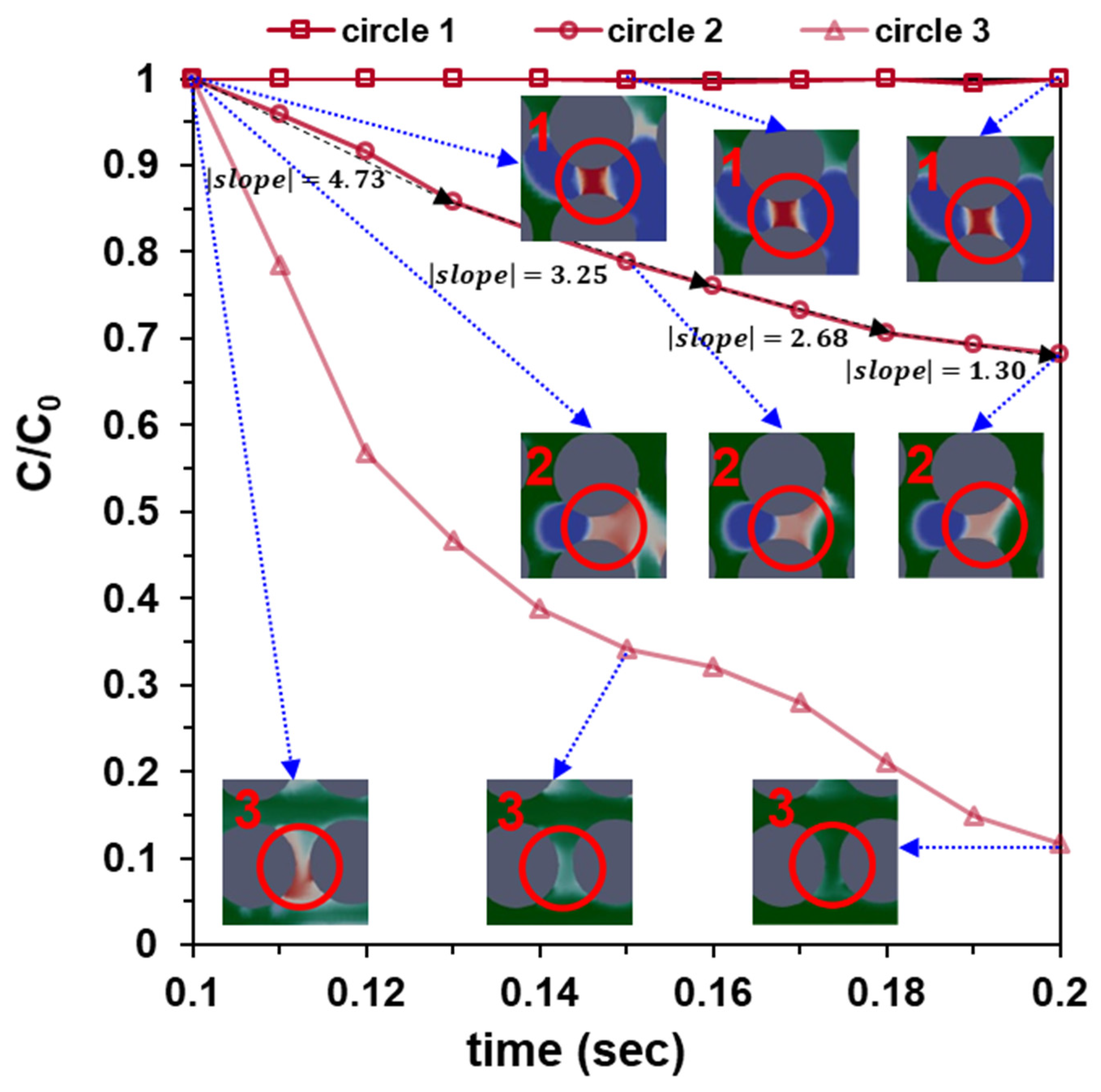
3.1. Effect of the Non-Wetting Phase (nw)

Figure 1 compares the displacement processes of w₁ by w₂ in porous media under the condition without nw to the condition with nw. From Figure 1a, it can be observed that w₁ in the porous system (Micromodel 1) without nw gradually mixed with w₂ and was displaced. On the other hand, Figure 1b shows that when nw existed in the porous system, nw would hinder the displacement of w₁. Even though nw was partially flushed out of the system, nw remained in the system and hindered the displacement of w₁ either by trapping it, such as the red circle 1 region in Figure 1b (C/C₀ remained constant in Figure 2), or by limiting the interaction of w₂ with w₁, such as in Figure 1b shown by the red circle 2 region. In the red circle 1 region, w₁ was trapped by nw and could not contact w₂. In the red circle 2 region, nw occupied the main flow path of the displacement, thus impeding the mixing of w₁ and w₂. This result indicated that the remaining nw in the porous system would affect the displacement of w₁ by w₂.

Ideally, w₁ should be totally displaced by w₂ after a long period of flushing. However, based on the column experiments implemented by Gouet-Kaplan et al. (2012) [13], the old water was still released from the unsaturated porous media over a long period of flushing by the new water. The phenomenon can be interpreted from pore scale observation and quantification based on simulation results in this study. Figure 2 shows the normalized concentration (C/C₀) of w₁ in Figure 1b red circle regions versus time. In Figure 2, the time span was from t = 0.1 s to t = 0.2 s in Figure 1b, where t = 0.1 s represented the start of monitoring and t = 0.2 s represented the end of monitoring. In the red circle 1 region, C/C₀ remained constant, which meant that w₁ was totally trapped by nw. In the red circle 2 region, C/C₀ decreased to 85.8% (|slope| = 4.73) from t = 0.1 s to t = 0.13 s, decreased to 76.0% (|slope| = 3.25) from t = 0.13 s to t = 0.16 s, decreased to 70.7% (|slope| = 2.68) from t = 0.16 s to t = 0.18 s, and decreased to 68.1% (|slope| = 1.30) from t = 0.18 s to t = 0.2 s. The more and more slow decrease in C/C₀ implied that w₁ would be continuously released even after a long period of flushing. In the red circle 3 region, C/C₀ significantly decreased to 34.2% from t = 0.1 s to t = 0.15 s and continuously decreased to 11.8% from t = 0.15 s to t = 0.2 s. This indicated that w₁ would be gradually displaced without the interference of nw. The results of Figure 2 illustrated that when nw occupied the main path for displacement, w₁ nearby nw would not be easily displaced completely and only be partially released very slowly.

Although not all the remaining nw in porous media hindered the displacement of w₁, more nw pockets indicated more opportunity to cause the phenomenon of slow release of w₁ mentioned above.

Table 2. Summary of the displacement results under the condition with nw.

Micromodel	Porosity (%)	Average Pore Radius (m)	Average Pore Throat (m)	Number of the Remaining nw Pockets	Final Image
Micromodel 1	49.73	3.53 × 10−4	2.39 × 10−4	4
Micromodel 2	49.73	3.53 × 10−4	2.36 × 10−4	3
Micromodel 3	49.73	3.53 × 10−4	2.38 × 10−4	6
Micromodel 4	48.39	2.63 × 10−4	1.66 × 10−4	12
Micromodel 5	49.73	4.41 × 10−4	2.73 × 10−4	1
Micromodel 6	65.09	5.24 × 10−4	4.37 × 10−4	3

summarizes the displacement results of all six micromodels under the conditions with nw. Micromodel 1, Micromodel 2, and Micromodel 3 (the three micromodels were slightly different in the grain distribution) had different remaining nw pockets and distributions, which resulted in very different displacement and mixing of w₁. The slight differences in geometry could result in significant displacement results when nw is involved.

Theoretically, the capillary pressure increases with decreasing the pore throat size (Young–Laplace equation $p_c=\frac{2\sigma cos\theta }{r}$, where p_c is the capillary pressure, r is the mean curvature, σ is the interfacial tension, and θ is the contact angle). Therefore, the snap-off phenomenon occurs more easily in porous media with narrower pore channels due to the larger interfacial instability between two immiscible fluids, leading to more nw pockets trapped in the pores. For the micromodels (Micromodel 1, Micromodel 4, and Micromodel 5) with similar porosity and different average pore throats, the number of remaining nw pockets increased with decreasing the average pore throat. Micromodel 4, with the smallest average pore throat (1.66 × 10⁻⁴ m), had the maximum number of the remaining nw pockets, which implied that it was the most difficult to completely displace w₁ in Micromodel 4. As for Micromodel 6, whose porosity (65.09%) is much larger than the other five micromodels (49.73% or 48.39%), the number of the remaining nw pockets was basically smaller than others, except Micromodel 5.

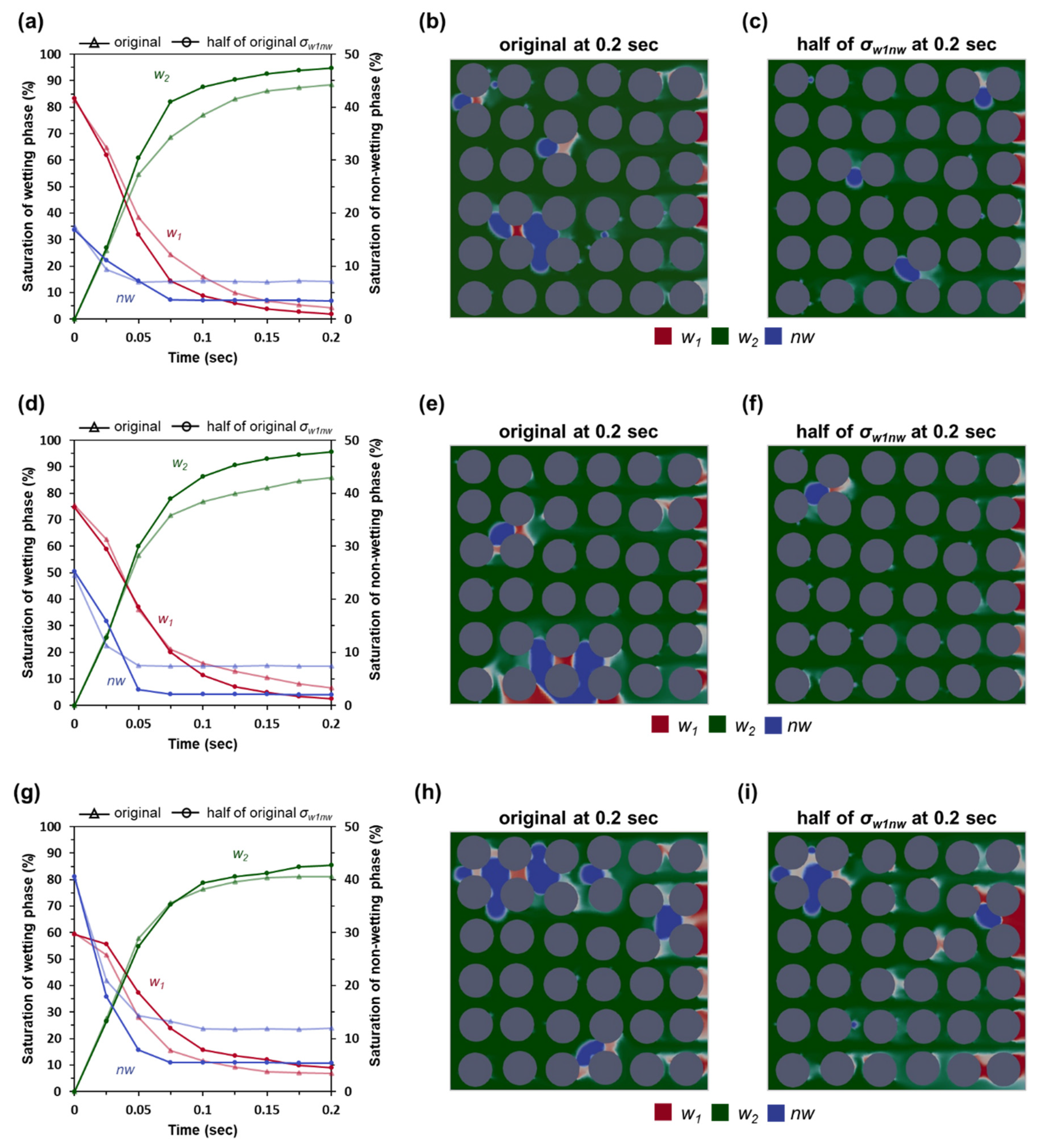
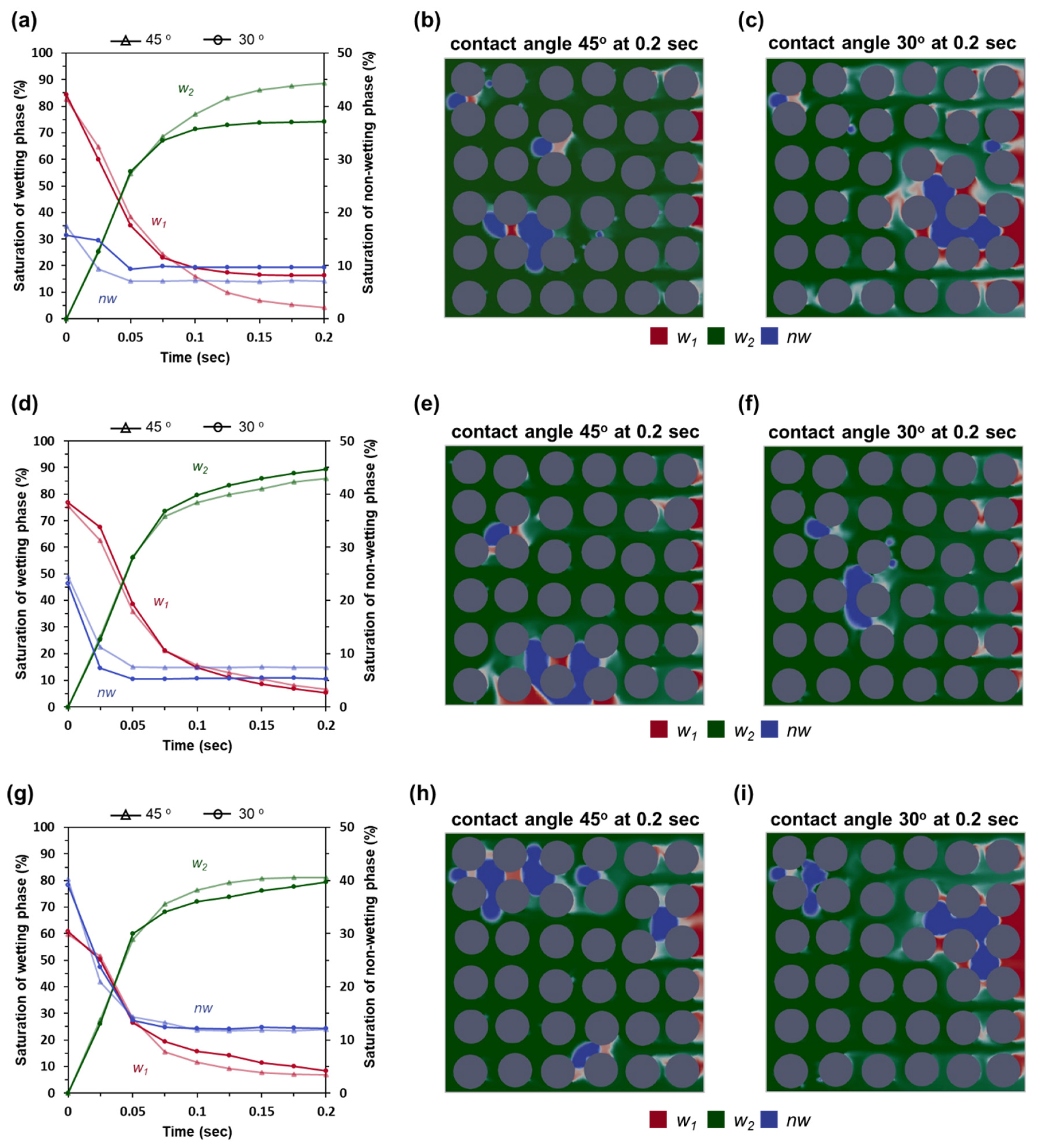
3.2. Effects of Interfacial Tension (σ_w1nw) and Contact Angle (θ)

Figure 3 shows fluid saturations versus time during displacement with different interfacial tensions (σ_w1nw) between w₁ and nw and images of displacement results at t = 0.2 s. All the properties of fluids for simulation were the same as in Table 1 and σ_w1nw decreased to half of the original value for comparison when w₂ started entering the system. When the properties listed in Table 1 were applied to the simulations of Micromodel 1, Micromodel 2, and Micromodel 3, in which w₁ and w₂ have the same density (ρ), viscosity (ν), and interfacial tension (σ), the S_w1 of Micromodel 1, Micromodel 2, and Micromodel 3 were 4.30%, 6.67%, and 6.85% at t = 0.2 s, respectively. All three cases had a similar phenomenon in that some w₁ were trapped by nw and some nw occupied the main flow paths, resulting in the incomplete mixing zones of w₁ and w₂ (Figure 3b,e,h).

When σ_w1nw decreased to 0.03535 kg/s² (half of the original value), S_w1 of Micromodel 1 and Micromodel 2 decreased to 1.88% and 2.48% at t = 0.2 s, but that of Micromodel 3 increased to 9.10%, even higher than the original simulation result (6.85%). Based on Figure 3c,f,i, it could be found that, unlike the original simulation results, most of nw were flushed out and could not interfere with the displacements of w₁. However, when nw remained in the system, the displacement of w₁ was still significantly hindered by nw.

Figure 4 showed fluid saturations versus time during displacement with different contact angles (θ) and images of displacement results at t = 0.2 s. All the properties of fluids for simulation were the same as in Table 1 and θ decreased from 45° to 30° for comparison when w₂ started entering the system. Figure 4a,d,g shows that when the contact angle (θ) was adjusted from 45° to 30°, the displacement results were different with no rules. For Micromodel 1, S_nw slightly increased from 7.13% to 9.67%, but S_w1 dramatically increased from 4.30% to 16.24%. For Micromodel 2, S_nw decreased from 7.42% to 5.32%, and S_w1 decreased from 6.67% to 5.34%. For Micromodel 3, S_nw increased from 11.95% to 12.17%, and S_w1 increased from 6.85% to 8.35%. Based on Figure 4b,c,e,f,h,i, it could be found that a change in the contact angle (θ) affected the distribution of the remaining nw in the porous system. This result implied that the contact angle (θ) influenced the immiscible fluids flow pattern, thus causing a different displacement efficiency of w₁.

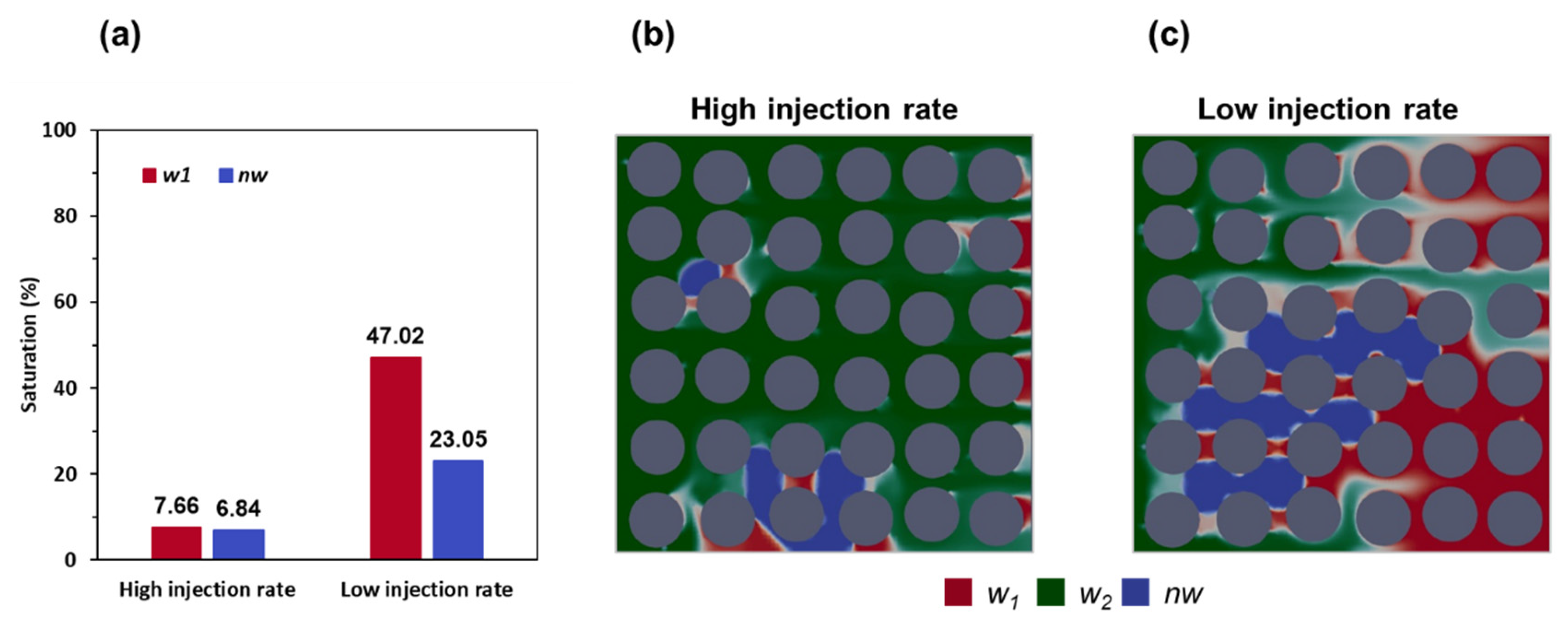
3.3. Effect of Injection Rate

Figure 5 shows fluid saturations under different injection rate conditions (Figure 5a) and images of displacement results (Figure 5b,c). All the properties of fluids for simulation were the same as in Table 1. Based on Figure 5a, it could be found that S_nw under a low injection rate condition (0.01 m/s) is much larger than under a high injection rate condition (0.05 m/s) because a lower driving force (Capillary number C_a = 1.41 × 10⁻⁴) could not effectively flush out nw. In addition, w₁ was not efficiently displaced by w₂ under low injection rate conditions. This result implied that low injection rates might cause more of nw to remain in the porous medium, which could hinder the displacement of w₁.

Figure 5c shows that although w₂ displaced w₁ through contact areas, nw did block some routes (longitudinal direction) and prevent w₂ from mixing with w₁. When there was more nw remaining in the porous medium, the displacement of w₁ was easier interfered with by the remaining nw. This result demonstrated that a very low injection rate (0.01 m/s) could not effectively displace w₁ by w₂ in porous media with nw.

3.4. Effect of Drainage–Imbibition Cycles

Figure 6 shows the fluid saturations after drainage–imbibition cycles. All the properties of fluids for simulation were the same as in Table 1. Initially, the system was assumed to be filled with w₁, and then two cycles of nw followed by w₂ were injected into the system. Based on Figure 6, it could be significantly observed that the S_w1 was lower after the second cycle than after the first cycle in all six micromodels (one cycle represented one drainage–imbibition process). This result inferred that the drainage–imbibition cycles could improve the displacement of w₁. For instance, the S_w1 decreased from 6.84% (first cycle) to 1.46% (second cycle) in Micromodel 1. However, it could be observed that the S_nw, the crucial factor affecting the displacement of w₁, decreased in Micromodel 3 (from 11.80% to 7.45%), Micromodel 4 (from 15.60% to 13.42%), and Micromodel 6 (from 13.26% to 10.57%), but increased in Micromodel 1 (from 7.01% to 12.03%), Micromodel 2 (from 7.51% to 14.28%), and Micromodel 5 (from 5.54% to 9.50%).

From Figure 6, it could be found that the distributions of nw after the first cycle were different from those after the second cycle. Some of w₁ originally trapped or limited by nw after the first cycle re-contacted w₂ and were displaced by them during the second cycle. Micromodel 1, Micromodel 2, and Micromodel 3 had the same porosity and similar average pore throats. Although the hindrance patterns of nw on the displacement of Micromodel 1, Micromodel 2, and Micromodel 3 were different, causing significantly different S_w1 after the first cycle, when the regions where nw hindered the displacements of w₁ were broken during the second cycle process, the S_w1 of the three micromodels were similar after the second cycle (Figure 6a–c).

However, not all the regions where nw hindered the displacements of w₁ formed during the first cycle would be broken during the second cycle. In Micromodel 4, the one originally with the maximum number of the remaining nw pockets due to its smallest average pore throat, the region where w₁ was trapped by nw (the upper middle area of the micromodel) still existed after the second cycle (Figure 6d). Even in a micromodel with a larger average pore throat, it did not mean that nw, which hindered the displacement, would be absolutely removed. In Micromodel 5, the one with similar porosity to Micromodel 1 and Micromodel 4 but with a larger average pore throat, the slightly upper right area in the middle of the micromodel continuously affected the displacement of w₁ after the second cycle (Figure 6e) although the S_w1 significantly decreased during the second cycle process.

In Micromodel 6, the one with the largest porosity of all six micromodels, the S_w1 decreased from 12.96% (first cycle) to 3.19% (second cycle). The decrease in S_w1 was more obvious than those of other micromodels with lower porosity. This was because when one nw pocket, which originally hindered the displacement of w₁ after the first cycle, was removed after the second cycle, a large amount of w₁ was rapidly displaced by w₂. This result implied that the effect of the drainage–imbibition cycle on the displacement of w₁ was more significant in micromodels with larger porosity.

3.5. Environmental Significance

Based on the above simulation results, we evaluated the factors affecting the displacement of w₁ by w₂ in the porous media and successfully investigated the potential mechanism. Furthermore, these simulation findings not only provided new directions for academic research but also contributed to a more comprehensive perspective and a deeper understanding of engineering applications.

In Section 3.1, it was demonstrated that the phenomena observed in Darcy-scale experiments or field experiments can be explained through pore-scale simulations without being limited by traditional experimental designs or quantitative techniques. For instance, this study utilized pore-scale simulation results to elucidate the “slow-release phenomenon of old water” observed in previous column experiments.

In Section 3.2, we gained a more comprehensive understanding of the removal of pollutants in the unsaturated zone. For instance, the surface tension of perfluorooctanesulfonic acid (PFOS), a type of PFAS, varies with its concentration [7], which could lead to significant variations in displacement efficiency, even under the same spatial distribution conditions. Moreover, as the water evaporated, the pollutants dissolved in the resident water within the porous system would change in concentration, thereby altering the surface tension of the solution and further affecting the displacement.

In Section 3.3, we learned that in contrast to what was presented in the literature [26], a high injection rate did not necessarily result in a lower opportunity for the interaction between new and old water due to preferential flow. In this study, a high injection rate may lead to significant displacement efficiency as it facilitated the effective flushing out of the non-wetting fluid.

In Section 3.4, we understood that the drainage–imbibition cycles facilitated the displacement of w₁. Since this cycle occurs repetitively naturally in the environment, this finding carries not only theoretical implications but also practical significance in guiding future soil remediation strategies.

In the porous system’s simulation, the capillary action of the wetting fluid was quite crucial because of the narrow pore channels, causing a significant pressure difference across the interface between two immiscible fluids. In SPH, the surface tension was not prescribed explicitly but was set by adding assumed forces between different particles [21]. Similar to SPH, the surface tension was modeled by using special forces between the lattice nodes in LBM [26,28]. With the advantage of DNS, parameters for simulation being the physical properties of the fluids, the computational method used in this study could authentically simulate other immiscible fluid–fluid flows in porous media. Combined with three-dimensional (3D) imaging techniques [35], which could reconstruct real porous structures, this method could easily predict the flow patterns in natural porous systems under different conditions by adjusting the physical properties (simulation parameters) without lab or field experiments.

4. Conclusions

This study simulated the displacement of w₁ by w₂ in porous media using DNS. A series of displacement simulations were carried out under different conditions. Using observation and quantification based on simulation results, the main conclusions can be summarized as follows:

(1)

When nw existed in the porous system, the displacement of w₁ by w₂ would be impeded. By calculating (C/C₀) of w₁ in the regions hindered by nw, it could be observed that w₁ was displaced very slowly. This result helped explain the “slow-release phenomenon of old water” in previous column experiments.

(2)

When σ_w1nw decreased to half of the original value, the S_w1 would decrease because most of nw was flushed out. A change in contact angle (θ) caused a different distribution of nw in the system, which could result in a different displacement efficiency of w₁.

(3)

At a very low injection rate = 0.01 m/s, w₂ could not effectively displace w₁ in porous media because of the remaining nw.

(4)

The drainage–imbibition cycles could improve the displacement of w₁ in porous media because the constrained regions caused by nw were broken during consecutive drainage–imbibition cycles.

(5)

The simulation results have significantly advanced our understanding of future research and applications. In addition, the DNS method authentically described the immiscible fluid–fluid flow in porous media and could be easily applied to study physical mechanisms in other natural or industrial systems.