Experimental Investigation of Coastal Flooding Hydrodynamics Using a Hybrid Defense System
Abstract
:1. Introduction
2. Materials and Methods
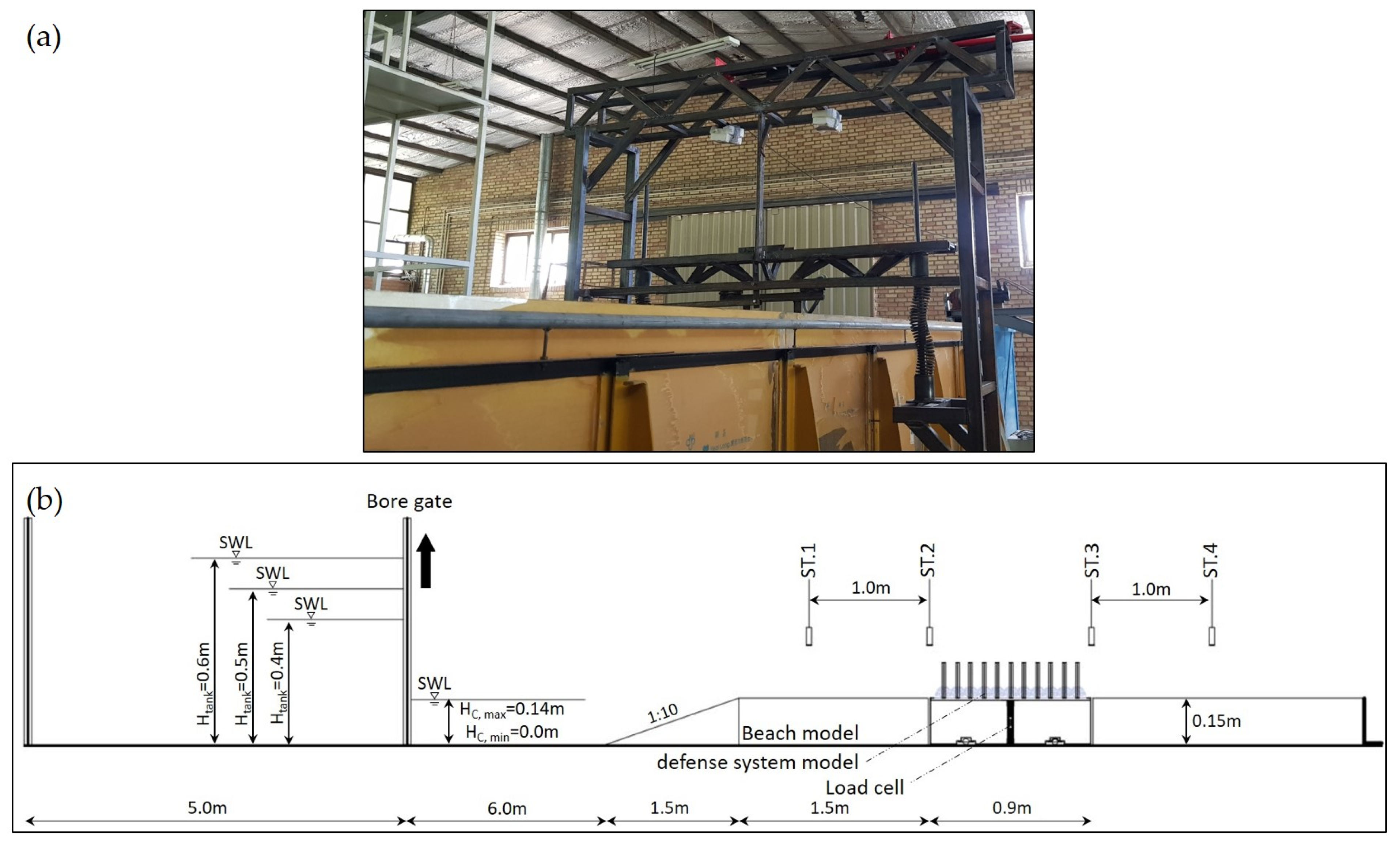
2.1. Experimental Apparatus and Procedures
2.2. Measurement Method
2.3. Examined Parameters
2.3.1. Flow Velocity Reduction
2.3.2. Reflection Coefficient
2.3.3. Hydrodynamic Force
2.3.4. Force and Moment Indices
3. Results and Discussion
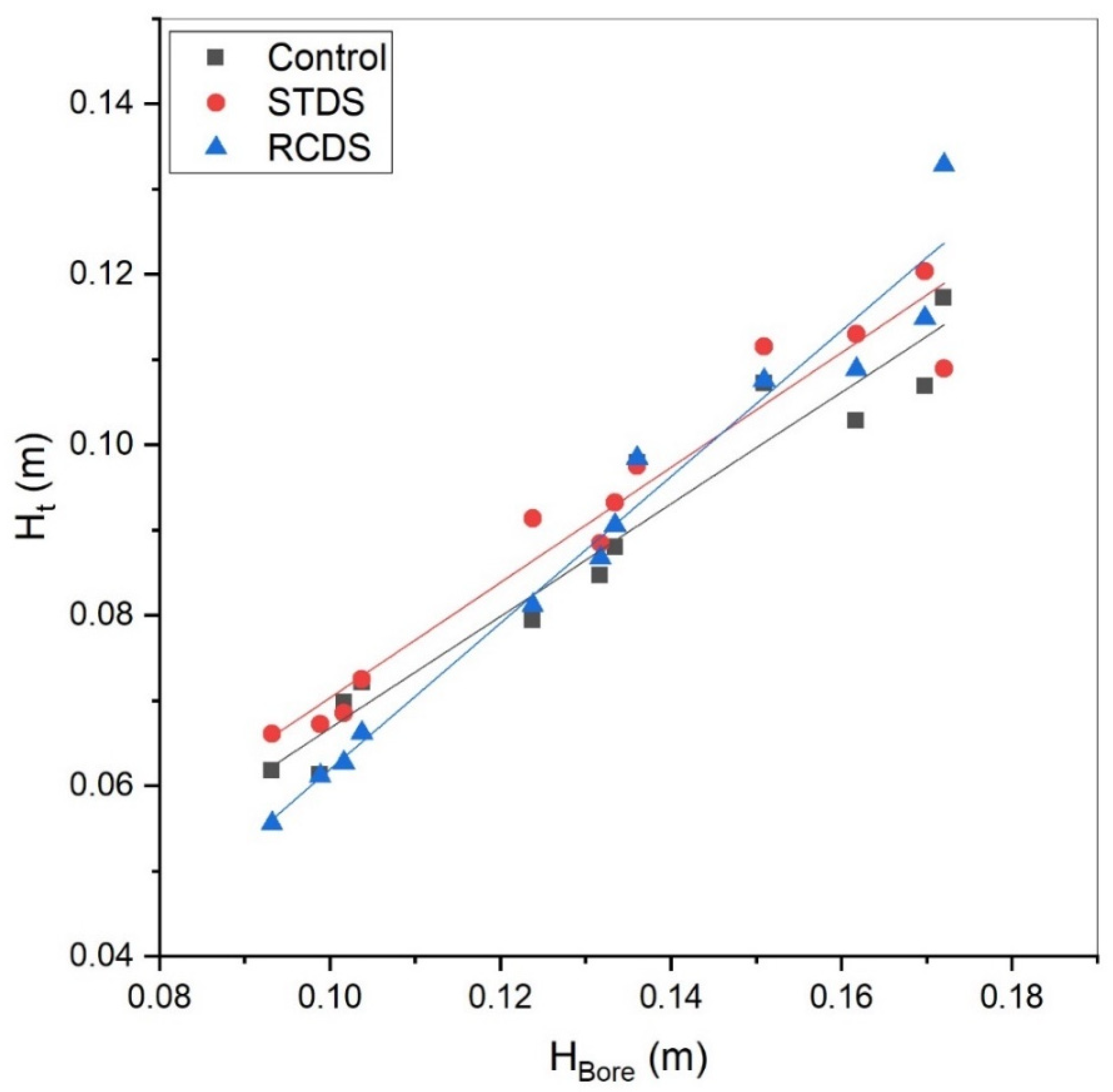
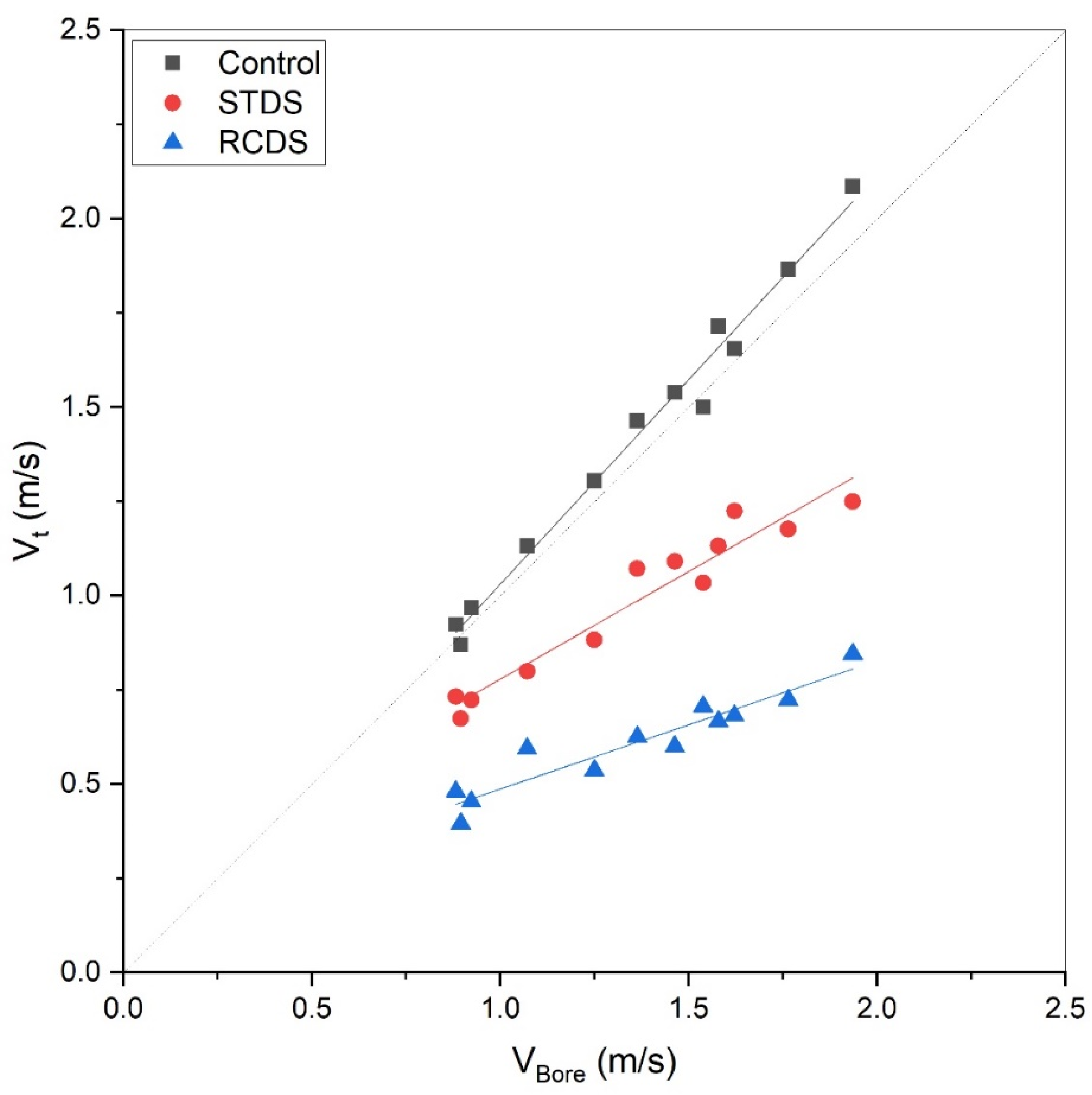
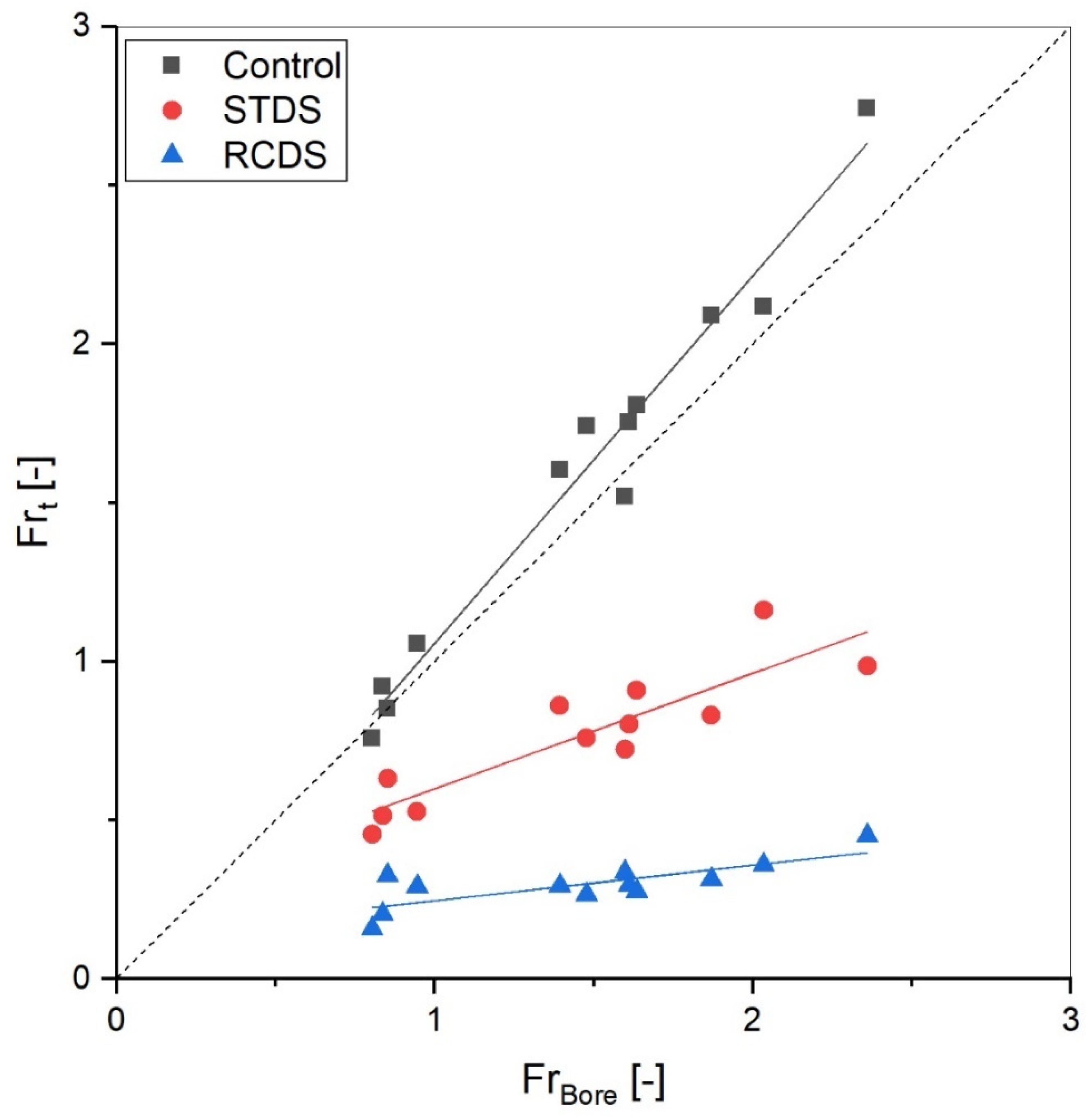
3.1. Generated Bore Characteristics
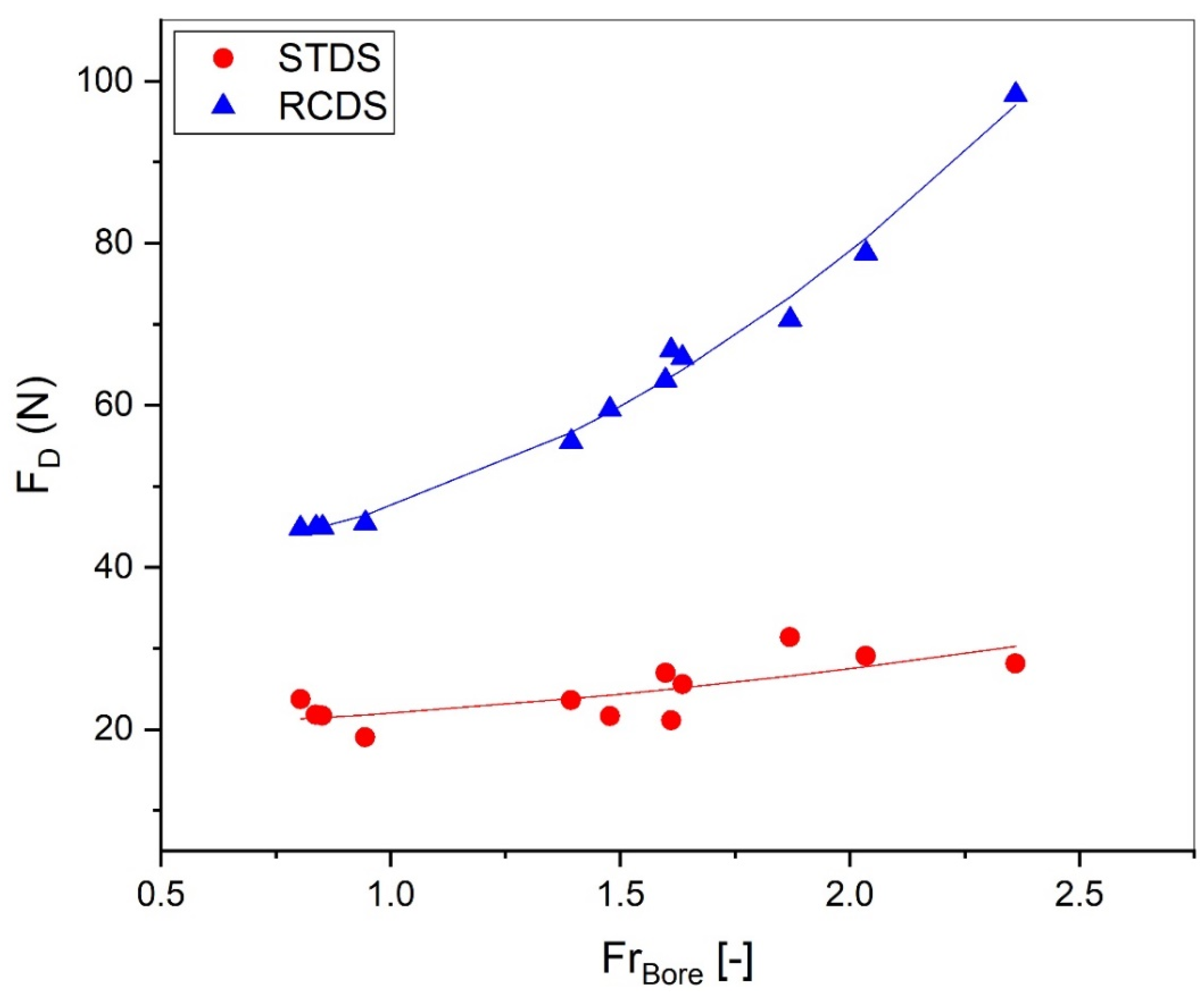
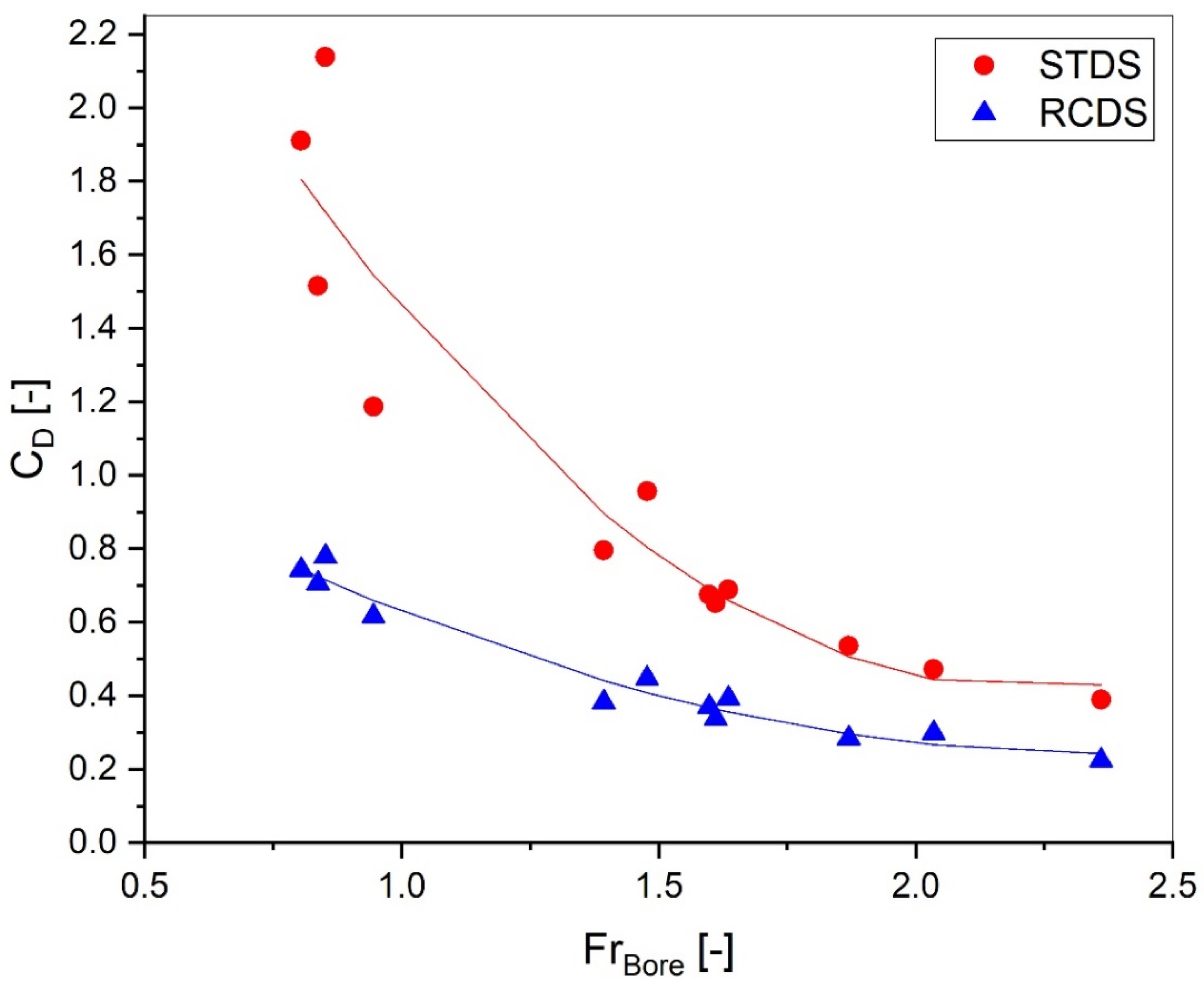
3.2. Drag Forces
3.3. Defense System Performance
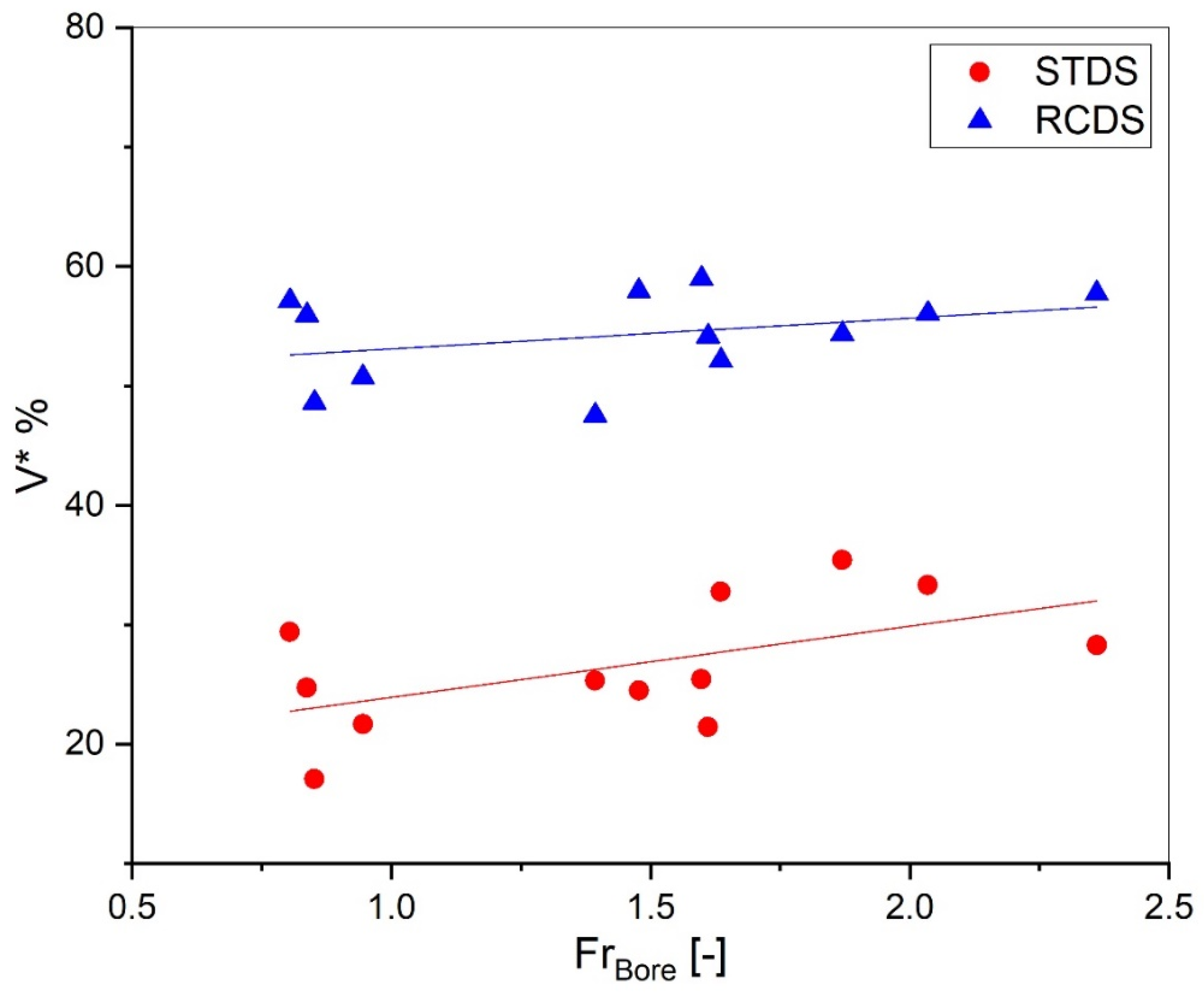
3.3.1. Effect on Velocity Reduction Rate
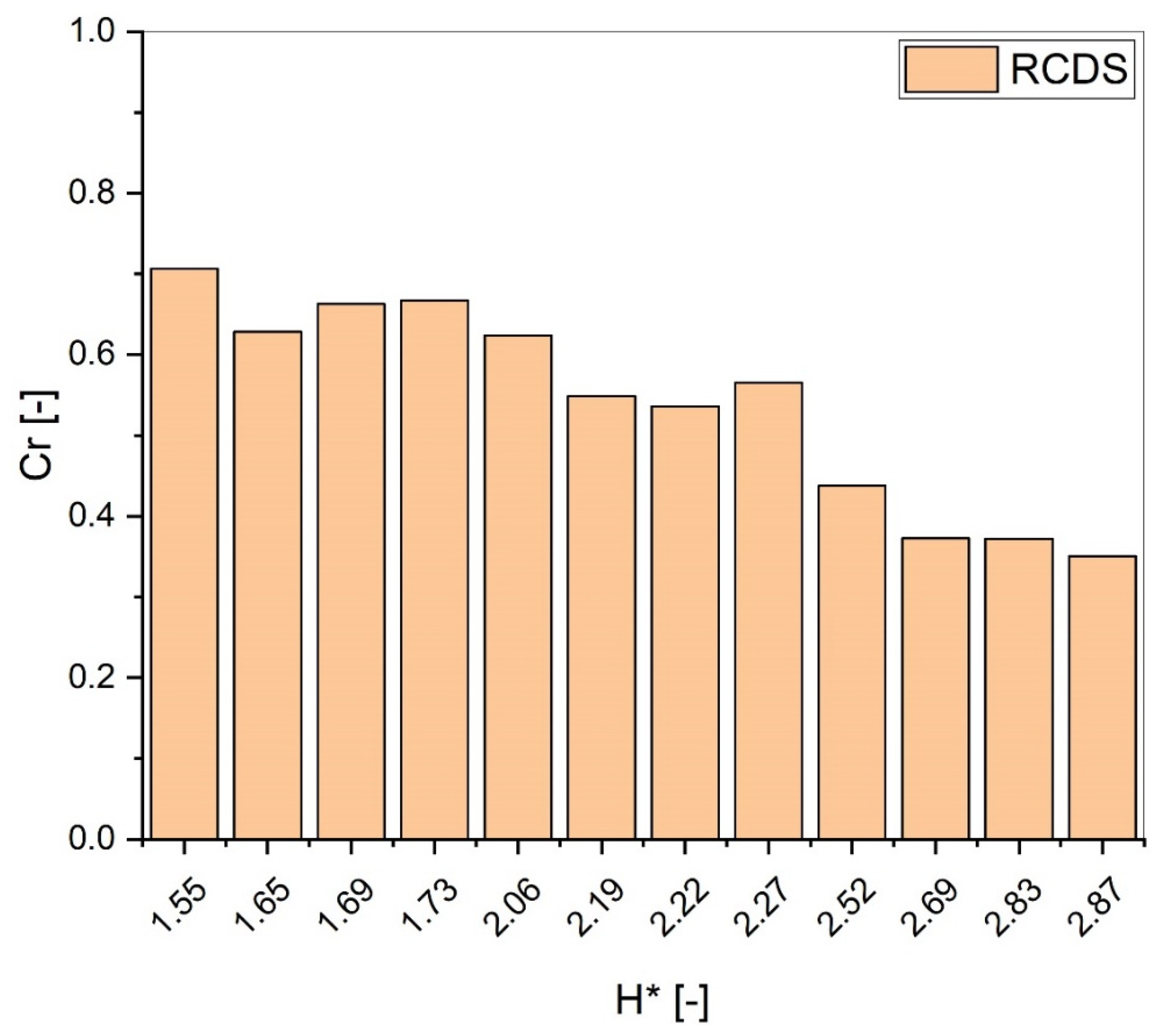
3.3.2. Effect on Reflection Coefficient
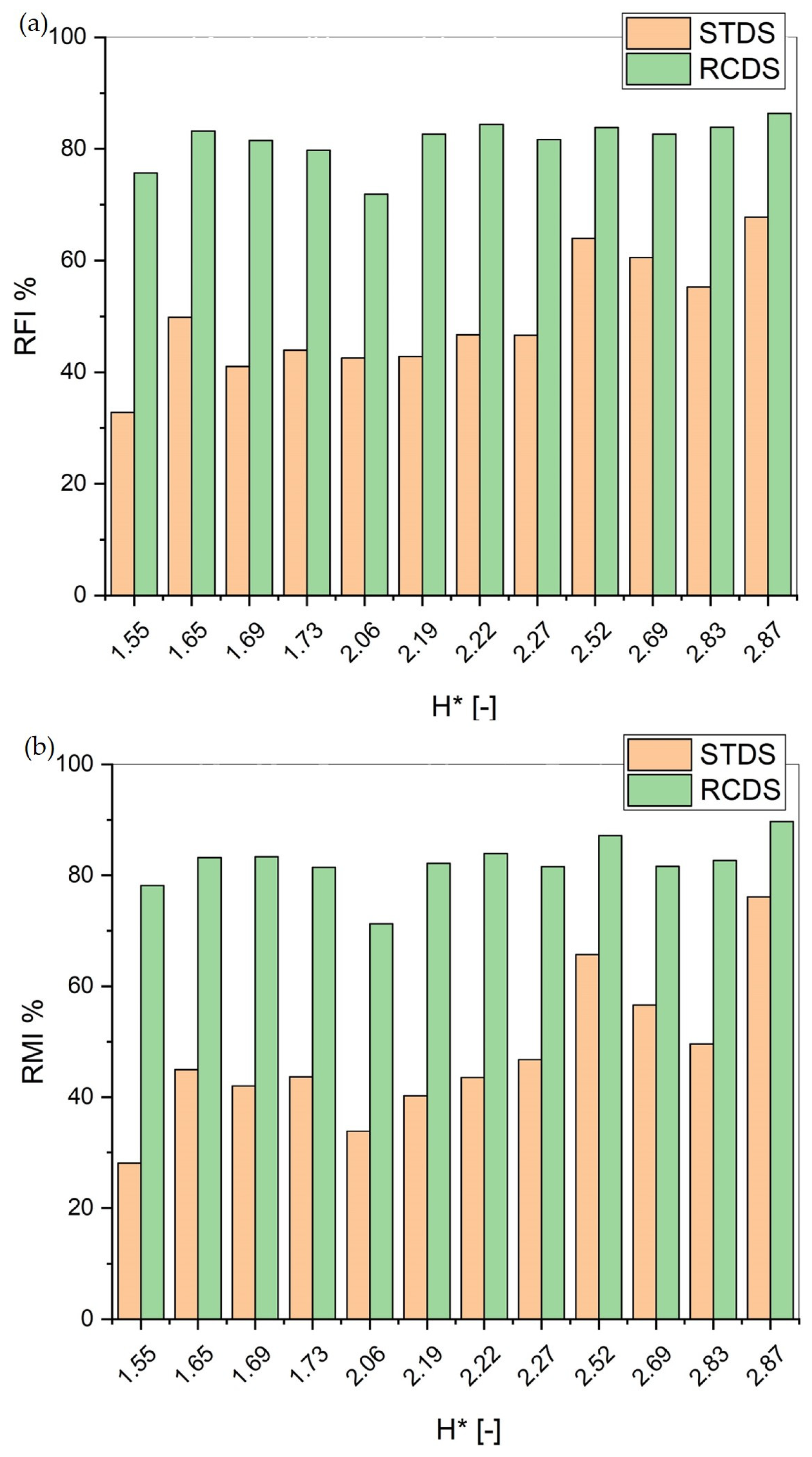
3.3.3. Effect on RFI and RMI
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, T.J.; Anderson, G.H.; Balentine, K.; Tiling, G.; Ward, G.A.; Whelan, K.R. Cumulative impacts of hurricanes on Florida mangrove ecosystems: Sediment deposition, storm surges and vegetation. Wetlands 2009, 29, 24–34. [Google Scholar] [CrossRef]
- Sutton-Grier, A.E.; Wowk, K.; Bamford, H. Future of our coasts: The potential for natural and hybrid infrastructure to enhance the resilience of our coastal communities, economies and ecosystems. Environ. Sci. Policy 2015, 51, 137–148. [Google Scholar] [CrossRef] [Green Version]
- Yeganeh-Bakhtiary, A.; Hamze Ziabari, S.M. Prediction of Infra-Gravity Swash Motions on Natural Beaches using Model Trees. Amirkabir J. Civ. Eng. 2018, 50, 445–452. [Google Scholar]
- Kalourazi, M.Y.; Siadatmousavi, S.M.; Yeganeh-Bakhtiary, A.; Jose, F. Simulating tropical storms in the Gulf of Mexico using analytical models. Oceanologia 2020, 62, 173–189. [Google Scholar] [CrossRef]
- Yeganeh-Bakhtiary, A.; EyvazOghli, H.; Shabakhty, N.; Kamranzad, B.; Abolfathi, S. Machine learning as a downscaling approach for prediction of wind characteristics under future climate change scenarios. Complexity 2022, 2022, 8451812. [Google Scholar]
- Marois, D.E.; Mitsch, W.J. Coastal protection from tsunamis and cyclones provided by mangrove wetlands–a review. Int. J. Biodivers. Sci. Ecosyst. Serv. Manag. 2015, 11, 71–83. [Google Scholar] [CrossRef]
- McIvor, A.L.; Spencer, T.; Möller, I.; Spalding, M. Storm Surge Reduction by Mangroves; Natural Coastal Protection Series: Rport 2; Cambridge Coastal Research Unit Working Paper 41; The Nature Conservancy and Wetlands International: Horapark, The Netherlands, 2012; 35p, ISSN 2050-7941; Available online: https://www.academia.edu/5420667/Natural_Coastal_Protection_Series_ISSN_2050_7941_Storm_Surge_Reduction_by_Mangroves_Natural_Coastal_Protection_Series_Report_2_Cambridge_Coastal_Research_Unit_Working_Paper_41 (accessed on 6 May 2023).
- Pranzini, E. Shore protection in Italy: From hard to soft engineering… and back. Ocean. Coast. Manag. 2018, 156, 43–57. [Google Scholar] [CrossRef]
- Almarshed, B.; Figlus, J.; Miller, J.; Verhagen, H.J. Innovative coastal risk reduction through hybrid design: Combining sand cover and structural defenses. J. Coast. Res. 2020, 36, 174–188. [Google Scholar] [CrossRef]
- Ferrario, F.; Beck, M.W.; Storlazzi, C.D.; Micheli, F.; Shepard, C.C.; Airoldi, L. The effectiveness of coral reefs for coastal hazard risk reduction and adaptation. Nat. Commun. 2014, 5, 3794. [Google Scholar] [CrossRef] [Green Version]
- Tashiro, A. Green self-efficacy for blue-green infrastructure management in a post-disaster recovery phase: Empirical research in a small rural community. Coast. Eng. J. 2021, 63, 408–421. [Google Scholar] [CrossRef]
- Harada, K.; Imamura, F. Effects of coastal forest on tsunami hazard mitigation—A preliminary investigation. Adv. Nat. Technol. Hazards Res. 2005, 23, 279. [Google Scholar]
- Iimura, K.; Tanaka, N. Numerical simulation estimating effects of tree density distribution in coastal forest on tsunami mitigation. Ocean. Eng. 2012, 54, 223–232. [Google Scholar] [CrossRef]
- Maza, M.; Lara, J.L.; Losada, I.J. Tsunami wave interaction with mangrove forests: A 3-D numerical approach. Coast. Eng. 2015, 98, 33–54. [Google Scholar] [CrossRef]
- Pasha, G.A.; Tanaka, N. Undular hydraulic jump formation and energy loss in a flow through emergent vegetation of varying thickness and density. Ocean. Eng. 2017, 141, 308–325. [Google Scholar] [CrossRef]
- Igarashi, Y.; Tanaka, N. Effectiveness of a compound defense system of sea embankment and coastal forest against a tsunami. Ocean. Eng. 2018, 151, 246–256. [Google Scholar] [CrossRef]
- Alongi, D.M. Mangrove forests: Resilience, protection from tsunamis, and responses to global climate change. Estuar. Coast. Shelf Sci. 2008, 76, 1–13. [Google Scholar] [CrossRef]
- Chang, C.W.; Mori, N. Green infrastructure for the reduction of coastal disasters: A review of the protective role of coastal forests against tsunami, storm surge, and wind waves. Coast. Eng. J. 2021, 63, 370–385. [Google Scholar] [CrossRef]
- Tanaka, N. Effectiveness and limitations of coastal forest in large tsunami: Conditions of Japanese pine trees on coastal sand dunes in tsunami caused by Great East Japan Earthquake. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2012, 68, II_7–II_15. [Google Scholar] [CrossRef] [Green Version]
- Montgomery, J.M.; Bryan, K.R.; Mullarney, J.C.; Horstman, E.M. Attenuation of storm surges by coastal mangroves. Geophys. Res. Lett. 2019, 46, 2680–2689. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.A.; Tanaka, N.; Rashedunnabi, A.H.M. Flume experiments on flow analysis and energy reduction through a compound tsunami mitigation system with a seaward embankment and landward vegetation over a mound. Geosciences 2021, 11, 90. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, H.; Li, Y.; Xu, H.; Shen, J.; Rhome, J.; Smith, T.J., III. The role of mangroves in attenuating storm surges. Estuar. Coast. Shelf Sci. 2012, 102, 11–23. [Google Scholar] [CrossRef]
- Dasgupta, S.; Islam, M.S.; Huq, M.; Huque Khan, Z.; Hasib, M.R. Quantifying the protective capacity of mangroves from storm surges in coastal Bangladesh. PLoS ONE 2019, 14, e0214079. [Google Scholar] [CrossRef] [PubMed]
- Lagomasino, D.; Fatoyinbo, T.; Castañeda-Moya, E.; Cook, B.D.; Montesano, P.M.; Neigh, C.S.; Morton, D.C. Storm surge and ponding explain mangrove dieback in southwest Florida following Hurricane Irma. Nat. Commun. 2021, 12, 4003. [Google Scholar] [CrossRef] [PubMed]
- Hoque, A.; Husrin, S.; Oumeraci, H. Laboratory studies of wave attenuation by coastal forest under storm surge. Coast. Eng. J. 2018, 60, 225–238. [Google Scholar] [CrossRef]
- Tanaka, N.; Yasuda, S.; Iimura, K.; Yagisawa, J. Combined effects of coastal forest and sea embankment on reducing the washout region of houses in the Great East Japan tsunami. J. Hydro-Environ. Res. 2014, 8, 270–280. [Google Scholar] [CrossRef]
- Rashedunnabi, A.H.M.; Tanaka, N.; Anjum, N. Effectiveness of a hybrid tsunami mitigation system consisting a seaward embankment and a landward horizontally double-layer forest. J. Jpn. Soc. Civ. Eng. Ser. B1 (Hydraul. Eng.) 2019, 75, I_715–I_720. [Google Scholar] [CrossRef]
- Usman, F.; Murakami, K.; Kurniawan, E.B. Study on reducing tsunami inundation energy by the modification of topography based on local wisdom. Procedia Environ. Sci. 2014, 20, 642–650. [Google Scholar] [CrossRef] [Green Version]
- Zaha, T.; Tanaka, N.; Kimiwada, Y. Flume experiments on optimal arrangement of hybrid defense system comprising an embankment, moat, and emergent vegetation to mitigate inundating tsunami current. Ocean. Eng. 2019, 173, 45–57. [Google Scholar] [CrossRef]
- Kimiwada, Y.; Tanaka, N.; Zaha, T. Differences in effectiveness of a hybrid tsunami defense system comprising an embankment, moat, and forest in submerged, emergent, or combined conditions. Ocean. Eng. 2020, 208, 107457. [Google Scholar] [CrossRef]
- Del Valle, A.; Eriksson, M.; Ishizawa, O.A.; Miranda, J.J. Mangroves protect coastal economic activity from hurricanes. Proc. Natl. Acad. Sci. USA 2020, 117, 265–270. [Google Scholar] [CrossRef]
- Ranasinghe, R.; Turner, I.L. Shoreline response to submerged structures: A review. Coast. Eng. 2006, 53, 65–79. [Google Scholar] [CrossRef]
- Buccino, M.; Del Vita, I.; Calabrese, M. Predicting wave transmission past Reef Ball™ submerged breakwaters. J. Coast. Res. 2013, 65, 171–176. [Google Scholar] [CrossRef]
- Srisuwan, C.; Rattanamanee, P. Modeling of Seadome as artificial reefs for coastal wave attenuation. Ocean. Eng. 2015, 103, 198–210. [Google Scholar] [CrossRef]
- Li, A.J.; Sun, X.L.; Liu, Y.; Li, H.J. Analysis of water wave interaction with multiple submerged porous reef balls. J. Eng. Math. 2021, 127, 26. [Google Scholar] [CrossRef]
- Krumholz, J.; Jadot, C. Demonstration of a New Technology Restoration of Red Mangrove (Rhizophora mangle) in High-Energy Environments. Mar. Technol. Soc. J. 2009, 43, 64–72. [Google Scholar] [CrossRef]
- Lukkunaprasit, P.; Ruangrassamee, A.; Thanasisathit, N. Tsunami loading on buildings with openings. Sci. Tsunami Hazards 2009, 28, 303. [Google Scholar]
- Matsutomi, H.; Okamoto, K. Inundation flow velocity of tsunami on land. Isl. Arc 2010, 19, 443–457. [Google Scholar] [CrossRef]
- Heidarzadeh, M.; Satake, K. A combined earthquake–landslide source model for the Tsunami from the 27 November 1945 M w 8.1 Makran earthquake. Bull. Seismol. Soc. Am. 2017, 107, 1033–1040. [Google Scholar] [CrossRef] [Green Version]
- Ghanavati, E.; Shah-Hosseini, M.; Marriner, N. Analysis of the makran coastline of Iran’s vulnerability to global sea-level rise. J. Mar. Sci. Eng. 2021, 9, 891. [Google Scholar] [CrossRef]
- Noarayanan, L.; Murali, K.; Sundar, V. Manning’s ‘n’co-efficient for flexible emergent vegetation in tandem configuration. J. Hydro-Environ. Res. 2012, 6, 51–62. [Google Scholar] [CrossRef]
- Mohamed, A. Characterization of Tsunami-like Bores in Support of Loading on Structures. Ph.D. Thesis, University of Hawaii at Manoa, Honolulu, HI, USA, 2008. [Google Scholar]
- Fathi-Moghadam, M.; Davoudi, L.; Motamedi-Nezhad, A. Modeling of solitary breaking wave force absorption by coastal trees. Ocean. Eng. 2018, 169, 87–98. [Google Scholar] [CrossRef]
- Huang, Z.; Yao, Y.; Sim, S.Y.; Yao, Y. Interaction of solitary waves with emergent, rigid vegetation. Ocean. Eng. 2011, 38, 1080–1088. [Google Scholar] [CrossRef]
- Imai, K.; Matsutomi, H. Fluid force on vegetation due to tsunami flow on a sand spit. Tsunamis Case Stud. Recent Dev. 2005, 23, 293–304. [Google Scholar]
- Ahmed, A.; Ghumman, A.R. Experimental Investigation of Flood Energy Dissipation by Single and Hybrid Defense System. Water 2019, 11, 1971. [Google Scholar] [CrossRef] [Green Version]
- Husrin, S. Attenuation of Solitary Waves and Wave Trains by Coastal Forests. Ph.D. Thesis, Technical University of Braunschweig, Braunschweig, Germany, 2013. [Google Scholar]
- Kothyari, U.C.; Hayashi, K.; Hashimoto, H. Drag coefficient of unsubmerged rigid vegetation stems in open channel flows. J. Hydraul. Res. 2009, 47, 691–699. [Google Scholar] [CrossRef]
- Ishikawa, Y.; Mizuhara, K.; Ashida, M. Drag Force on Multiple Rows of Cylinders in an Open Channel; Grant-in-aid research project report; Kyushu University: Fukuoka, Japan, 2000. [Google Scholar]
- D’Ippolito, A.; Lauria, A.; Alfonsi, G.; Calomino, F. Flow resistance in open channel with rigid emergent vegetation. In Proceedings of the 5th IAHR Europe Congress, Trento, Italy, 12–14 June 2018. [Google Scholar]
- Cavedon, V. Effects of Rigid Stems on Sediment Transport. Ph.D. Thesis, University of Trento, Trento, Italy, 2012. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeganeh-Bakhtiary, A.; Kolahian, M.; Eyvazoghli, H. Experimental Investigation of Coastal Flooding Hydrodynamics Using a Hybrid Defense System. Water 2023, 15, 2632. https://doi.org/10.3390/w15142632
Yeganeh-Bakhtiary A, Kolahian M, Eyvazoghli H. Experimental Investigation of Coastal Flooding Hydrodynamics Using a Hybrid Defense System. Water. 2023; 15(14):2632. https://doi.org/10.3390/w15142632
Chicago/Turabian StyleYeganeh-Bakhtiary, Abbas, Mohammadreza Kolahian, and Hossein Eyvazoghli. 2023. "Experimental Investigation of Coastal Flooding Hydrodynamics Using a Hybrid Defense System" Water 15, no. 14: 2632. https://doi.org/10.3390/w15142632





