Optimal Scheduling of Cascade Reservoirs Based on an Integrated Multistrategy Particle Swarm Algorithm
Abstract
:1. Introduction
- An IMPSO method is proposed that uses initialization, adaptive parameters, Lévy flight, and variable spiral search strategies to efficiently maximize performance.
- In conjunction with the proposed IMPSO algorithm, an explicit–implicit coupled constraint handling technique is introduced to solve the generation scheduling model of cascaded hydropower systems.
- The proposed scheme provides an effective tool for solving the complex problem of reservoir operation. Compared with several other schemes, it has the advantages of strong searching ability and robustness, which also can better utilize the collaborative generation effect of cascade hydropower units.
2. Operation Model of Cascade Reservoirs
2.1. Objective Function
2.2. Constraints
- (1)
- Water balance constraints
- (2)
- Storage capacity constraint
- (3)
- Hydraulic constraints
- (4)
- Outflow constraints
- (5)
- Generation flow constraints
- (6)
- Water level constraints
- (7)
- Water level head constraints
- (8)
- Output constraints
- (9)
- Initial and final water level control constraints
3. Integrated Multistrategy Particle Swarm Optimization Algorithm (IMPSO)
3.1. Introduction of the Particle Swarm Optimization Algorithm (PSO)
- (1)
- Random population initialization
- (2)
- Particle velocity update
- (3)
- Particle location update
3.2. Integrated Multistrategy Particle Swarm Optimization Algorithm (IMPSO)
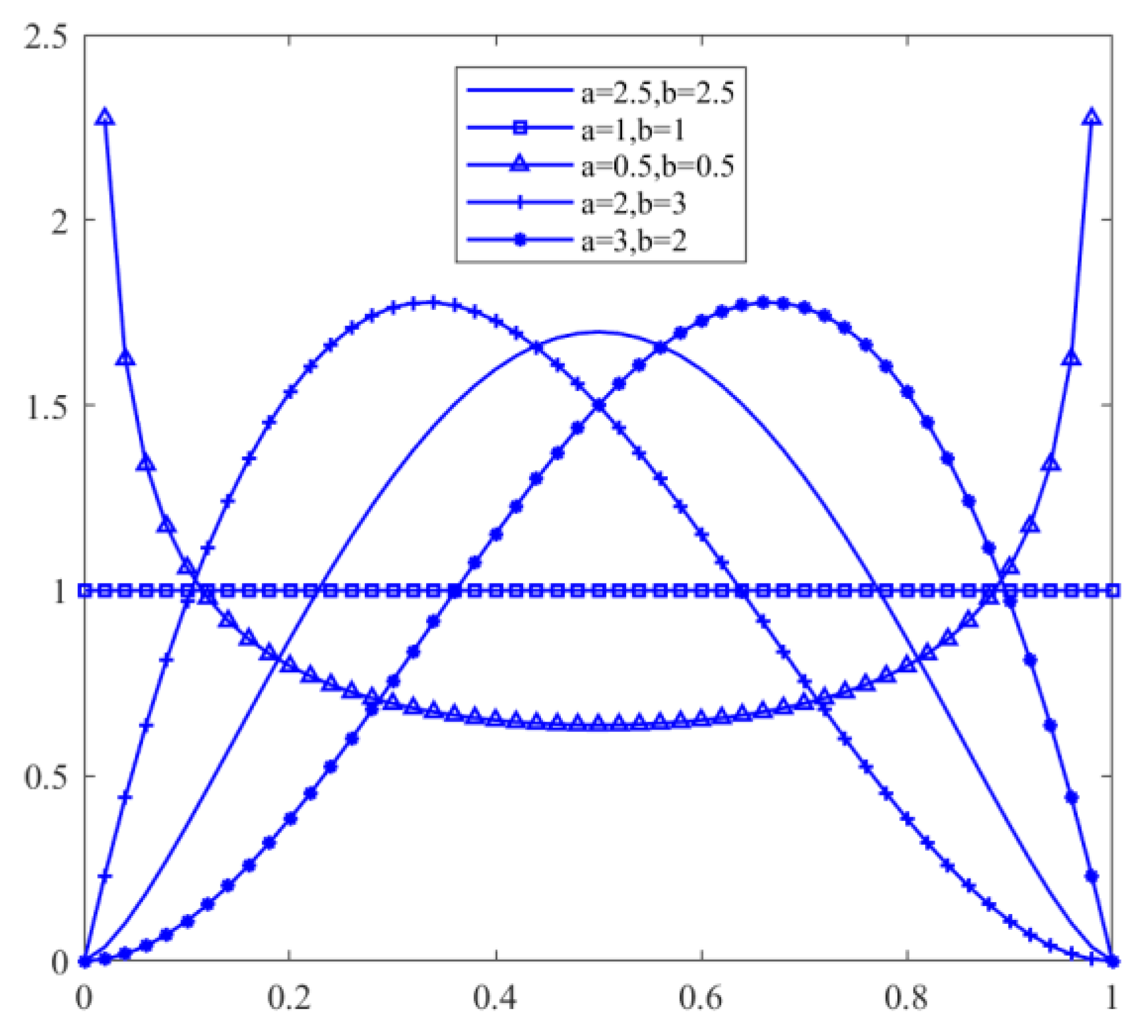
3.2.1. Population Initialization Based on the Beta Distribution
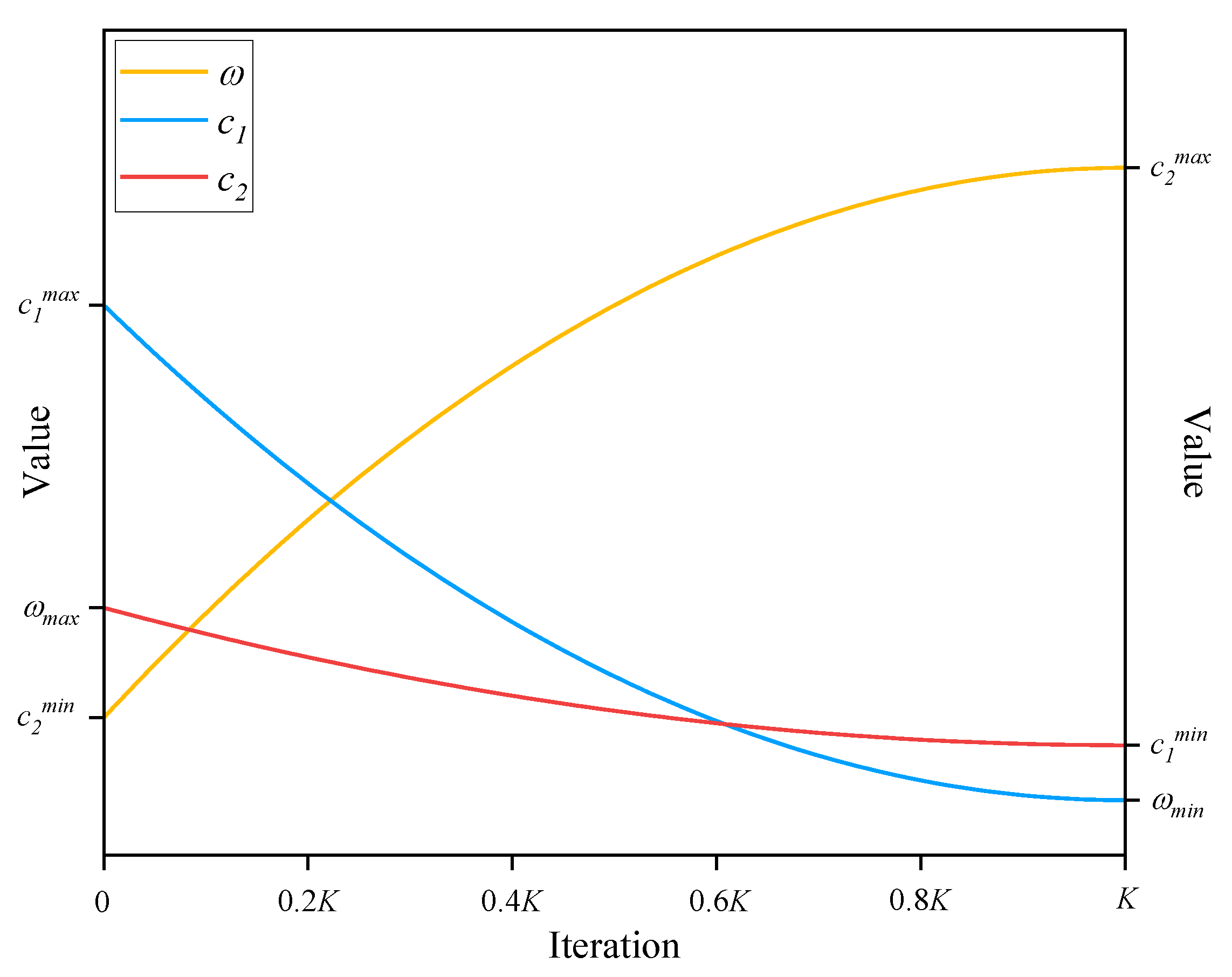
3.2.2. Nonlinear Adaptive Parameter Fitting Strategy
3.2.3. Lévy Flight Mechanism
3.2.4. Adaptive Variable Spiral Policy
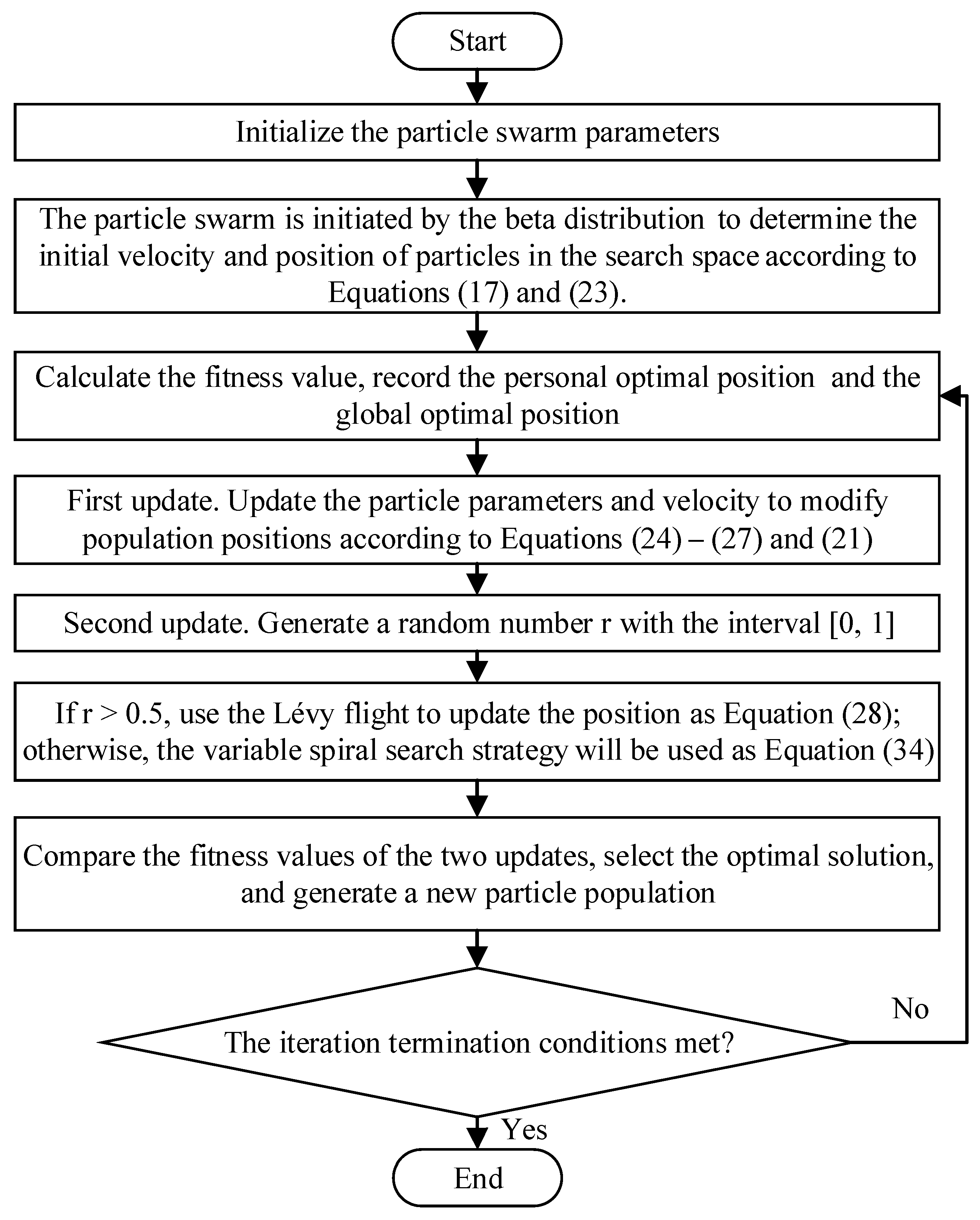
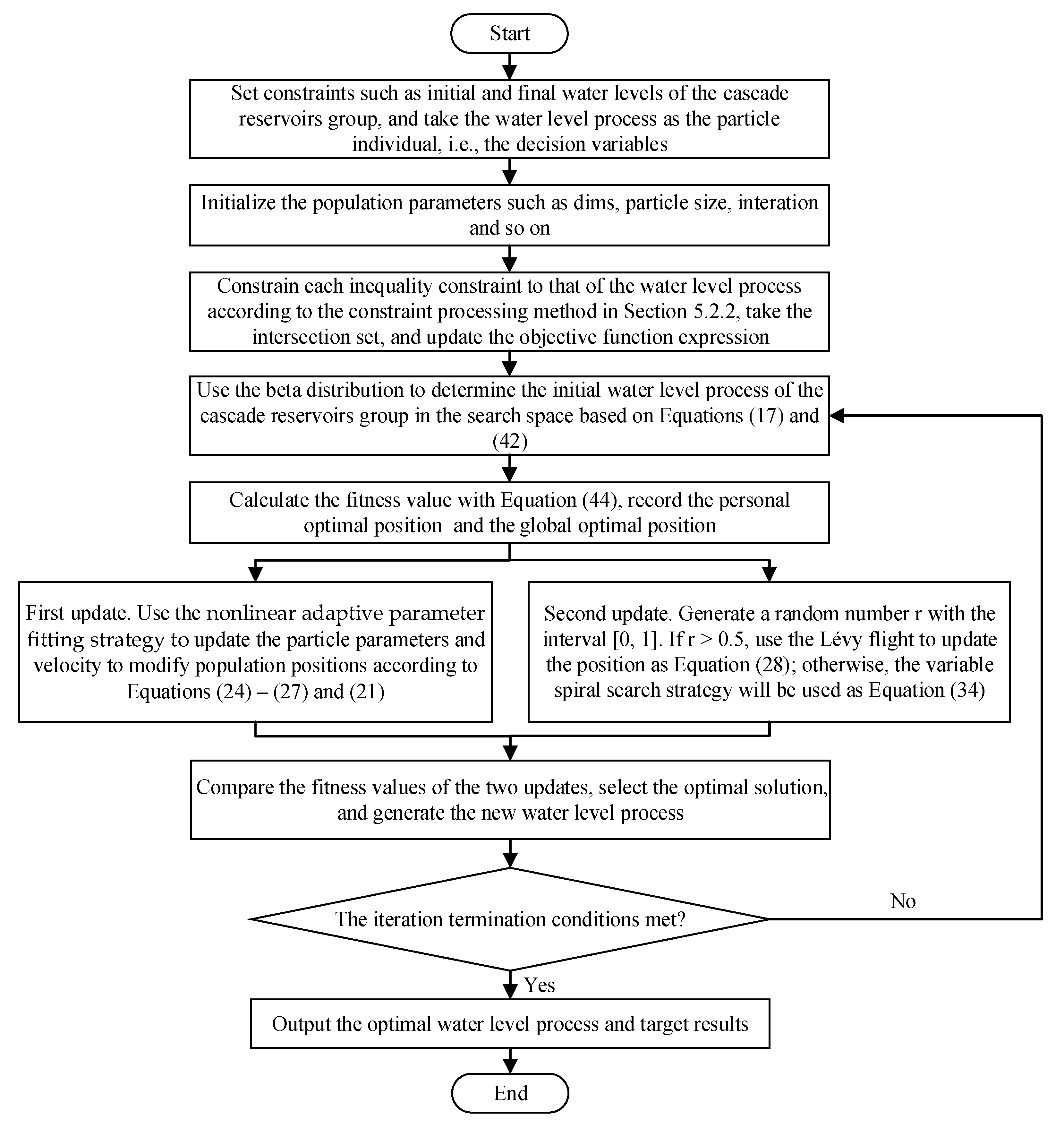
3.3. Framework of IMPSO
4. Constraint Handling Methods
4.1. Review of Constraint Handling Methods
4.2. Explicit–Implicit Coupled Constraint Handling Technique
5. Case Study
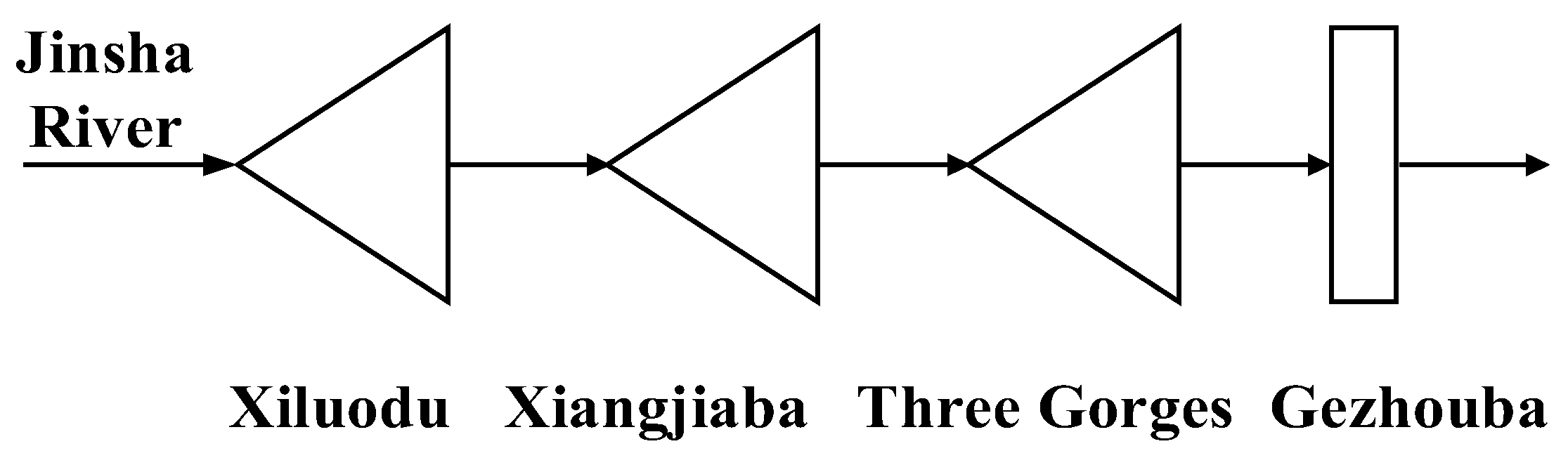
5.1. Study Area
5.2. Detailed Technical Procedures
5.2.1. Solution Structure and Population Initialization
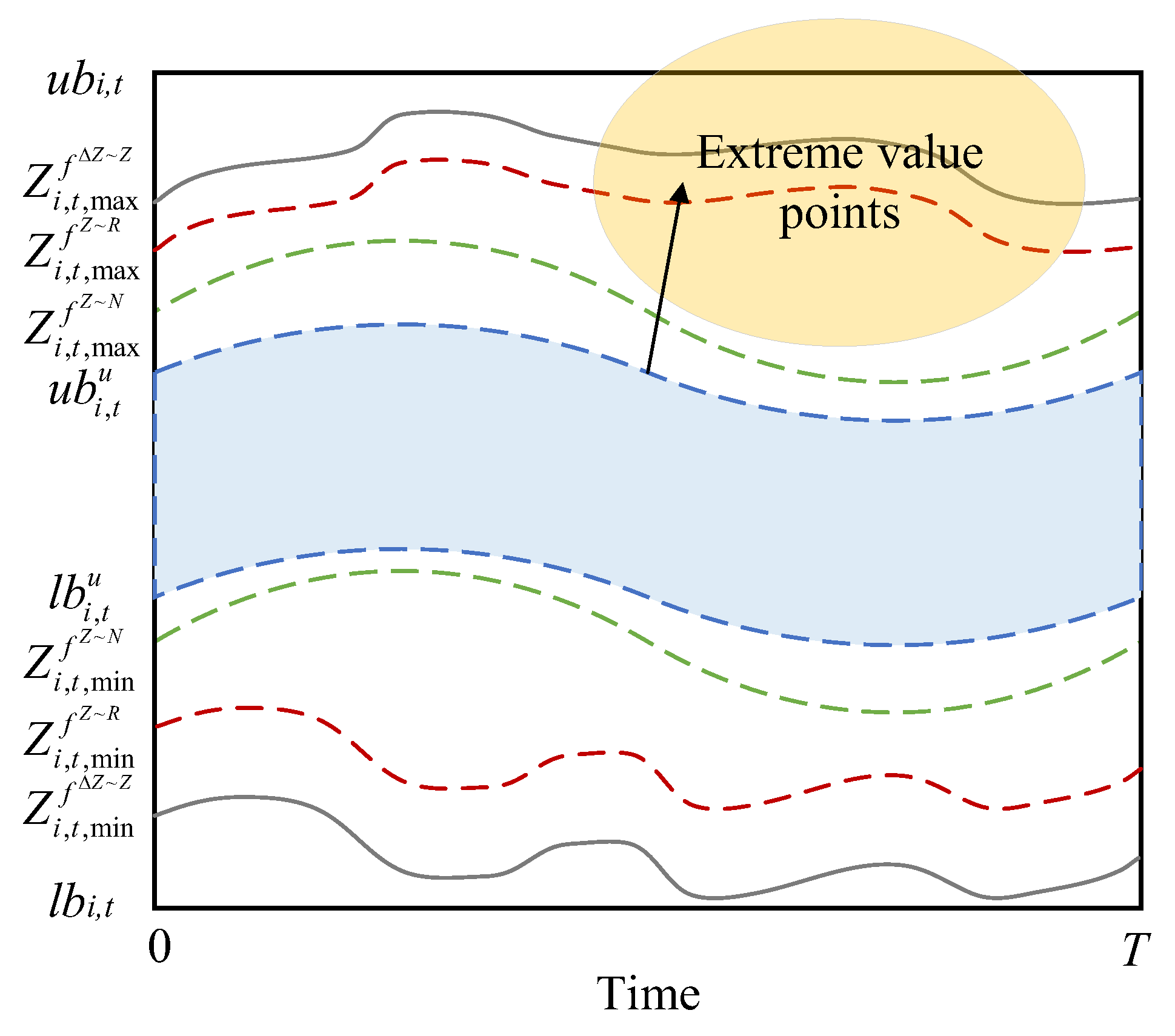
5.2.2. Explicit–Implicit Coupled Constraint Handling Method Based on Constraint Normalization
5.3. Overall Implementation Framework
5.4. Results and Analysis
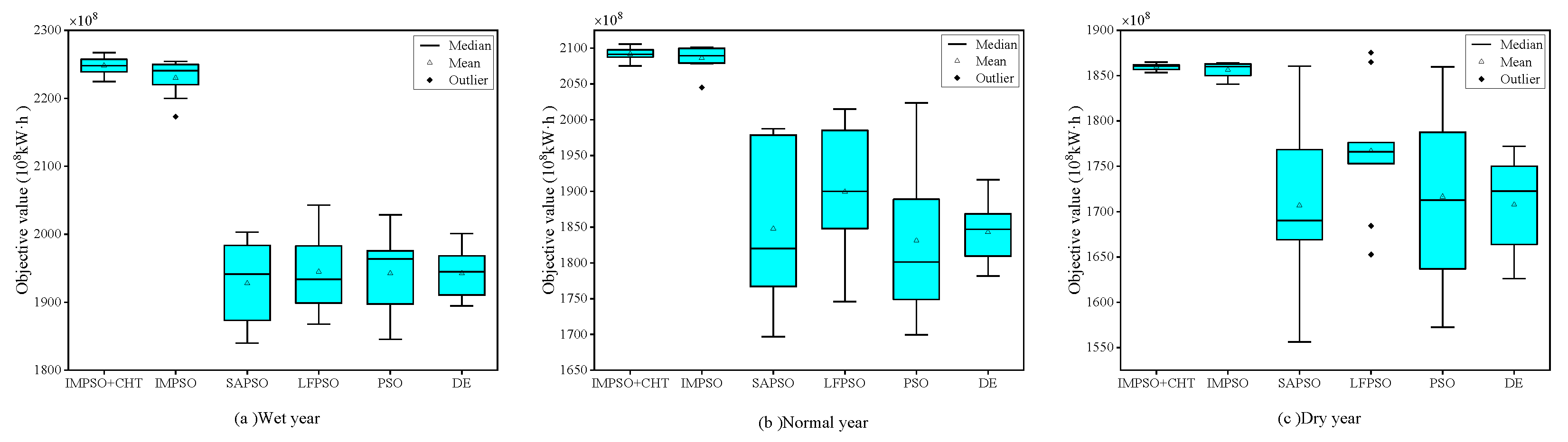
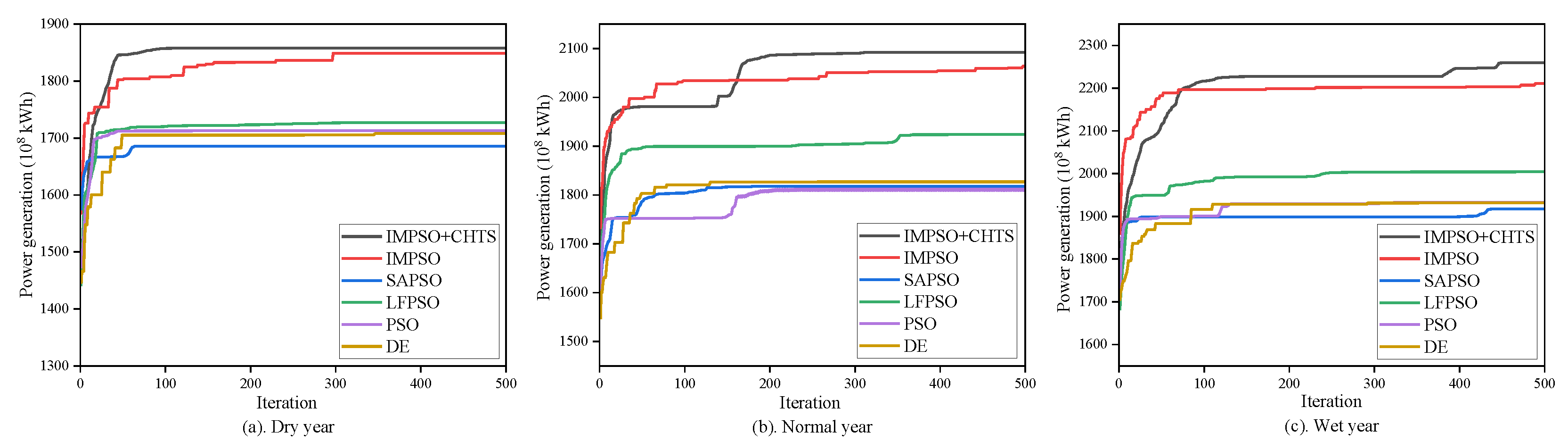
5.4.1. Statistical analysis
5.4.2. Analysis of Optimization Scheduling Results
6. Conclusions
- (1)
- Using beta distribution initialization to generate candidate solutions and adaptive nonlinear variation of the speed update-related parameters improves the proposed algorithm’s population diversity, resulting in faster convergence to the global optimal solution than the comparison schemes. Meanwhile, introducing the Lévy flight mechanism and variable helix search strategy, the optimization search is performed in a diverse exploration manner, which effectively enhances the local exploration capability and global exploitation capability of the algorithm.
- (2)
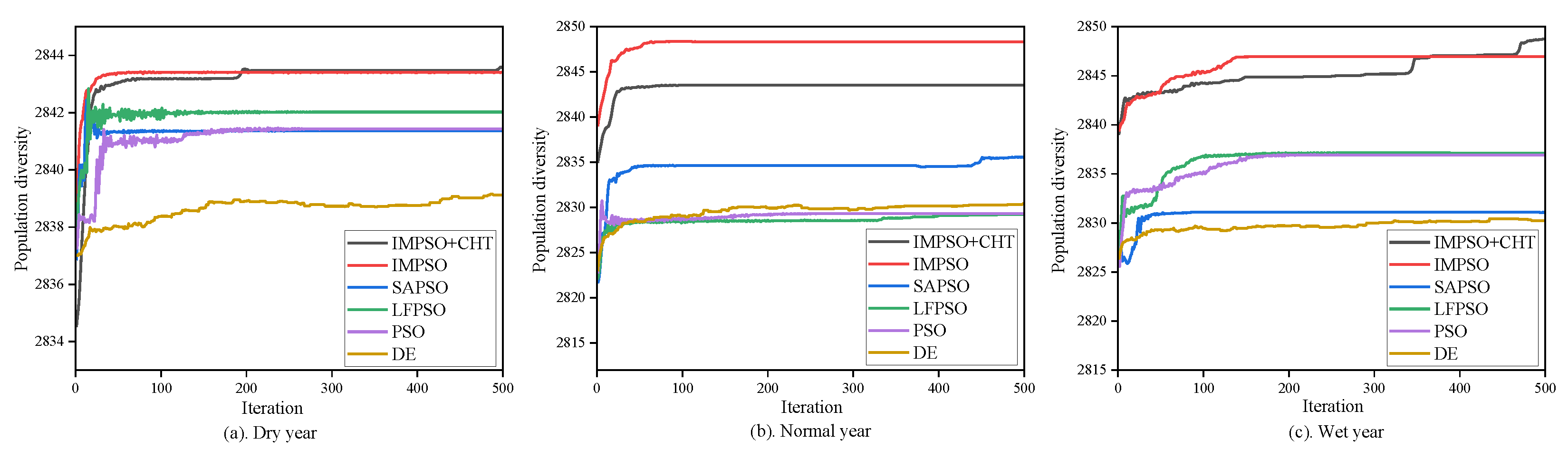
- The combined statistic results in Table 2 and Table 3 and Figure 9, Figure 10 and Figure 11 show that using the IMPSO algorithm in reservoir power generation scheduling engineering can achieve more robust and accurate results, increased population diversity, and algorithmic exploration than the comparison algorithms. Meanwhile, the IMPSO method combined with the explicit–implicit coupled constraint processing technique achieves superior results but falls short in terms of population variety when compared with the IMPSO scheme.
- (3)
- (4)
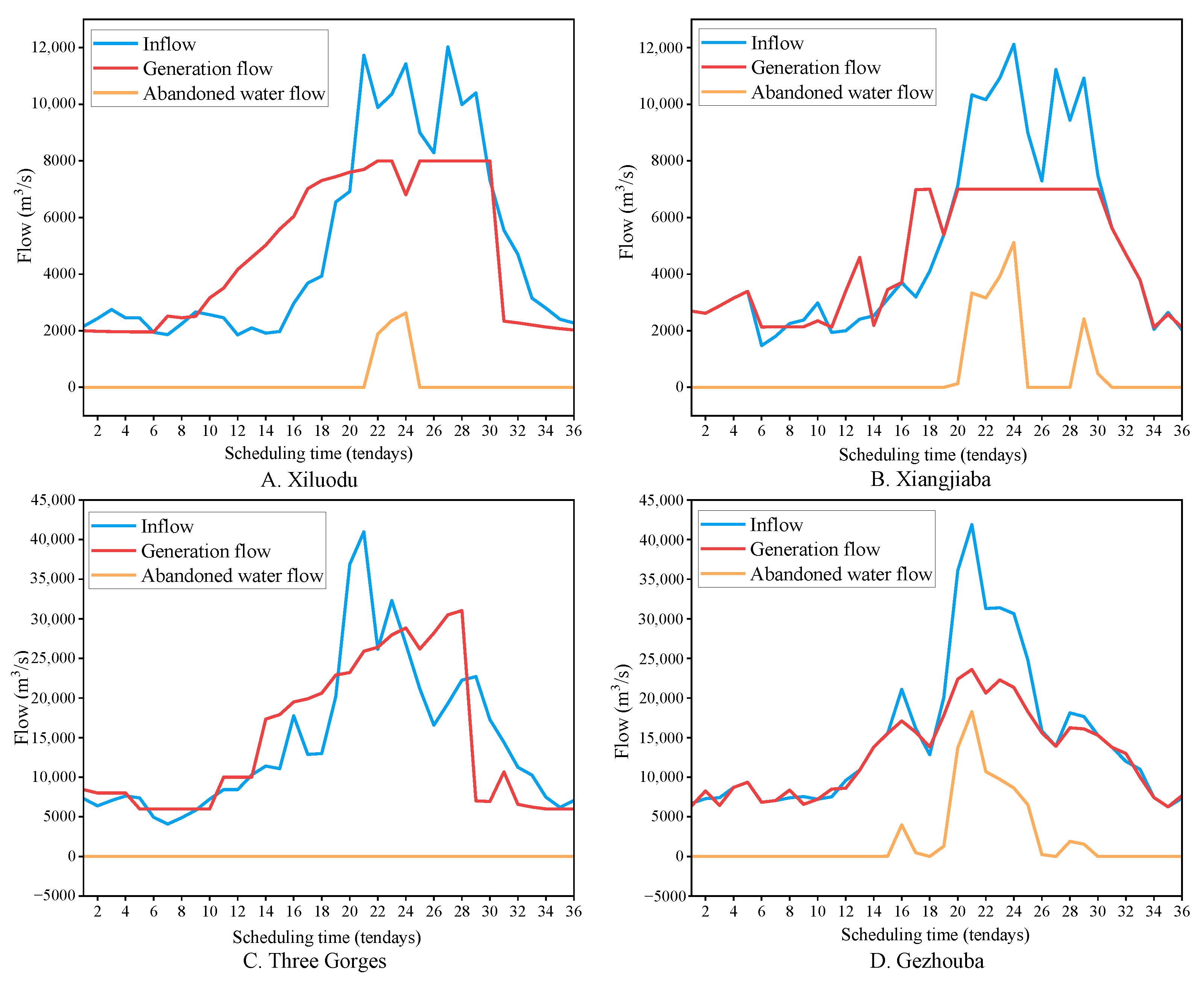
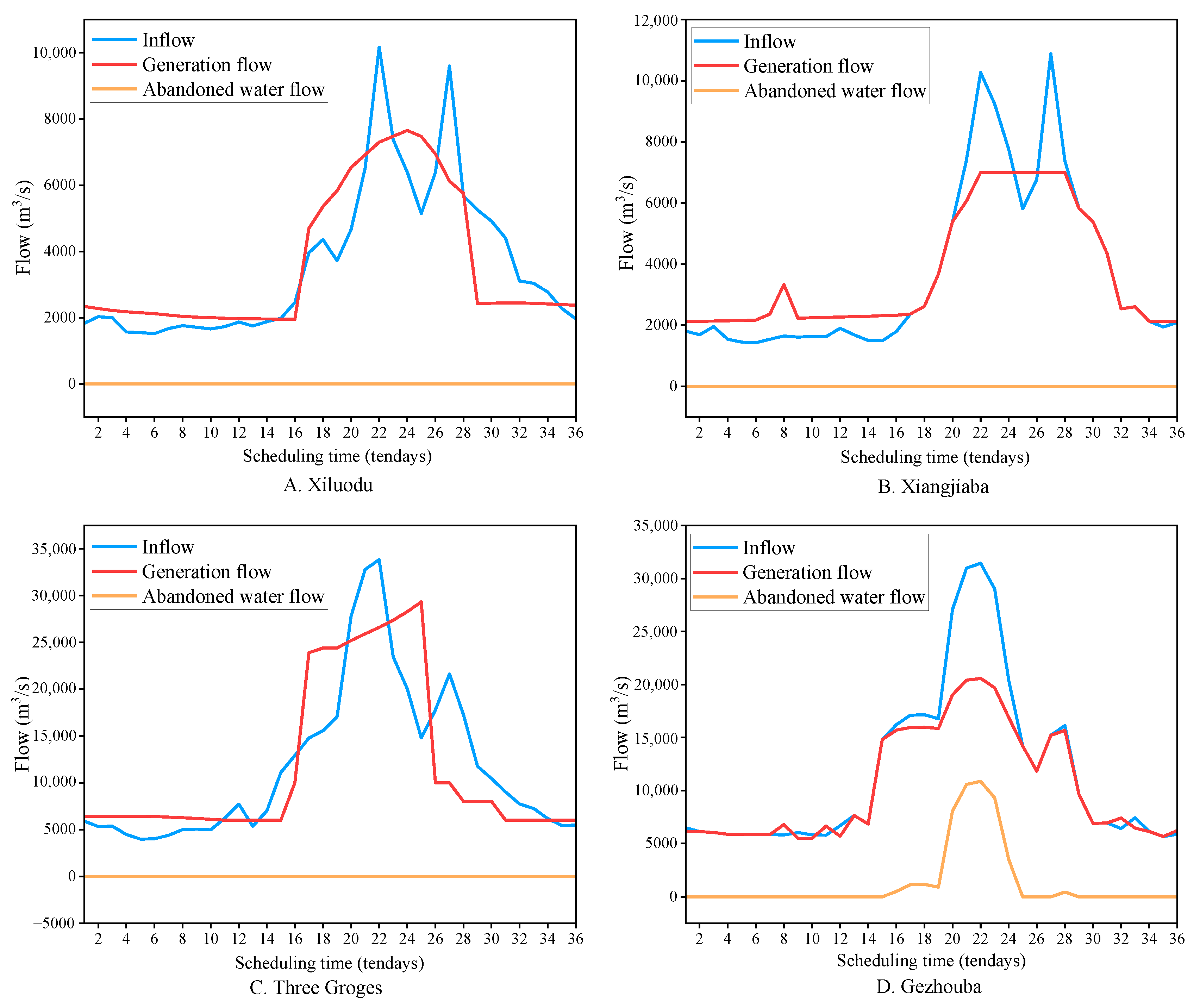
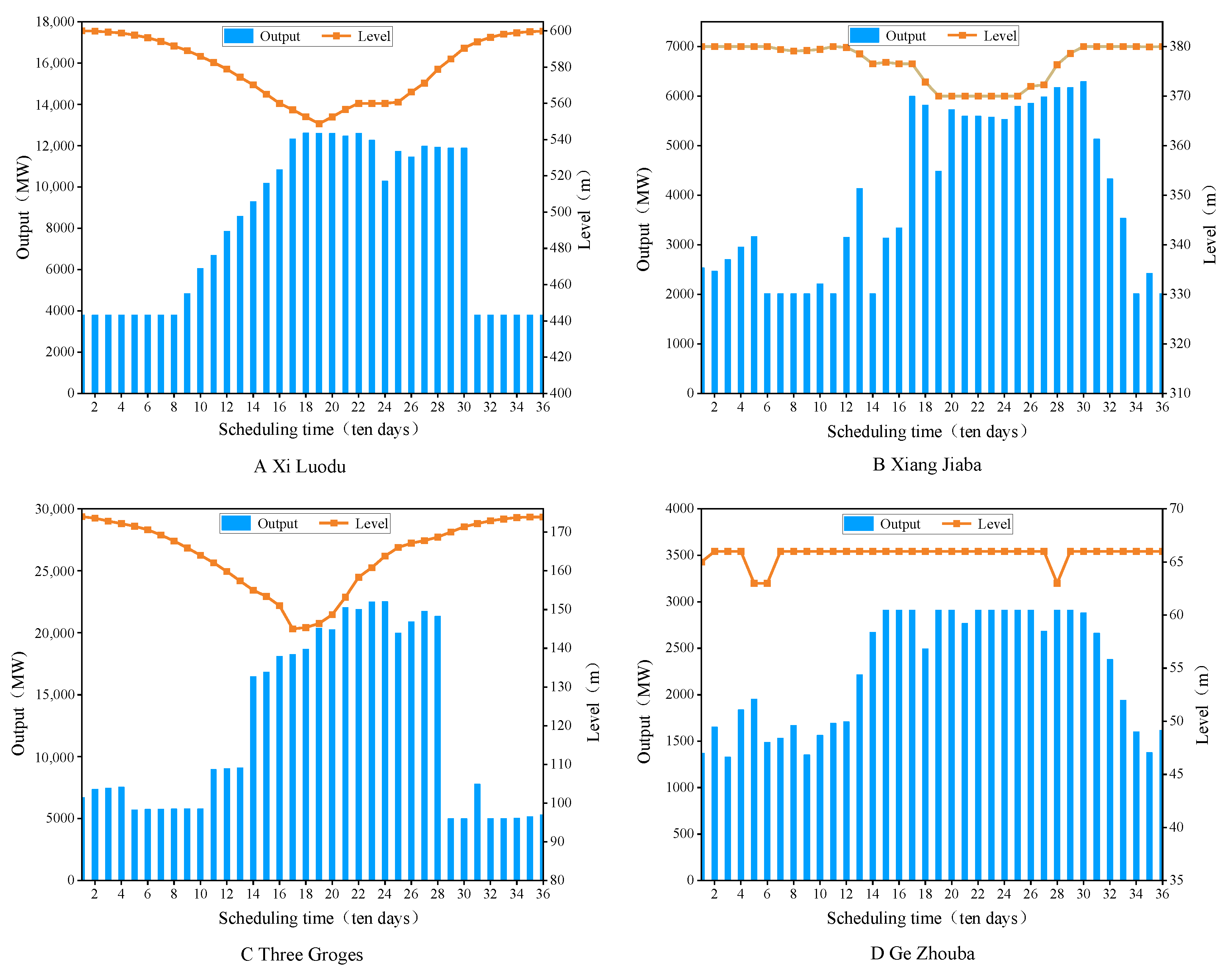
- The water level and treatment results from Figure 15, Figure 16 and Figure 17 obtained using the IMPSO+CHT method can not only meet the boundary conditions of cascade hydropower reservoirs, but also make better use of the abundant water resources in the catchment area and take full advantage of the regulatory and balancing functions of cascade reservoirs; moreover, these results produce a more efficient and reasonable regulation process for the operations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, L.; Niu, D.; Wang, K.; Xu, X. Sustainable development pathways of hydropower in China: Interdisciplinary qualitative analysis and scenario-based system dynamics quantitative modeling. J. Clean. Prod. 2020, 287, 125528. [Google Scholar] [CrossRef]
- Li, X.-Z.; Chen, Z.-J.; Fan, X.-C.; Cheng, Z.-J. Hydropower development situation and prospects in China. Renew. Sustain. Energy Rev. 2018, 82, 232–239. [Google Scholar] [CrossRef]
- Xie, Y.; Liu, S.; Fang, H.; Ding, M.; Wang, J. Three-Parameter Regulation Rules for the Long-Term Optimal Scheduling of Multiyear Regulating Storage Reservoirs. Water 2021, 13, 3593. [Google Scholar] [CrossRef]
- Jiang, Z.; Qin, H.; Wu, W.; Qiao, Y. Studying Operation Rules of Cascade Reservoirs Based on Multi-Dimensional Dynamics Programming. Water 2018, 10, 20. [Google Scholar] [CrossRef] [Green Version]
- Chang, J.; Wang, X.; Li, Y.; Wang, Y.; Zhang, H. Hydropower plant operation rules optimization response to climate change. Energy 2018, 160, 886–897. [Google Scholar] [CrossRef]
- Suwal, N.; Huang, X.; Kuriqi, A.; Chen, Y.; Pandey, K.P.; Bhattarai, K.P. Optimisation of cascade reservoir operation considering environmental flows for different environmental management classes. Renew. Energy 2020, 158, 453–464. [Google Scholar] [CrossRef]
- Guo, Y.; Ming, B.; Huang, Q.; Wang, Y.; Zheng, X.; Zhang, W. Risk-averse day-ahead generation scheduling of hydro–wind–photovoltaic complementary systems considering the steady requirement of power delivery. Appl. Energy 2022, 309, 118467. [Google Scholar] [CrossRef]
- Qiu, H.; Chen, L.; Zhou, J.; He, Z.; Zhang, H. Risk analysis of water supply-hydropower generation-environment nexus in the cascade reservoir operation. J. Clean. Prod. 2021, 283, 124239. [Google Scholar] [CrossRef]
- Liu, B.; Yao, K.; Wang, F.; Chi, X.; Gong, Y. Benefit Sharing in Hydropower Development: A Model Using Game Theory and Cost–Benefit Analysis. Water 2022, 14, 1208. [Google Scholar] [CrossRef]
- Ren, Y.; Yao, X.; Liu, D.; Qiao, R.; Zhang, L.; Zhang, K.; Jin, K.; Li, H.; Ran, Y.; Li, F. Optimal design of hydro-wind-PV multi-energy complementary systems considering smooth power output. Sustain. Energy Technol. Assess. 2022, 50, 101832. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi-Ivatloo, B.; Gharehpetian, G.B. Short-term scheduling of hydro-based power plants considering application of heuristic algorithms: A comprehensive review. Renew. Sustain. Energy Rev. 2017, 74, 116–129. [Google Scholar] [CrossRef]
- He, S.; Guo, S.; Chen, K.; Deng, L.; Liao, Z.; Xiong, F.; Yin, J. Optimal impoundment operation for cascade reservoirs coupling parallel dynamic programming with importance sampling and successive approximation. Adv. Water Resour. 2019, 131, 103375. [Google Scholar] [CrossRef]
- Zhou, B.; Feng, S.; Xu, Z.; Jiang, Y.; Wang, Y.; Chen, K.; Wang, J. A Monthly Hydropower Scheduling Model of Cascaded Reservoirs with the Zoutendijk Method. Water 2022, 14, 3978. [Google Scholar] [CrossRef]
- Needham, J.T.; Watkins, D.W.; Lund, J.R.; Nanda, S.K. Linear Programming for Flood Control in the Iowa and Des Moines Rivers. J. Water Resour. Plan. Manag. Am. Soc. Civ. Eng. 2000, 126, 118–127. [Google Scholar] [CrossRef] [Green Version]
- Barros, M.T.L.; Tsai, F.T.-C.; Yang, S.-L.; Lopes, J.E.G.; Yeh, W.W.-G. Optimization of Large-Scale Hydropower System Operations. J. Water Resour. Plan. Manag. Am. Soc. Civ. Eng. 2003, 129, 178–188. [Google Scholar] [CrossRef]
- Dogan, M.S.; Lund, J.R.; Medellin-Azuara, J. Hybrid Linear and Nonlinear Programming Model for Hydropower Reservoir Optimization. J. Water Resour. Plan. Manag. 2021, 147, 06021001. [Google Scholar] [CrossRef]
- Van Dau, Q.; Kangrang, A.; Kuntiyawichai, K. Probability-Based Rule Curves for Multi-Purpose Reservoir System in the Seine River Basin, France. Water 2023, 15, 1732. [Google Scholar] [CrossRef]
- Hjelmeland, M.N.; Zou, J.; Helseth, A.; Ahmed, S. Nonconvex Medium-Term Hydropower Scheduling by Stochastic Dual Dynamic Integer Programming. IEEE Trans. Sustain. Energy 2018, 10, 481–490. [Google Scholar] [CrossRef] [Green Version]
- Agushaka, J.O.; Ezugwu, A.E. Initialisation Approaches for Population-Based Metaheuristic Algorithms: A Comprehensive Review. Appl. Sci. 2022, 12, 896. [Google Scholar] [CrossRef]
- Lai, V.; Huang, Y.F.; Koo, C.H.; Ahmed, A.N.; El-Shafie, A. A Review of Reservoir Operation Optimisations: From Traditional Models to Metaheuristic Algorithms. Arch. Comput. Methods Eng. 2022, 29, 3435–3457. [Google Scholar] [CrossRef]
- Azad, A.S.; Rahaman, S.A.; Watada, J.; Vasant, P.; Vintaned, J.A.G. Optimization of the hydropower energy generation using Meta-Heuristic approaches: A review. Energy Rep. 2020, 6, 2230–2248. [Google Scholar] [CrossRef]
- Thaeer Hammid, A.; Awad, O.I.; Sulaiman, M.H.; Gunasekaran, S.S.; Mostafa, S.A.; Manoj Kumar, N.; Khalaf, B.A.; Al-Jawhar, Y.A.; Abdulhasan, R.A. A Review of Optimization Algorithms in Solving Hydro Generation Scheduling Problems. Energies 2020, 13, 2787. [Google Scholar] [CrossRef]
- He, Z.; Zhou, J.; Xie, M.; Jia, B.; Bao, Z.; Qin, H.; Zhang, H. Study on guaranteed output constraints in the long term joint optimal scheduling for the hydropower station group. Energy 2019, 185, 1210–1224. [Google Scholar] [CrossRef]
- Mao, J.-Q.; Tian, M.-M.; Hu, T.-F.; Ji, K.; Dai, L.-Q.; Dai, H.-C. Shuffled complex evolution coupled with stochastic ranking for reservoir scheduling problems. Water Sci. Eng. 2019, 12, 307–318. [Google Scholar] [CrossRef]
- Hu, H.; Yang, K.; Su, L.; Yang, Z. A Novel Adaptive Multi-Objective Particle Swarm Optimization Based on Decomposition and Dominance for Long-term Generation Scheduling of Cascade Hydropower System. Water Resour. Manag. 2019, 33, 4007–4026. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, J.; Lu, P.; Yuan, L. Long-term scheduling of large cascade hydropower stations in Jinsha River, China. Energy Convers. Manag. 2015, 90, 476–487. [Google Scholar] [CrossRef]
- Baldo, A.; Boffa, M.; Cascioli, L.; Fadda, E.; Lanza, C.; Ravera, A. The polynomial robust knapsack problem. Eur. J. Oper. Res. 2022, 305, 1424–1434. [Google Scholar] [CrossRef]
- Lu, Y.; Liang, M.; Ye, Z.; Cao, L. Improved particle swarm optimization algorithm and its application in text feature selection. Appl. Soft Comput. 2015, 35, 629–636. [Google Scholar] [CrossRef]
- Liu, D.; Xiao, Z.; Li, H.; Hu, X.; Malik, O. Accurate Parameter Estimation of a Hydro-Turbine Regulation System Using Adaptive Fuzzy Particle Swarm Optimization. Energies 2019, 12, 3903. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Pan, H. Energy-Efficient Cooperative Spectrum Sensing Strategy for Cognitive Wireless Sensor Networks Based on Particle Swarm Optimization. IEEE Access 2020, 8, 214707–214715. [Google Scholar] [CrossRef]
- Dahmani, S.; Yebdri, D. Hybrid Algorithm of Particle Swarm Optimization and Grey Wolf Optimizer for Reservoir Operation Management. Water Resour. Manag. 2020, 34, 4545–4560. [Google Scholar] [CrossRef]
- Shi, Y.H.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the IEEE World Congress on Computational Intelligence, 1998 IEEE International Conference on Evolutionary Computation Proceedings, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S.; Zhao, Y.-X.; Fong, S.; He, X. Swarm intelligence: Past, present and future. Soft Comput. 2018, 22, 5923–5933. [Google Scholar] [CrossRef] [Green Version]
- Agushaka, J.O.; Ezugwu, A.E. Evaluation of several initialization methods on arithmetic optimization algorithm performance. J. Intell. Syst. 2022, 31, 70–94. [Google Scholar] [CrossRef]
- Li, Q.; Liu, S.-Y.; Yang, X.-S. Influence of initialization on the performance of metaheuristic optimizers. Appl. Soft Comput. 2020, 91, 106193. [Google Scholar] [CrossRef] [Green Version]
- Rauf, H.T.; Shoaib, U.; Lali, M.I.; Alhaisoni, M.; Irfan, M.N.; Khan, M.A. Particle Swarm Optimization with Probability Sequence for Global Optimization. IEEE Access 2020, 8, 110535–110549. [Google Scholar] [CrossRef]
- Li, J.; An, Q.; Lei, H.; Deng, Q.; Wang, G.-G. Survey of Lévy Flight-Based Metaheuristics for Optimization. Mathematics 2022, 10, 2785. [Google Scholar] [CrossRef]
- Liu, L.; Bai, K.; Dan, Z.; Zhang, S.; Liu, Z. Whale Optimization Algorithm with Global Search Strategy. J. Chin. Comput. Syst. 2020, 41, 1820–1825. Available online: https://scholar.google.com/scholar_lookup?title=Whale+Optimization+Algorithm+with+Global+Search+Strategy&author=Liu,+L.&author=Bai,+K.&author=Dan,+Z.&author=Zhang,+S.&author=Liu,+Z.&publication_year=2020&journal=J.+Chin.+Comput.+Syst.&volume=41&pages=1820%E2%80%931825 (accessed on 4 September 2020).
- Zhang, C.; Lin, Q.; Gao, L.; Li, X. Backtracking Search Algorithm with three constraint handling methods for constrained optimization problems. Expert Syst. Appl. 2015, 42, 7831–7845. [Google Scholar] [CrossRef]
- Li, Z.; Chen, S.; Zhang, S.; Jiang, S.; Gu, Y.; Nouioua, M. FSB-EA: Fuzzy search bias guided constraint handling technique for evolutionary algorithm. Expert Syst. Appl. 2019, 119, 20–35. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Deb, K. Implicit constraints handling for efficient search of feasible solutions. Comput. Methods Appl. Mech. Eng. 2020, 363, 112917. [Google Scholar] [CrossRef]
- Harrison, K.R.; Engelbrecht, A.P.; Ombuki-Berman, B.M. Self-adaptive particle swarm optimization: A review and analysis of convergence. Swarm Intell. 2018, 12, 187–226. [Google Scholar] [CrossRef] [Green Version]
- Haklı, H.; Uğuz, H. A novel particle swarm optimization algorithm with Levy flight. Appl. Soft Comput. 2014, 23, 333–345. [Google Scholar] [CrossRef]
- Yan, Z.; Zhaobin, L.; Zhang, B. A Novel Differential Evolution Algorithm for Constrained Optimization. In Proceedings of the 2017 IEEE International Conference on Computational Science and Engineering (CSE) and IEEE International Conference on Embedded and Ubiquitous Computing (EUC), Guangzhou, China, 21–24 July 2017. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. QANA: Quantum-based avian navigation optimizer algorithm. Eng. Appl. Artif. Intell. 2021, 104, 104314. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. Starling murmuration optimizer: A novel bio-inspired algorithm for global and engineering optimization. Comput. Methods Appl. Mech. Eng. 2022, 392, 114616. [Google Scholar] [CrossRef]



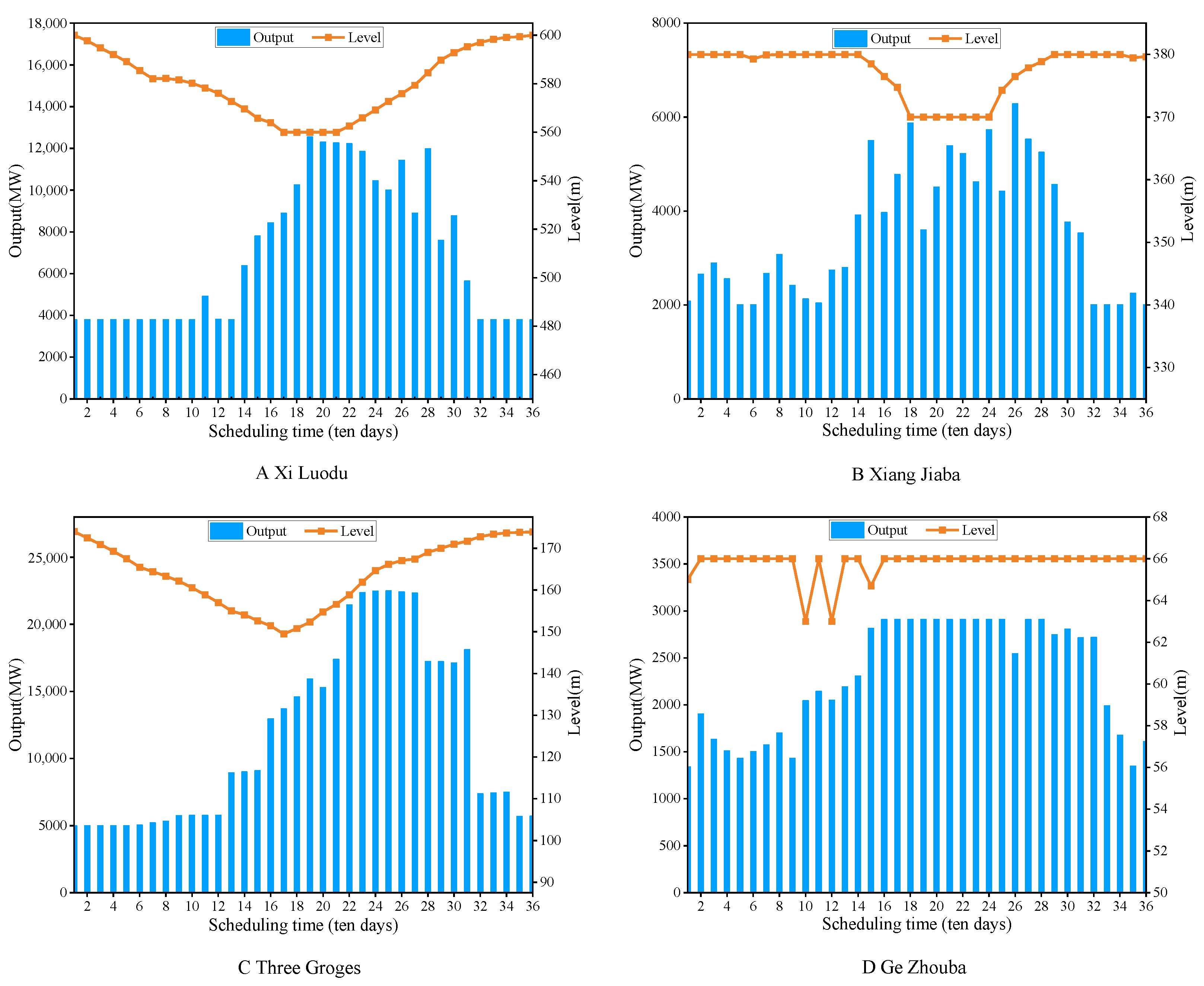
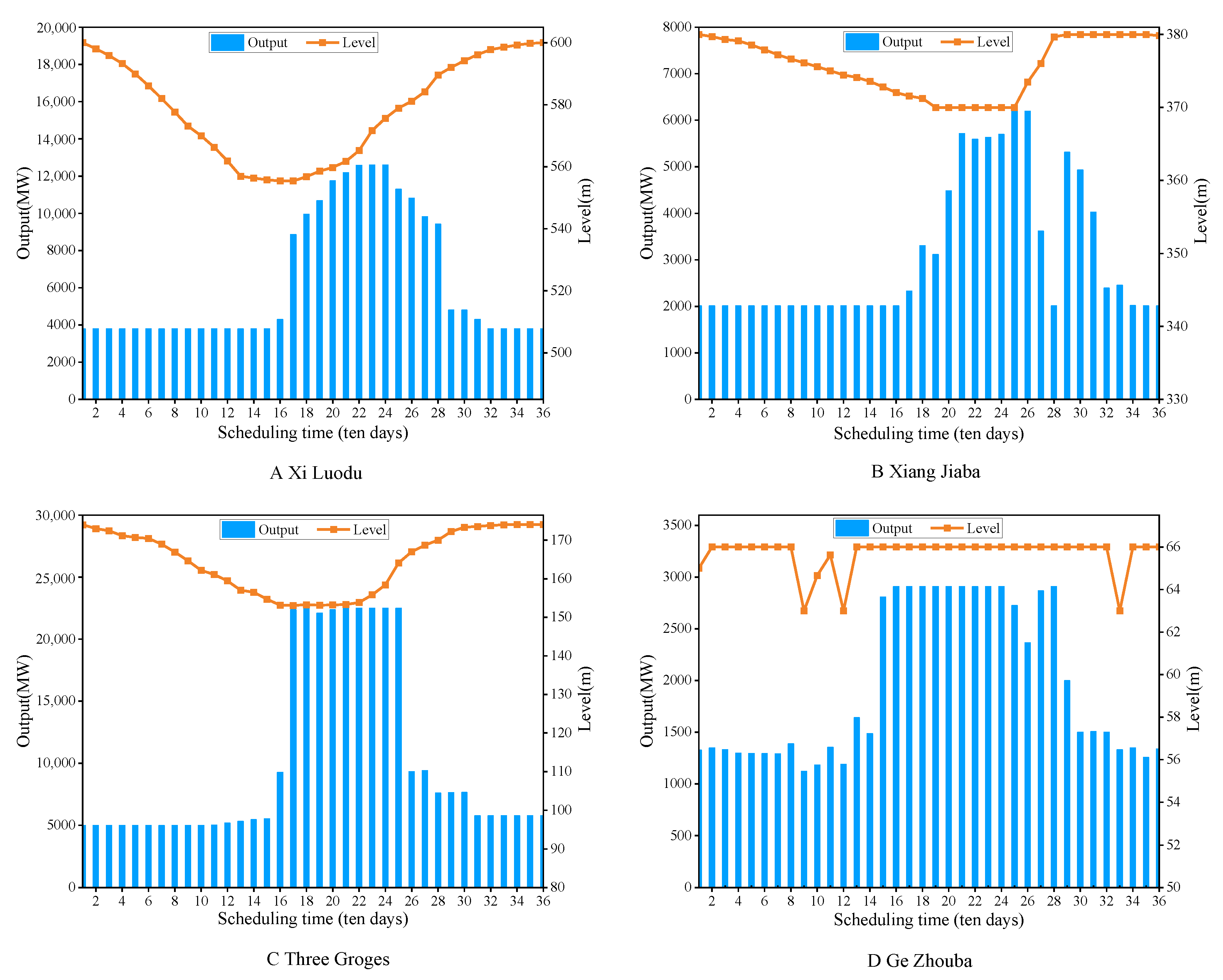
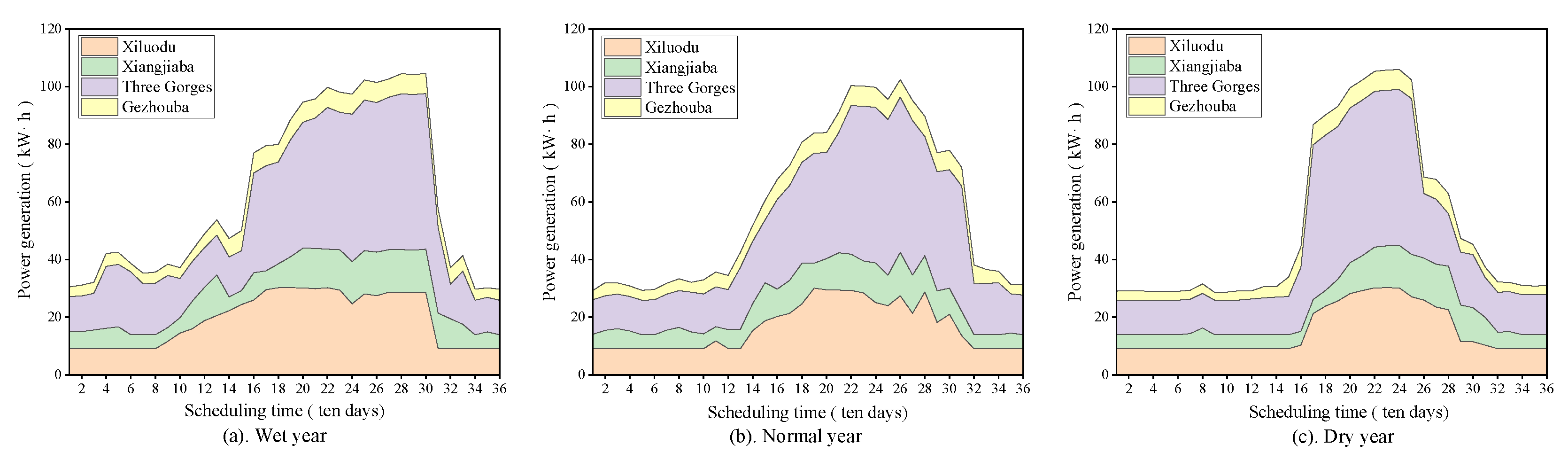
| Reservoir Feature | Xiluodu | Xiangjiaba | Three Gorges | Gezhouba |
|---|---|---|---|---|
| Regulation performance | Annually | Seasonally | Annually | Daily |
| Generation coefficient | 8.5 | 8.35 | 8.8 | 8.5 |
| Normal water level (m) | 600 | 380 | 175 | 66 |
| Dead water level (m) | 540 | 370 | 145 | 63 |
| Guaranteed capacity (MW) | 3795 | 2009 | 4990 | 1040 |
| Installed capacity (MW) | 12,600 | 6400 | 22,500 | 2910 |
| Minimum outflow (m3/s) | 1700 | 1700 | 6000 | 5500 |
| Runoff Scenarios | Objective Value (108 kW·h) | |||||
|---|---|---|---|---|---|---|
| Methods | Average | Median | Best | Worst | Standard Deviation | |
| Wet year | IMPSO+CHT | 2244.86 | 2244.41 | 2267.39 | 2224.81 | 15.95 |
| IMPSO | 2229.94 | 2240.86 | 2254.41 | 2173.14 | 25.12 | |
| SAPSO | 1927.66 | 1941.31 | 2003.24 | 1839.86 | 54.99 | |
| LFPSO | 1944.84 | 1933.59 | 2042.93 | 1867.86 | 56.08 | |
| PSO | 1942.49 | 1963.76 | 2028.84 | 1845.59 | 55.88 | |
| DE | 1942.35 | 1944.82 | 2001.02 | 1894.85 | 34.07 | |
| Normal year | IMPSO+CHT | 2091.76 | 2091.57 | 2105.61 | 2075.34 | 8.59 |
| IMPSO | 2086.25 | 2089.53 | 2101.46 | 2045.12 | 16.08 | |
| SAPSO | 1847.68 | 1820.32 | 1987.33 | 1697.08 | 103.22 | |
| LFPSO | 1899.35 | 1899.90 | 2015.22 | 1745.75 | 90.79 | |
| PSO | 1830.97 | 1801.22 | 2023.52 | 1699.34 | 102.77 | |
| DE | 1842.75 | 1846.89 | 1916.32 | 1781.71 | 41.10 | |
| Dry year | IMPSO+CHT | 1859.84 | 1860.77 | 1864.86 | 1853.50 | 3.14 |
| IMPSO | 1856.33 | 1859.99 | 1864.10 | 1840.60 | 7.91 | |
| SAPSO | 1706.79 | 1690.30 | 1860.61 | 1556.13 | 83.64 | |
| LFPSO | 1766.92 | 1766.00 | 1875.46 | 1652.74 | 64.51 | |
| PSO | 1717.39 | 1712.80 | 1859.58 | 1572.45 | 100.16 | |
| DE | 1707.64 | 1722.54 | 1771.95 | 1626.00 | 49.92 | |
| Runoff Scenarios | Methods | |||||
|---|---|---|---|---|---|---|
| IMPSO+CHT | IMPSO | SAPSO | LFPSO | PSO | DE | |
| Wet year | 1.5 | 1.5 | 4.4 | 4.5 | 4.4 | 4.8 |
| Normal year | 1.4 | 1.6 | 4.4 | 3.8 | 5.3 | 4.5 |
| Dry year | 1.7 | 1.8 | 4.6 | 3.7 | 4.5 | 4.7 |
| Mean rank | 1.53(1) | 1.63(2) | 4.67(4) | 4(3) | 4.73(5) | 4.67(4) |
| Methods | Runoff Scenarios | ||
|---|---|---|---|
| Wet Year | Normal Year | Dry Year | |
| IMPSO+CHT | 102,496.94 | 58,496.09 | 46,525.09 |
| IMPSO | 10,9926.80 | 58,995.86 | 53,199.21 |
| SAPSO | 150,642.80 | 98,511.19 | 69,218.02 |
| LFPSO | 111,575.85 | 94,364.46 | 69,667.44 |
| PSO | 155,965.26 | 139,110.53 | 69,218.02 |
| DE | 159,466.37 | 134,618.88 | 71,089.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Mo, L.; Yang, Y.; Tao, Y. Optimal Scheduling of Cascade Reservoirs Based on an Integrated Multistrategy Particle Swarm Algorithm. Water 2023, 15, 2593. https://doi.org/10.3390/w15142593
Liu Y, Mo L, Yang Y, Tao Y. Optimal Scheduling of Cascade Reservoirs Based on an Integrated Multistrategy Particle Swarm Algorithm. Water. 2023; 15(14):2593. https://doi.org/10.3390/w15142593
Chicago/Turabian StyleLiu, Yixuan, Li Mo, Yuqi Yang, and Yitao Tao. 2023. "Optimal Scheduling of Cascade Reservoirs Based on an Integrated Multistrategy Particle Swarm Algorithm" Water 15, no. 14: 2593. https://doi.org/10.3390/w15142593
APA StyleLiu, Y., Mo, L., Yang, Y., & Tao, Y. (2023). Optimal Scheduling of Cascade Reservoirs Based on an Integrated Multistrategy Particle Swarm Algorithm. Water, 15(14), 2593. https://doi.org/10.3390/w15142593





