Research on the Hydraulic Characteristics of Island Fishways by Experimental and Numerical Methods
Abstract
:1. Introduction
2. Materials and Methods
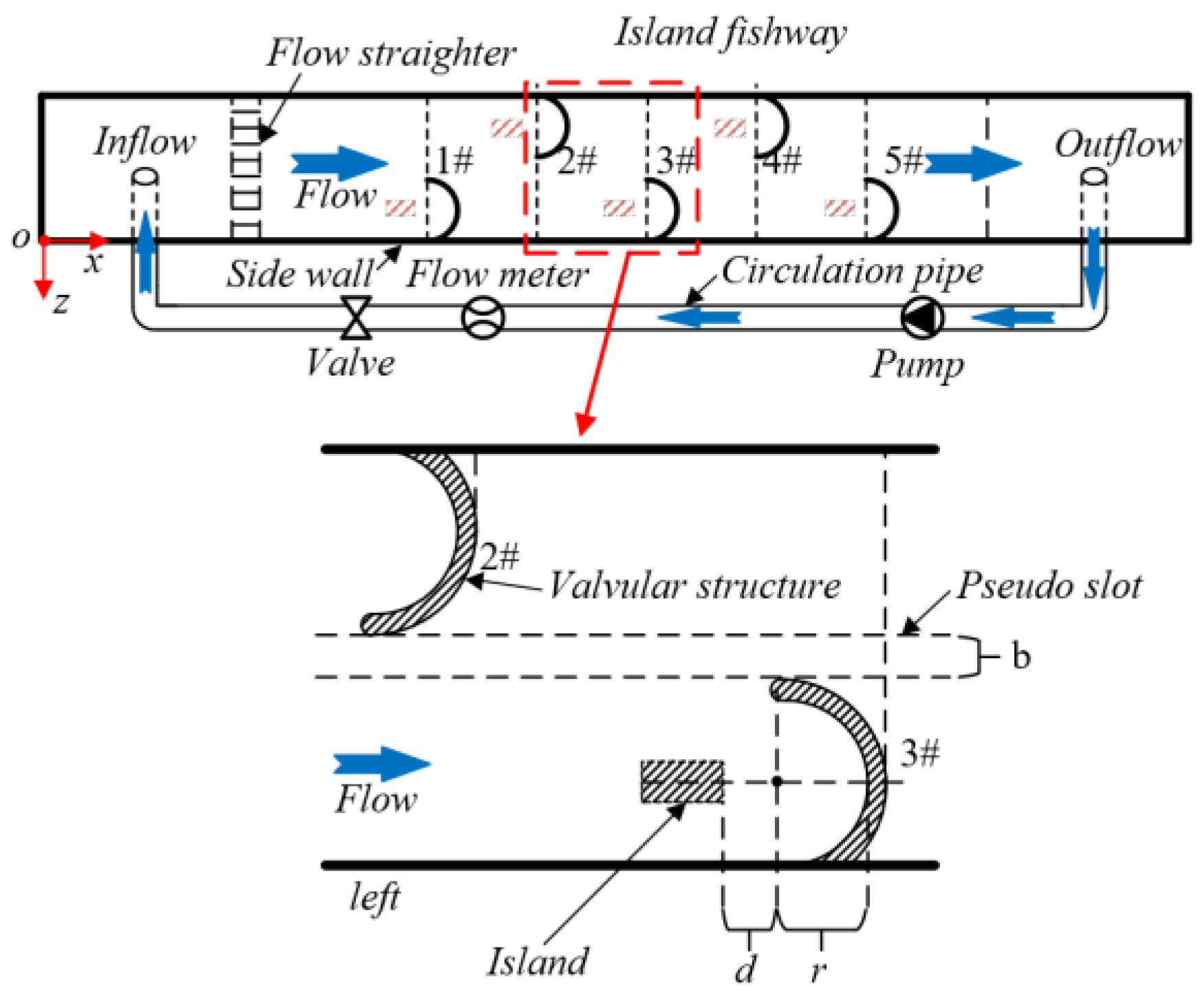
2.1. Experimental Method
2.2. Numerical Simulation
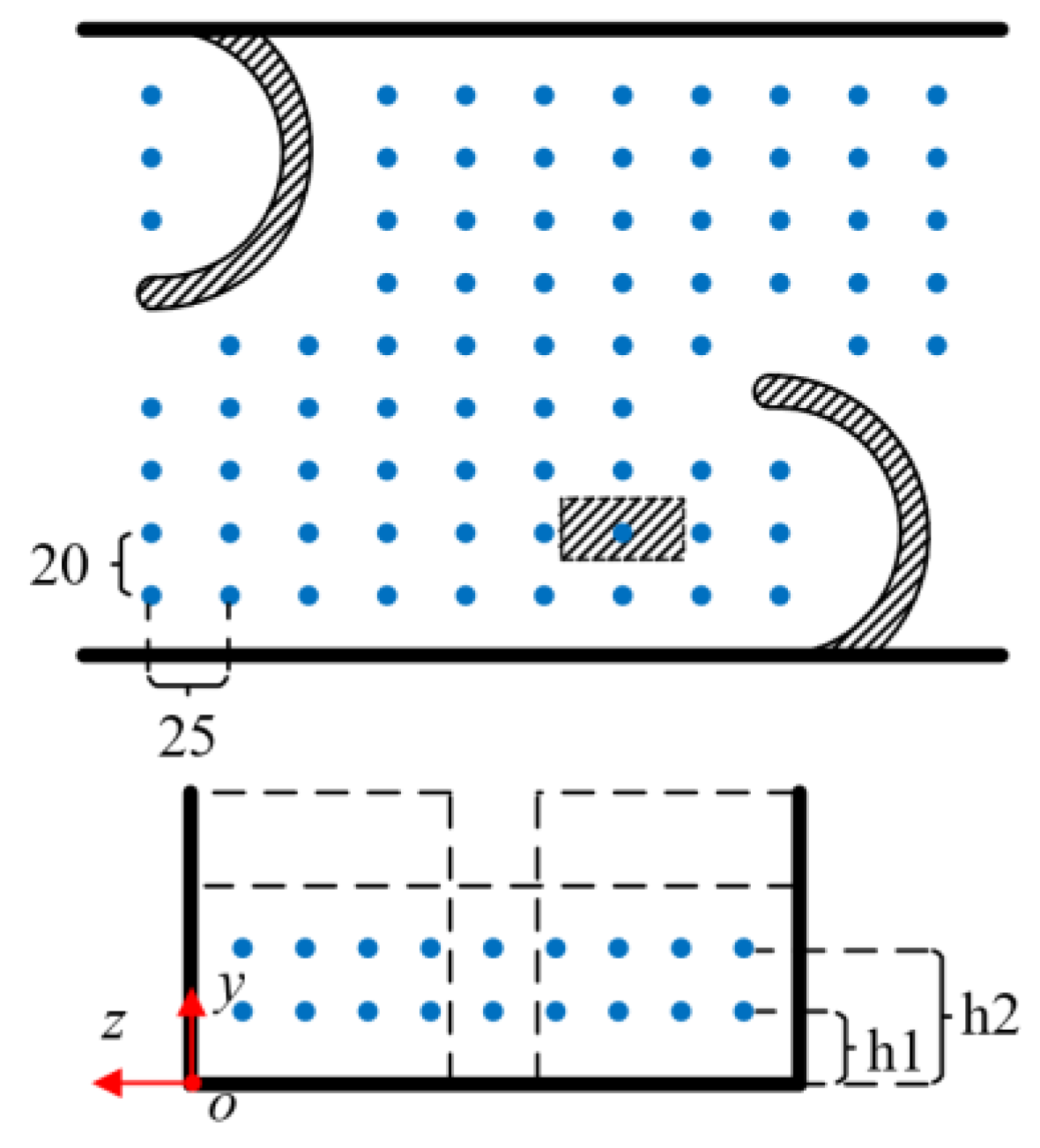
2.2.1. Model Domain and Design Parameters
2.2.2. Governing Equations
- (i)
- Turbulence control equation
- (ii)
- Free surface control equation
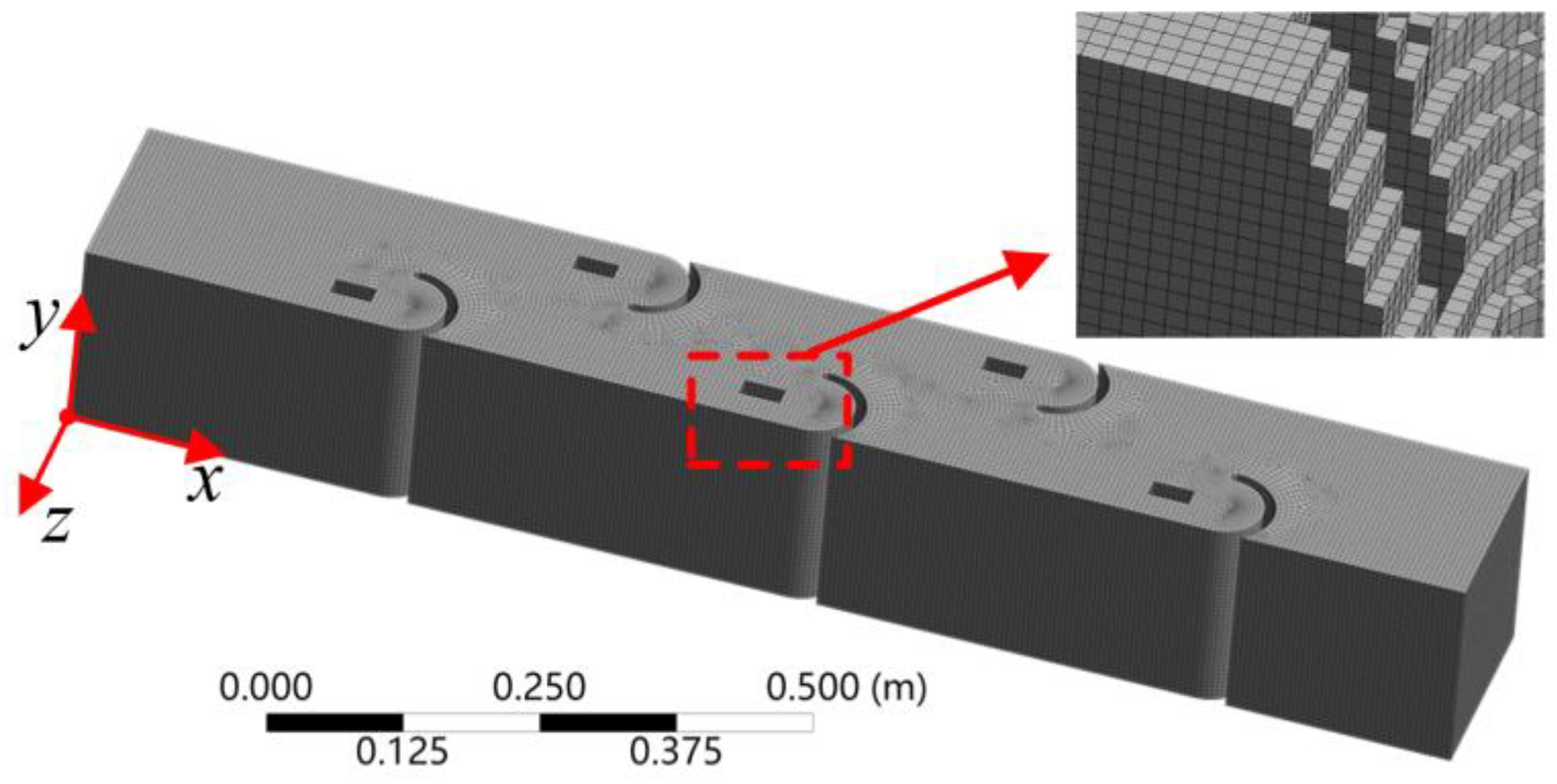
2.2.3. Mesh and Boundary Conditions
3. Results and Discussion
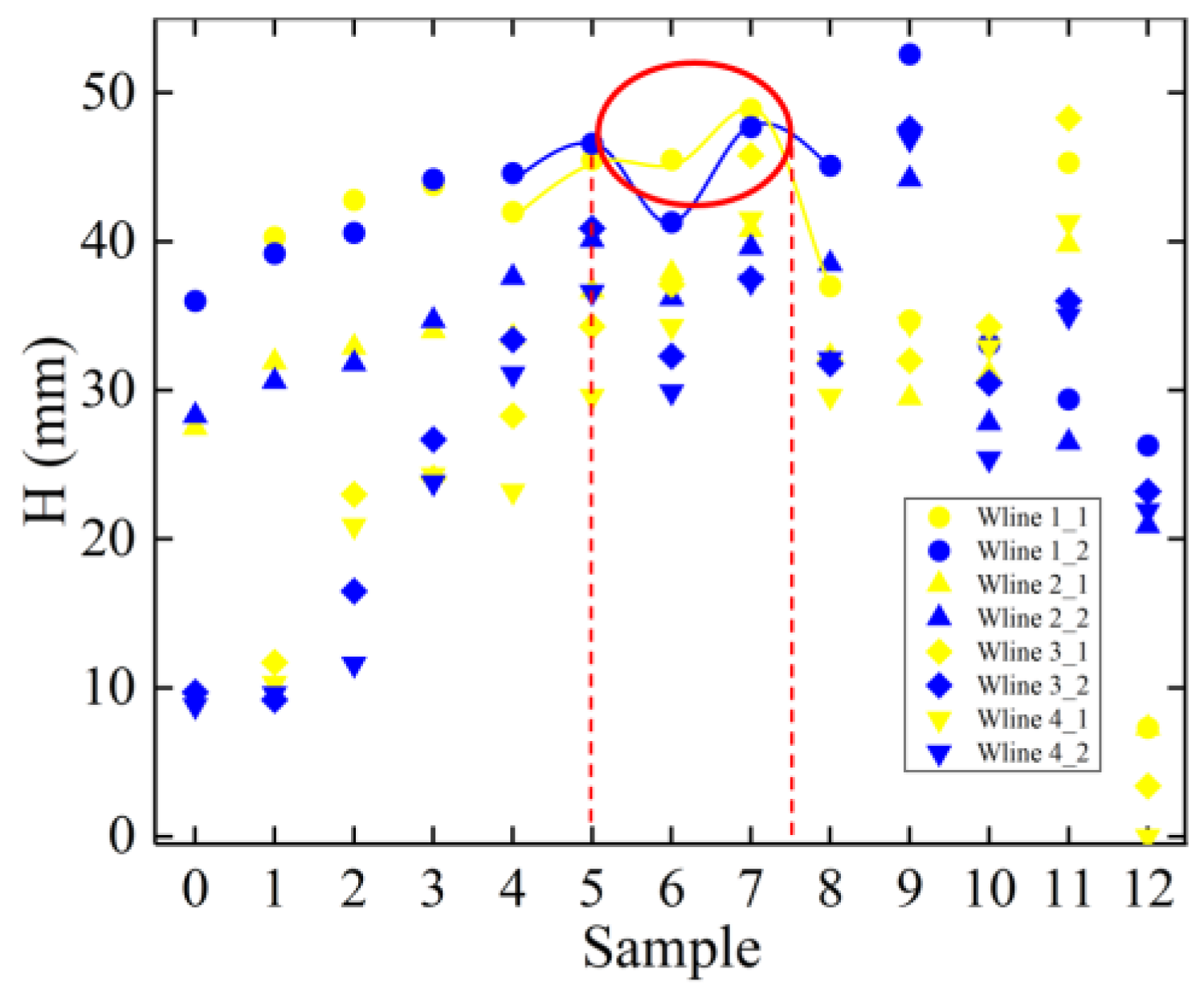
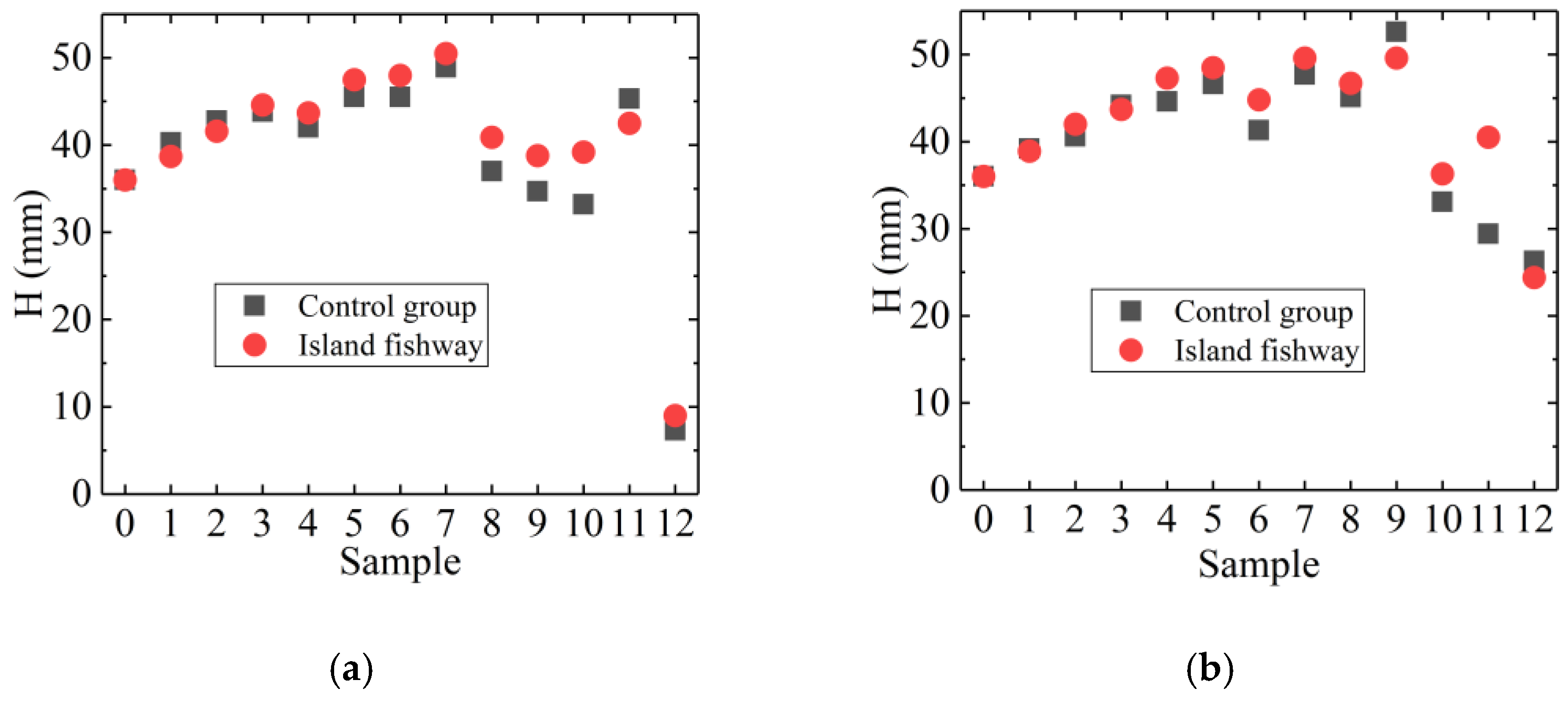
3.1. Experimental Results and Model Performance Validation
3.2. Hydraulic Characteristic Analysis
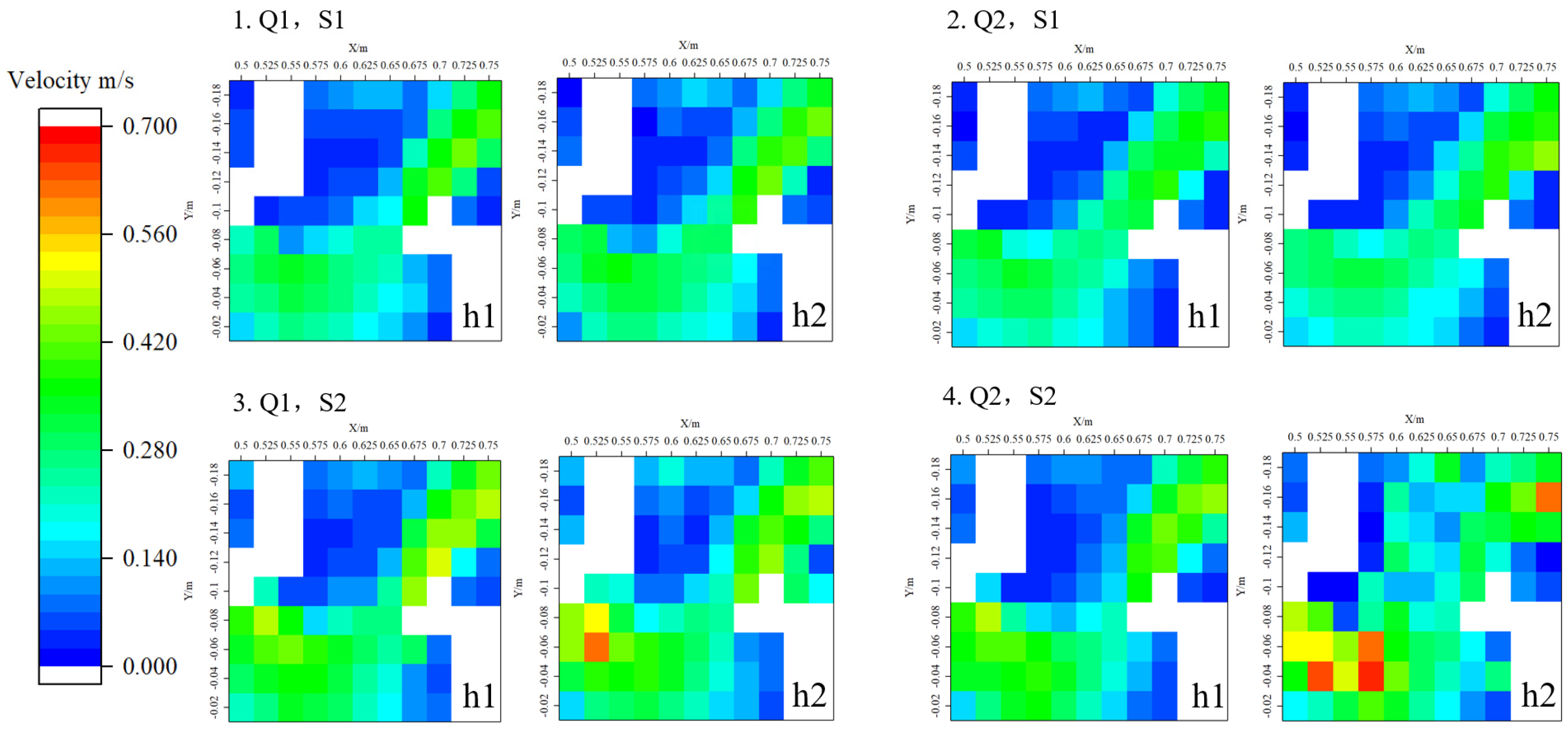
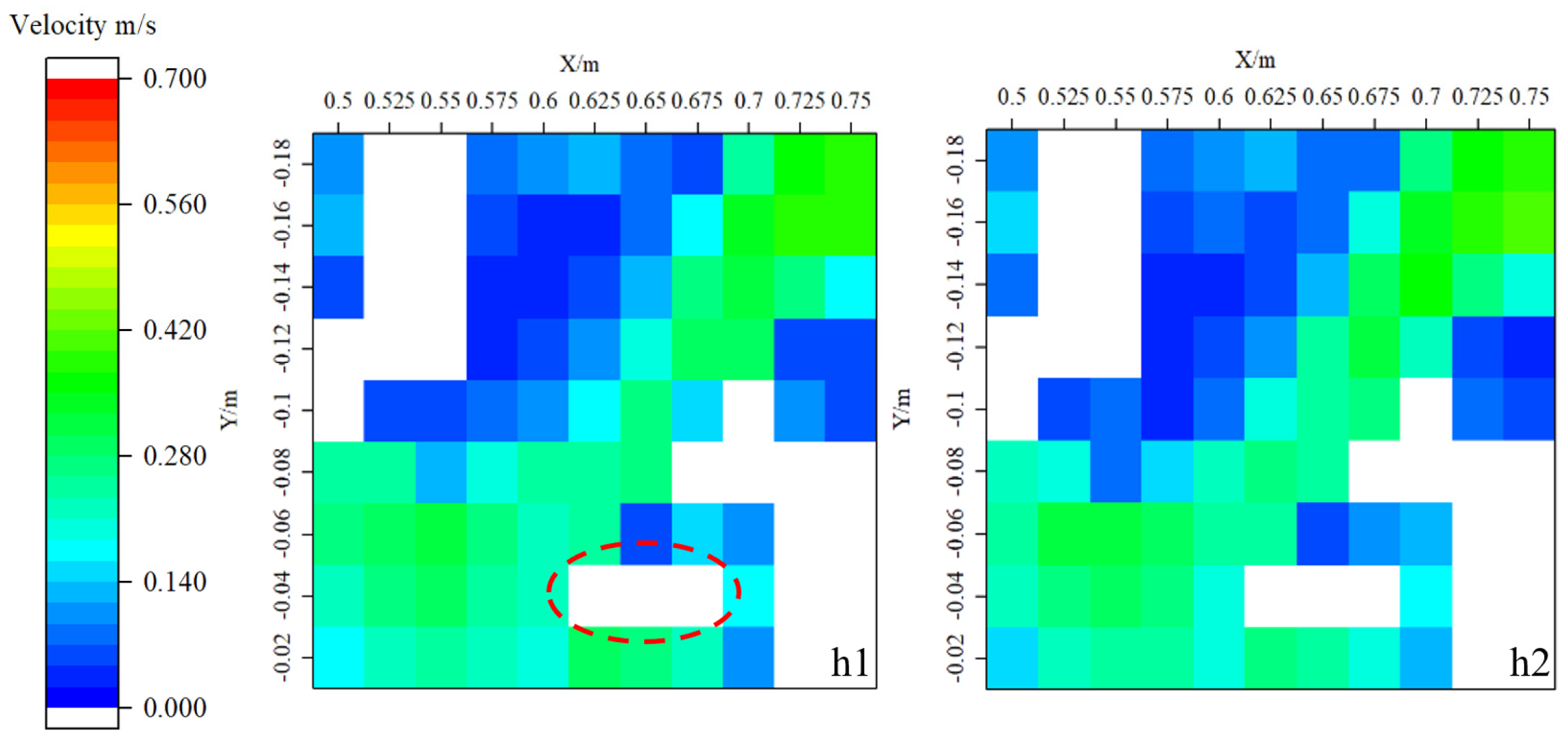
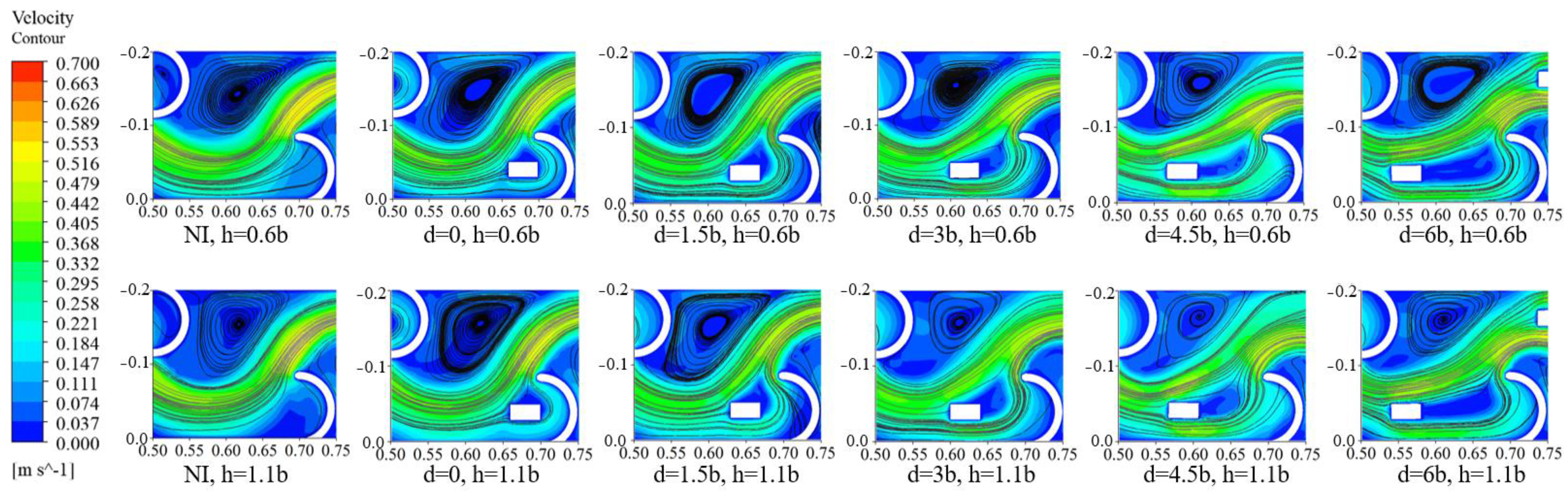
3.2.1. Velocity Field Distribution
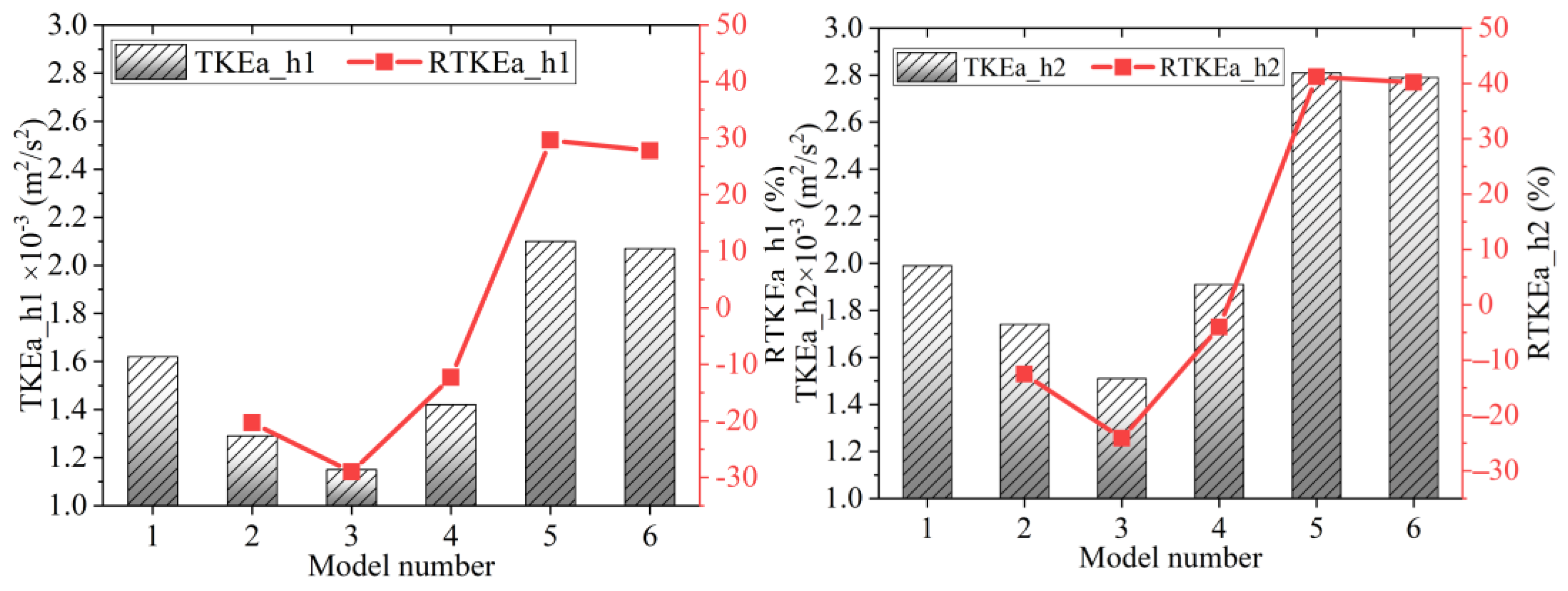
3.2.2. Turbulent Kinetic Energy
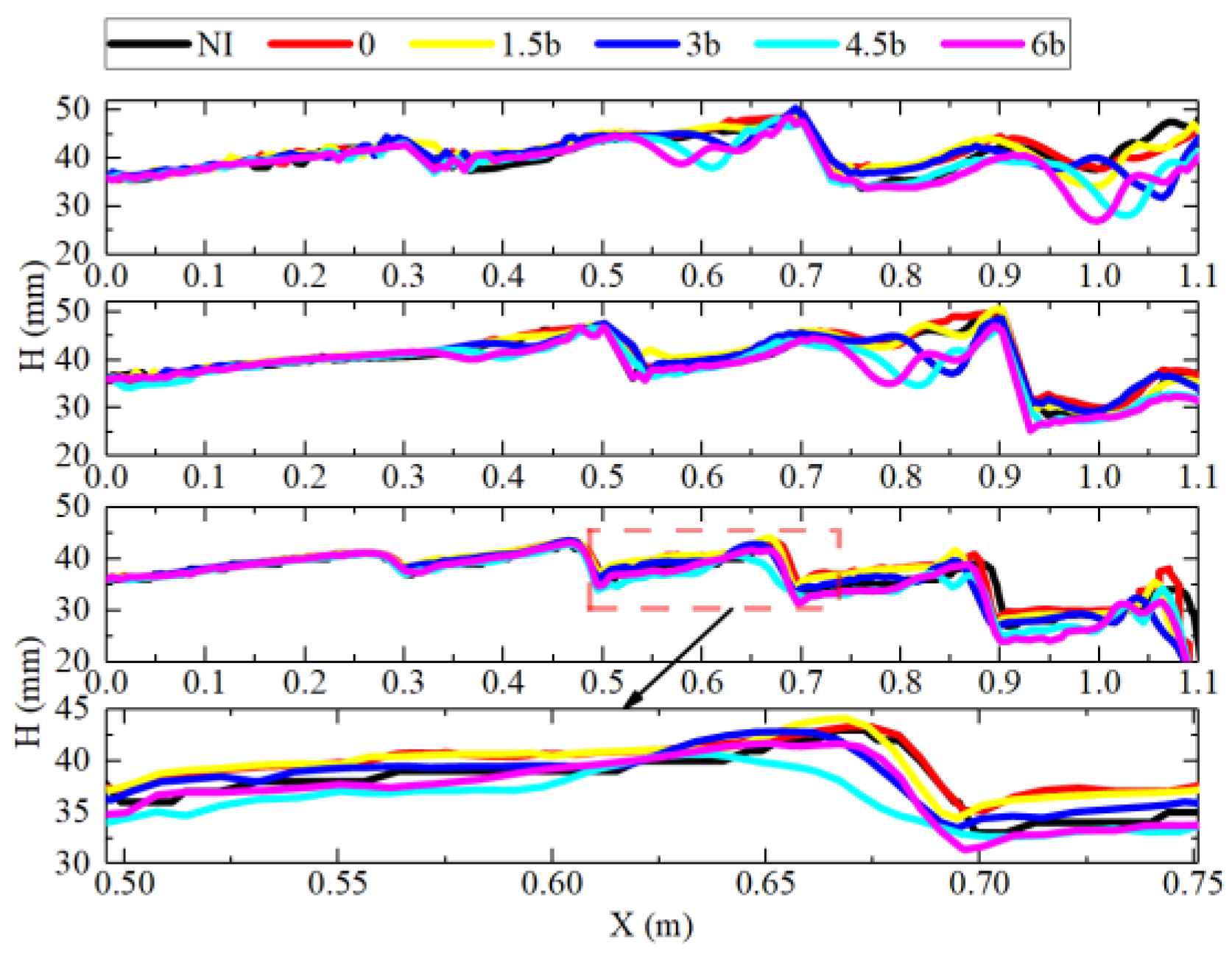
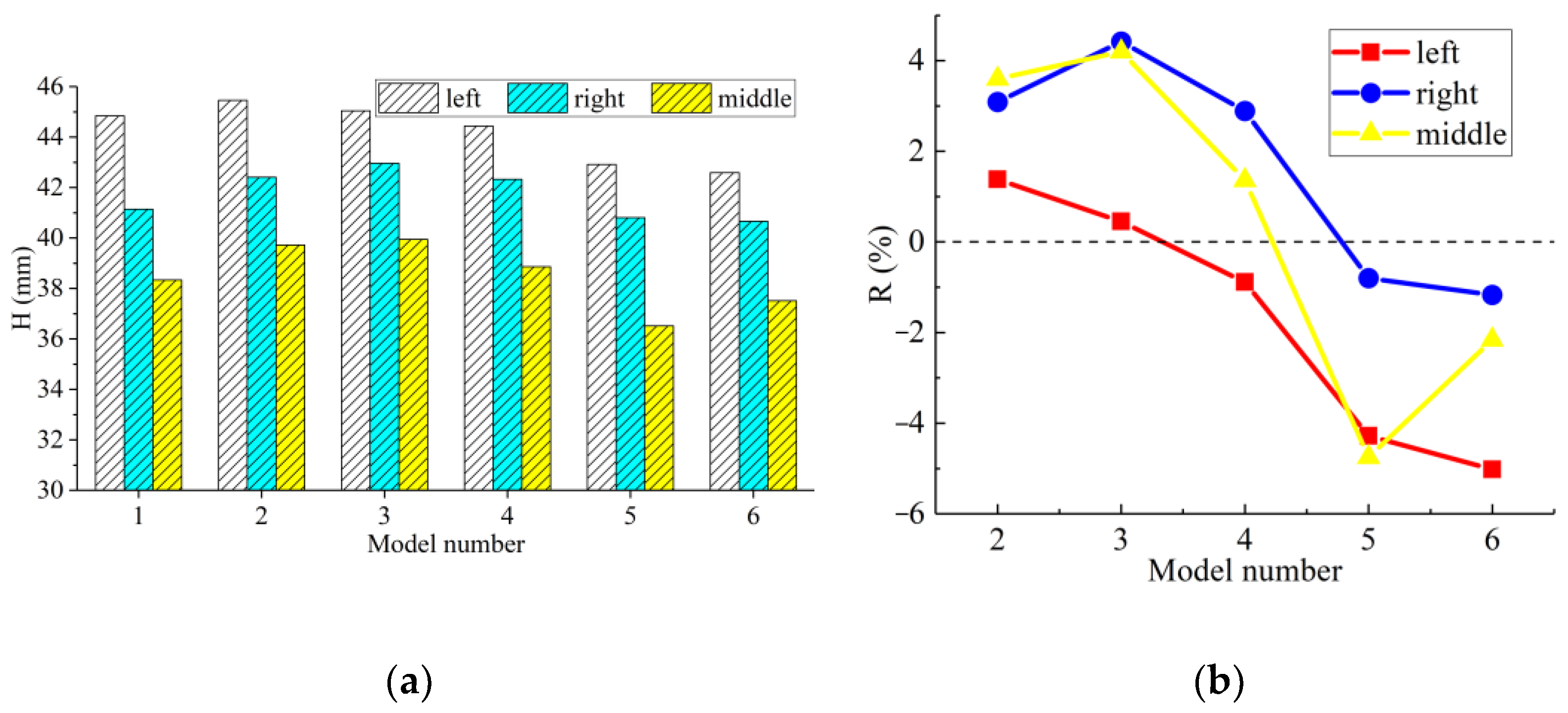
3.2.3. Water Depth Distribution
4. Conclusions
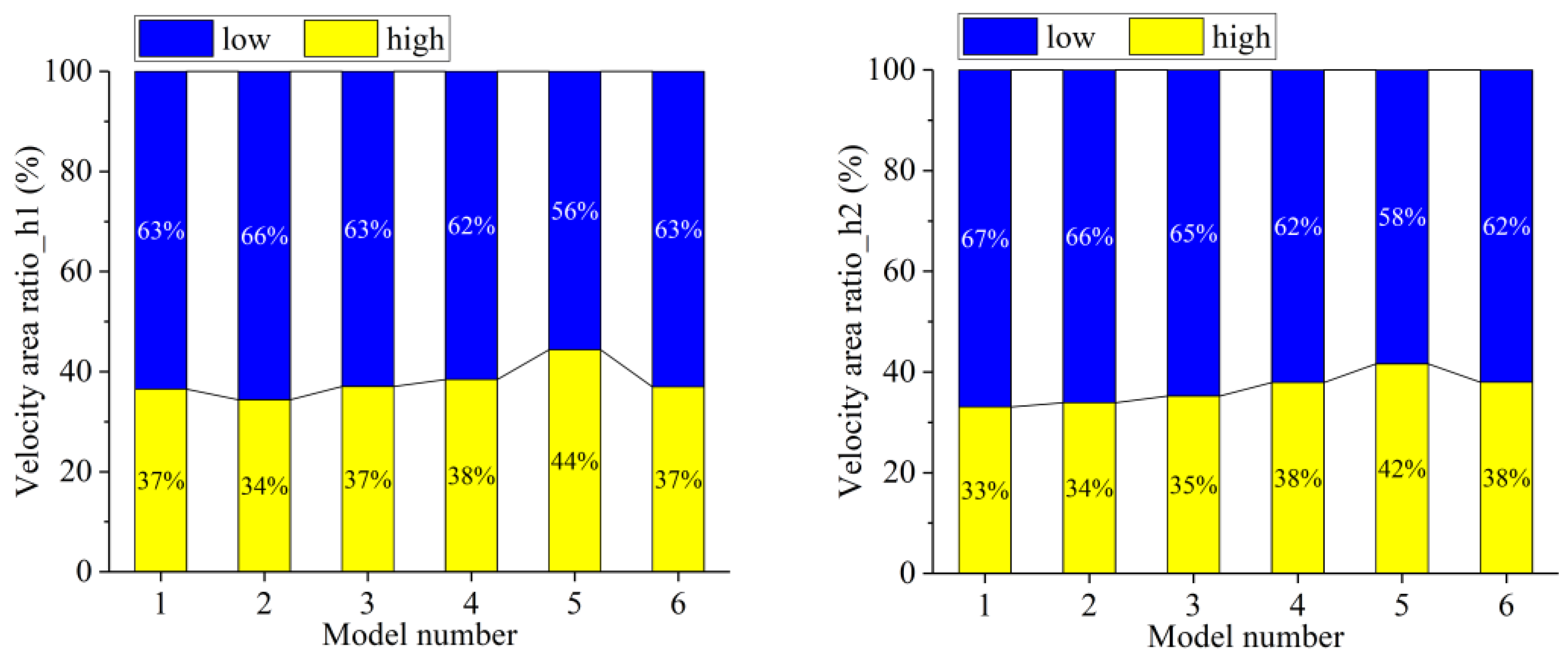
- (1)
- The main flow area of the fishway was evident in the pool chamber. Additionally, the rear of the island structure presented a small area of low flow velocity, and this area tended to elongate with the increase in island distance setting. The proportion of high and low flow velocity areas varied little under different pool layout schemes, while low flow velocity areas often accounted for over 60% of the pool area.
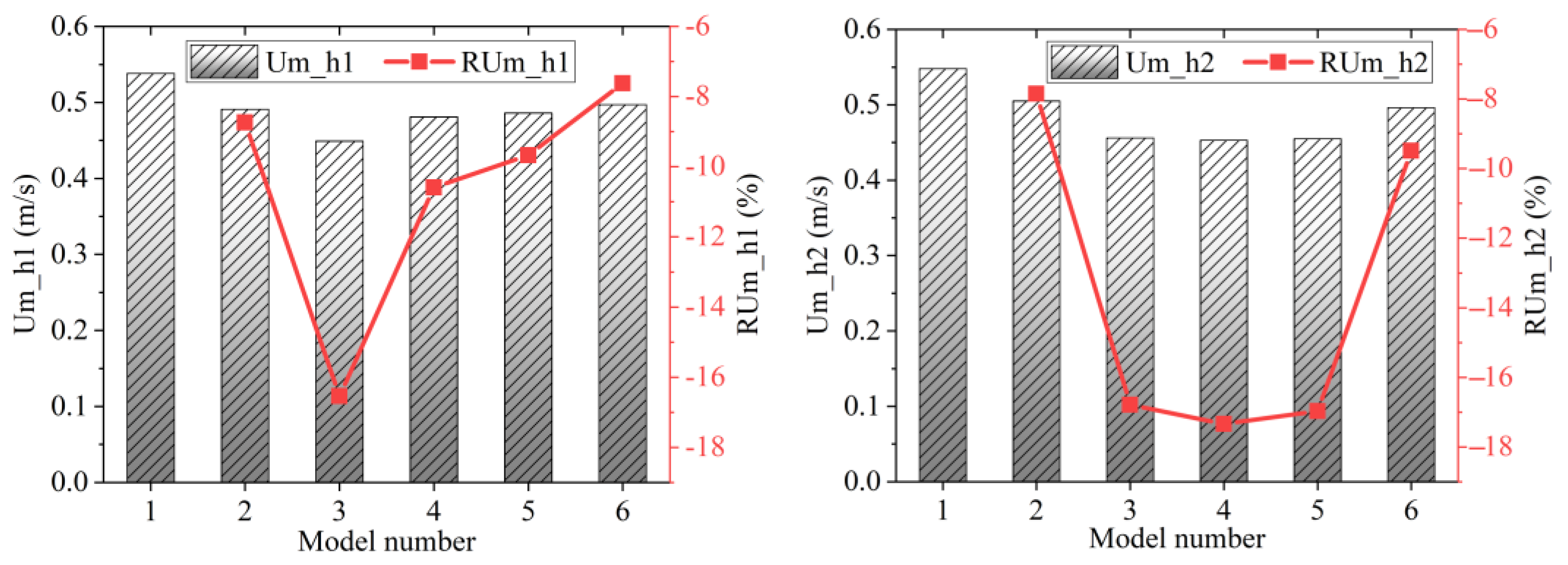
- (2)
- The upper layer’s maximum flow velocity was higher than that of the lower layer, while the average velocity was similar. The arrangement of the island significantly suppresses the maximum flow velocity of different water layers (d = 1.5b having a better effect). However, this inhibitory effect weakens as the island distance increases; for the average flow velocity, the effect of the island leads to a slight increase, and as the island distance increases, the overall effect tends to intensify.
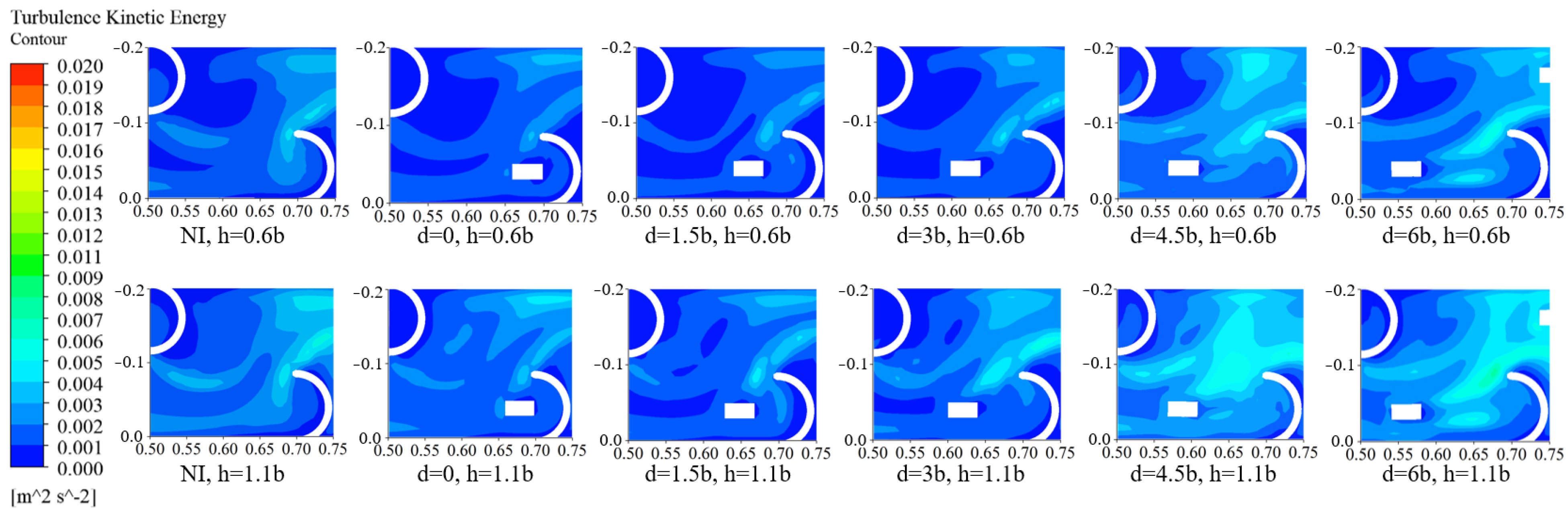
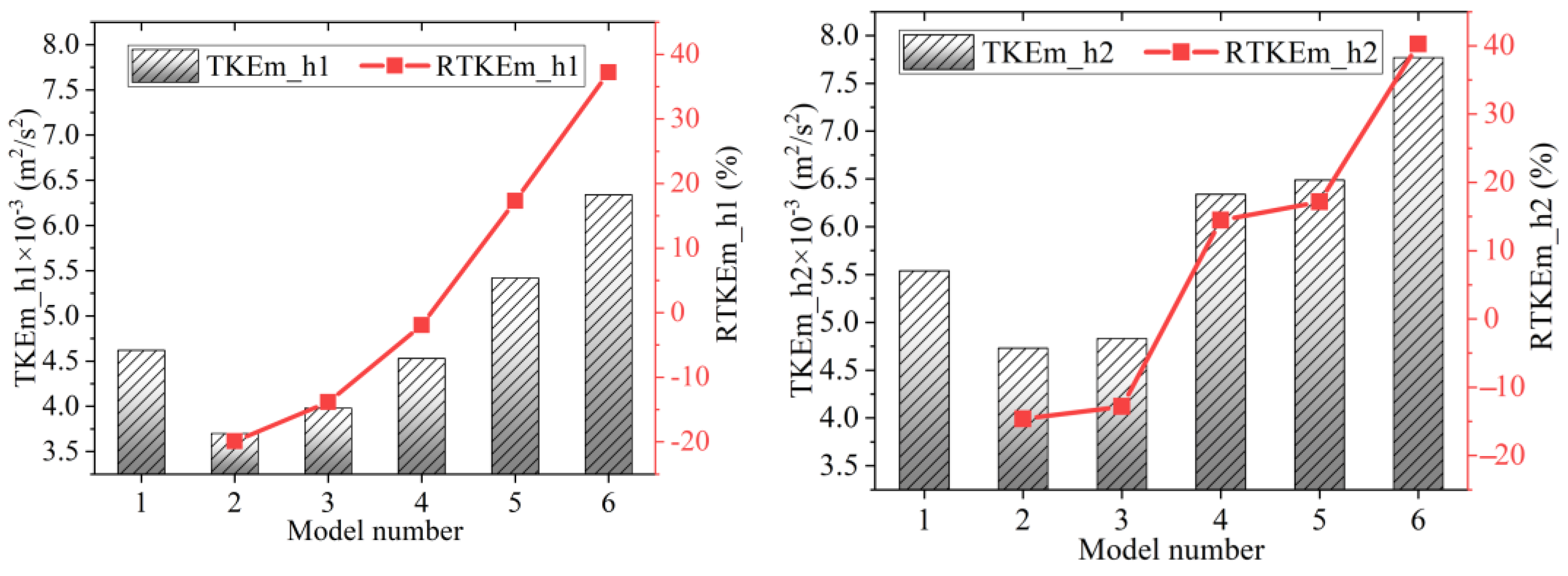
- (3)
- The distribution of TKE values in the upper layer was significantly higher than that in the lower layer. When d was taken as 0 or 1.5b, it had an excellent inhibitory effect on TKE, with a maximum weakening TKE value of up to 30%. Overall, TKE values showed an increasing trend with increasing d values, with a maximum increase of approximately 40% (d = 6b; h2). The average turbulent kinetic energy in the pool chamber was relatively small, and the maximum turbulent kinetic energy in the pool chamber was less than 0.01s2/m2.
- (4)
- The water level showed a stepped distribution as a whole. The results show that its changes were not significant under different models, and there was only a certain effect of raising the water level when d = 0 and 1.5b. However, further increasing the d value might even lead to a slight decrease in the water level. Combined with the above flow rate and TKE analysis, it could be considered appropriate to take a value near 1.5b for d.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Katopodis, C.; Cai, L.; Johnson, D. Sturgeon survival: The role of swimming performance and fish passage research. Fish. Res. 2019, 212, 162–171. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, L. Yangtze dams increasingly threaten the survival of the Chinese sturgeon. Curr. Biol. 2018, 28, 3640–3647.e3618. [Google Scholar] [CrossRef]
- Mallen-Cooper, M.; Brand, D. Non-salmonids in a salmonid fishway: What do 50 years of data tell us about past and future fish passage. Fish. Manag. Ecol. 2007, 14, 319–332. [Google Scholar] [CrossRef]
- Williams, J.G.; Armstrong, G.; Katopodis, C.; Larinier, M.; Travade, F. Thinking like a fish: A key ingredient for development of effective fish passage facilities at river obstructions. River Res. Appl. 2012, 28, 407–417. [Google Scholar] [CrossRef] [Green Version]
- Mao, X. Review of fishway research in China. Ecol. Eng. 2018, 115, 91–95. [Google Scholar] [CrossRef]
- Kasischke, K.; Oertel, M. Discharge Coefficients of a Specific Vertical Slot Fishway Geometry—New Fitting Parameters. Water 2023, 15, 1193. [Google Scholar] [CrossRef]
- Qie, Z.; Guo, L.; Wu, X.; Ran, Y. Experimental study and numerical simulation of hydraulic characteristics of Tai Chi fishway. Trans. Chin. Soc. Agric. Eng. 2018, 34, 182–188. [Google Scholar]
- Baharvand, S.; Lashkar-Ara, B. Hydraulic design criteria of the modified meander C-type fishway using the combined experimental and CFD models. Ecol. Eng. 2021, 164, 106207. [Google Scholar] [CrossRef]
- Masumoto, T.; Nakai, M.; Asaeda, T.; Rahman, M. Effectiveness of New Rock-Ramp Fishway at Miyanaka Intake Dam Compared with Existing Large and Small Stair-Type Fishways. Water 2022, 14, 1991. [Google Scholar] [CrossRef]
- Dong, Z.; Tong, J.; Huang, Z. Turbulence characteristics in a weir-orifice-slot combined fishway with an identical layout. J. Turbul. 2022, 23, 327–351. [Google Scholar] [CrossRef]
- Thompson, S.M.; Paudel, B.; Jamal, T.; Walters, D. Numerical investigation of multistaged tesla valves. J. Fluids Eng. 2014, 136, 081102. [Google Scholar] [CrossRef]
- Qian, J.-Y.; Wu, J.-Y.; Gao, Z.-X.; Wu, A.; Jin, Z.-J. Hydrogen decompression analysis by multi-stage Tesla valves for hydrogen fuel cell. Int. J. Hydrogen Energy 2019, 44, 13666–13674. [Google Scholar] [CrossRef]
- Zhang, S.; Winoto, S.; Low, H. Performance simulations of Tesla microfluidic valves. In Proceedings of the International Conference on Integration and Commercialization of Micro and Nanosystems, Sanya, China, 10–13 January 2007; pp. 15–19. [Google Scholar]
- Keizer, K. Determination Whether a Large Scale Tesla Valve Could Be Applicable as a Fish Passage. Additional Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Hoek, S.; Jin, R.; van der Schaar, E.; Shanitbayeva, S.; de Visser, M.; Wallace, N.; Lavooij, H. The Return of Fish Migration to the Dutch River Delta. 2021. Available online: https://www.delta21.nl/wp-content/uploads/2022/02/ACT-Vismigratierivier.pdf (accessed on 13 July 2023).
- Zeng, G.; Xu, M.; Mou, J.; Hua, C.; Fan, C. Application of Tesla Valve’s Obstruction Characteristics to Reverse Fluid in Fish Migration. Water 2022, 15, 40. [Google Scholar] [CrossRef]
- Błotnicki, J.; Gruszczyński, M. Modelling of Tesla Valvular Concuit as an Energy Dissipation System in Fish Pass Pools. In Proceedings of the 2nd International Scientific Conference on Ecological and Environmental Engineering COEE21, Wrocław, Poland, 30 June–1 July 2021; p. 6. [Google Scholar]
- Webb, P.W.; Kostecki, P.T.; Don Stevens, E. The Effect of Size and Swimming Speed on Locomotor Kinematics of Rainbow Trout. J. Exp. Biol. 1984, 109, 77–95. [Google Scholar] [CrossRef]
- Sullivan, C.J.; Weber, M.J.; Pierce, C.L.; Camacho, C.A. A Comparison of Grass Carp Population Characteristics Upstream and Downstream of Lock and Dam 19 of the Upper Mississippi River. J. Fish Wildl. Manag. 2020, 11, 99–111. [Google Scholar] [CrossRef] [Green Version]
- Masser, M.P. Using Grass Carp in Aquaculture and Private Impoundments; SRAC: Mississippi, MS, USA, 2002. [Google Scholar]
- Mu, X.; Zhen, W.; Li, X.; Cao, P.; Gong, L.; Xu, F. A Study of the Impact of Different Flow Velocities and Light Colors at the Entrance of a Fish Collection System on the Upstream Swimming Behavior of Juvenile Grass Carp. Water 2019, 11, 322. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Ji, B.; Zou, J.; Long, X. Experimental investigation on the transport of different fish species in a jet fish pump. Aquac. Eng. 2017, 79, 42–48. [Google Scholar] [CrossRef]
- General Institute of Water Resources and Hydropower Planning and Design. Guidelines for Fishway Design of Water Conservancy and Hydropower Projects; SL 609-2013; China Water & Power Press: Beijing, China, 2013. [Google Scholar]
- Keming, A. Basic Points and Engineering Examples of Hydraulic Design for Fishways. Water Conserv. Sci. Technol. Econ. 2012, 18, 82–85. [Google Scholar]
- Yagci, O. Hydraulic aspects of pool-weir fishways as ecologically friendly water structure. Ecol. Eng. 2010, 36, 36–46. [Google Scholar] [CrossRef]
- Tan, J.; Liu, Z.; Wang, Y.; Wang, Y.; Ke, S.; Shi, X. Analysis of Movements and Behavior of Bighead Carps (Hypophthalmichthys nobilis) Considering Fish Passage Energetics in an Experimental Vertical Slot Fishway. Animals 2022, 12, 1725. [Google Scholar] [CrossRef] [PubMed]
- Shi, K.; Li, G.; Liu, S.; Sun, S. Experimental study on the passage behavior of juvenile Schizothorax prenanti by configuring local colors in the vertical slot fishways. Sci. Total Environ. 2022, 843, 156989. [Google Scholar] [CrossRef]
- Cea, L.; Pena, L.; Puertas, J.; Vázquez-Cendón, M.; Peña, E. Application of several depth-averaged turbulence models to simulate flow in vertical slot fishways. J. Hydraul. Eng. 2007, 133, 160–172. [Google Scholar] [CrossRef]
- Tan, J.; Gao, Z.; Dai, H.; Yang, Z.; Shi, X. Effects of turbulence and velocity on the movement behaviour of bighead carp (Hypophthalmichthys nobilis) in an experimental vertical slot fishway. Ecol. Eng. 2019, 127, 363–374. [Google Scholar] [CrossRef]
- Barton, A.F.; Keller, R.J. 3D free surface model for a vertical slot fishway. In Proceedings of the XXX IAHR Congress, AUTh, Thessaloniki, Greece, 24 August 2003; pp. 409–416. [Google Scholar]
- Zhong, Z.; Ruan, T.; Hu, Y.; Liu, J.; Liu, B.; Xu, W. Experimental and numerical assessment of hydraulic characteristic of a new semi-frustum weir in the pool-weir fishway. Ecol. Eng. 2021, 170, 106362. [Google Scholar] [CrossRef]
- Xu, M.; Zeng, G.; Wu, D.; Mou, J.; Zhao, J.; Zheng, S.; Huang, B.; Ren, Y. Structural Optimization of Jet Fish Pump Design Based on a Multi-Objective Genetic Algorithm. Energies 2022, 15, 4104. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Jiang, Y.; Alexander, D.; Jenkins, H.; Arthur, R.; Chen, Q. Natural ventilation in buildings: Measurement in a wind tunnel and numerical simulation with large-eddy simulation. J. Wind. Eng. Ind. Aerodyn. 2003, 91, 331–353. [Google Scholar] [CrossRef]
- Qie, Z.; Liu, H.; Wu, M.; Ran, Y. Establishment of swirling-flow fishway and analysis of its hydraulic characteristics. Trans. Chin. Soc. Agric. Eng. 2020, 36, 126–131. [Google Scholar]
- Li, H.; Wang, X.; Zheng, F. Analysis of three-dimensional characteristics of water flow in trapezoidal fishways. J. Hohai Univ. (Nat. Sci.) 2022, 51, 1–7. [Google Scholar]
- Yang, Q.; Hu, P.; Yang, Z.; Chu, L.; Yang, J. Suitable Flow Rate and Adaptive Threshold for Grass Carp (Ctenopharyngodon idellus) Migration. J. Hydroecol. 2019, 40, 93–100. [Google Scholar]
- Lu, B.; Liu, W.; Liang, Y.; Chen, Q.; Huang, Y.; Pan, L.; Liu, D.; Shi, X. The burst-coast swimming behavior of grass carp (Ctenopharyngodon idellus) during fast-start. J. Fish. China 2014, 38, 6. [Google Scholar]
- O’Connor, J.; Hale, R.; Mallen-Cooper, M.; Cooke, S.J.; Stuart, I. Developing performance standards in fish passage: Integrating ecology, engineering and socio-economics. Ecol. Eng. 2022, 182, 106732. [Google Scholar] [CrossRef]
- Hou, Y.; Yang, Z.; An, R.; Cai, L.; Chen, X.; Zhao, X.; Zou, X. Water flow and substrate preferences of Schizothorax wangchiachii (Fang, 1936). Ecol. Eng. 2019, 138, 1–7. [Google Scholar] [CrossRef]
- Chen, B.; Yuan, H.; He, X.; Sun, Q.; Xu, G. Research on the Influence of Tank Chamber Structure on the Hydraulic Characteristics of Vertical Fishway. J. Yangtze River Sci. Res. Inst. 2022, 1–8. [Google Scholar]
- Gao, L.; Gao, B.; Xu, D.; Peng, W.; Lu, J. Multiple assessments of trace metals in sediments and their response to the water level fluctuation in the Three Gorges Reservoir, China. Sci. Total Environ. 2019, 648, 197–205. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Rajaratnam, N.; Katopodis, C. Structure of flow in vertical slot fishway. J. Hydraul. Eng. 1999, 125, 351–360. [Google Scholar] [CrossRef]
- Enders, E.C.; Boisclair, D.; Roy, A.G. The effect of turbulence on the cost of swimming for juvenile Atlantic salmon (Salmo salar). Can. J. Fish. Aquat. Sci. 2003, 60, 1149–1160. [Google Scholar] [CrossRef]
- Quaranta, E.; Katopodis, C.; Revelli, R.; Comoglio, C. Turbulent flow field comparison and related suitability for fish passage of a standard and a simplified low-gradient vertical slot fishway. River Res. Appl. 2017, 33, 1295–1305. [Google Scholar] [CrossRef]


| Mesh Number | Size (m) | Elements | Error (%) |
|---|---|---|---|
| M1 | 0.01 | 59,460 | 7 |
| M2 | 0.008 | 112,900 | 6.08 |
| M3 | 0.006 | 257,268 | 5.95 |
| M4 | 0.005 | 461,720 | 5.98 |
| No. | ||
|---|---|---|
| 1 | 38.6 | 40.5 |
| 2 | 31.9 | 33.6 |
| 3 | 28.1 | 28.8 |
| 4 | 25.4 | 26.9 |
| 1(I) | 40.1 | 42.2 |
| No. | H | |||||
|---|---|---|---|---|---|---|
| 1 | h1 | 0.538 | - | 0.167 | - | 0.575 |
| h2 | 0.548 | - | 0.155 | - | 0.494 | |
| 2 (0b) | h1 | 0.491 | −8.740 | 0.169 | 1.200 | 0.524 |
| h2 | 0.505 | −7.850 | 0.167 | 7.740 | 0.513 | |
| 3 (1.5b) | h1 | 0.449 | −16.540 | 0.162 | 3.000 | 0.588 |
| h2 | 0.456 | −16.790 | 0.156 | 0.650 | 0.544 | |
| 4 (3b) | h1 | 0.481 | −10.590 | 0.167 | 0 | 0.624 |
| h2 | 0.453 | −17.340 | 0.166 | 7.100 | 0.611 | |
| 5 (4.5b) | h1 | 0.486 | −9.670 | 0.182 | 8.980 | 0.797 |
| h2 | 0.455 | −16.970 | 0.179 | 15.480 | 0.713 | |
| 6 (6b) | h1 | 0.497 | −7.620 | 0.169 | 1.200 | 0.587 |
| h2 | 0.496 | −9.490 | 0.173 | 11.610 | 0.612 |
| No. | H | ||||
|---|---|---|---|---|---|
| 1 | h1 | 4.62 | - | 1.62 | - |
| h2 | 5.54 | - | 1.99 | - | |
| 2 (0b) | h1 | 3.70 | −19.91 | 1.29 | −20.37 |
| h2 | 4.73 | −14.62 | 1.74 | −12.56 | |
| 3 (1.5b) | h1 | 3.98 | −13.85 | 1.15 | −29.01 |
| h2 | 4.83 | −12.82 | 1.51 | −24.12 | |
| 4 (3b) | h1 | 4.53 | −1.95 | 1.42 | −12.35 |
| h2 | 6.34 | 14.44 | 1.91 | −4.02 | |
| 5 (4.5b) | h1 | 5.42 | 17.32 | 2.10 | 29.63 |
| h2 | 6.49 | 17.15 | 2.81 | 41.21 | |
| 6 (6b) | h1 | 6.34 | 37.23 | 2.07 | 27.78 |
| h2 | 7.77 | 40.25 | 2.79 | 40.20 |
| No. | Hsl (mm) | RHsl (%) | Hsr (mm) | RHsr (%) | Hsm (mm) | RHsm (%) |
|---|---|---|---|---|---|---|
| 1 | 44.84 | - | 41.14 | - | 38.34 | - |
| 2 | 45.46 | 1.38 | 42.41 | 3.09 | 39.72 | 3.60 |
| 3 | 45.04 | 0.45 | 42.96 | 4.42 | 39.95 | 4.20 |
| 4 | 44.44 | −0.89 | 42.33 | 2.89 | 38.86 | 1.36 |
| 5 | 42.92 | −4.28 | 40.81 | −0.80 | 36.52 | −4.75 |
| 6 | 42.59 | −5.02 | 40.66 | −1.17 | 37.51 | −2.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, G.; Xu, M.; Mou, J.; Wang, K.; Ren, Y. Research on the Hydraulic Characteristics of Island Fishways by Experimental and Numerical Methods. Water 2023, 15, 2592. https://doi.org/10.3390/w15142592
Zeng G, Xu M, Mou J, Wang K, Ren Y. Research on the Hydraulic Characteristics of Island Fishways by Experimental and Numerical Methods. Water. 2023; 15(14):2592. https://doi.org/10.3390/w15142592
Chicago/Turabian StyleZeng, Guorui, Maosen Xu, Jiegang Mou, Keke Wang, and Yun Ren. 2023. "Research on the Hydraulic Characteristics of Island Fishways by Experimental and Numerical Methods" Water 15, no. 14: 2592. https://doi.org/10.3390/w15142592
APA StyleZeng, G., Xu, M., Mou, J., Wang, K., & Ren, Y. (2023). Research on the Hydraulic Characteristics of Island Fishways by Experimental and Numerical Methods. Water, 15(14), 2592. https://doi.org/10.3390/w15142592







