Research on the Development and Application of a Deep Learning Model for Effective Management and Response to Harmful Algal Blooms
Abstract
1. Introduction
- The relationship between harmful algae and water quality is nonlinear. Of the various ANN-based algorithms, DNN, in particular, has the advantage of enabling nonlinear combinations between input variables. Additionally, it is a powerful tool for modeling complex systems [39,40]. Furthermore, to address the data imbalance in the data of cyanobacteria cell counts in the study area, a model combining DNN with SMOTE was proposed, and its applicability was evaluated. In this study, the DNN algorithm was used to simultaneously predict the number of cyanobacteria cells and the HAB alert levels. To allow for the prediction of both continuous and categorical data, the DNN algorithm was improved to support multiple outputs in this study.
- In terms of prediction accuracy, we evaluated the results of the DNN algorithm, which predicts cyanobacteria cells and HAB alert level, to assess their applicability in the field and recommend research directions for future AI-based HAB prediction research.
2. Materials and Methods
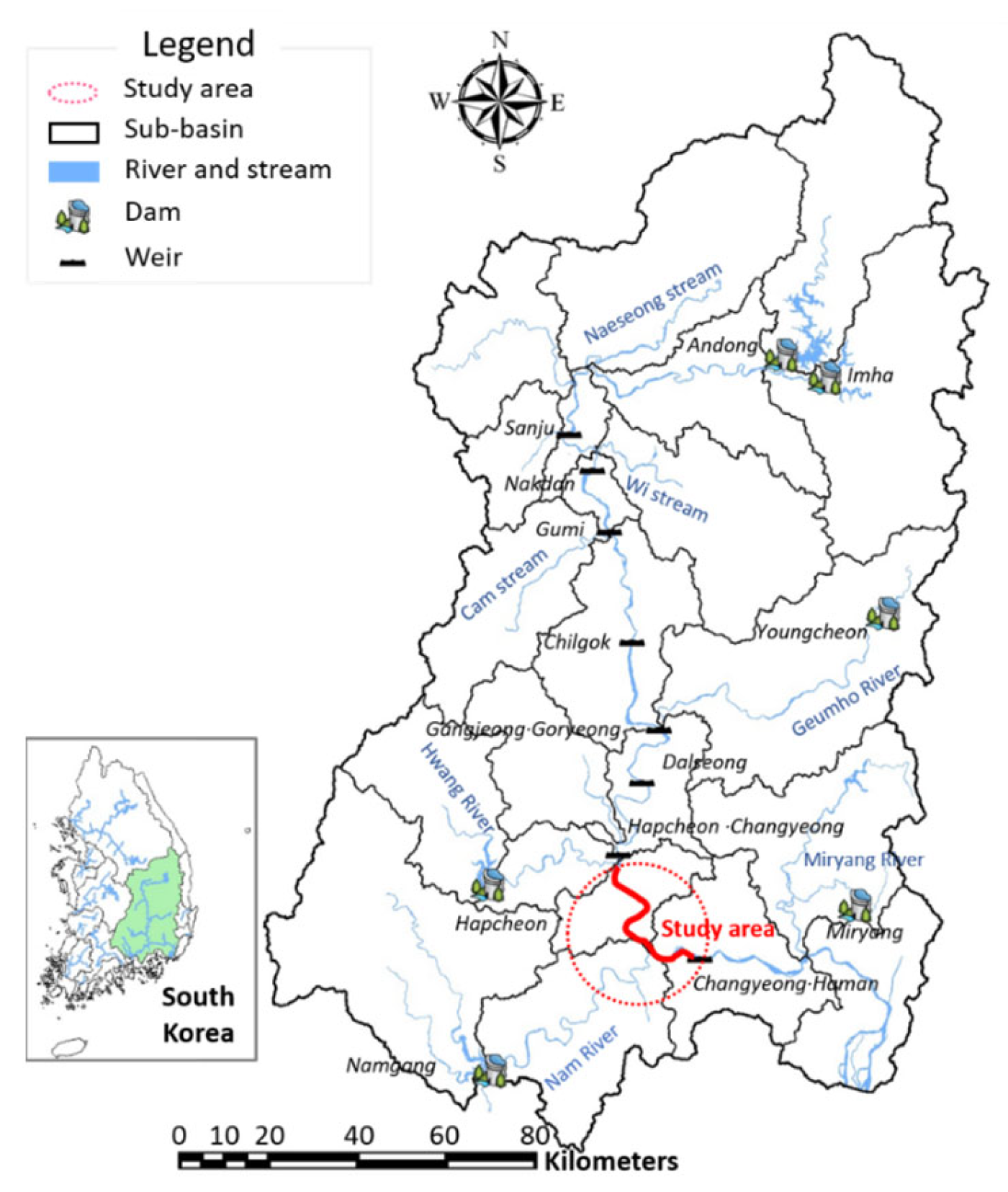
2.1. Study Area
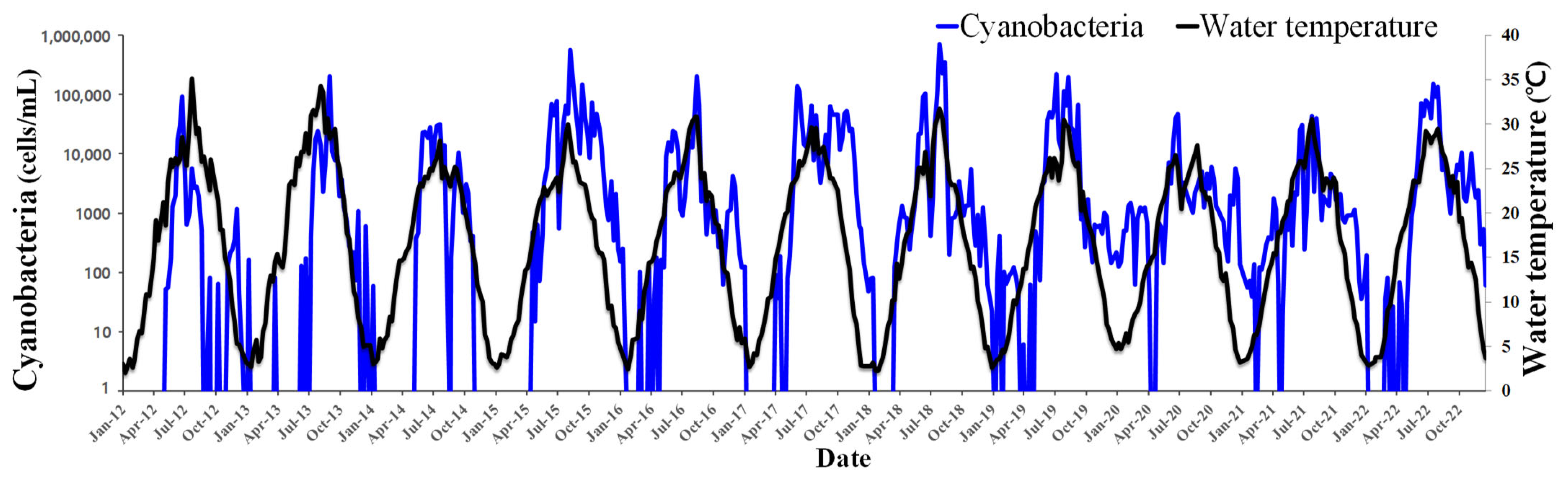
2.2. Water Quality, Algae, and HAB Alert Levels Data
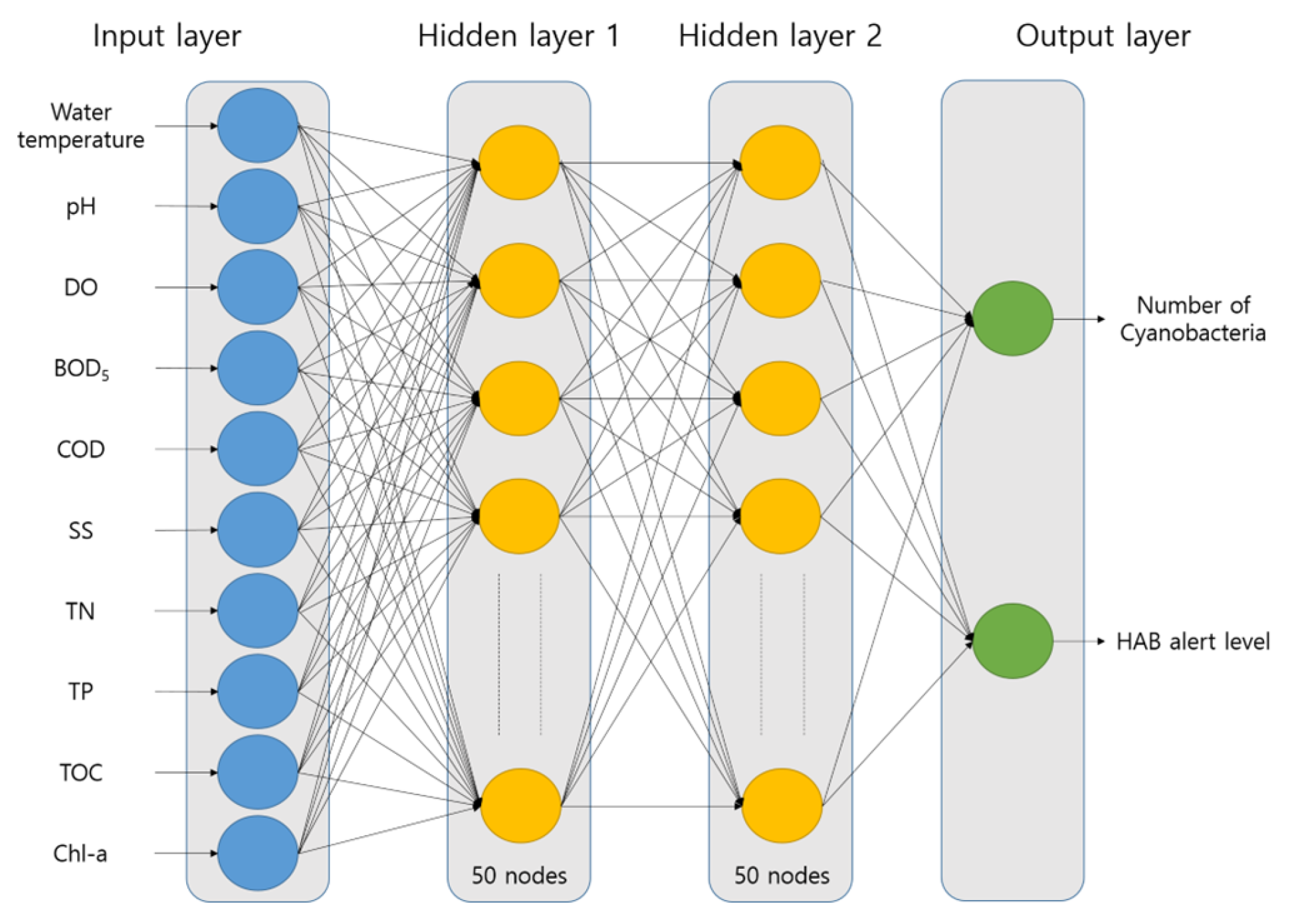
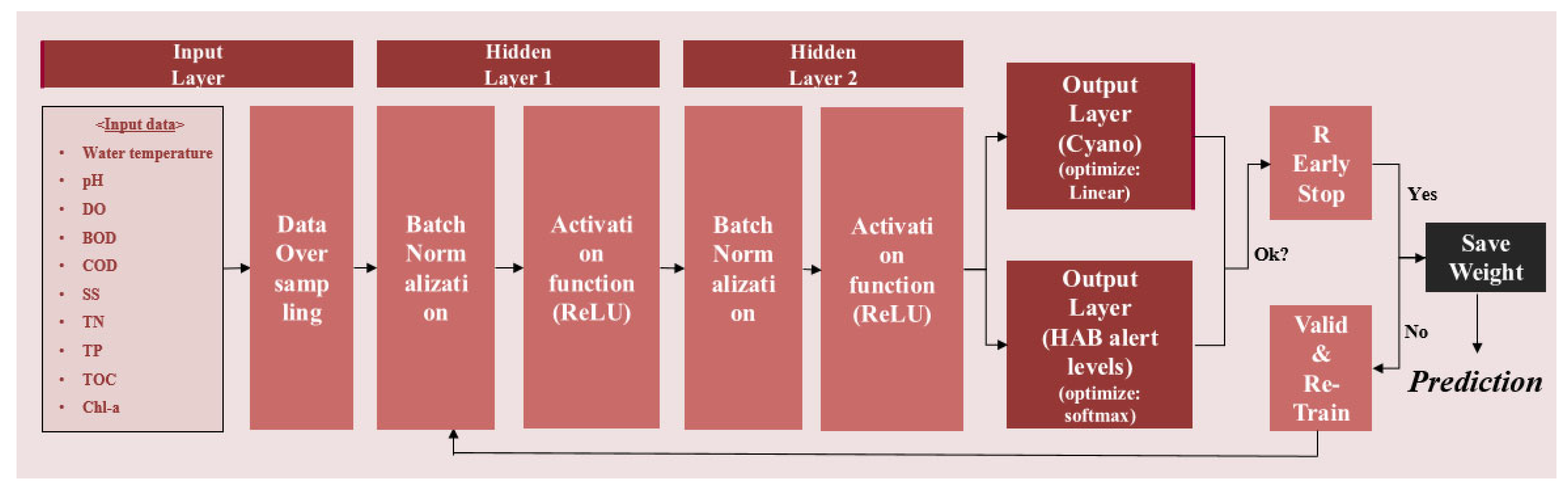
2.3. DNN Algorithm
2.4. Method for Analyzing the Predictive Performance
3. Construction of Deep Learning Model and Prediction Results
3.1. Data Preprocessing
3.2. Hidden Layers and Nodes for Optimal DNN Model
3.3. Improvement of DNN Architecture for Multi-Output of Continuous and Categorical Data
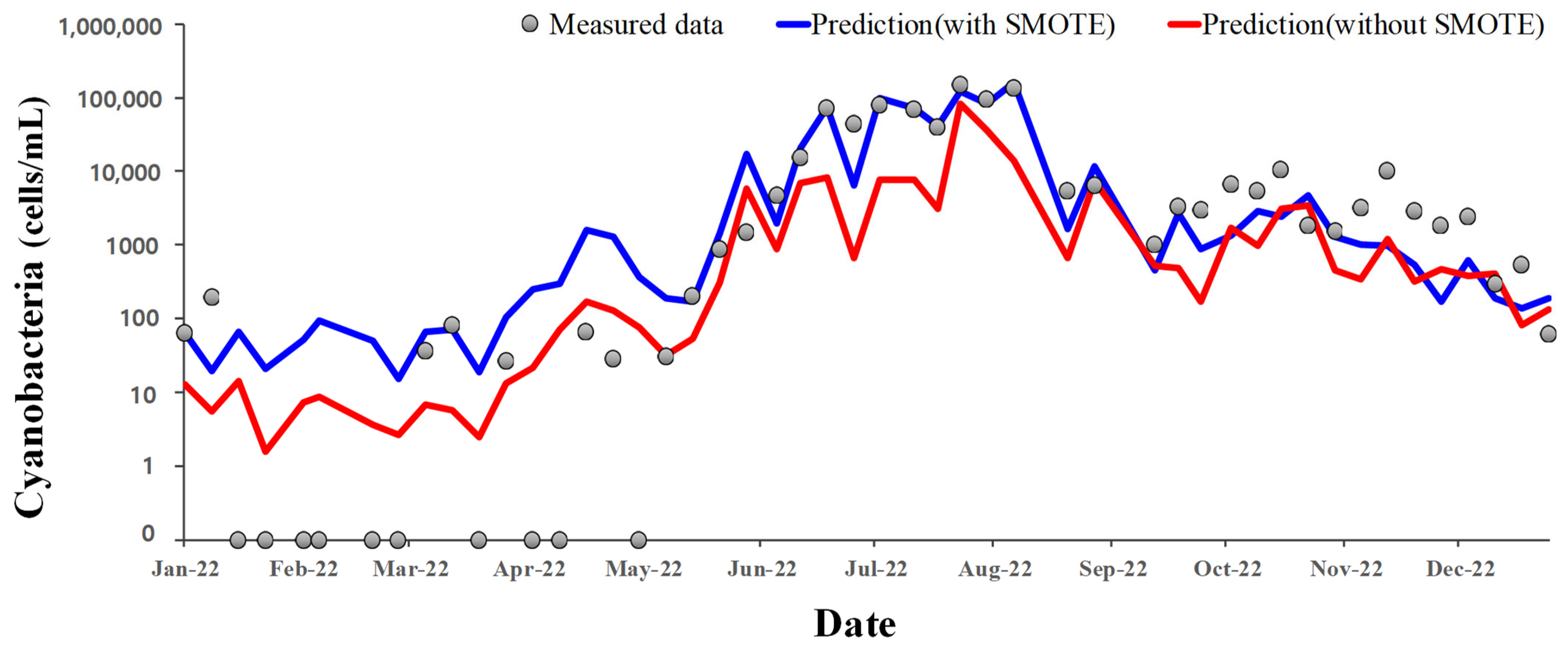
3.4. Result of Cyanobacteria Prediction
3.5. Result of HAB Alert Levels Prediction
4. Discussion
5. Conclusions
- (1)
- The DNN algorithm showed sufficient predictive power to estimate the number of cyanobacteria cells and HAB alert levels. It is essential to supplement the imbalanced data on cyanobacteria and HAB alert levels and secure the lacking data in order to ensure sufficient predictive power. The model combining the DNN algorithm with SMOTE showed better performance than the model that did not combine them.
- (2)
- High prediction accuracy was shown for the number of cyanobacteria cells during summer and for the serious alert level of HABs categorized as levels 2 and 3. In this aspect, it can be said that the developed HAB prediction deep learning model has sufficient applicability in responding to and managing HABs.
- (3)
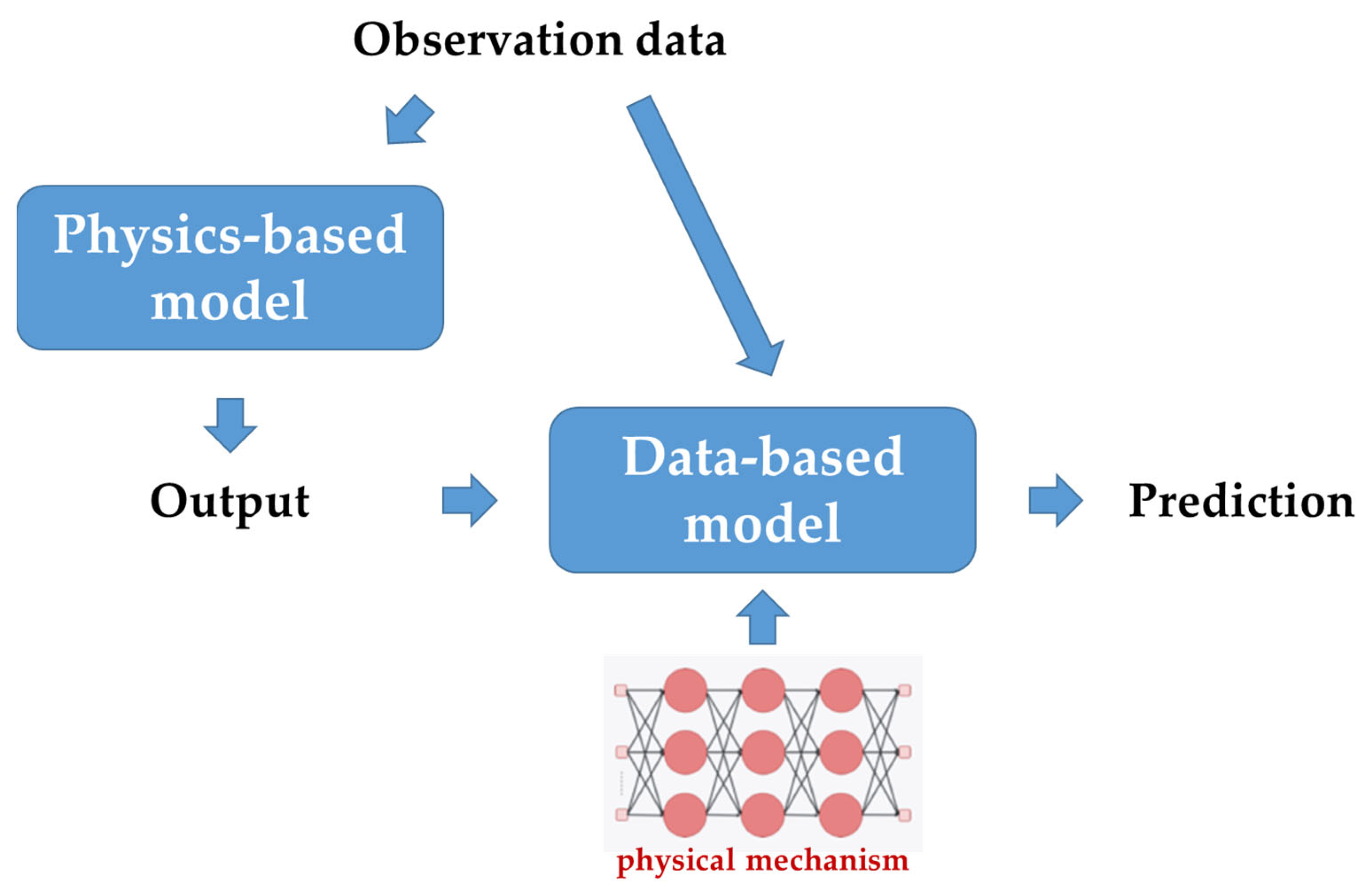
- Algal blooms can be determined through algae concentrations and the HAB alert level. Therefore, these study-built deep learning models that can predict algae concentrations and HAB alert levels were used to prevent algal bloom-induced damage. To further advance this study, it is necessary to utilize the deep learning model developed in this study along with the existing physics-based model, EFDC-NIER, to respond to HABs.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Date | Observation | Predicted Probabilities for Each Level (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Simulation without SMOTE | Simulation with SMOTE | ||||||||
| Level | 0 | 1 | 2 | 3 | 0 | 1 | 2 | ||
| 3 January 2022 | 0 | 99.2 | 0.8 | 0.0 | 0.0 | 94.1 | 5.9 | 0.0 | 0.0 |
| 10 January 2022 | 0 | 99.9 | 0.1 | 0.0 | 0.0 | 89.5 | 10.5 | 0.0 | 0.0 |
| 17 January 2022 | 0 | 98.6 | 1.4 | 0.0 | 0.0 | 85.3 | 14.7 | 0.0 | 0.0 |
| 24 January 2022 | 0 | 100.0 | 0.0 | 0.0 | 0.0 | 99.9 | 0.1 | 0.0 | 0.0 |
| 3 February 2022 | 0 | 100.0 | 0.0 | 0.0 | 0.0 | 96.2 | 3.8 | 0.0 | 0.0 |
| 7 February 2022 | 0 | 99.8 | 0.2 | 0.0 | 0.0 | 96.5 | 3.5 | 0.0 | 0.0 |
| 21 February 2022 | 0 | 100.0 | 0.0 | 0.0 | 0.0 | 95.9 | 4.1 | 0.0 | 0.0 |
| 28 February 2022 | 0 | 100.0 | 0.0 | 0.0 | 0.0 | 98.9 | 1.1 | 0.0 | 0.0 |
| 7 March 2022 | 0 | 99.5 | 0.5 | 0.0 | 0.0 | 88.9 | 11.1 | 0.0 | 0.0 |
| 14 March 2022 | 0 | 100.0 | 0.0 | 0.0 | 0.0 | 99.7 | 0.3 | 0.0 | 0.0 |
| 21 March 2022 | 0 | 100.0 | 0.0 | 0.0 | 0.0 | 99.8 | 0.2 | 0.0 | 0.0 |
| 28 March 2022 | 0 | 99.9 | 0.0 | 0.1 | 0.0 | 96.6 | 3.4 | 0.0 | 0.0 |
| 4 April 2022 | 0 | 99.3 | 0.4 | 0.3 | 0.0 | 71.3 | 28.7 | 0.0 | 0.0 |
| 11 April 2022 | 0 | 99.9 | 0.1 | 0.0 | 0.0 | 92.9 | 7.1 | 0.0 | 0.0 |
| 18 April 2022 | 0 | 89.7 | 0.5 | 9.6 | 0.2 | 44.7 | 38.5 | 16.8 | 0.0 |
| 25 April 2022 | 0 | 96.5 | 3.5 | 0.0 | 0.0 | 95.0 | 4.9 | 0.1 | 0.0 |
| 2 May 2022 | 0 | 42.3 | 57.5 | 0.2 | 0.0 | 5.7 | 94.0 | 0.3 | 0.0 |
| 9 May 2022 | 0 | 98.6 | 1.4 | 0.0 | 0.0 | 95.3 | 4.0 | 0.7 | 0.0 |
| 16 May 2022 | 0 | 58.6 | 40.3 | 1.1 | 0.0 | 80.8 | 18.2 | 1.0 | 0.0 |
| 23 May 2022 | 0 | 75.2 | 18.6 | 5.4 | 0.8 | 74.8 | 21.7 | 3.5 | 0.0 |
| 30 May 2022 | 1 | 0.1 | 83.4 | 12.3 | 4.2 | 0.0 | 81.8 | 17.5 | 0.7 |
| 7 June 2022 | 1 | 1.0 | 96.7 | 1.8 | 0.5 | 12.2 | 56.6 | 31.2 | 0.0 |
| 13 June 2022 | 2 | 0.0 | 1.1 | 88.9 | 10.0 | 0.0 | 0.0 | 100.0 | 0.0 |
| 20 June 2022 | 2 | 0.0 | 0.1 | 90.2 | 9.7 | 0.0 | 0.0 | 100.0 | 0.0 |
| 27 June 2022 | 2 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 | 100.0 | 0.0 |
| 4 July 2022 | 2 | 0.0 | 0.3 | 99.2 | 0.5 | 0.0 | 0.0 | 100.0 | 0.0 |
| 13 July 2022 | 2 | 0.0 | 62.3 | 37.6 | 0.1 | 0.0 | 0.0 | 100.0 | 0.0 |
| 19 July 2022 | 2 | 0.0 | 87.2 | 7.6 | 5.2 | 0.0 | 0.0 | 100.0 | 0.0 |
| 25 July 2022 | 3 | 0.0 | 0.0 | 97.0 | 3.0 | 0.0 | 0.0 | 1.0 | 99.0 |
| 1 August 2022 | 2 | 0.0 | 72.0 | 28.0 | 0.0 | 0.0 | 11.6 | 42.6 | 45.8 |
| 8 August 2022 | 3 | 0.0 | 0.7 | 99.1 | 0.2 | 0.0 | 0.0 | 0.0 | 100.0 |
| 22 August 2022 | 1 | 7.0 | 93.0 | 0.1 | 0.0 | 0.6 | 99.4 | 0.0 | 0.0 |
| 29 August 2022 | 1 | 0.3 | 53.6 | 45.8 | 0.3 | 0.0 | 93.8 | 6.2 | 0.0 |
| 14 September 2022 | 0 | 38.3 | 61.7 | 0.0 | 0.0 | 9.5 | 90.5 | 0.0 | 0.0 |
| 20 September 2022 | 1 | 38.8 | 61.2 | 0.0 | 0.0 | 11.7 | 88.3 | 0.0 | 0.0 |
| 26 September 2022 | 1 | 96.0 | 3.9 | 0.1 | 0.0 | 17.5 | 40.1 | 42.4 | 0.0 |
| 4 October 2022 | 1 | 0.3 | 97.6 | 1.3 | 0.8 | 0.2 | 94.1 | 5.7 | 0.0 |
| 11 October 2022 | 1 | 75.8 | 17.1 | 0.7 | 6.4 | 0.3 | 0.5 | 99.0 | 0.2 |
| 17 October 2022 | 2 | 20.2 | 79.4 | 0.2 | 0.2 | 12.9 | 86.7 | 0.1 | 0.3 |
| 24 October 2022 | 1 | 28.1 | 8.5 | 61.8 | 1.6 | 3.0 | 3.2 | 93.7 | 0.1 |
| 31 October 2022 | 1 | 65.8 | 34.2 | 0.0 | 0.0 | 43.9 | 52.5 | 3.6 | 0.0 |
| 7 November 2022 | 1 | 52.5 | 47.5 | 0.0 | 0.0 | 50.2 | 49.8 | 0.0 | 0.0 |
| 14 November 2022 | 2 | 15.4 | 84.6 | 0.0 | 0.0 | 0.1 | 34.6 | 65.3 | 0.0 |
| 21 November 2022 | 1 | 35.6 | 64.4 | 0.0 | 0.0 | 48.8 | 51.2 | 0.0 | 0.0 |
| 28 November 2022 | 1 | 41.0 | 59.0 | 0.0 | 0.0 | 43.8 | 56.2 | 0.0 | 0.0 |
| 5 December 2022 | 1 | 29.0 | 71.0 | 0.0 | 0.0 | 41.6 | 58.4 | 0.0 | 0.0 |
| 12 December 2022 | 0 | 32.0 | 68.0 | 0.0 | 0.0 | 26.5 | 73.5 | 0.0 | 0.0 |
| 19 December 2022 | 0 | 36.5 | 63.5 | 0.0 | 0.0 | 36.9 | 63.1 | 0.0 | 0.0 |
| 26 December 2022 | 0 | 57.7 | 42.3 | 0.0 | 0.0 | 69.5 | 30.5 | 0.0 | 0.0 |
References
- Kim, J.; Kwak, J.; Ahn, J.M.; Kim, H.; Jeon, J.; Kim, K. Oscillation flow dam operation method for algal bloom mitigation. Water 2022, 14, 1315. [Google Scholar] [CrossRef]
- Ghiasi, B.; Noori, R.; Sheikhian, H. Uncertainty quantification of granular computing-neural network model for prediction of pollutant longitudinal dispersion coefficient in aquatic streams. Sci. Rep. 2022, 12, 4610. [Google Scholar] [CrossRef] [PubMed]
- Modabberi, A.; Noori, R.; Madani, K.; Ehsani, A.H.; Mehr, A.D.; Hooshyaripor, F.; Klove, B. Caspian Sea is eutrophying: The alarming message of satellite data. Environ. Res. Lett. 2020, 15, 124047. [Google Scholar] [CrossRef]
- Downing, J.; Polasky, S.; Olmstead, S.; Newbold, S. Protecting local water quality has global benefits. Nat. Commun. 2021, 12, 2709. [Google Scholar] [CrossRef]
- Kleinman, P.; Sharpley, A. Eutrophication of Lakes and Rivers. In Encyclopedia of Life Sciences; Wiley Online Library, John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar] [CrossRef]
- Cressey, D. Climate change is making algal blooms worse. Nature 2017. [Google Scholar] [CrossRef]
- Sharma, P.; Sivaramakrishnaiah, M.; Deepanraj, B.; Saravanan, R.; Reddy, M.V. A novel optimization approach for biohydrogen production using algal biomass. Int. J. Hydrogen Energy 2022, in press. [Google Scholar] [CrossRef]
- National Institute of Environmental Research. Operation Manual of Harmful Algal Blooms Alert System (2020); NIER: Incheon, Republic of Korea, 2020.
- Zhang, J.; Shi, K.; Paerl, H.W.; Ruhland, K.M.; Yuan, Y.; Wang, R.; Chen, J.; Ge, M.; Zheng, L.; Zhang, Z.; et al. Ancient DNA reveals potentially toxic cyanobacteria increasing with climate change. Water Res. 2023, 229, 119435. [Google Scholar] [CrossRef]
- Oh, H.-M.; Lee, S.J.; Jang, M.-H.; Yoon, B.-D. Microcystin Production by Microcystis aeruginosa in a Phosphorus-Limited chemostat. Appl Env. Microbiol. 2000, 66, 176–179. [Google Scholar] [CrossRef]
- Pimentel, J.; Giani, A. Microcystin Production and Regulation under Nutrient Stress Conditions in Toxic Microcystis Strains. Appl Env. Microbiol. 2014, 80, 5836–5843. [Google Scholar] [CrossRef] [PubMed]
- Jung, E.; Joo, G.-J.; Kim, H.G.; Kim, D.-K.; Kim, H.-W. Effects of seasonal and diel variations in thermal stratification on phytoplankton in a regulated river. Biogeosci. Discuss. 2022, in press. [Google Scholar] [CrossRef]
- Wu, G.; Xu, Z. Prediction of algal blooming using EFDC model: Case study in the Daoxiang Lake. Ecol. Model. 2011, 222, 1245–1252. [Google Scholar] [CrossRef]
- Tang, C.; Li, Y.; Acharya, K. Modeling the effects of external nutrient reductions on algal blooms in hyper-eutrophic Lake Taihu. China Ecol. Eng. 2016, 94, 164–173. [Google Scholar] [CrossRef]
- Ahn, J.M.; Kim, B.; Jong, J.; Nam, G.; Park, L.J.; Park, S.; Kang, T.; Lee, J.-K.; Kim, J. Predicting Cyanobacterial Blooms Using Hyperspectral Images in a Regulated River. Sensors 2021, 21, 530. [Google Scholar] [CrossRef]
- Jiang, L.; Li, Y.P.; Zhao, X.; Tillostson, M.R.; Wang, W.C.; Zhang, S.S.; Sarpong, L.; Asmaa, Q.; Pan, B.Z. Parameter uncertainty and sensitivity analysis of water quality model in Lake Taihu, China. Ecol. Model. 2018, 375, 1–12. [Google Scholar] [CrossRef]
- Su, J.J.; Du, X.Z.; Li, X.Y. Developing a non-point source P loss indicator in R and its parameter uncertainty assessment using GLUE: A case study in northern China. Environ. Sci. Pollut. Res. 2018, 25, 21070–21085. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, H.; Wang, L.; Hua, Z.; He, C.; Cheng, J. A combination method for multicriteria uncertainty analysis and parameter estimation: A case study of Chaohu Lake in Eastern China. Environ. Sci. Pollut. Res. 2020, 27, 20934–20949. [Google Scholar] [CrossRef]
- Ahn, J.M.; Kim, J.; Park, L.J.; Jeon, J.; Jong, J.; Min, J.-H.; Kang, T. Predicting Cyanobacterial Harmful Algal Blooms (CyanoHABs) in a Regulated River Using a Revised EFDC model. Water 2021, 13, 439. [Google Scholar] [CrossRef]
- Korea Environment Institute. Development and Application of Algal Bloom Using Artificial Intelligence Deep Learning; KEI: Seoul, Republic of Korea, 2020. [Google Scholar]
- Lek, S.; Park, Y.S. Artificial Neural Network. In Encyclopedia of Ecology; Academic Press, Elservier Inc.: Amsterdam, The Netherlands, 2008; pp. 237–245. [Google Scholar] [CrossRef]
- Jeong, K.S.; Recknagel, F.; Joo, G.J. Prediction and Elucidation of Population Dynamics of the Blue-green Algae Microcystis aeruginosa and the Diatom Stephanodiscus hantzschii in the Nakdong River-Reservoir System (South Korea) by a Recurrent Artificial Neural Network. In Ecological Informatics; Recknagel, F., Ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Velo-Suarez, L.; Gutierrez-Estrada, J.C. Artificial neural network approaches to one-step weekly prediction of Dinophysis acuminata blooms in Huelva (Western Andalucia, Spain). Harmful Algae 2007, 6, 361–371. [Google Scholar] [CrossRef]
- Maier, H.; Dandy, G.; Burch, M. Use of artificial neural networks for modelling cyanobacteria Anabaena spp. in the River Murray, South Australia. Ecol. Model. 1998, 105, 257–272. [Google Scholar] [CrossRef]
- Thai-Nghe, N.; Thanh-Hai, N.; Chi Ngon, N. Deep learning approach for forecasting water quality in iot systems. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 686–693. [Google Scholar] [CrossRef]
- Pyo, J.C.; Cho, K.H.; Kim, K.; Baek, S.S.; Nam, G.; Park, S. Cyanobacteria cell prediction using interpretable deep learning model with observed, numerical, and sensing data assemblage. Water Res. 2021, 203, 117483. [Google Scholar] [CrossRef]
- Ni, J.; Liu, R.; Tang, G.; Xie, Y. An Improved Attention-based Bidirectional LSTM Model for Cyanobacterial Bloom Prediction. Int. J. Control. Autom. Syst. 2022, 20, 3445–3455. [Google Scholar] [CrossRef]
- Yu, J.-W.; Kim, J.-S.; Li, X.; Jong, Y.-C.; Kim, K.-H.; Ryang, G.-I. Water quality forecasting based on data decomposition, fuzzy clustering and deep learning neural network. Environ. Pollut. 2022, 303, 119136. [Google Scholar] [CrossRef]
- Yim, I.; Shin, J.; Lee, H.; Park, S.; Nam, G.; Kang, T.; Cho, K.H.; Cha, Y. Deep learning-based retrieval of cyanobacteria pigment in inland water for in-situ and airborne hyperspectral data. Ecol. Indic. 2020, 110, 105879. [Google Scholar] [CrossRef]
- Yang, Y.; Xiong, Q.; Wu, C.; Zou, Q.; Yu, Y.; Yi, H.; Gao, M. A study on water quality prediction by a hybrid CNN-LSTM model with attention mechanism. Environ. Sci. Pollut. Res. 2021, 28, 55129–55139. [Google Scholar] [CrossRef]
- Bilali, A.E.; Lamane, H.; Taleb, A.; Nafii, A. A framework based on multivariate distribution-based virtual sample generation and DNN for predicting water quality with small data. J. Clean. Prod. 2022, 368, 133227. [Google Scholar] [CrossRef]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, S.; Basak, S.; Saikia, P.; Paul, S.; Tsalavoutis, V.; Atiah, F.; Ravi, V.; Peters, A. A review of deep learning with special emphasis on architectures, applications and recent trends. Knowl. Based Syst. 2020, 194, 105596. [Google Scholar] [CrossRef]
- Campolo, A.; Crawford, K. Enchanted determinism: Power without responsibility in artificial intelligence. Engag. Sci. Technol. Soc. 2020, 6, 1–19. [Google Scholar] [CrossRef]
- Orr, W.; Davis, J.L. Attributions of ethical responsibility by Artificial Intelligence practitioners. Inf. Commun. Soc. 2020, 23, 719–735. [Google Scholar] [CrossRef]
- Ewing, G.; Demir, I. An ethical decision-making framework with serious gaming: A smart water case study on flooding. J. Hydroinform. 2021, 23, 466–482. [Google Scholar] [CrossRef]
- TRACTICA. Global AI Software Market Set to Rise Sixfold to Reach Nearly $100 Billion in 2025; TRACTICA: Boulder, Colorado, USA, 2020. [Google Scholar]
- TRACTICA. Deep Learning Chipsets; TRACTICA: Boulder, CO, USA, 2020. [Google Scholar]
- Barthwal, M.; Rakshit, D. Artificial neural network coupled building-integrated photovoltaic thermal system for Indian montane climate. Energy Rep. 2021, 7, 1338–1348. [Google Scholar] [CrossRef]
- Gopi, A.; Sharma, P.; Sudhakar, K.; Ngui, W.K.; Kirpichnikova, I.; Cuce, E. Weather Impact on Solar Farm Performance: A Comparative Analysis of Machine Learning Techniques. Sustainability 2023, 15, 439. [Google Scholar] [CrossRef]
- National Institute of Environmental Research. Development of a Quantification Technique for Water Quality Prediction Uncertainty (Ⅰ)—Global Sensitivity Analysis of EFDC-NIER Model; NIER: Incheon, Republic of Korea, 2019.
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Miles, J. R Squared, Adjusted R Squared; Wiley Online Library, John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Willmott, C.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A New Over-Sampling Method in Imbalanced Data Sets Learning. ICIC 2005, 3644, 878–887. [Google Scholar] [CrossRef]
- Yang, W.; Pan, C.; Zhang, Y. An oversampling method for imbalanced data based on spatial distribution of minority samples SD-KMSMOTE. Sci. Rep. 2022, 12, 16820. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Calvo-Pardo, H.; Mancini, T.; Olmo, J. Optimal deep neural networks by maximization of the approximation power. Comput. Oper. Res. 2023, 156, 106264. [Google Scholar] [CrossRef]
- Thomas, A.; Walters, S.; Gheytassi, S.M.; Morgan, R.; Petridis, M. On the Optimal Node Ratio between Hidden Layers: A Probabilistic Study. Int. J. Mach. Learn. Comput. 2016, 6, 241–247. [Google Scholar] [CrossRef]
- Karsoliya, S. Approximating Number of Hidden layer Neurons in Multiple hidden layer BPNN Architecture. Int. J. Eng. Trends Technol. 2012, 3, 714–717. [Google Scholar]
- Gupta, T.K.; Raza, K. Optimizing Deep Feedforward Neural Network Architecture: A Tabu Search Based Approach. Neural Process. Lett. 2020, 51, 2855–2870. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Dahl, G.E.; Sainath, T.N.; Hinton, G.E. Improving deep neural networks for LVCSR using rectified linear units and dropout. In Proceedings of the 2013 IEEE International Conference on Acoustics Speech, and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 8609–8613. [Google Scholar] [CrossRef]
- Afaq, S.; Rao, S. Significance of Epochs on Training a Neural Network. Int. J. Sci. Technol. Res. 2020, 9, 485–488. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
| Variables | Changnyeong-Haman Weir | |
|---|---|---|
| MIN–MAX 1 | AVG ± SD 2 | |
| Water temperature (°C) | 2.0–35.1 | 16.6 ± 8.6 |
| pH | 6.7–9.7 | 8.1 ± 0.6 |
| DO (mg/L) | 6.4–21.5 | 11.2 ± 2.5 |
| BOD5 (mg/L) | 0.7–5.6 | 2.3 ± 0.8 |
| COD (mg/L) | 3.9–12.8 | 6.3 ± 1.1 |
| SS (mg/L) | 1.6–72.0 | 10.1 ± 6.9 |
| TN (mg/L) | 1.157–5.483 | 2.767 ± 0.771 |
| TP (mg/L) | 0.013–0.174 | 0.050 ± 0.029 |
| TOC (mg/L) | 2.6–11.1 | 4.3 ± 0.9 |
| Chl-a (mg/m3) | 2.2–134.4 | 26.6 ± 19.3 |
| Number of Cyanobacteria (cells/mL) | 13,557–715,993 | 13,557 ± 51,435 |
| Level | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Cyanobacteria (cells/mL) | <1000 | ≥1000 <10,000 | ≥10,000 <100,000 | ≥100,000 <1,000,000 | ≥1,000,000 |
| Counts | 314 | 126 | 93 | 17 | 0 |
| Cyanobacteria | HAB Alert Levels | ||||
|---|---|---|---|---|---|
| DNN with SMOTE | DNN without SMOTE | DNN with SMOTE | DNN without SMOTE | ||
| Train | R2 | 0.82 | 0.76 | 0.92 | 0.93 |
| MAE | 0.5 | 0.7 | 0.1 | 0.1 | |
| RMSE | 0.7 | 0.8 | 0.1 | 0.1 | |
| Validation | R2 | 0.78 | 0.7 | 0.79 | 0.18 |
| MAE | 0.6 | 0.7 | 0.1 | 0.2 | |
| RMSE | 0.7 | 0.9 | 0.2 | 0.3 | |
| Counts | Accuracy (%) | |||||
|---|---|---|---|---|---|---|
| Observation | Simulation without SMOTE | Simulation with SMOTE | Without SMOTE | With SMOTE | ||
| Level | 0 | 24 | 20 | 20 | 83.3 | 83.3 |
| 1 | 14 | 9 | 10 | 64.3 | 71.4 | |
| 2 | 9 | 7 | 7 | 44.4 | 77.8 | |
| 3 | 2 | 0 | 2 | 0.0 | 100.0 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Kim, H.; Kim, K.; Ahn, J.M. Research on the Development and Application of a Deep Learning Model for Effective Management and Response to Harmful Algal Blooms. Water 2023, 15, 2293. https://doi.org/10.3390/w15122293
Kim J, Kim H, Kim K, Ahn JM. Research on the Development and Application of a Deep Learning Model for Effective Management and Response to Harmful Algal Blooms. Water. 2023; 15(12):2293. https://doi.org/10.3390/w15122293
Chicago/Turabian StyleKim, Jungwook, Hongtae Kim, Kyunghyun Kim, and Jung Min Ahn. 2023. "Research on the Development and Application of a Deep Learning Model for Effective Management and Response to Harmful Algal Blooms" Water 15, no. 12: 2293. https://doi.org/10.3390/w15122293
APA StyleKim, J., Kim, H., Kim, K., & Ahn, J. M. (2023). Research on the Development and Application of a Deep Learning Model for Effective Management and Response to Harmful Algal Blooms. Water, 15(12), 2293. https://doi.org/10.3390/w15122293








