Development of a Three-Dimensional Hydrodynamic Model Based on the Discontinuous Galerkin Method
Abstract
1. Introduction
| Grid Type | Numerical Method | ||
|---|---|---|---|
| Finite Difference Method | Finite Volume Method | Finite Element Method | |
| Structured grid | ROMS [6], POM [7], MoM [8], GETM [9], TRIM [10], DELFT3D [11], EFDC [12], ECOMSED [13], COHERENS [14] | MITgcm [15], MOHID [16] | |
| Unstructured grid | FVCOM [17], UnTRIM [18], HydroInfo [19] | FESOM [20], ICOM, SELFE [21], ADCIRC [22], SCHISM [23], TELEMAC [24] | |
2. Governing Equations
3. Numerical Implementation
3.1. Domain Partition and Polynomial Space
3.2. Numerical Discretization of Momentum Equations
3.2.1. Convective and Bottom Topography Terms
3.2.2. Horizontal Eddy Viscosity Terms
3.2.3. Vertical Eddy Viscosity and Coriolis Acceleration Terms
3.3. Numerical Discretization of the Primitive Continuity Equation
3.4. Calculation of Vertical Velocity
3.5. Time Stepping
- Calculate the explicit terms and for the three-dimensional momentum equations and primitive continuity equation according to the variables at .
- Calculate the intermediate water depth asLikewise, the intermediate conservative variables and areWith available, the intermediate depth-averaged momenta and are calculated through the depth-integration of , followed by the calculation of the intermediate vertical velocity . Later, the explicit terms and for the three-dimensional momentum equations and primitive continuity equation, are calculated according to the intermediate variables.
- Calculate the water depth and the conservative variables at as
- Integrate along the water depth to obtain the final depth-averaged momenta and , followed by the calculation of the final vertical velocity .
4. Numerical Tests
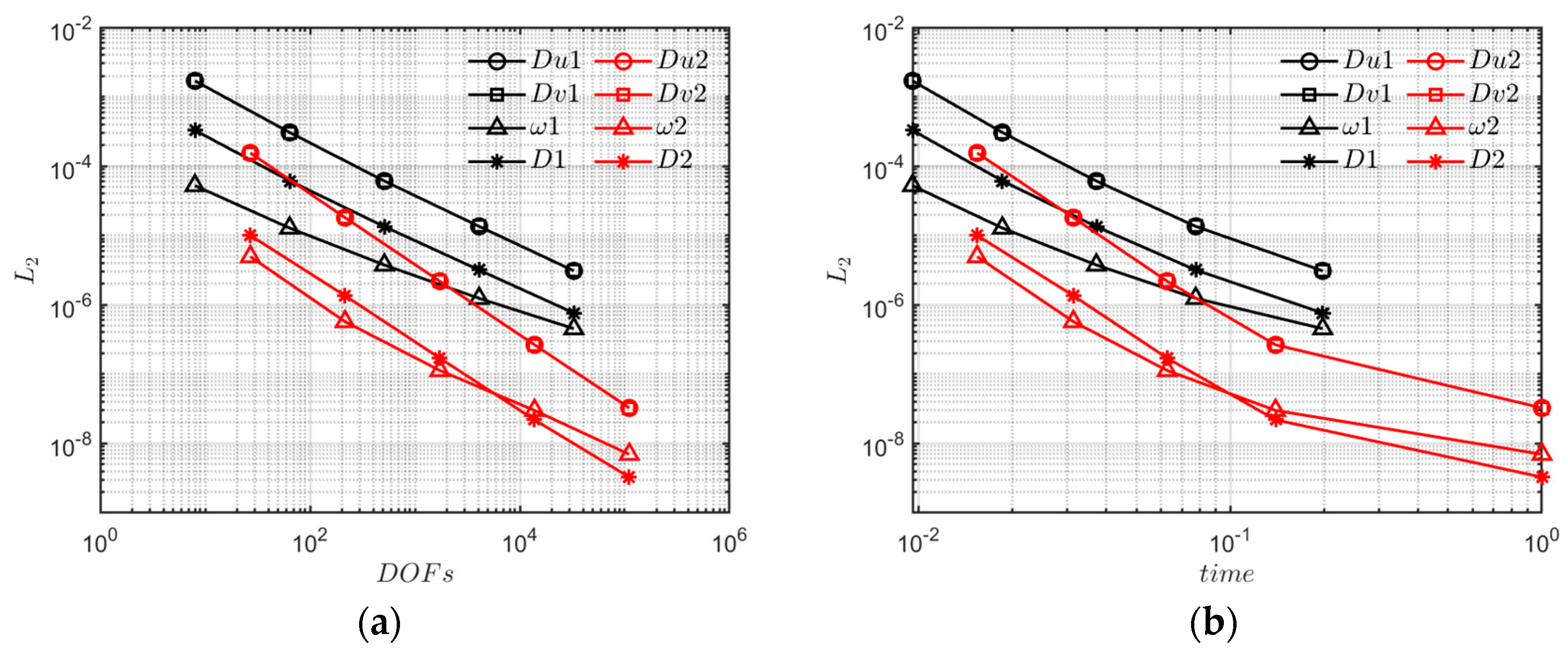
4.1. Manufactured Solution
4.2. Tide Wave Propagation in a Semi-Closed Bay
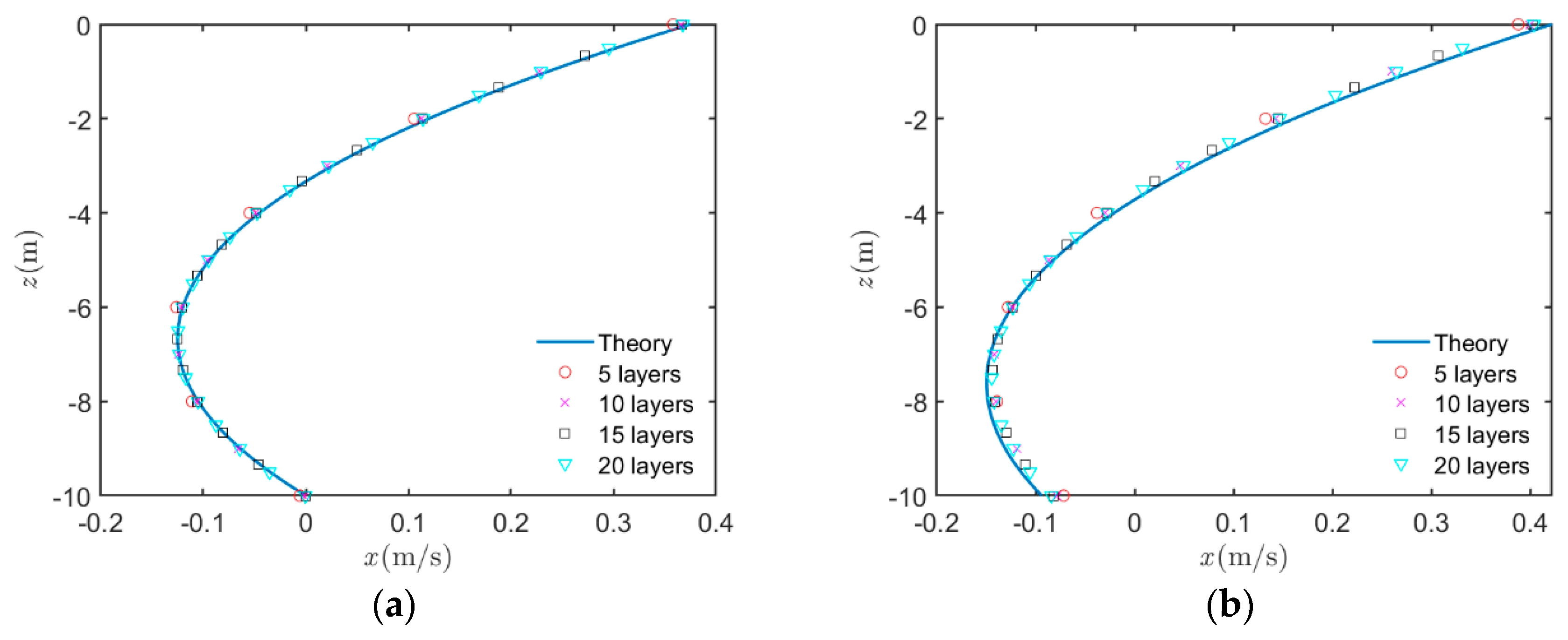
4.3. Wind-Induced Water Circulation
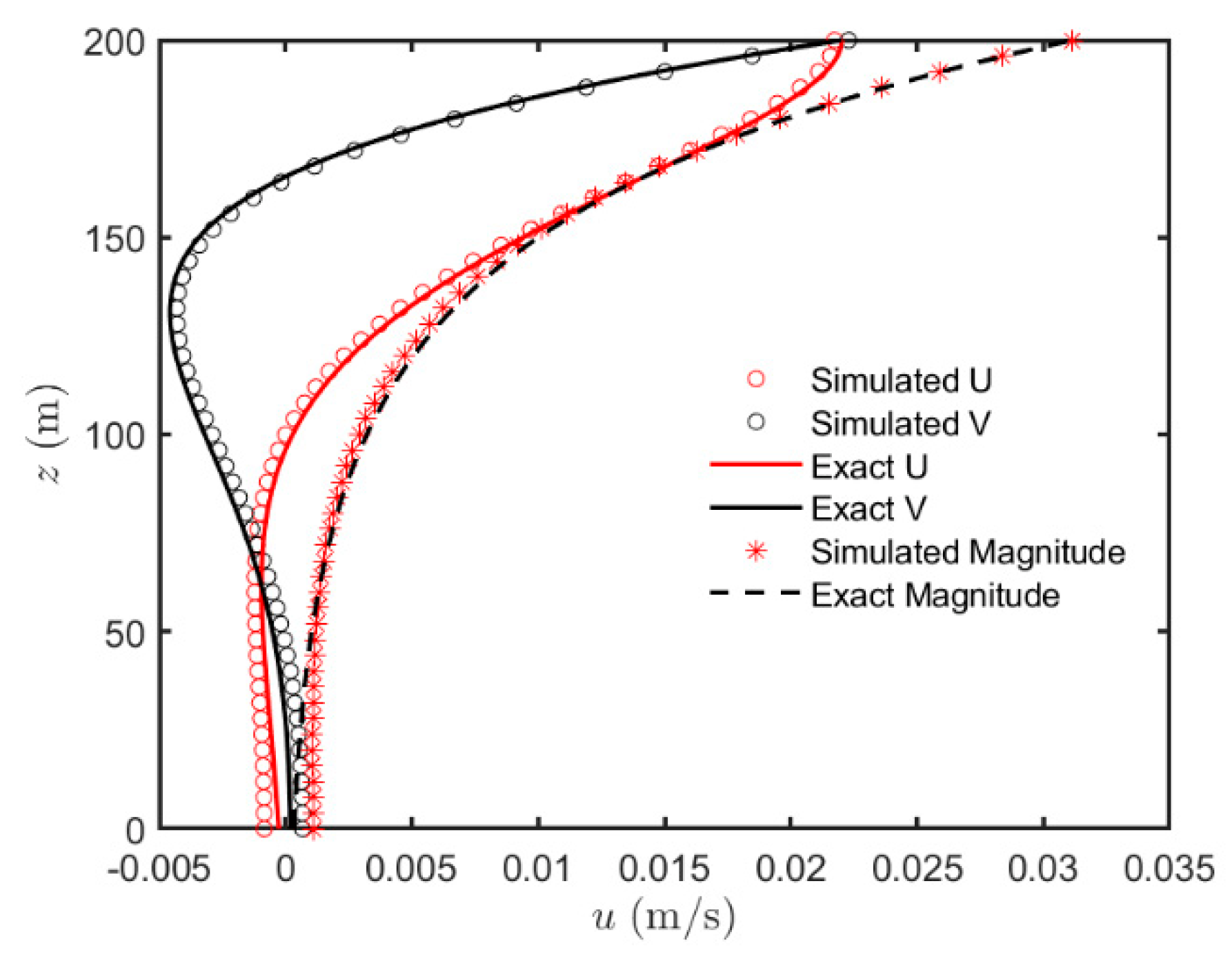
4.4. Generation of the Ekman Profile
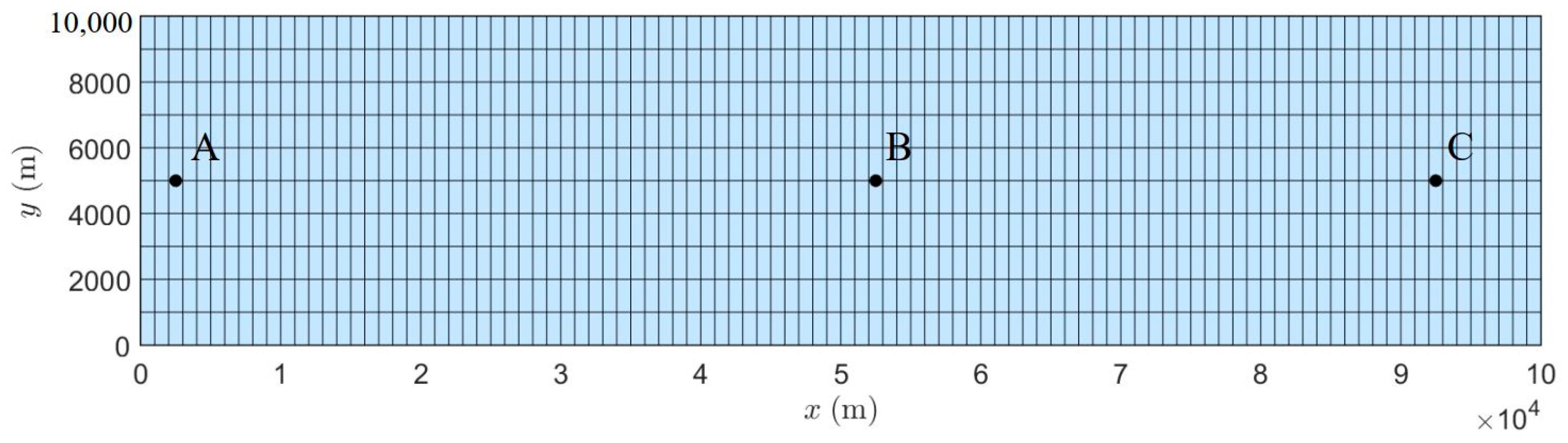
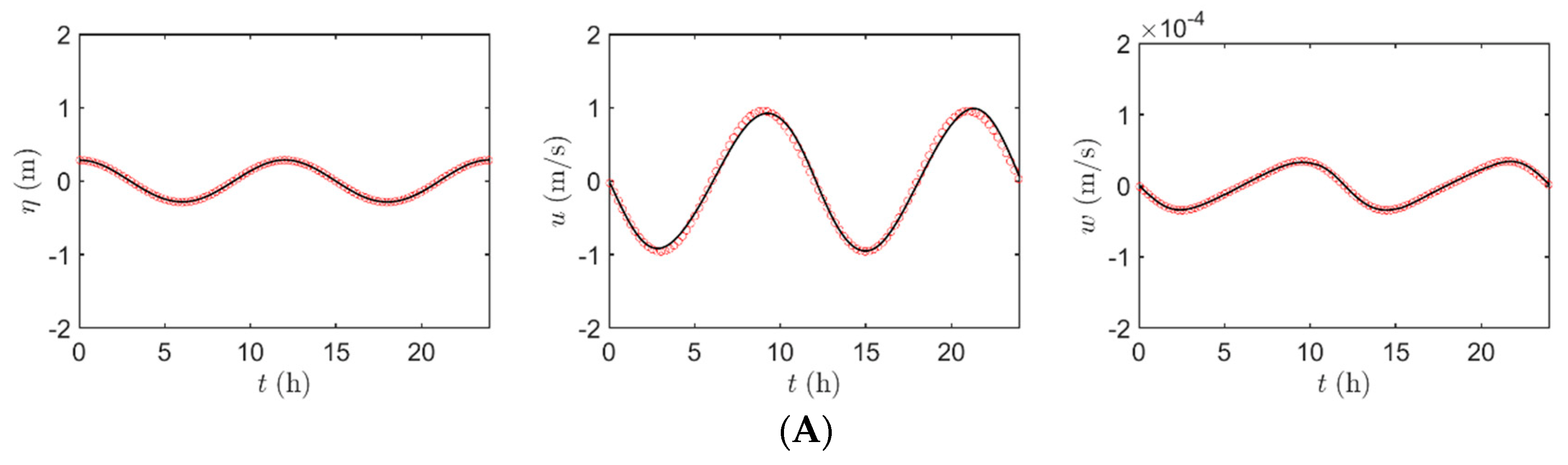
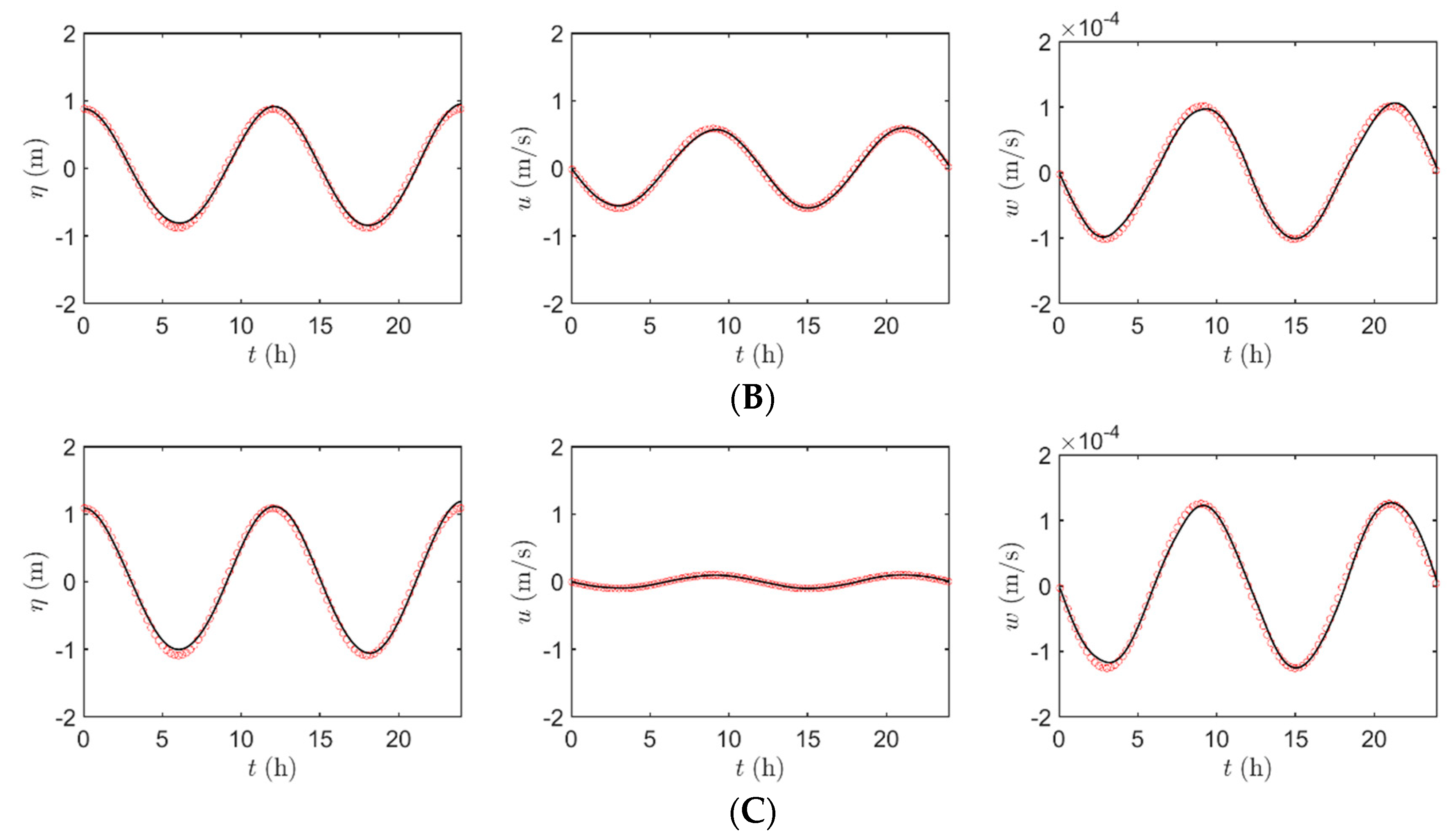
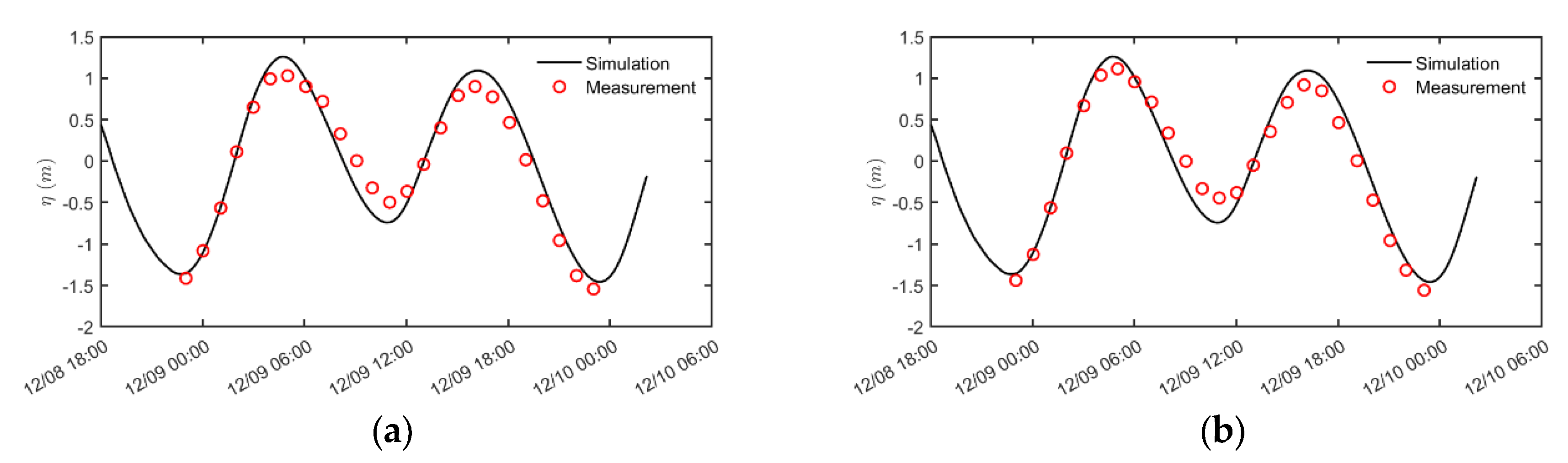
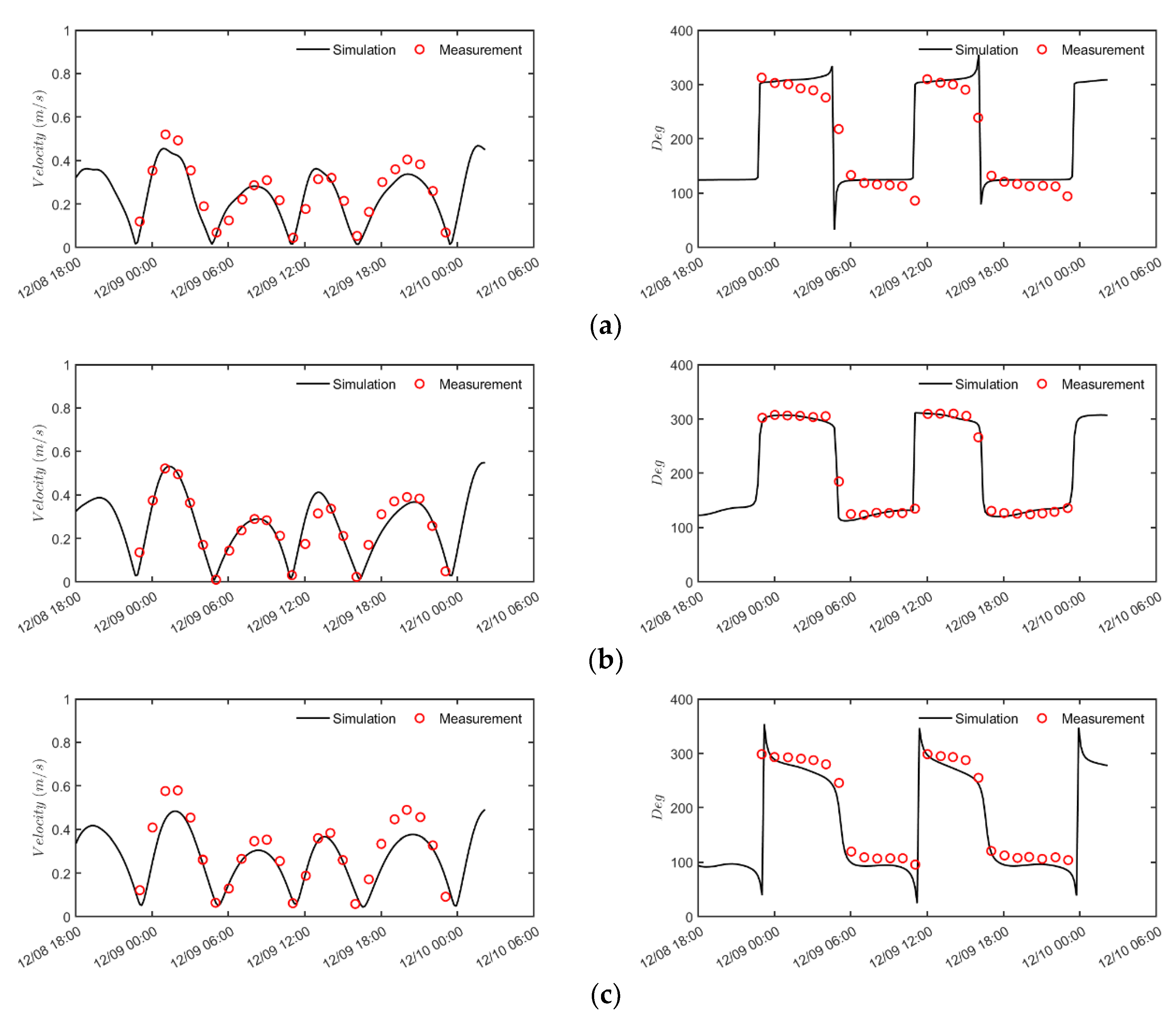
4.5. Tidal Flow in Bohai Bay
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lee, J.; Lee, J.; Yun, S.-L.; Kim, S.-K. Three-Dimensional Unstructured Grid Finite-Volume Model for Coastal and Estuarine Circulation and Its Application. Water 2020, 12, 2752. [Google Scholar] [CrossRef]
- Blaise, S.; Comblen, R.; Legat, V.; Remacle, J.-F.; Deleersnijder, E.; Lambrechts, J. A discontinuous finite element baroclinic marine model on unstructured prismatic meshes. Ocean. Dyn. 2010, 60, 1371–1393. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Q. Development of an efficient wetting and drying treatment for shallow-water modeling using the quadrature-free Runge-Kutta discontinuous Galerkin method. Int. J. Numer. Methods Fluids 2021, 93, 314–338. [Google Scholar] [CrossRef]
- Ran, G.; Zhang, Q.; Li, L. A depth-integrated non-hydrostatic model for nearshore wave modelling based on the discontinuous Galerkin method. Ocean. Eng. 2021, 232, 108661. [Google Scholar] [CrossRef]
- Di Pietro, D.A.; Marche, F. Weighted interior penalty discretization of fully nonlinear and weakly dispersive free surface shallow water flows. J. Comput. Phys. 2018, 355, 285–309. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean. Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Mellor, G. Users Guide for a Three-Dimensional, Primitive Equation, Numerical Ocean Model; Princeton University: Princeton, NJ, USA, 2004. [Google Scholar]
- Griffies, S.M. Elements of the Modular Ocean Model (MOM); GFDL Ocean Group Technical Report; NOAA: Princeton, NJ, USA, 2012. [Google Scholar]
- Burchard, H.; Bolding, K. GETM: A General Estuarine Transport Model. Scientific Documentation; European Commission Technical Report EUR 20253 EN; European Commission: Brussels, Belgium, 2002; p. 157. [Google Scholar]
- Casulli, V.; Cheng, R.T. Semi-implicit finite difference methods for three-dimensional shallow water flow. Int. J. Numer. Methods Fluids 1992, 15, 629–648. [Google Scholar] [CrossRef]
- Deltares Systems. User Manual of Delft3D-FLOW—Simulation of Multi-Dimensional Hydrodynamic Flows and Transport Phenomena, Including Sediments; Report of Delft Hydraulics; Deltares: Delft, The Netherlands, 2003; p. 497. [Google Scholar]
- Hamrick, J.; Wu, T. Computational Design and Optimization of the EFDC/HEM3D Surface Water Hydrodynamic and Eutrophication. In Next Generation Environmental Models and Computational Methods; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1997; pp. 143–161. [Google Scholar]
- Blumberg, A.F.; Mellor, G.L. A Description of a Three-Dimensional Coastal Ocean Circulation Model; AGU: Washington, DC, USA, 1987; pp. 1–16. [Google Scholar]
- Luyten, P.J.; Jones, J.E.; Proctor, R. A numerical study of the long-and short-term temperature variability and thermal circulation in the North Sea. J. Phys. Oceanogr. 2003, 33, 37–56. [Google Scholar] [CrossRef]
- Alistair, A.; Jean-Michel, C.; Stephanie, D.; Constantinos, E.; David, F.; Gael, F.; Baylor, F.-K.; Patrick, H.; Chris, H.; Ed, H. Mitgcm User Manual; MIT: Cambridge, MA, USA, 2018. [Google Scholar]
- Martins, F.; Leitão, P.; Silva, A.; Neves, R. 3D modelling in the Sado estuary using a new generic vertical discretization approach. Oceanol. Acta 2001, 24, 51–62. [Google Scholar] [CrossRef]
- Chen, C.; Beardsley, R.; Cowles, G.; Qi, J.; Lai, Z.; Gao, G.; Stuebe, D.; Xu, Q.; Xue, P.; Ge, J. An Unstructured-Grid, Finite-Volume Community Ocean Model: FVCOM User Manual; SMAST/UMASSD Technical Report-13-0701; MIT: Cambridge, MA, USA, 2012; p. 404. [Google Scholar]
- Casulli, V.; Walters, R.A. An unstructured grid, three-dimensional model based on the shallow water equations. Int. J. Numer. Methods Fluids 2000, 32, 331–348. [Google Scholar] [CrossRef]
- Nan, Z.; Sheng, J.; Congfang, A.; Weiye, D. An integrated water-conveyance system based on Web GIS. J. Hydroinform. 2018, 20, 668–686. [Google Scholar] [CrossRef]
- Wang, Q. The Finite Element Ocean Model and Its Aspect of Vertical Discretization. Ph.D. Thesis, Universität Bremen, Bremen, Germany, 2007. [Google Scholar]
- Zhang, Y.; Baptista, A.M. SELFE: A semi-implicit Eulerian–Lagrangian finite-element model for cross-scale ocean circulation. Ocean. Model. 2008, 21, 71–96. [Google Scholar] [CrossRef]
- Luettich, R.A.; Westerink, J.J.; Scheffner, N.W. ADCIRC: An Advanced Three-Dimensional Circulation Model for Shelves, Coasts, and Estuaries. Report 1, Theory and methodology of ADCIRC-2DD1 and ADCIRC-3DL; Department of the Army, US Army Corps of Engineers Waterways Experiment Station, Coastal Engineering Research Center: Vicksburg, MS, USA, 1992. [Google Scholar]
- Zhang, Y.J.; Ye, F.; Stanev, E.V.; Grashorn, S. Seamless cross-scale modeling with SCHISM. Ocean. Model. 2016, 102, 64–81. [Google Scholar] [CrossRef]
- Hervouet, J.-M. Hydrodynamics of Free Surface Flows: Modelling with the Finite Element Method; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Dawson, C.; Aizinger, V. A discontinuous Galerkin method for three-dimensional shallow water equations. J. Sci. Comput. 2005, 22, 245–267. [Google Scholar] [CrossRef]
- Aizinger, V.; Dawson, C. The local discontinuous Galerkin method for three-dimensional shallow water flow. Comput. Methods Appl. Mech. Eng. 2007, 196, 734–746. [Google Scholar] [CrossRef]
- Aizinger, V.; Proft, J.; Dawson, C.; Pothina, D.; Negusse, S. A three-dimensional discontinuous Galerkin model applied to the baroclinic simulation of Corpus Christi Bay. Ocean. Dyn. 2013, 63, 89–113. [Google Scholar] [CrossRef]
- Blaise, S. Development of a Finite Element Marine Model. Ph.D. Thesis, UCL-Université Catholique de Louvain, Ottignies-Louvain-la-Neuve, Belgium, 2009. [Google Scholar]
- Comblen, R. Discontinuous Finite-Element Methods for Two-and Three-Dimensional Marine Flows. Ph.D. Thesis, UCL-Université Catholique de Louvain, Ottignies-Louvain-la-Neuve, Belgium, 2010. [Google Scholar]
- Gandham, R. High Performance High-Order Numerical Methods: Applications in Ocean Modeling. Ph.D. Thesis, Rice University, Houston, TX, USA, 2015. [Google Scholar]
- Conroy, C.J.; Kubatko, E.J. Hp discontinuous Galerkin methods for the vertical extent of the water column in coastal settings part I: Barotropic forcing. J. Comput. Phys. 2016, 305, 1147–1171. [Google Scholar] [CrossRef]
- Kärnä, T.; Legat, V.; Deleersnijder, E.; Burchard, H. Coupling of a discontinuous Galerkin finite element marine model with a finite difference turbulence closure model. Ocean. Model. 2012, 47, 55–64. [Google Scholar] [CrossRef]
- Phillips, N.A. A coordinate system having some special advantages for numerical forecasting. J. Atmos. Sci. 1957, 14, 184–195. [Google Scholar] [CrossRef]
- Toro, E.F. Shock-Capturing Methods for Free-Surface Shallow Flows; John Wiley and Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Hesthaven, J.S.; Warburton, T. Nodal Discontinuous Galerkin Methods: Algorithms, Analysis, and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Cockburn, B.; Shu, C.-W. The local discontinuous Galerkin method for time-dependent convection-diffusion systems. SIAM J. Numer. Anal. 1998, 35, 2440–2463. [Google Scholar] [CrossRef]
- Di Pietro, D.A.; Ern, A. Mathematical Aspects of Discontinuous Galerkin Methods; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 69. [Google Scholar]
- Ascher, U.M.; Ruuth, S.J.; Spiteri, R.J. Implicit-explicit Runge-Kutta methods for time-dependent partial differential equations. Appl. Numer. Math. 1997, 25, 151–167. [Google Scholar] [CrossRef]
- Salari, K.; Knupp, P. Code Verification by the Method of Manufactured Solutions; SAND2000-1444; Sandia National Laboratories: Albuquerque, NM, USA, 2000. [Google Scholar]
- Neumann, G.; Pierson, W.J., Jr. Principles of Physical Oceanography; Prentice-Hall: Englewood Cliffs, NJ, USA, 1966. [Google Scholar]
- Liu, X.; Mohammadian, A.; Sedano, J.Á.I.; Kurganov, A. Three-dimensional shallow water system: A relaxation approach. J. Comput. Phys. 2017, 333, 160–179. [Google Scholar] [CrossRef]
- Koutitas, C.; O’Connor, B. Modeling three-dimensional wind-induced flows. J. Hydraul. Div. ASCE 1980, 106, 1843–1865. [Google Scholar] [CrossRef]
- Huang, W. Three Dimensional Numerical Modeling Of Circulation And Water Quality Induced By Combined Sewage Overflow Discharges. Ph.D. Thesis, Department of Ocean Engineering, University of Rhode Island, Kingston, RI, USA, 1993. [Google Scholar]
- Trahan, C.; Savant, G.; Berger, R.; Farthing, M.; McAlpin, T.; Pettey, L.; Choudhary, G.; Dawson, C.N. Formulation and application of the adaptive hydraulics three-dimensional shallow water and transport models. J. Comput. Phys. 2018, 374, 47–90. [Google Scholar] [CrossRef]
- Price, J.F.; Weller, R.A.; Schudlich, R.R. Wind-driven ocean currents and Ekman transport. Science 1987, 238, 1534–1538. [Google Scholar] [CrossRef]
- Li, M.; Zheng, J. Introduction to Chinatide software for tide prediction in China seas. J. Waterw. Harb. 2007, 28, 65–68. (In Chinese) [Google Scholar]
- Burchard, H.; Bolding, K.; Villarreal, M.R. GOTM, a General Ocean Turbulence Model: Theory, Implementation and Test Cases; Technical Report EUR 18745 EN; European Commission: Brussels, Belgium, 1999.



| Variables | Explanation |
|---|---|
| velocity of water in x direction | |
| velocity of water in y direction | |
| velocity of water in z direction | |
| g | acceleration due to gravity |
| angle of geographical latitude | |
| magnitude of the angular velocity of the Earth | |
| Coriolis parameter | |
| vertical eddy viscosity coefficient | |
| horizontal eddy viscosity coefficient | |
| density | |
| wind stress in x direction | |
| wind stress in y direction | |
| the surface elevation | |
| surface velocity of water in x direction | |
| surface velocity of water in y direction | |
| bottom elevation | |
| bottom velocity of water in x direction | |
| bottom velocity of water in y direction | |
| half height of the bottommost element | |
| in x direction | |
| in y direction | |
| drag coefficient | |
| von Karman constant | |
| bottom roughness parameter | |
| vertical velocity in the computational domain | |
| depth-averaged velocity in x direction | |
| depth-averaged velocity in y direction | |
| water depth |
| Ne | NL | Er(D) | CR(D) | Er(Du) | CR(Du) | Er(Dv) | CR(Dv) | Er(ω) | CR(ω) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.00033 | 0.00169 | 0.00169 | |||||
| 4 | 2 | 2.42 | 0.00031 | 2.47 | 0.00031 | 2.47 | 2.03 | ||
| 16 | 4 | 2.19 | 2.33 | 2.33 | 1.77 | ||||
| 64 | 8 | 2.08 | 2.17 | 2.17 | 1.60 | ||||
| 256 | 16 | 2.06 | 2.13 | 2.13 | 1.45 |
| Ne | NL | Er(D) | CR(D) | Er(Du) | CR(Du) | Er(Dv) | CR(Dv) | Er(ω) | CR(ω) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.00015 | 0.00015 | ||||||
| 4 | 2 | 3.10 | 3.10 | 3.10 | 3.11 | ||||
| 16 | 4 | 3.04 | 3.04 | 3.04 | 2.33 | ||||
| 64 | 8 | 3.05 | 3.05 | 3.05 | 1.91 | ||||
| 256 | 16 | 3.02 | 3.02 | 3.02 | 2.10 |
| NL | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| Homogeneous Dirichlet boundary condition | ||||
| RMSE | 0.0107 | 0.0051 | 0.0041 | 0.0037 |
| Neumann boundary condition | ||||
| RMSE | 0.0219 | 0.0138 | 0.0114 | 0.0103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, G.; Zhang, Q.; Chen, Z. Development of a Three-Dimensional Hydrodynamic Model Based on the Discontinuous Galerkin Method. Water 2023, 15, 156. https://doi.org/10.3390/w15010156
Ran G, Zhang Q, Chen Z. Development of a Three-Dimensional Hydrodynamic Model Based on the Discontinuous Galerkin Method. Water. 2023; 15(1):156. https://doi.org/10.3390/w15010156
Chicago/Turabian StyleRan, Guoquan, Qinghe Zhang, and Zereng Chen. 2023. "Development of a Three-Dimensional Hydrodynamic Model Based on the Discontinuous Galerkin Method" Water 15, no. 1: 156. https://doi.org/10.3390/w15010156
APA StyleRan, G., Zhang, Q., & Chen, Z. (2023). Development of a Three-Dimensional Hydrodynamic Model Based on the Discontinuous Galerkin Method. Water, 15(1), 156. https://doi.org/10.3390/w15010156







