A Review of Sources of Uncertainty in Optimization Objectives of Water Distribution Systems
Abstract
:1. Introduction
2. Sources of Uncertainty and Their Relative Importance in Relation to Optimization Objectives
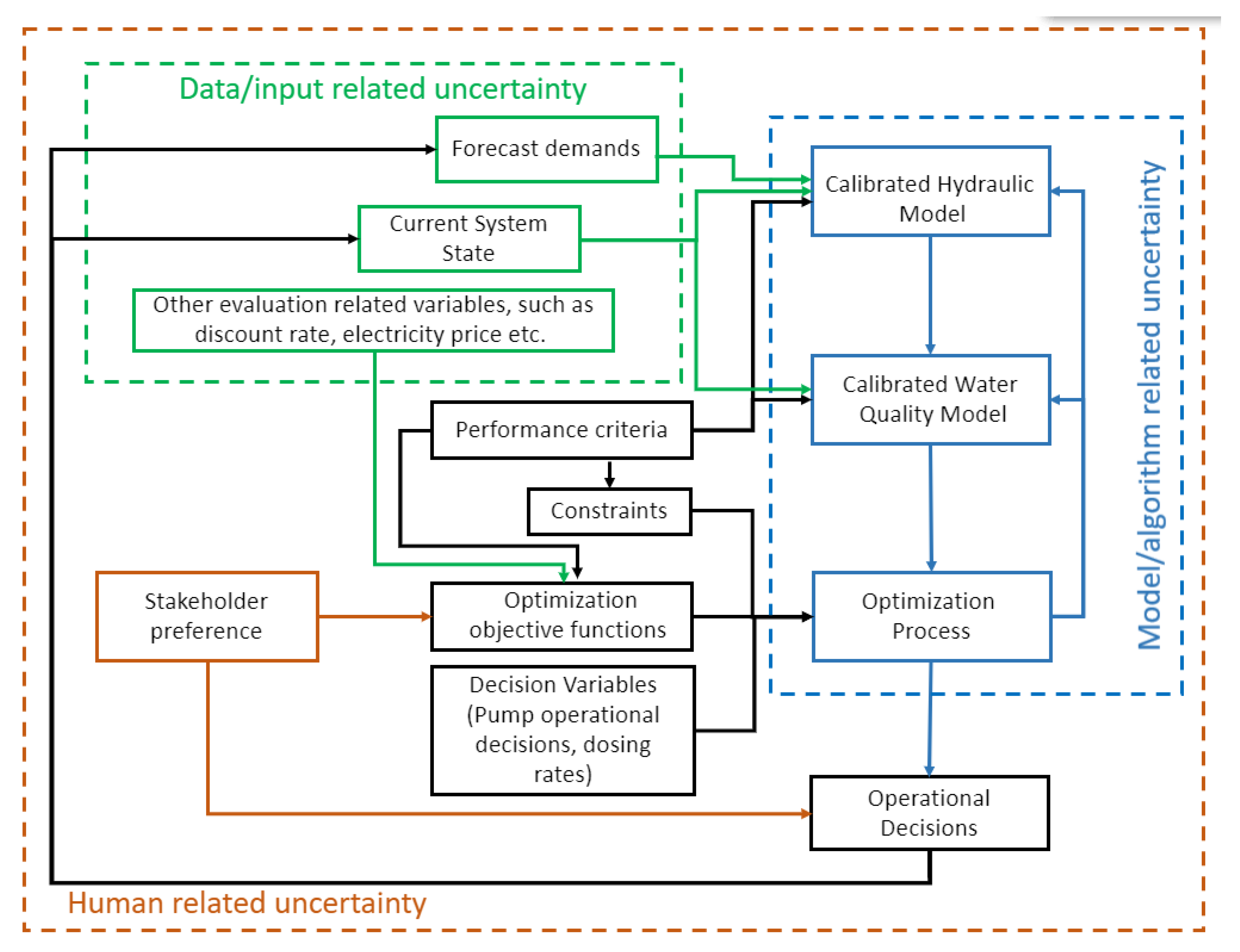
- Model/algorithm uncertainty (e.g., pipe roughness values or chemical reaction rates);
- Data/input related uncertainty (e.g., uncertainty in water demands due to natural variability, population growth and/or climate change); and
- Human related uncertainty (e.g., lack of knowledge about the network or ambiguity in the framing or decision making process).
2.1. Water Distribution System Planning and Design
2.2. Water Distribution System Rehabilitation
2.3. Water Distribution System Operations
3. Review of Literature on Sources of Uncertainty on Optimization Objectives
3.1. Water Distribution System Planning and Design
3.2. Water Distribution System Rehabilitation
3.3. Water Distribution System Operations
4. Conclusions
5. Recommendations for Further Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in optimisation of water distribution systems? A literature review of system operation. Environ. Mod. Softw. 2017, 93, 209–254. [Google Scholar] [CrossRef] [Green Version]
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in Optimisation of Water Distribution Systems? A literature review of system design. Water 2018, 10, 307. [Google Scholar] [CrossRef] [Green Version]
- Balekelayi, N.; Tesfamariam, S. Optimization techniques used in design and operations of water distribution networks: A review and comparative study. Sustain. Resil. Infrastruct. 2017, 2, 153–168. [Google Scholar] [CrossRef]
- Sarbu, I. Optimization of urban water distribution networks using deterministic and heuristic techniques: Comprehensive revie. J. Pipeline Syst. Eng. Prac. ASCE 2021, 12, 03121001. [Google Scholar] [CrossRef]
- Creaco, E.; Campisano, A.; Fontana, N.; Marini, G.; Page, P.R.; Walski, T. Real time control of water distribution networks: A state-of-the-art review. Water Res. 2019, 161, 517–530. [Google Scholar] [CrossRef] [PubMed]
- Hutton, C.; Kapelan, Z.; Vamvakeridou-Lyroudia, L.; Savic, D.A. Dealing with uncertainty in water distribution system models: A framework for real-time modeling and data assimilation. J. Water Resour. Plan. Manag. ASCE 2014, 140, 169–183. [Google Scholar] [CrossRef]
- Zhao, Q.; Wu, W.; Simpson, A.R.; Willis, A. Simpler Is Better—Calibration of Pipe Roughness in Water Distribution Systems. Water 2022, 14, 3276. [Google Scholar] [CrossRef]
- Shang, F.; Uber, J.G.; Rossman, L.A. Modeling reaction and transport of multiple species in water distribution systems. Environ. Sci. Technol. 2008, 42, 808–814. [Google Scholar] [CrossRef]
- Maier, H.R.; Kapelan, Z.; Kasprzyk, J.; Kollat, J.; Matott, L.S.; Cunha, M.C.; Dandy, G.C.; Gibbs, M.S.; Keedwell, E.; Marchi, A.; et al. Evolutionary algorithms and other metaheuristics in water resources: Current status, research challenges and future directions. Environ. Mod. Softw. 2014, 62, 271–299. [Google Scholar] [CrossRef] [Green Version]
- Jun, S.; Arbesser-Rastburg, G.; Fuchs-Hanusch, D.; Lansey, K. Response surfaces for water distribution system pipe roughness calibration. J. Water Resour. Plan. Manag. ASCE 2022, 148, 04021105. [Google Scholar] [CrossRef]
- Salehi, S.; Ghazizadeh, M.J.; Tabesh, M. A comprehensive criteria-base multi-attribute decision-making model for rehabilitation of water distribution systems. Struct. Infrastruct. Eng. 2018, 14, 743–765. [Google Scholar] [CrossRef]
- Skogen, M.D.; Ji, R.; Akimova, A.; Daewel, U.; Hansen, C.; Hjøllo, S.S.; van Leeuwen, S.M.; Maar, M.; Macias, D.; Mousing, E.A.; et al. Disclosing the truth: Are models better than observations? Mar. Ecol. Prog. Ser. 2021, 680, 7–13. [Google Scholar] [CrossRef]
- Mair, M.; Rauch, W.; Sitzenfrei, R. Improving incomplete water distribution system data. Procedia Eng. 2014, 70, 1055–1062. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Song, Z.; Ouyang, M. Lifecycle operational resilience assessment of urban water distribution networks. Reliab. Eng. Syst. Saf. 2020, 198, 106859. [Google Scholar] [CrossRef]
- Boindala, S.P.; Jaykrishnan, G.; Ostfeld, A. Robust multi-objective optimization of water distribution systems. In Proceedings of the World Environmental and Water Resources Congress 2022, Atlanta, GA, USA, 5–8 June 2022; pp. 1085–1095. [Google Scholar]
- Choi, Y.H. Development of optimal water distribution system design and operation approach considering hydraulic and water quality criteria in many-objective optimization framework. J. Comput. Des. Eng. 2022, 9, 507–518. [Google Scholar] [CrossRef]
- Creaco, E.; Franchini, M.; Walski, T.M. Accounting for phasing of construction within the design of water distribution networks. J. Water Resour. Plan. Manag. ASCE 2013, 140, 598–606. [Google Scholar] [CrossRef]
- Creaco, E.; Franchini, M.; Walski, T.M. Comparison of various phased approaches for the constrained minimum-cost design of water distribution networks. Urban Water J. 2016, 13, 270–283. [Google Scholar] [CrossRef] [Green Version]
- Sirsant, S.; Reddy, M.J. Performance-based multi-objective design and expansion of water distribution networks considering life cycle costs and future demands. Water Supply 2022, 22, 1388–1408. [Google Scholar] [CrossRef]
- Wu, W.; Simpson, A.R.; Maier, H.R. Accounting for greenhouse gas emissions in multi-objective genetic algorithm optimization of water distribution systems. J. Water Resour. Plan. Manag. ASCE 2010, 136, 146–155. [Google Scholar] [CrossRef] [Green Version]
- Bondank, E.N.; Chester, M.V.; Ruddell, B.L. Water distribution system failure risks with increasing temperatures. Environ. Sci. Technol. 2018, 52, 9605–9614. [Google Scholar] [CrossRef]
- Jensen, H.A.; Jerez, D.J. A stochastic framework for reliability and sensitivity analysis of large scale water distribution networks. Reliab. Eng. Syst. Saf. 2018, 176, 80–92. [Google Scholar] [CrossRef]
- Monsef, H.; Naghashzadegan, M.; Farmani, R.; Jamali, A. Deficiency of reliability indicators in water distribution networks. J. Water Resour. Plan. Manag. ASCE 2019, 145, 04019022. [Google Scholar] [CrossRef]
- McInerney, D.; Thyer, M.; Kavetski, D.; Bennett, B.; Lerat, J.; Gibbs, M.; Kuczera, G. A simplified approach to produce probabilistic hydrological model predictions. Environ. Mod. Softw. 2018, 109, 306–314. [Google Scholar] [CrossRef]
- Kapelan, Z.; Savic, D.A.; Walters, G.A.; Babayan, A.V. Risk- and robustness-based solutions to a multi-objective water distribution system rehabilitation problem under uncertainty. Water Sci. Technol. 2006, 53, 61–75. [Google Scholar] [CrossRef]
- Olsson, R.; Kapelan, Z.; Savic, D.A.; Savic, D.A. Probabilistic building block identification for the optimal design and rehabilitation of water distribution systems. J. Hydroinform. 2009, 11, 89–105. [Google Scholar] [CrossRef] [Green Version]
- Rahmani, F.; Behzadian, K.; Ardeshir, A. Rehabilitation of a water distribution system using sequential multiobjective optimization models. J. Water Resour. Plan. Manag. ASCE 2016, 142, C4015003. [Google Scholar] [CrossRef]
- Roshani, E.; Filion, Y. The effect of future water demand reduction on WDS rehabilitation planning. Procedia Eng. 2014, 89, 796–803. [Google Scholar] [CrossRef] [Green Version]
- Roshani, E.; Filion, Y.R. Event-based approach to optimize the timing of water main rehabilitation with asset management strategies. J. Water Resour. Plan. Manag. ASCE 2014, 140, 04014004. [Google Scholar] [CrossRef] [Green Version]
- Roshani, E.; Filion, Y.R. Water distribution system rehabilitation under climate change mitigation scenarios in Canada. J. Water Resour. Plan. Manag. ASCE 2015, 141, 04014066. [Google Scholar] [CrossRef] [Green Version]
- Hong, H.P.; Allouche, E.N.; Trivedi, M. Optimal scheduling of replacement and rehabilitation of water distribution systems. J. Infrastrust. Syst. 2006, 12, 184–191. [Google Scholar] [CrossRef]
- Dandy, G.C.; Engelhardt, M. Optimal scheduling of water pipe replacement using genetic algorithms. J. Water Resour. Plan. Manag. ASCE 2001, 127, 214–223. [Google Scholar] [CrossRef]
- Dandy, G.C.; Engelhardt, M.O. Multi-objective trade-offs between cost and reliability in the replacement of water mains. J. Water Resour. Plan. Manag. ASCE 2006, 132, 79–88. [Google Scholar] [CrossRef]
- Alvisi, S.; Franchini, M. Multiobjective optimization of rehabilitation and leakage detection scheduling in water distribution systems. J. Water Resour. Plan. Manag. ASCE 2009, 135, 426–439. [Google Scholar] [CrossRef]
- Siew, C.; Tanyimboh, T.; Seyoum, A.G. Assessment of penalty-free multi-objective evolutionary optimization approach for the design and rehabilitation of water distribution systems. Water Resour. Manag. 2014, 28, 373–389. [Google Scholar] [CrossRef] [Green Version]
- Meirelles, G.; Brentan, B.; Izquierdo, J.; Ramos, H.; Luvizotto, E. Trunk network rehabilitation for resilience improvement and energy recovery in water distribution networks. Water 2018, 10, 693. [Google Scholar] [CrossRef] [Green Version]
- Dell’Aira, F.; Cancelliere, A.; Creaco, E.; Pezzinga, G. Novel comprehensive approach for phasing design and rehabilitation of water distribution networks. J. Water Resour. Plan. Manag. ASCE 2021, 147, 04021001. [Google Scholar] [CrossRef]
- Souza, R.G.; Meirelles, G.; Brentan, B.; Izquierdo, J. Rehabilitation in intermittent water distribution networks for optimal operation. Water 2022, 14, 88. [Google Scholar] [CrossRef]
- Filion, Y.R.; MacLean, H.L.; Karney, B.W. Life-cycle energy analysis of a water distribution system. J. Infrastrust. Syst. 2004, 10, 120–130. [Google Scholar] [CrossRef] [Green Version]
- Farahmandfar, Z.; Piratla, K.R.; Piratla, K.R. Resilience-based water main rehabilitation planning in a multi-hazard context. AQUA 2017, 66, 651–664. [Google Scholar] [CrossRef]
- Tabesh, M.; Saber, H. A prioritization model for rehabilitation of water distribution networks using GIS. Water Resour. Manag. 2012, 26, 225–241. [Google Scholar] [CrossRef]
- Pudasaini, B.; Shahandashti, M. Seismic rehabilitation optimization of water pipe networks considering spatial variabilities of demand criticalities and seismic ground motion intensities. J. Infrastrust. Syst. 2021, 27, 04021028. [Google Scholar] [CrossRef]
- Karmakar, S. Propagation of uncertainties in water distribution systems modeling. Desal. Water Treat. 2011, 33, 107–117. [Google Scholar] [CrossRef]
- Hu, S.H. Theory and development of uncertainty analysis in water distribution system model. Adv. Educ. Res. 2011, 2, 224–227. [Google Scholar]
- Emerton, R.E.; Stephens, E.M.; Pappenberger, F.; Pagano, T.C.; Weerts, A.H.; Wood, A.W.; Salamon, P.; Brown, J.D.; Hjerdt, N.; Donnelly, C.; et al. Continental and global scale flood forecasting systems. WIREs Water 2016, 3, 391–418. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Huang, W.; Yang, X.; Wang, L.; Wang, Z.; Wang, Y. Impact of problem formulations, pipe selection methods, and optimization algorithms on the rehabilitation of water distribution systems. AQUA 2020, 69, 769–784. [Google Scholar] [CrossRef]
- Salomons, E.; Goryashko, A.; Shamir, U.; Rao, Z.; Alvisi, S. Optimizing the operation of the Haifa-a water distribution network. J. Hydroinf. 2007, 9, 51–64. [Google Scholar] [CrossRef] [Green Version]
- Brion, L.M.; Mays, L.W. Methodology for optimal operation of pumping stations in water distribution systems. J. Hydraul. Eng. ASCE 1991, 117, 1551–1569. [Google Scholar] [CrossRef]
- van Zyl, J.E.; Savic, D.A.; Walters, G.A. Operational optimization of water distribution systems using a hybrid genetic algorithm. J. Water Resour. Plan. Manag. ASCE 2004, 130, 160–170. [Google Scholar] [CrossRef]
- Zessler, U.; Shamir, U. Optimal operation of water distribution systems. J. Water Resour. Plan. Manag. ASCE 1989, 115, 735–752. [Google Scholar] [CrossRef]
- Jamieson, D.G.; Shamir, U.; Martinez, F.; Franchini, M. Conceptual design of a generic, real-time, near-optimal control system for water-distribution networks. J. Hydroinf. 2007, 9, 3–14. [Google Scholar] [CrossRef]
- Khatavkar, P.; Mays, L.W. Optimization-simulation model for real-time pump and valve operation of water distribution systems under critical conditions. Urban Water J. 2019, 16, 45–55. [Google Scholar] [CrossRef]
- Sakarya, B.A.; Mays, L.W. Optimal operation of water distribution pumps considering water quality. J. Water Resour. Plan. Manag. ASCE 2000, 126, 210–220. [Google Scholar] [CrossRef]
- Boccelli, D.L.; Tryby, M.E.; Uber, J.G.; Rossman, L.A.; Zierolf, M.L.; Polycarpou, M.M. Optimal scheduling of booster disinfection in water distribution systems. J. Water Resour. Plan. Manag. ASCE 1998, 124, 99–111. [Google Scholar] [CrossRef]
- Kang, D.S.; Lansey, K. Real-time optimal valve operation and booster disinfection for water quality in water distribution systems. J. Water Resour. Plan. Manag. ASCE 2010, 136, 463–473. [Google Scholar] [CrossRef]
- Schwartz, R.; Housh, M.; Ostfeld, A. Least-cost robust design optimization of water distribution systems under multiple loading. J. Water Resour. Plan. Manag. ASCE 2016, 142, 04016031. [Google Scholar] [CrossRef]
- Khatavkar, P.; Mays, L.W. Model for optimal operation of water distribution pumps with uncertain demand patterns. Water Resour. Manag. 2017, 31, 3867–3880. [Google Scholar] [CrossRef]
- Goryashko, A.P.; Nemirovski, A.S. Robust energy cost optimization of water distribution systems with uncertain demand. Autom. Rem. Control 2014, 75, 1754–1769. [Google Scholar] [CrossRef] [Green Version]
- Kastl, G.J.; Fisher, I.H.; Jegatheesan, V. Evaluation of chlorine decay kinetics expressions for drinking water distribution systems modelling. J. Water Supply Res. Technol. AQUA 1999, 48, 219–226. [Google Scholar] [CrossRef]
- Fisher, I.; Kastl, G.; Sathasivan, A. New model of chlorine-wall reaction for simulating chlorine concentration in drinking water distribution systems. Water Res. 2017, 125, 427–437. [Google Scholar] [CrossRef]
- Fisher, I.; Kastl, G.; Sathasivan, A.; Jegatheesan, V. Suitability of chlorine bulk decay models for planning and management of water distribution systems. Crit. Rev. Environ. Sci. Technol. 2011, 41, 1843–1882. [Google Scholar] [CrossRef]
- Grayman, W.M.; Deininger, R.A.; Green, A.; Boulos, P.F.; Bowcock, R.W.; Godwin, C.C. Water quality and mixing models for tanks and reservoirs. J. AWWA—Am. Water Works Assoc. 1996, 88, 60–73. [Google Scholar] [CrossRef]
- Basupi, I.; Kapelan, Z. Flexible water distribution system design under future demand uncertainty. J. Water Resour. Plan. Manag. ASCE 2015, 141, 04014067. [Google Scholar] [CrossRef]
- Xing, L.; Raviv, T.; Sela, L. Sensor placement for robust burst identification in water systems: Balancing modeling accuracy, parsimony, and uncertainties. Adv. Eng. Inform. 2022, 51, 101484. [Google Scholar] [CrossRef]
- Nicklow, J.; Reed, P.; Savic, D.; Dessalegne, T.; Harrell, L.; Chan-Hilton, A.; ASCE Task Committee on Evolutionary Computation in Environmental and Water Resources Engineering. State of the art for genetic algorithms and beyond in water resources planning and management. J. Water Resour. Plan. Manag. ASCE 2010, 136, 412–432. [Google Scholar] [CrossRef]
- Sitzenfrei, R.; Rauch, W. Optimizing small hydropower systems in water distribution systems based on long-time-series simulation and future scenarios. J. Water Resour. Plan. Manag. ASCE 2015, 141, 04015021. [Google Scholar] [CrossRef]
- Creaco, E.; Franchini, M.; Walski, T.M. Taking account of uncertainty in demand growth when phasing the construction of a water distribution network. J. Water Resour. Plan. Manag. ASCE 2015, 141, 04014049. [Google Scholar] [CrossRef]
- Xu, C.; Goulter, I.C. Reliability-based optimal design of water distribution networks. J. Water Resour. Plan. Manag. ASCE 1999, 125, 352–362. [Google Scholar] [CrossRef] [Green Version]
- Babayan, A.; Kapelan, Z.; Savic, D.; Walters, G. Least-cost design of water distribution networks under demand uncertainty. J. Water Resour. Plan. Manag. ASCE 2005, 131, 375–382. [Google Scholar] [CrossRef]
- Marques, J.; Cunha, M.; Savić, D. Many-objective optimization model for the flexible design of water distribution networks. J. Environ. Manag. 2018, 226, 308–319. [Google Scholar] [CrossRef]
- Basupi, I.; Kapelan, Z. Evaluating flexibility in water distribution system design under future demand uncertainty. J. Infrastrust. Syst. 2015, 21, 04014034. [Google Scholar] [CrossRef]
- Maier, H.R.; Guillaume, J.H.A.; van Delden, H.; Riddell, G.A.; Haasnoot, M.; Kwakkel, J.H. An uncertain future, deep uncertainty, scenarios, robustness and adaptation: How do they fit together? Environ. Mod. Softw. 2016, 81, 154–164. [Google Scholar] [CrossRef]
- McPhail, C.; Maier, H.R.; Kwakkel, J.H.; Giuliani, M.; Castelletti, A.; Westra, S. Robustness metrics: How are they calculated, when should they be used and why do they give different results? Earths Future 2018, 6, 169–191. [Google Scholar] [CrossRef]
- Simpson, A.R. Selecting a discount rate for evaluating water distribution projects—The sustainability controversy. In WDSA 2008, Proceedings of the 10th Annual Water Distribution Systems Analysis Conference, Kruger National Park, South Africa, 17–20 August 2008; van Zyl, K., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2008; pp. 1–12. ISBN 9780784410240. [Google Scholar]
- Paez, D.; Filion, Y. Water distribution systems reliability under extended-period simulations. J. Water Resour. Plan. Manag. ASCE 2020, 146, 04020062. [Google Scholar] [CrossRef]
- Wu, W.; Maier, H.R.; Dandy, G.C.; Leonard, R.; Bellette, K.; Cuddy, S.; Maheepala, S. Including stakeholder input in formulating and solving real-world optimisation problems: Generic framework and case study. Environ. Mod. Softw. 2016, 79, 197–213. [Google Scholar] [CrossRef]
- Ezzeldin, R.M.; Djebedjian, B. Optimal design of water distribution networks using whale optimization algorithm. Urban Water J. 2020, 17, 14–22. [Google Scholar] [CrossRef]
- Djebedjian, B.; Abdel-Gawad, H.A.; Ezzeldin, R.M. Global performance of metaheuristic optimization tools for water distribution networks. Ain Shams Eng. J. 2021, 12, 223–239. [Google Scholar] [CrossRef]
- Sopasakis, P.; Sampathirao, A.K.; Bemporad, A.; Patrinos, P. Uncertainty-aware demand management of water distribution networks in deregulated energy markets. Environ. Mod. Softw. 2018, 101, 10–22. [Google Scholar] [CrossRef] [Green Version]
- Nono, D.; Basupi, I. Robust booster chlorination in water distribution systems: Design and operational perspectives under uncertainty. J. Water Supply Res. Technol. AQUA 2019, 68, 399–410. [Google Scholar] [CrossRef]
- Housh, M.; Ostfeld, A.; Shamir, U. Implicit mean-variance approach for optimal management of a water supply system under uncertainty. J. Water Resour. Plan. Manag. ASCE 2013, 13, 634–643. [Google Scholar] [CrossRef] [Green Version]
- Cohen, D.; Shamir, U.; Sinai, G. Comparison of models for optimal operation of multiquality water supply networks. Eng. Optim. 2003, 35, 579–605. [Google Scholar] [CrossRef]
- Baran, B.; von Lucken, C.; Sotelo, A. Multi-objective pump scheduling optimisation using evolutionary strategies. Adv. Eng. Softw. 2005, 36, 39–47. [Google Scholar] [CrossRef]
- Lopez-Ibanez, M.; Prasad, T.D.; Paechter, B. Ant colony optimization for optimal control of pumps in water distribution networks. J. Water Resour. Plan. Manag. ASCE 2008, 134, 337–346. [Google Scholar] [CrossRef]
- Bene, J.G.; Hos, C.J. Finding least-cost pump schedules for reservoir filling with a variable speed pump. J. Water Resour. Plan. Manag. ASCE 2012, 138, 682–686. [Google Scholar] [CrossRef]
- Selek, I.; Bene, J.G.; Hos, C. Optimal (short-term) pump schedule detection for water distribution systems by neutral evolutionary search. Appl. Soft Comput. 2012, 12, 2336–2351. [Google Scholar] [CrossRef]
- Ghaddar, B.; Naoum-Sawaya, J.; Kishimoto, A.; Taheri, N.; Eck, B. A Lagrangian. decomposition approach for the pump scheduling problem in water networks. Eur. J. Oper. Res. 2015, 241, 490–501. [Google Scholar] [CrossRef]
- Price, E.; Ostfeld, A. Discrete pump scheduling and leakage control using linear programming for optimal operation of water distribution systems. J. Hydraul. Eng. ASCE 2014, 140, 04014017. [Google Scholar] [CrossRef]
- Bene, J.G.; Selek, I.; Hos, C. Comparison of deterministic and heuristic optimization solvers for water network scheduling problems. Water Sci. Technol. Water Supply 2013, 13, 1367–1376. [Google Scholar] [CrossRef]
- Kougias, I.P.; Theodossiou, N.P. Multiobjective pump scheduling optimization using harmony search algorithm (HSA) and polyphonic HSA. Water Resour. Manag. 2013, 27, 1249–1261. [Google Scholar] [CrossRef]
- Ewald, G.; Kurek, W.; Brdys, M.A. Grid implementation of a parallel multiobjective genetic algorithm for optimized allocation of chlorination stations in drinking water distribution systems: Chojnice case study. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2008, 38, 497–509. [Google Scholar] [CrossRef]

| Sources of Uncertainty | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Optimization Category | Optimization Objectives | Model | Optimization Method | Data—Randomness in Demand | Data—Randomness in Other Variables (e.g., Mechanical, Water Quality, …) | Data—Long-term Changes in Demand | Data—Long-term Changes in Other Variables | Human—Lack of Knowledge | Human—Stakeholders Preferences |
| WDS planning/design | Min capital cost | ✓ | ✓ | ✓✓ | ✓ | ✓✓ | ✓✓ | ✓✓✓ | ✓ |
| Min life-cycle cost | ✓✓ | ✓ | ✓✓✓ | ✓ | ✓✓✓ | ✓✓ | ✓✓✓ | ✓ | |
| Min life-cycle energy/emissions | ✓✓ | ✓ | ✓✓✓ | ✓ | ✓✓✓ | ✓✓ | ✓✓✓ | ✓ | |
| Max flexibility | ✓✓✓ | ✓ | ✓✓✓ | ✓ | ✓✓✓ | ✓✓ | ✓✓✓ | ✓✓✓ | |
| Max hydraulic performance (e.g., hydraulic capacity, system reliability) | ✓ | ✓ | ✓✓✓ | ✓✓ | ✓✓✓ | ✓✓ | ✓✓✓ | ✓✓ | |
| Max water quality performance | ✓✓✓ | ✓ | ✓✓✓ | ✓✓ | ✓✓✓ | ✓✓ | ✓✓✓ | ✓ | |
| WDS rehabilitation | Min capital cost | ✓ | ✓ | ✓ | ✓✓ | ✓✓ | ✓✓ | ✓✓✓ | ✓ |
| Min operation cost | ✓ | ✓ | ✓✓ | ✓✓ | ✓✓✓ | ✓ | ✓✓✓ | ✓ | |
| Min life-cycle cost | ✓ | ✓ | ✓✓ | ✓✓ | ✓✓✓ | ✓✓ | ✓✓✓ | ✓ | |
| Min life-cycle energy/emissions | ✓ | ✓ | ✓✓ | ✓✓ | ✓✓✓ | ✓✓ | ✓✓✓ | ✓ | |
| Min water loss | ✓ | ✓ | ✓ | ✓ | ✓✓ | ✓ | ✓✓✓ | ✓ | |
| Max hydraulic performance (e.g., hydraulic capacity, supply reliability) | ✓ | ✓ | ✓✓✓ | ✓✓ | ✓✓✓ | ✓✓ | ✓✓✓ | ✓ | |
| WDS operation | Min life cycle cost | ✓ | ✓ | ✓✓ | ✓✓ | n/a | n/a | ✓✓✓ | ✓ |
| Min operating cost | ✓ | ✓ | ✓✓ | ✓✓ | n/a | n/a | ✓✓✓ | ✓ | |
| Max hydraulic efficiency (e.g., pump power, pump switches) | ✓ | ✓ | ✓✓ | ✓✓ | n/a | n/a | ✓✓✓ | ✓ | |
| Min energy consumption/GHG emissions | ✓✓ | ✓ | ✓✓✓ | ✓✓ | n/a | n/a | ✓✓✓ | ✓ | |
| Max water quality | ✓✓✓ | ✓ | ✓✓✓ | ✓✓ | n/a | n/a | ✓✓✓ | ✓ | |
| Min average/maximum water age | ✓ | ✓ | ✓✓✓ | ✓✓ | n/a | n/a | ✓✓✓ | ✓ | |
| Sources of Uncertainty | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Optimization Category | Optimization Objectives | Model (e.g., Model Structure and Parameter, e.g., Pipe Roughness or Chemical Reaction Rates for Water Quality Considerations) | Optimization Algorithm (e.g., Algorithm and Algorithm Parameters) | Data—Randomness (Natural Variability) in Demand | Data—Randomness (Natural Variability) in Other Variables (Mechanical, Water Quality, …) | Data—Long-term Changes in Demand (Due to Population Growth, Climate Change) | Data - Long-term Changes in Other Variables, e.g., Carbon Tax, Hazards | Human—Lack of Knowledge | Human—Stakeholders Preferences |
| WDS planning/design | Min capital cost | ✓✓✓ | ✓✓✓ | ✓✓✓ | ✓✓ | ✓✓✓ | ✓ | ✓ | ✓ |
| Min life-cycle cost | ✓✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Min life-cycle energy/emissions | ✓ | ✓ | ✓✓✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Max flexibility | ✓ | ✓✓✓ | ✓✓✓ | ✓ | ✓✓ | ✓ | ✓ | ✓ | |
| Max hydraulic performance (e.g., hydraulic capacity, system reliability) | ✓✓✓ | ✓✓✓ | ✓✓✓ | ✓✓ | ✓✓ | ✓✓ | ✓ | ✓ | |
| Max water quality performance | ✓✓✓ | ✓✓✓ | ✓✓✓ | ✓✓ | ✓✓✓ | ✓ | ✓✓ | ✓ | |
| WDS rehabilitation | Min capital cost | ✓ | ✓✓ | ✓ | ✓ | ✓✓ | ✓✓ | ✓✓ | ✓✓ |
| Min operation cost | ✓ | ✓ | ✓ | ✓ | ✓✓ | ✓✓ | ✓✓ | ✓ | |
| Min life-cycle cost | ✓ | ✓ | ✓✓✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Min life-cycle energy/emissions | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Min water loss | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Max hydraulic performance (e.g., hydraulic capacity, system reliability) | ✓ | ✓✓✓ | ✓✓✓ | ✓✓✓ | ✓ | ✓✓ | ✓ | ✓✓✓ | |
| WDS operation | Min life cycle cost | ✓ | ✓✓✓ | ✓ | ✓✓ | n/a | n/a | ✓ | ✓ |
| Min operating cost | ✓ | ✓✓✓ | ✓✓✓ | ✓✓ | n/a | n/a | ✓ | ✓ | |
| Max hydraulic efficiency (e.g., pump power, pump switches) | ✓ | ✓✓ | ✓✓ | ✓✓ | n/a | n/a | ✓ | ✓ | |
| Min energy consumption/GHG emissions | ✓ | ✓ | ✓ | ✓ | n/a | n/a | ✓ | ✓ | |
| Max water quality | ✓✓ | ✓ | ✓✓ | ✓ | n/a | n/a | ✓ | ✓ | |
| Min average/maximum water age | ✓ | ✓ | ✓ | ✓ | n/a | n/a | ✓ | ✓ | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dandy, G.; Wu, W.; Simpson, A.; Leonard, M. A Review of Sources of Uncertainty in Optimization Objectives of Water Distribution Systems. Water 2023, 15, 136. https://doi.org/10.3390/w15010136
Dandy G, Wu W, Simpson A, Leonard M. A Review of Sources of Uncertainty in Optimization Objectives of Water Distribution Systems. Water. 2023; 15(1):136. https://doi.org/10.3390/w15010136
Chicago/Turabian StyleDandy, Graeme, Wenyan Wu, Angus Simpson, and Michael Leonard. 2023. "A Review of Sources of Uncertainty in Optimization Objectives of Water Distribution Systems" Water 15, no. 1: 136. https://doi.org/10.3390/w15010136
APA StyleDandy, G., Wu, W., Simpson, A., & Leonard, M. (2023). A Review of Sources of Uncertainty in Optimization Objectives of Water Distribution Systems. Water, 15(1), 136. https://doi.org/10.3390/w15010136







