How Heterogeneous Pore Scale Distributions of Wettability Affect Infiltration into Porous Media
Abstract
:1. Introduction
2. Method
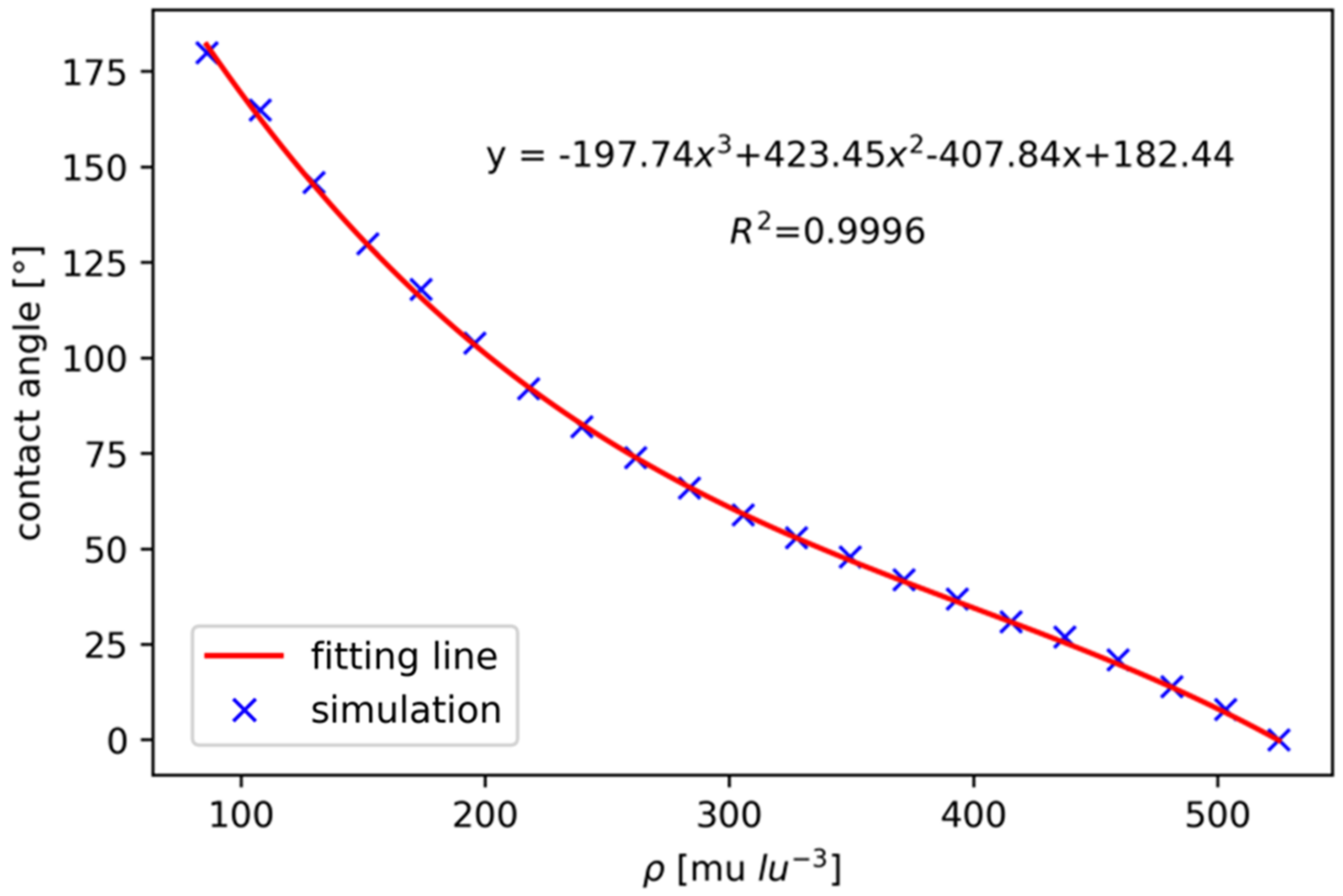
2.1. Theory of Effective Contact Angles
2.2. Multiphase Lattice Boltzmann Model
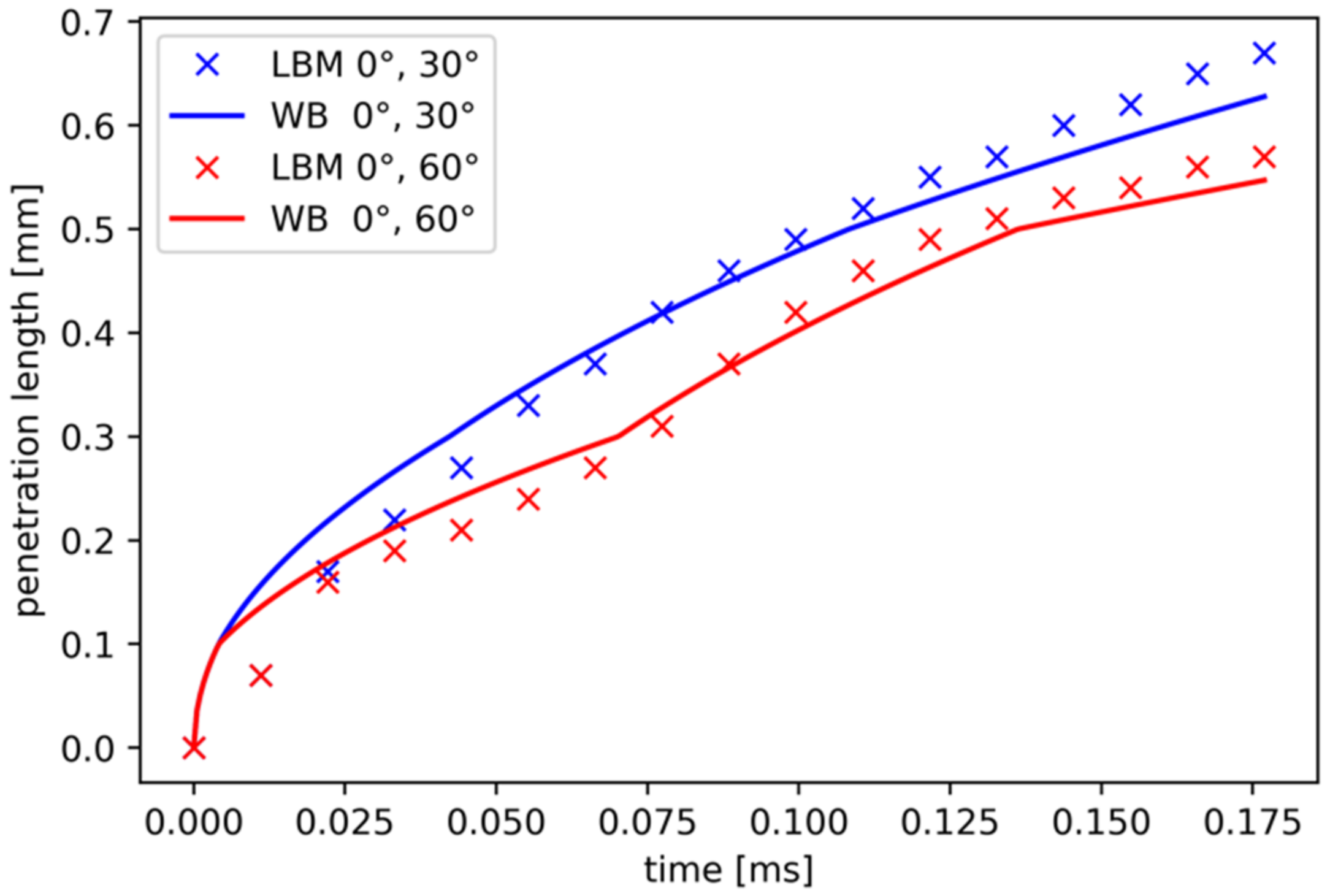
2.3. Model Validation
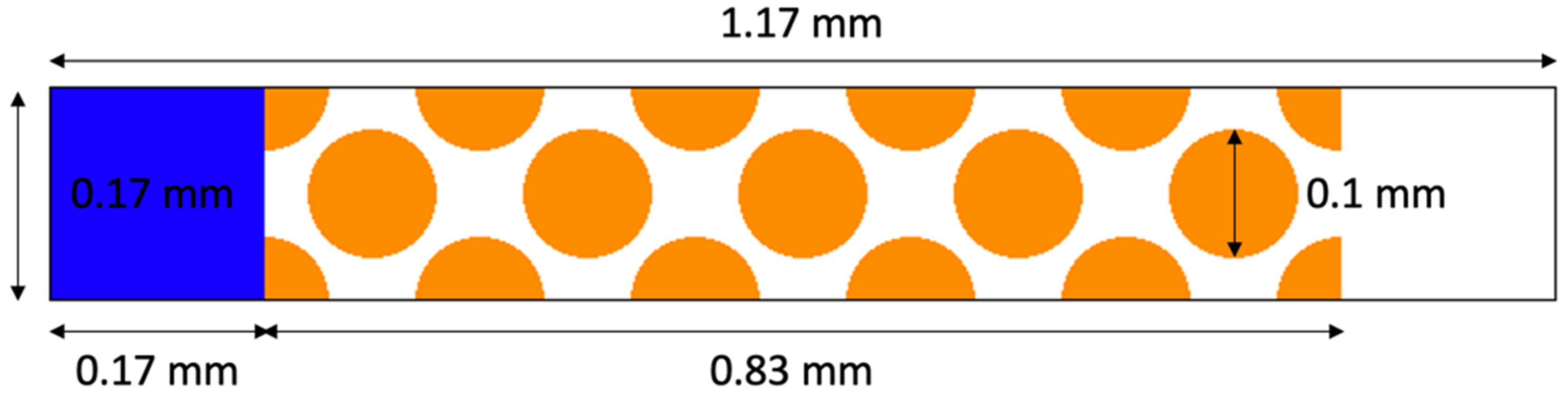
2.4. Infiltration into Porous Media Depending on Contact Angle Distribution
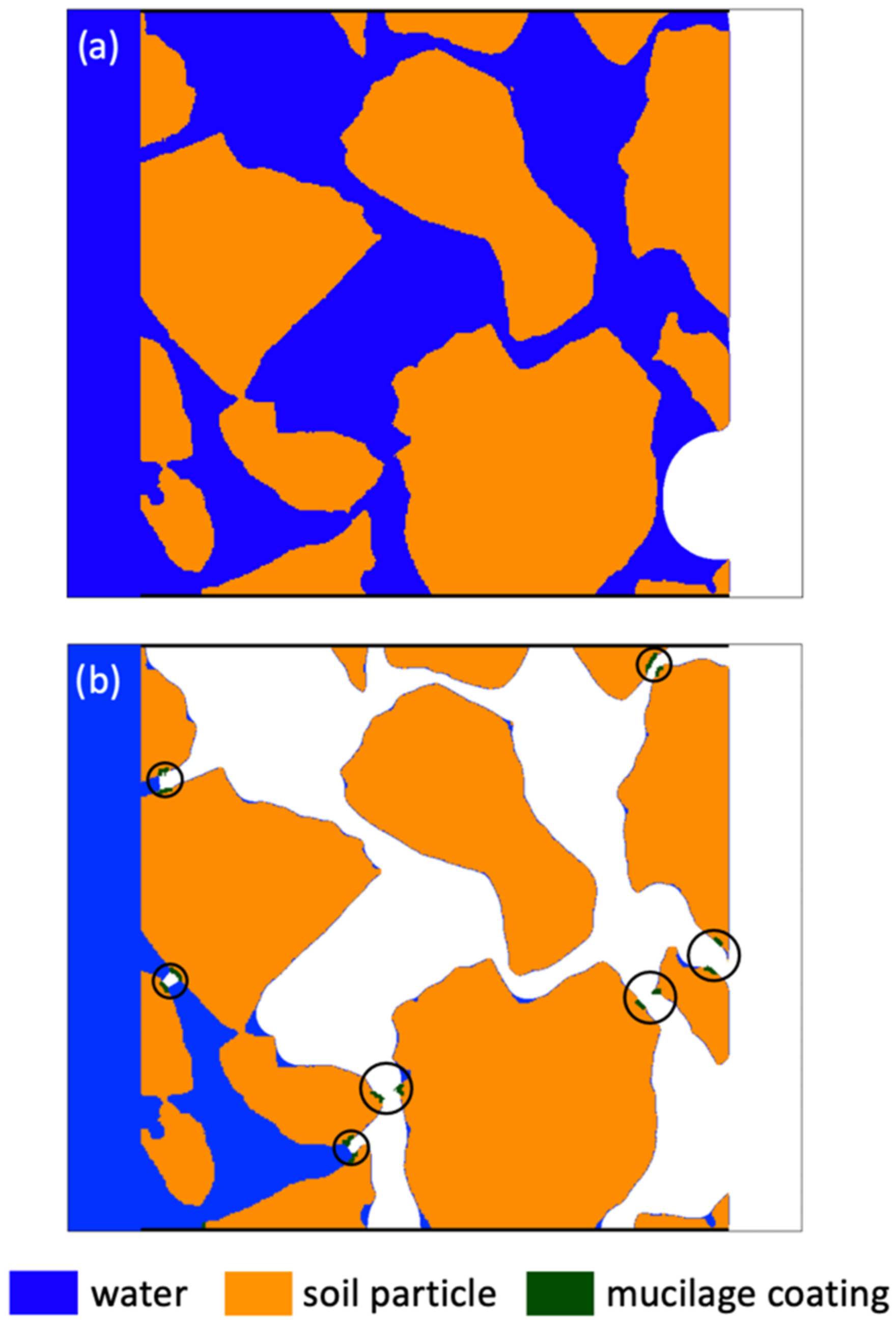
2.5. Infiltration into Soil
3. Results and Discussion
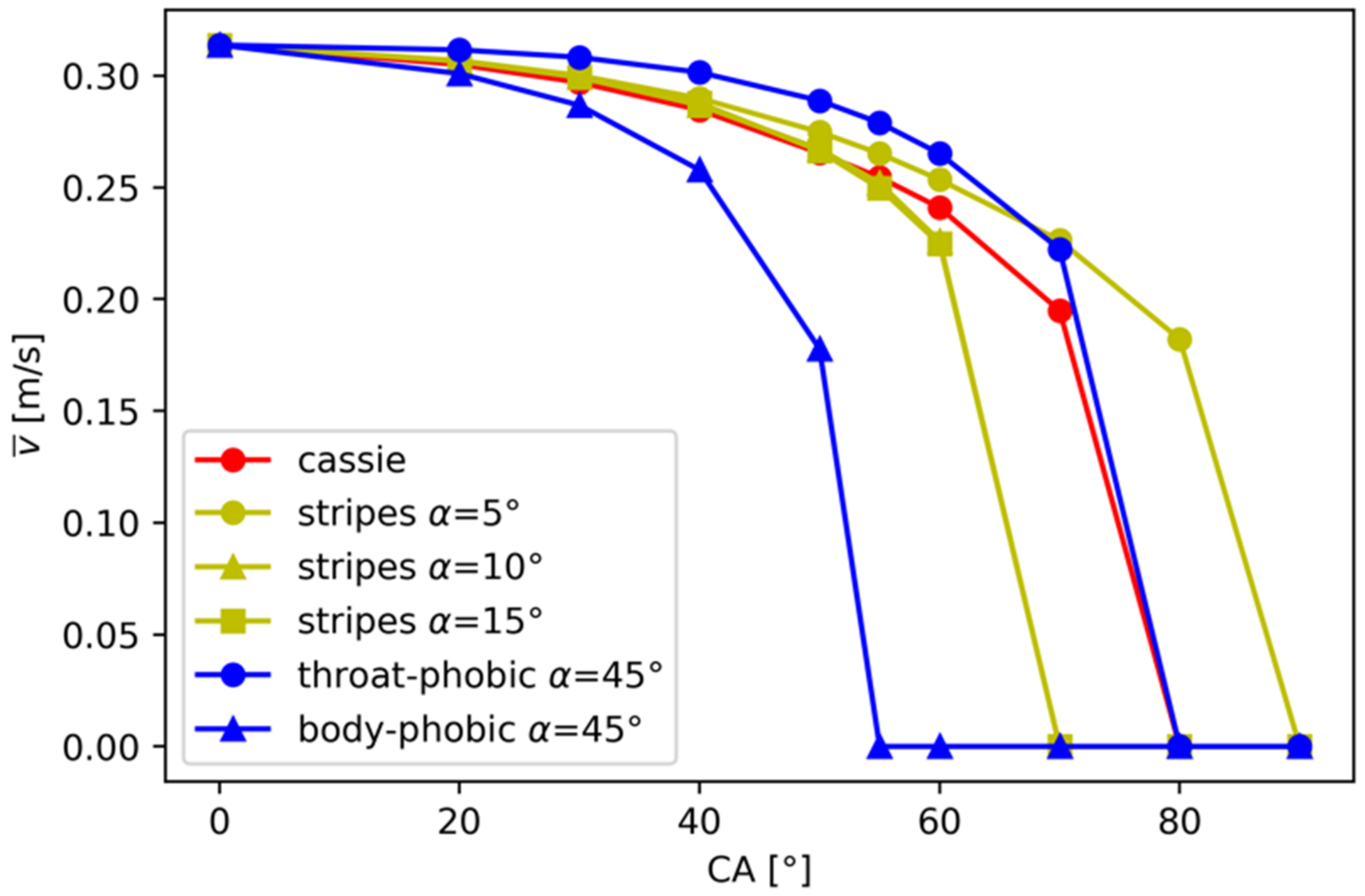
3.1. Dynamic: Simplified Porous System
3.1.1. Homogeneous Coating Pattern
3.1.2. Body-Throat Coating Patterns
3.1.3. Stripes Coating Pattern
3.1.4. Comparison with Cassie Equation
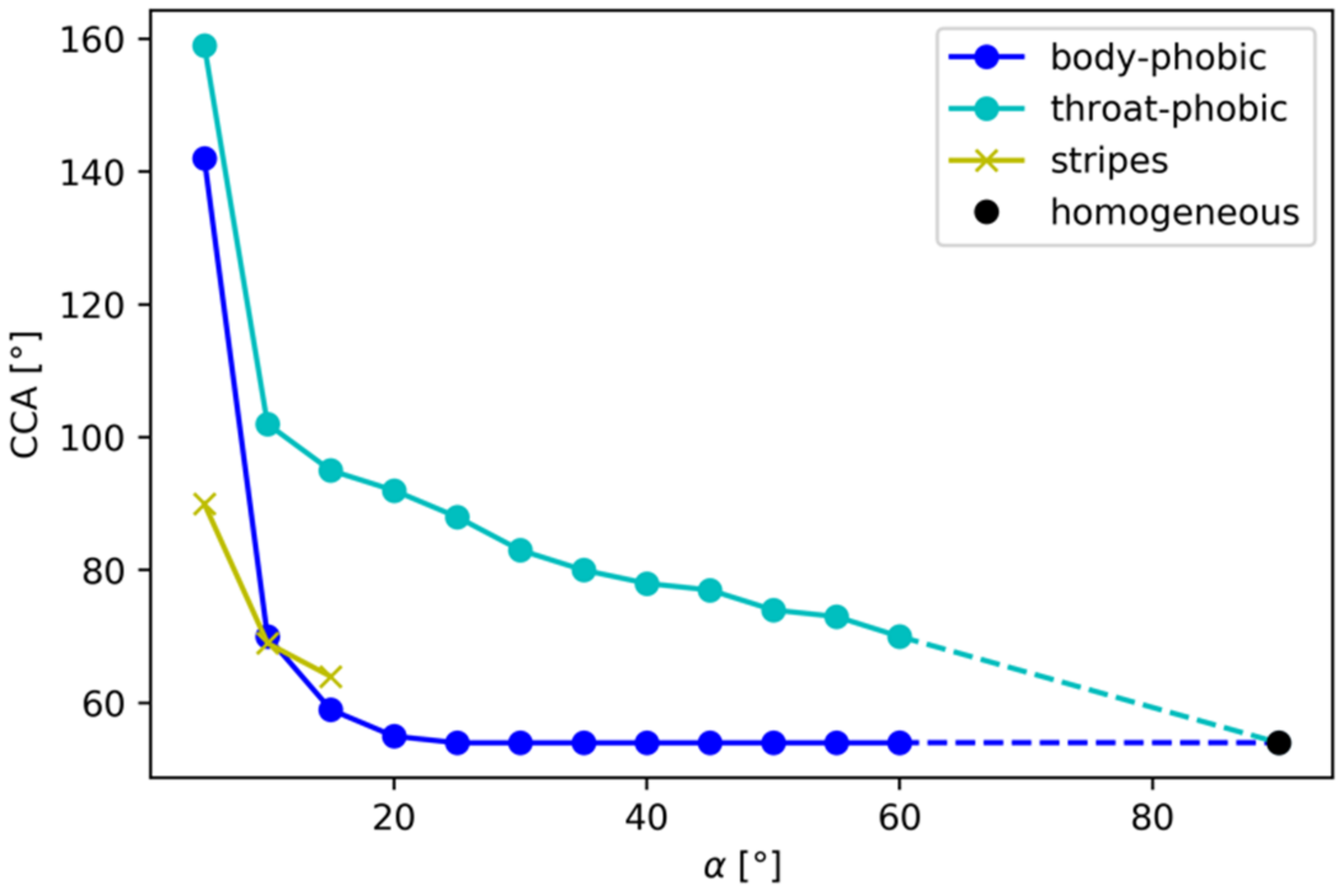
3.2. Critical Contact Angle (CCA)
3.3. Cassie Equation in Soil
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CA | contact angle |
| CCA | critical contact angle |
| CFD | computational fluid dynamics |
| LBM | Lattice Boltzmann Method |
| lu | length unit |
| mu | mass unit |
| SC | Shan-Chen |
| SEM | scanning electron microscope |
| SOM | soil organic matter |
| SRXTM | synchrotron-based X-ray tomographic microscopy |
| SWR | soil water repellency |
| ts | time steps |
| WB: | Washburn |
| Symbols: | |
| surface fraction | |
| grid spacing | |
| conversion factor of length | |
| conversion factors of mass | |
| conversion factors of time | |
| conversion factors of surface tension | |
| conversion factors of dynamic viscosity | |
| plate spacing or particle diameter | |
| discrete velocities along direction | |
| body force | |
| gravitational force | |
| interparticle force | |
| particle distribution function along direction | |
| equilibrium particle distribution function along direction | |
| interaction strength | |
| position of the contact line | |
| physical length | |
| error norm | |
| number of lattice nodes | |
| pressure | |
| correlation coefficient | |
| time | |
| macroscopic velocity | |
| infiltration front velocity | |
| weighting factor along direction | |
| penetration length | |
| penetration length of finest grid | |
| penetrated length after short system settling | |
| stripe width | |
| stripe width of the body of a body-phobic coating | |
| stripe width of the body of a body-phobic coating | |
| surface tension | |
| time step | |
| porosity | |
| dynamic viscosity | |
| kinematic viscosity | |
| macroscopic density | |
| constant of interaction potential function | |
| pseudo density of the wall | |
| effective total infiltration rate | |
| relaxation time | |
| contact angle | |
| effective contact angle | |
| interaction potential | |
| constant of interaction potential function | |
Appendix A. Unit Conversion

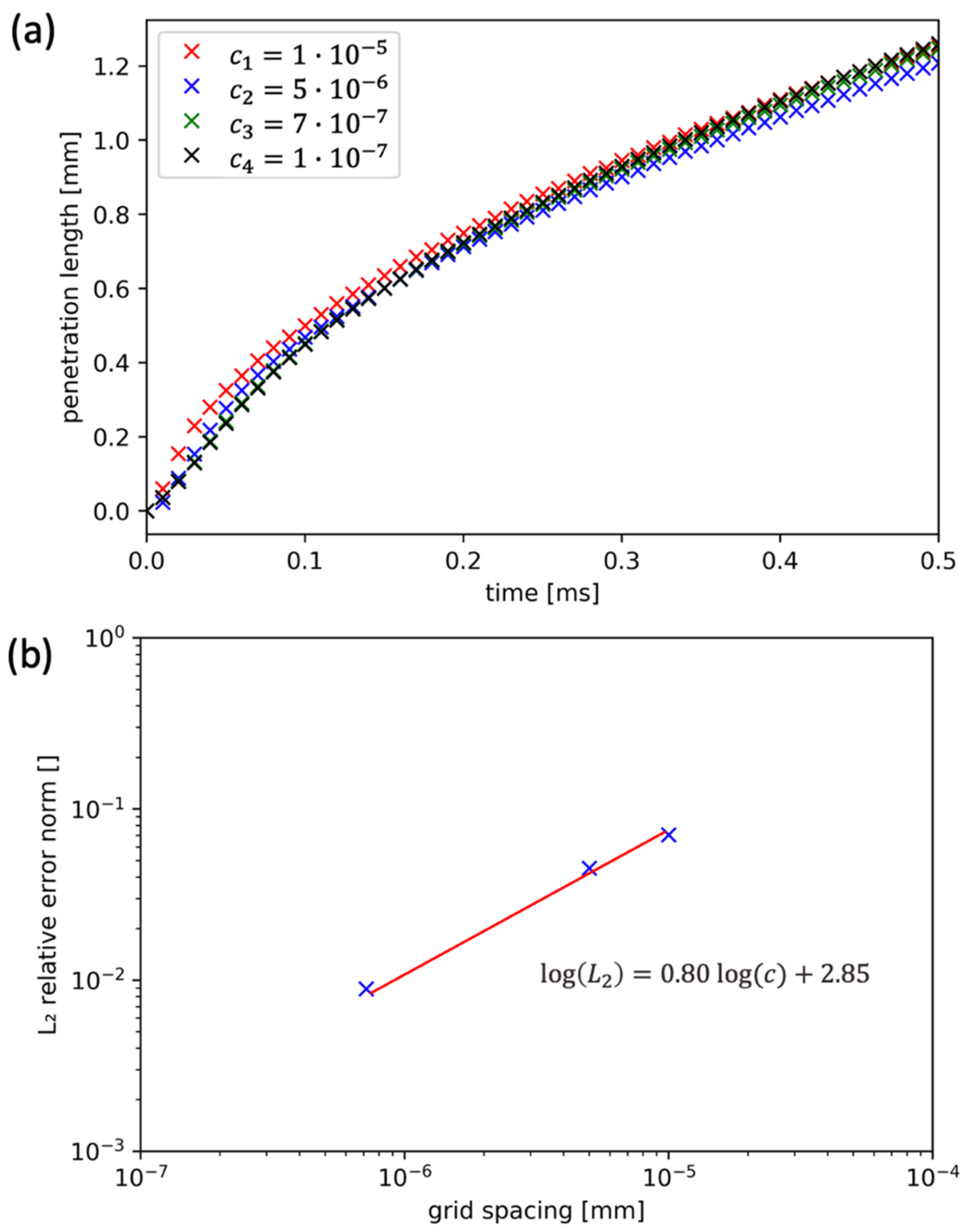
Appendix B. Grid Convergence
References
- Vereecken, H.; Schnepf, A.; Hopmans, J.W.; Javaux, M.; Or, D.; Roose, T.; Vanderborght, J.; Young, M.H.; Amelung, W.; Aitkenhead, M.; et al. Modeling Soil Processes: Review, Key Challenges, and New Perspectives. Vadose Zone J. 2016, 15, vzj2015.09.0131. [Google Scholar] [CrossRef] [Green Version]
- Vogel, H.-J.; Roth, K. Moving through Scales of Flow and Transport in Soil. J. Hydrol. 2003, 272, 95–106. [Google Scholar] [CrossRef]
- Doerr, S.H.; Shakesby, R.A.; Walsh, R.P.D. Soil Water Repellency: Its Causes, Characteristics and Hydro-Geomorphological Significance. Earth-Sci. Rev. 2000, 51, 33–65. [Google Scholar] [CrossRef]
- Young, T. III. An Essay on the Cohesion of Fluids. Philos. Trans. R. Soc. Lond. 1805, 95, 65–87. [Google Scholar] [CrossRef]
- Tschapek, M. Criteria for Determining the hydrophilicity-hydrophobicity of Soils. Z. Pflanz. Bodenkd. 1984, 147, 137–149. [Google Scholar] [CrossRef]
- Ma’Shum, M.; Tate, M.E.; Jones, G.P.; Oades, J.M. Extraction and Characterization of Water-Repellent Materials from Australian Soils. J. Soil Sci. 1988, 39, 99–110. [Google Scholar] [CrossRef]
- Woche, S.K.; Goebel, M.-O.; Mikutta, R.; Schurig, C.; Kaestner, M.; Guggenberger, G.; Bachmann, J. Soil Wettability Can Be Explained by the Chemical Composition of Particle Interfaces—An XPS Study. Sci. Rep. 2017, 7, 42877. [Google Scholar] [CrossRef]
- Cerdà, A.; Doerr, S.H. Soil Wettability, Runoff and Erodibility of Major Dry-Mediterranean Land Use Types on Calcareous Soils. Hydrol. Process. 2007, 21, 2325–2336. [Google Scholar] [CrossRef]
- Goebel, M.-O.; Bachmann, J.; Woche, S.K. Modified Technique to Assess the Wettability of Soil Aggregates: Comparison with Contact Angles Measured on Crushed Aggregates and Bulk Soil. Eur. J. Soil Sci. 2008, 59, 1241–1252. [Google Scholar] [CrossRef]
- Madsen, M.D.; Zvirzdin, D.L.; Petersen, S.L.; Hopkins, B.G.; Roundy, B.A.; Chandler, D.G. Soil Water Repellency within a Burned Piñon-Juniper Woodland: Spatial Distribution, Severity, and Ecohydrologic Implications. Soil Sci. Soc. Am. J. 2011, 75, 1543–1553. [Google Scholar] [CrossRef] [Green Version]
- Bachmann, J.; Goebel, M.-O.; Woche, S.K. Small-Scale Contact Angle Mapping on Undisturbed Soil Surfaces. J. Hydrol. Hydromech. 2013, 61, 3–8. [Google Scholar] [CrossRef] [Green Version]
- Kaltenbach, R.; Diehl, D.; Schaumann, G.E. Links between Nanoscale and Macroscale Surface Properties of Natural Root Mucilage Studied by Atomic Force Microscopy and Contact Angle. J. Colloid Interface Sci. 2018, 516, 446–455. [Google Scholar] [CrossRef]
- Gregory, P.J. Roots, Rhizosphere and Soil: The Route to a Better Understanding of Soil Science? Eur. J. Soil Sci. 2006, 57, 2–12. [Google Scholar] [CrossRef]
- Bais, H.P.; Weir, T.L.; Perry, L.G.; Gilroy, S.; Vivanco, J.M. The role of root exudates in rhizosphere interactions with plants and other organisms. Annu. Rev. Plant Biol. 2006, 57, 233–266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carminati, A.; Benard, P.; Ahmed, M.A.; Zarebanadkouki, M. Liquid Bridges at the Root-Soil Interface. Plant Soil 2017, 417, 1–15. [Google Scholar] [CrossRef]
- Hinsinger, P.; Bengough, A.G.; Vetterlein, D.; Young, I.M. Rhizosphere: Biophysics, Biogeochemistry and Ecological Relevance. Plant Soil 2009, 321, 117–152. [Google Scholar] [CrossRef]
- Whalley, W.R.; Riseley, B.; Leeds-Harrison, P.B.; Bird, N.R.A.; Leech, P.K.; Adderley, W.P. Structural Differences between Bulk and Rhizosphere Soil. Eur. J. Soil Sci. 2005, 56, 353–360. [Google Scholar] [CrossRef]
- Carminati, A.; Moradi, A.B.; Vetterlein, D.; Vontobel, P.; Lehmann, E.; Weller, U.; Vogel, H.-J.; Oswald, S.E. Dynamics of Soil Water Content in the Rhizosphere. Plant Soil 2010, 332, 163–176. [Google Scholar] [CrossRef]
- Kroener, E.; Holz, M.; Zarebanadkouki, M.; Ahmed, M.; Carminati, A. Effects of Mucilage on Rhizosphere Hydraulic Functions Depend on Soil Particle Size. Vadose Zone J. 2018, 17, 170056. [Google Scholar] [CrossRef] [Green Version]
- Kroener, E.; Zarebanadkouki, M.; Kaestner, A.; Carminati, A. Nonequilibrium Water Dynamics in the Rhizosphere: How Mucilage Affects Water Flow in Soils. Water Resour. Res. 2014, 50, 6479–6495. [Google Scholar] [CrossRef] [Green Version]
- Muñoz, L.A.; Cobos, A.; Diaz, O.; Aguilera, J.M. Chia Seeds: Microstructure, Mucilage Extraction and Hydration. J. Food Eng. 2012, 108, 216–224. [Google Scholar] [CrossRef]
- Read, D.B.; Gregory, P.J.; Bell, A.E. Physical Properties of Axenic Maize Root Mucilage. Plant Soil 1999, 211, 87–91. [Google Scholar] [CrossRef]
- Ahmed, M.A.; Kroener, E.; Benard, P.; Zarebanadkouki, M.; Kaestner, A.; Carminati, A. Drying of Mucilage Causes Water Repellency in the Rhizosphere of Maize: Measurements and Modelling. Plant Soil 2016, 407, 161–171. [Google Scholar] [CrossRef]
- Moradi, A.B.; Carminati, A.; Lamparter, A.; Woche, S.K.; Bachmann, J.; Vetterlein, D.; Vogel, H.-J.; Oswald, S.E. Is the Rhizosphere Temporarily Water Repellent? Vadose Zone J. 2012, 11, vzj2011.0120. [Google Scholar] [CrossRef]
- Benard, P.; Zarebanadkouki, M.; Brax, M.; Kaltenbach, R.; Jerjen, I.; Marone, F.; Couradeau, E.; Felde, V.J.M.N.L.; Kaestner, A.; Carminati, A. Microhydrological Niches in Soils: How Mucilage and EPS Alter the Biophysical Properties of the Rhizosphere and Other Biological Hotspots. Vadose Zone J. 2019, 18, 180211. [Google Scholar] [CrossRef] [Green Version]
- Benard, P.; Zarebanadkouki, M.; Hedwig, C.; Holz, M.; Ahmed, M.A.; Carminati, A. Pore-Scale Distribution of Mucilage Affecting Water Repellency in the Rhizosphere. Vadose Zone J. 2018, 17, 170013. [Google Scholar] [CrossRef] [Green Version]
- Ahrenholz, B.; Tölke, J.; Lehmann, P.; Peters, A.; Kaestner, A.; Krafczyk, M.; Durner, W. Prediction of Capillary Hysteresis in a Porous Material Using Lattice-Boltzmann Methods and Comparison to Experimental Data and a Morphological Pore Network Model. Adv. Water Resour. 2008, 31, 1151–1173. [Google Scholar] [CrossRef]
- Garg, A.; Garg, A.; Tai, K.; Barontini, S.; Stokes, A. A Computational Intelligence-Based Genetic Programming Approach for the Simulation of Soil Water Retention Curves. Transp. Porous Media 2014, 103, 497–513. [Google Scholar] [CrossRef]
- Daly, K.R.; Mooney, S.J.; Bennett, M.J.; Crout, N.M.J.; Roose, T.; Tracy, S.R. Assessing the Influence of the Rhizosphere on Soil Hydraulic Properties Using X-ray Computed Tomography and Numerical Modelling. J. Exp. Bot. 2015, 66, 2305–2314. [Google Scholar] [CrossRef] [Green Version]
- Baveye, P.C.; Otten, W.; Kravchenko, A.; Balseiro-Romero, M.; Beckers, É.; Chalhoub, M.; Darnault, C.; Eickhorst, T.; Garnier, P.; Hapca, S.; et al. Emergent Properties of Microbial Activity in Heterogeneous Soil Microenvironments: Different Research Approaches Are Slowly Converging, Yet Major Challenges Remain. Front. Microbiol. 2018, 9, 1929. [Google Scholar] [CrossRef] [PubMed]
- Portell, X.; Pot, V.; Garnier, P.; Otten, W.; Baveye, P.C. Microscale Heterogeneity of the Spatial Distribution of Organic Matter Can Promote Bacterial Biodiversity in Soils: Insights from Computer Simulations. Front. Microbiol. 2018, 9, 1583. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deurer, M.; Bachmann, J. Modeling Water Movement in Heterogeneous Water-Repellent Soil: 2. A Conceptual Numerical Simulation. Vadose Zone J. 2007, 6, 446–457. [Google Scholar] [CrossRef]
- Jafari, I.; Masihi, M.; Nasiri Zarandi, M. Numerical Simulation of Counter-Current Spontaneous Imbibition in Water-Wet Fractured Porous Media: Influences of Water Injection Velocity, Fracture Aperture, and Grains Geometry. Phys. Fluids 2017, 29, 113305. [Google Scholar] [CrossRef]
- Aljasmi, A.; Sahimi, M. Speeding-up Image-Based Simulation of Two-Phase Flow in Porous Media with Lattice-Boltzmann Method Using Three-Dimensional Curvelet Transforms. Phys. Fluids 2021, 33, 113313. [Google Scholar] [CrossRef]
- Lin, W.; Xiong, S.; Liu, Y.; He, Y.; Chu, S.; Liu, S. Spontaneous Imbibition in Tight Porous Media with Different Wettability: Pore-Scale Simulation. Phys. Fluids 2021, 33, 032013. [Google Scholar] [CrossRef]
- Seta, T.; Takegoshi, E.; Okui, K. Lattice Boltzmann Simulation of Natural Convection in Porous Media. Math. Comput. Simul. 2006, 72, 195–200. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, T.S. Lattice Boltzmann Model for Incompressible Flows through Porous Media. Phys. Rev. E 2002, 66, 036304. [Google Scholar] [CrossRef]
- Abouei Mehrizi, A.; Farhadi, M.; Sedighi, K.; Latif Aghili, A. Lattice Boltzmann Simulation of Heat Transfer Enhancement in a Cold Plate Using Porous Medium. J. Heat Transf. 2013, 135, 111006. [Google Scholar] [CrossRef]
- Cruz, B.C.; Furrer, J.M.; Guo, Y.-S.; Dougherty, D.; Hinestroza, H.F.; Hernandez, J.S.; Gage, D.J.; Cho, Y.K.; Shor, L.M. Pore-Scale Water Dynamics during Drying and the Impacts of Structure and Surface Wettability: Pore-scale water dynamics during drying. Water Resour. Res. 2017, 53, 5585–5600. [Google Scholar] [CrossRef]
- Li, Y.; LeBoeuf, E.J.; Basu, P.K.; Mahadevan, S. Stochastic Modeling of the Permeability of Randomly Generated Porous Media. Adv. Water Resour. 2005, 28, 835–844. [Google Scholar] [CrossRef] [Green Version]
- Sukop, M.C.; Or, D. Invasion Percolation of Single Component, Multiphase Fluids with Lattice Boltzmann Models. Phys. B Condens. Matter 2003, 338, 298–303. [Google Scholar] [CrossRef]
- Grunau, D.; Chen, S.; Eggert, K. A Lattice Boltzmann Model for Multiphase Fluid Flows. Phys. Fluids Fluid Dyn. 1993, 5, 2557–2562. [Google Scholar] [CrossRef] [Green Version]
- Shan, X.; Chen, H. Simulation of Nonideal Gases and Liquid-Gas Phase Transitions by the Lattice Boltzmann Equation. Phys. Rev. E 1994, 49, 2941–2948. [Google Scholar] [CrossRef] [Green Version]
- Shan, X.; Chen, H. Lattice Boltzmann Model for Simulating Flows with Multiple Phases and Components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef] [Green Version]
- Swift, M.R.; Orlandini, E.; Osborn, W.R.; Yeomans, J.M. Lattice Boltzmann Simulations of Liquid-Gas and Binary Fluid Systems. Phys. Rev. E 1996, 54, 5041–5052. [Google Scholar] [CrossRef]
- Swift, M.R.; Osborn, W.R.; Yeomans, J.M. Lattice Boltzmann Simulation of Nonideal Fluids. Phys. Rev. Lett. 1995, 75, 830–833. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Sukop, M.C.; Lu, X.-Y. Multiphase Lattice Boltzmann Methods: Theory and Application; John Wiley and Sons, Inc.: Chichester, UK, 2015; ISBN 978-1-118-97133-8. [Google Scholar]
- Li, Q.; Luo, K.H.; Kang, Q.J.; He, Y.L.; Chen, Q.; Liu, Q. Lattice Boltzmann Methods for Multiphase Flow and Phase-Change Heat Transfer. Prog. Energy Combust. Sci. 2016, 52, 62–105. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Kang, Q.; Mu, Y.; He, Y.-L.; Tao, W.-Q. A Critical Review of the Pseudopotential Multiphase Lattice Boltzmann Model: Methods and Applications. Int. J. Heat Mass Transf. 2014, 76, 210–236. [Google Scholar] [CrossRef]
- Son, S.; Chen, L.; Kang, Q.; Derome, D.; Carmeliet, J. Contact Angle Effects on Pore and Corner Arc Menisci in Polygonal Capillary Tubes Studied with the Pseudopotential Multiphase Lattice Boltzmann Model. Computation 2016, 4, 12. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Ju, Y.; Wang, M. Pore-Scale Modeling of Spontaneous Imbibition Behavior in a Complex Shale Porous Structure by Pseudopotential Lattice Boltzmann Method. J. Geophys. Res. Solid Earth 2018, 123, 9586–9600. [Google Scholar] [CrossRef]
- Liu, H.; Kang, Q.; Leonardi, C.R.; Schmieschek, S.; Narváez, A.; Jones, B.D.; Williams, J.R.; Valocchi, A.J.; Harting, J. Multiphase Lattice Boltzmann Simulations for Porous Media Applications: A Review. Comput. Geosci. 2016, 20, 777–805. [Google Scholar] [CrossRef] [Green Version]
- Akai, T.; Alhammadi, A.M.; Blunt, M.J.; Bijeljic, B. Modeling Oil Recovery in Mixed-Wet Rocks: Pore-Scale Comparison between Experiment and Simulation. Transp. Porous Media 2019, 127, 393–414. [Google Scholar] [CrossRef] [Green Version]
- Guo, R.; Dalton, L.E.; Fan, M.; McClure, J.; Zeng, L.; Crandall, D.; Chen, C. The Role of the Spatial Heterogeneity and Correlation Length of Surface Wettability on Two-Phase Flow in a CO2-Water-Rock System. Adv. Water Resour. 2020, 146, 103763. [Google Scholar] [CrossRef]
- Cooper, L.J.; Daly, K.R.; Hallett, P.D.; Naveed, M.; Koebernick, N.; Bengough, A.G.; George, T.S.; Roose, T. Fluid Flow in Porous Media Using Image-Based Modelling to Parametrize Richards’ Equation. Proc. R. Soc. Math. Phys. Eng. Sci. 2017, 473, 20170178. [Google Scholar] [CrossRef] [Green Version]
- Czachor, H. Modelling the Effect of Pore Structure and Wetting Angles on Capillary Rise in Soils Having Different Wettabilities. J. Hydrol. 2006, 328, 604–613. [Google Scholar] [CrossRef]
- Murison, J.; Semin, B.; Baret, J.-C.; Herminghaus, S.; Schröter, M.; Brinkmann, M. Wetting Heterogeneities in Porous Media Control Flow Dissipation. Phys. Rev. Appl. 2014, 2, 034002. [Google Scholar] [CrossRef] [Green Version]
- Benard, P.; Kroener, E.; Vontobel, P.; Kaestner, A.; Carminati, A. Water Percolation through the Root-Soil Interface. Adv. Water Resour. 2016, 95, 190–198. [Google Scholar] [CrossRef]
- Cassie, A.B.D. Contact Angles. Discuss. Faraday Soc. 1948, 3, 11–16. [Google Scholar] [CrossRef]
- Patel, R.A. Yantra. Available online: https://bitbucket.org/yantralbm/yantra (accessed on 1 January 2022).
- Patel, R.A. Lattice Boltzmann Method Based Framework for Simulating Physico-Chemical Processes in Heterogeneous Porous Media and Its Application to Cement Paste. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2016. [Google Scholar]
- Sukop, M.C.; Or, D. Lattice Boltzmann Method for Modeling Liquid-Vapor Interface Configurations in Porous Media: Lattice Boltzmann for Interface Configurations. Water Resour. Res. 2004, 40, W01509. [Google Scholar] [CrossRef]
- Sukop, M.C.; Thorne, D.T. Lattice Boltzmann Modeling: An Introduction for Geoscientists and Engineers; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2006; ISBN 978-3-540-27981-5. [Google Scholar]
- Wen, B.; Huang, B.; Qin, Z.; Wang, C.; Zhang, C. Contact Angle Measurement in Lattice Boltzmann Method. Comput. Math. Appl. 2018, 76, 1686–1698. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Valocchi, A.J.; Kang, Q.; Werth, C. Pore-Scale Simulations of Gas Displacing Liquid in a Homogeneous Pore Network Using the Lattice Boltzmann Method. Transp. Porous Media 2013, 99, 555–580. [Google Scholar] [CrossRef]
- Diotallevi, F.; Biferale, L.; Chibbaro, S.; Lamura, A.; Pontrelli, G.; Sbragaglia, M.; Succi, S.; Toschi, F. Capillary Filling Using Lattice Boltzmann Equations: The Case of Multi-Phase Flows. Eur. Phys. J. Spec. Top. 2009, 166, 111–116. [Google Scholar] [CrossRef]
- Pooley, C.M.; Kusumaatmaja, H.; Yeomans, J.M. Modelling Capillary Filling Dynamics Using Lattice Boltzmann Simulations. Eur. Phys. J. Spec. Top. 2009, 171, 63–71. [Google Scholar] [CrossRef]
- Lu, G.; Wang, X.-D.; Duan, Y.-Y. Study on Initial Stage of Capillary Rise Dynamics. Colloids Surf. Physicochem. Eng. Asp. 2013, 433, 95–103. [Google Scholar] [CrossRef]
- Sun, C.; McClure, J.E.; Mostaghimi, P.; Herring, A.L.; Berg, S.; Armstrong, R.T. Probing Effective Wetting in Subsurface Systems. Geophys. Res. Lett. 2020, 47, e2019GL086151. [Google Scholar] [CrossRef]
- McHale, G.; Newton, M.I.; Shirtcliffe, N.J. Water-Repellent Soil and Its Relationship to Granularity, Surface Roughness and Hydrophobicity: A Materials Science View. Eur. J. Soil Sci. 2005, 56, 445–452. [Google Scholar] [CrossRef] [Green Version]
- Carmeliet, J.; Chen, L.; Kang, Q.; Derome, D. Beyond-Cassie Mode of Wetting and Local Contact Angles of Droplets on Checkboard-Patterned Surfaces. Langmuir 2017, 33, 6192–6200. [Google Scholar] [CrossRef]
- Zhang, B.; Wang, J.; Liu, Z.; Zhang, X. Beyond Cassie Equation: Local Structure of Heterogeneous Surfaces Determines the Contact Angles of Microdroplets. Sci. Rep. 2015, 4, 5822. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Ju, Z.; Bachmann, J.; Horton, R.; Ren, T. Moisture-Dependent Wettability of Artificial Hydrophobic Soils and Its Relevance for Soil Water Desorption Curves. Soil Sci. Soc. Am. J. 2012, 76, 342–349. [Google Scholar] [CrossRef]
- Landl, M.; Phalempin, M.; Schlüter, S.; Vetterlein, D.; Vanderborght, J.; Kroener, E.; Schnepf, A. Modeling the Impact of Rhizosphere Bulk Density and Mucilage Gradients on Root Water Uptake. Front. Agron. 2021, 3, 622367. [Google Scholar] [CrossRef]



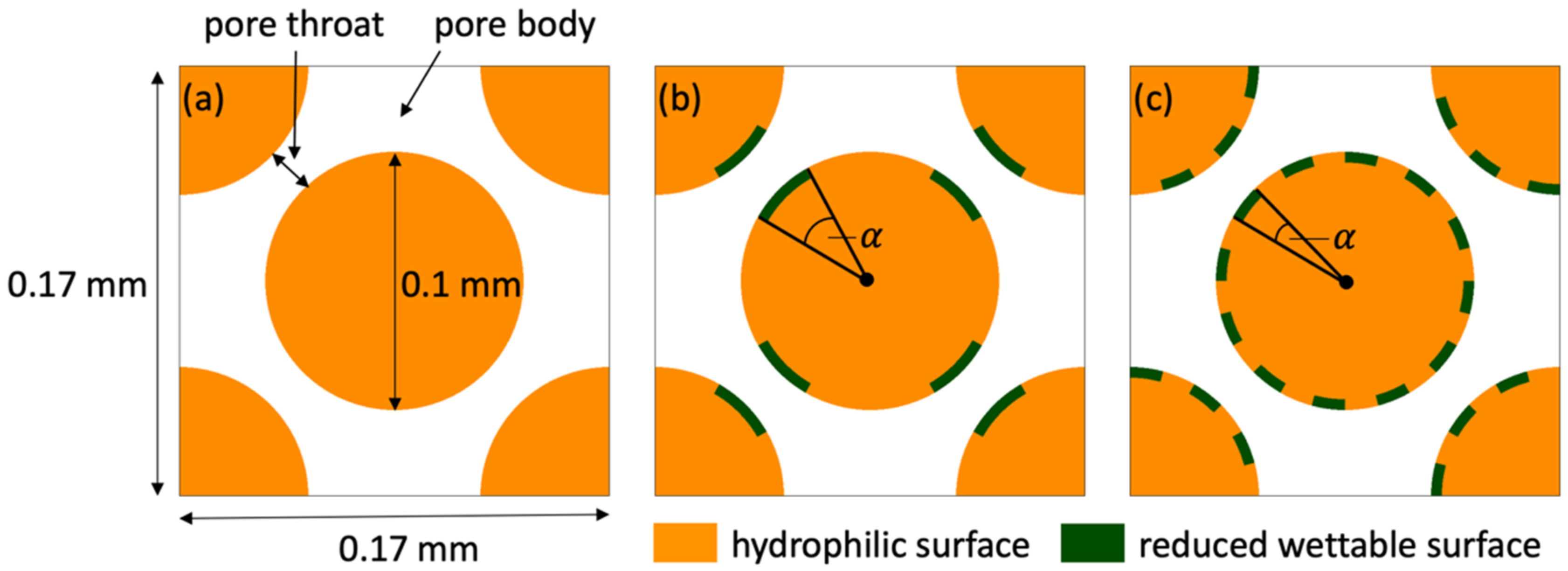
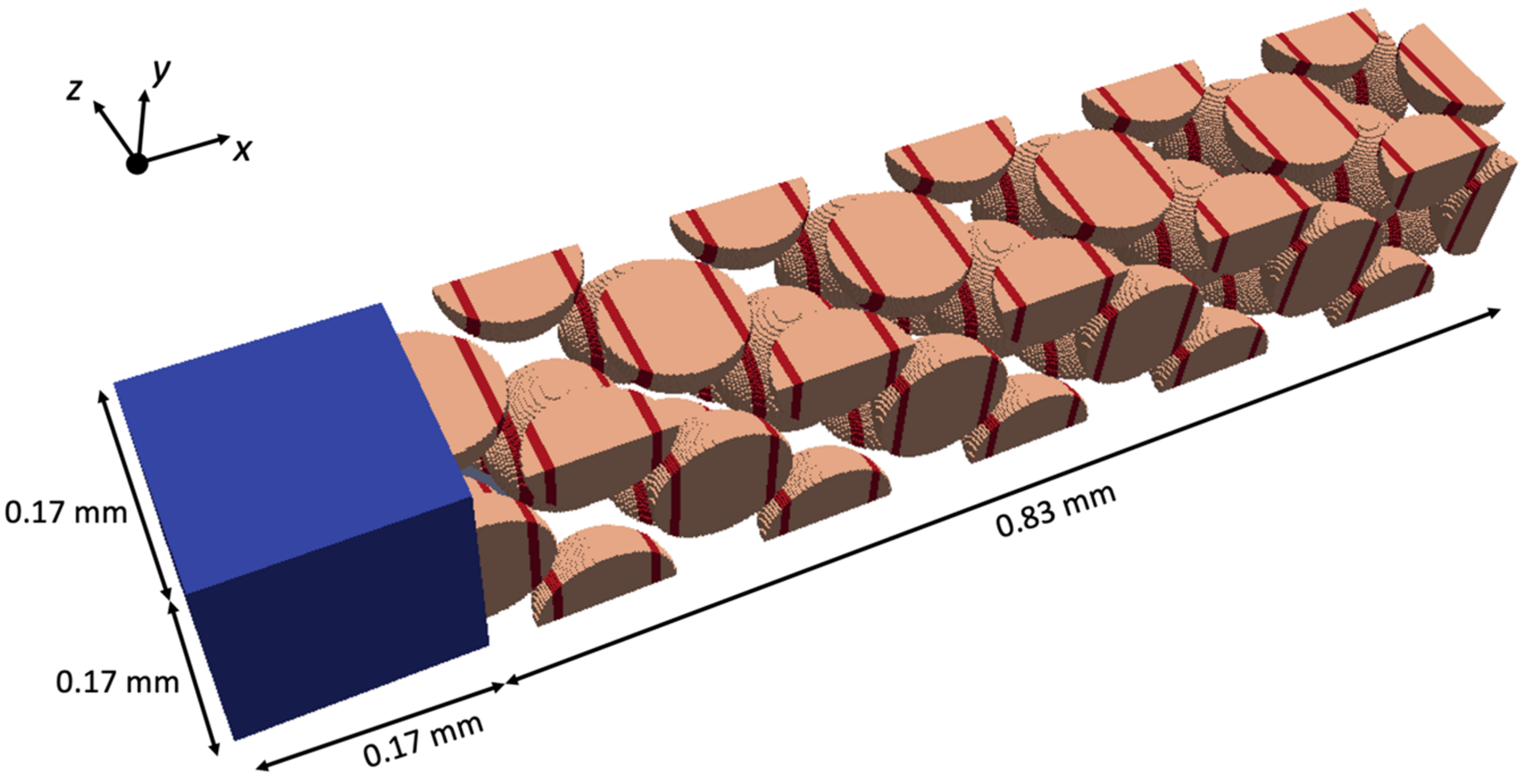
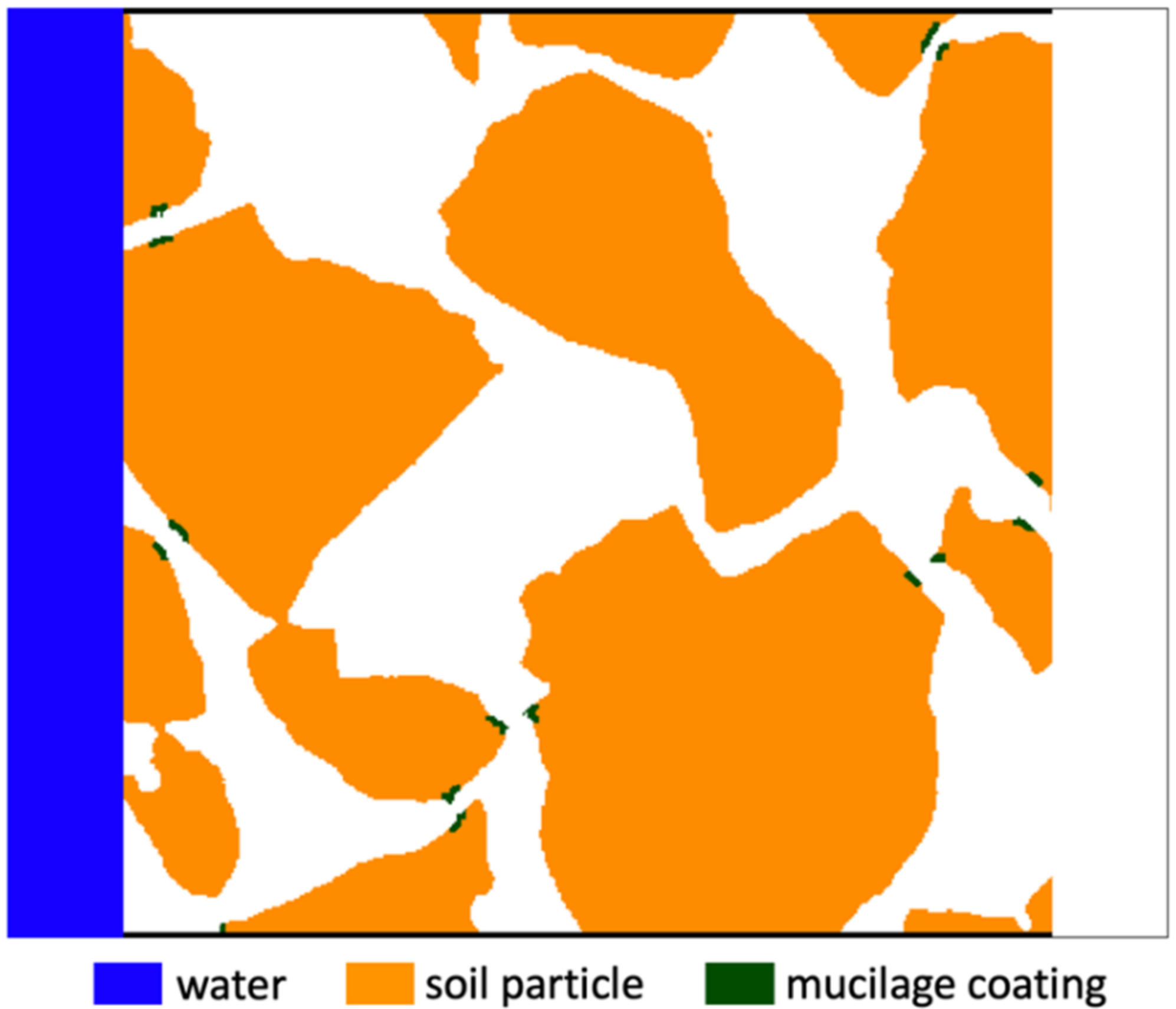
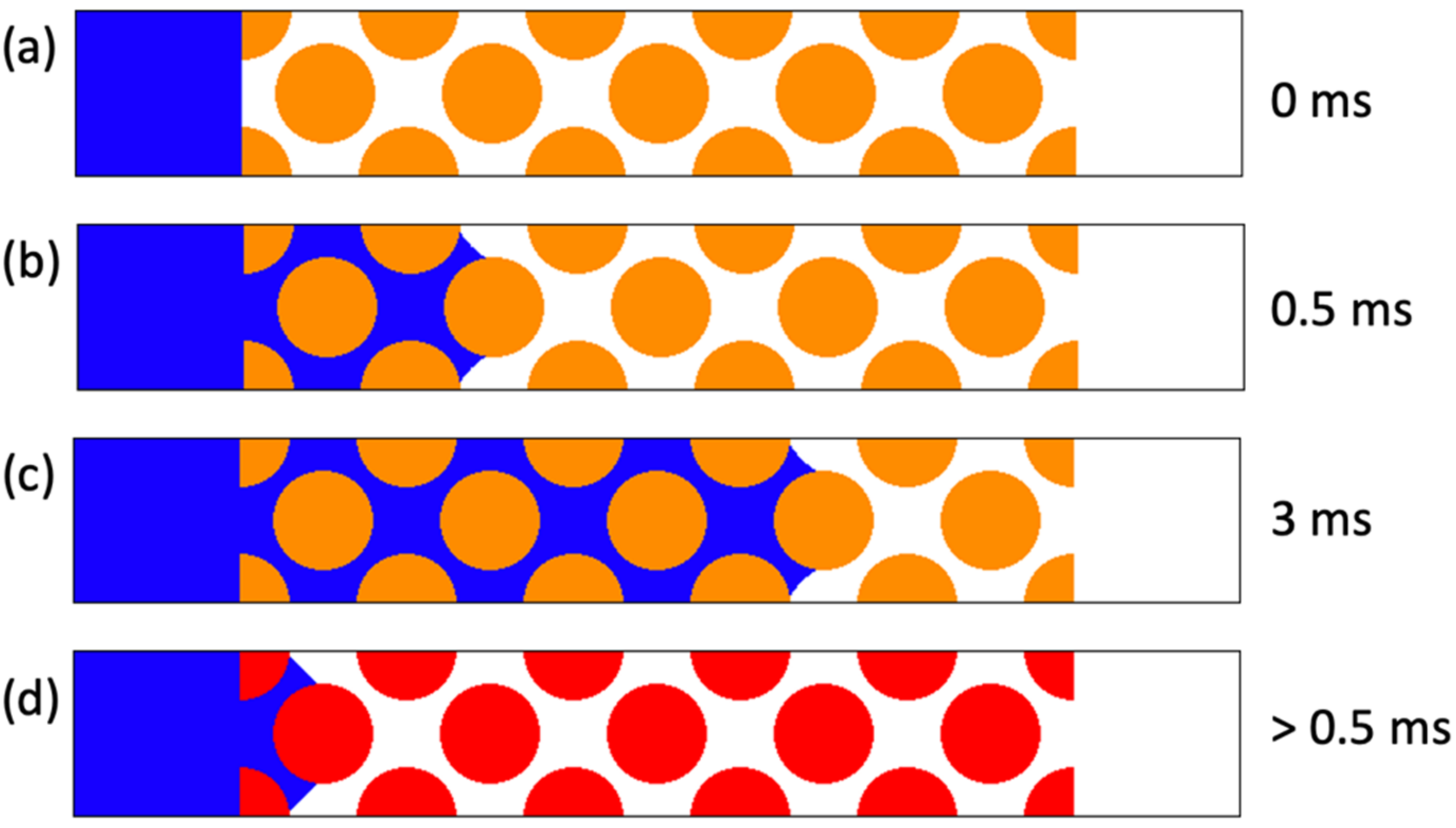
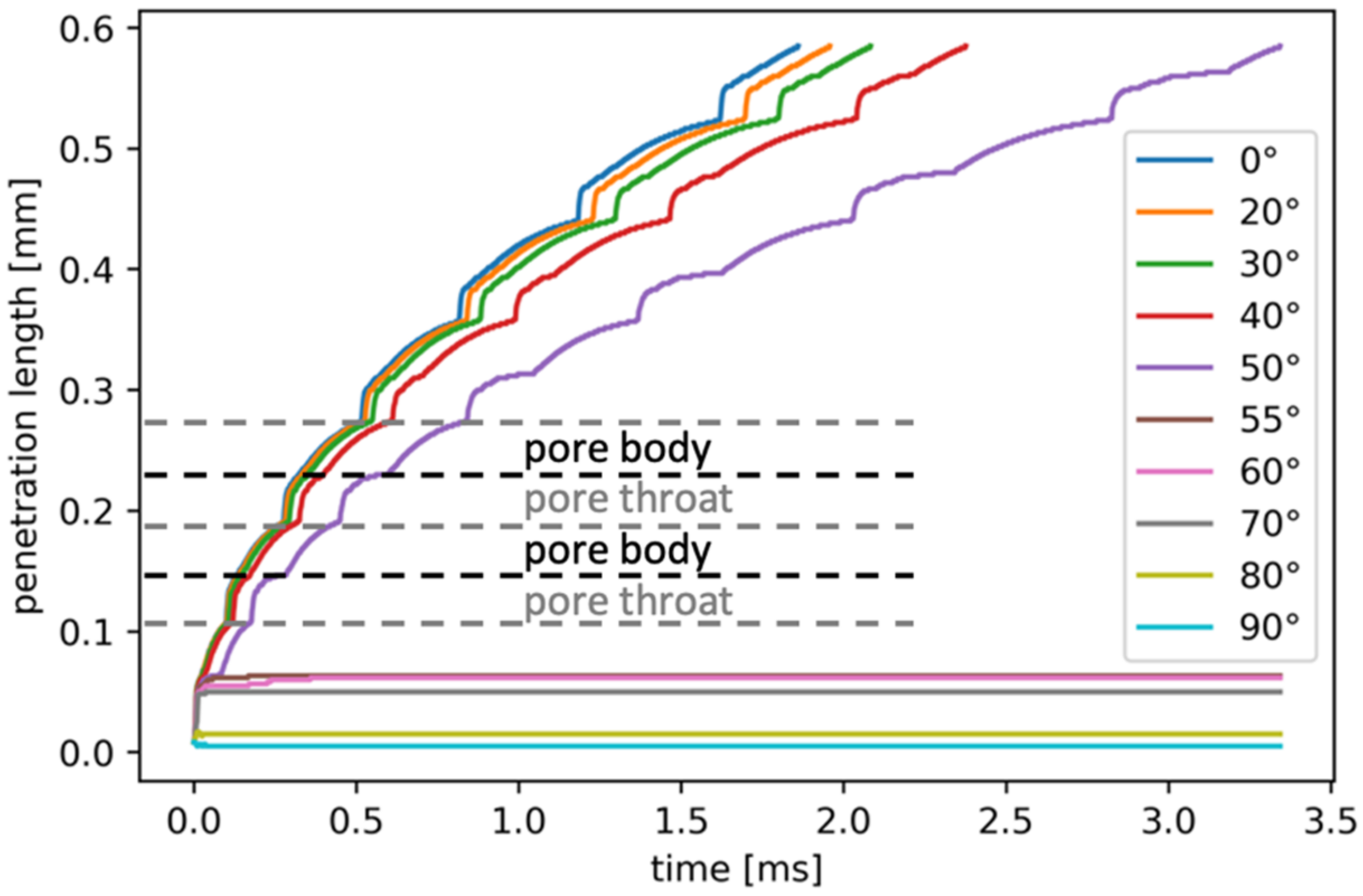
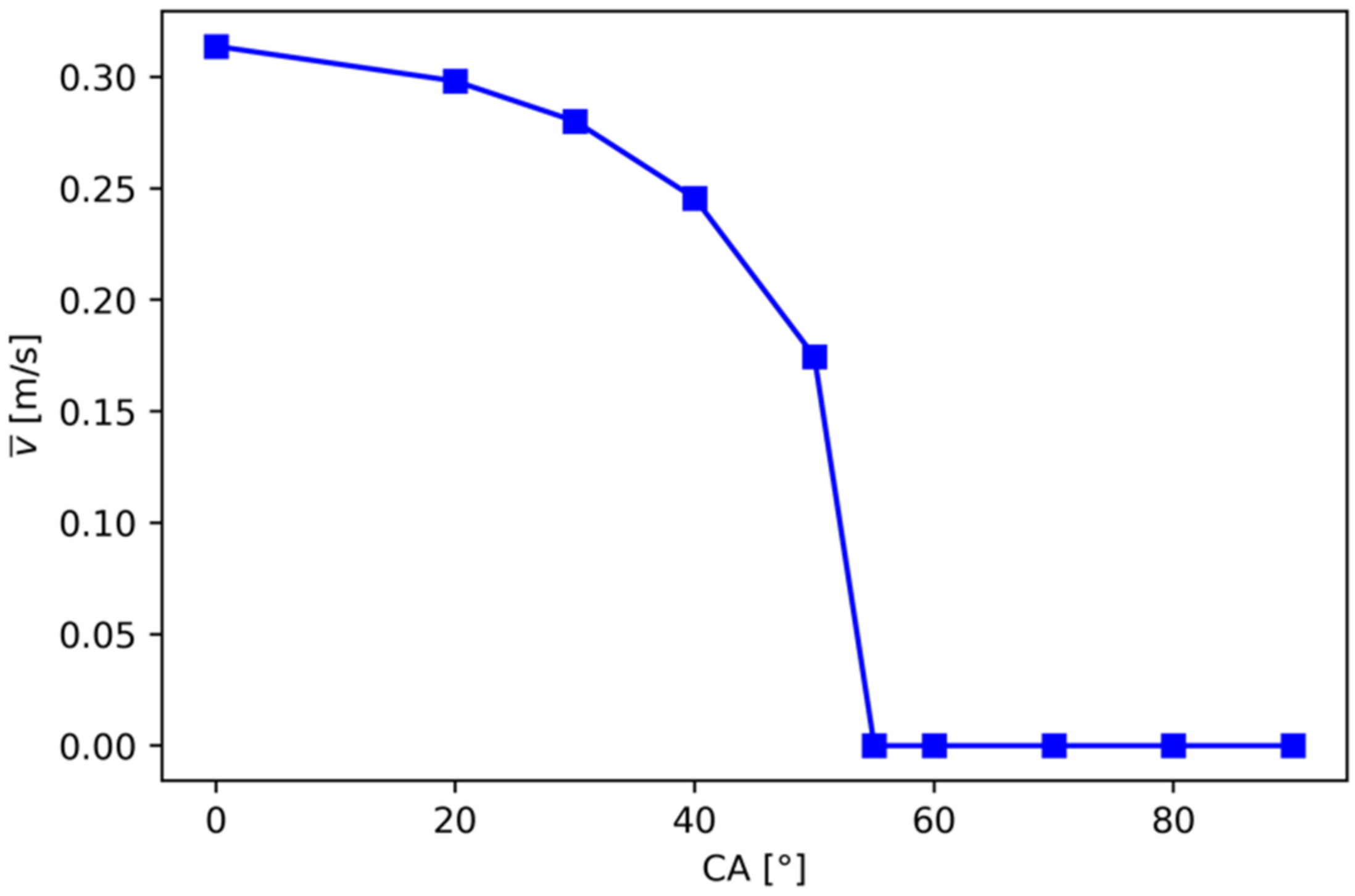
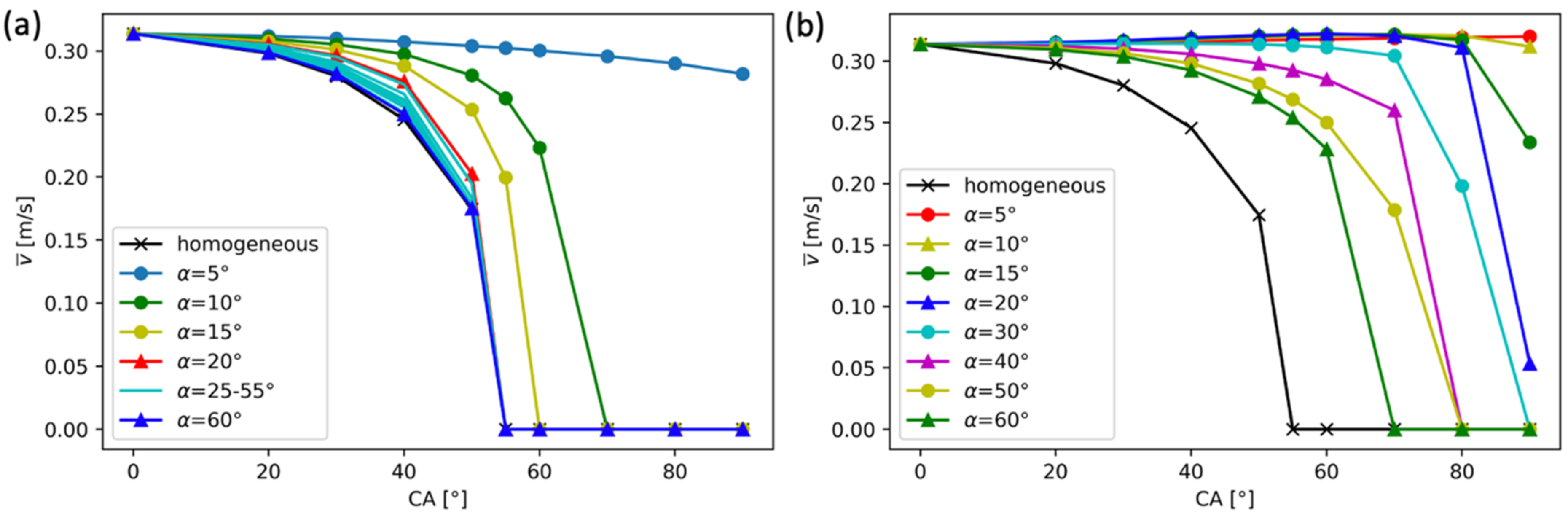
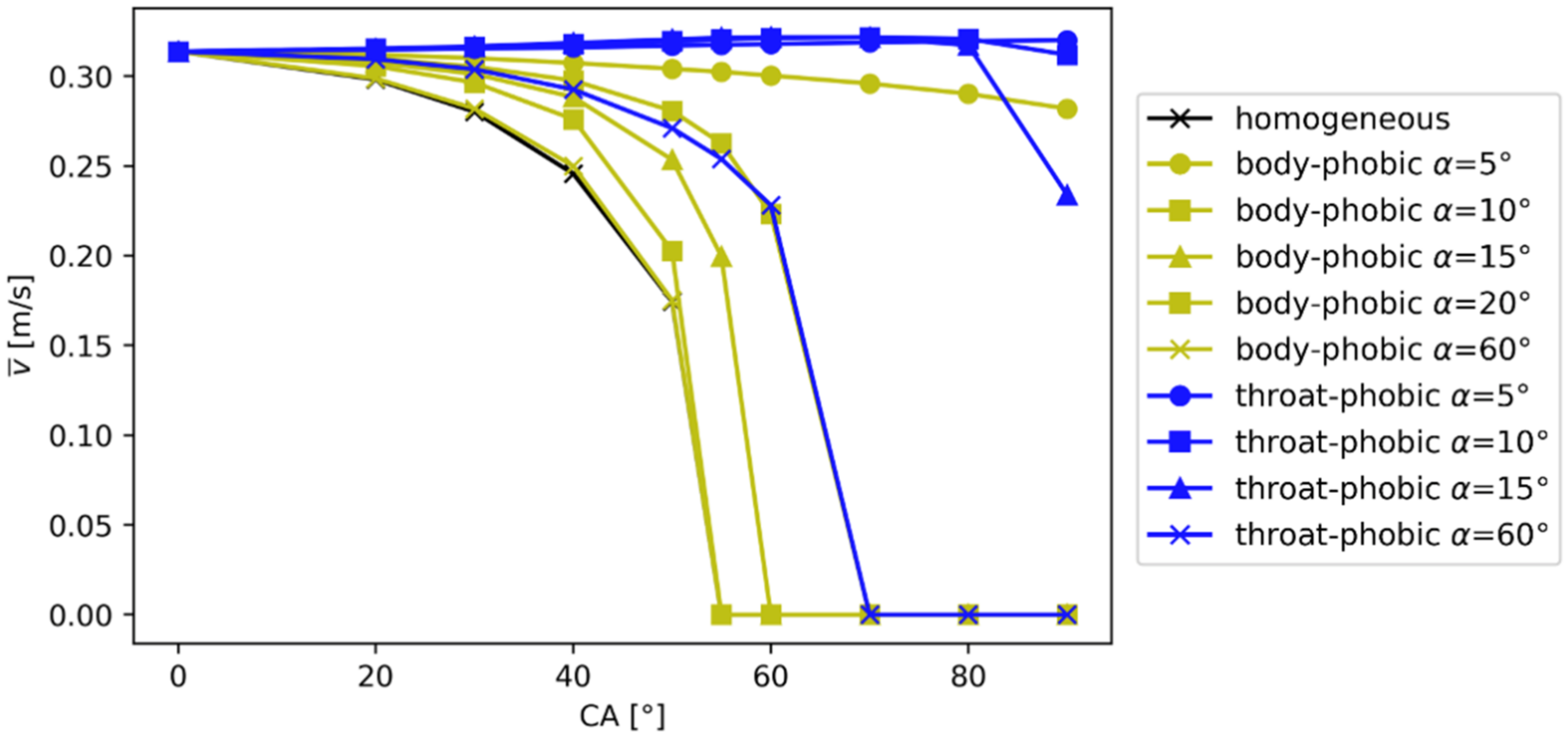


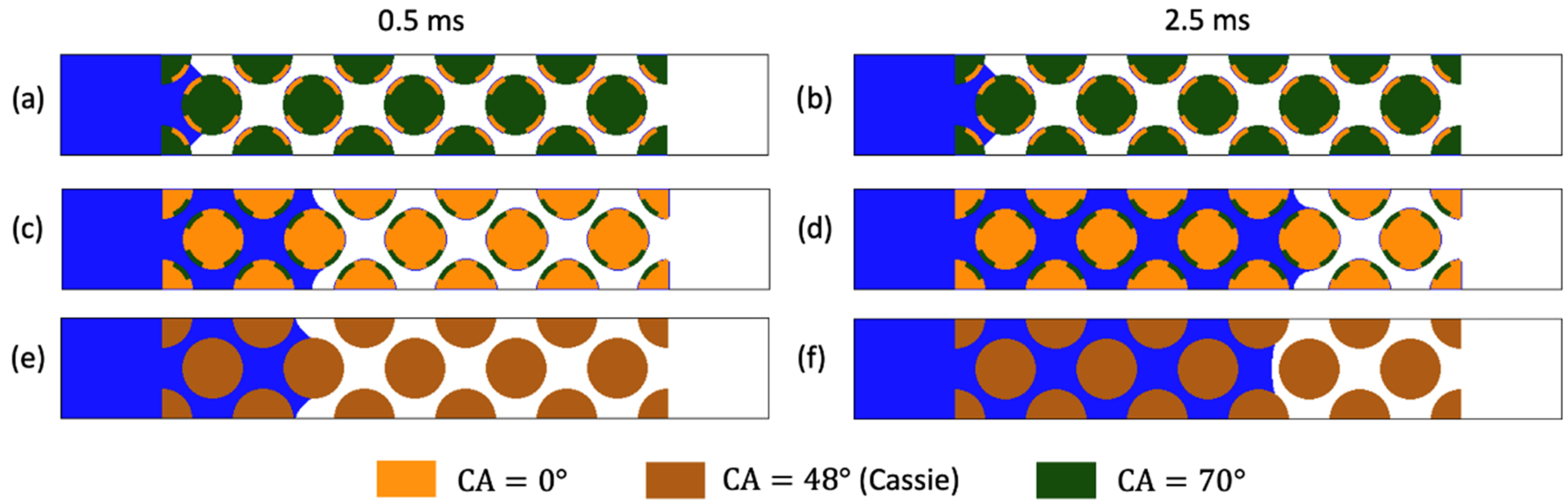
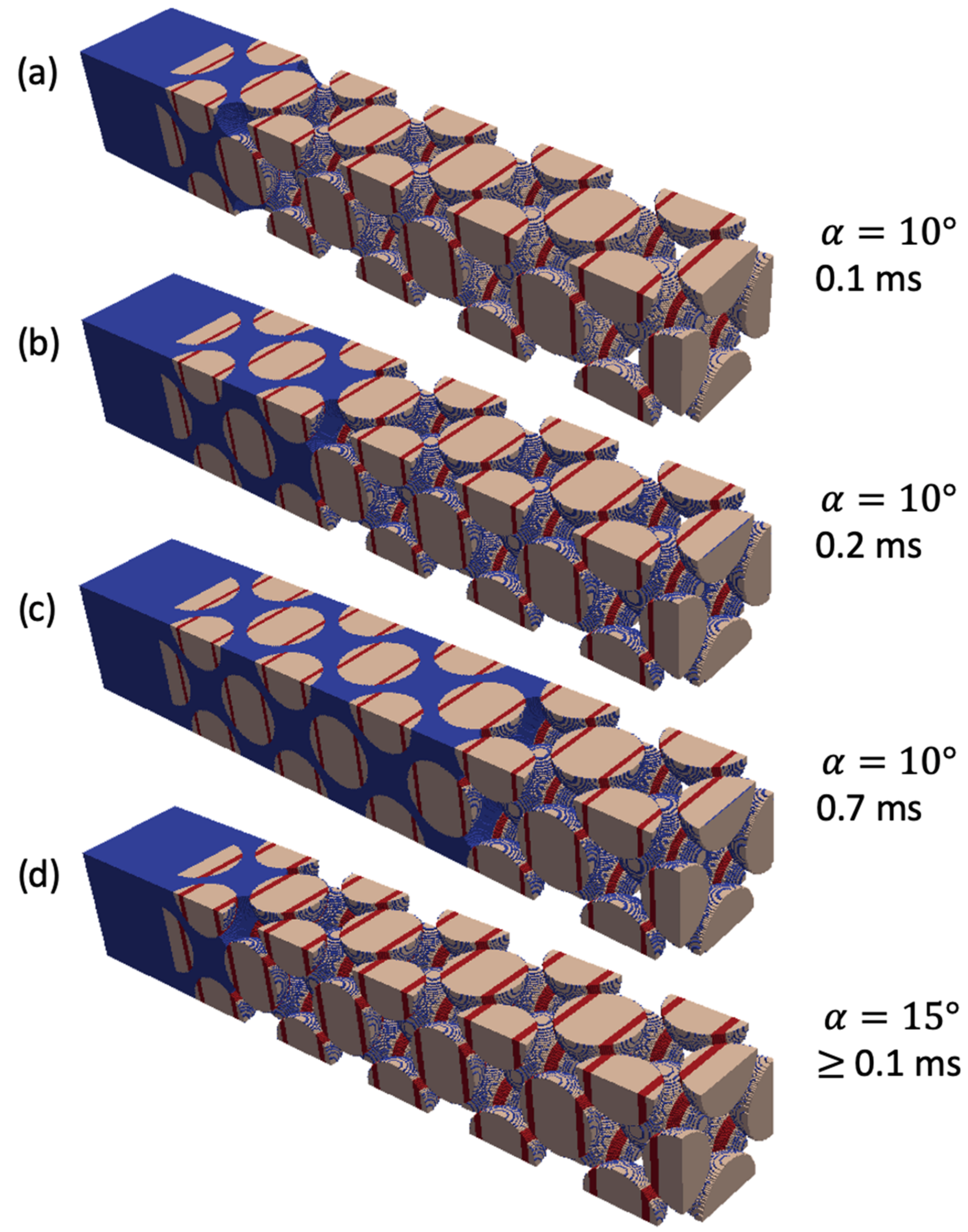
| Coating Pattern | Description |
|---|---|
| homogeneous pattern | all particles homogeneously coated with the same (Figure 7a) |
| body-throat pattern | particle surface of the pore throat and pore body having different (Figure 7b) |
| stripes pattern | particle surface divided into stripes of equal size, which alternately have two different (Figure 7c) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bentz, J.; Patel, R.A.; Benard, P.; Lieu, A.; Haupenthal, A.; Kroener, E. How Heterogeneous Pore Scale Distributions of Wettability Affect Infiltration into Porous Media. Water 2022, 14, 1110. https://doi.org/10.3390/w14071110
Bentz J, Patel RA, Benard P, Lieu A, Haupenthal A, Kroener E. How Heterogeneous Pore Scale Distributions of Wettability Affect Infiltration into Porous Media. Water. 2022; 14(7):1110. https://doi.org/10.3390/w14071110
Chicago/Turabian StyleBentz, Jonas, Ravi A. Patel, Pascal Benard, Alice Lieu, Adrian Haupenthal, and Eva Kroener. 2022. "How Heterogeneous Pore Scale Distributions of Wettability Affect Infiltration into Porous Media" Water 14, no. 7: 1110. https://doi.org/10.3390/w14071110
APA StyleBentz, J., Patel, R. A., Benard, P., Lieu, A., Haupenthal, A., & Kroener, E. (2022). How Heterogeneous Pore Scale Distributions of Wettability Affect Infiltration into Porous Media. Water, 14(7), 1110. https://doi.org/10.3390/w14071110







