Agricultural Productive Carrying Capacity Improve and Water Optimal Allocation under Uncertainty Based on Remote Sensing Data in Lancang County, Southwest China
Abstract
1. Introduction
2. Overview of the Studying Area
2.1. The Water Resources System in Lancang County
2.2. The Agricultural Resources System in Lancang County
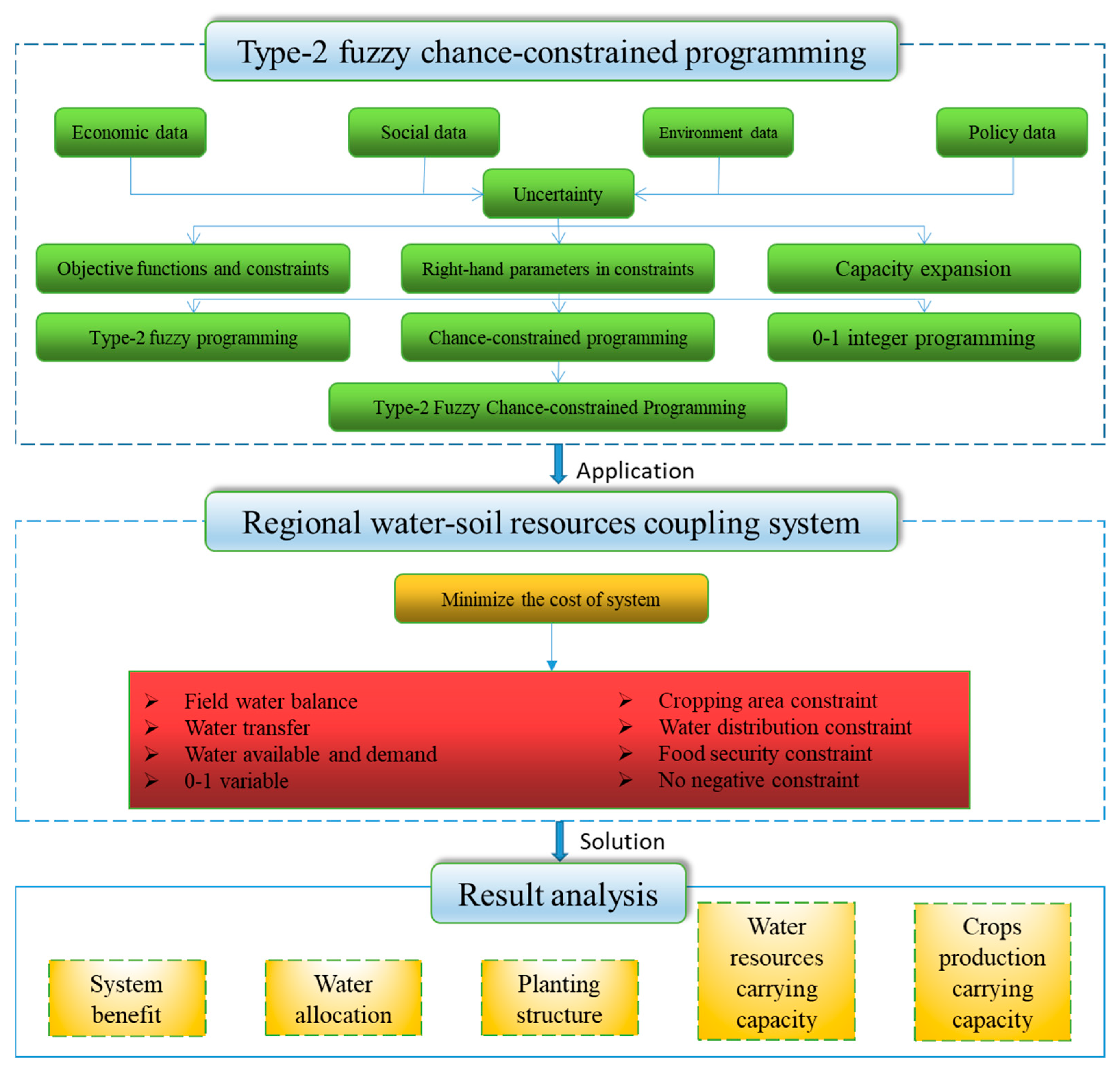
3. Methods
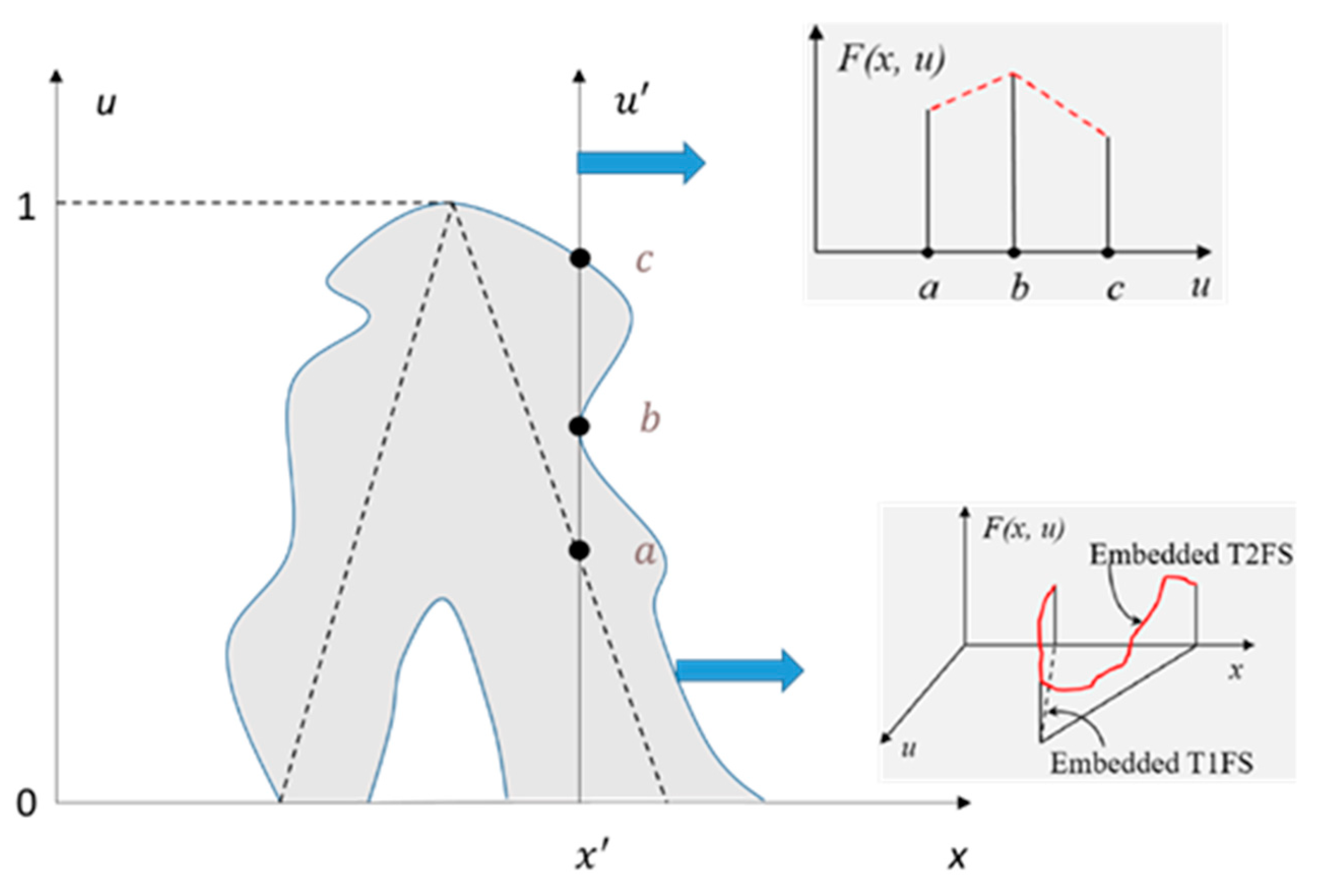
3.1. Type-2 Triangular Fuzzy Sets
- (1)
- Calculate the relative distance matrix D = |dij|t×t, where dij = |hi − hj|;
- (2)
- Calculate the average of relative distances ;
- (3)
- Introduce the pairwise comparison number pij, /, the pairwise matrix P = |pij|t×t;
- (4)
- Calculate the real weight wj of hj, ;
- (5)
- Calculate the core of the fuzzy number, ;
- (6)
- Define the mean deviation σ, choose and calculate to replace σ;
- (7)
- Define η as the distance from the left end to the right end of the fuzzy number, select and calculate /, /, A = {i|hi < a2, i ∈ I}, B = {i|hi > a2, i ∈ I};
- (8)
- Calculate a1 = a2 − 3(1 + η) ησ/(1 + η2), a3 = a2 + 3(1 + η) σ/(1 + η2). From this, the traditional fuzzy number F = (a1, a2, a3) of cij can be obtained.
3.2. Chance-Constrained Programming (CCP)
3.3. Type-2 Fuzzy Chance-Constrained Programming (T2FCCP) Construction and Its Solution
- (1)
- Surface water supply constraints
- (2)
- Groundwater supply constraints
- (3)
- Water demand constraints
- (4)
- Water balance constraints
- (5)
- Water distribution constraints
- (6)
- Cropping area constraints
- (7)
- Food security constraints
- (8)
- Water transfer constraints
- (9)
- Structure constraintswhere i, j, and t represent tributaries, crops, and time interval, respectively; f is the cost of system (¥106); , , , and are the canal irrigation cost (yuan/m3), well irrigation cost (yuan/m3), reclaimed water treatment, distribution, operation and maintenance costs (yuan/m3), and water resource dispatch cost (yuan/m3), respectively; , and are the i tributary j crop canal irrigation area (hm2), i tributary j crop well irrigation area (hm2), and i tributary j crop reclaimed water irrigation area (hm2), respectively; is the planting cost (yuan/hm2); and are the net canal irrigation water volume (m3/hm2) and net well irrigation water volume (m3/hm2), respectively; and are the canal water utilization coefficient and effective use coefficient of field water, respectively; and are 0–1 variables; and are the reclaimed water quota and external water transfer quota (m3/hm2), respectively; is the canal water supply (m3); is the residual surface water (m3); is the canal irrigation water intake coefficient; is the surface water availability (m3); is the confidence level of canal irrigation; is the well irrigation water intake coefficient; is the groundwater availability (m3); is the well irrigation area of i tributary (hm2); is the confidence level of well irrigation; is the effective precipitation; is the water requirements to ensure the basic normal growth of crops (m3); is the effective utilization rate of cultivated land irrigation water; is the irrigation water quota for the j th major crop (m3/hm2); is the proportion of the sown area of the j th major crop (%); and are the maximum canal irrigation area (hm2) and minimum canal irrigation area (hm2), respectively; and are the maximum well irrigation area (hm2) and minimum well irrigation area (hm2), respectively; and are the maximum reclaimed water irrigation area (hm2) and minimum reclaimed water irrigation area (hm2), respectively; is the yield (kg/hm2); is the population for i tributary; is the food demand per capita (kg/capita); is the minimum water requirement (m3/hm2).
3.4. Harmony Evaluation Method
- (1)
- Single-index quantification. According to the relationship between the changes from small to large indicators and the changes in the harmony degree of their representations, they can be divided into positive indicators and reverse indicators. The positive index harmony degree increases with the increase of the index value; the reverse index harmony degree decreases with the increase of the index value. Suppose a, b, c, d, and e are the worst value, poor value, passing value, better value and optimal value of a positive or negative index, respectively. Using feature points (a, 0), (b, 0.3), (c, 0.6), (d, 0.8), and (e, 1), then the calculation formula of harmony degree of the positive index and the reverse index are, respectively:where is the harmony degree of the i-th indicator at time t, i = 1, 2, …, n, n is the number of indicators; is the indicator value of the i-th indicator at time t.
- (2)
- Multi-indicator synthesis. Based on the calculation of the harmony degree of a single index, the harmony degree of each subsystem and the water resources–economic society–ecological environment system is calculated separately according to the method of weighted summation. Assume that the value of a quantitative index at time t is , its harmony degree is , then the water resources subsystem harmony degree (WHD), the economic and social subsystem harmony degree (SEHD), and the environmental subsystem harmony degree (EHD) are, respectively:where , , and take values from 0 to 1, , , and are the number of subsystem indicators, respectively, and is the index weight calculated by using the entropy weight method and the analytic hierarchy process.
- (3)
- Multi-criteria integration. Based on the WHD, SEHD, and EHD calculated above, the water resources–economical society–environmental system harmony degree (WSEHD) is calculated by the weighted sum method, and the formula iswhere the value of ranges from 0 to 1; , , and are weights of the corresponding subsystems; all take 1/3. In order to intuitively and objectively reflect the harmony level of the water resources–economical society–ecological environment system, according to the calculation results of WSEHD, seven harmony levels are set with a step size of 0.2, as shown in Table 2.
4. Application
4.1. Data Preparation
4.2. Result Analysis and Discussions
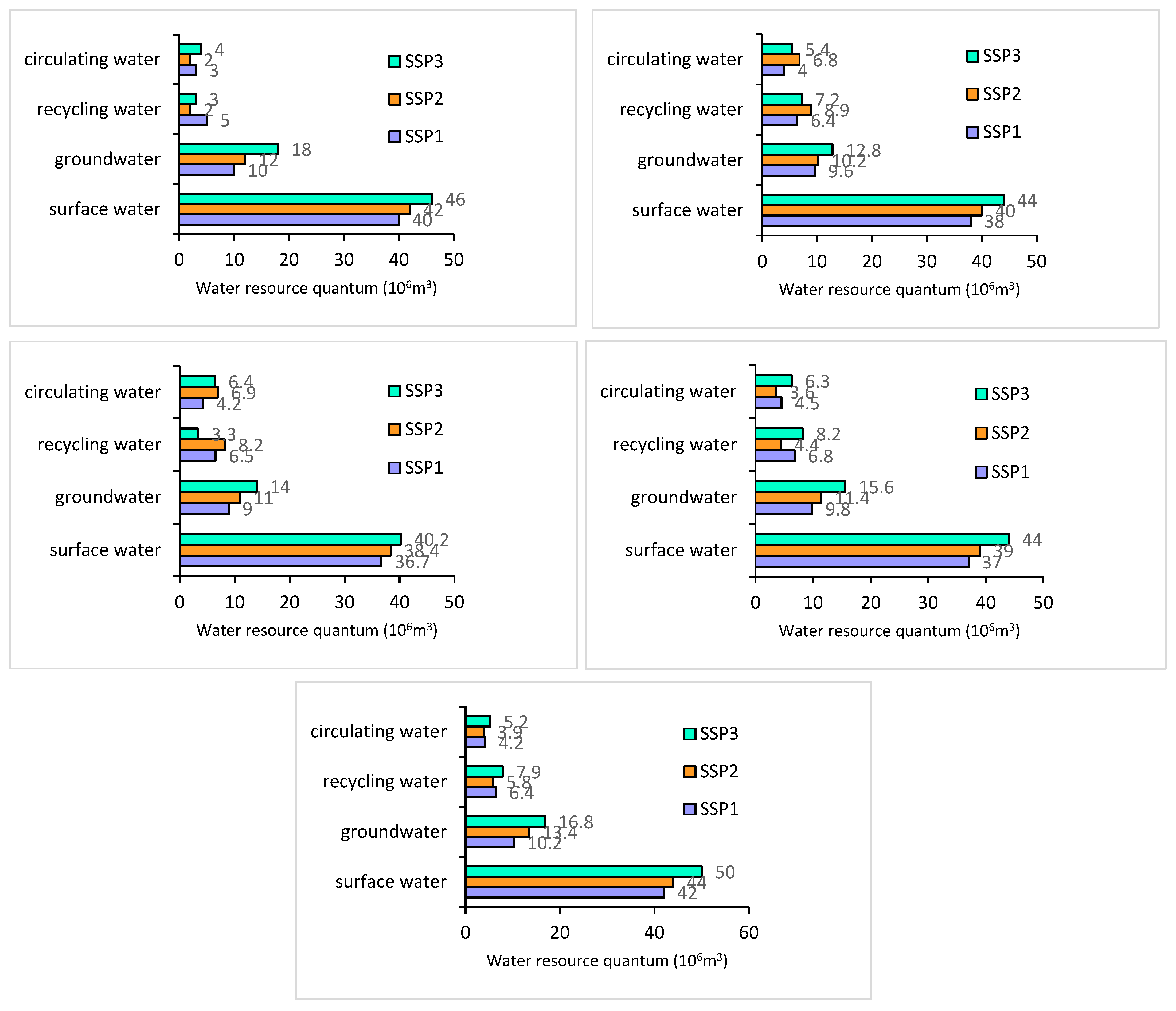
4.2.1. Water Resources Optimal Allocation in Lancang County
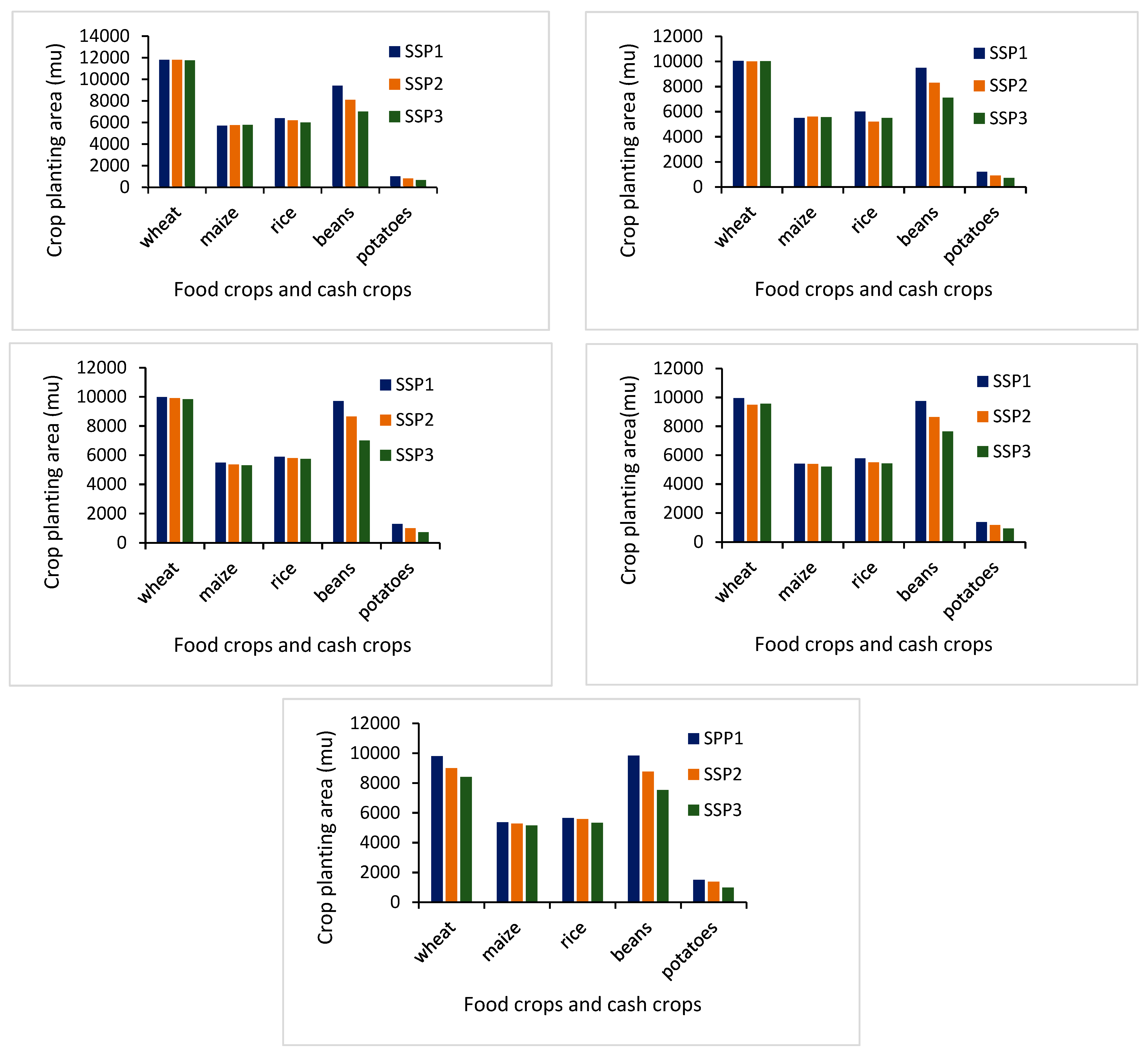
4.2.2. Planting Area Results of Different Crops in Lancang County
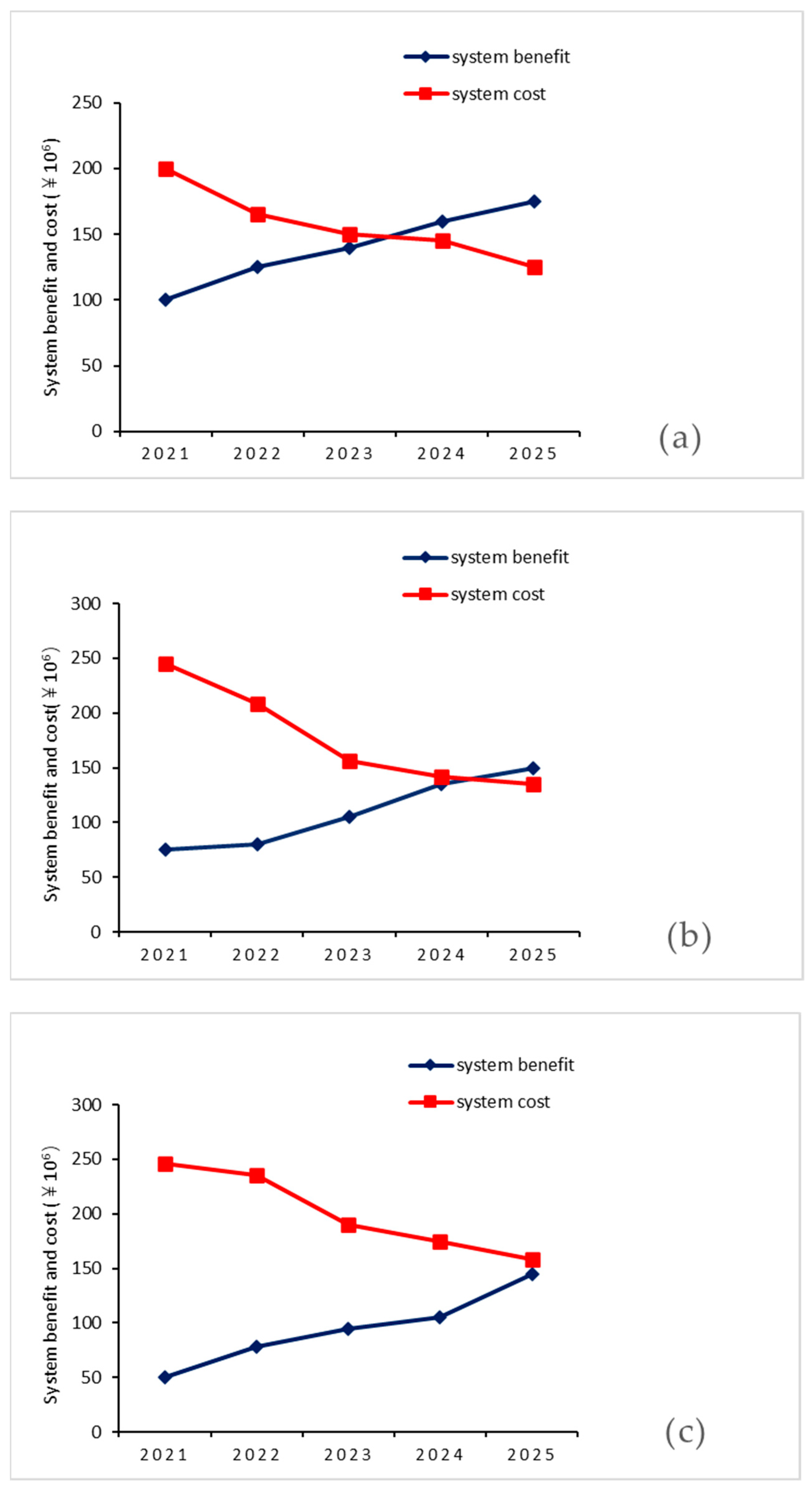
4.2.3. The System Costs and Benefits in Lancang County
4.2.4. Harmony Evaluation in Lancang County
4.2.5. Evaluation of Agricultural Production Irrigation Carrying Capacity in Lancang County
- (1)
- Dry year scenario
- (2)
- Wet year scenario
- (3)
- Planning Scenario
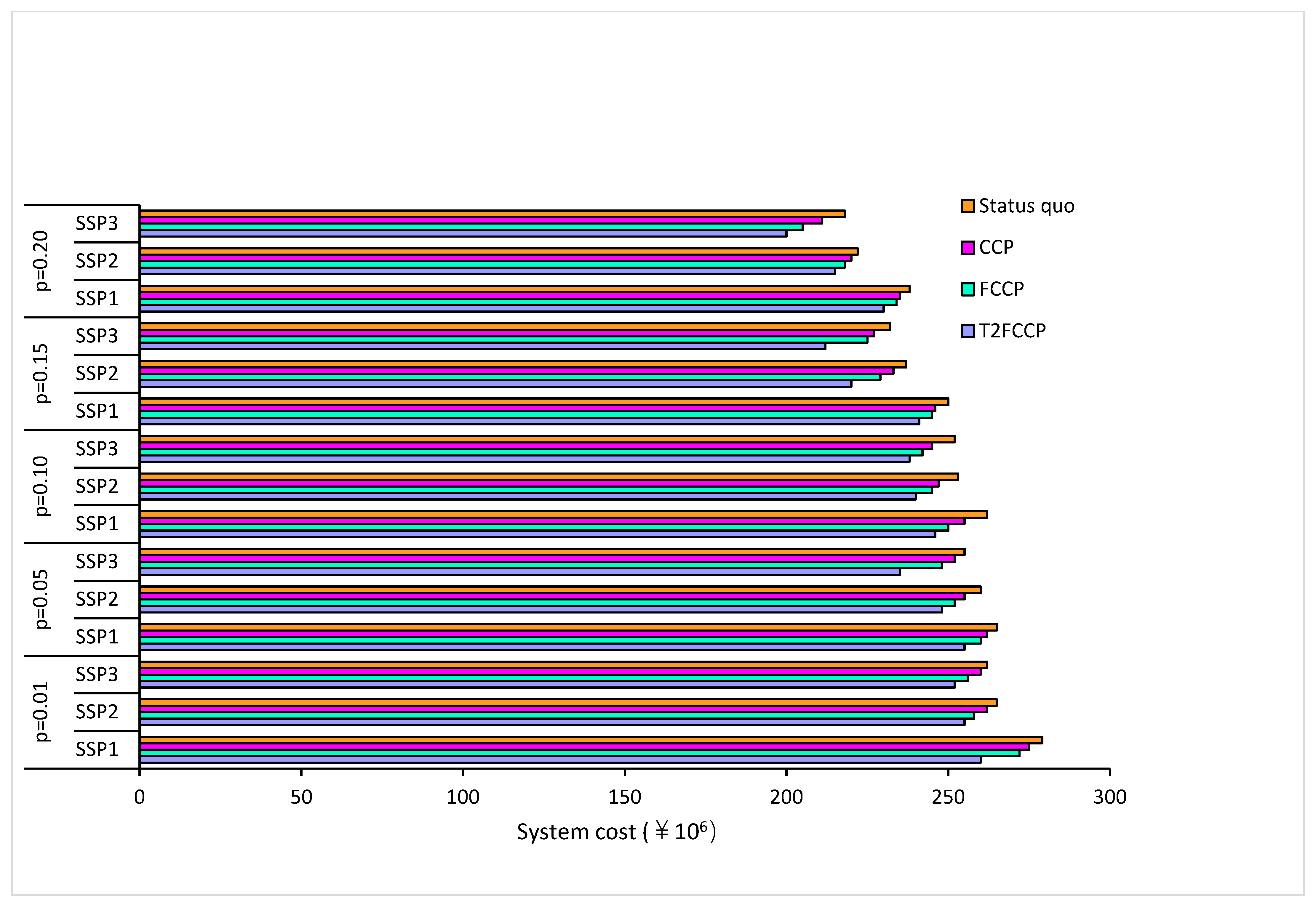
4.2.6. Cost Comparison between CCP, FCCP, T2FCCP Model and Status Quo
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cao, R.; Huang, G.H.; Chen, J.P.; Li, Y.P.; He, C.Y. A chance-constrained urban agglomeration energy model for cooperative carbon emission management. Energy 2021, 223, 119885. [Google Scholar] [CrossRef]
- Cao, R.; Huang, G.H.; Chen, J.P.; Li, Y.P. A fractional multi-stage simulation-optimization energy model for carbon emission management of urban agglomeration. Sci. Total Environ. 2021, 774, 144963. [Google Scholar] [CrossRef]
- Cao, R.; Jin, X.M. Distribution Characteristics of Soil Moisture in the Three Rivers Headwaters Region, China. J. Environ. Inf. Lett. 2021, 6, 55–65. [Google Scholar] [CrossRef]
- Gu, W.; Shao, D.; Tan, X.; Shu, C.; Wu, Z. Simulation and optimization of multi-reservoir operation in inter-basin water transfer system. Water Res. Manag. 2017, 33, 3401–3412. [Google Scholar] [CrossRef]
- Chen, S.; Shao, D.; Tan, X.; Gu, W.; Lei, C. An interval multistage classified model for regional inter- and intra-seasonal water management under uncertain and nonstationary condition. Agric. Water Manag. 2017, 191, 98–112. [Google Scholar] [CrossRef]
- Zhang, C.L.; Li, M.; Guo, P. Two-Stage Stochastic Chance-Constrained Fractional Programming Model for Optimal Agricultural Cultivation Scale in an Arid Area. J. Irri. Drain. Eng. 2017, 143, 0001216. [Google Scholar] [CrossRef]
- Zhang, C.L.; Guo, P. An inexact CVaR two-stage mixed-integer linear programming approach for agricultural water management under uncertainty considering ecological water requirement. Ecol. Ind. 2018, 92, 342–353. [Google Scholar] [CrossRef]
- Zhang, C.L.; Li, M.; Guo, P. An interval multistage joint-probabilistic chance-constrained programming model with left-hand-side randomness for crop area planning under uncertainty. J. Clean. Prod. 2017, 167, 1276–1289. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, P.; Liu, X.; Adeloye, A.J. Simulation and Optimization Coupling Model for Soil Salinization and Waterlogging Control in the Urad Irrigation Area, North China. J. Hydrol. 2021, 607, 127408. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Yang, P.L. Agricultural Water Optimal Allocation Using Minimum Cross-Entropy and Entropy-Weight-Based TOPSIS Method in Hetao Irrigation District, Northwest China. Agriculture 2022, 12, 853. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, K.; Wang, S.; Wu, T.; Li, X.; Wang, J.; Wang, D.; Zhu, H.; Tan, C.; Ji, Y. Spatiotemporal evolution of ecological vulnerability in the Yellow River Basin under ecological restoration initiatives. Ecol. Indic. 2022, 135, 108586. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, K.; Li, X.; Wang, S.; Wang, J. Vulnerability assessment and its driving forces in terms of NDVI and GPP over the Loess Plateau, China. Phys. Chem. Earth Parts A B C 2022, 125, 103106. [Google Scholar] [CrossRef]
- Liu, K.; Li, X.K.; Long, X. Trends in groundwater changes driven by precipitation and anthropogenic activities on the southeast side of the Hu Line. Environ. Res. Lett. 2021, 16, 094032. [Google Scholar] [CrossRef]
- Maqsood, I.; Huang, G.H.; Scott Yeomans, J. An interval parameter fuzzy two-stage stochastic program for water resources management under uncertainty. Eur. J. Oper. Res. 2005, 167, 208–225. [Google Scholar] [CrossRef]
- Akhtari, S.; Sowlati, T. Hybrid optimization-simulation for integrated planning of bioenergy and biofuel supply chains. Appl. Energy 2020, 259, 114124. [Google Scholar] [CrossRef]
- Shabani, N.; Sowlati, T. A hybrid multi-stage stochastic programming-robust optimization model for maximizing the supply chain of a forest-based biomass power plant considering uncertainties. J. Clean. Prod. 2016, 112, 3285–3293. [Google Scholar] [CrossRef]
- Kamjoo, A.; Maheri, A.; Dizqah, A.M.; Putrus, G.A. Multi-objective design under uncertainties of hybrid renewable energy system using NSGA-II and chance constrained programming. Int. J. Electr. Power Energy Syst. 2016, 74, 187–194. [Google Scholar] [CrossRef]
- Daneshvar, M.; Mohammadi-Ivatloo, B.; Zare, K. Two-stage optimal robust scheduling of hybrid energy system considering the demand response programs. J. Clean. Prod. 2020, 248, 119267. [Google Scholar] [CrossRef]
- Cui, H.; Guo, P.; Li, M.; Guo, S.; Zhang, F. A multi-risk assessment framework for agricultural land use optimization. Stoch. Environ. Res. Risk Asses. 2019, 33, 563–579. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Singh, V.P.; Yang, G. An uncertainty-based framework for agricultural water-land resources allocation and risk evaluation. Agric. Water Manag. 2016, 177, 10–23. [Google Scholar] [CrossRef]
- Sun, H.Y.; Wang, S.F.; Hao, X.M. An Improved Analytic Hierarchy Process Method for the evaluation of agricultural water management in irrigation districts of north China. Agric. Water Manag. 2017, 179, 324–337. [Google Scholar] [CrossRef]
- Zhang, F.; Guo, S.; Ren, C.; Guo, P. Integrated IMO-TSP and AHP Method for Regional Water Allocation under Uncertainty. J. Water Res. Plan. Manag. 2018, 144, 04018025. [Google Scholar] [CrossRef]
- Zhao, J.; Li, M.; Guo, P.; Zhang, C.; Tan, Q. Agricultural Water Productivity Oriented Water Resources Allocation Based on the Coordination of Multiple Factors. Water 2017, 9, 490. [Google Scholar] [CrossRef]
- Chen, S.; Wang, S.; Shukla, M.K.; Wu, D.; Guo, X.; Li, D.; Du, T. Delineation of management zones and optimization of irrigation scheduling to improve irrigation water productivity and revenue in a farmland of Northwest China. Prec. Agric. 2020, 21, 655–677. [Google Scholar] [CrossRef]
- Ren, C.; Guo, P.; Li, M.; Li, R. An innovative method for water resources carrying capacity research—Metabolic theory of regional water resources. J. Environ. Manag. 2016, 167, 139–146. [Google Scholar] [CrossRef]
- He, L.; Wang, S.; Peng, C.; Tan, Q. Optimization of Water Consumption Distribution Based on Crop Suitability in the Middle Reaches of Heihe River. Sustainability 2018, 10, 2119. [Google Scholar] [CrossRef]
- Wang, S.F.; Singh, V.P. Spatio-Temporal Variability of Soil Water Content under Different Crop Covers in Irrigation Districts of Northwest China. Entropy 2017, 19, 410. [Google Scholar] [CrossRef]
- Gui, Z.Y.; Li, M.; Guo, P. Simulation-based inexact fuzzy semi-infinite programming method for agricultural cultivated area planning in the Shiyang River basin. J. Irri. Drain. Eng. 2017, 143, 0001118. [Google Scholar] [CrossRef]
- Zhang, C.L.; Li, M.; Guo, P. Trend detection and stochastic simulation prediction of streamflow at Yingluoxia hydrological station, Heihe River Basin, China. Front. Agric. Sci. Eng. 2017, 4, 81–96. [Google Scholar] [CrossRef]
- Zhang, F.; Li, M.; Guo, S.; Zhang, C.; Guo, P. Integrated uncertain models for runoff forecasting and crop planting structure optimization of the Shiyang River Basin, north-west China. Front. Agric. Sci. Eng. 2018, 5, 177–187. [Google Scholar] [CrossRef]
- Gui, Z.; Zhang, C.; Li, M.; Guo, P. Risk analysis methods of the water resources system under uncertainty. Front. Agric. Sci. Eng. 2015, 2, 205–215. [Google Scholar] [CrossRef]
- Lu, H.W.; Huang, G.H.; Liu, L.; He, L. An interval-parameter fuzzy-stochastic programming approach for air quality management under uncertainty. Environ. Eng. Sci. 2008, 25, 895–910. [Google Scholar] [CrossRef]
- Huang, G.H.; He, L.; Zeng, G.M.; Lu, H.W. Identification of Optimal Urban Solid Waste Flow Schemes under Impacts of Energy Prices. Environ. Eng. Sci. 2008, 25, 685–696. [Google Scholar] [CrossRef]
- He, L.; Huang, G.H.; Lu, H.W.; Zeng, G.M. Optimization of surfactant-enhanced aquifer remediation for a laboratory BTEX system under parameter uncertainty. Environ. Sci. Technol. 2008, 42, 2009–2014. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Huang, G.H.; Zeng, G.; Lu, H. An Interval Mixed-Integer Semi-Infinite Programming Method for Municipal Solid Waste Management. J. Air Waste Manag. Ass. 2012, 59, 236–246. [Google Scholar] [CrossRef]
- He, L.; Huang, G.H.; Zeng, G.M.; Lu, H.W. Identifying optimal regional solid waste management strategies through an inexact integer programming model containing infinite objectives and constraints. Waste Manag. 2009, 29, 21–31. [Google Scholar] [CrossRef]
- Lu, H.W.; Huang, G.H.; He, L. A Two-Phase Optimization Model Based on Inexact Air Dispersion Simulation for Regional Air Quality Control. Water Air Soil. Poll. 2010, 211, 121–134. [Google Scholar] [CrossRef]
- Lu, H.W.; Huang, G.H.; He, L. Inexact rough-interval two-stage stochastic programming for conjunctive water allocation problems. J. Environ. Manag. 2009, 91, 261–269. [Google Scholar] [CrossRef]
- Lu, H.W.; Huang, G.H.; He, L. An inexact rough-interval fuzzy linear programming method for generating conjunctive water-allocation strategies to agricultural irrigation systems. Appl. Math. Model. 2011, 35, 4330–4340. [Google Scholar] [CrossRef]
- He, L.; Huang, G.H.; Lu, H.W. Greenhouse gas emissions control in integrated municipal solid waste management through mixed integer bilevel decision-making. J. Hazar. Mater. 2011, 193, 112–119. [Google Scholar] [CrossRef]
- He, L.; Huang, G.H.; Lu, H.W. Bivariate interval semi-infinite programming with an application to environmental decision-making analysis. Eur. J. Oper. Res. 2011, 211, 452–465. [Google Scholar] [CrossRef]
- He, L.; Huang, G.; Lu, H.; Wang, S.; Xu, Y. Quasi-Monte Carlo based global uncertainty and sensitivity analysis in modeling free product migration and recovery from petroleum-contaminated aquifers. J. Hazar. Mater. 2012, 219–220, 133–140. [Google Scholar] [CrossRef] [PubMed]
- Shi, B.; Lu, H.W.; Ren, L.X.; He, L. A fuzzy inexact two-phase programming approach to solving optimal allocation problems in water resources management. Appl. Math. Model. 2014, 38, 5502–5514. [Google Scholar] [CrossRef]
| Document | Author | Location | Method | How to Use Optimization Model | Index for Water Allocation | Temporal Scale | Spatial Scale | Scenarios |
|---|---|---|---|---|---|---|---|---|
| An inexact modeling approach for supporting water resources allocation under natural and social complexities in a border city of China and Myanmar | Chen et al., 2021 | Southwest China | ITSFCCP | Reflect the trade-offs between the system benefits and risks | Fuzzy sets, discrete intervals, probability distribution and credibility levels | 2005–2016 | Prefecture-level city | Flow levels |
| A Stochastic Optimization Model for Agricultural Irrigation Water Allocation Based on the Field Water Cycle | Yan et al., 2018 | Northwest China | TSCCP | Considering field water cycle process | Different crops and months | 2000–2015 | Irrigation District level | Different flow levels and constraint-violation risk levels |
| Efficient and Economical Allocation of Irrigation Water under a Changing Environment: a Stochastic Multi-Objective Nonlinear Programming Model | Yan et al., 2018 | Northwest China | SMONLP | Trade-offs between NEB and IWUE | Different crops and months | From April to September in 2016 | Irrigation District level | weighting factor of objective functions and violating probability |
| This study | Zhang et al., 2022 | Southwest China | T2FCCP | Conjunction with the Harmony Evaluation Method | Harmony level | 2021–2025 | County area | Three SSPs |
| WSEHD | 0 | (0, 0.2) | [0.2, 0.4) | [0.4, 0.6) | [0.6, 0.8) | [0.8, 1) | 1 |
|---|---|---|---|---|---|---|---|
| Harmony level | totally discordant | less harmonious | basic dissonance | close to harmony | basic harmony | more harmonious | complete harmony |
| 2021 | 2022 | 2023 | 2024 | 2025 | ||
|---|---|---|---|---|---|---|
| Number | Tributaries | WSEHD Harmony Level | WSEHD Harmony Level | WSEHD Harmony Level | WSEHD Harmony Level | WSEHD Harmony Level |
| 1 | Shangyun River | 0.42 close to harmony | 0.41 close to harmony | 0.48 close to harmony | 0.62 basic harmony | 0.64 basic harmony |
| 2 | Hei River | 0.43 close to harmony | 0.42 close to harmony | 0.54 close to harmony | 0.63 basic harmony | 0.71 basic harmony |
| 3 | Mangpa River | 0.46 close to harmony | 0.51 close to harmony | 0.47 close to harmony | 0.65 basic harmony | 0.74 basic harmony |
| 4 | Nanlang River | 0.36 basic dissonance | 0.38 basic dissonance | 0.42 close to harmony | 0.44 close to harmony | 0.72 basic harmony |
| Total Water Resources | Total Amount of Water Resources Is Higher than the Average over the Years | Precipitation Is Higher than the Multi-Year Average | Groundwater Resources | Farmland Irrigation Water Consumption | Non-Farmland Irrigation Water Consumption | Groundwater Supply | Surface Water Supply | Reclaimed Water Volume | Total Water Supply |
|---|---|---|---|---|---|---|---|---|---|
| 125.96 | −28.62% | −35.72% | 108.06 | 110.52 | 115.34 | 118.08 | 78.08 | 12.8 | 260.78 |
| Total Surface Water Supply and Reclaimed Water | Non-Agricultural Water Use Exceeds Surface Water | Remaining after Deduction of Groundwater | 60% of the Groundwater Resources of the Year |
|---|---|---|---|
| 80.21 | 70.62 | 135.28 | 64.85 |
| Total Water Resources | Total Amount of Water Resources Is Higher than the Average over the Years | Precipitation Is Higher than the Multi-Year Average | Groundwater Resources | Farmland Irrigation Water Consumption | Non-Farmland Irrigation Water Consumption | Groundwater Supply | Surface Water Supply | Reclaimed Water Volume | Total Water Supply |
|---|---|---|---|---|---|---|---|---|---|
| 135.68 | 25.48% | 28.20% | 112.65 | 56.48 | 58.25 | 65.4 | 30.5 | 18.2 | 280.2 |
| Total Surface Water Supply and Reclaimed Water | Non-Agricultural Water Use Exceeds Surface Water | Remaining after Deduction of Groundwater | 60% of the Groundwater Resources of the Year |
|---|---|---|---|
| 85.28 | 66.4 | 140.6 | 67.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yang, P. Agricultural Productive Carrying Capacity Improve and Water Optimal Allocation under Uncertainty Based on Remote Sensing Data in Lancang County, Southwest China. Water 2022, 14, 3641. https://doi.org/10.3390/w14223641
Zhang Y, Yang P. Agricultural Productive Carrying Capacity Improve and Water Optimal Allocation under Uncertainty Based on Remote Sensing Data in Lancang County, Southwest China. Water. 2022; 14(22):3641. https://doi.org/10.3390/w14223641
Chicago/Turabian StyleZhang, Yunquan, and Peiling Yang. 2022. "Agricultural Productive Carrying Capacity Improve and Water Optimal Allocation under Uncertainty Based on Remote Sensing Data in Lancang County, Southwest China" Water 14, no. 22: 3641. https://doi.org/10.3390/w14223641
APA StyleZhang, Y., & Yang, P. (2022). Agricultural Productive Carrying Capacity Improve and Water Optimal Allocation under Uncertainty Based on Remote Sensing Data in Lancang County, Southwest China. Water, 14(22), 3641. https://doi.org/10.3390/w14223641






