1. Introduction
Surface water connected with rivers and streams is a key component in controlling the hydrological cycle, ecology, social wellbeing, and economic growth [
1]. Environmental events, including annual precipitation and erosion, and also social elements like agricultural, urban, and industrial production procedures, all have an impact on river water quality [
2]. Surface water contributes as a dominant and major source of fresh water throughout the world. Its diminishment can have serious implications on the accessibility of drinking water, and quite significant consequences in terms of economic and financial growth and technological strategies [
3]. The interplay of river systems and their surroundings, as well as the interchange of industrial, agricultural, and urban wastes across their trajectory results in water contamination [
4]. The poor and contaminated water quality is a critical issue that poses a vulnerable situation to human welfare, agricultural, and the environment [
2].
One of the major factors contributing towards the poor and contaminated water quality is the salinity. The saline environment of waterbodies has continuously grown over the last decade, compromising the quality of drinking water, and water utilized for irrigation, and in industrial processing units [
5]. The salt accumulation caused by saltiness creates an adverse hydrological condition within water, inhibiting its household, agricultural and commercial consumption. Water quality assessment and saltwater monitoring and regulation is becoming crucial, and thus the stability between water supply and demand has met the required threshold [
6]. One of the key parameters that can be used as a substantial indicator for the assessment of water quality is total dissolved solids (TDS), which can be used to determine its appropriateness for irrigation and drinking [
7]. TDS is primarily made up of dissolved inorganic salts like sodium (Na
+), calcium (Ca
2+), magnesium (Mg
2+), nitrates (NO
3−), chloride (Cl
−), and sulfate (SO
42−), as well as other dissolved organic particles. Higher level of salts and organic matter indicates substandard water quality [
8].
Electric conductivity (EC) and TDS measurements have been the subject of scientific laboratory analysis and experimental procedures [
7]. However, manual laboratory experiments, have several drawbacks, like the time required, their unreliable nature, and their inaccurate and ambiguous results due to the systematic errors and thus the lack of ability to be generalized [
9]. Moreover, larger projects with passing time limit are inappropriate for labor-intensive tests. As a result, computer simulated models can be utilized to evaluate and forecast the water quality [
10,
11]. Numerous scientific publications have attempted to analyze a diverse collection of different water quality attributes employing numerical, stochastic, and mechanistic methods [
12]. Such conventional means can still provide predictions for linear and homogeneous data sources [
13]. The researchers also used other different techniques for the modelling of water quality indices, such as the driver-pressure-state-impact-response (DPSIR) method [
14] and the advanced classification techniques i.e., the ground directive (GWD) and the water framework directive (WFD) [
15]. Recently, machine learning (ML) based supervised models have been claimed to handle broad, non-linear, asymmetric, and complicated mechanisms of ecological and hydrologic systems, thereby avoiding the limitations of previous traditional models. Consequently, novel methods that are computationally fast, reliable, and effective for the determination and evaluation of EC and TDS are necessary. These advancements in measuring, analyzing, and monitoring water quality can benefit the environmental engineering sector.
During the last couple of decades, the sub-field of artificial intelligence (AI) i.e., machine learning (ML) has been widely used to tackle varied ecological technical challenges, especially water quality index simulation [
2,
16,
17,
18,
19]. ML techniques are indeed a technological breakthrough in the development on management and surveillance of many engineering activities [
20,
21,
22]. These algorithmic procedures can help to make appropriate forecasts without needing sophisticated programming officials. ML models are eventually supported by the collected data and the interpretation of configurations among data. These models are accomplished via the application of algorithms with the help of data subsets, including training and validation sets, and testing (unseen dataset) for evaluating the performance of predictive models [
23,
24,
25].
The literature review shows a great intention towards the use of AI techniques for water quality prediction [
26]. Tripathi and Singal [
27] focused on the development of a novel water quality index (WQI) calculation approach for the Indian Ganges River. The authors used a principal components analysis (PCA) approach to lessen the total twenty-eight variables to just the nine best combinations of explanatory parameters, which includes Hydrogen Power (pH), EC, TDS, Sulfate (SO
42−), Dissolved Oxygen (DO), Chlorine (Cl
−), Total Coliform (TC), Magnesium (Mg), and Biochemical Oxygen Demand (BOD). The use of only nine variables results in quicker calculations, consequently reducing the computational duration. Similarly, Zali et al. [
28] used the ML technique i.e., artificial neural networks (ANNs) to investigate the impacts of six key explanatory variables (i.e., Chemical Oxygen Demand (COD), Suspended Solids (SS), Nitrate (NO
3−), BOD, DO, and pH) for the computation of WQI. Determining the comparative relevance of every variable in WQI prediction using a sensitivity analysis showed that DO, SS, and NO
3− are indeed the essential input variables. Nigam and SM [
29] compared the prediction performance of fuzzy based models and conventional computation techniques for the calculation of WQI of ground water, reporting comparatively the outburst predictive power of fuzzy (an intelligent model). Thus, this categorizes the water quality and surpasses the predictions of conventional calculation techniques. Srinivas and Singh [
30] extended their study to an Interactive Fuzzy model (IFM) for establishment of a unique fuzzy decision-making technique for predicting WQI in rivers. The results of their research show a considerable enhancement in WQI predictive accuracy in comparison with a conventional fuzzy approach. Yaseen et al. [
31] investigated the estimation efficiency of adaptive-neuro-fuzzy-inference-system (ANFIS)-based hybrid models combined with subtractive clustering (SC), Fuzzy C-mean data clustering (FCM), and grid partitioning (GP). They found that ANFIS-SC is the best and most consistent model. Radial-basis-function-neural-networks (RBFN) and back-propagation-neural-network (BPNN) algorithms were used to propose a model for the establishment of the relation between WQI and many biological variables (like COD, SS, BOD, DO, Nitrate, and pH) in tropical and subtropical environments [
32]. The RBFNN model produced comparatively good predictive outcomes. Bozorg-Haddad et al. [
10] tested the performance of genetic-programming (GP) and least-square-support-vector-regression (LSSVR) for the estimation of K, Na, Mg, EC, SO
4, EC, TDS, and pH, in the Sefidrood River located in Iran. For all the computed models, the
R2 values is greater than 0.9, indicating good correlation. Al-Mukhtar and Al-Yaseen [
33] used ANN, ANFIS and multiple-linear-regression (MLR) techniques to assess the water quality of the Abu-Ziriq River, located in Iraq. They forecasted the EC and TDS with most significant input variables (nitrate, chloride, calcium, magnesium, hardness and sulfate) and found that the ANFIS technique yielded the best outcomes. Sarkar and Pandey [
34] used the ANN approach to analyze the amount of dissolved oxygen (DO) in river water over three distinct sites using four different variables i.e., pH, temperature, DO, and biochemical oxygen demand (BOD) and reported a correlation coefficient (R) value above 0.90 between the forecasted and actual DO data. Zhang et al. [
35] used the combined hybridized model of ANN and GP algorithm to forecast the production of drinking water from chemical treatment plants. The findings showed that these created models performed well in forecasting the output capacity of the water treatment processing unit. Incorporation of additional data to the algorithm during training enhanced the model performance significantly. Chen et al. [
36] utilized a comprehensive database to examine the water quality predictive ability of ten distinct ML models (three ensemble and seven conventional). The study indicated that utilizing a larger number of datapoints for water quality assessment can improve the predictive accuracy of the model. Some other prominent methodologies have been used effectively for different meteorological, environmental, and hydrological challenges (like rainfall forecasting), and these include tree-based algorithmic procedures, like random forest (RF), decision tree (DT) and support vector machine (SVM) models. These models are also recognized as a remarkable ML approach for both linear and complex non-linear engineering problems. Different researchers have utilized these algorithms with excellent predictive performance in a variety of scientific challenges [
37]. Granata et al. [
38] generated the SVM and RF model to forecast the content of TDS, TSS, BOD and COD, finding that the SVM model provided superior predictions. However, the efficacy is reduced when subjected to unseen data. In brief, the various mathematical models are developed that contributed to the betterment of human life [
39,
40,
41,
42,
43,
44,
45,
46].
Although conventional AI algorithms rely on ANN and ANFIS, are extensively used for WQP modeling. Environmentalists have been investigating new resilient and robust intelligent algorithms [
18,
19]. It is worthy to mention that the neural networks work like a black box and do not consider any physical phenomenon of the issue being resolved. Most of the neural networks deliver a complex expression for the prediction of outcome on the basis of inputs [
47]. In fact, ANN based models are considered as a correlation amongst the inputs and outputs, and the relation is either linear or relies on the pre-defined base functions [
48,
49]. Also, the tree-based algorithms are only good at capturing the linear relationship [
50]. To overcome these issues, researchers used EA algorithms like GEP for simulation of water WQPs [
51,
52]. The EAs are advantageous in the condition where realistic and practical expression with higher generalization and prediction capabilities is required. However, the GEP is unable to incorporate the diverging data for the establishment of an ultimate model and must be excluded from the training and validation phase for the enhancement of the model’s performance. Also, the GEP encode a single chromosome (expression) and present it as a program. Thus, they are only appropriate when there exists a simple relationship between inputs and outputs [
53]. In contrast, the MEP is a comparatively new variant of genetic programming (GP) and has an ability to code a multiple number of chromosomes (expressions) in just one computer program [
53]. It has the potential to predict the outcome accurately given the unknown complexity of the targeted parameter [
54]. Unlike other ML algorithms, MEP does not need the identification of the final expression. In addition, the evolution process can effectively read and eliminate the complex mathematical errors from the resulting expression. The decoding procedure of MEP is fairly intuitive in comparison with other ML methods. Given the immense benefits of MEP algorithmic process over other evolutionary algorithms, it is scarcely adopted by environmentalists.
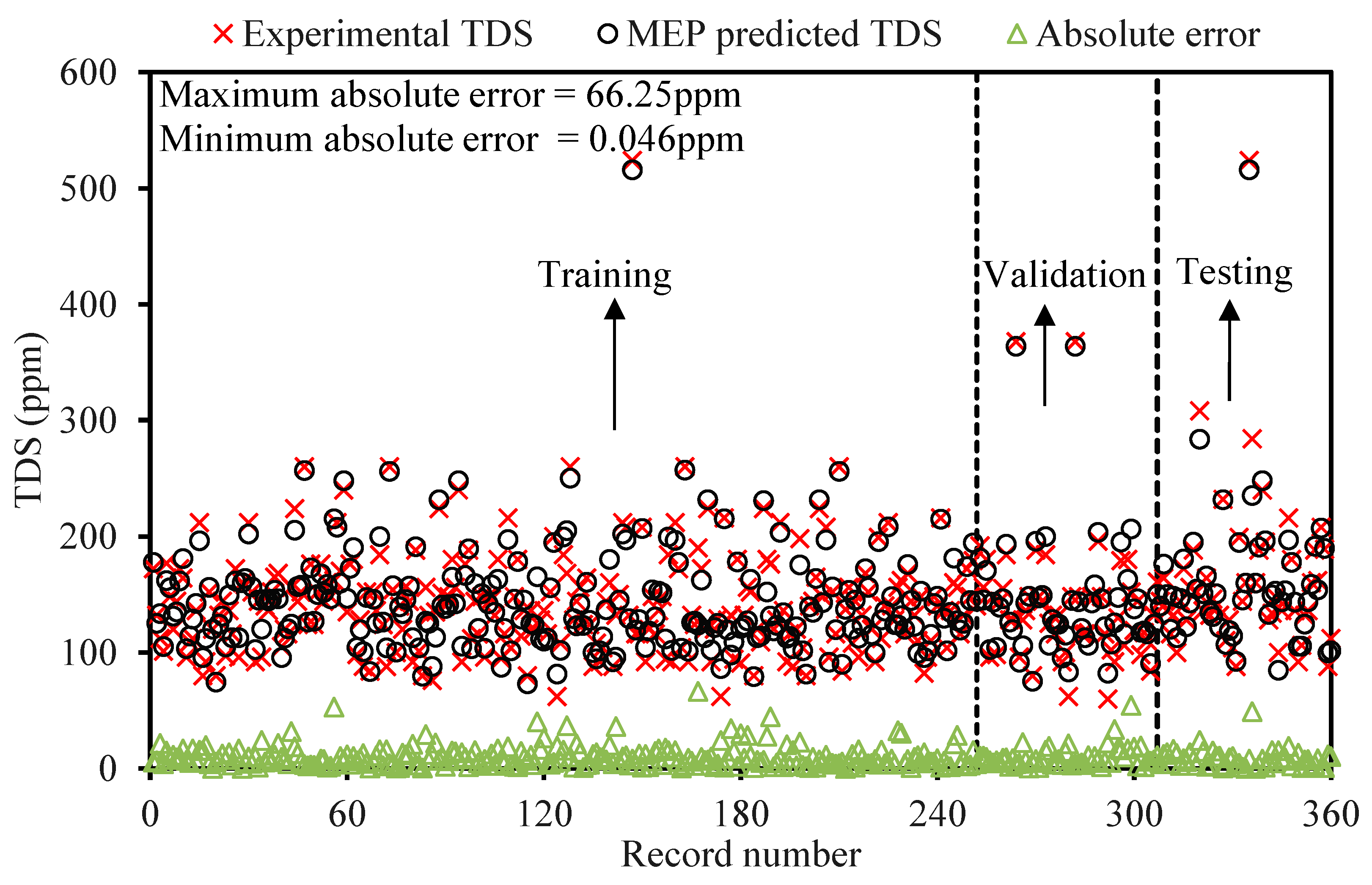
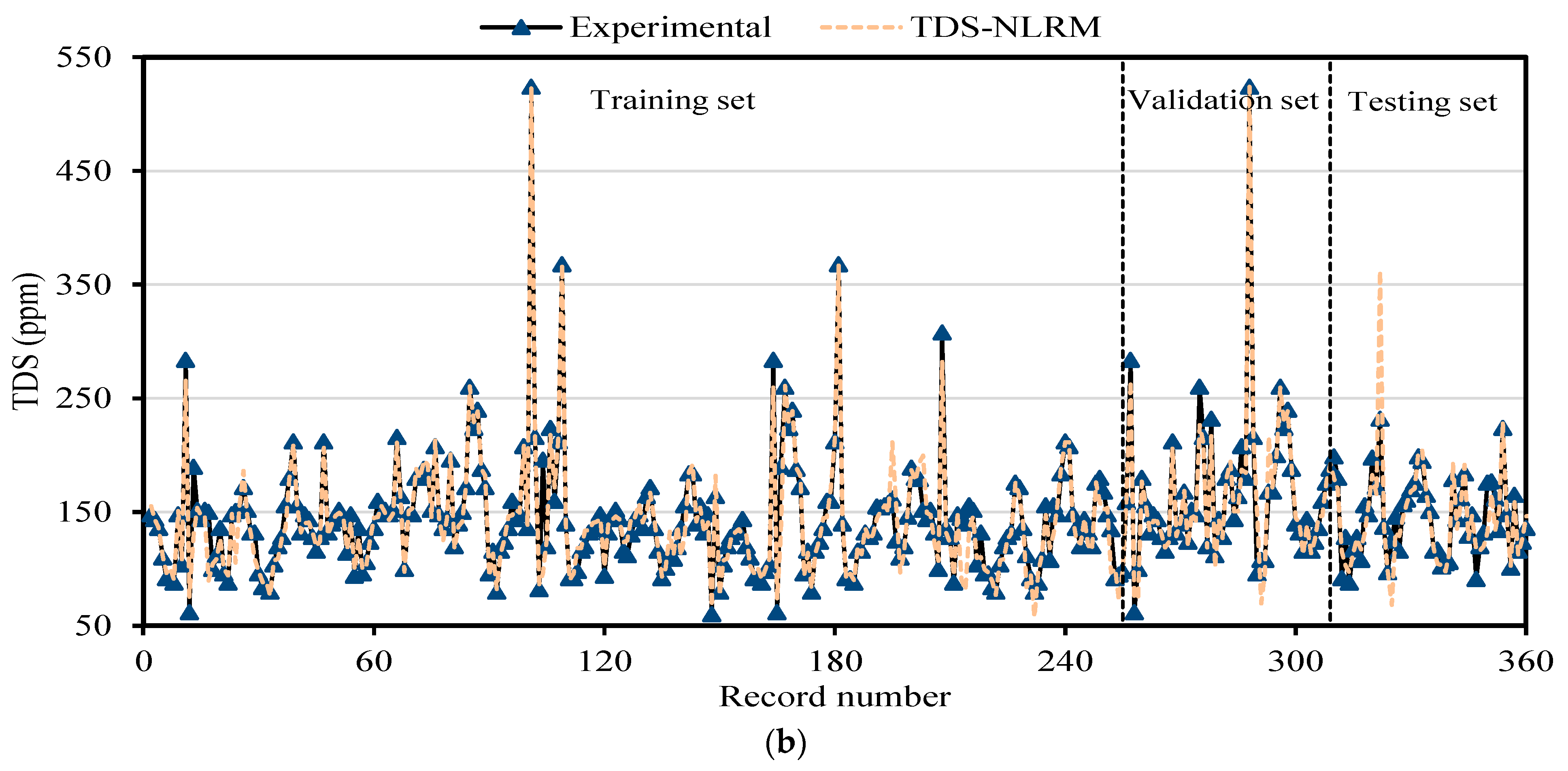
In the present research, water quality parameters like EC and TDS of the Upper Indus Basin (UIB) at the Bisham Qilla monitoring stations were modeled employing MEP algorithmic procedures and the traditional non-linear regression (NLR) approach based on the most affecting variables. A comprehensive dataset of 360 monthly readings taken from the Water and Power Development Authority (WAPDA) is being partitioned into three sets (training, validation, and testing) to verify the efficiency of the training process. To guarantee model efficacy, reliability and applicability, an in-depth statistical error test and sensitivity study is performed on the developed MEP models. The models that effectively predict TDS and EC concentrations by employing a small set of variables considerably minimize the trouble and expense involved in environmental surveillance.
5. Conclusions
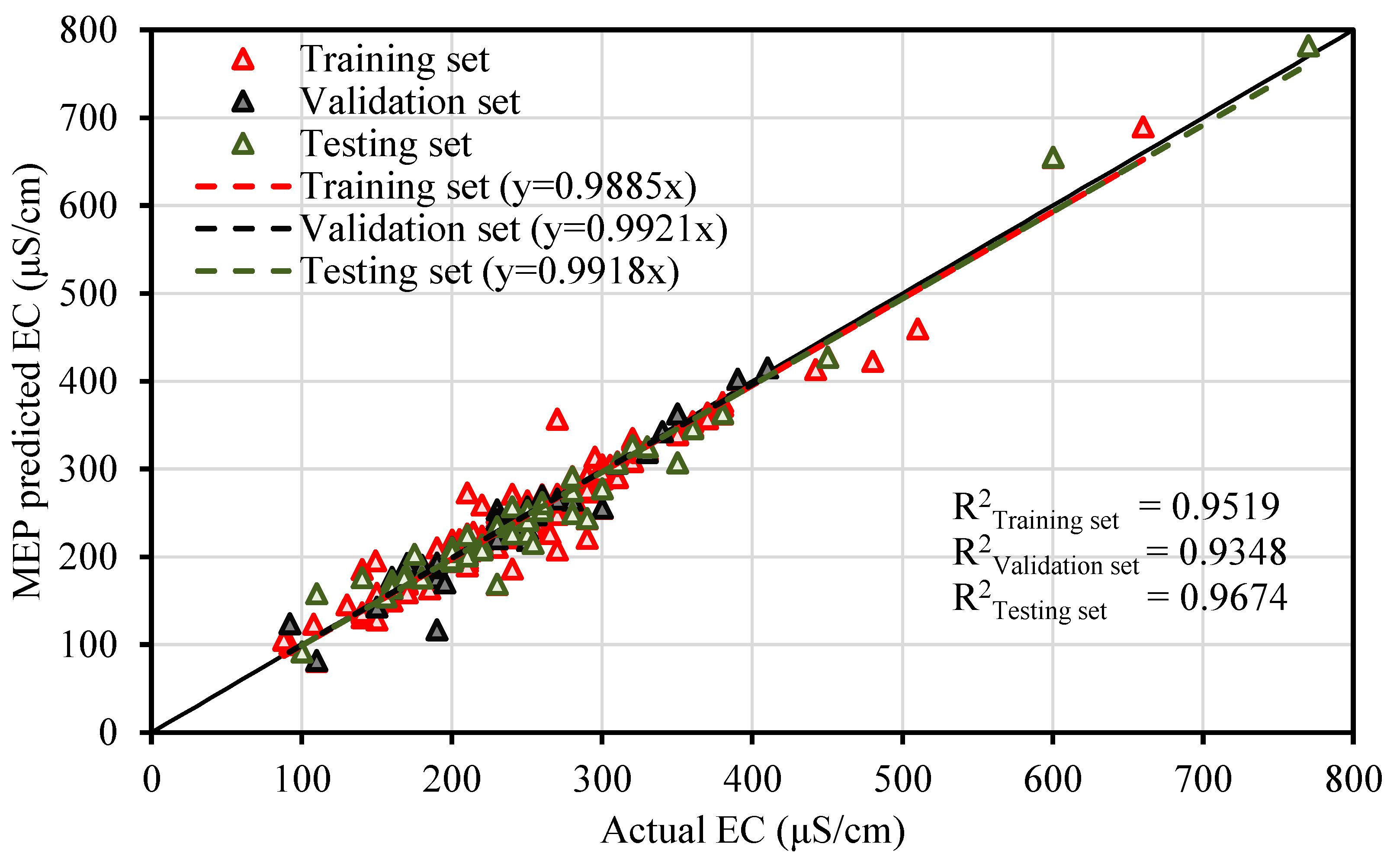
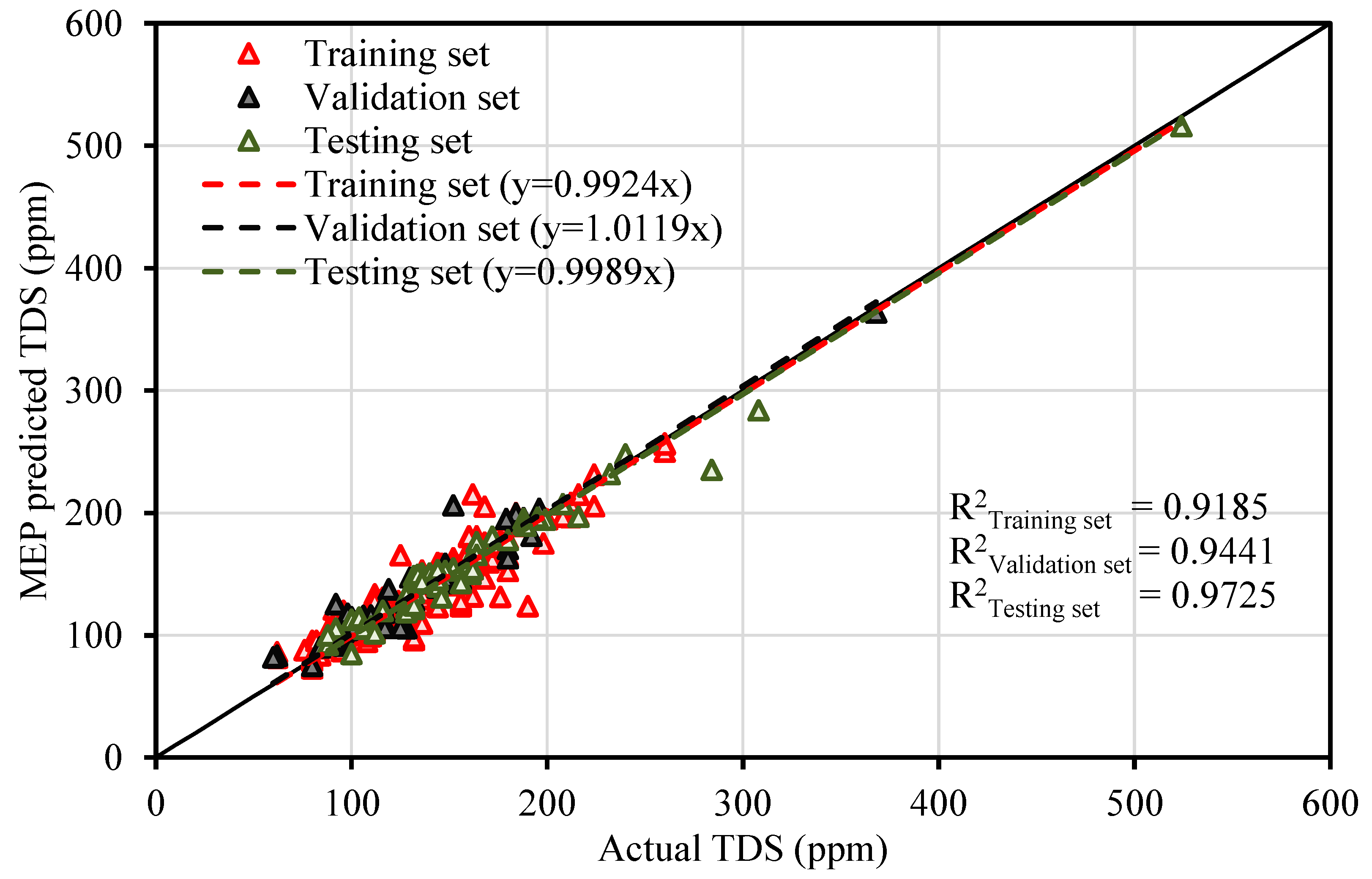
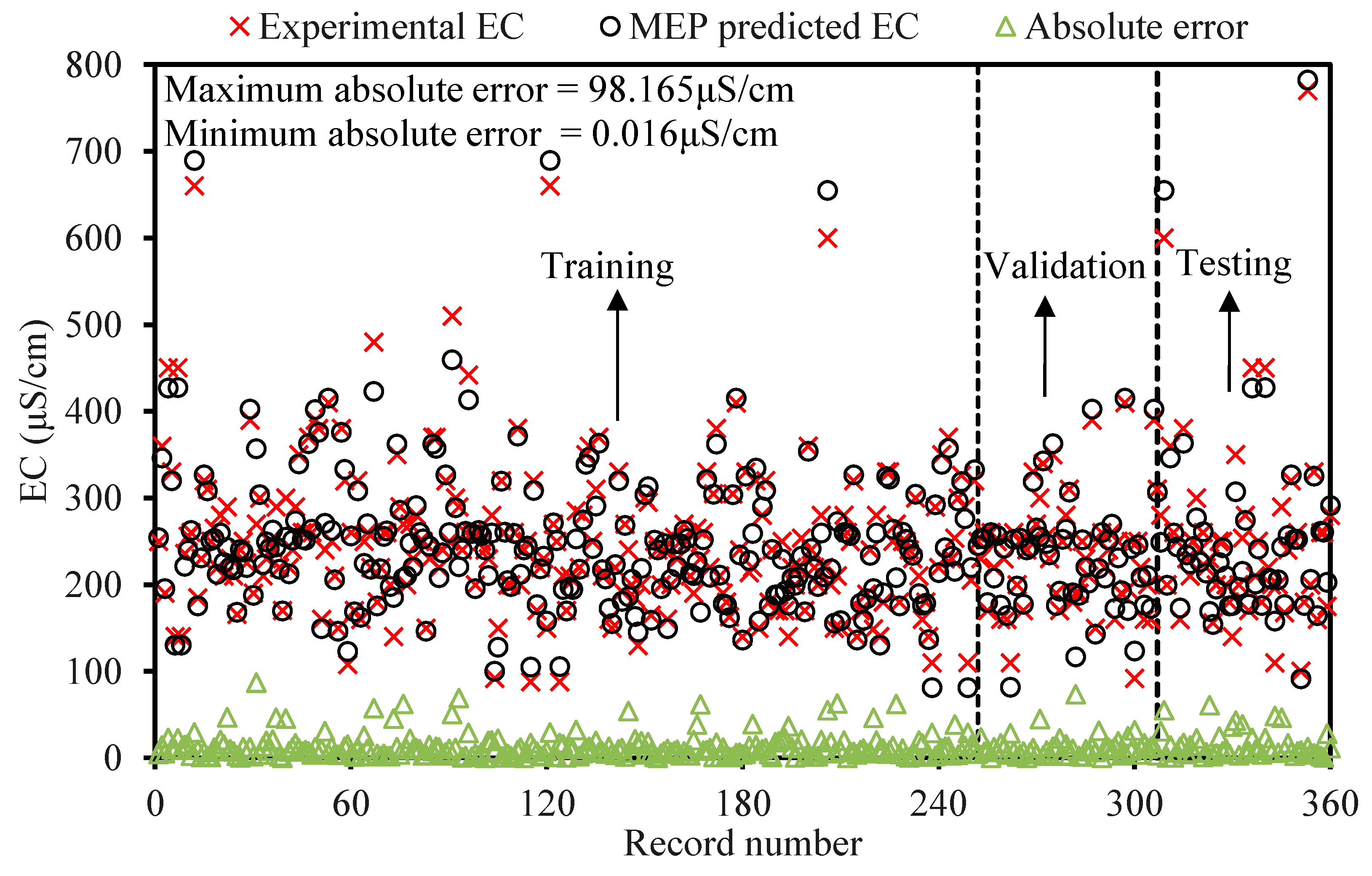
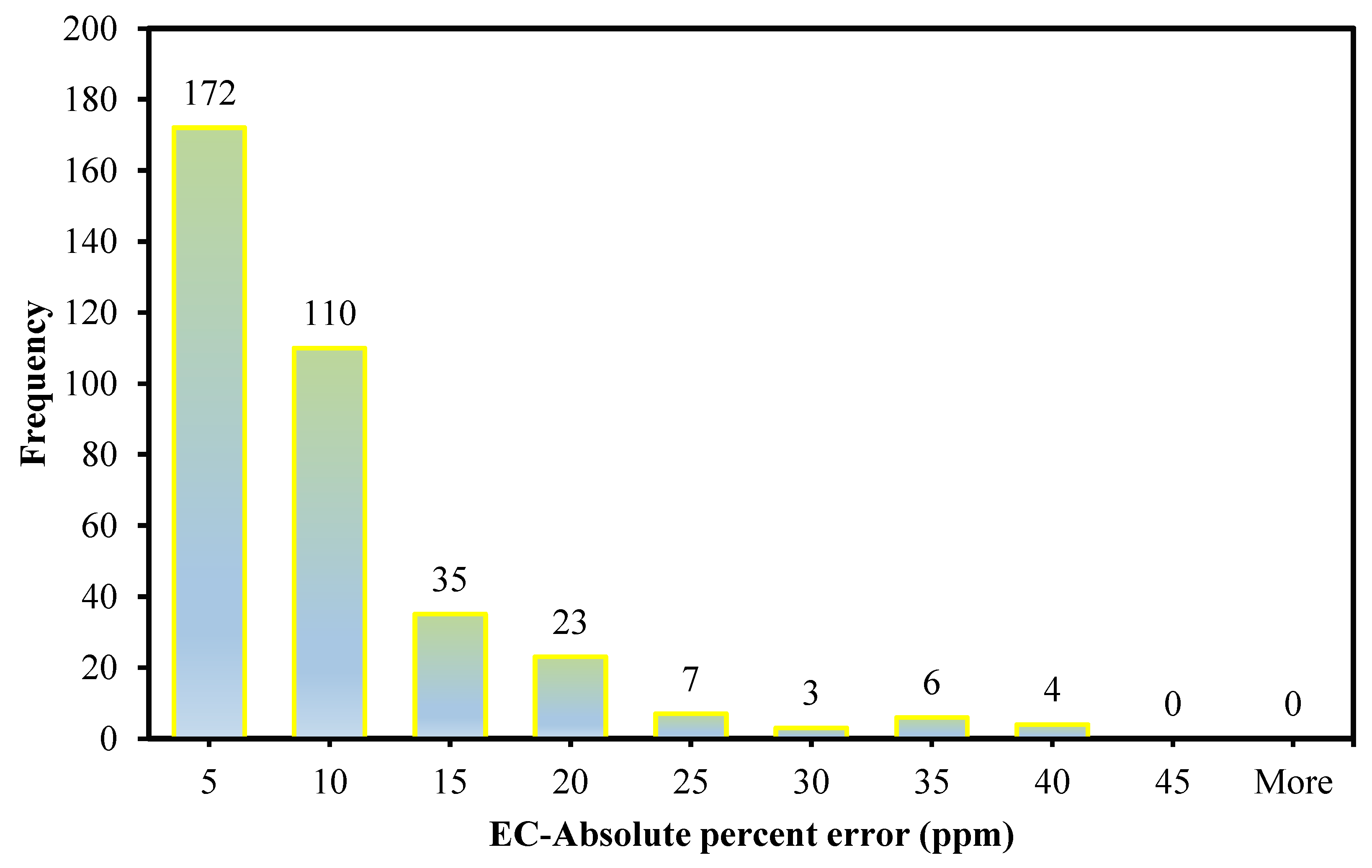
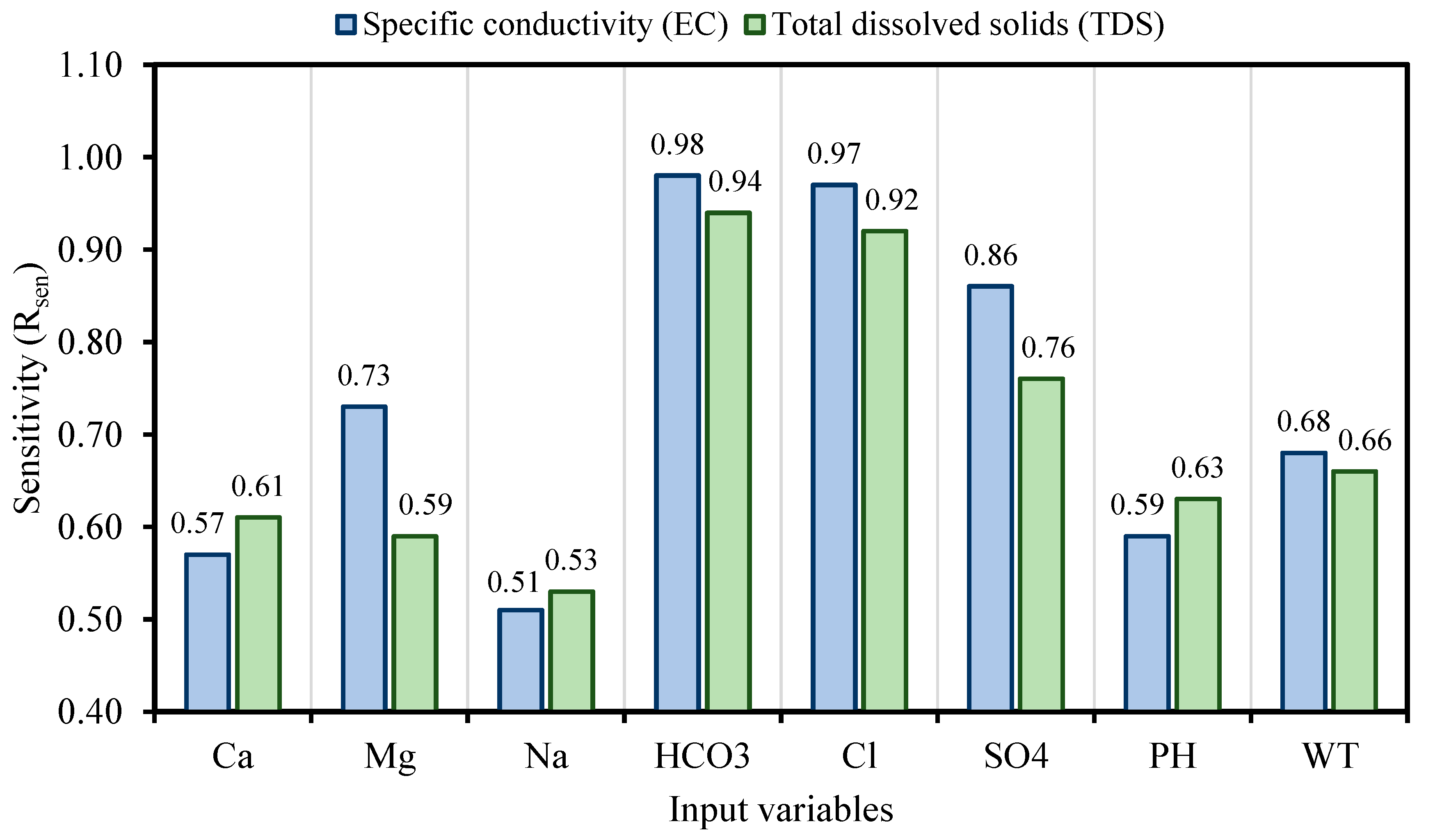
The contamination of water is a big issue that directly threatens both human health and the environment, and also poses a serious issue for agricultural productivity. This study proposed evolutionary algorithm- (EA) based multi-expression programming (MEP) models for the prediction of specific conductivity (EC) and total dissolved solids (TDS). A bigger water quality dataset of 360 readings collected on a monthly basis was used in the modeling process. The eight most influential water quality input variables were selected, i.e., water temperature (°C), magnesium (Mg), calcium (Ca), sodium (Na), sulphate (SO4), chloride (Cl), pH, and bicarbonates (HCO3). The accuracy, reliability and generalization of the established models were evaluated using various well-known of statistical measures, i.e., slope and coefficient of determination (R2), mean-absolute-present error (MAPE), mean-absolute-error (MAE), root-mean-square-logarithmic error (RMSLE), and root-mean-square error (RMSE). The performance of the models was compared with traditional multiple non-linear regression (NLRM) models. The regression results of EC-MEP and TDS-MEP showed excellent accuracy with coefficient of regression (R2) and slope above 0.95 in the testing phase on unseen data. Also, the error statistics are minimum, showing the generalized and reliable performance. The projected (RMSE and MAE) in EC prediction were (18.54 μS/cm and 12.36 μS/cm), (17.19 μS/cm and 12.14 μS/cm) and (16.43 μS/cm and 11.22 μS/cm) for training, validation and testing sets, respectively, and for the TDS modeling they were (13.36 ppm and 9.75 ppm), (13.33 ppm and 9.80 ppm) and (11.36 ppm and 8.27 ppm), respectively. The RMSLE approaches 0, indicating an outburst performance. According to MAPE, the performance of the established models was categorized as “excellent” and thus can be confidently used for future predictions. The predictions of NLRMs show a significant deviation from the targeted results, reflecting the reduced performance statistics that made the reliability of the NLRMs doubtful. However, the MAPE of the NLRMs also falls within acceptable limits i.e., below 50%. In essence, the traditional regression models (i.e., NLRMs) are not useful for the prediction of complex problems because of their inefficiency and least generalization capability. Furthermore, the sensitivity analysis of the developed MEP models revealed that all of the eight variables considered in current research influences the prediction of the water quality parameters (EC and TDS), with distinct effects having a sensitiveness index above 0.5. Thus, the developed EA-based MEP models are not merely the correlations but can be helpful for practitioners and decision-makers that will eventually save the time and money required for monitoring water quality parameters.