Spatio-Temporal Interpolation and Bias Correction Ordering Analysis for Hydrological Simulations: An Assessment on a Mountainous River Basin
Abstract
:1. Introduction
2. Materials and Methods
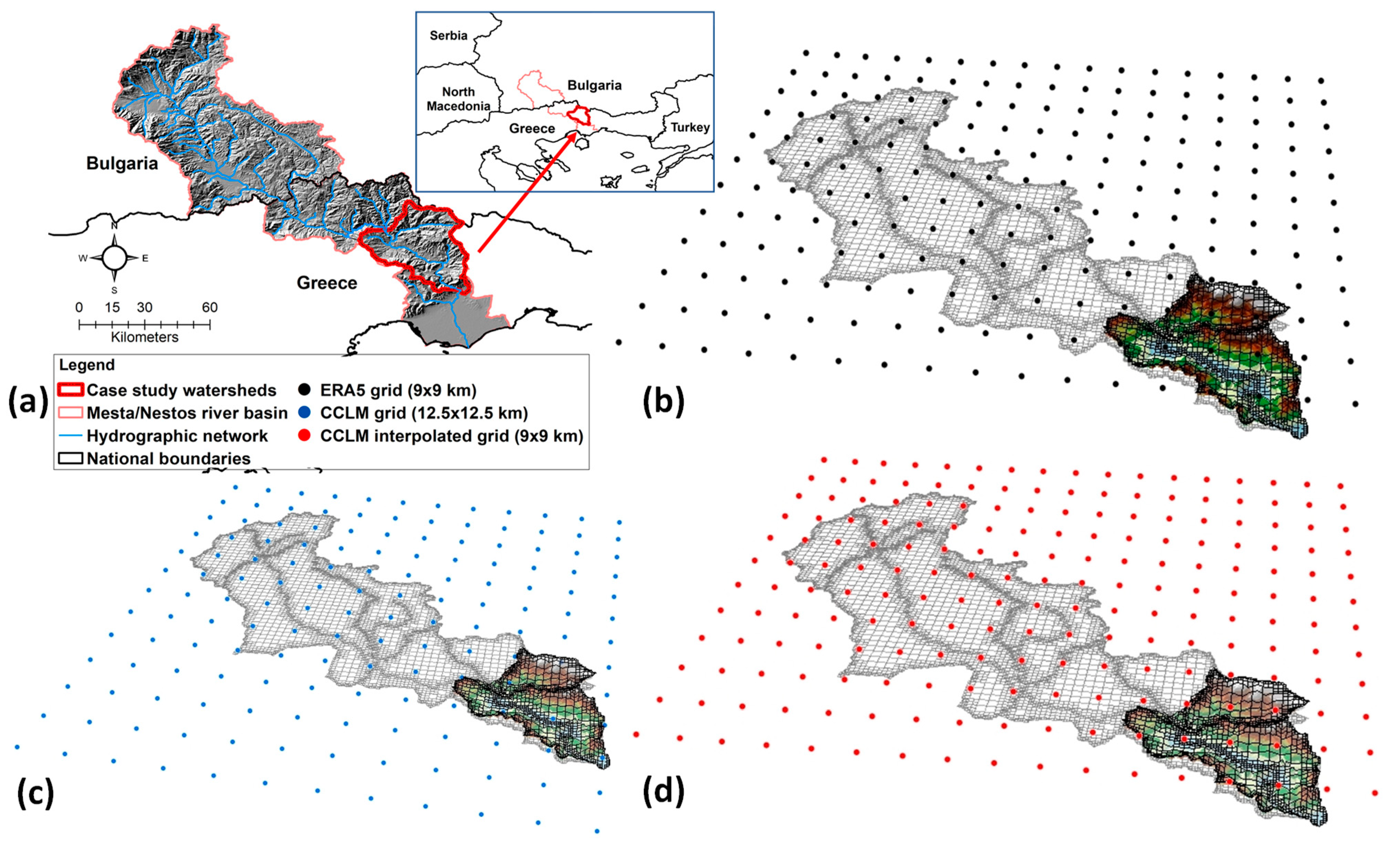
2.1. Case Study Area
2.2. Utilized Datasets, bias Correction, and Spatio-Temporal Methods
2.2.1. ERA5 Precipitation and Temperature
2.2.2. Climate Model
2.2.3. Bias Correction Methods
2.2.4. Spatio-Temporal Kriging Method
2.3. Hydrological Modeling
3. Results
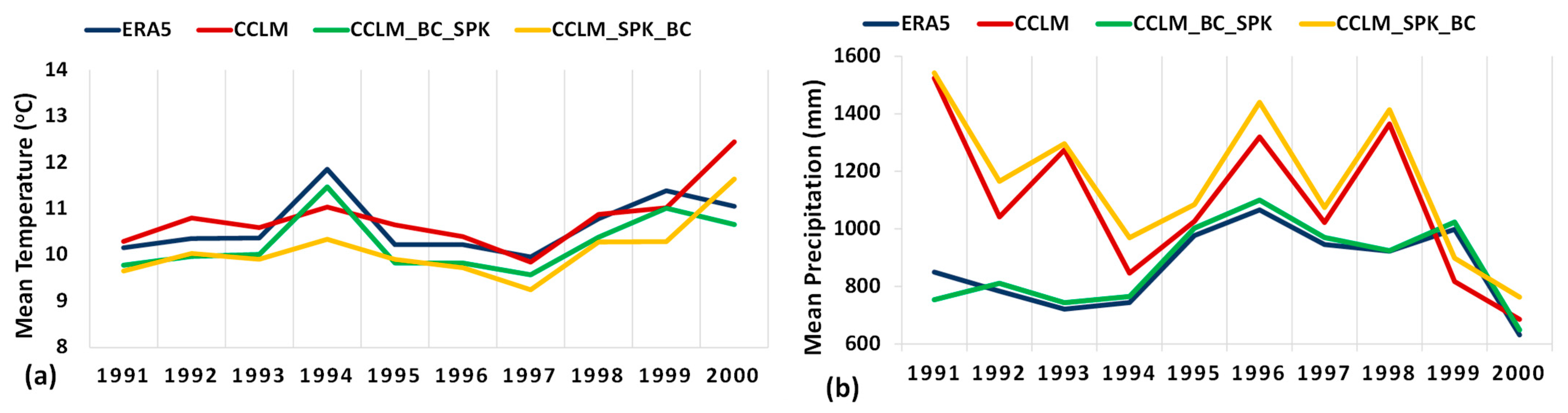
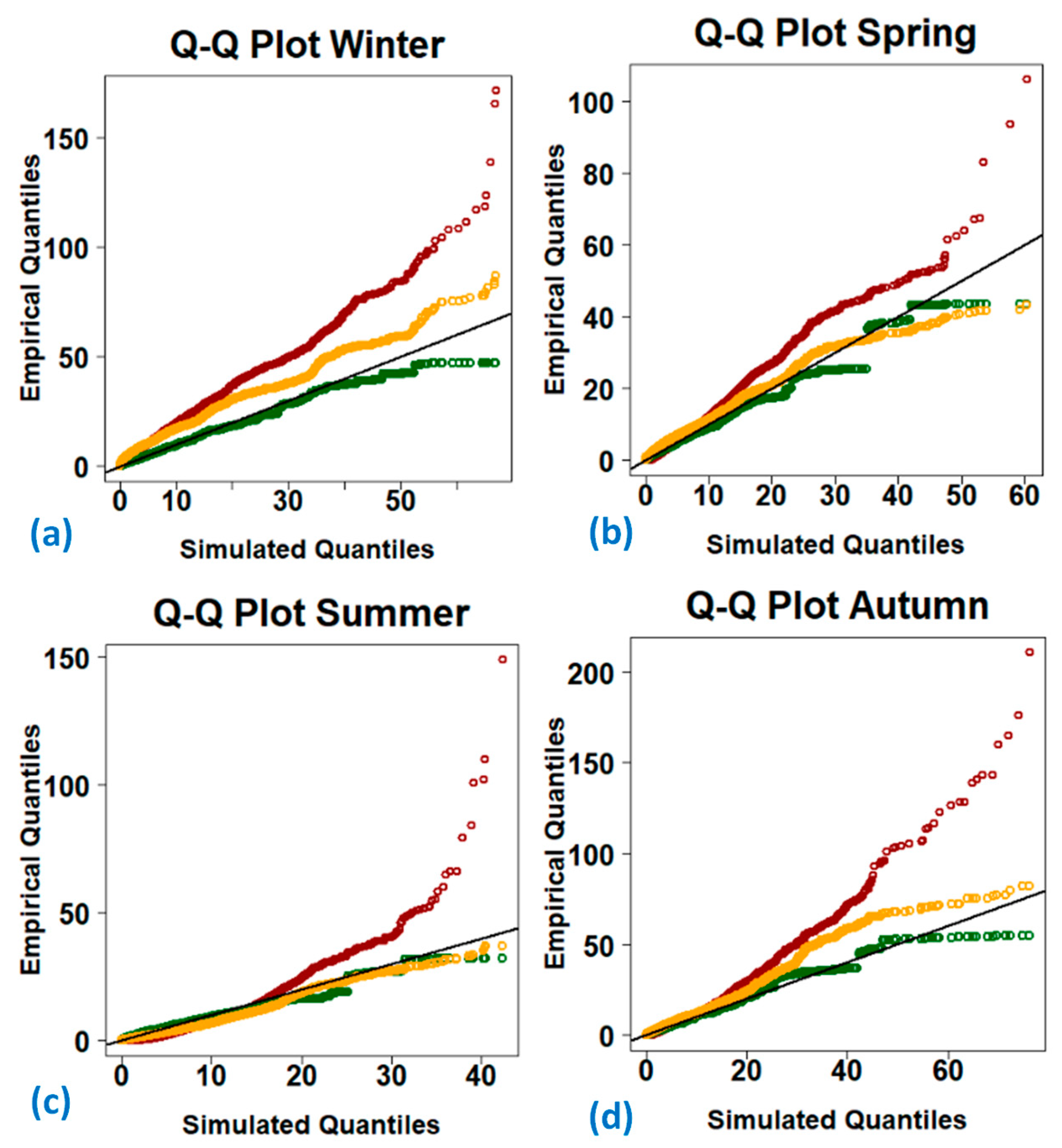
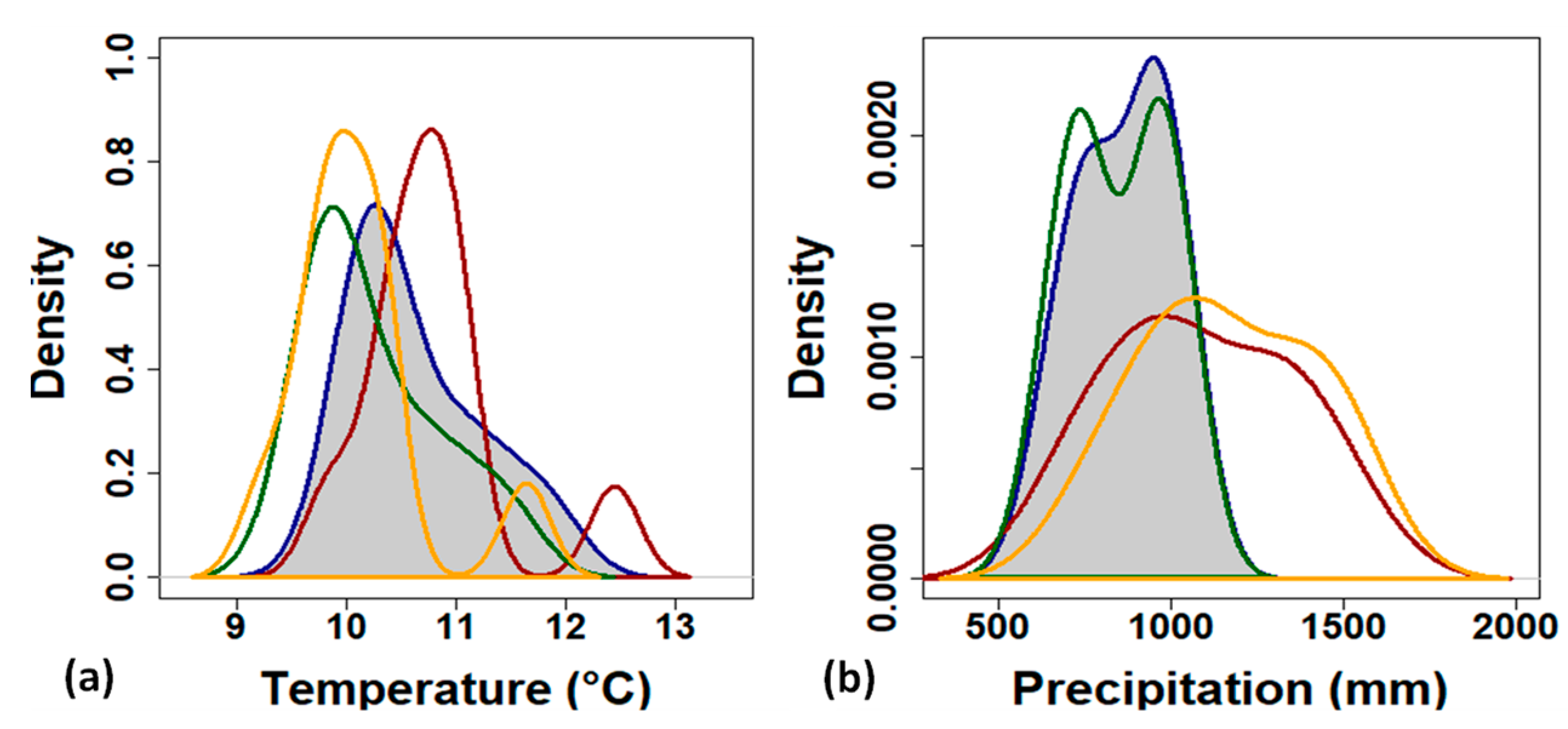
3.1. Climate Datasets Analysis’ Outputs
3.1.1. Precipitation Data
3.1.2. Temperature Data
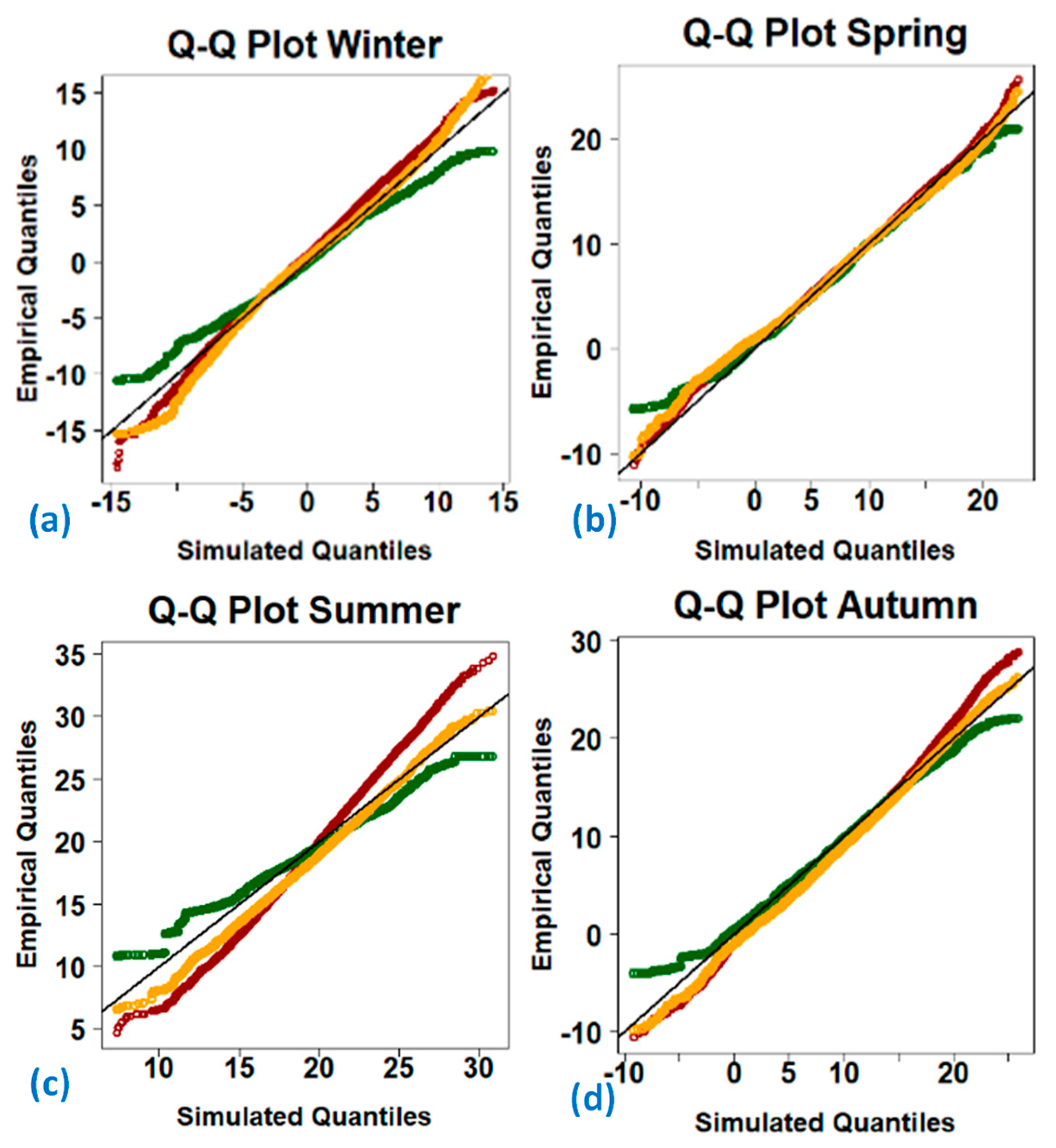
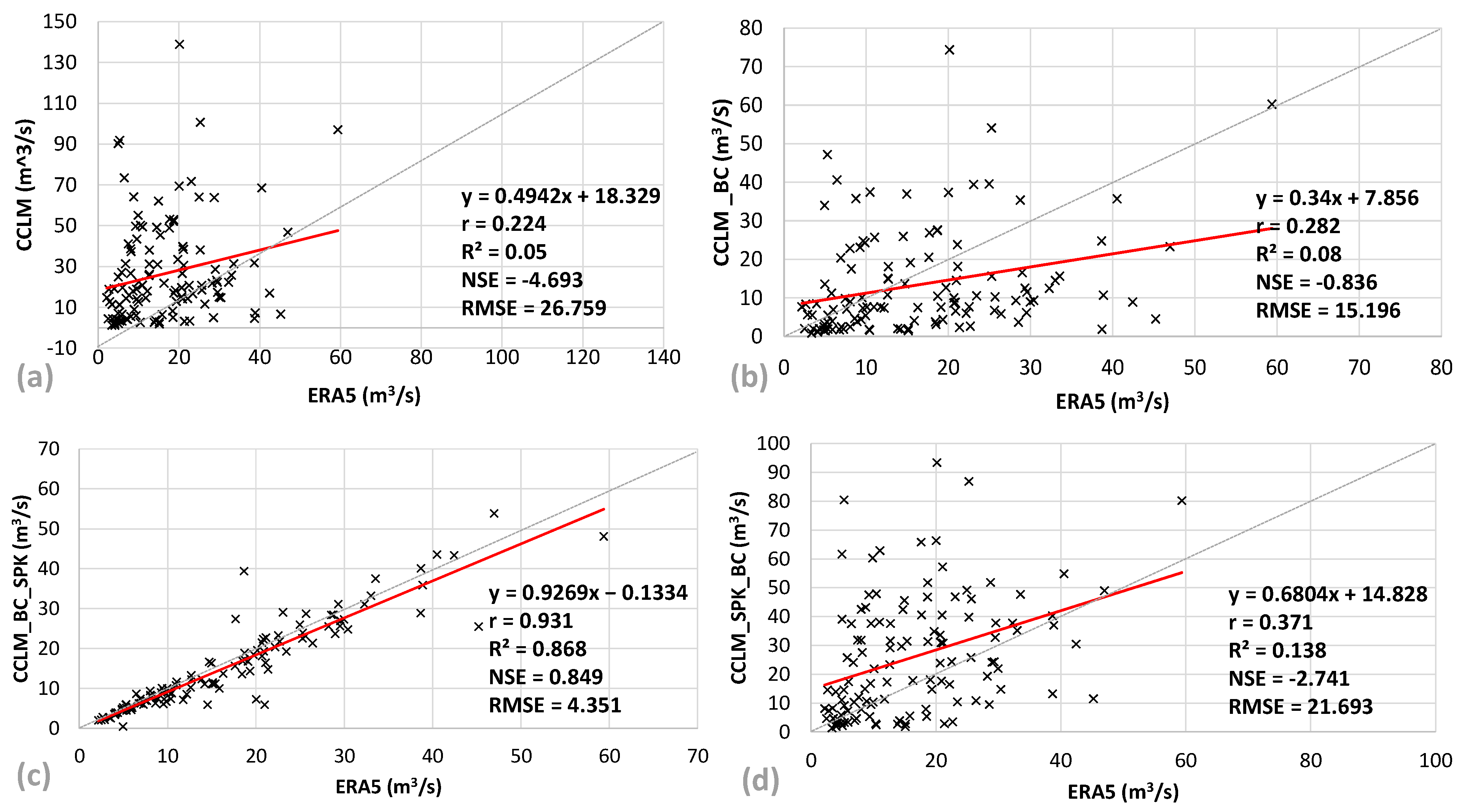
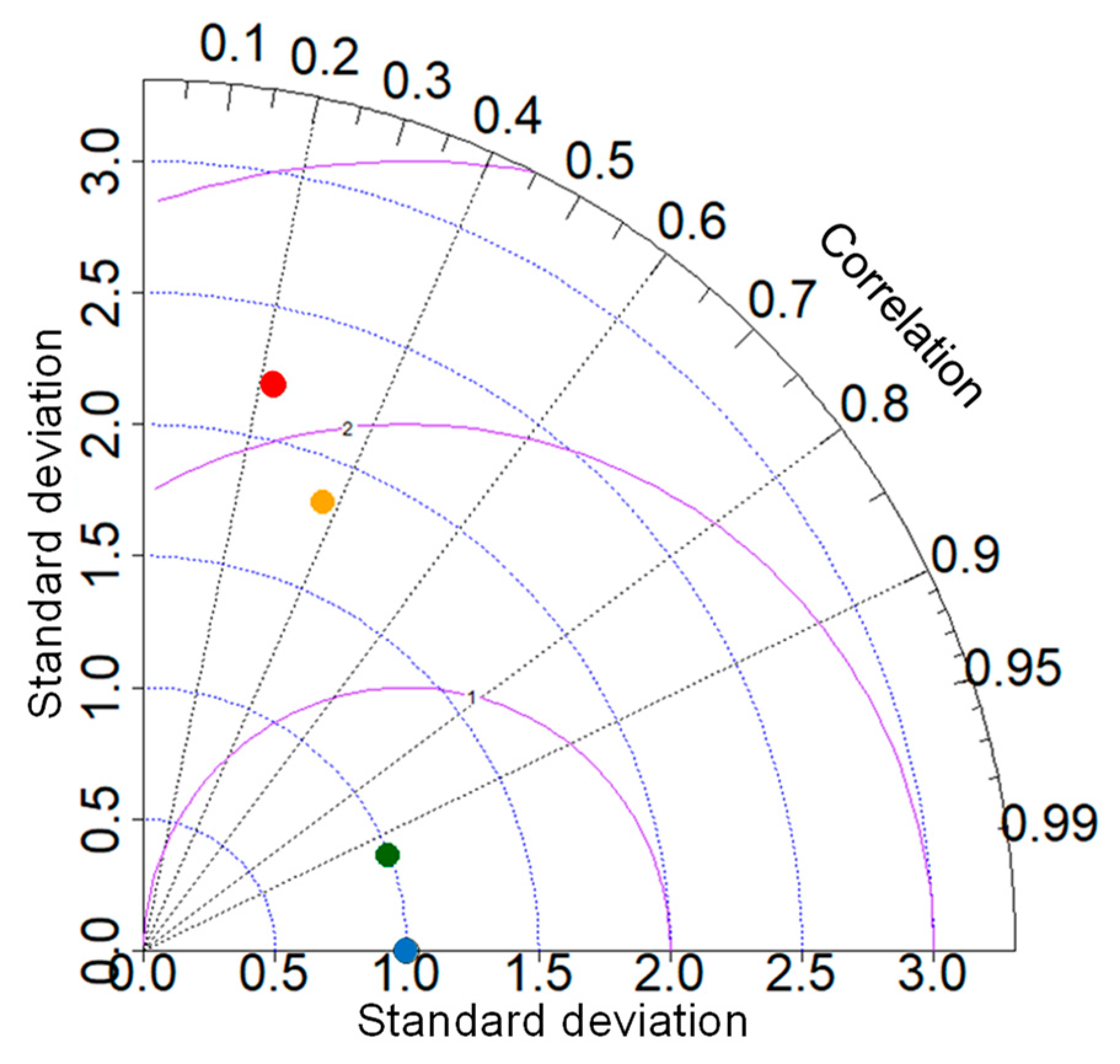
3.2. Hydrological Simulation Outputs
4. Discussion
4.1. Accuracy of Data, Methods, and Models
4.2. Interpretation of Findings
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raimonet, M.; Oudin, L.; Thieu, V.; Silvestre, M.; Vautard, R.; Rabouille, C.; Moigne, P.L. Evaluation of Gridded Meteorological Datasets for Hydrological Modeling. J. Hydrometeorol. 2017, 18, 3027–3041. [Google Scholar] [CrossRef]
- Fréjaville, T.; Benito Garzón, M. The EuMedClim database: Yearly climate data (1901–2014) of 1 km resolution grids for Europe and the Mediterranean Basin. Front. Ecol. Evol. 2018, 6, 31. [Google Scholar] [CrossRef] [Green Version]
- Arshad, M.; Ma, X.; Yin, J.; Ullah, W.; Liu, M.; Ullah, I. Performance evaluation of ERA-5, JRA-55, MERRA-2, and CFS-2 reanalysis datasets, over diverse climate regions of Pakistan. Weather Clim. Extrem. 2021, 33, 100373. [Google Scholar] [CrossRef]
- Xu, X.; Frey, S.K.; Boluwade, A.; Erler, A.R.; Khader, O.; Lapen, D.R.; Sudicky, E. Evaluation of variability among different precipitation products in the Northern Great Plains. J. Hydrol. Reg. Stud. 2019, 24, 100608. [Google Scholar] [CrossRef]
- Dhanya, C.T.; Villarini, G. An investigation of predictability dynamics of temperature and precipitation in reanalysis datasets over the continental United States. Atmos. Res. 2017, 183, 341–350. [Google Scholar] [CrossRef]
- Wong, J.S.; Razavi, S.; Bonsal, B.R.; Wheater, H.S.; Asong, Z.E. Inter-comparison of daily precipitation products for large-scale hydro-climatic applications over Canada. Hydrol. Earth Syst. Sci. 2017, 21, 2163–2185. [Google Scholar] [CrossRef] [Green Version]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979–present). J. Hydrometeorol. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The tropical rainfall measuring mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.-K.; Hnilo, J.J.; Fiorino, M.; Potter, G.L. NCEP–DOE AMIP-II Reanalysis (R-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- Mesinger, F.; DiMego, G.; Kalnay, E.; Mitchell, K.; Shafran, P.C.; Ebisuzaki, W.; Jović, D.; Woollen, J.; Rogers, E.; Berbery, E.H.; et al. North American regional reanalysis. Bull. Am. Meteorol. Soc. 2006, 87, 343–360. [Google Scholar] [CrossRef] [Green Version]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Pan, H.L.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Kistler, R.; Woollen, J.; Behringer, D.; et al. The NCEP climate forecast system reanalysis. Bull. Am. Meteorol. Soc. 2015, 91, 1015–1057. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horanyi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Pelosi, A.; Terribile, F.; D’Urso, G.; Chirico, G.B. Comparison of ERA5-Land and UERRA MESCAN-SURFEX Reanalysis Data with Spatially Interpolated Weather Observations for the Regional Assessment of Reference Evapotranspiration. Water 2020, 12, 1669. [Google Scholar] [CrossRef]
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global surface temperature change. Rev. Geophys. 2010, 48, RG4004. [Google Scholar] [CrossRef] [Green Version]
- Jones, P.D.; Lister, D.H.; Osborn, T.J.; Harpham, C.; Salmon, M.; Morice, C.P. Hemispheric and large-scale land-surface air temperature variations: An extensive revision and an update to 2010. J. Geophys. Res. Atmos. 2012, 117, D05127. [Google Scholar] [CrossRef] [Green Version]
- Hofstra, N.; Haylock, M.; New, M.; Jones, P.; Frei, C. Comparison of six methods for the interpolation of daily, European climate data. J. Geophys. Res.-Atmos. 2008, 113, D21110. [Google Scholar] [CrossRef] [Green Version]
- Mavromatis, T.; Voulanas, D. Evaluating ERA-Interim, Agri4Cast, and E-OBS gridded products in reproducing spatiotemporal characteristics of precipitation and drought over a data poor region: The Case of Greece. Int. J. Climatol. 2021, 41, 2118–2136. [Google Scholar] [CrossRef]
- Bosilovich, M.G.; Kennedy, J.; Dee, D.; Allan, R.; O’Neill, A. On the reprocessing and reanalysis of observations for climate. In Climate Science for Serving Society; Asrar, G.R., Hurrell, J.W., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 51–72. [Google Scholar]
- Krysanova, V.; Donnelly, C.; Gelfan, A.; Gerten, D.; Arheimer, B.; Hattermann, F.; Kundzewicz, Z.W. How the performance of hydrological models relates to credibility of projections under climate change. Hydrol. Sci. J. 2018, 63, 696–720. [Google Scholar] [CrossRef]
- Hay, L.E.; Clark, M.P.; Wilby, R.; Gutowski, W.J.; Leavesley, G.H.; Pan, Z.; Arritt, R.W.; Takle, E.S. Use of Regional Climate Model Output for Hydrologic Simulations. J. Hydrometeorol. 2002, 3, 571–590. [Google Scholar] [CrossRef]
- Kleinn, J.; Frei, C.; Gurtz, J.; Lüthi, D.; Vidale, P.L.; Schär, C. Hydrologic simulations in the Rhine basin driven by a regional climate model. J. Geophys. Res. D Atmos. 2005, 110, D04102. [Google Scholar] [CrossRef]
- Johnson, F.; Sharma, A. Accounting for interannual variability: A comparison of options for water resources climate change impact assessments. Water Resour. Res. 2011, 47, W04508.I. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Chaumont, D.; Braun, M. Finding Appropriate Bias Correction Methods in Downscaling Precipitation for Hydrologic Impact Studies over North America. Water Resour. Res. 2013, 49, 4187–4205. [Google Scholar] [CrossRef]
- Chen, C.; Haerter, J.O.; Hagemann, S.; Piani, C. On the contribution of statistical bias correction to the uncertainty in the projected hydrological cycle. Geophys. Res. Lett. 2011, 38, L20403. [Google Scholar] [CrossRef] [Green Version]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456, 12–29. [Google Scholar] [CrossRef]
- Fujihara, Y.; Tanaka, K.; Watanabe, T.; Nagano, T.; Kojiri, T. Assessing the impacts of climate change on the water resources of the Seyhan River Basin in Turkey: Use of dynamically downscaled data for hydrologic simulations. J. Hydrol. 2008, 353, 33–48. [Google Scholar] [CrossRef]
- Kidd, C.; Becker, A.; Huffman, G.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D. So, How Much of the Earth’s Surface Is Covered by Rain Gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef]
- Fuka, D.R.; Walter, M.T.; MacAlister, C.; Degaetano, A.T.; Steenhuis, T.S.; Easton, Z.M. Using the Climate Forecast System Reanalysis as weather input data for watershed models. Hydrol. Process. 2014, 28, 5613–5623. [Google Scholar] [CrossRef]
- Soriano, E.; Mediero, L.; Garijo, C. Selection of Bias Correction Methods to Assess the Impact of Climate Change on Flood Frequency Curves. Water 2019, 11, 2266. [Google Scholar] [CrossRef] [Green Version]
- Lazoglou, G.; Anagnostopoulou, C.; Skoulikaris, C.; Tolika, K. Bias Correction of Climate Model’s Precipitation Using the Copula Method and Its Application in River Basin Simulation. Water 2019, 11, 600. [Google Scholar] [CrossRef] [Green Version]
- Lagouvardos, K.; Kotroni, V.; Bezes, A.; Koletsis, I.; Kopania, T.; Lykoudis, S.; Mazarakis, N.; Papagiannaki, K.; Vougioukas, S. The automatic weather stations NOANN network of the National Observatory of Athens: Operation and database. Geosci. Data J. 2017, 4, 4–16. [Google Scholar] [CrossRef]
- Liu, D.; Zhao, Q.; Fu, D.; Guo, S.; Liu, P.; Zeng, Y. Comparison of spatial interpolation methods for the estimation of precipitation patterns at different time scales to improve the accuracy of discharge simulations. Hydrol. Res. 2020, 51, 583–601. [Google Scholar] [CrossRef]
- Cheng, M.; Wang, Y.; Engel, B.; Zhang, W.; Peng, H.; Chen, X.; Xia, H. Performance Assessment of Spatial Interpolation of Precipitation for Hydrological Process Simulation in the Three Gorges Basin. Water 2017, 9, 838. [Google Scholar] [CrossRef] [Green Version]
- Teegavarapu, R.S.; Meskele, T.; Pathak, C.S. Geo-spatial grid-based transformations of precipitation estimates using spatial interpolation methods. Comput. Geosci. 2012, 40, 28–39. [Google Scholar] [CrossRef]
- Yang, X.; Xie, X.; Liu, D.L.; Ji, F.; Wang, L. Spatial Interpolation of Daily Rainfall Data for Local Climate Impact Assessment over Greater Sydney Region. Adv. Meteorol. 2015, 2015, 563629. [Google Scholar] [CrossRef] [Green Version]
- Heuvelink, G.B.; Griffith, D.A.; Hengl, T.; Melles, S.J. Sampling design optimization for space-time kriging. In Spatio-Temporal Design; John Wiley & Sons, Ltd.: Chichester, UK, 2012; pp. 207–230. ISBN 9781118441862. [Google Scholar]
- Heuvelink, G.B.M.; Griffth, D.A. Space-time geostatistics for geography: A case study of radiation monitoring across parts of Germany. Geog. Anal. 2010, 42, 161–179. [Google Scholar] [CrossRef]
- Gräler, B.; Rehr, M.; Gerharz, L.; Pebesma, E.J. Spatio-Temporal Analysis and Interpolation of PM10 Measurements in Europe for 2009. ETC/ACM Tech. Paper 2012/08 2013, 30p. Available online: https://www.eionet.europa.eu/etcs/etc-atni/products/etc-atni-reports/etcacm_2012_8_spatio-temp_pm10analyses (accessed on 4 January 2021).
- Venetsanou, P.; Anagnostopoulou, C.; Loukas, A.; Lazoglou, G.; Voudouris, K. Minimizing the uncertainties of RCMs climate data by using spatio-temporal geostatistical modeling. Earth Sci. Inform. 2019, 12, 183–196. [Google Scholar]
- Leta, O.T.; Nossent, J.; Velez, C.; Shrestha, N.K.; van Griensven, A.; Bauwens, W. Assessment of the different sources of uncertainty in a SWAT model of the River Senne (Belgium). Environ. Modell. Softw. 2015, 68, 129–146. [Google Scholar] [CrossRef]
- Lobligeois, F.; Andréassian, V.; Perrin, C.; Tabary, P.; Loumagne, C. When does higher spatial resolution rainfall information improve streamflow simulation? An evaluation using 3620 flood events. Hydrol. Earth Syst. Sci. 2014, 18, 575–594. [Google Scholar] [CrossRef] [Green Version]
- Sridharan, V.; Broad, O.; Shivakumar, A.; Howells, M.; Boehlert, B.; Groves, D.G.; Rogner, H.-H.; Taliotis, C.; Neumann, J.E.; Strzepek, K.M.; et al. Resilience of the Eastern African electricity sector to climate driven changes in hydropower generation. Nat. Commun. 2019, 10, 302. [Google Scholar] [CrossRef] [Green Version]
- Rabiei, E.; Haberlandt, U. Applying bias correction for merging rain gauge and radar data. J. Hydrol. 2015, 522, 544–557. [Google Scholar] [CrossRef]
- Skoulikaris, C.; Makris, C.; Katirtzidou, M.; Baltikas, V.; Krestenitis, Y. Assessing the vulnerability of a deltaic environment due to climate change impact on surface and coastal waters: The case of Nestos River (Greece). Environ. Mod. Assess. 2021, 26, 459–486. [Google Scholar] [CrossRef]
- Special Secretariat for Water (SSW). The River Basin Management Plan of Thrace Water District (GR11); Ministry of Environment and Energy: Athens, Greece, 2013. (In Greek) [Google Scholar]
- Pothapakula, P.K.; Primo, C.; Sørland, S.; Ahrens, B. The synergistic impact of ENSO and IOD on Indian summer monsoon rainfall in observations and climate simulations—An information theory perspective. Earth Syst. Dynam. 2020, 11, 903–923. [Google Scholar] [CrossRef]
- Vautard, R.; Kadygrov, N.; Iles, C.; Boberg, F.; Buonomo, E.; Bülow, K.; Coppola, E.; Corre, L.; Meijgaard, E.; Nogherotto, R.; et al. Evaluation of the large EURO-CORDEX regional climate model ensemble. J. Geophys. Res. Atmos. 2020, 126, e2019JD032344. [Google Scholar] [CrossRef]
- Panofsky, H.G.; Brier, G.W. Some Applications of Statistics to Meteorology; Mineral Industries Extension Services; College of Mineral Industries, Pennsylvania State University: State College, PA, USA, 1958. [Google Scholar]
- Angus, J.E. The Probability Integral Transform and Related Results. SIAM Rev. 1994, 36, 652–654. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.O.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef] [Green Version]
- Cannon, A.J. Probabilistic Multisite Precipitation Downscaling by an Expanded Bernoulli Gamma Density Network. J. Hydrometeorol. 2008, 9, 1284–1300. [Google Scholar] [CrossRef]
- Li, H.; Sheffield, J.; Wood, E.F. Bias correction of monthly precipitation and temperature fields from Intergovernmental Panel on Climate Change AR4 models using equidistant 15 quantile matching. J. Geophys. Res. 2010, 115, D10101. [Google Scholar] [CrossRef]
- Casanueva, A.; Herrera, S.; Iturbide, M.; Lange, S.; Jury, M.; Dosio, A.; Maraun, D.; Gutiérrez, J.M. Testing bias adjustment methods for regional climate change applications under observational uncertainty and resolution mismatch. Atmos. Sci. Lett. 2020, 21, e978. [Google Scholar] [CrossRef] [Green Version]
- Bedia, J.; Baño-Medina, J.; Legasa, M.N.; Iturbide, M.; Manzanas, R.; Herrera, S.; Casanueva, A.; San-Martín, D.; Cofiño, A.S.; Gutiérrez, J.M. Statistical downscaling with the downscaleR package (v3.1.0): Contribution to the VALUE intercomparison experiment. Geosci. Model Dev. 2020, 13, 1711–1735. [Google Scholar] [CrossRef] [Green Version]
- Iturbide, M.; Bedia, J.; Herrera, S.; Baño-Medina, J.; Fernández, J.; Frías, M.D.; Manzanas, R.; San-Martínc, D.; Cimadevill, E.; Cofiño, A.S.; et al. The R-based climate4R open framework for reproducible climate data access and post-processing. Environ. Model. Softw. 2019, 111, 42–54. [Google Scholar] [CrossRef]
- Cannon, A.J. Neural networks for probabilistic environmental prediction: Conditional Density Estimation Network Creation and Evaluation (CaDENCE) in R. Comput. Geosci. 2012, 41, 126–135. [Google Scholar] [CrossRef]
- Gräler, B.; Gerharz, L.; Pebesma, E. Spatio-Temporal Interpolation using gstat. R J. 2016, 8, 204–218. [Google Scholar] [CrossRef]
- Pebesma, E.; Graler, B. Introduction to Spatio-Temporal Variography; University of Münster: Münster, Germany, 2021. [Google Scholar]
- Bilonick, R.A. Monthly hydrogen ion deposition maps for the northeastern U.S. from July 1982 to September 1984. Atmos. Environ. 1988, 22, 1909–1924. [Google Scholar] [CrossRef]
- Snepvangers, J.; Heuvelink, G.; Huisman, J. Soil water content interpolation using spatio-temporal kriging with external drift. Geoderma 2003, 112, 253–271. [Google Scholar] [CrossRef]
- Pebesma, E. spacetime: Spatio-Temporal Data in R. J. Stat. Softw. 2012, 51, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Ledoux, E.; Girard, G.; de Marsily, G.; Deschenes, J. Spatially distributed modelling: Conceptual approach, coupling surface water and ground water. In Unsaturated Flow Hydrologic Modelling-Theory and Practice; Morel-Seytoux, H.J., Ed.; NATO ASI Series S 275; Kluwer Academic: Boston, CA, USA, 1989; pp. 435–454. [Google Scholar]
- Skoulikaris, C.; Anagnostopoulou, C.; Lazoglou, G. Hydrological Modeling Response to Climate Model Spatial Analysis of a South Eastern Europe International Basin. Climate 2020, 8, 1. [Google Scholar] [CrossRef] [Green Version]
- Skoulikaris, C.; Ganoulis, J. Climate change impacts on river catchment hydrology using dynamic downscaling of global climate models. In National Security and Human Health Implications of Climate Change; Fernando, H.J.S., Klaic, Z.B., McCulley, J.L., Eds.; Springer: Dordrecht, The Netherlands, 2011; Volume 125, pp. 281–287. [Google Scholar]
- Sepaskhah, A.R.; Razzaghi, F. Evaluation of the adjusted Thornthwaite and Hargreaves-Samani methods for estimation of daily evapotranspiration in a semi-arid region of Iran. Arch. Agron. Soil Sci. 2009, 55, 51–66. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Sharma, D.; Das Gupta, A.; Babel, M.S. Spatial disaggregation of bias-corrected GCM precipitation for improved hydrologic simulation: Ping River Basin, Thailand. Hydrol. Earth Syst. Sci. 2007, 11, 1373–1390. [Google Scholar] [CrossRef] [Green Version]
- Chiaravalloti, F.; Caloiero, T.; Coscarelli, R. The Long-Term ERA5 Data Series for Trend Analysis of Rainfall in Italy. Hydrology 2022, 9, 18. [Google Scholar] [CrossRef]
- Gleixner, S.; Demissie, T.; Diro, G.T. Did ERA5 Improve Temperature and Precipitation Reanalysis over East Africa? Atmosphere 2020, 11, 996. [Google Scholar] [CrossRef]
- Tarek, M.; Brissette, F.; Arsenault, R. Evaluation of the ERA5 reanalysis as a potential reference dataset for hydrological modeling over North-America. Hydrol. Earth Syst. Sci. 2019, 10, 1009–1012. [Google Scholar]
- Xu, J.; Ma, Z.; Yan, S.; Peng, J. Do ERA5 and ERA5-Land Precipitation Estimates Outperform Satellite-based Precipitation Products? A Comprehensive Comparison between State-of-the-art Model-based and Satellite-based Precipitation Products over Mainland China. J. Hydrol. 2022, 605, 127353. [Google Scholar] [CrossRef]
- Mendez, M.; Maathuis, B.; Hein-Griggs, D.; Alvarado-Gamboa, L.-F. Performance Evaluation of Bias Correction Methods for Climate Change Monthly Precipitation Projections over Costa Rica. Water 2020, 12, 482. [Google Scholar] [CrossRef] [Green Version]
- Acharya, N.; Chattopadhyay, S.; Mohanty, U.C.; Dash, S.K.; Sahoo, L.N. On the bias correction of general circulation model output for Indian summer monsoon. Meteorol. Appl. 2013, 20, 349–356. [Google Scholar] [CrossRef]
- Sangelantoni, L.; Russo, A.; Gennaretti, F. Impact of bias correction and downscaling through quantile mapping on simulated climate change signal: A case study over Central Italy. Theor. Appl. Climatol. 2019, 135, 725–740. [Google Scholar] [CrossRef]
- Mishra, B.K.; Rafiei Emam, A.; Masago, Y.; Kumar, P.; Regmi, R.K.; Fukushi, K. Assessment of Future Flood Inundations under Climate and Land Use Change Scenarios in the Ciliwung River Basin, Jakarta. J. Flood Risk Manag. 2018, 11, S1105–S1115. [Google Scholar] [CrossRef]
- Kilibarda, M.; Hengl, T.; Heuvelink, G.B.M.; Gräler, B.; Pebesma, E.; Perčec Tadić, M.; Bajat, B. Spatio-temporal interpolation of daily temperatures for global land areas at 1 km resolution. J. Geophys. Res. Atmos. 2014, 119, 2294–2313. [Google Scholar] [CrossRef] [Green Version]
- Artinyan, E.; Habets, F.; Noilhan, J.; Ledoux, E.; Dimitrov, D.; Martin, E.; Le Moigne, P. Modelling the water budget and the riverflows of the Maritsa basin in Bulgaria. Hydrol. Earth Syst. Sci. 2008, 12, 21–37. [Google Scholar] [CrossRef] [Green Version]
- Rousset, F.; Habets, F.; Gomez, E.; Le Moigne, P.; Morel, S.; Noilhan, J.; Ledoux, E. Hydrometeorological modeling of the Seine basin using the SAFRAN-ISBA-MODCOU system. J. Geophys. Res. Atmos. 2004, 109, D14105. [Google Scholar] [CrossRef]
- Quintana-Seguí, P.; Ribes, A.; Martin, E.; Habets, F.; Boé, J. Comparison of three downscaling methods in simulating the impact of climate change on the hydrology of Mediterranean basins. J. Hydrol. 2010, 383, 111–124. [Google Scholar] [CrossRef] [Green Version]

| Abbreviation | Definition |
|---|---|
| ERA5 | ERA5-Land dataset |
| CCLM | CLMcom-ETH-COSMO-crCLIM_v1 climate model outputs |
| CCLM_BC | Empirical quantile mapping bias correction on CCLM climate data |
| CCLM_BC_SPK | Empirical quantile mapping bias correction on CCLM climate data followed by spatio-temporal kriging |
| CCLM_SPK_BC | Spatio-temporal kriging on CCLM climate outputs followed by bias correction with the empirical quantile mapping method |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skoulikaris, C.; Venetsanou, P.; Lazoglou, G.; Anagnostopoulou, C.; Voudouris, K. Spatio-Temporal Interpolation and Bias Correction Ordering Analysis for Hydrological Simulations: An Assessment on a Mountainous River Basin. Water 2022, 14, 660. https://doi.org/10.3390/w14040660
Skoulikaris C, Venetsanou P, Lazoglou G, Anagnostopoulou C, Voudouris K. Spatio-Temporal Interpolation and Bias Correction Ordering Analysis for Hydrological Simulations: An Assessment on a Mountainous River Basin. Water. 2022; 14(4):660. https://doi.org/10.3390/w14040660
Chicago/Turabian StyleSkoulikaris, Charalampos, Panagiota Venetsanou, Georgia Lazoglou, Christina Anagnostopoulou, and Konstantinos Voudouris. 2022. "Spatio-Temporal Interpolation and Bias Correction Ordering Analysis for Hydrological Simulations: An Assessment on a Mountainous River Basin" Water 14, no. 4: 660. https://doi.org/10.3390/w14040660
APA StyleSkoulikaris, C., Venetsanou, P., Lazoglou, G., Anagnostopoulou, C., & Voudouris, K. (2022). Spatio-Temporal Interpolation and Bias Correction Ordering Analysis for Hydrological Simulations: An Assessment on a Mountainous River Basin. Water, 14(4), 660. https://doi.org/10.3390/w14040660







_S._Voudouris.png)

