A Digital Twin of a Water Distribution System by Using Graph Convolutional Networks for Pump Speed-Based State Estimation
Abstract
:1. Introduction
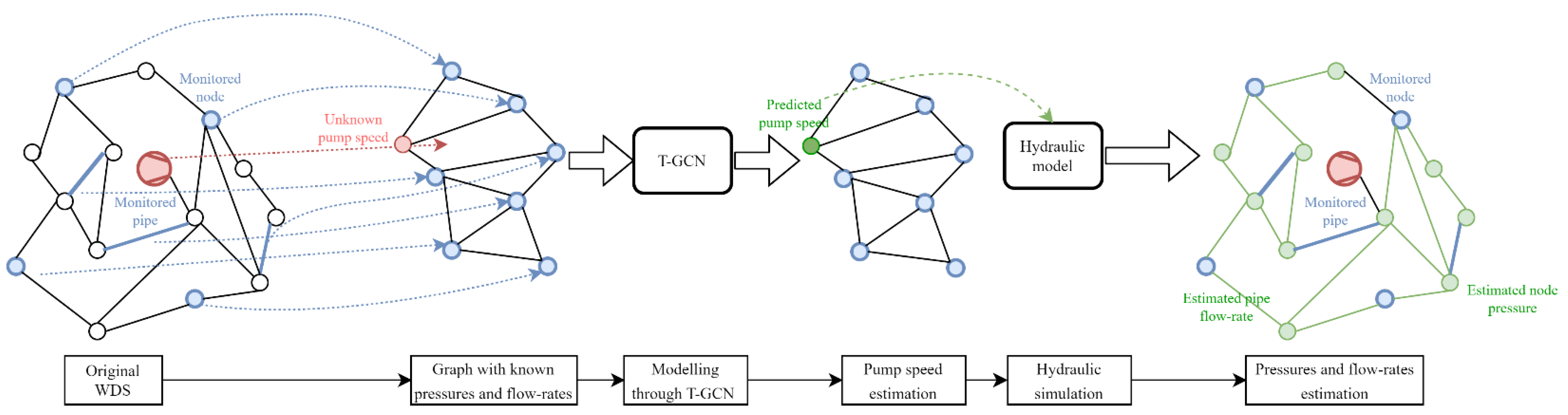
2. Materials and Methods
2.1. Temporal-Graph Convolutional Neural Networks
2.2. Evaluation Parameters
2.3. Pressure and Flow Calculation from the Estimated Relative Speed
3. Case Studies
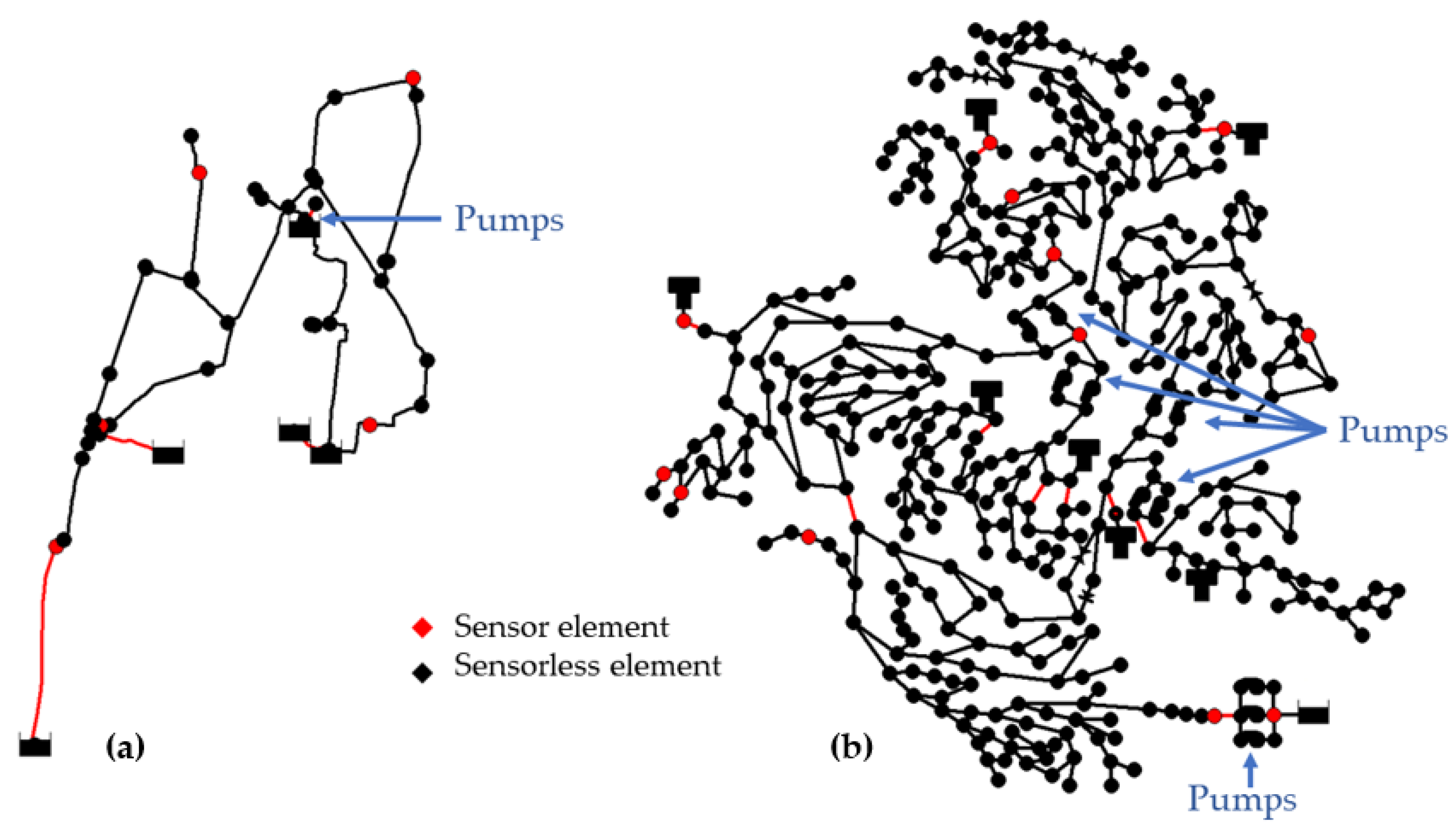
3.1. Network 1: Patios Network-Villa del Rosario
3.2. Network 2: C-Town Network
3.3. Data Set Generation for T-GCN Application
4. Results
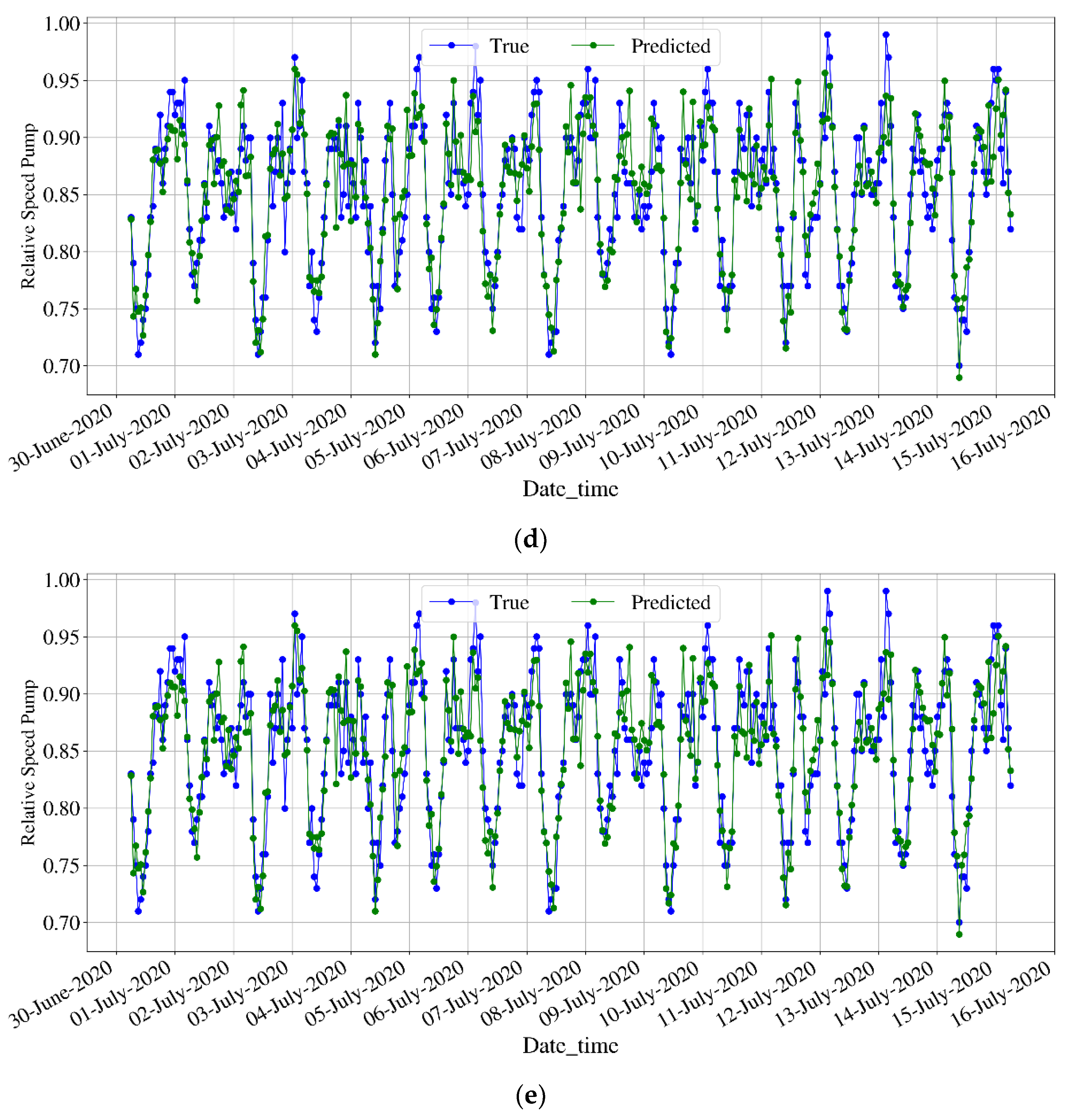
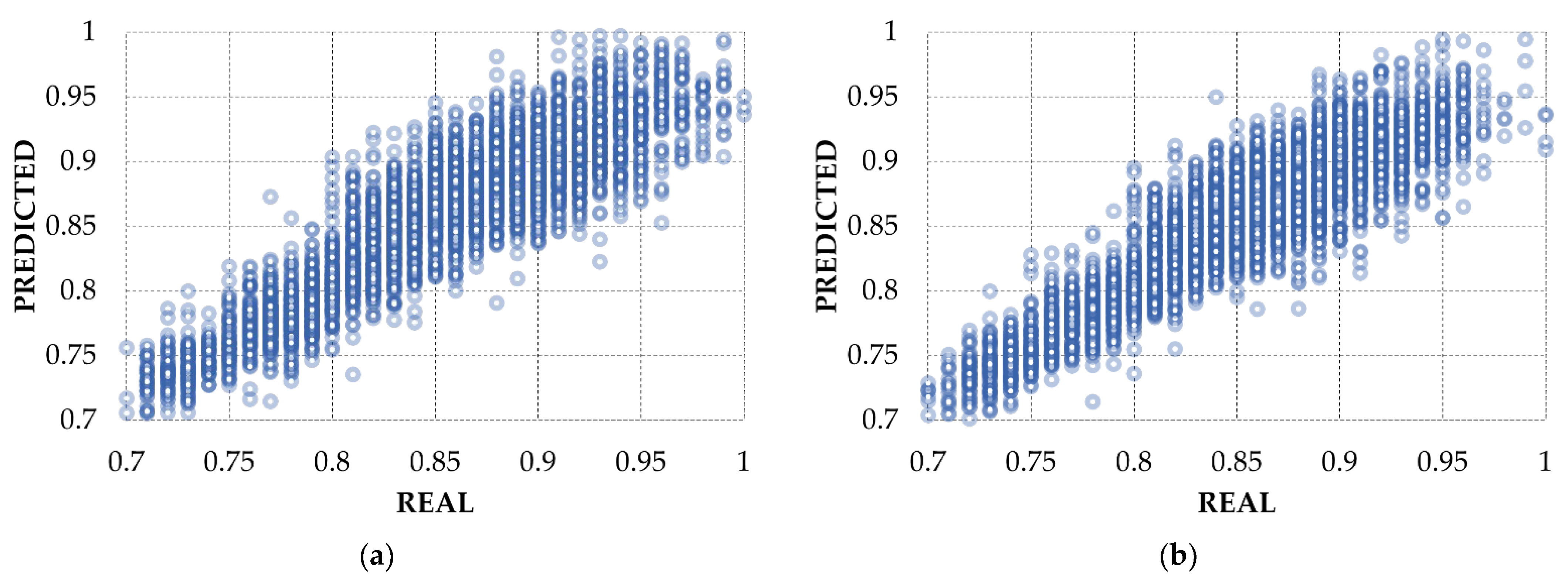
4.1. T-GCN Evaluation for Pump Speed Estimation
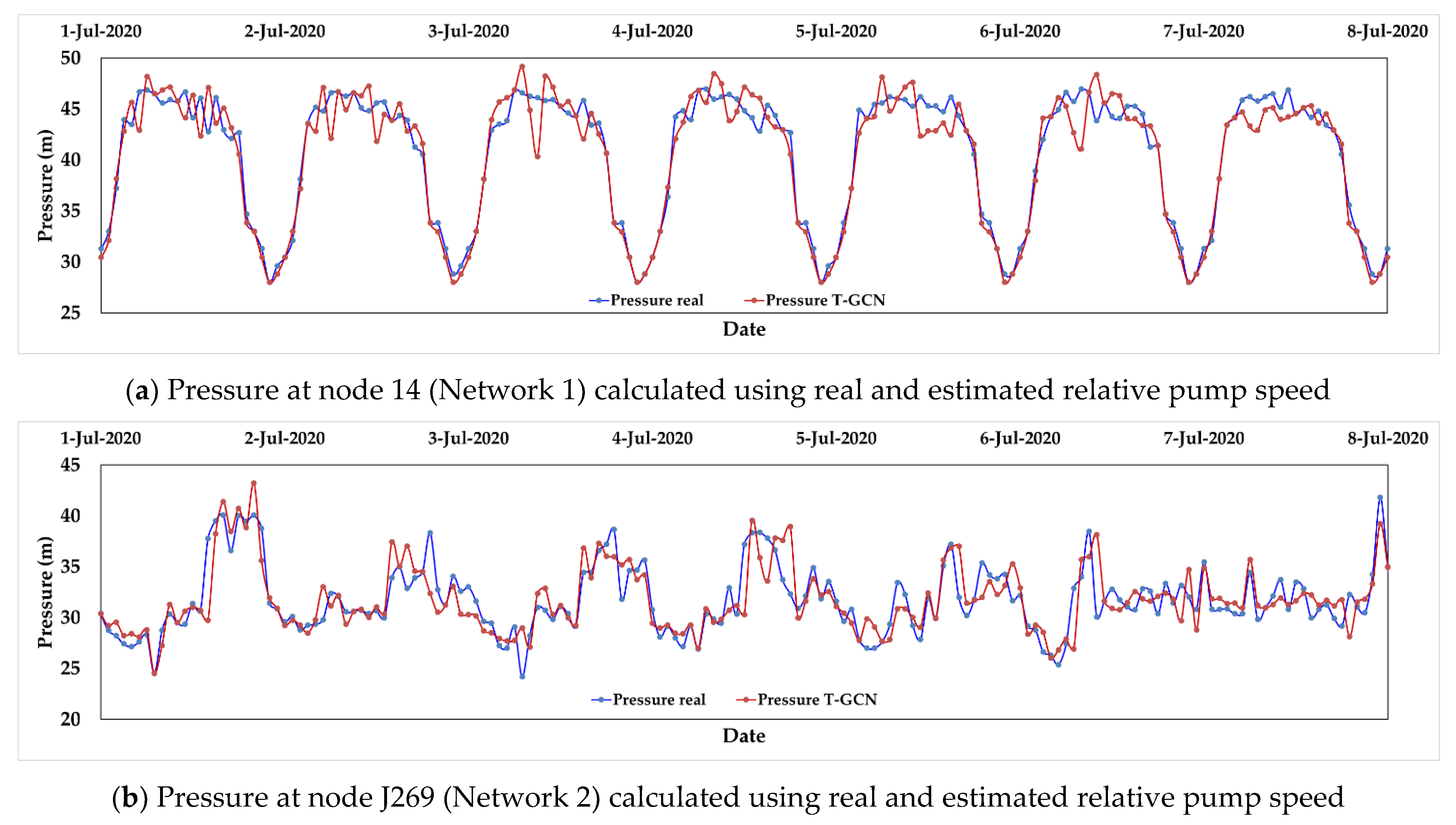
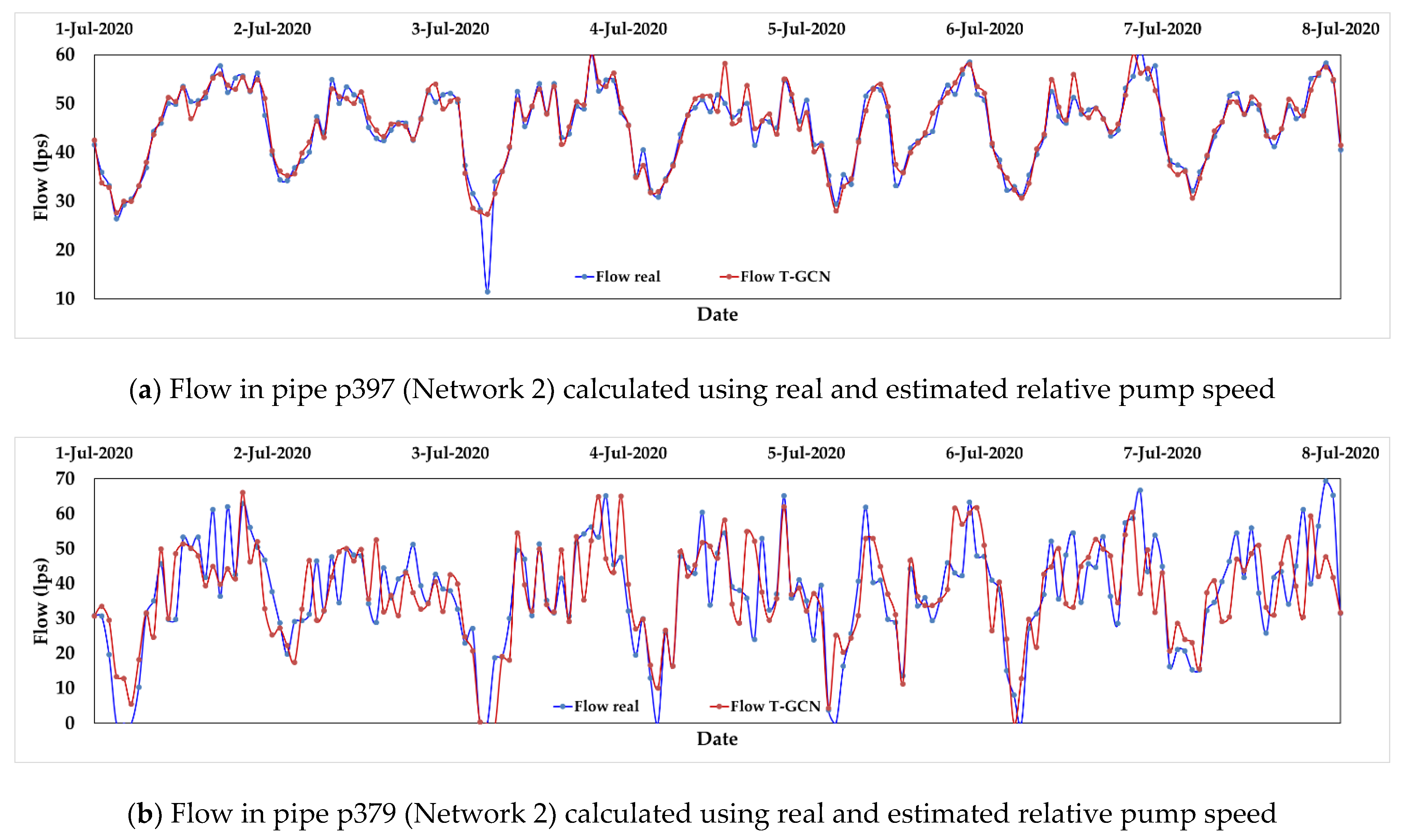
4.2. Estimation of Pressure and Flowrate Using Estimated Pump Speeds
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Herrera, M.; Ayala-Cabrera, D.; Izquierdo, J.; Montalvo, I. Smart Data Analysis for Smart Water Networks. In Proceedings of the Congress on Numerical Methods in Engineering—CMN 2017, Valencia, Spain, 3–5 July 2017; pp. 1665–1677. [Google Scholar]
- Herrera, M.; García-Díaz, J.; Izquierdo, J.; Pérez-García, R. Municipal Water Demand Forecasting: Tools for Intervention Time Series. Stoch. Anal. Appl. 2011, 29, 998–1007. [Google Scholar] [CrossRef]
- Mala-Jetmarova, H.; Sultanova, N.; Savic, D. Lost in optimisation of water distribution systems? A literature review of system operation. Environ. Model. Softw. 2017, 93, 209–254. [Google Scholar] [CrossRef] [Green Version]
- Makropoulos, C.; Savić, D. Urban Hydroinformatics: Past, Present and Future. Water 2019, 11, 1959. [Google Scholar] [CrossRef] [Green Version]
- Gutiérrez-Pérez, J. Monitorización, detección y estimación de estados de fallo en la calidad del agua de redes de distribución urbanas. Ph.D. Thesis, Universitat Politècnica de València, Valencia, Spain, 2021. [Google Scholar]
- Taormina, R.; Galelli, S.; Tippenhauer, N.; Salomons, E.; Ostfeld, A. Characterizing Cyber-Physical Attacks on Water Distribution Systems. J. Water Resour. Plan. Manag. 2017, 143, 04017009. [Google Scholar] [CrossRef]
- Tshehla, K.; Hamam, Y.; Abu-Mahfouz, A. State estimation in water distribution network: A review. In Proceedings of the 2017 IEEE 15th International Conference on Industrial Informatics (INDIN), Emden, Germany, 24–26 July 2017; pp. 1247–1252. [Google Scholar]
- Righetti, M.; Bort, C.; Bottazzi, M.; Menapace, A.; Zanfe, A. Optimal selection and monitoring of nodes aimed at supporting leakages identification in WDS. Water 2019, 11, 629. [Google Scholar] [CrossRef] [Green Version]
- Zanfei, A.; Menapace, A.; Santopietro, S.; Righetti, M. Calibration Procedure for Water Distribution Systems: Comparison among Hydraulic Models. Water 2020, 12, 1421. [Google Scholar] [CrossRef]
- Díaz, S.; González, J.; Mínguez, R. Observability Analysis in Water Transport Networks: Algebraic Approach. J. Water Resour. Plan. Manag. 2016, 142, 04015071. [Google Scholar] [CrossRef]
- Letting, L.; Hamam, Y.; Abu-Mahfouz, A. Estimation of water demand in water distribution systems using particle swarm optimization. Water 2017, 9, 593. [Google Scholar] [CrossRef] [Green Version]
- Díaz-García, S. Comprehensive Approach for On-Line Monitoring Water Distribution Systems via State Estimation Related Techniques. Ph.D. Thesis, Universidad de Castilla-La Mancha, Ciudad Real, Spain, 2017. [Google Scholar]
- Díaz, S.; Mínguez, R.; González, J. Aproximación estocástica al análisis de observabilidad en redes de abastecimiento de agua. Ing. Del Agua 2016, 20, 139. [Google Scholar] [CrossRef] [Green Version]
- Díaz, S.; Mínguez, R.; González, J.; Savic, D. Explicit Expressions for State Estimation Sensitivity Analysis in Water Systems. J. Water Resour. Plan. Manag. 2018, 144, 06018001. [Google Scholar] [CrossRef]
- Díaz, S.; Mínguez, R.; González, J. Calibration via Multi-period State Estimation in Water Distribution Systems. Water Resour. Manag. 2017, 31, 4801–4819. [Google Scholar] [CrossRef]
- Díaz, S.; Mínguez, R.; González, J. Topological State Estimation in Water Distribution Systems: Mixed-Integer Quadratic Programming Approach. J. Water Resour. Plan. Manag. 2018, 144, 04018026. [Google Scholar] [CrossRef]
- Díaz, S.; Mínguez, R.; González, J. Topological Observability Analysis in Water Distribution Systems. J. Water Resour. Plan. Manag. 2017, 143, 06017001. [Google Scholar] [CrossRef]
- Díaz, S.; Mínguez, R.; González, J. Probabilistic leak detectability assessment via state estimation in water transport networks. Stoch. Environ. Res. Risk Assess. 2018, 32, 2111–2128. [Google Scholar] [CrossRef]
- Fusco, F.; Arandia, E. State Estimation for Water Distribution Networks in the Presence of Control Devices with Switching Behavior. Procedia Eng. 2017, 186, 592–600. [Google Scholar] [CrossRef]
- Holz, K.; Cunge, J.; Lehfeldt, R.; Savic, D. Hydroinformatics Vision 2011. In Advances in Hydroinformatics; Springer: Singapore, 2014; pp. 545–560. [Google Scholar]
- Rozos, E. Machine learning, urbanwater resources management and operating policy. Resources 2019, 8, 173. [Google Scholar] [CrossRef] [Green Version]
- Novarini, B.; Brentan, B.M.; Meirelles, G.; Luvizotto-Junior, E. Optimal pressure management in water distribution networks through district metered area creation based on machine learning. Rev. Bras. Recur. Hidricos. 2019, 24, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Mounce, S.R.; Machell, J. Burst detection using hydraulic data from water distribution systems with artificial neural networks. Urban Water J. 2006, 3, 21–31. [Google Scholar] [CrossRef]
- Capelo, D.; Brentan, M.; Monteiro, B.; Covas, L. Near–Real Time Burst Location and Sizing in Water Distribution Systems Using Artificial Neural Networks. Water 2021, 13, 1841. [Google Scholar] [CrossRef]
- Manzi, D.; Brentan, B.; Meirelles, G.; Izquierdo, J.; Luvizotto, E. Pattern recognition and clustering of transient pressure signals for burst location. Water 2019, 11, 2279. [Google Scholar] [CrossRef] [Green Version]
- Bohorquez, J.; Alexander, B.; Simpson, A.R.; Lambert, M.F. Leak Detection and Topology Identification in Pipelines Using Fluid Transients and Artificial Neural Networks. J. Water Resour. Plan. Manag. 2020, 146, 04020040. [Google Scholar] [CrossRef]
- Bohorquez, J.; Simpson, A.R.; Lambert, M.F.; Alexander, B. Merging Fluid Transient Waves and Artificial Neural Networks for Burst Detection and Identification in Pipelines. J. Water Resour. Plan. Manag. 2021, 147, 04020097. [Google Scholar] [CrossRef]
- Brentan, B.M.; Luvizotto, E.; Herrera, M.; Izquierdo, J.; Pérez-García, R. Hybrid regression model for near real-time urban water demand forecasting. J. Comput. Appl. Math. 2017, 309, 532–541. [Google Scholar] [CrossRef]
- Bennett, C.; Stewart, R.A.; Beal, C.D. ANN-based residential water end-use demand forecasting model. Expert Syst. Appl. 2013, 40, 1014–1023. [Google Scholar] [CrossRef] [Green Version]
- Msiza, I.S.; Nelwamondo, F.V.; Marwala, T. Artificial neural networks and support vector machines for water demand time series forecasting. In Proceedings of the 2007 IEEE International Conference on Systems, Man and Cybernetics, Montreal, QC, Canada, 7–10 October 2007; pp. 638–643. [Google Scholar]
- Tsiami, L.; Makropoulos, C. Cyber—Physical attack detection in water distribution systems with temporal graph convolutional neural networks. Water 2021, 13, 1247. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiang, J.; Qian, K.; Ding, Y.; Yang, S.H.; He, L. Graph convolutional networks based contamination source identification across water distribution networks. Process Saf. Environ. Prot. 2021, 155, 317–324. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the 5th International Conference on Learning Representations, Conference Track Proceedings, Toulon, France, 24–26 April 2017; pp. 1–14. [Google Scholar]
- Zhou, J. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef] [Green Version]
- Singh, R.; Bathla, S.; Meel, P. State-of-the-Art Applications of Graph Convolutional Neural Networks. In Proceedings of the 6th International Conference on Recent Trends in Computing, Delhi, India, 3–4 July 2020; pp. 107–115. [Google Scholar]
- Michaël-Defferrard, P.V.; Xavier, B. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering. Adv. Neural Inf. Process. Syst. 2016, 59, 395–398. [Google Scholar]
- Bai, J. A3t-gcn: Attention temporal graph convolutional network for traffic forecasting. ISPRS Int. J. Geo-Inf. 2021, 10, 485. [Google Scholar] [CrossRef]
- Zhao, L. T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction. IEEE Trans. Intell. Transp. Syst. 2020, 21, 3848–3858. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Wang, Q.; Tao, C.; Deng, H.; Zhao, L.; Li, H. AST-GCN: Attribute-augmented spatiotemporal graph convolutional network for traffic forecasting. IEEE Access 2021, 9, 35973–35983. [Google Scholar] [CrossRef]
- Bai, L.; Yao, L.; Wang, X.; Li, C.; Zhang, X. Deep spatial–temporal sequence modeling for multi-step passenger demand prediction. Future Gener. Comput. Syst. 2021, 121, 25–34. [Google Scholar] [CrossRef]
- Hüttel, F.; Peled, I.; Rodrigues, F.; Pereira, F. Deep Spatio-Temporal Forecasting of Electrical Vehicle Charging Demand; Cornell University: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Ding, Y.; Zhu, Y.; Feng, J.; Zhang, P.; Cheng, Z. Interpretable spatio-temporal attention LSTM model for flood forecasting. Neurocomputing 2020, 403, 348–359. [Google Scholar] [CrossRef]
- Curl, J.; Nading, T.; Hegger, K.; Barhoumi, A.; Smoczynski, M. Digital twins: The next generation of water treatment technology. J.-Am. Water Work. Assoc. 2019, 111, 44–50. [Google Scholar] [CrossRef]
- Callcut, M.; Cerceau, J.; Varga, L.; McMillan, L. Digital Twins in Civil Infrastructure Systems. Sustainability 2021, 13, 11549. [Google Scholar] [CrossRef]
- Bronstein, M.M.; Bruna, J.; LeCun, Y.; Szlam, A.; Vandergheynst, P. Geometric deep learning: Going beyond euclidean data. IEEE Signal Process. Mag. 2017, 34, 18–42. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Mei, G.; Prezioso, E.; Zhang, Z.; Xu, N. A deep learning approach using graph convolutional networks for slope deformation prediction based on time-series displacement data. Neural Comput. Appl. 2021, 33, 14441–14457. [Google Scholar] [CrossRef]
- Grattarola, D.; Alippi, C. Graph Neural Networks in TensorFlow and Keras with Spektral [Application Notes]. IEEE Comput. Intell. Mag. 2021, 16, 99–106. [Google Scholar] [CrossRef]
- Chollet, F. Deep learning with Python, 2nd ed.; Manning Pubkications: New York, NY, USA, 2021; p. 504. [Google Scholar]
- Klise, K.; Murray, R.; Haxton, T. An overview of the Water Network Tool for Resilience (WNTR). In Proceedings of the 1st International WDSA/CCWI Joint Conference, Kingston, ON, Canada, 23–25 July 2018. [Google Scholar]






| Parameter | Network 1 | Network 2 |
|---|---|---|
| Total length | 43.54 km | 56.73 km |
| Roughness Coefficient | 0.0015 mm (Darcy-Weisbach) | 60–140 (Hazen-Williams) |
| Pipe diameter | 75–762 mm | 51–610 mm |
| Number of pipes | 67 | 429 |
| Number of nodes | 62 | 388 |
| Number of reservoirs | 5 | 1 |
| Number of pumps | 2 | 11 |
| Number of tanks | 0 | 7 |
| Number of valves | 0 | 5 |
| Parameter | PU2 | PU4 | PU6 | PU8 | PU10 |
|---|---|---|---|---|---|
| 0.028 | 0.026 | 0.026 | 0.027 | 0.027 | |
| 0.021 | 0.020 | 0.020 | 0.021 | 0.021 | |
| 0.801 | 0.815 | 0.799 | 0.802 | 0.802 |
| Network 1 | Network 2 | ||||
|---|---|---|---|---|---|
| Parameter | Node 14 | Node J269 | Node J256 | Pipe p397 | Pipe J379 |
| 1.8 | 2.9 | 1.7 | 1.8 | 9.7 | |
| 1.1 | 2.0 | 1.3 | 1.2 | 2.6 | |
| 0.923 | 0.448 | 0.592 | 0.949 | 0.632 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonilla, C.A.; Zanfei, A.; Brentan, B.; Montalvo, I.; Izquierdo, J. A Digital Twin of a Water Distribution System by Using Graph Convolutional Networks for Pump Speed-Based State Estimation. Water 2022, 14, 514. https://doi.org/10.3390/w14040514
Bonilla CA, Zanfei A, Brentan B, Montalvo I, Izquierdo J. A Digital Twin of a Water Distribution System by Using Graph Convolutional Networks for Pump Speed-Based State Estimation. Water. 2022; 14(4):514. https://doi.org/10.3390/w14040514
Chicago/Turabian StyleBonilla, Carlos A., Ariele Zanfei, Bruno Brentan, Idel Montalvo, and Joaquín Izquierdo. 2022. "A Digital Twin of a Water Distribution System by Using Graph Convolutional Networks for Pump Speed-Based State Estimation" Water 14, no. 4: 514. https://doi.org/10.3390/w14040514








