Rehabilitation in Intermittent Water Distribution Networks for Optimal Operation
Abstract
:1. Introduction
2. Materials and Methods
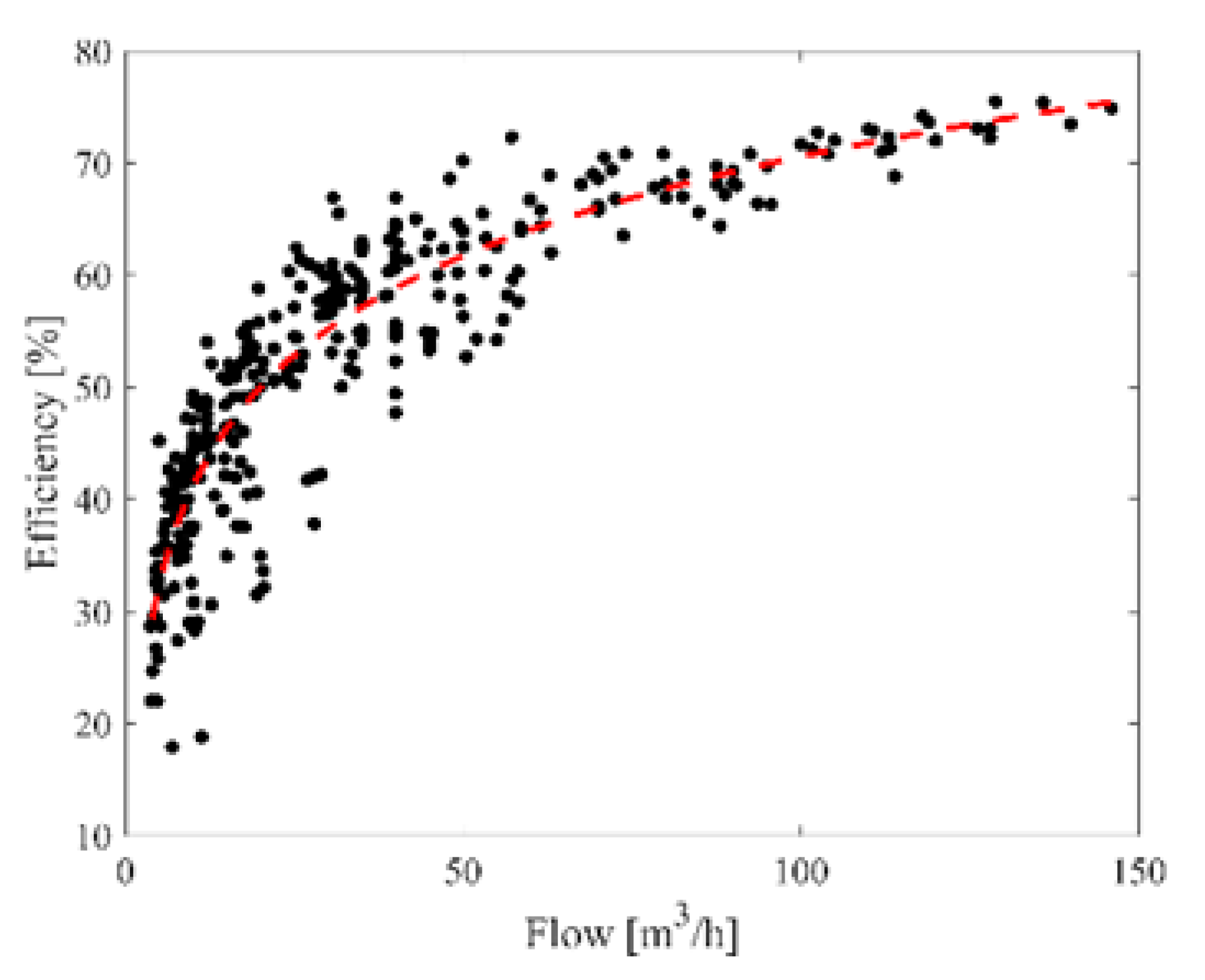
2.1. Pump Selection
2.2. Leakage Modeling
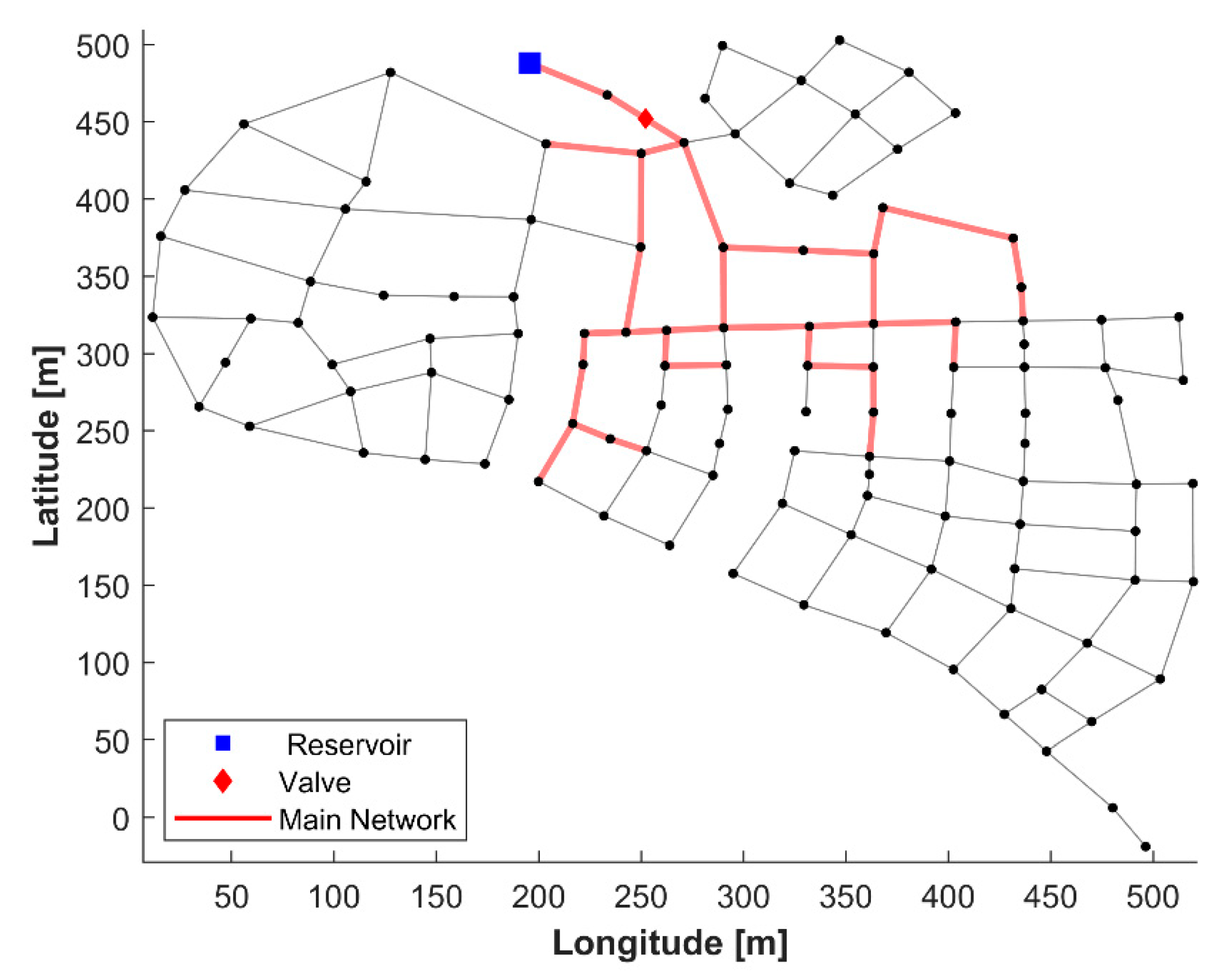
2.3. Main Network Modeling
2.4. Cost Modeling
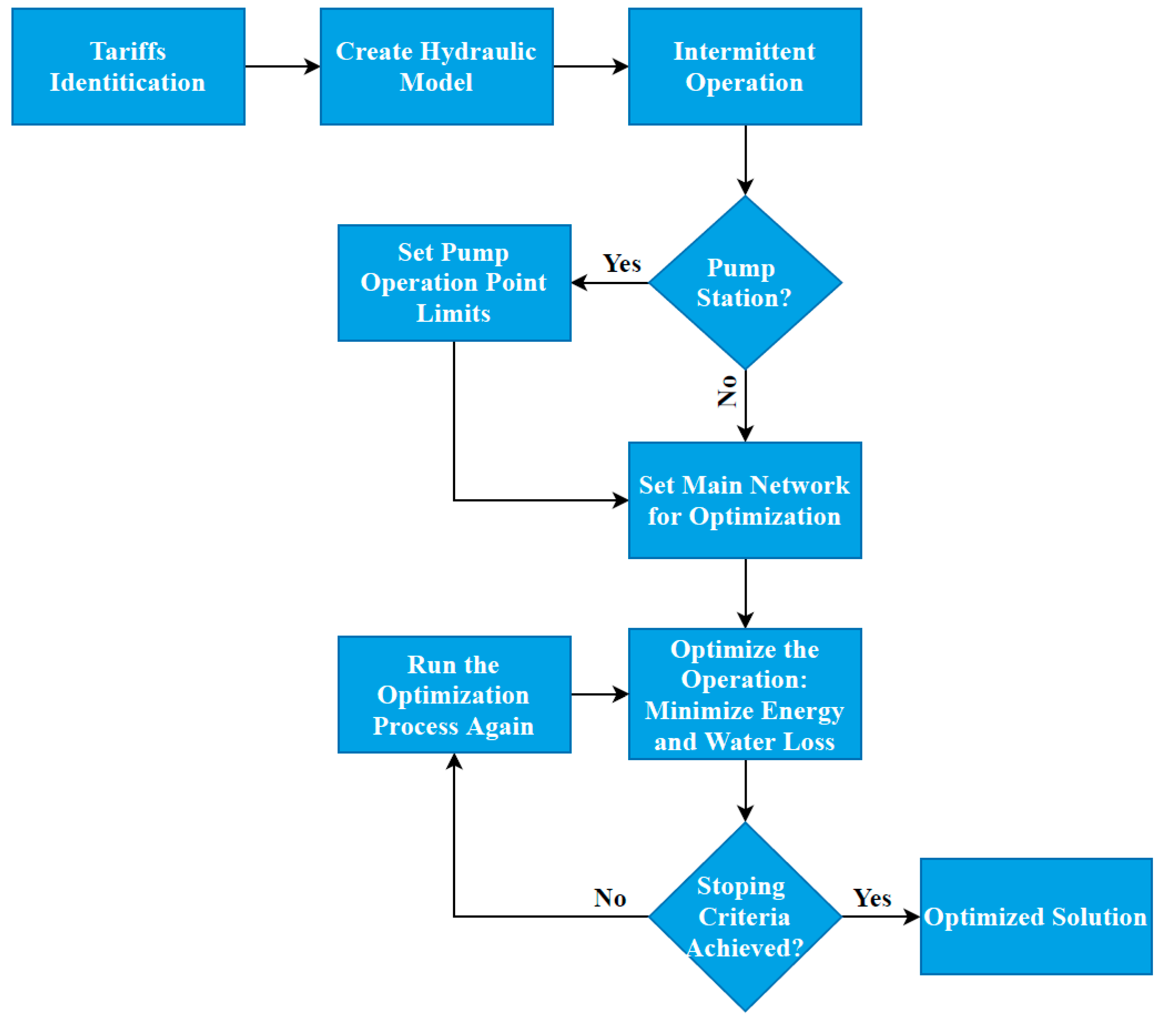
2.5. Optimization Procedure
3. Case Studies
3.1. Case Study 1: ZJ Network
3.2. Case Study 2: OBCL-1 Network
4. Results
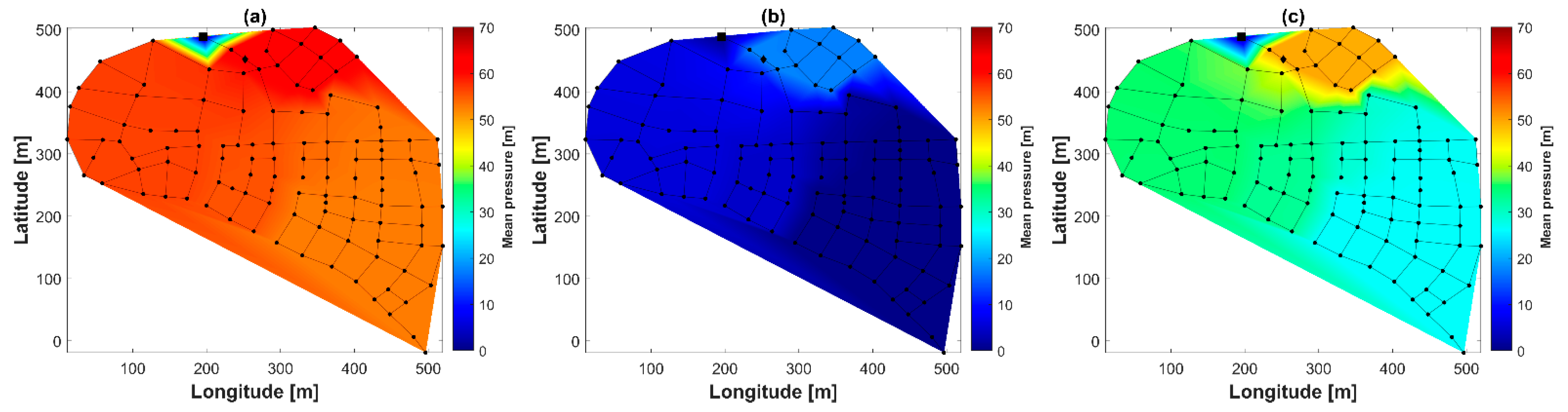
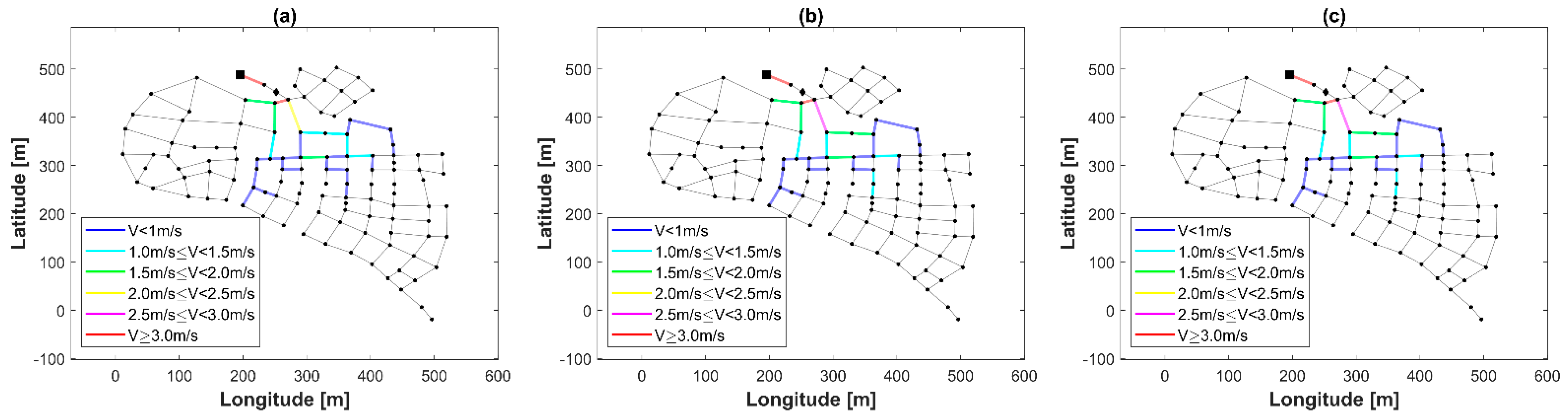
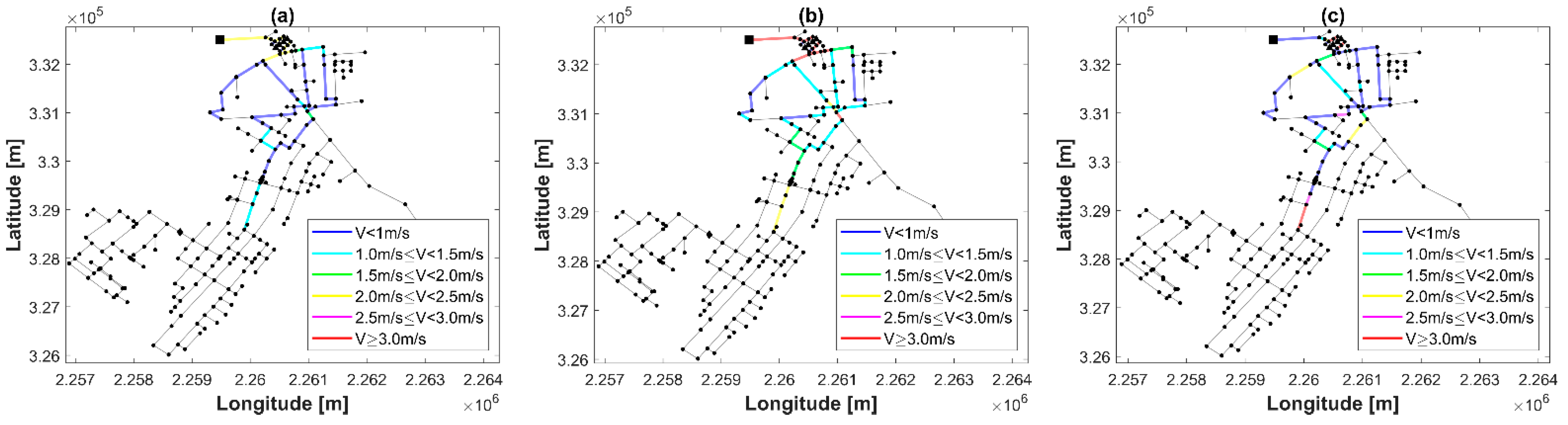
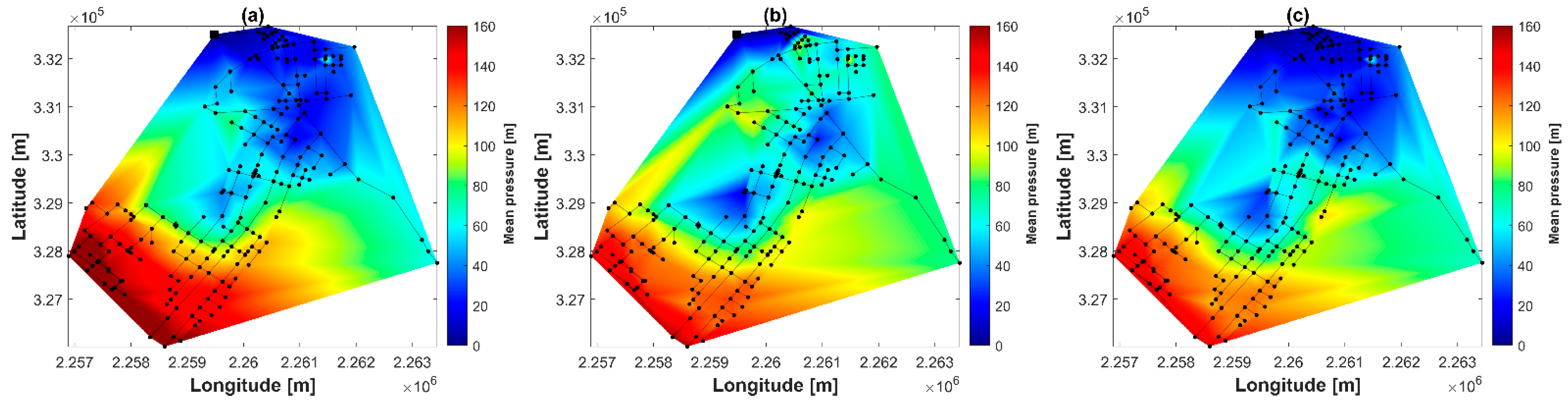
4.1. ZJ Network Results
4.2. OBCL-1 Network Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kummu, M.; Guillaume, J.H.A.; de Moel, H.; Eisner, S.; Flörke, M.; Porkka, M.; Siebert, S.; Veldkamp, T.I.E.; Ward, P.J. The world’s road to water scarcity: Shortage and stress in the 20th century and pathways towards sustainability. Sci. Rep. 2016, 6, 38495. [Google Scholar] [CrossRef] [Green Version]
- Moreira, M.D.S.; dos Santos, I.F.S.; Freitas, L.F.; Freitas, F.F.; Barros, R.M.; Filho, G.L.T. Energy and economic analysis for a desalination plant powered by municipal solid waste incineration and natural gas in Brazil. Environ. Dev. Sustain. 2021, 1–28. [Google Scholar] [CrossRef]
- ANSA. Lack of Water Affected 5 Billion People by 2050. Época Magazine. Available online: https://epocanegocios.globo.com/Mundo/noticia/2018/03/falta-de-agua-afetara-5-bilhoes-de-pessoas-ate-2050-diz-onu.html (accessed on 8 November 2021).
- Andey, S.P.; Kelkar, P.S. Performance of water distribution systems during intermittent versus continuous water supply. J. Am. Water Work. Assoc. 2007, 99, 99–106. [Google Scholar] [CrossRef]
- WHO; UNICEF. Progress on Drinking Water and Sanitation; WHO/UNICEF: Geneva, Switzerland, 2012. [Google Scholar]
- Kumpel, E.; Nelson, K.L. Intermittent Water Supply: Prevalence, Practice, and Microbial Water Quality. Environ. Sci. Technol. 2016, 50, 542–553. [Google Scholar] [CrossRef]
- WHO. Guidelines for Drinking-Water Quality; WHO Library Cataloguing-in-Publication Data: Geneva, Switzerland, 2008; p. 668. [Google Scholar]
- Preciado, C.C.; Husband, S.; Boxall, J.; del Olmo, G.; Soria-Carrasco, V.; Maeng, S.K.; Douterelo, I. Intermittent Water Supply Impacts on Distribution System Biofilms and Water Quality. Water Res. 2021, 201, 117372. [Google Scholar] [CrossRef]
- Companhia de Saneamento Básico do Estado de São Paulo—SABESP. CHESS—Crise Hídrica, Estratégia e Soluções da SABESP: Para a Região Metropolitana de São Paulo; SABESP: São Paulo, Brazil, 2015; p. 95. [Google Scholar]
- EPA. Brazilian Energy Balance 2020 Year 2019; EPA—Empresa de Pesquisa Energética: Rio de Janeiro, Brazil, 2020; p. 292. [Google Scholar]
- Ministério do Desenvolvimento Regional; Secretaria Nacional de Saneamento—SNS. Sistema Nacional de Informações Sobre Saneamento: 25 Diagnóstico dos Serviços de Água e Esgotos—2019; SNS/MDR: Brasília, Brazil, 2020; p. 183. [Google Scholar]
- Ministério de Minas e Energia—MME; Secretaria de Planejamento e Desenvolvimento Energético—SPDE; Departamento de Desenvolvimento Energético. Plano Nacional de Eficiência Energética: Premissas e Diretrizes Básicas; SPDE/MDR: Brasília, Brazil, 2010; p. 156. [Google Scholar]
- Palod, N.; Prasad, V.; Khare, R. Redefining the application of an evolutionary algorithm for the optimal pipe sizing problem. J. Water Clim. Chang. 2021, 12, 2299–2313. [Google Scholar] [CrossRef]
- Bianchotti, J.D.; Denardi, M.; Castro-Gama, M.; Puccini, G.D. Sectorization for Water Distribution Systems with Multiple Sources: A Performance Indices Comparison. Water 2021, 13, 131. [Google Scholar] [CrossRef]
- Świętochowska, M.; Bartkowska, I.; Gwoździej-Mazur, J. Energy Optimization of the Pumping Station. Environ. Sci. Proc. 2021, 9, 37. [Google Scholar] [CrossRef]
- Capelo, M.; Brentan, B.; Monteiro, L.; Covas, D. Near–Real Time Burst Location and Sizing in Water Distribution Systems Using Artificial Neural Networks. Water 2021, 13, 1841. [Google Scholar] [CrossRef]
- Hu, S.; Gao, J.; Zhong, D.; Deng, L.; Ou, C.; Xin, P. An Innovative Hourly Water Demand Forecasting Preprocessing Framework with Local Outlier Correction and Adaptive Decomposition Techniques. Water 2021, 13, 582. [Google Scholar] [CrossRef]
- Sambito, M.; Piazza, S.; Freni, G. Stochastic Approach for Optimal Positioning of Pumps as Turbines (PATs). Sustainability 2021, 13, 12318. [Google Scholar] [CrossRef]
- Creaco, E.; Galuppini, G.; Campisano, A.; Ciaponi, C.; Pezzinga, G. A Bi-Objective Approach for Optimizing the Installation of PATs in Systems of Transmission Mains. Water 2020, 12, 330. [Google Scholar] [CrossRef] [Green Version]
- Souza, R.G.M. Avaliação Hidroenergética de Sistemas de Distribuição de Água: Suprimento Contínuo versus Intermitente. Master’s Thesis, Federal University of Minas Gerais—UFMG, Belo Horizonte, Brazil, November 2021. [Google Scholar]
- Rossman, L.A. EPANET User’s Manual; US Environmental Protection Agency (EPA): Cincinnati, OH, USA, 1994; p. 200. [Google Scholar]
- Gomes, H.P. Abastecimento de Água; LENHS/UFPB: João Pessoa, Brazil, 2019; p. 464. [Google Scholar]
- Móller, D.S.; Lima, G.M.; Brentan, B.M.; Barros, D.B. Optimal pump selection for variable speed operation in water distribution network. RBRH 2020, 25. [Google Scholar] [CrossRef]
- Brazil. Instituto Nacional de Metrologia, Normalização e Qualidade Industrial—INMETRO. Portaria n° 455, de 01 de Dezembro 2010. Requisitos de Avaliação da Conformidade para Bombas e Motobombas Centrífugas. Diário Oficial União Brasília. Available online: http://www2.aladi.org/nsfaladi/normasTecnicas.nsf/09267198f1324b64032574960062343c/e380ed588b45568f032579e4004f416e/$FILE/Portaria%20N%C2%B0%20455-2010.pdf (accessed on 1 January 2012).
- Van Zyl, J.E.; Lambert, A.O.; Collins, R. Realistic Modeling of Leakage and Intrusion Flows through Leak Openings in Pipes. J. Hydraul. Eng. 2017, 143, 04017030. [Google Scholar] [CrossRef]
- Schwaller, J.; Van Zyl, J.E.; Kabaasha, A.M. Characterising the pressure-leakage response of pipe networks using the FAVAD equation. Water Supply 2015, 15, 1373–1382. [Google Scholar] [CrossRef]
- Van Zyl, J.E.; Malde, R. Evaluating the pressure-leakage behaviour of leaks in water pipes. J. Water Supply Res. Technol. 2017, 66, 287–299. [Google Scholar] [CrossRef]
- Associação Brasileira de Normas Técnicas—ABNT. NBR 12215-1: Projeto de Adutora de Água Parte 1: Conduto Forçado; ABNT: Rio de Janeiro, Brazil, 2017; p. 26. [Google Scholar]
- Campbell, E.; Izquierdo, J.; Montalvo, I.; Ilaya-Ayza, A.E.; Pérez-García, R.; Tavera, M. A flexible methodology to sectorize water supply networks based on social network theory concepts and multi-objective optimization. J. Hydroinform. 2016, 18, 62–76. [Google Scholar] [CrossRef] [Green Version]
- Maiolo, M.; Pantusa, D.; Carini, M.; Capano, G.; Chiaravalloti, F.; Procopio, A. A New Vulnerability Measure for Water Distribution Network. Water 2018, 10, 1005. [Google Scholar] [CrossRef] [Green Version]
- Meijer, D.; Post, J.; Van der Hoek, J.P.; Korving, H.; Langeveld, J.; Clemens, F. Identifying critical elements in drinking water distribution networks using graph theory. Struct. Infrastruct. Eng. 2021, 17, 347–360. [Google Scholar] [CrossRef] [Green Version]
- El-Ghandour, H.A.; Elabd, S.M.; Elbeltagi, E. Assessment of optimal water distribution systems design under steady-state and transient conditions due to pipe roughness uncertainty. Ain Shams Eng. J. 2021, 12, 465–473. [Google Scholar] [CrossRef]
- Di Nardo, A.; Giudicianni, C.; Greco, R.; Herrera, M.; Santonastaso, G.F. Applications of Graph Spectral Techniques to Water Distribution Network Management. Water 2018, 10, 45. [Google Scholar] [CrossRef] [Green Version]
- Hajebi, S.; Roshani, E.; Cardozo, N.; Barrett, S.; Clarke, A.; Clarke, S. Water distribution network sectorisation using graph theory and many-objective optimisation. J. Hydroinform. 2015, 18, 77–95. [Google Scholar] [CrossRef] [Green Version]
- Companhia Energética de Minas Gerais—CEMIG. Valores de Tarifas e Serviços; CEMIG: Belo Horizonte, Brazil, 2020; Available online: https://www.cemig.com.br/atendimento/valores-de-tarifas-e-servicos/ (accessed on 13 December 2020).
- Gomes, H.P. Avaliação Econômica: Eficiência Energética, 1st ed.; Editora UFPB: João Pessoa, Brazil, 2014; p. 100. ISBN 978-85-237-0818-4. [Google Scholar]
- Sistema Nacional de Pesquisa de Custos e Índices da Construção Civil—SINAPI. Preço de Insumos e Composições. Mês de Referência: Março de 2021. Belo Horizonte. 2021. Available online: https://www.caixa.gov.br/site/Paginas/downloads.aspx#categoria_648 (accessed on 30 April 2021).
- Secretaria da Infraestrutura do Estado do Ceará—SEINFRA. Tabela de custos. Mês de Referência: Março de 2021. Fortaleza. 2021. Available online: https://www.seinfra.ce.gov.br/tabela-de-custos/ (accessed on 30 April 2021).
- Companhia Paulista de Obras e Serviços—CPOS. Tabela de Custos. Mês de Referência: Março de 2021. São Paulo. 2021. Available online: https://www.prefeitura.sp.gov.br/cidade/secretarias/obras/tabelas_de_custos/index.php?p=310197 (accessed on 30 April 2021).
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, USA, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Goldbarg, E.; Goldbarg, M.; Luna, H. Otimização Combinatória e Metaheurísticas: Algoritmos e Apliacações; Elsevier: Rio de Janeiro, Brasil, 2017. [Google Scholar]
- Hernandez, E.; Hoagland, S.; Ormsbee, L.E. WDSRD: A Database for Research Applications. 2016. Available online: http://www.uky.edu/WDST/database.html (accessed on 28 December 2020).


| Description | Tariff |
|---|---|
| Energy—non-peak hour (NPH) (R$/kWh) | 0.3567 |
| Energy—peak hour (PH) (R$/kWh) | 0.5342 |
| Power—non-peak hour (NPH) (R$/kW) | 13.950 |
| Power—peak hour (PH) (R$/kW) | 43.950 |
| Description | Range of Average Total Expenditure Amounts (IN003) (R$/m³) | Average Total Expenditure Amounts (IN003) (R$/m³) |
|---|---|---|
| Regional | 1.87 to 7.61 | 3.96 |
| Micro-regional | 1.05 to 5.53 | 3.48 |
| Local | 0.30 to 7.82 | 2.68 |
| Brazil | 0.30 to 7.82 | 3.57 |
| = 0.30 R$/m³ | = 7.82 R$/m³ | = 3.50 R$/m³ | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Description | 24 h 1 | 15 h 1 | 12 h 1 | 12 h * | 24 h 1 | 15 h 1 | 12 h 1 | 12 h * | 24 h 1 | 15 h 1 | 12 h 1 | 12 h * |
| Mean pressure (m) | 55 | 22 | 4 | 33 | 55 | 22 | 4 | 33 | 55 | 22 | 4 | 33 |
| Daily distribution (103 m³) | 158.1 | 129.6 | - | 129.1 | 158.1 | 129.6 | - | 129.1 | 158.1 | 129.6 | - | 129.1 |
| Daily consumption (103 m³) | 110.9 | 110.9 | - | 110.9 | 110.9 | 110.9 | - | 110.9 | 110.9 | 110.9 | - | 110.9 |
| Daily leakage (103 m³) | 47.2 | 18.7 | - | 18.2 | 47.2 | 18.7 | - | 18.2 | 47.206 | 18.7 | - | 18.2 |
| Daily leakage (%) | 29.9 | 14.5 | - | 14.1 | 29.9 | 14.5 | - | 14.1 | 29.9 | 14.5 | - | 14.1 |
| Daily energy cost (103 R$) | - | - | - | - | - | - | - | - | - | - | - | - |
| Daily leakage cost (103 R$) | 14.2 | 5.6 | - | 5.5 | 369.1 | 146.5 | - | 142.6 | 168.5 | 66.9 | - | 65.1 |
| Implantation cost (106 R$) | - | - | - | 4.9 | - | - | - | 4.9 | - | - | - | 4.9 |
| Project horizon cost (106 R$) | 41.6 | 16.5 | - | 21.0 | 1085.3 | 430.8 | - | 424.1 | 495.5 | 196.7 | - | 196.3 |
| Economic efficiency (%) | - | 60.3 | - | 49.6 | - | 60.3 | - | 60.9 | - | 60.3 | - | 60.4 |
| = 0.30 R$/m³ | = 7.82 R$/m³ | = 3.50 R$/m³ | ||||
|---|---|---|---|---|---|---|
| Description | 15 h * | 12 h * | 15 h * | 12 h * | 15 h * | 12 h * |
| Resized extensions (m) | 10,626 | 9513 | 9727 | 10,671 | 11,741 | 12,057 |
| = 0.30 R$/m³ | = 7.82 R$/m³ | = 3.50 R$/m³ | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Description | 24 h 1 | 15 h 1 | 15 h * | 12 h 1 | 12 h * | 24 h 1 | 15 h 1 | 15 h * | 12 h 1 | 12 h * | 24 h 1 | 15 h 1 | 15 h * | 12 h 1 | 12 h * |
| Power-PH (kW) | 35 | 67 | 10 | 211 | 14 | 41 | 71 | 18 | 199 | 14 | 36 | 70 | 17 | 211 | 9 |
| Energy-PH (kWh) | 92 | 180 | 29 | 416 | 41 | 97 | 181 | 33 | 417 | 34 | 94 | 173 | 43 | 416 | 19 |
| Power-NPH (kW) | 54 | 182 | 41 | 261 | 22 | 33 | 180 | 33 | 258 | 22 | 66 | 180 | 32 | 262 | 19 |
| Energy-NPH (kWh) | 489 | 1063 | 253 | 1272 | 148 | 512 | 1046 | 117 | 1250 | 99 | 463 | 1080 | 224 | 1410 | 100 |
| Total Energy (kWh/day) | 581 | 1243 | 282 | 1689 | 189 | 608 | 1227 | 150 | 1668 | 134 | 556 | 1253 | 267 | 1825 | 120 |
| Mean pressure (m) | 82 | 84 | 74 | 85 | 79 | 80 | 82 | 73 | 84 | 68 | 81 | 81 | 77 | 81 | 67 |
| Daily distribution (103 m³) | 20.2 | 18.1 | 17.8 | 17.3 | 17.2 | 20.1 | 18.0 | 17.7 | 17.3 | 17.0 | 20.1 | 18.0 | 17.8 | 17.2 | 16.9 |
| Daily consumption (103 m³) | 14.3 | 14.3 | 14.3 | 14.3 | 14.3 | 14.3 | 14.3 | 14.3 | 14.3 | 14.3 | 14.3 | 14.3 | 14.3 | 14.3 | 14.3 |
| Daily leakage (103 m³) | 5.9 | 3.8 | 3.5 | 3.1 | 2.9 | 5.8 | 3.7 | 3.5 | 3.1 | 2.7 | 5.8 | 3.7 | 3.6 | 2.9 | 2.7 |
| Daily leakage (%) | 29.3 | 21.0 | 19.8 | 17.7 | 16.9 | 28.9 | 20.7 | 19.5 | 17.7 | 15.8 | 29.0 | 20.7 | 20.0 | 17.1 | 15.8 |
| Daily energy cost (103 R$) | 2.5 | 5.9 | 1.1 | 13.6 | 1.0 | 2.5 | 6.1 | 1.3 | 13.0 | 1.0 | 2.7 | 6.1 | 1.3 | 13.6 | 0.7 |
| Daily leakage cost (103 R$) | 1.8 | 1.1 | 1.1 | 0.9 | 0.9 | 45.6 | 29.2 | 27.0 | 24.0 | 21.0 | 20.8 | 13.3 | 12.8 | 10.5 | 9.5 |
| Implantation cost (106 R$) | - | - | 5.0 | - | 5.4 | - | - | 7.2 | - | 9.6 | - | - | 7.8 | - | 8.4 |
| Project horizon cost (106 R$) | 12.7 | 21.0 | 11.4 | 43.0 | 10.9 | 141.3 | 103.9 | 90.5 | 109.3 | 74.3 | 69.3 | 57.2 | 49.0 | 71.4 | 38.5 |
| Efficiency (%) | - | −65.8 | 10.0 | −239.5 | 14.0 | - | 26.4 | 36.0 | 22.7 | 47.4 | - | 17.5 | 29.2 | −3.1 | 44.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Souza, R.G.; Meirelles, G.; Brentan, B.; Izquierdo, J. Rehabilitation in Intermittent Water Distribution Networks for Optimal Operation. Water 2022, 14, 88. https://doi.org/10.3390/w14010088
Souza RG, Meirelles G, Brentan B, Izquierdo J. Rehabilitation in Intermittent Water Distribution Networks for Optimal Operation. Water. 2022; 14(1):88. https://doi.org/10.3390/w14010088
Chicago/Turabian StyleSouza, Rui Gabriel, Gustavo Meirelles, Bruno Brentan, and Joaquín Izquierdo. 2022. "Rehabilitation in Intermittent Water Distribution Networks for Optimal Operation" Water 14, no. 1: 88. https://doi.org/10.3390/w14010088
APA StyleSouza, R. G., Meirelles, G., Brentan, B., & Izquierdo, J. (2022). Rehabilitation in Intermittent Water Distribution Networks for Optimal Operation. Water, 14(1), 88. https://doi.org/10.3390/w14010088









