Waved-Shape Accumulation of Ice Jam—Analysis and Experimental Study
Abstract
:1. Introduction
2. Materials and Methods
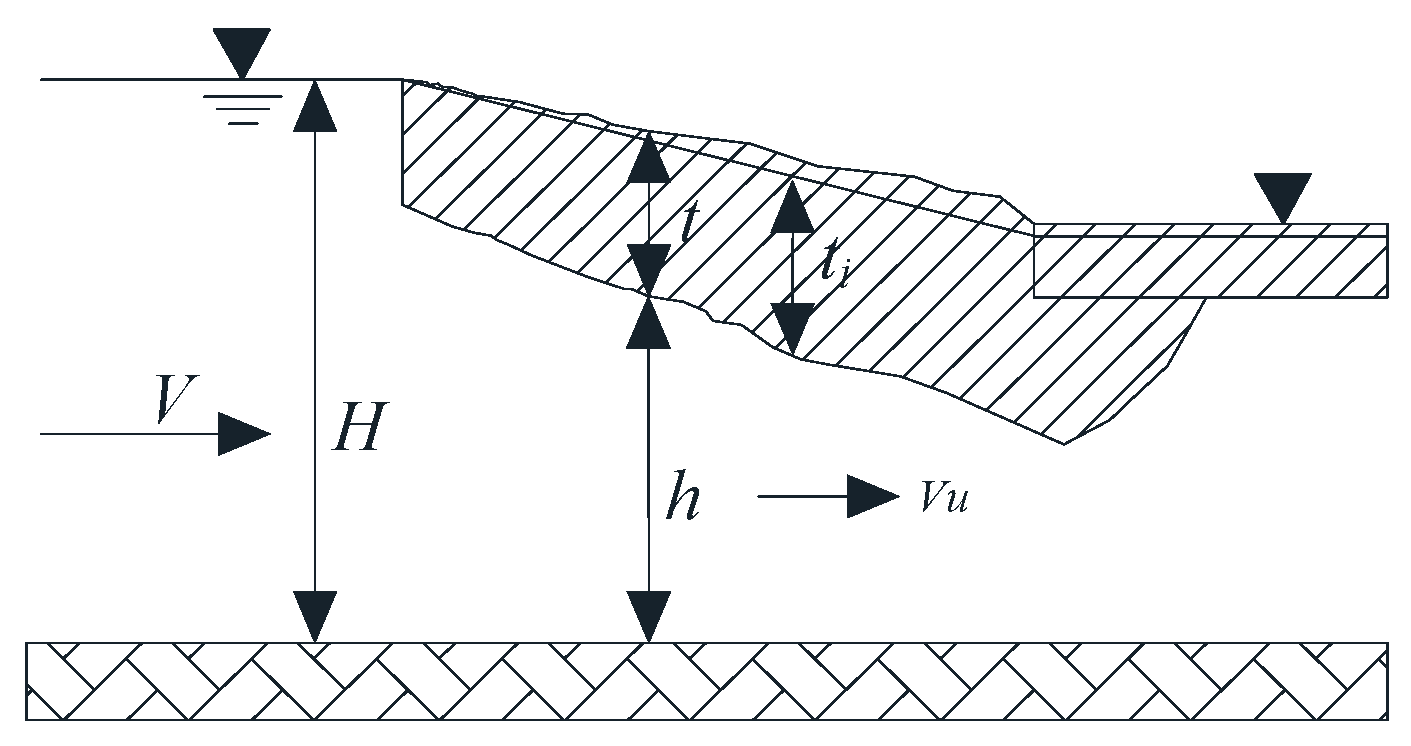
2.1. Laboratory Experiment Setup
2.2. Mechanical Analysis of an Equilibrium Ice Jam
3. Results and Discussion
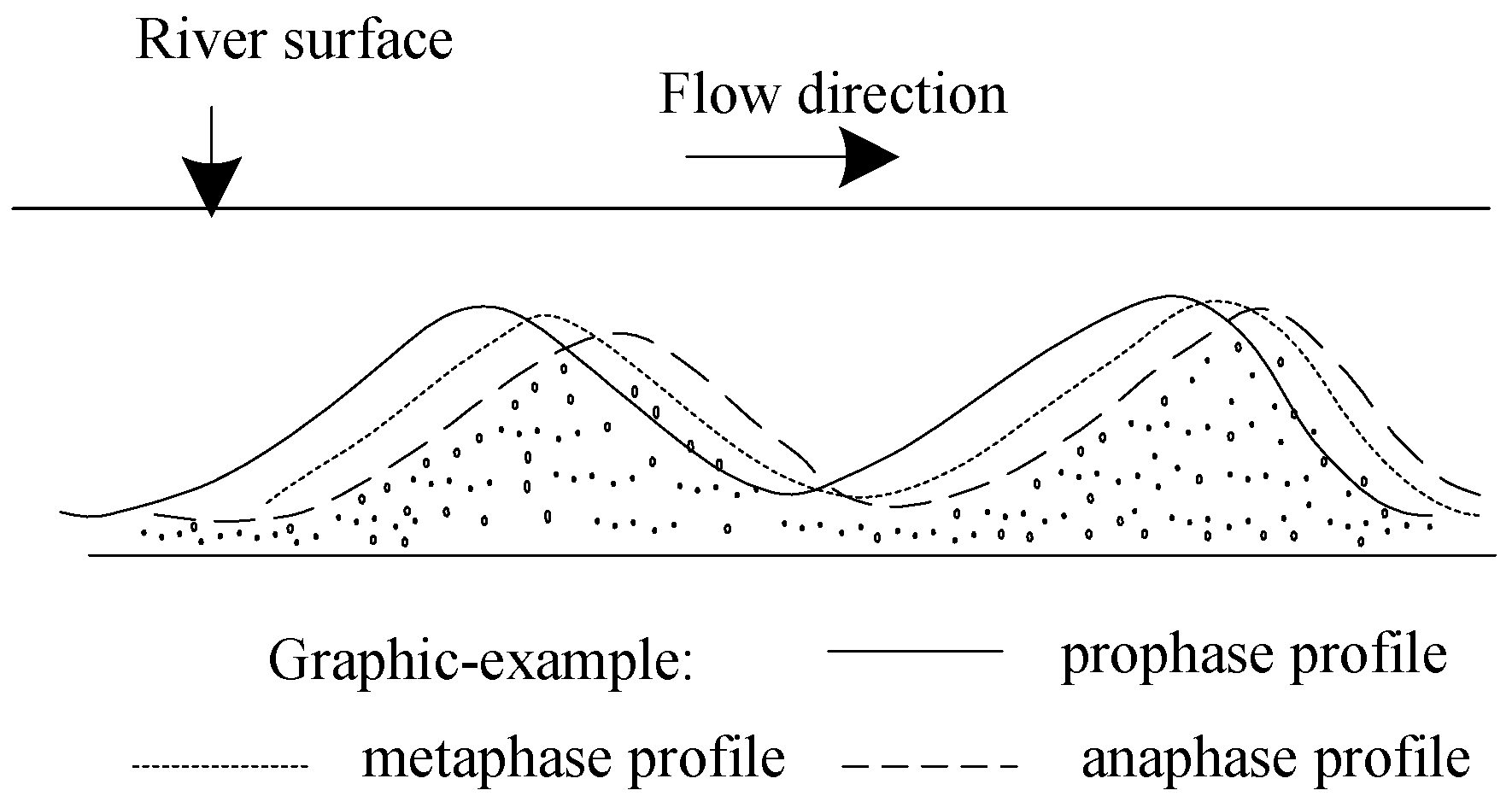
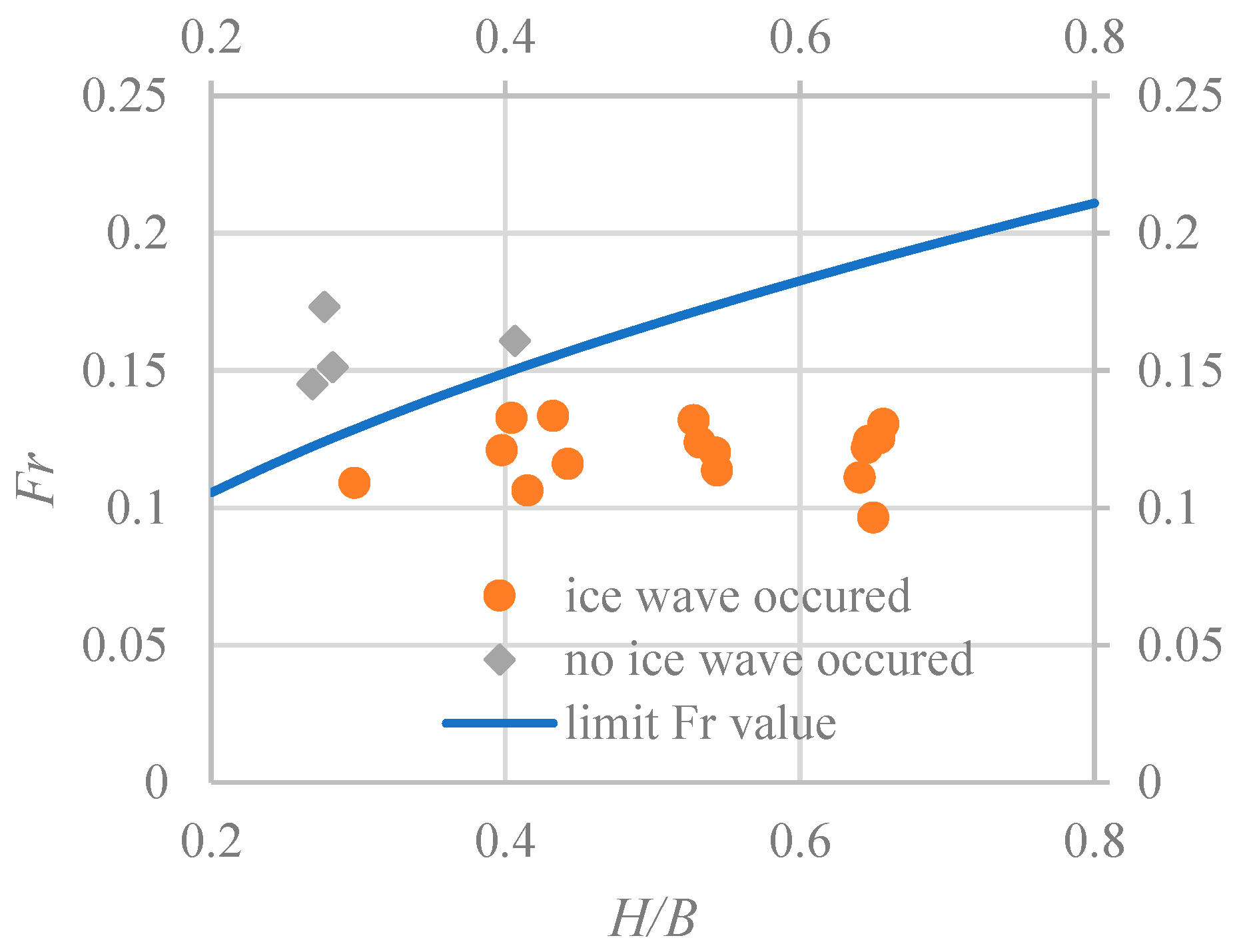
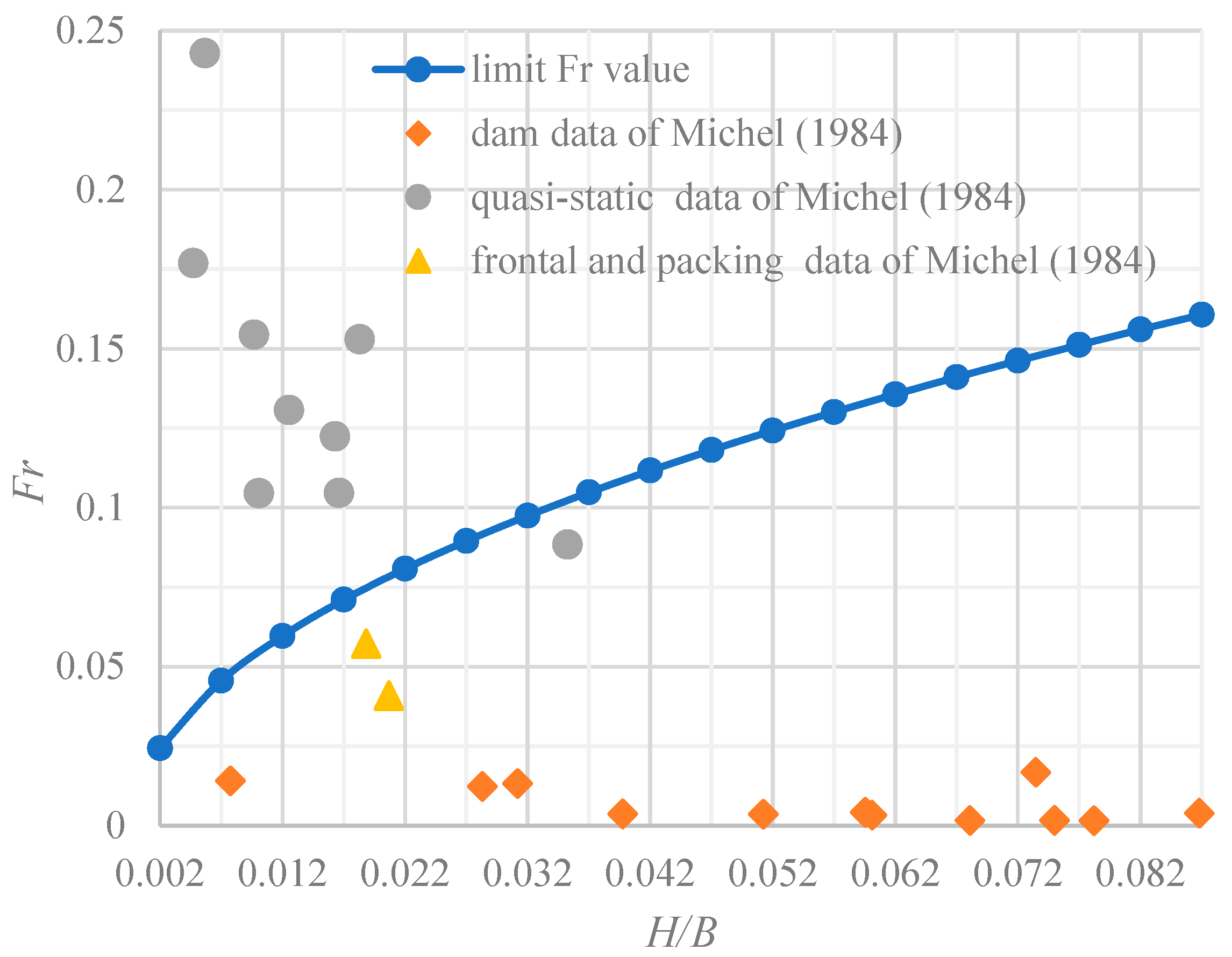
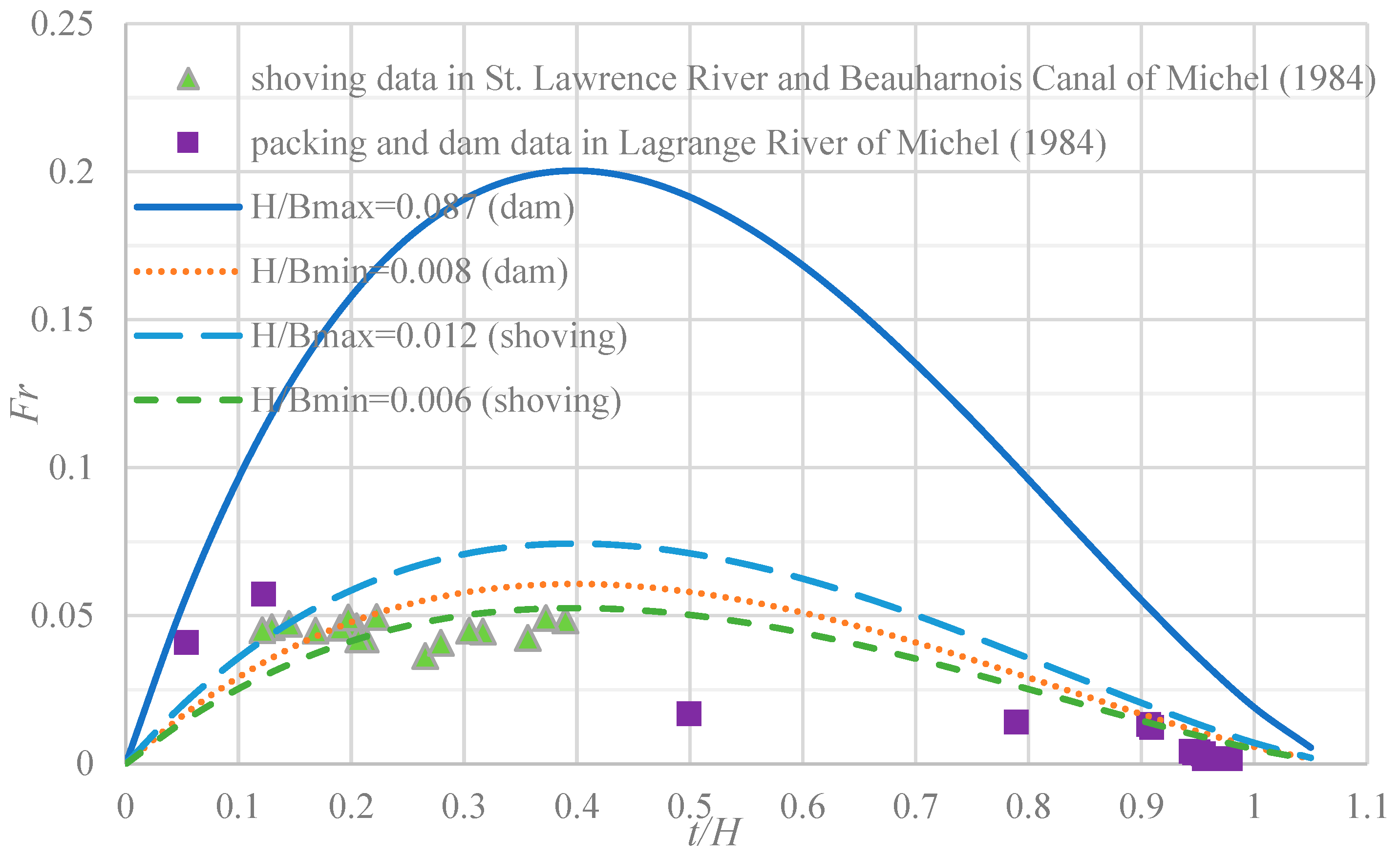
3.1. The Limiting Conditions for the Occurrence of Ice Wave Phenomenon
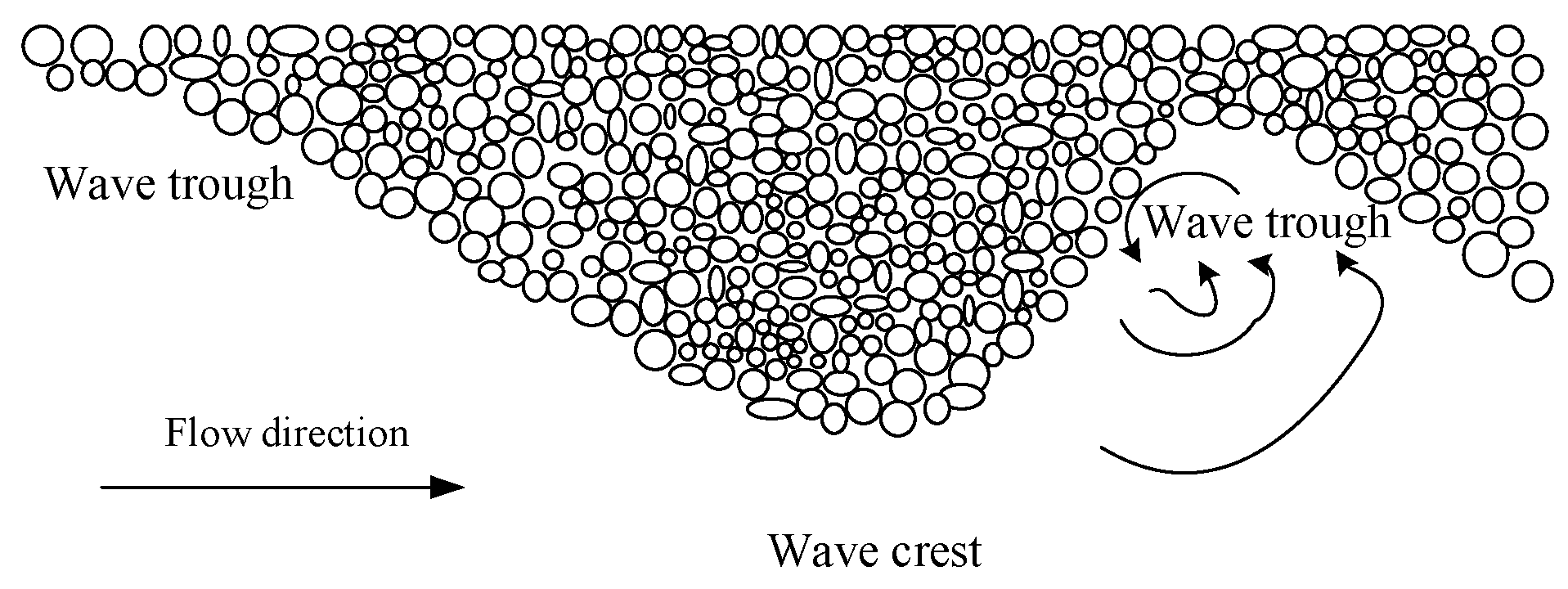
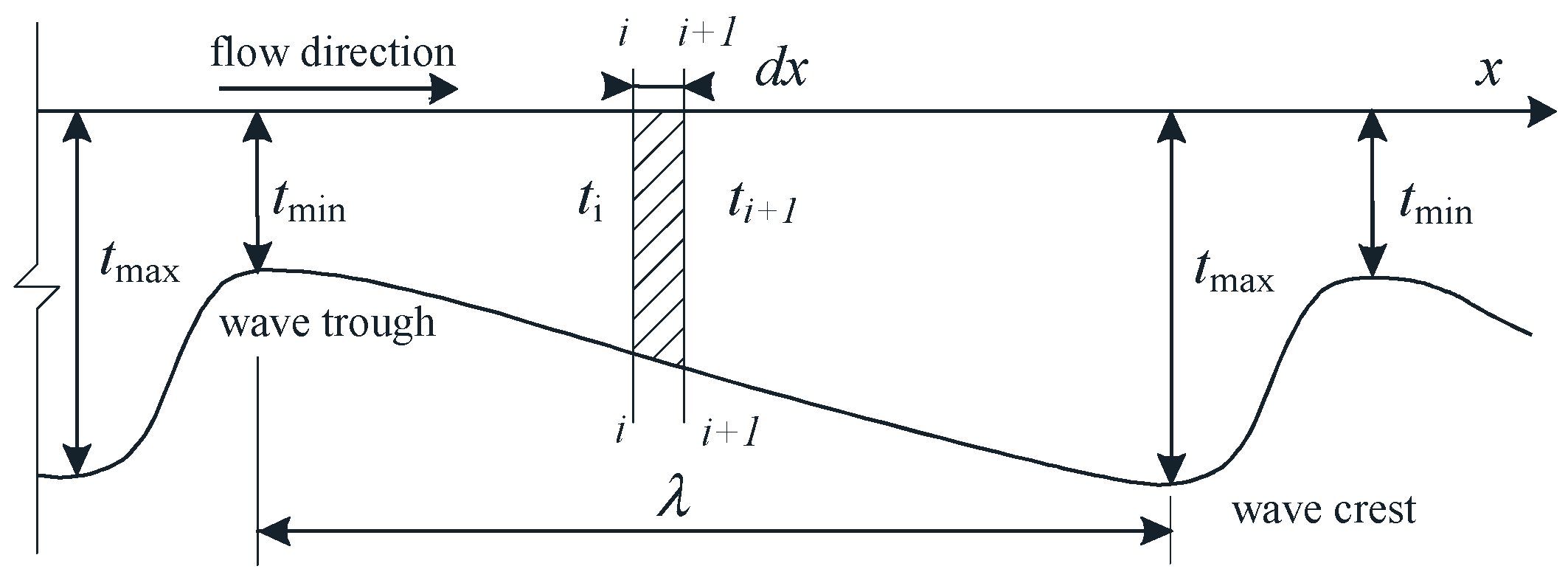
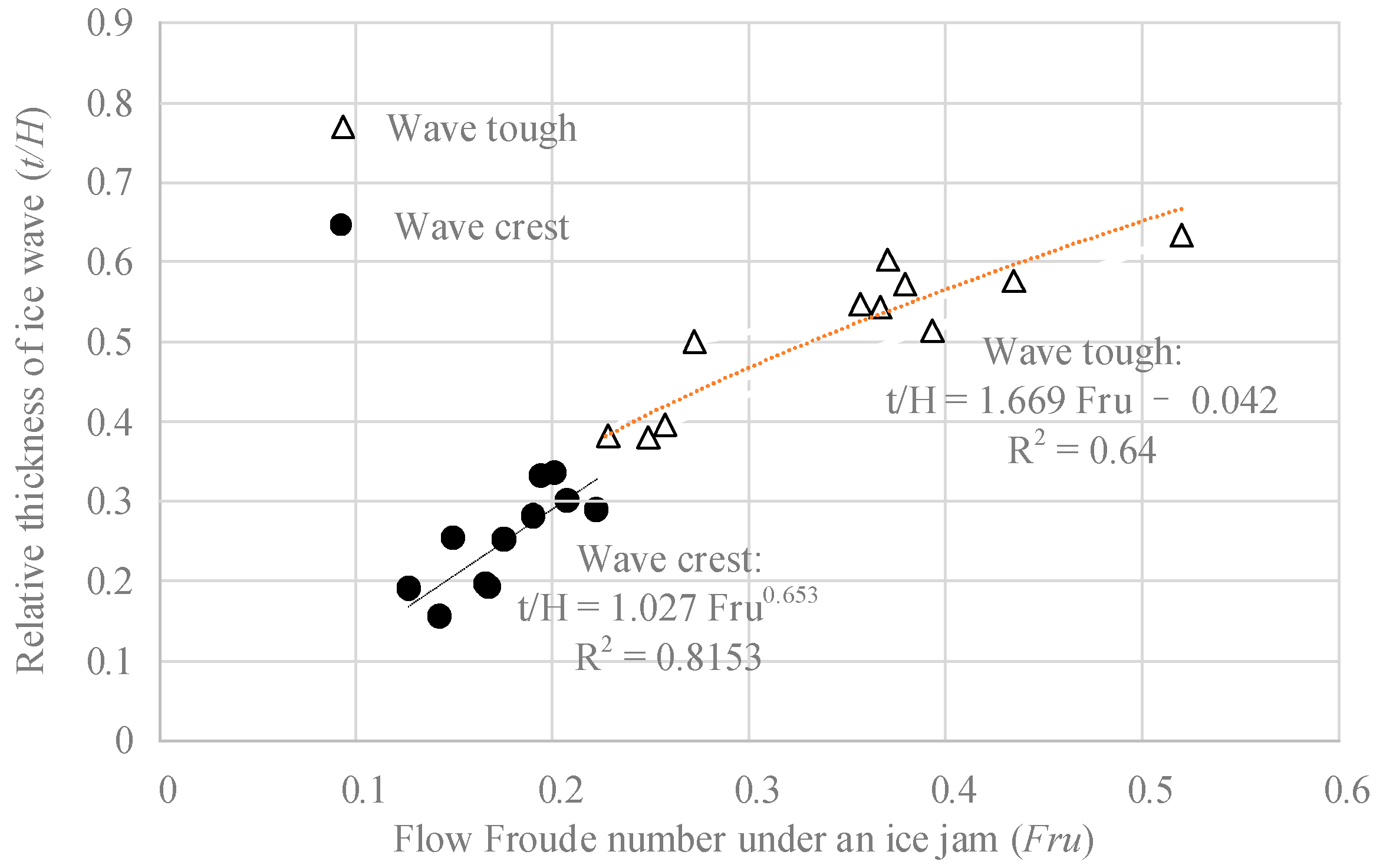
3.2. Ice Jam Thickness of Wave Crest and Wave Trough
3.3. Flow Froude Number under the Ice Jam
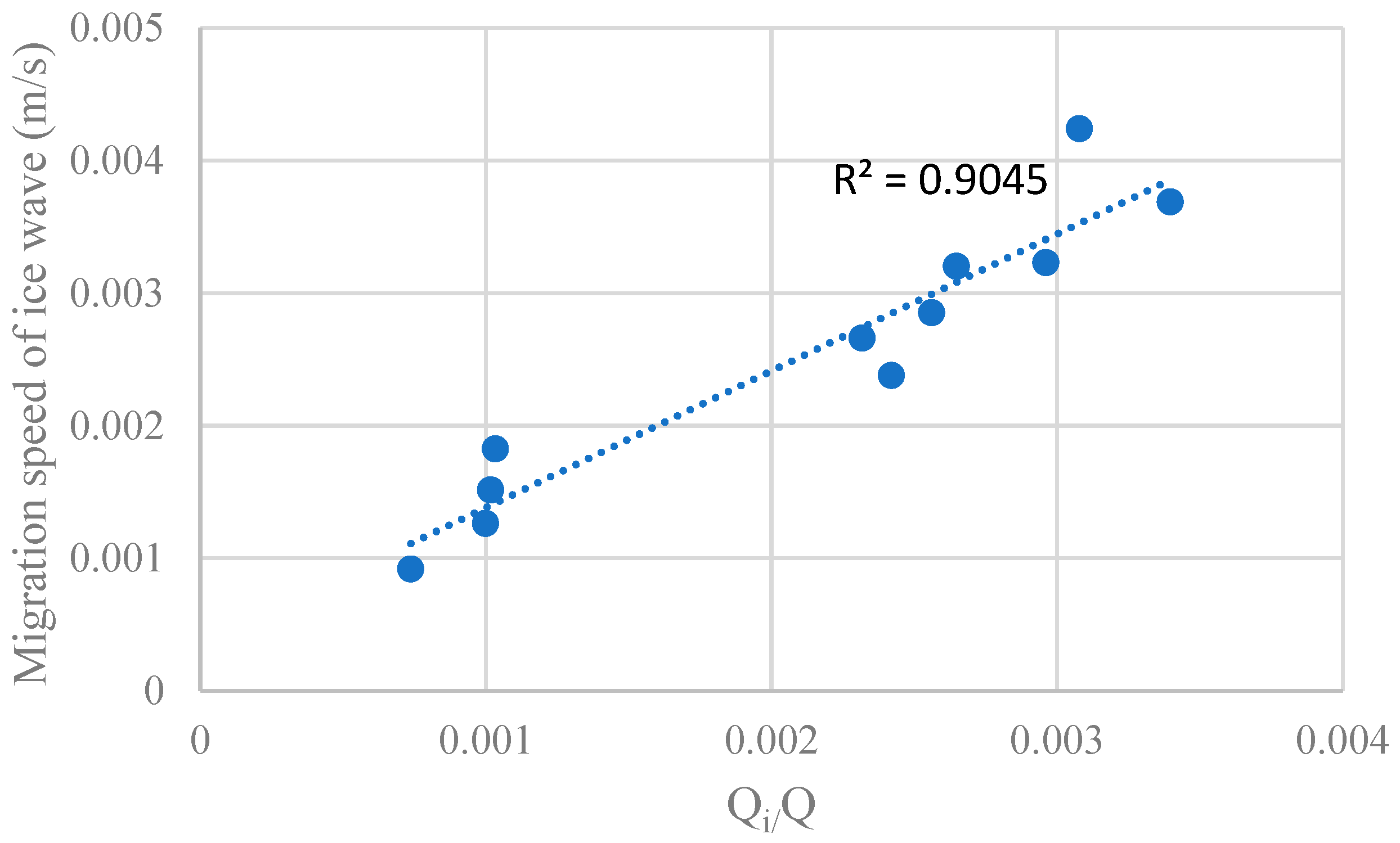
3.4. Wave Length and Migration Speed
3.5. Case Studies
- (a)
- Quasi-static ice jam: This kind of ice jam is also known as the continuous juxtaposition form. It is characterized by the continuous juxtaposition of a layer of ice floes with a specific thickness. The ice jam thickness completely depends on the initial ice thickness and the thermal effect during winter period, which is similar to but slightly different from the static ice cover in lakes.
- (b)
- Frontal progression: The kind of accumulation refers to an ice jam whose thickness exceeds its initial thickness after the submerged ice floes accumulate at the front of an ice jam (or the leading edge of an ice jam). A relatively stable ice jam head in a river is essential for the development of this kind of ice jam.
- (c)
- Packing ice jam: The front edge of an ice jam in rivers may advance and retreat during ice-jammed period, and when it advances upstream, local accumulation (packing) will often occur.
- (d)
- Shoving ice jam: In natural rivers, when the cohesive force of an ice jam is not enough to support the positive stress at the front edge of an ice jam, a long and thin ice cover is often broken suddenly and leads to a thick accumulation body at the downstream. During the period of the initial stage, this accumulation body is normally loose without cohesion, but it may form a solid accumulation ice jam later due to the influence of thermal factors.
- (e)
- Hanging dam: A hanging ice dam is referred to the development of an ice jam along a specific river section (such as the junction of rapid flow and slow flow), where the flow velocity is too high for ice floes to accumulate upstream. Under such a flow condition, the incoming ice floes will be entrained by water and accumulate under the bottom of the ice cover. The cross sectional area for flow under the ice accumulation decreases until the flow velocity is high enough to erode ice floes further to downstream.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiao, Y.; Pavelsky, T.M.; Allen, G.H. The past and future of global river ice. Nature 2020, 577, 69–73. [Google Scholar]
- Sui, J.; Karney, B.; Fang, D. Variation in water level under ice-jammed condition—Field investigation and experimental study. Hydrol. Res. 2005, 36, 65–84. [Google Scholar] [CrossRef]
- Beltaos, S.; Burrell, B.C. Hydrotechnical Advances in Canadian River-Ice Science and Engineering during the Past 35 Years. Can. J. Civ. Eng. 2015, 42, 583–591. [Google Scholar] [CrossRef]
- Sui, J.; Hicks, F.; Menounos, B. Observations of riverbed scour under a developing hanging ice dam. Can. J. Civ. Eng. 2006, 33, 214–218. [Google Scholar] [CrossRef]
- White, K.D. Review of prediction methods for breakup ice jams. Can. J. Civ. Eng. 2003, 30, 89–100. [Google Scholar] [CrossRef]
- Lindenschmidt, K.E.; Das, A.; Rokaya, P.; Chu, T. Ice jam flood risk assessment and mapping. Hydrol. Process. 2016, 30, 3754–3769. [Google Scholar] [CrossRef]
- Sui, J.; Wang, J.; Balachandar, R. Accumulation of frazil ice along a river bend. Can. J. Civ. Eng. 2008, 35, 158–169. [Google Scholar] [CrossRef]
- Sui, J.; Karney, B.W.; Sun, Z.; Wang, D. Field Investigation of Frazil Jam Evolution: A Case Study. J. Hydraul. Eng. 2002, 128, 781–787. [Google Scholar] [CrossRef]
- Beltaos, S.; Carter, T. Field studies of ice breakup and jamming in lower Peace River, Canada. Cold Reg. Sci. Technol. 2009, 56, 102–114. [Google Scholar] [CrossRef]
- Healy, D.; Hicks, F.E. Experimental study of ice jam formation dynamics. J. Cold Reg. Eng. 2006, 20, 117–139. [Google Scholar] [CrossRef]
- Wang, J.; Hua, J.; Chen, P.; Sui, J.; Wu, P.; Whitcombe, T. Initiation of ice jam in front of bridge piers—An experimental study. J. Hydrodyn. 2019, 31, 117–123. [Google Scholar] [CrossRef]
- Daly, S.F.; Axelson, K.D. Stability of floating and submerged blocks. J. Hydraul. Res. 1990, 28, 737–752. [Google Scholar] [CrossRef]
- Wang, J.; Sui, J.Y.; Zhang, H.Y.; Chen, P.P.; Hirshfield, F. Mechanisms of ice accumulation in a river bend—An experimental study. Int. J. Sediment Res. 2012, 27, 521–537. [Google Scholar] [CrossRef]
- Hicks, F.E.; Healy, D. Determining winter discharge based on hydraulic modeling. Can. J. Civ. Eng. 2003, 30, 101–112. [Google Scholar] [CrossRef]
- Wang, J.; Chen, P.; Sui, J. Progress in studies on ice accumulation in river bends. J. Hydrodyn. 2011, 23, 737–744. [Google Scholar] [CrossRef]
- Beltaos, S. Progress in the study and management of river ice jams. Cold Reg. Sci. Technol. 2008, 51, 2–19. [Google Scholar] [CrossRef]
- Beltaos, S. Numerical prediction of ice-jam profiles in lower Athabasca River. Can. J. Civ. Eng. 2019, 46, 722–731. [Google Scholar] [CrossRef]
- Wang, J.; Sui, J.; Chen, P. Numerical simulations of ice accumulation under ice cover along a river bend. Int. J. Environ. Sci. Technol. 2009, 6, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Sola, D.; Scott, K.A. Efficient Shallow Network for River Ice Segmentation. Remote Sens. 2022, 14, 2378. [Google Scholar] [CrossRef]
- Altena, B.; Kääb, A. Quantifying river ice movement through a combination of European satellite monitoring services. Int. J. Appl. Earth Obs. Geoinf. 2021, 98, 102315. [Google Scholar] [CrossRef]
- Sui, J.; Faruque, M.A.A.; Balachandar, R. Local scour caused by submerged square jets under ice cover. ASCE J. Hydraul. Eng. 2009, 135, 316–319. [Google Scholar] [CrossRef]
- Sui, J.; Wang, J.; He, Y.; Krol, F. Velocity profiles and incipient motion of frazil particles under ice cover. Int. J. Sediment Res. 2010, 25, 39–51. [Google Scholar] [CrossRef]
- Jafari, R.; Sui, J. Velocity field and turbulence structure around spur dikes with different angles of orientation under ice covered flow conditions. Water 2021, 13, 1844. [Google Scholar] [CrossRef]
- Namaee, M.; Sui, J. Velocity profiles and turbulence intensities around side-by-side bridge piers under ice-covered flow condition. J. Hydrol. Hydromech. 2020, 68, 70–82. [Google Scholar] [CrossRef] [Green Version]
- Cheng, T.; Wang, J.; Chen, P.; Sui, J. Simulation of ice accumulation around bridge piers during river breakup periods using a discrete element model. J. Hydrodyn. 2022, 34, 94–105. [Google Scholar] [CrossRef]
- Shen, H.T.; Wang, D.S. Under cover transport and accumulation of frazil granules. J. Hydraul. Eng. 1995, 121, 184–195. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Sui, J.; Karney, B. Formation and movement of ice accumulation waves under ice cover—An experimental study. J. Hydrol. Hydromech. 2019, 67, 171–178. [Google Scholar] [CrossRef] [Green Version]
- Beltaos, S. River Ice Jams; Water Resources Publications: Littleton, CO, USA, 1995. [Google Scholar]
- Pariset, E.; Hausser, R.; Gagnon, A. Formation of ice covers and ice jams in rivers. J. Hydraul. Div. 1966, 92, 1–24. [Google Scholar] [CrossRef]
- Michel, B. Comparison of field data with theories on ice cover progression in large rivers. Can. J. Civ. Eng. 1984, 11, 798–814. [Google Scholar] [CrossRef]



| Initial Condition | Equilibrium Ice Jam | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Flow Depth (cm) | Flow Rate (L/s) | Ice Discharge (L/s) | Fr | Flow Depth (cm) | Average Ice Thickness (cm) | Water Head (cm) | Ice Jam Length (cm) | Hydraulic Gradient | Chézy Coefficient |
| 10 | 5.61 | 0.01299 | 0.109 | 11.9 | 5.25 | 2.71 | 7.08 | 1.07 × 10−3 | 14.10 |
| 15 | 9.00 | 0.02177 | 0.106 | 16.6 | 7.5 | 2.74 | 11.39 | 9.77 × 10−4 | 14.83 |
| 15 | 9.60 | 0.00993 | 0.121 | 15.9 | 5.55 | 3.35 | 9.83 | 6.32 × 10−4 | 16.22 |
| 15 | 10.81 | 0.0367 | 0.116 | 17.7 | 8.1 | 3.19 | 11.75 | 1.52 × 10−3 | 13.17 |
| 15 | 12.02 | 0.03699 | 0.133 | 17.3 | 6.95 | 4.07 | 10.14 | 1.09 × 10−3 | 15.45 |
| 20 | 12.02 | 0.03558 | 0.093 | 22.04 | 8.75 | 2.49 | 17.08 | 1.38 × 10−3 | 9.45 |
| 20 | 14.43 | 0.03694 | 0.114 | 21.75 | 8.65 | 3.25 | 15.49 | 1.26 × 10−3 | 12.10 |
| 20 | 15.20 | 0.04025 | 0.120 | 21.7 | 8.375 | 3.51 | 14.99 | 1.01 × 10−3 | 13.94 |
| 25 | 16.00 | 0.01599 | 0.096 | 26 | 9.8 | 2.78 | 20.44 | 7.18 × 10−4 | 12.95 |
| 25 | 18.01 | 0.01327 | 0.111 | 25.62 | 6.9 | 3.30 | 19.11 | 3.69 × 10−4 | 16.36 |
| 25 | 20.00 | 0.02034 | 0.122 | 25.82 | 7.4 | 3.77 | 18.51 | 5.54 × 10−4 | 15.20 |
| Initial Flow Depth (cm) | Flow Discharge (L/s) | Ice Discharge (L/s) | Flow Depth during Equilibrium Ice Jam (cm) | Fr during Equilibrium Ice Jam | Location of Ice Jam Head at CS | Occurrence of Ice Wave |
|---|---|---|---|---|---|---|
| 10 | 5.61 | 0.01299 | 11.90 | 0.109 | 5 | Yes |
| 10 | 6.40 | 0.00625 | 10.75 | 0.145 | 5 | No |
| 10 | 6.40 | 0.0105 | 10.75 | 0.145 | 5 | No |
| 10 | 7.20 | 0.01054 | 11.31 | 0.151 | 18 | No |
| 10 | 8.00 | 0.0274 | 11.08 | 0.173 | 17 | No |
| 15 | 9.00 | 0.02177 | 16.60 | 0.106 | 5 | Yes |
| 15 | 9.60 | 0.00993 | 15.90 | 0.121 | 5 | Yes |
| 15 | 10.81 | 0.00613 | 16.17 | 0.132 | 15 | Yes |
| 15 | 10.81 | 0.0367 | 17.70 | 0.116 | 5 | Yes |
| 15 | 12.02 | 0.03699 | 17.30 | 0.133 | 5 | Yes |
| 15 | 13.20 | 0.02365 | 16.26 | 0.161 | 14 | No |
| 20 | 14.43 | 0.03694 | 21.75 | 0.114 | 5 | Yes |
| 20 | 15.20 | 0.04025 | 21.70 | 0.120 | 5 | Yes |
| 20 | 15.20 | 0.00743 | 21.28 | 0.124 | 17 | Yes |
| 20 | 16.03 | 0.0259 | 21.12 | 0.132 | 15 | Yes |
| 25 | 16.00 | 0.01599 | 26.00 | 0.096 | 5 | Yes |
| 25 | 18.01 | 0.01327 | 25.62 | 0.111 | 6 | Yes |
| 25 | 20.00 | 0.02034 | 25.82 | 0.122 | 5 | Yes |
| 25 | 20.50 | 0.01298 | 25.88 | 0.124 | 16 | Yes |
| 25 | 21.00 | 0.01327 | 26.16 | 0.125 | 18 | Yes |
| 25 | 22.00 | 0.02579 | 26.27 | 0.130 | 19 | Yes |
| Initial Condition | Equilibrium Ice Jam | Calculated Ice Jam Thickness (cm) | Measured Ice Jam Thickness (cm) | Diff. Btw. Calculated and Measured Results | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Flow Depth (cm) | Flow Rate (L/s) | Ice Discharge (L/s) | Fr | Flow Depth (cm) | Lower Limiting (tLL) | Upper Limiting (tUL) | At Wave Trough (tWT) | At Wave Crest (tWC) | Ratio: tWC/tWT | (tLL − tWT) (cm) | (tUL − tWc) (cm) |
| 10 | 5.61 | 0.01299 | 0.109 | 11.9 | 2.71 | 7.08 | 4.0 | 6.5 | 1.63 | −1.29 | 0.58 |
| 15 | 9.00 | 0.02177 | 0.106 | 16.6 | 2.74 | 11.39 | 5.5 | 9.5 | 1.73 | −2.76 | 1.89 |
| 15 | 9.60 | 0.00993 | 0.121 | 15.9 | 3.35 | 9.83 | 4.8 | 6.3 | 1.31 | −1.45 | 3.53 |
| 15 | 10.81 | 0.0367 | 0.116 | 17.7 | 3.19 | 11.75 | 5.0 | 11.2 | 2.24 | −1.81 | 0.55 |
| 15 | 12.02 | 0.03699 | 0.133 | 17.3 | 4.07 | 10.14 | 5.0 | 8.9 | 1.78 | −0.93 | 1.24 |
| 20 | 12.02 | 0.03558 | 0.093 | 22.04 | 2.49 | 17.08 | 4.2 | 13.3 | 3.17 | −1.71 | 3.78 |
| 20 | 14.43 | 0.03694 | 0.114 | 21.75 | 3.25 | 15.49 | 5.5 | 11.8 | 2.15 | −2.25 | 3.69 |
| 20 | 15.20 | 0.04025 | 0.120 | 21.7 | 3.51 | 14.99 | 4.25 | 12.5 | 2.94 | −0.74 | 2.49 |
| 25 | 16.00 | 0.01599 | 0.096 | 26 | 2.78 | 20.44 | 6.6 | 13.0 | 1.97 | −3.82 | 7.44 |
| 25 | 18.01 | 0.01327 | 0.111 | 25.62 | 3.30 | 19.11 | 4.0 | 9.8 | 2.45 | −0.7 | 9.31 |
| 25 | 20.00 | 0.02034 | 0.122 | 25.82 | 3.77 | 18.51 | 5.0 | 9.8 | 1.96 | −1.23 | 8.71 |
| Initial Condition | Equilibrium Ice Jam | Wave Length (cm) | Measured Results | |||||
|---|---|---|---|---|---|---|---|---|
| Flow Depth (cm) | Flow Rate (L/s) | Ice Discharge (L/s) | Fr | Flow Depth (cm) | Calculated Result | Measured Result | Ice Wave Periodic Migration Time (s) | Ice Wave Migration Speed (m/s) |
| 10 | 5.61 | 0.01299 | 0.109 | 11.90 | 33.11 | 29 | 109 | 0.00266 |
| 15 | 9.00 | 0.02177 | 0.106 | 16.60 | 40.50 | 34 | 143 | 0.00238 |
| 15 | 9.60 | 0.00993 | 0.121 | 15.90 | 23.98 | 25 | 137 | 0.00182 |
| 15 | 10.81 | 0.03699 | 0.116 | 17.70 | 70.76 | 66 | 179 | 0.00369 |
| 15 | 12.02 | 0.03699 | 0.133 | 17.30 | 69.93 | 64 | 151 | 0.00424 |
| 20 | 12.02 | 0.03558 | 0.093 | 22.04 | 66.70 | 62 | 192 | 0.00323 |
| 20 | 14.43 | 0.03699 | 0.114 | 21.75 | 68.23 | 69 | 242 | 0.00285 |
| 20 | 15.20 | 0.04025 | 0.120 | 21.70 | 74.70 | 81 | 253 | 0.00320 |
| 25 | 16.00 | 0.01599 | 0.096 | 26.00 | 38.07 | 54 | 428 | 0.00126 |
| 25 | 18.01 | 0.01327 | 0.111 | 25.62 | 24.27 | 61 | 664 | 0.00092 |
| 25 | 20.00 | 0.02034 | 0.122 | 25.82 | 24.80 | 50 | 330 | 0.00152 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Sui, J.; Cao, G.; Cheng, T. Waved-Shape Accumulation of Ice Jam—Analysis and Experimental Study. Water 2022, 14, 3945. https://doi.org/10.3390/w14233945
Chen P, Sui J, Cao G, Cheng T. Waved-Shape Accumulation of Ice Jam—Analysis and Experimental Study. Water. 2022; 14(23):3945. https://doi.org/10.3390/w14233945
Chicago/Turabian StyleChen, Pangpang, Jueyi Sui, Guangxue Cao, and Tiejie Cheng. 2022. "Waved-Shape Accumulation of Ice Jam—Analysis and Experimental Study" Water 14, no. 23: 3945. https://doi.org/10.3390/w14233945
APA StyleChen, P., Sui, J., Cao, G., & Cheng, T. (2022). Waved-Shape Accumulation of Ice Jam—Analysis and Experimental Study. Water, 14(23), 3945. https://doi.org/10.3390/w14233945





