RANS Modeling of Turbulent Flow and Heat Transfer in a Droplet-Laden Mist Flow through a Ribbed Duct
Abstract
:1. Introduction
2. Mathematical Models
2.1. Governing Equations for the Two-Phase Turbulent Mist Phase
2.2. Evaporation Model
2.3. The Elliptic Blending Reynolds Stress Model (RSM) for the Gas Phase
2.4. Governing Equations for the Dispersed Phase
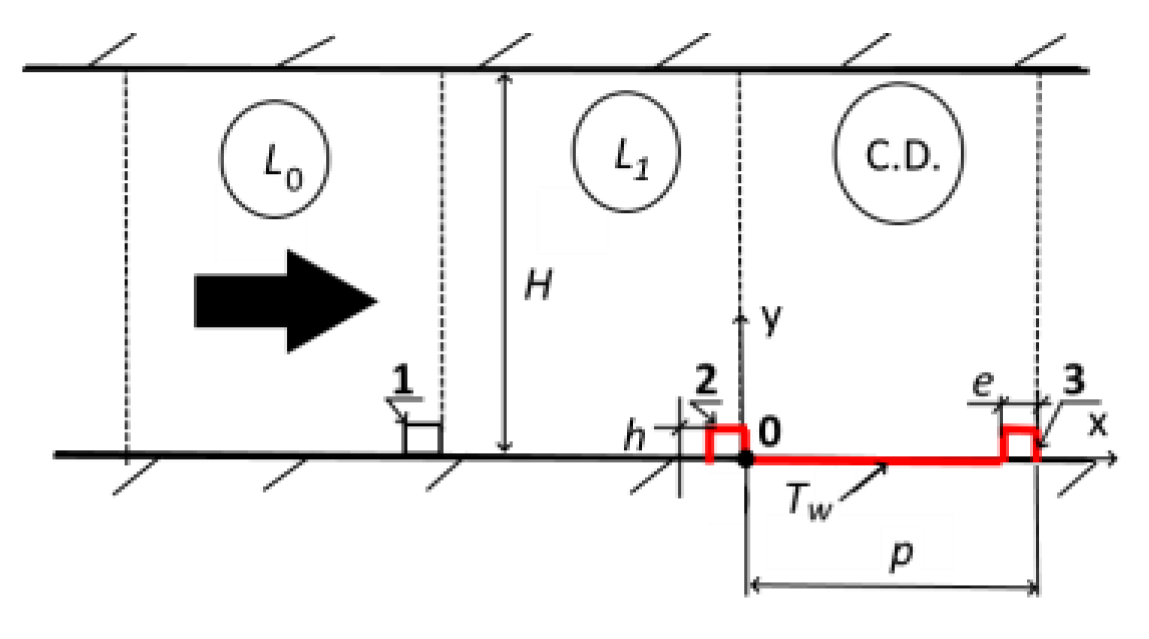
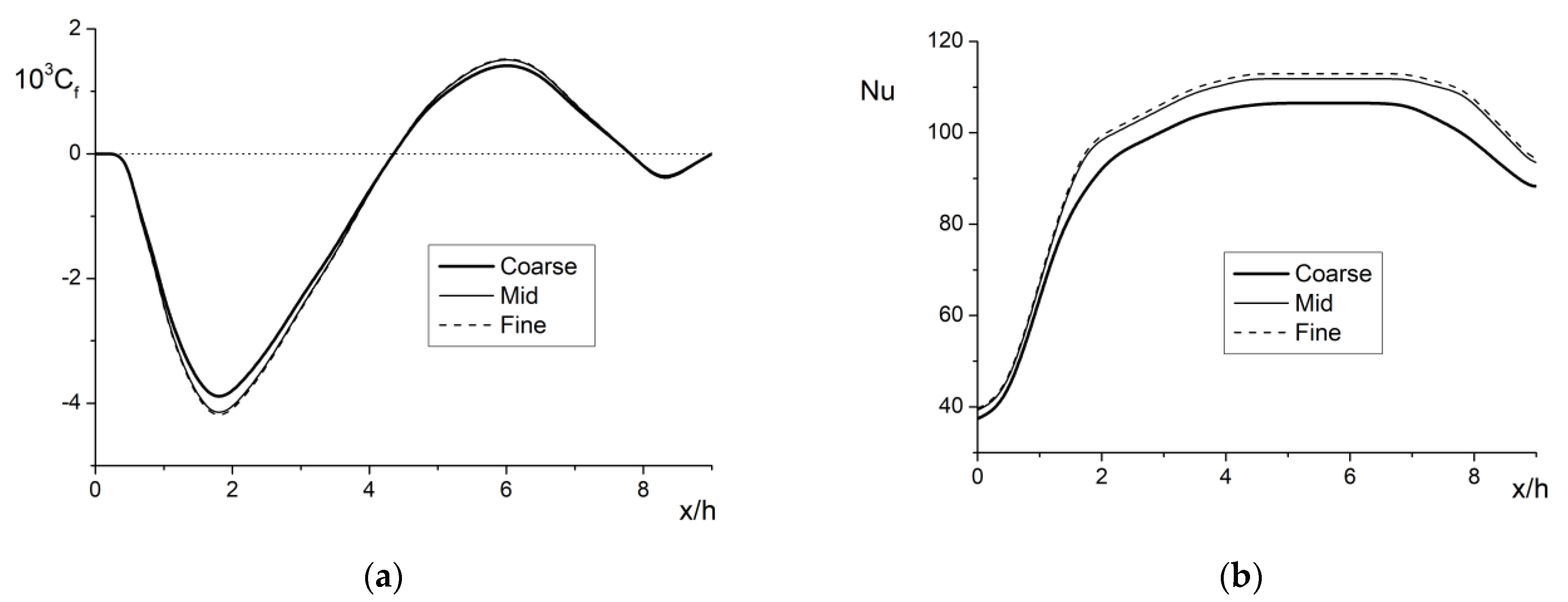
3. Numerical Solution and Model Validation
3.1. Numerical Solution
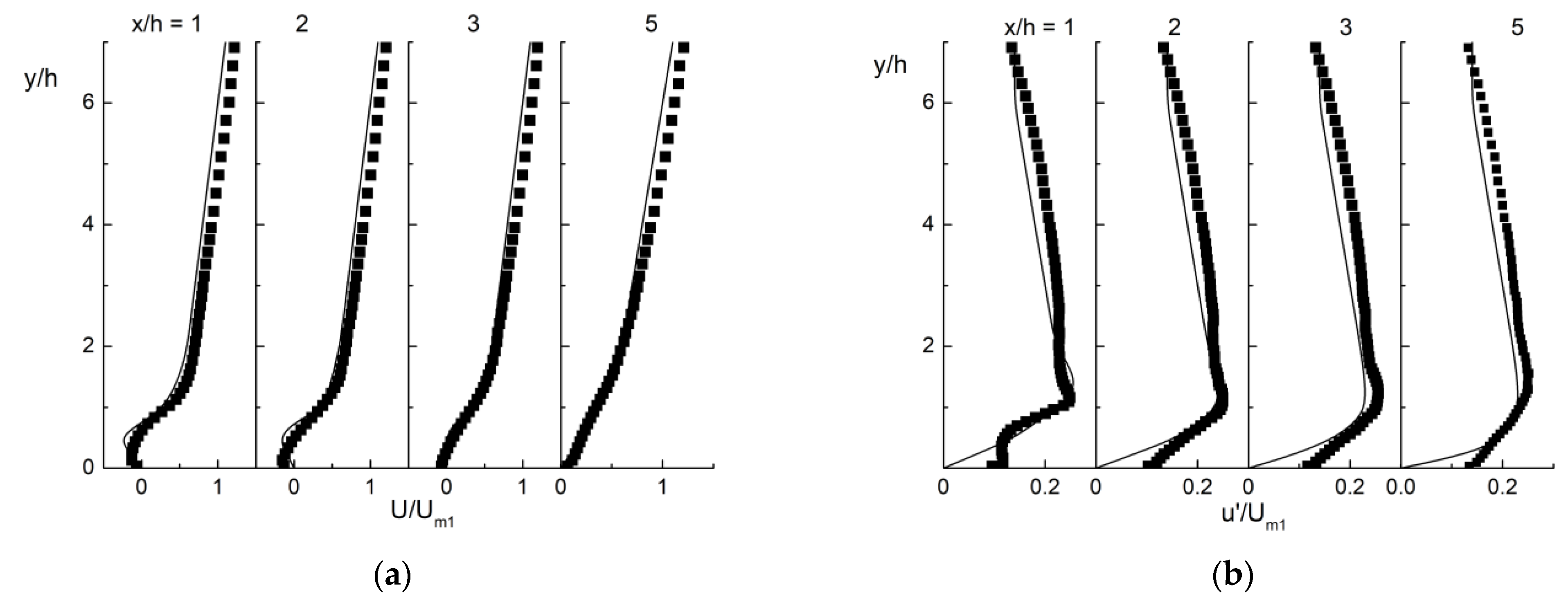
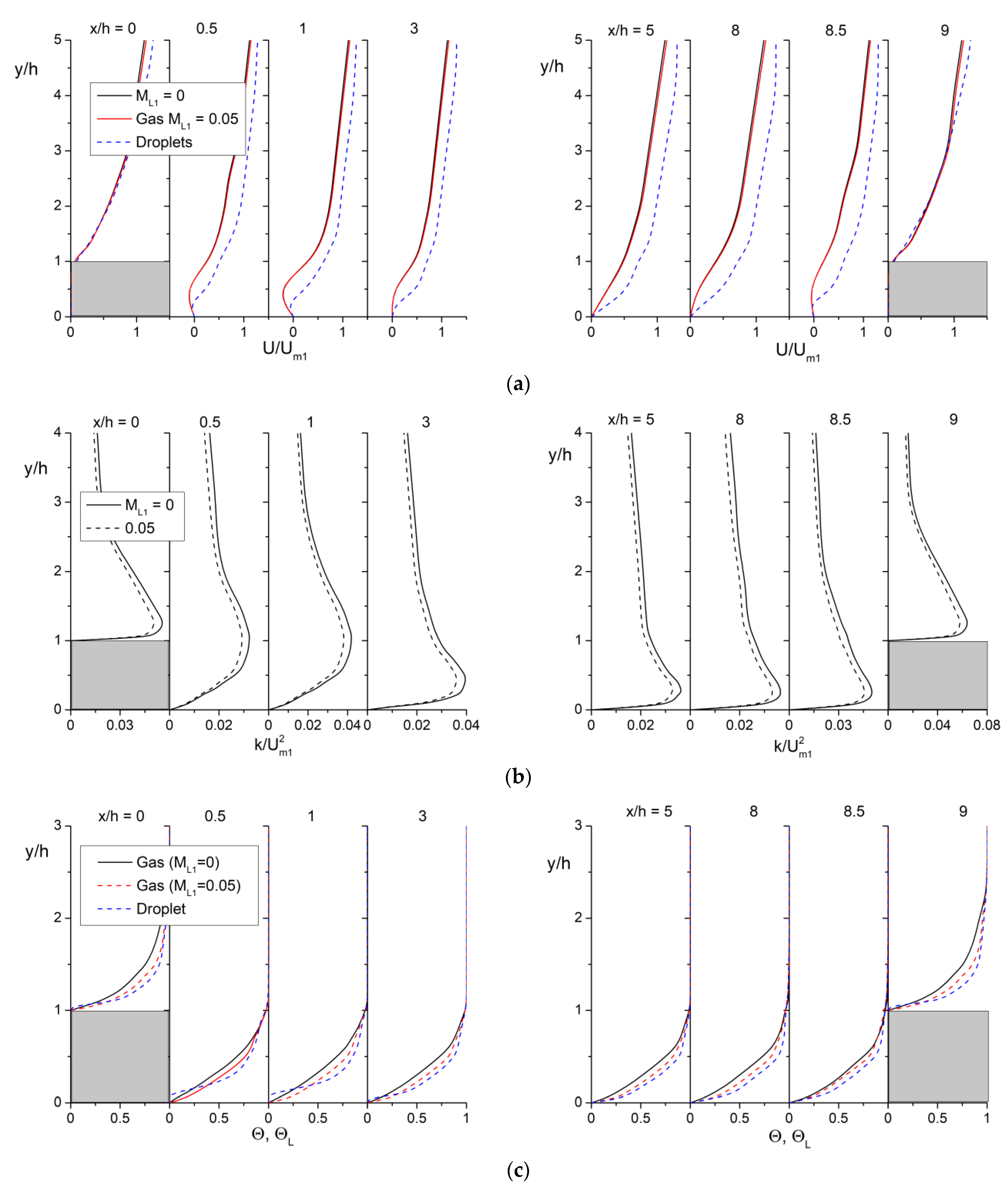
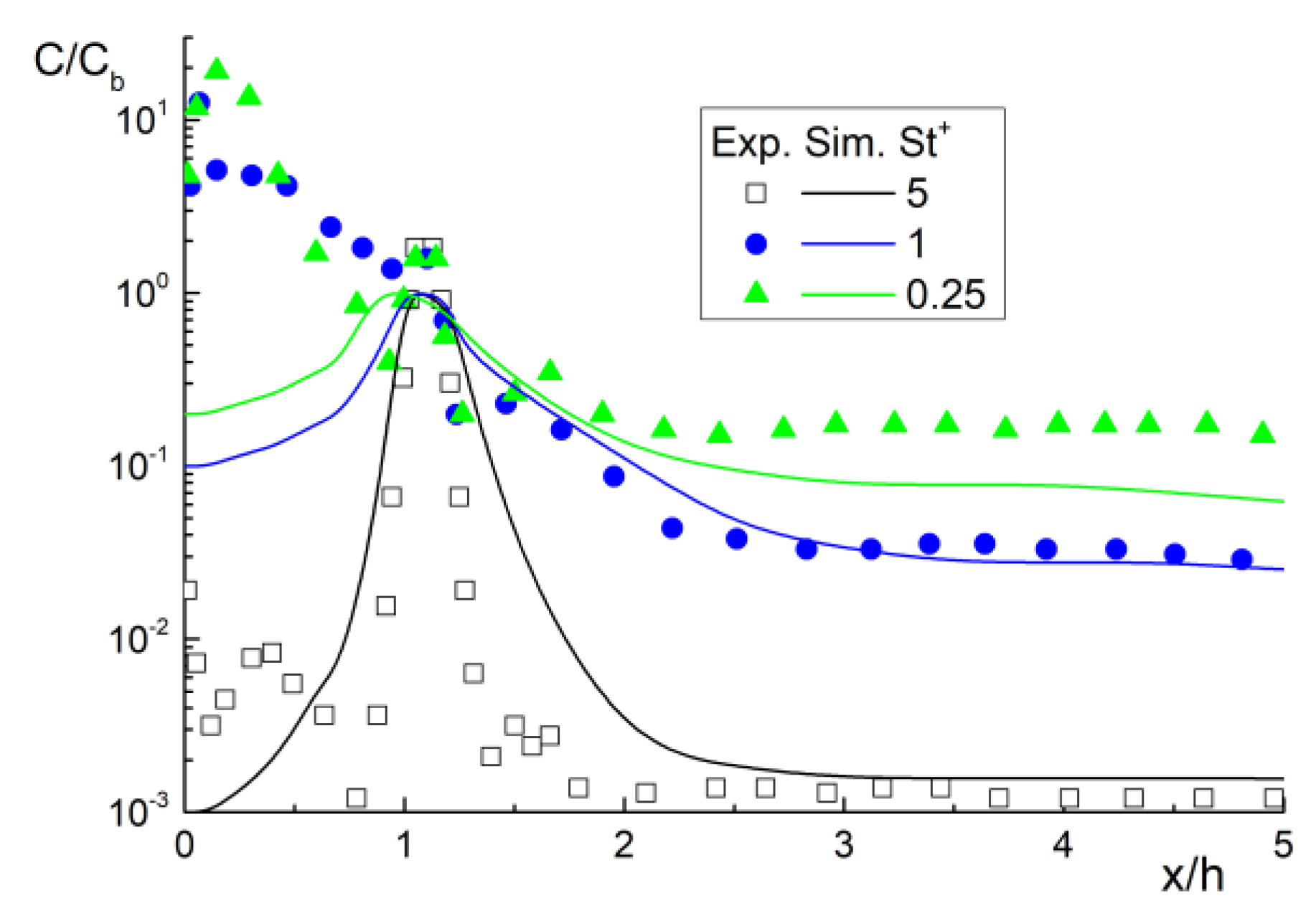
3.2. Model Validation
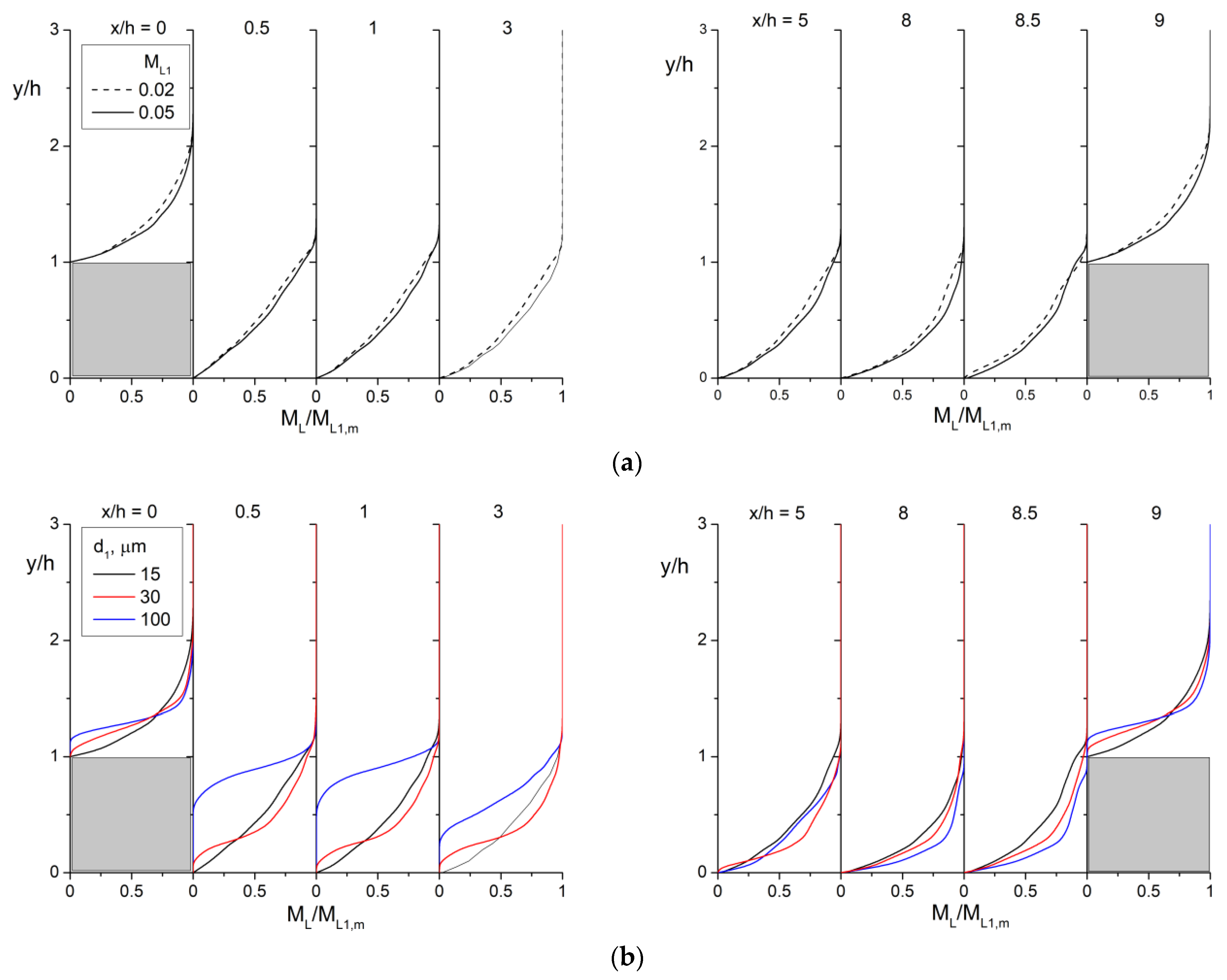
4. The RANS Results and Discussion
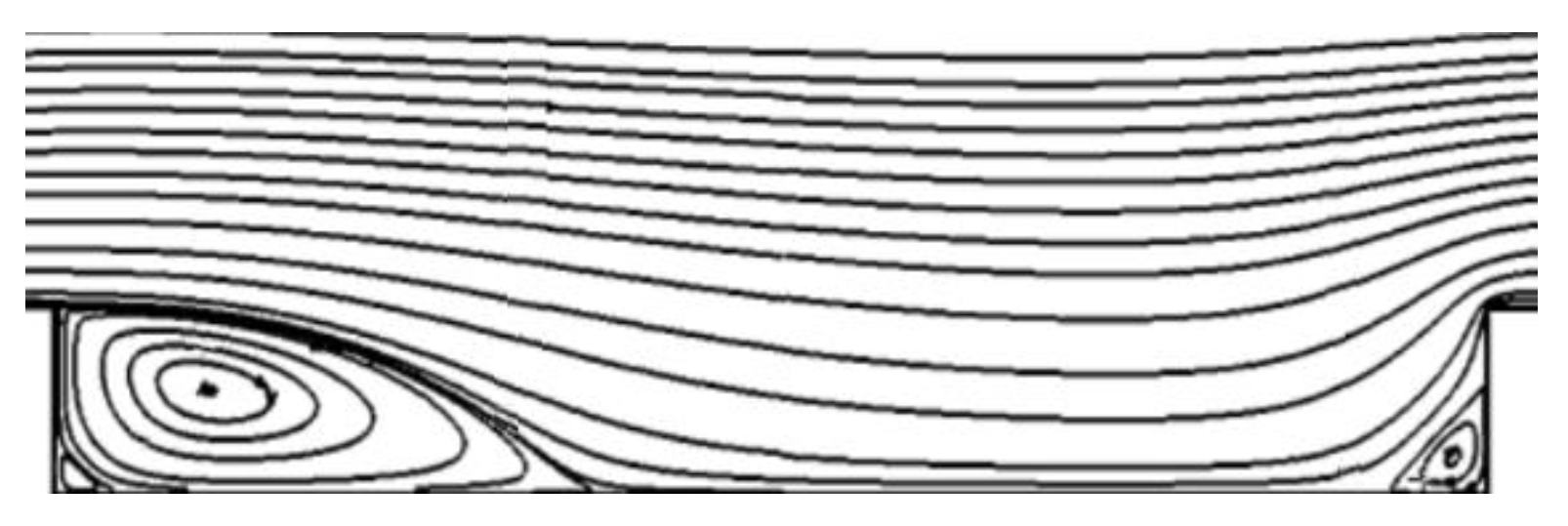
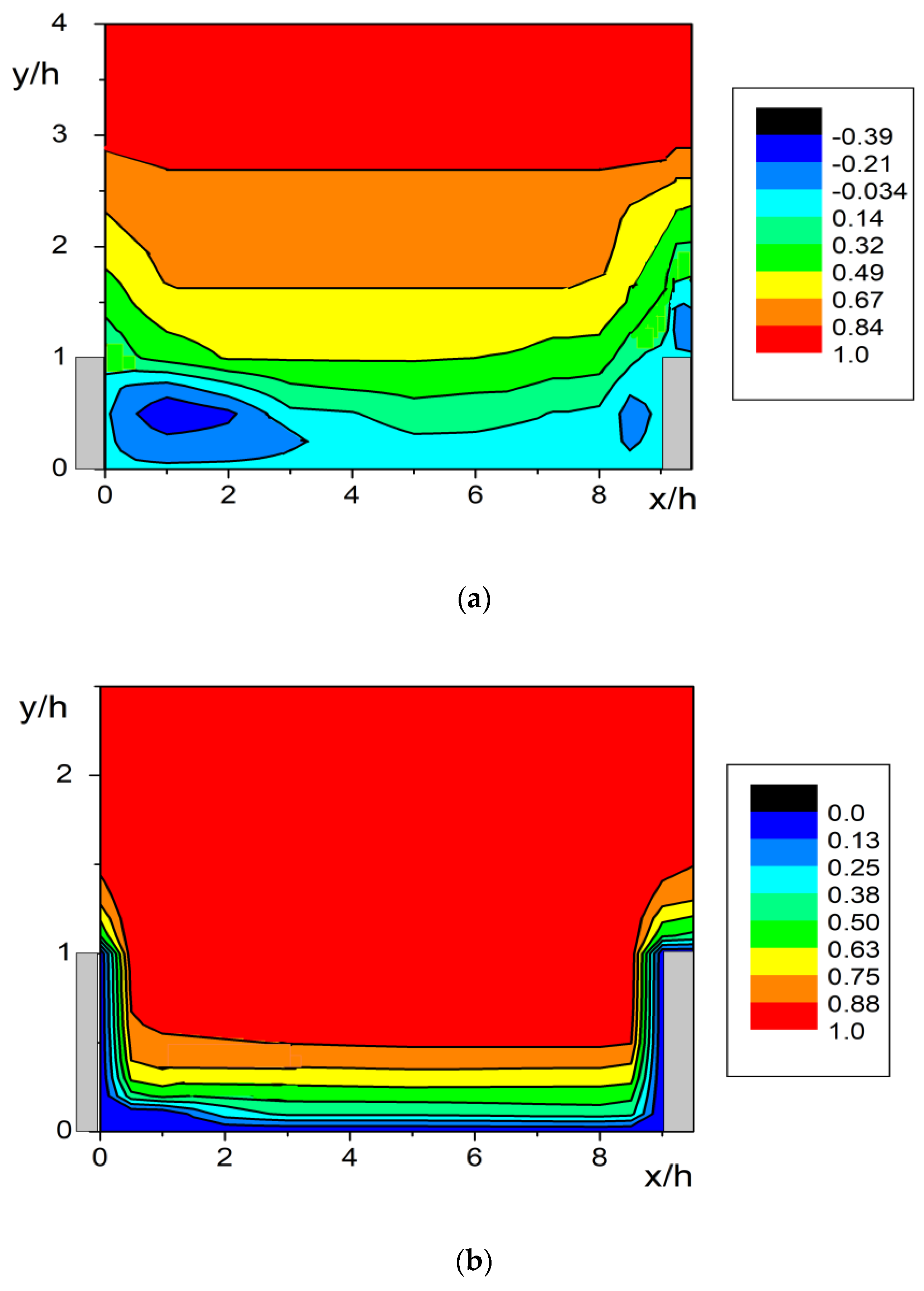
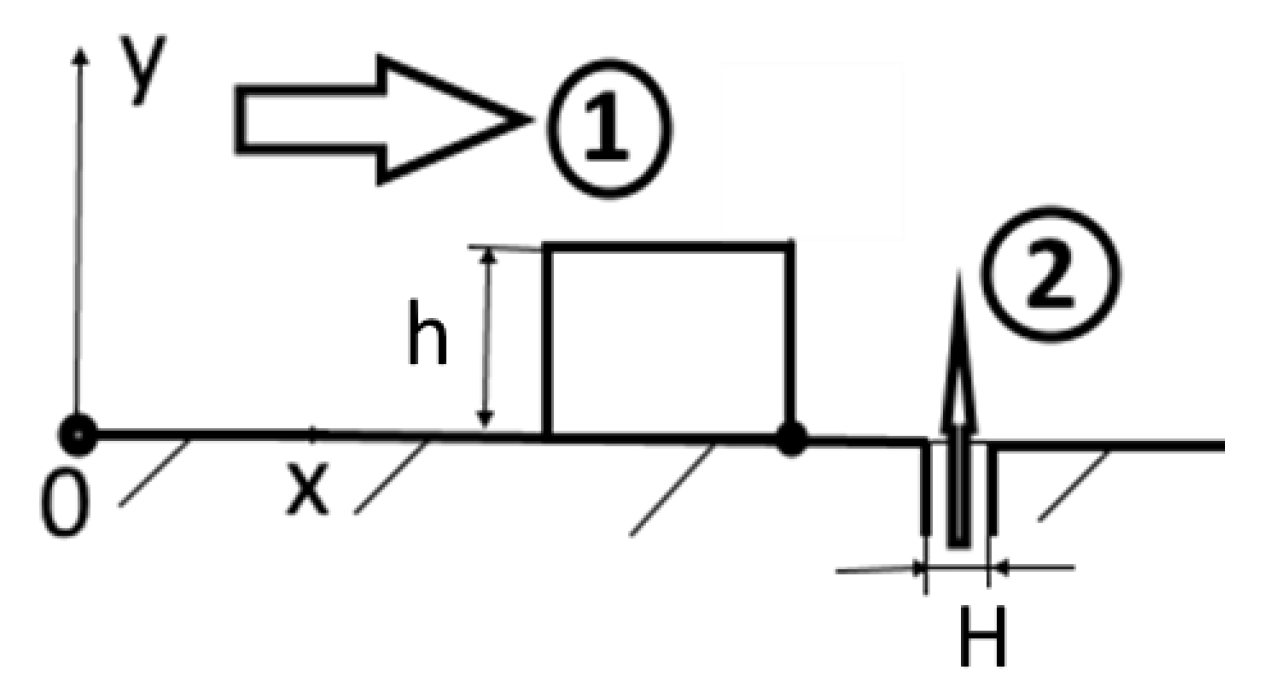
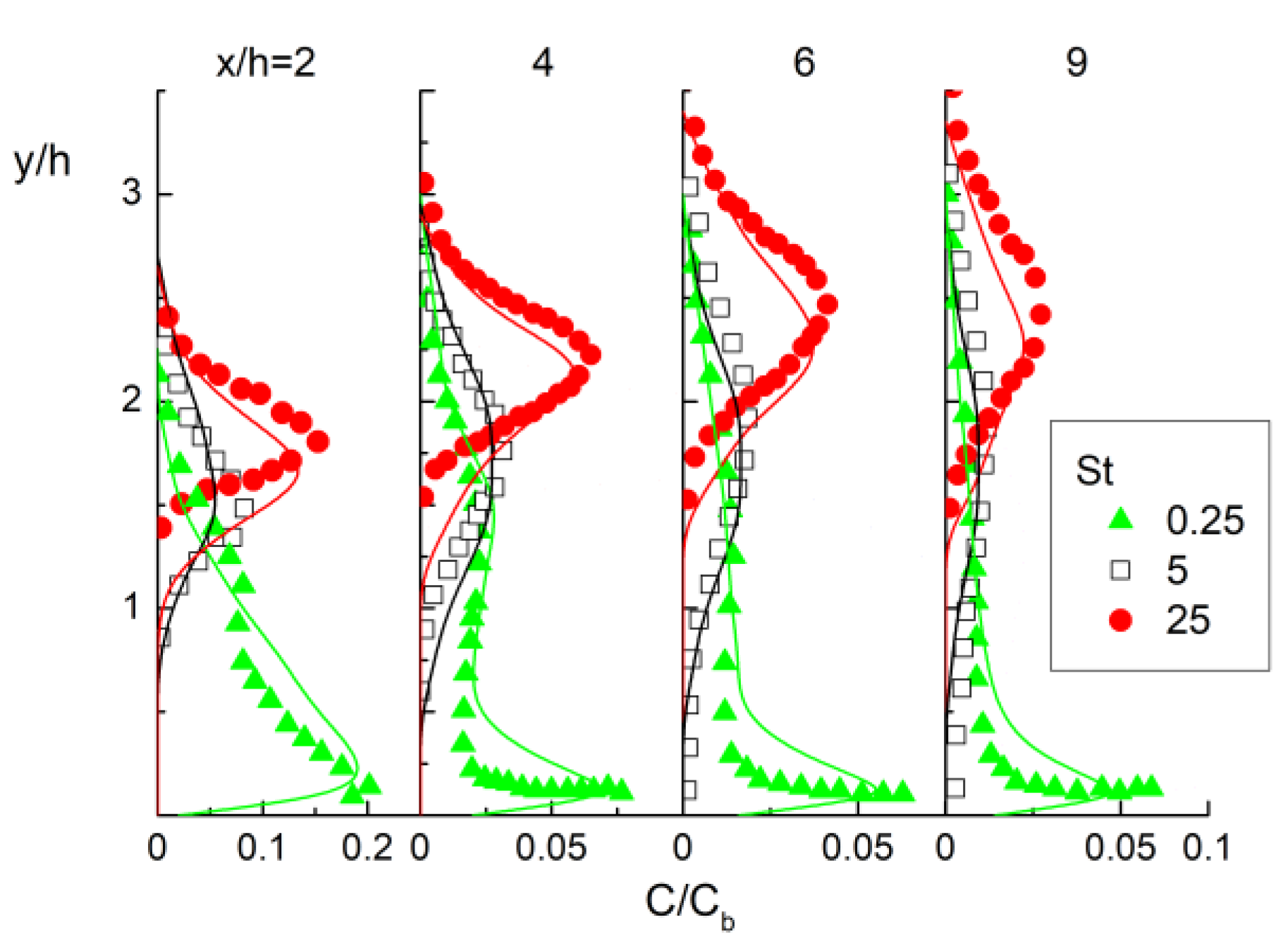
4.1. Flow Structure
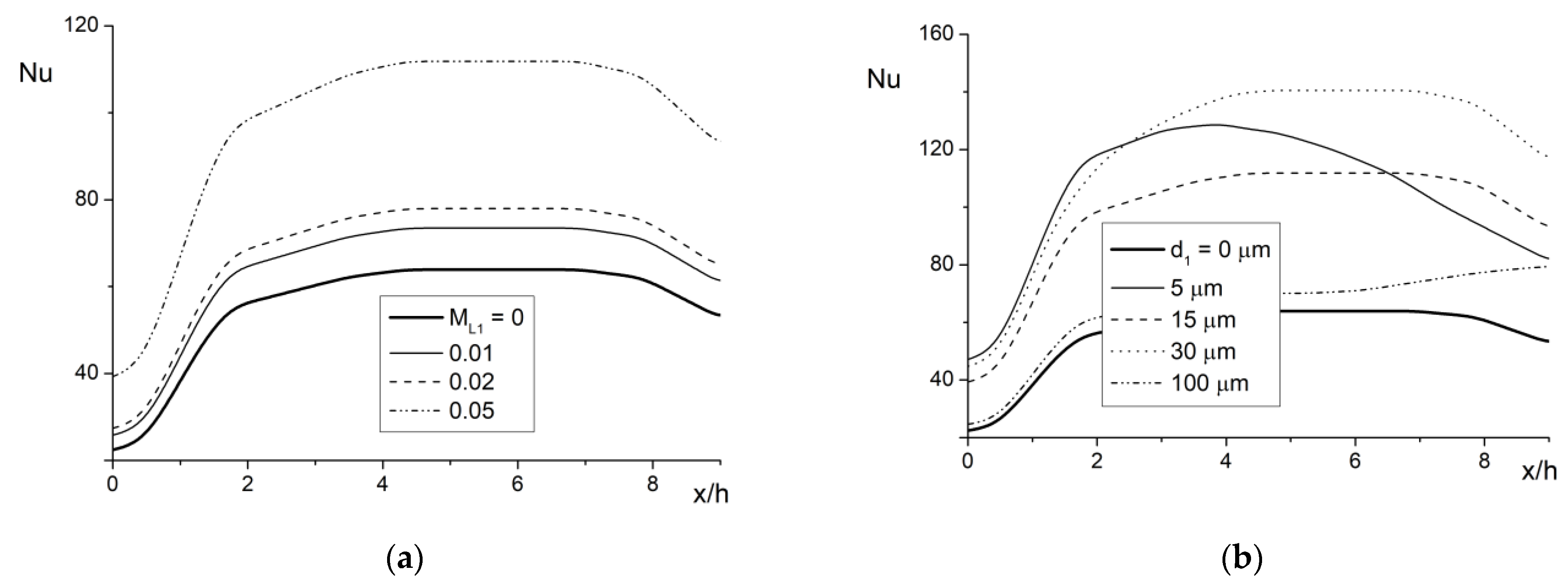
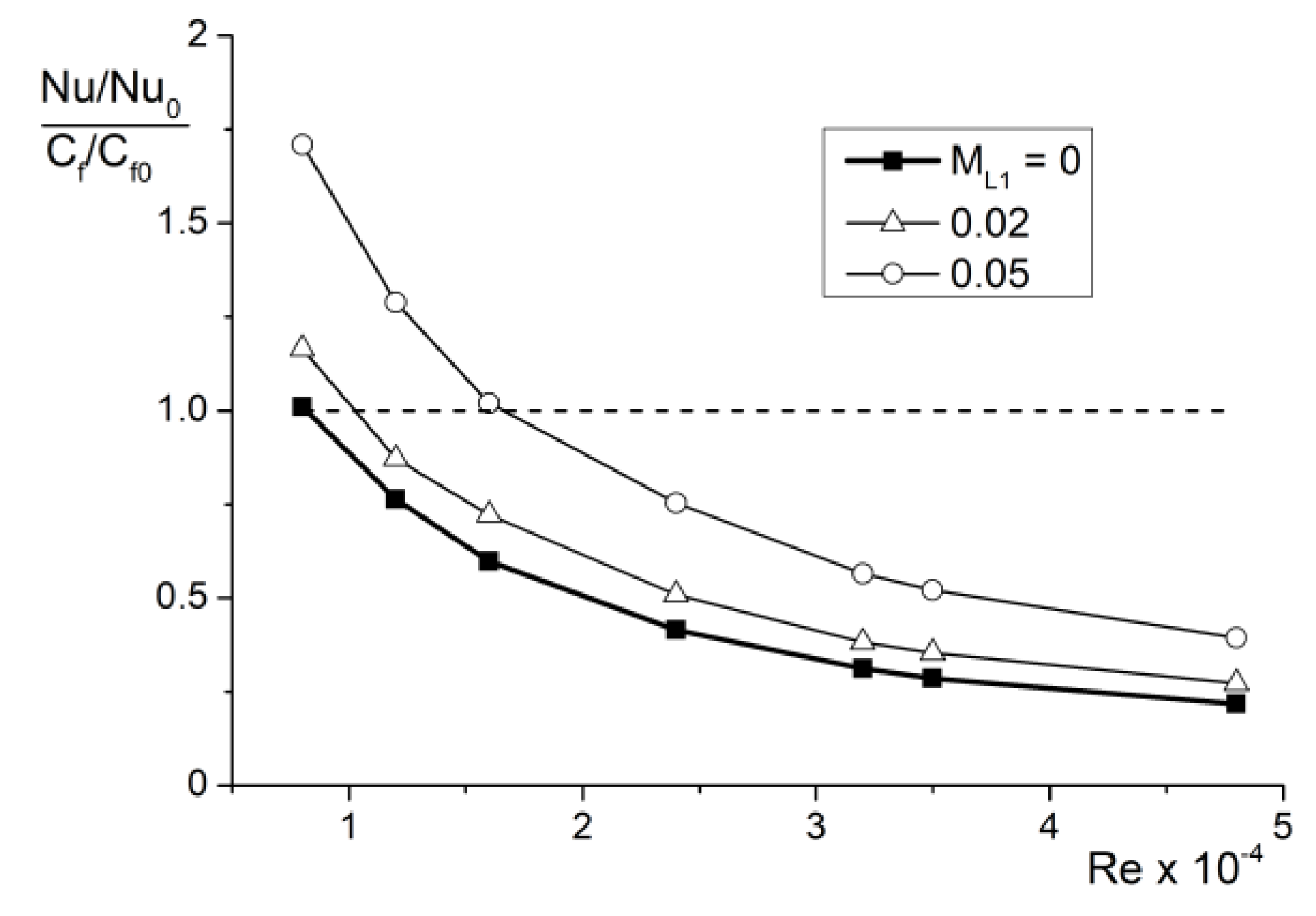
4.2. Heat Transfer
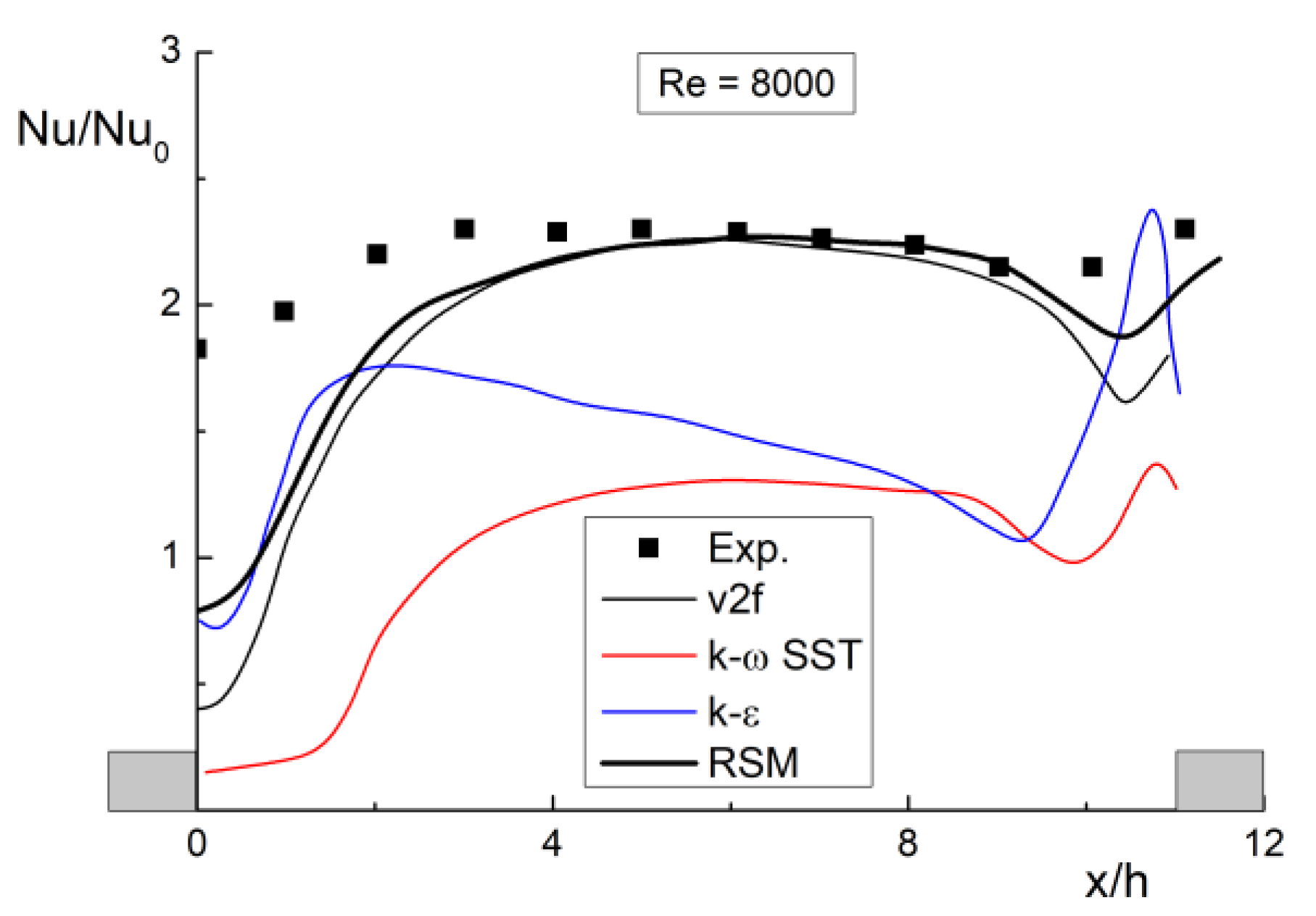
5. Comparison with Results of Other Authors
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| wall friction coefficient | |
| D | droplet diameter |
| H | rib height |
| turbulent kinetic energy | |
| ML | mass fraction |
| Nusselt number | |
| p | rib pitch |
| qW | heat flux density |
| ReD = UmDh/ν | Reynolds number, based on hydraulic diameter |
| Re = Um1H/ν | Reynolds number, based on the duct height |
| Stk = τ/τf | the mean Stokes number |
| T | temperature |
| UL | the mean droplet velocity |
| Um1 | mean mass flow velocity |
| US | the fluid (gas) velocity seen by the droplet |
| u* | wall friction velocity |
| x | streamwise coordinate |
| xR | position of the flow reattachment point |
| y | distance normal from the wall |
| Subscripts | |
| 0 | two-phase mist flow in a smooth duct |
| 1 | initial condition |
| W | wall |
| L | liquid |
| M | mean mass |
| Greek | |
| Φ | volume fraction |
| Ρ | density |
| μ | the dynamic viscosity |
| ν | kinematic viscosity |
| τ | the droplet relaxation time |
| τW | wall shear stress |
| Acronym | |
| BFS | backward-facing step |
| CV | control volume |
| FFS | forward-facing step |
| THE | heat transfer enhancement |
| RANS | Reynolds-averaged Navier–Stokes |
| SMC | second-moment closure |
| TKE | turbulent kinetic energy |
References
- Webb, R.L.; Kim, N.N. Principles of Enhanced Heat Transfer, 2nd ed.; Taylor & Francis: New York, NY, USA, 2005. [Google Scholar]
- Han, J.C.; Dutta, S.; Ekkad, S. Gas Turbine Heat Transfer and Cooling Technology, 2nd ed.; CRC Press: New York, NY, USA, 2012; pp. 363–441. [Google Scholar]
- Kalinin, E.K.; Dreitser, G.A.; Yarkho, S.A. Enhancement of Heat Transfer in Channels; Mashinostroenie: Moscow, Russia, 1990. (In Russian) [Google Scholar]
- Terekhov, V.; Dyachenko, A.; Smulsky, Y.; Bogatko, T.; Yarygina, N. Heat Transfer in Subsonic Separated Flows; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Han, J.C.; Glicksman, L.R.; Rohsenow, W.M. An investigation of heat transfer and friction for rib-roughened surfaces. Int. J. Heat Mass Transf. 1978, 21, 1143–1156. [Google Scholar] [CrossRef]
- Liou, T.M.; Hwang, J.J.; Chen, S.H. Simulation and measurement of enhanced turbulent heat transfer in a channel with periodic ribs on one principal wall. Int. J. Heat Mass Transf. 1993, 36, 507–517. [Google Scholar] [CrossRef]
- Leontiev, A.I.; Olimpiev, V.V. Thermal physics and heat engineering of promising heat transfer intensifiers. Rep. Russ. Acad. Sci. Energetics 2011, 7–31. (In Russian) [Google Scholar]
- Fitzpatrick, X.A.; Lambert, B.; Murray, D.B. Measurements in the separation region of a gas-particle cross flow. Exp. Fluids 1992, 12, 329–341. [Google Scholar] [CrossRef]
- Marchioli, C.; Armenio, V.; Salvetti, M.V.; Soldati, A. Mechanisms for deposition and resuspension of heavy particles in turbulent flow over wavy interfaces. Phys. Fluids 2006, 18, 025102. [Google Scholar] [CrossRef]
- Grigoriadis, D.G.E.; Kassinos, S.C. Lagrangian particle dispersion in turbulent flow over a wall mounted obstacle. Int. J. Heat Fluid Flow 2009, 30, 462–470. [Google Scholar] [CrossRef]
- Lin, S.; Liu, J.; Xia, H.; Zhang, Z.; Ao, X. A numerical study of particle-laden flow around an obstacle: Flow evolution and Stokes number effects. Appl. Math. Model. 2022, 103, 287–307. [Google Scholar] [CrossRef]
- Varaksin, A.Y. Gas-solid flows past bodies. High Temp. 2018, 56, 275–295. [Google Scholar] [CrossRef]
- Krepper, E.; Beyer, M.; Frank, T.; Lucas, D.; Prasser, H.-M. CFD modelling of polydispersed bubbly two-phase flow around an obstacle. Nucl. Eng. Des. 2009, 239, 2372–2381. [Google Scholar] [CrossRef]
- Tas-Koehler, S.; Neumann-Kipping, M.; Liao, Y.; Krepper, E.; Hampel, U. CFD simulation of bubbly flow around an obstacle in a vertical pipe with a focus on breakup and coalescence modelling. Int. J. Multiph. Flow 2021, 135, 10352. [Google Scholar] [CrossRef]
- Lakehal, D. On the modelling of multiphase turbulent flows for environmental and hydrodynamic applications. Int. J. Multiph. Flow 2002, 28, 823–863. [Google Scholar] [CrossRef]
- Huang, Y.-H.; Chen, C.-H.; Liu, Y.-H. Nonboiling heat transfer and friction of air/water mist flow in a square duct with orthogonal ribs. ASME J. Therm. Sci. Eng. Appl. 2017, 9, 041014. [Google Scholar] [CrossRef]
- Jiang, G.; Shi, X.; Chen, G.; Gao, J. Study on flow and heat transfer characteristics of the mist/steam two-phase flow in rectangular channels with 60 deg. ribs. Int. J. Heat Mass Transf. 2018, 120, 1101–1117. [Google Scholar] [CrossRef]
- Huang, K.-T.; Liu, Y.-H. Enhancement of mist flow cooling by using V-shaped broken ribs. Energies 2019, 12, 3785. [Google Scholar] [CrossRef] [Green Version]
- Dhanasekaran, T.S.; Wang, T. Computational analysis of mist/air cooling in a two-pass rectangular rotating channel with 45-deg angled rib turbulators. Int. J. Heat Mass Transf. 2013, 61, 554–564. [Google Scholar] [CrossRef]
- Elwekeel, F.N.M.; Zheng, Q.; Abdala, A.M.M. Air/mist cooling in a rectangular duct with varying shapes of ribs. Proc. IMechE Part C J. Mech. Eng. Sci. 2014, 228, 1925–1935. [Google Scholar] [CrossRef]
- Gong, J.; Ma, C.; Lu, J.; Gao, T. Effect of rib orientation on heat transfer and flow characteristics of mist/steam in square channels. Int. Comm. Heat Mass Transf. 2020, 118, 104900. [Google Scholar] [CrossRef]
- Thangam, S.; Speziale, C.S. Turbulent flow past a backward-facing step: A critical evaluation of two-equation models. AIAA J. 1992, 30, 1314–1320. [Google Scholar] [CrossRef]
- Zaikov, L.A.; Strelets, M.K.; Shur, M.L. A comparison between one- and two-equation differential models of turbulence in application to separated and attached flows: Flow in channels with counterstep. High Temp. 1996, 34, 713–725. [Google Scholar]
- Heyerichs, K.; Pollard, A. Heat transfer in separated and impinging turbulent flows. Int. J. Heat Mass Transf. 1996, 39, 2385–2400. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. Second moment closure modelling of flow, turbulence and heat transfer in droplet-laden mist flow in a vertical pipe with sudden expansion. Int. J. Heat Mass Transf. 2013, 66, 210–222. [Google Scholar] [CrossRef]
- Derevich, I.V.; Zaichik, L.I. Particle deposition from a turbulent flow. Fluid Dyn. 1988, 23, 722–729. [Google Scholar] [CrossRef]
- Reeks, M.W. On a kinetic equation for the transport of particles in turbulent flows. Phys. Fluids A 1991, 3, 446–456. [Google Scholar] [CrossRef]
- Fadai-Ghotbi, A.; Manceau, R.; Boree, J. Revisiting URANS computations of the backward-facing step flow using second moment closures. Influence of the numerics. Flow Turbul. Combust. 2008, 81, 395–410. [Google Scholar] [CrossRef]
- Zaichik, L.I. A statistical model of particle transport and heat transfer in turbulent shear flows. Phys. Fluids 1999, 11, 1521–1534. [Google Scholar] [CrossRef]
- Derevich, I.V. Statistical modelling of mass transfer in turbulent two-phase dispersed flows. 1. Model development. Int. J. Heat Mass Transf. 2000, 43, 3709–3723. [Google Scholar] [CrossRef]
- Terekhov, V.I.; Pakhomov, M.A. Numerical study of heat transfer in a laminar mist flow over an isothermal flat plate. Int. J. Heat Mass Transfer 2002, 45, 2077–2085. [Google Scholar] [CrossRef]
- Elgobashi, S. An updated classification map of particle-laden turbulent flows. In IUTAM Symposium on Computational Approaches to Multiphase Flow, Fluid Mechanics and Its Applications; Balachandar, S., Prosperetti, A., Eds.; Springer: Dordrecht, The Netherlands, 2006; Volume 81, pp. 3–10. [Google Scholar]
- Lin, S.P.; Reitz, R.D. Drop and spray formation from a liquid jet. Ann. Rev. Fluid Mech. 1998, 30, 85–105. [Google Scholar] [CrossRef]
- Mukin, R.V.; Zaichik, L.I. Nonlinear algebraic Reynolds stress model for two-phase turbulent flows laden with small heavy particles. Int. J. Heat Fluid Flow 2012, 33, 81–91. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. let evaporation in a gas-droplet mist dilute turbulent flow behind a backward-facing step. Water 2021, 13, 2333. [Google Scholar] [CrossRef]
- Hanjalic, K.; Jakirlic, S. Contribution towards the second-moment closure modelling of separating turbulent flows. Comput. Fluids 1998, 27, 137–156. [Google Scholar] [CrossRef]
- Anderson, D.A.; Tannehill, J.C.; Pletcher, R.H. Computational Fluid Mechanics and Heat Transfer, 2nd ed.; Taylor & Francis: New York, NY, USA, 1997. [Google Scholar]
- Mastanaiah, K.; Ganic, E.N. Heat transfer in two-component dispersed flow. ASME J. Heat Transf. 1981, 103, 300–306. [Google Scholar] [CrossRef]
- Ruck, S.; Arbeiter, F. LDA measurements in a one-sided ribbed square channel at Reynolds numbers of 50 000 and 100 000. Exp. Fluids 2021, 62, 232. [Google Scholar] [CrossRef]
- Wang, L.; Sunden, B. Experimental investigation of local heat transfer in a square duct with continuous and truncated ribs. Exp. Heat Transf. 2005, 18, 179–197. [Google Scholar] [CrossRef]
- Liu, J.; Xie, G.N.; Simon, T.W. Turbulent flow and heat transfer enhancement in rectangular channels with novel cylindrical grooves. Int. J. Heat Mass Transf. 2015, 81, 563–577. [Google Scholar] [CrossRef]
- Fessler, J.R.; Eaton, J.K. Turbulence modification by particles in a backward-facing step flow. J. Fluid Mech. 1999, 314, 97–117. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pakhomov, M.A.; Terekhov, V.I. RANS Modeling of Turbulent Flow and Heat Transfer in a Droplet-Laden Mist Flow through a Ribbed Duct. Water 2022, 14, 3829. https://doi.org/10.3390/w14233829
Pakhomov MA, Terekhov VI. RANS Modeling of Turbulent Flow and Heat Transfer in a Droplet-Laden Mist Flow through a Ribbed Duct. Water. 2022; 14(23):3829. https://doi.org/10.3390/w14233829
Chicago/Turabian StylePakhomov, Maksim A., and Viktor I. Terekhov. 2022. "RANS Modeling of Turbulent Flow and Heat Transfer in a Droplet-Laden Mist Flow through a Ribbed Duct" Water 14, no. 23: 3829. https://doi.org/10.3390/w14233829




