Two-Phase Annular Flow in Vertical Pipes: A Critical Review of Current Research Techniques and Progress
Abstract
1. Introduction
2. Investigation Methodologies
2.1. Visualization and Photography
2.2. Laser-Induced Fluorescence (LIF)
2.3. Particle Image Velocimetry (PIV)
2.4. Laser Focus Displacement Meter (LFD)
2.5. Ultrasonic Flow Meter and Near-Infrared Sensor
2.6. Conductance Sensor
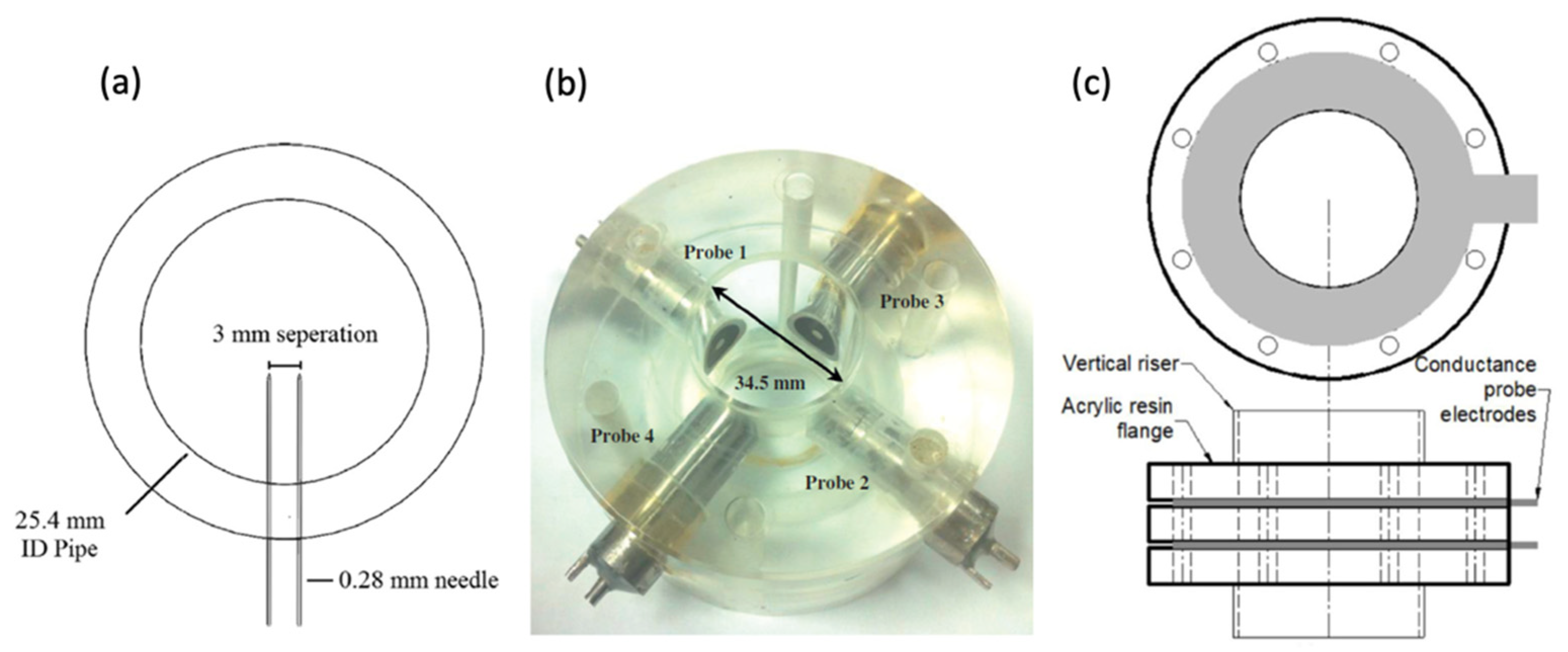
2.7. Capacitance Sensor
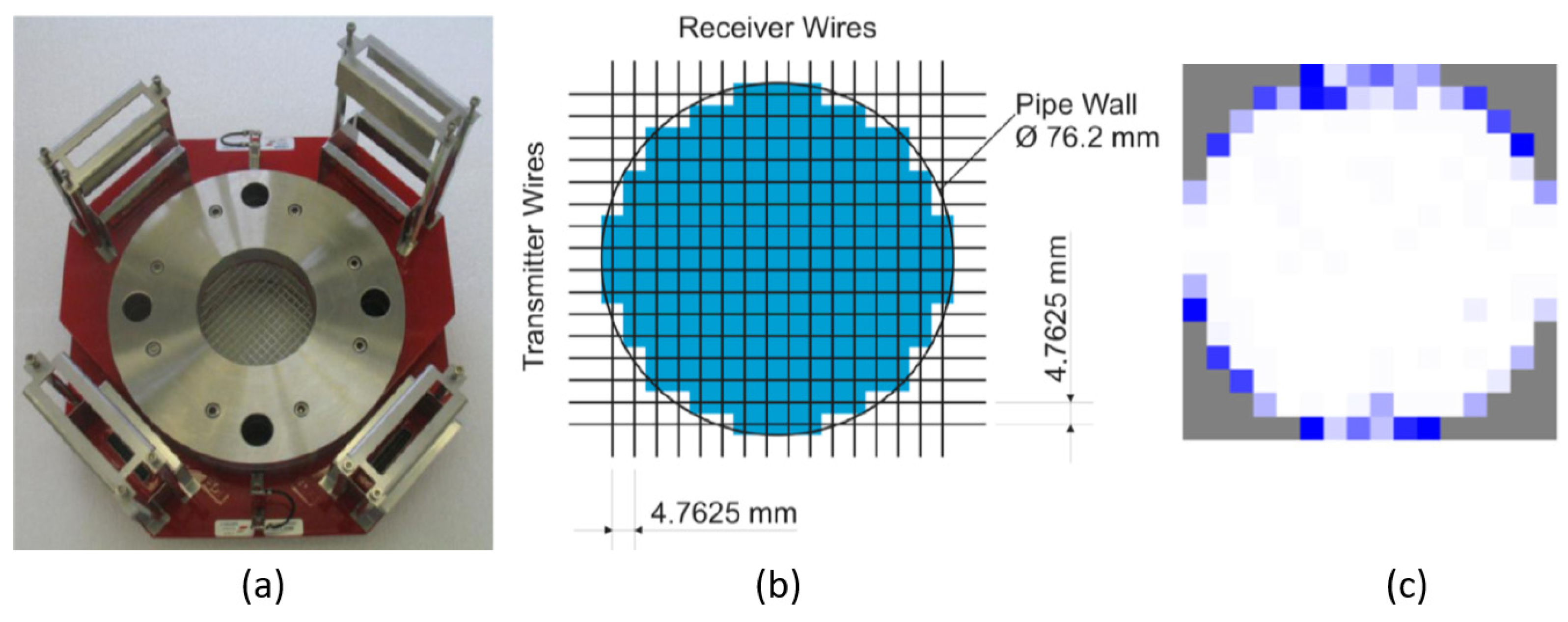
2.8. Wire-Mesh Sensor (WMS)
2.9. Radiative Imaging
2.10. Film Extraction
2.11. Shadow Photography and Laser Diffraction
2.12. Laser Doppler Anemometry (LDA)
2.13. Other Mechanical Methods
2.14. Numerical Simulation
2.15. Challenges of Current Experimental Techniques
3. The Wavy Liquid Film
3.1. Fundamental Understanding of the Liquid Film
3.2. Disturbance Wave Characteristics
3.3. Correlations of the Film Thickness
3.4. The Void Fraction of Annular Two-Phase Flow
4. The Entrained Droplets in the Central Gas Core
4.1. Droplet Behaviour
4.2. Correlation of Droplet Entrainment
5. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature List | |||
| Symbols | Greek Characters | ||
| a | Void fraction | δ | Film thickness |
| C | Friction factor | Time-averaged film thickness | |
| d | Diameter of the drop | ε | Entrainment rate |
| D | Diameter of the pipe | λ | Wavelength |
| E | Entrainment fraction | μ | Dynamic viscosity |
| f | Friction factor | ν | Kinematic viscosity |
| Fr | Froude number | ρ | Density |
| g | acceleration of gravity | σ | Surface tension coefficient |
| h | Disturbance wave height | τ | Shear stress |
| j | Superficial velocity | Subscripts | |
| k | Wave number | * | Friction |
| Ka | Kapitza number | 32 | Sauter diameter |
| L | Length | base | The base of the disturbance wave |
| Mass flow rate | c | Gas core | |
| Nu | Viscosity number | DW | Disturbance wave |
| Nuf | Non-dimensional viscosity number | e | Entrained |
| Δp | Pressure difference | m | Modified |
| Re | Reynolds number | max | Maximum condition |
| St | Strouhal number | G | Gas |
| u | Velocity | Gc | Critical gas state |
| V | Volume | L | Liquid |
| We | Weber number | La | Laplace length |
| x | Vaper quality | lf | Liquid film |
| Xtt | Lockhart-Martinelli parameter | lfc | Critical film flow |
| Pressure gradient due to friction loss | L, ref | Liquid at reference condition (at 20 °C) | |
| i | Interfacial | ||
| v | Volume mean | ||
| w | Wall | ||
References
- Gormley, M.; Aspray, T.J.; Kelly, D.A. COVID-19: Mitigating transmission via wastewater plumbing systems. Lancet Glob. Health 2020, 8, e643. [Google Scholar] [CrossRef]
- Gormley, M.; Swaffield, J.; Sleigh, P.; Noakes, C. An assessment of, and response to, potential cross-contamination routes due to defective appliance water trap seals in building drainage systems. Build. Serv. Eng. Res. Technol. 2012, 33, 203–222. [Google Scholar] [CrossRef]
- Stewart, C.; Gormley, M.; Xue, Y.; Kelly, D.; Campbell, D. Steady-State Hydraulic Analysis of High-Rise Building Wastewater Drainage Networks: Modelling Basis. Buildings 2021, 11, 344. [Google Scholar] [CrossRef]
- Wong, L.-T.; Mui, K.-W.; Cheng, C.-L.; Leung, P.H.-M. Time-Variant Positive Air Pressure in Drainage Stacks as a Pathogen Transmission Pathway of COVID-19. Int. J. Environ. Res. Public Health 2021, 18, 6068. [Google Scholar] [CrossRef] [PubMed]
- Gormley, M.; Aspray, T.J.; Kelly, D.A. Aerosol and bioaerosol particle size and dynamics from defective sanitary plumbing systems. Indoor Air 2021, 31, 1427–1440. [Google Scholar] [CrossRef] [PubMed]
- Hewitt, G.F.; Hall-Taylor, N.S. Annular Two-Phase Flow; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Azzopardi, B.J. Drops in annular two-phase flow. Int. J. Multiph. Flow 1997, 23, 1–53. [Google Scholar]
- Berna, C.; Escrivá, A.; Muñoz-Cobo, J.L.; Herranz, L.E. Review of droplet entrainment in annular flow: Characterization of the entrained droplets. Prog. Nucl. Energy 2015, 79, 64–86. [Google Scholar] [CrossRef]
- Berna, C.; Escrivá, A.; Muñoz-Cobo, J.L.; Herranz, L.E. Review of droplet entrainment in annular flow: Interfacial waves and onset of entrainment. Prog. Nucl. Energy 2014, 74, 14–43. [Google Scholar] [CrossRef]
- Wu, B.; Firouzi, M.; Mitchell, T.; Rufford, T.E.; Leonardi, C.; Towler, B. A critical review of flow maps for gas-liquid flows in vertical pipes and annuli. Chem. Eng. J. 2017, 326, 350–377. [Google Scholar] [CrossRef]
- Rahman, M.; Heidrick, T.; Fleck, B. A critical review of advanced experimental techniques to measure two-phase gas/liquid flow. Open Fuels Energy Sci. J. 2009, 2, 54–70. [Google Scholar]
- Tibiriçá, C.B.; Nascimento, F.J.d.; Ribatski, G. Film thickness measurement techniques applied to micro-scale two-phase flow systems. Exp. Therm. Fluid Sci. 2010, 34, 463–473. [Google Scholar] [CrossRef]
- Cherdantsev, A.V.; An, J.S.; Charogiannis, A.; Markides, C.N. Simultaneous application of two laser-induced fluorescence approaches for film thickness measurements in annular gas-liquid flows. Int. J. Multiph. Flow 2019, 119, 237–258. [Google Scholar] [CrossRef]
- Qiao, S.; Mena, D.; Kim, S. Inlet effects on vertical-downward air–water two-phase flow. Nucl. Eng. Des. 2017, 312, 375–388. [Google Scholar] [CrossRef]
- van Nimwegen, A.T.; Portela, L.M.; Henkes, R.A.W.M. The effect of the diameter on air-water annular and churn flow in vertical pipes with and without surfactants. Int. J. Multiph. Flow 2017, 88, 179–190. [Google Scholar] [CrossRef]
- Van Nimwegen, A.; Portela, L.; Henkes, R. The effect of surfactants on air–water annular and churn flow in vertical pipes. Part 1: Morphology of the air–water interface. Int. J. Multiph. Flow 2015, 71, 133–145. [Google Scholar] [CrossRef]
- Van Nimwegen, A.; Portela, L.; Henkes, R. The effect of surfactants on air–water annular and churn flow in vertical pipes. Part 2: Liquid holdup and pressure gradient dynamics. Int. J. Multiph. Flow 2015, 71, 146–158. [Google Scholar] [CrossRef]
- Van der Meulen, G.P. Churn-Annular Gas-Liquid Flows in Large Diameter Vertical Pipes. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2012. [Google Scholar]
- Adomeit, P.; Renz, U. Hydrodynamics of three-dimensional waves in laminar falling films. Int. J. Multiph. Flow 2000, 26, 1183–1208. [Google Scholar] [CrossRef]
- Takamasa, T.; Hazuku, T.; Hibiki, T. Experimental Study of gas-liquid two-phase flow affected by wall surface wettability. Int. J. Heat Fluid Flow 2008, 29, 1593–1602. [Google Scholar] [CrossRef]
- Pham, S.H.; Kawara, Z.; Yokomine, T.; Kunugi, T. Detailed observations of wavy interface behaviors of annular two-phase flow on rod bundle geometry. Int. J. Multiph. Flow 2014, 59, 135–144. [Google Scholar] [CrossRef]
- Bhagwat, S.M.; Ghajar, A.J. Similarities and differences in the flow patterns and void fraction in vertical upward and downward two phase flow. Exp. Therm. Fluid Sci. 2012, 39, 213–227. [Google Scholar] [CrossRef]
- Waltrich, P.J.; Falcone, G.; Barbosa, J.R. Axial development of annular, churn and slug flows in a long vertical tube. Int. J. Multiph. Flow 2013, 57, 38–48. [Google Scholar] [CrossRef]
- Posada, C.; Waltrich, P.J. Effect of forced flow oscillations on churn and annular flow in a long vertical tube. Exp. Therm. Fluid Sci. 2017, 81, 345–357. [Google Scholar] [CrossRef]
- Milan, M.; Borhani, N.; Thome, J.R. Adiabatic vertical downward air–water flow pattern map: Influence of inlet device, flow development length and hysteresis effects. Int. J. Multiph. Flow 2013, 56, 126–137. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, Y.; Wang, Z.; Hu, Q.; Wang, D. Experimental study on radial evolution of droplets in vertical gas-liquid two-phase annular flow. Int. J. Multiph. Flow 2020, 129, 103325. [Google Scholar] [CrossRef]
- Raeiszadeh, F.; Hajidavalloo, E.; Behbahaninejad, M.; Hanafizadeh, P. Effect of pipe rotation on downward co-current air-water flow in a vertical pipe. Int. J. Multiph. Flow 2016, 81, 1–14. [Google Scholar] [CrossRef]
- Vijayan, M.; Jayanti, S.; Balakrishnan, A.R. Effect of tube diameter on flooding. Int. J. Multiph. Flow 2001, 27, 797–816. [Google Scholar] [CrossRef]
- Dasgupta, A.; Chandraker, D.K.; Kshirasagar, S.; Reddy, B.R.; Rajalakshmi, R.; Nayak, A.K.; Walker, S.P.; Vijayan, P.K.; Hewitt, G.F. Experimental investigation on dominant waves in upward air-water two-phase flow in churn and annular regime. Exp. Therm. Fluid Sci. 2017, 81, 147–163. [Google Scholar] [CrossRef]
- Da Hlaing, N.; Sirivat, A.; Siemanond, K.; Wilkes, J.O. Vertical two-phase flow regimes and pressure gradients: Effect of viscosity. Exp. Therm. Fluid Sci. 2007, 31, 567–577. [Google Scholar] [CrossRef]
- Kumar, A.; Bhowmik, S.; Ray, S.; Das, G. Flow pattern transition in gas-liquid downflow through narrow vertical tubes. AIChE J. 2017, 63, 792–800. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Liu, H.; Gao, Y.; Li, H.; Sun, B. Experimental study on entrained droplets in vertical two-phase churn and annular flows. Int. J. Heat Mass Transf. 2019, 138, 1346–1358. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Liu, H.; Gao, Y.; Li, H.; Sun, B. Experimental study on bubble and droplet entrainment in vertical churn and annular flows and their relationship. Chem. Eng. Sci. 2019, 206, 387–400. [Google Scholar] [CrossRef]
- Wang, L.-S.; Liu, S.; Hou, L.; Yang, M.; Zhang, J.; Xu, J. Prediction of the liquid film reversal of annular flow in vertical and inclined pipes. Int. J. Multiph. Flow 2022, 146, 103853. [Google Scholar] [CrossRef]
- Schmid, D.; Verlaat, B.; Petagna, P.; Revellin, R.; Schiffmann, J. Flow pattern observations and flow pattern map for adiabatic two-phase flow of carbon dioxide in vertical upward and downward direction. Exp. Therm. Fluid Sci. 2022, 131, 110526. [Google Scholar] [CrossRef]
- Dang, Z.; Yang, Z.; Yang, X.; Ishii, M. Experimental study on void fraction, pressure drop and flow regime analysis in a large ID piping system. Int. J. Multiph. Flow 2019, 111, 31–41. [Google Scholar] [CrossRef]
- Chen, L.; Tian, Y.S.; Karayiannis, T.G. The effect of tube diameter on vertical two-phase flow regimes in small tubes. Int. J. Heat Mass Transf. 2006, 49, 4220–4230. [Google Scholar] [CrossRef]
- Coleman, J.W.; Garimella, S. Characterization of two-phase flow patterns in small diameter round and rectangular tubes. Int. J. Heat Mass Transf. 1999, 42, 2869–2881. [Google Scholar] [CrossRef]
- Pan, L.M.; He, H.; Ju, P.; Hibiki, T.; Ishii, M. Experimental study and modeling of disturbance wave height of vertical annular flow. Int. J. Heat Mass Transf. 2015, 89, 165–175. [Google Scholar] [CrossRef]
- Pan, L.M.; He, H.; Ju, P.; Hibiki, T.; Ishii, M. The influences of gas-liquid interfacial properties on interfacial shear stress for vertical annular flow. Int. J. Heat Mass Transf. 2015, 89, 1172–1183. [Google Scholar] [CrossRef]
- Schubring, D.; Shedd, T.A.; Hurlburt, E.T. Studying disturbance waves in vertical annular flow with high-speed video. Int. J. Multiph. Flow 2010, 36, 385–396. [Google Scholar] [CrossRef]
- Lin, R.; Wang, K.; Liu, L.; Zhang, Y.; Dong, S. Study on the characteristics of interfacial waves in annular flow by image analysis. Chem. Eng. Sci. 2020, 212, 115336. [Google Scholar] [CrossRef]
- Lin, R.; Wang, K.; Liu, L.; Zhang, Y.; Dong, S. Application of the image analysis on the investigation of disturbance waves in vertical upward annular two-phase flow. Exp. Therm. Fluid Sci. 2020, 114, 110062. [Google Scholar] [CrossRef]
- Moreira, T.A.; Morse, R.W.; Dressler, K.M.; Ribatski, G.; Berson, A. Liquid-film thickness and disturbance-wave characterization in a vertical, upward, two-phase annular flow of saturated R245fa inside a rectangular channel. Int. J. Multiph. Flow 2020, 132, 103412. [Google Scholar] [CrossRef]
- Barbosa, J.R., Jr.; Govan, A.H.; Hewitt, G.F. Visualisation and modelling studies of churn flow in a vertical pipe. Int. J. Multiph. Flow 2001, 27, 2105–2127. [Google Scholar] [CrossRef]
- Häber, T.; Gebretsadik, M.; Bockhorn, H.; Zarzalis, N. The effect of total reflection in PLIF imaging of annular thin films. Int. J. Multiph. Flow 2015, 76, 64–72. [Google Scholar] [CrossRef]
- van Eckeveld, A.C.; Gotfredsen, E.; Westerweel, J.; Poelma, C. Annular two-phase flow in vertical smooth and corrugated pipes. Int. J. Multiph. Flow 2018, 109, 150–163. [Google Scholar] [CrossRef]
- Zadrazil, I.; Matar, O.K.; Markides, C.N. An experimental characterization of downwards gas-liquid annular flow by laser-induced fluorescence: Flow regimes and film statistics. Int. J. Multiph. Flow 2014, 60, 87–102. [Google Scholar] [CrossRef]
- Schubring, D.; Ashwood, A.C.; Shedd, T.A.; Hurlburt, E.T. Planar laser-induced fluorescence (PLIF) measurements of liquid film thickness in annular flow. Part I: Methods and data. Int. J. Multiph. Flow 2010, 36, 815–824. [Google Scholar] [CrossRef]
- Schubring, D.; Shedd, T.A.; Hurlburt, E.T. Planar laser-induced fluorescence (PLIF) measurements of liquid film thickness in annular flow. Part II: Analysis and comparison to models. Int. J. Multiph. Flow 2010, 36, 825–835. [Google Scholar] [CrossRef]
- Kokomoor, W.; Schubring, D. Improved visualization algorithms for vertical annular flow. J. Vis. 2014, 17, 77–86. [Google Scholar] [CrossRef]
- Xue, T.; Yang, L.; Ge, P.; Qu, L. Error analysis and liquid film thickness measurement in gas–liquid annular flow. Optik 2015, 126, 2674–2678. [Google Scholar] [CrossRef]
- Liu, J.; Xue, T. Experimental investigation of liquid entrainment in vertical upward annular flow based on fluorescence imaging. Prog. Nucl. Energy 2022, 152, 104383. [Google Scholar] [CrossRef]
- Xue, T.; Li, Z.; Li, C.; Wu, B. Measurement of thickness of annular liquid films based on distortion correction of laser-induced fluorescence imaging. Rev. Sci. Instrum. 2019, 90, 033103. [Google Scholar] [CrossRef] [PubMed]
- Xue, T.; Li, C.; Wu, B. Distortion correction and characteristics measurement of circumferential liquid film based on PLIF. AIChE J. 2019, 65, e16612. [Google Scholar] [CrossRef]
- Vasques, J.; Cherdantsev, A.; Cherdantsev, M.; Isaenkov, S.; Hann, D. Comparison of disturbance wave parameters with flow orientation in vertical annular gas-liquid flows in a small pipe. Exp. Therm. Fluid Sci. 2018, 97, 484–501. [Google Scholar] [CrossRef]
- Fan, W.; Cherdantsev, A.; Anglart, H. Experimental and numerical study of formation and development of disturbance waves in annular gas-liquid flow. Energy 2020, 207, 118309. [Google Scholar]
- Alekseenko, S.V.; Cherdantsev, A.V.; Cherdantsev, M.V.; Isaenkov, S.V.; Markovich, D.M. Study of formation and development of disturbance waves in annular gas-liquid flow. Int. J. Multiph. Flow 2015, 77, 65–75. [Google Scholar] [CrossRef]
- Alekseenko, S.V.; Cherdantsev, A.V.; Heinz, O.M.; Kharlamov, S.M.; Markovich, D.M. Analysis of spatial and temporal evolution of disturbance waves and ripples in annular gas-liquid flow. Int. J. Multiph. Flow 2014, 67, 122–134. [Google Scholar] [CrossRef]
- Alekseenko, S.; Cherdantsev, A.; Cherdantsev, M.; Isaenkov, S.; Kharlamov, S.; Markovich, D. Application of a high-speed laser-induced fluorescence technique for studying the three-dimensional structure of annular gas-liquid flow. Exp. Fluids 2012, 53, 77–89. [Google Scholar] [CrossRef]
- Alekseenko, S.; Antipin, V.; Cherdantsev, A.; Kharlamov, S.; Markovich, D. Two-wave structure of liquid film and wave interrelation in annular gas-liquid flow with and without entrainment. Phys. Fluids 2009, 21, 061701. [Google Scholar] [CrossRef]
- Farias, P.; Martins, F.; Sampaio, L.; Serfaty, R.; Azevedo, L. Liquid film characterization in horizontal, annular, two-phase, gas–liquid flow using time-resolved laser-induced fluorescence. Exp. Fluids 2012, 52, 633–645. [Google Scholar] [CrossRef]
- Karimi, G.; Kawaji, M. An experimental study of freely falling films in a vertical tube. Chem. Eng. Sci. 1998, 53, 3501–3512. [Google Scholar] [CrossRef]
- Zadrazil, I.; Markides, C.N. An experimental characterization of liquid films in downwards co-current gas-liquid annular flow by particle image and tracking velocimetry. Int. J. Multiph. Flow 2014, 67, 42–53. [Google Scholar] [CrossRef]
- Zadrazil, I.; Markides, C.; Matar, O.; Náraigh, L.; Hewitt, G. Characterisation of downwards co-current gas-liquid annular flows. In Proceedings of the Seventh International Symposium On Turbulence, Heat and Mass Transfer, Palermo, Italy, 24–27 September 2012. [Google Scholar]
- Ashwood, A.C.; Hogen, S.J.V.; Rodarte, M.A.; Kopplin, C.R.; Rodríguez, D.J.; Hurlburt, E.T.; Shedd, T.A. A multiphase, micro-scale PIV measurement technique for liquid film velocity measurements in annular two-phase flow. Int. J. Multiph. Flow 2015, 68, 27–39. [Google Scholar] [CrossRef]
- Charogiannis, A.; An, J.S.; Voulgaropoulos, V.; Markides, C.N. Structured planar laser-induced fluorescence (S-PLIF) for the accurate identification of interfaces in multiphase flows. Int. J. Multiph. Flow 2019, 118, 193–204. [Google Scholar] [CrossRef]
- Hazuku, T.; Takamasa, T.; Matsumoto, Y. Experimental study on axial development of liquid film in vertical upward annular two-phase flow. Int. J. Multiph. Flow 2008, 34, 111–127. [Google Scholar] [CrossRef]
- Okawa, T.; Goto, T.; Yamagoe, Y. Liquid film behavior in annular two-phase flow under flow oscillation conditions. Int. J. Heat Mass Transf. 2010, 53, 962–971. [Google Scholar] [CrossRef]
- Shedd, T.A.; Newell, T. Automated optical liquid film thickness measurement method. Rev. Sci. Instrum. 1998, 69, 4205–4213. [Google Scholar] [CrossRef]
- Hurlburt, E.; Newell, T. Optical measurement of liquid film thickness and wave velocity in liquid film flows. Exp. Fluids 1996, 21, 357–362. [Google Scholar] [CrossRef]
- Ohba, K.; Nagae, K. Characteristics and behavior of the interfacial wave on the liquid film in a vertically upward air-water two-phase annular flow. Nucl. Eng. Des. 1993, 141, 17–25. [Google Scholar] [CrossRef]
- Lel, V.V.; Al-Sibai, F.; Leefken, A.; Renz, U. Local thickness and wave velocity measurement of wavy films with a chromatic confocal imaging method and a fluorescence intensity technique. Exp. Fluids 2005, 39, 856–864. [Google Scholar] [CrossRef]
- Liang, F.; Fang, Z.; Chen, J.; Sun, S. Investigating the liquid film characteristics of gas–liquid swirling flow using ultrasound Doppler velocimetry. AIChE J. 2017, 63, 2348–2357. [Google Scholar] [CrossRef]
- Wang, M.; Zheng, D.; Xu, Y. A new method for liquid film thickness measurement based on ultrasonic echo resonance technique in gas-liquid flow. Meas. J. Int. Meas. Confed. 2019, 146, 447–457. [Google Scholar] [CrossRef]
- Al-Aufi, Y.A.; Hewakandamby, B.N.; Dimitrakis, G.; Holmes, M.; Hasan, A.; Watson, N.J. Thin film thickness measurements in two phase annular flows using ultrasonic pulse echo techniques. Flow Meas. Instrum. 2019, 66, 67–78. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, N.; Fang, L.; Zhang, T.; Feng, Y. Void fraction measurement using NIR technology for horizontal wet-gas annular flow. Exp. Therm. Fluid Sci. 2016, 76, 98–108. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, N.; Feng, Y.; Sun, H.; Fang, L. Interfacial wave velocity of vertical gas-liquid annular flow at different system pressures. Exp. Therm. Fluid Sci. 2018, 92, 20–32. [Google Scholar] [CrossRef]
- Li, C.; Liu, M.; Zhao, N.; Wang, F.; Zhao, Z.; Guo, S.; Fang, L.; Li, X. Void fraction measurement using modal decomposition and ensemble learning in vertical annular flow. Chem. Eng. Sci. 2022, 247, 116929. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, B.; Wang, J.; Fang, L.; Li, X.; Wang, F.; Zhao, N. Liquid film characteristics measurement based on NIR in gas–liquid vertical annular upward flow. Meas. Sci. Technol. 2022, 33, 065014. [Google Scholar] [CrossRef]
- Hawkes, N.J.; Lawrence, C.J.; Hewitt, G.F. Studies of wispy-annular flow using transient pressure gradient and optical measurements. Int. J. Multiph. Flow 2000, 26, 1565–1582. [Google Scholar] [CrossRef]
- Coney, M.W.E. The theory and application of conductance probes for the measurement of liquid film thickness in two-phase flow. J. Phys. E: Sci. Instrum. 1973, 6, 903–911. [Google Scholar] [CrossRef]
- Hewitt, G.F. Measurement of two phase flow parameters. Nasa Sti/recon Tech. Rep. A 1978, 79, 47262. [Google Scholar]
- Damsohn, M.; Prasser, H.M. High-speed liquid film sensor with high spatial resolution. Meas. Sci. Technol. 2009, 20, 114001. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, N.; Chen, C.; Sun, H. A method for direct thickness measurement of wavy liquid film in gas-liquid two-phase annular flow using conductance probes. Flow Meas. Instrum. 2018, 62, 66–75. [Google Scholar] [CrossRef]
- Polansky, J.; Wang, M. Vertical annular flow pattern characterisation using proper orthogonal decomposition of Electrical Impedance Tomography. Flow Meas. Instrum. 2018, 62, 281–296. [Google Scholar] [CrossRef]
- Brown, R.C.; Andreussi, P.; Zanelli, S. The use of wire probes for the measurement of liquid film thickness in annular gas-liquid flows. Can. J. Chem. Eng. 1978, 56, 754–757. [Google Scholar] [CrossRef]
- Zabaras, G.; Dukler, A.E.; Moalem-Maron, D. Vertical upward cocurrent gas-liquid annular flow. AIChE J. 1986, 32, 829–843. [Google Scholar] [CrossRef]
- Karapantsios, T.D.; Paras, S.V.; Karabelas, A.J. Statistical characteristics of free falling films at high reynolds numbers. Int. J. Multiph. Flow 1989, 15, 1–21. [Google Scholar] [CrossRef]
- Koskie, J.E.; Mudawar, I.; Tiederman, W.G. Parallel-wire probes for measurement of thick liquid films. Int. J. Multiph. Flow 1989, 15, 521–530. [Google Scholar] [CrossRef]
- Ruder, Z.; Hanratty, T.J. A definition of gas-liquid plug flow in horizontal pipes. Int. J. Multiph. Flow 1990, 16, 233–242. [Google Scholar] [CrossRef]
- Kumar, R.; Gottmann, M.; Sridhar, K. Film thickness and wave velocity measurements in a vertical duct. J. Fluids Eng. 2002, 124, 634–642. [Google Scholar] [CrossRef]
- Usui, K.; Sato, K. Vertically downward two-phase flow,(I) Void distribution and average void fraction. J. Nucl. Sci. Technol. 1989, 26, 670–680. [Google Scholar] [CrossRef]
- Fukano, T.; Furukawa, T. Prediction of the effects of liquid viscosity on interfacial shear stress and frictional pressure drop in vertical upward gas-liquid annular flow. Int. J. Multiph. Flow 1998, 24, 587–603. [Google Scholar] [CrossRef]
- Al-Sarkhi, A.; Sarica, C.; Magrini, K. Inclination effects on wave characteristics in annular gas–liquid flows. AIChE J. 2012, 58, 1018–1029. [Google Scholar] [CrossRef]
- Fore, L.B.; Beus, S.G.; Bauer, R.C. Interfacial friction in gas-liquid annular flow: Analogies to full and transition roughness. Int. J. Multiph. Flow 2000, 26, 1755–1769. [Google Scholar] [CrossRef]
- Paras, S.V.; Karabelas, A.J. Properties of the liquid layer in horizontal annular flow. Int. J. Multiph. Flow 1991, 17, 439–454. [Google Scholar] [CrossRef]
- Li, W.; Zhou, F.; Li, R.; Zhou, L. Experimental study on the characteristics of liquid layer and disturbance waves in horizontal annular flow. J. Therm. Sci. 1999, 8, 235–242. [Google Scholar] [CrossRef]
- Alamu, M.B.; Azzopardi, B.J. Simultaneous investigation of entrained liquid fraction, liquid film thickness and pressure drop in vertical annular flow. J. Energy Resour. Technol. Trans. ASME 2011, 133, 023103. [Google Scholar] [CrossRef]
- Alamu, M.B.; Azzopardi, B.J. Wave and drop periodicity in transient annular flow. Nucl. Eng. Des. 2011, 241, 5079–5092. [Google Scholar] [CrossRef]
- Al-Yarubi, Q. Phase Flow Rate Measurements of Annular Flows. Ph.D. Thesis, University of Huddersfield, Huddersfield, UK, 2010. [Google Scholar]
- Han, H.; Zhu, Z.; Gabriel, K. A study on the effect of gas flow rate on the wave characteristics in two-phase gas–liquid annular flow. Nucl. Eng. Des. 2006, 236, 2580–2588. [Google Scholar] [CrossRef]
- Smith, T.R.; Schlegel, J.P.; Hibiki, T.; Ishii, M. Two-phase flow structure in large diameter pipes. Int. J. Heat Fluid Flow 2012, 33, 156–167. [Google Scholar] [CrossRef]
- Posada, C.; Waltrich, P.J. Similarities and differences in churn and annular flow regimes in steady-state and oscillatory flows in a long vertical tube. Exp. Therm. Fluid Sci. 2018, 93, 272–284. [Google Scholar] [CrossRef]
- Dao, E.K.; Balakotaiah, V. Experimental study of wave occlusion on falling films in a vertical pipe. AIChE J. 2000, 46, 1300–1306. [Google Scholar] [CrossRef]
- Wang, G.; Zhu, Q.; Ishii, M.; Buchanan, J.R. Four-sensor droplet capable conductivity probe for measurement of churn-turbulent to annular transition flow. Int. J. Heat Mass Transf. 2020, 157, 119949. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, G.; Schlegel, J.P.; Yan, Y.; Yang, X.; Liu, Y.; Ishii, M.; Buchanan, J.R. Experimental study of two-phase flow structure in churn-turbulent to annular flows. Exp. Therm. Fluid Sci. 2021, 129, 110397. [Google Scholar] [CrossRef]
- Abdulkadir, M.; Azzi, A.; Zhao, D.; Lowndes, I.S.; Azzopardi, B.J. Liquid film thickness behaviour within a large diameter vertical 180° return bend. Chem. Eng. Sci. 2014, 107, 137–148. [Google Scholar] [CrossRef]
- Wang, G.; Dang, Z.; Ishii, M. Wave structure and velocity in vertical upward annular two-phase flow. Exp. Therm. Fluid Sci. 2021, 120, 110205. [Google Scholar] [CrossRef]
- Fukano, T. Measurement of time varying thickness of liquid film flowing with high speed gas flow by a constant electric current method (CECM). Nucl. Eng. Des. 1998, 184, 363–377. [Google Scholar] [CrossRef]
- Wolf, A.; Jayanti, S.; Hewitt, G.F. Flow development in vertical annular flow. Chem. Eng. Sci. 2001, 56, 3221–3235. [Google Scholar] [CrossRef]
- Sawant, P.; Ishii, M.; Hazuku, T.; Takamasa, T.; Mori, M. Properties of disturbance waves in vertical annular two-phase flow. Nucl. Eng. Des. 2008, 238, 3528–3541. [Google Scholar] [CrossRef]
- Tiwari, R.; Damsohn, M.; Prasser, H.-M.; Wymann, D.; Gossweiler, C. Multi-range sensors for the measurement of liquid film thickness distributions based on electrical conductance. Flow Meas. Instrum. 2014, 40, 124–132. [Google Scholar] [CrossRef]
- Setyawan, A. The effect of the fluid properties on the wave velocity and wave frequency of gas–liquid annular two-phase flow in a horizontal pipe. Exp. Therm. Fluid Sci. 2016, 71, 25–41. [Google Scholar] [CrossRef]
- Omebere-Iyari, N.K.; Azzopardi, B.J. A Study of Flow Patterns for Gas/Liquid Flow in Small Diameter Tubes. Chem. Eng. Res. Des. 2007, 85, 180–192. [Google Scholar] [CrossRef]
- Kaji, R.; Azzopardi, B.J. The effect of pipe diameter on the structure of gas/liquid flow in vertical pipes. Int. J. Multiph. Flow 2010, 36, 303–313. [Google Scholar] [CrossRef]
- Wang, Z.; Gabriel, K.S.; Manz, D.L. The influences of wave height on the interfacial friction in annular gas-liquid flow under normal and microgravity conditions. Int. J. Multiph. Flow 2004, 30, 1193–1211. [Google Scholar] [CrossRef]
- Zhao, Y.; Markides, C.N.; Matar, O.K.; Hewitt, G.F. Disturbance wave development in two-phase gas-liquid upwards vertical annular flow. Int. J. Multiph. Flow 2013, 55, 111–129. [Google Scholar] [CrossRef]
- Azzopardi, B.J. Disturbance wave frequencies, velocities and spacing in vertical annular two-phase flow. Nucl. Eng. Des. 1986, 92, 121–133. [Google Scholar] [CrossRef]
- Abdulkadir, M.; Zhao, D.; Azzi, A.; Lowndes, I.S.; Azzopardi, B.J. Two-phase air-water flow through a large diameter vertical 180 o return bend. Chem. Eng. Sci. 2012, 79, 138–152. [Google Scholar] [CrossRef]
- Dang, Z.; Yang, Z.; Yang, X.; Ishii, M. Experimental study of vertical and horizontal two-phase pipe flow through double 90 degree elbows. Int. J. Heat Mass Transf. 2018, 120, 861–869. [Google Scholar] [CrossRef]
- Alekseenko, S.V.; Aktershev, S.P.; Cherdantsev, A.V.; Kharlamov, S.M.; Markovich, D.M. Primary instabilities of liquid film flow sheared by turbulent gas stream. Int. J. Multiph. Flow 2009, 35, 617–627. [Google Scholar] [CrossRef]
- Belt, R.J.; Westende, J.M.C.V.; Prasser, H.M.; Portela, L.M. Time and spatially resolved measurements of interfacial waves in vertical annular flow. Int. J. Multiph. Flow 2010, 36, 570–587. [Google Scholar] [CrossRef]
- Muñoz-Cobo, J.-L.; Rivera, Y.; Berna, C.; Escrivá, A. Analysis of Conductance Probes for Two-Phase Flow and Holdup Applications. Sensors 2020, 20, 7042. [Google Scholar] [CrossRef]
- Rivera, Y.; Muñoz-Cobo, J.L.; Cuadros, J.L.; Berna, C.; Escrivá, A. Experimental study of the effects produced by the changes of the liquid and gas superficial velocities and the surface tension on the interfacial waves and the film thickness in annular concurrent upward vertical flows. Exp. Therm. Fluid Sci. 2021, 120, 110224. [Google Scholar] [CrossRef]
- Fershtman, A.; Robers, L.; Prasser, H.-M.; Barnea, D.; Shemer, L. Interfacial structure of upward gas–liquid annular flow in inclined pipes. Int. J. Multiph. Flow 2020, 132, 103437. [Google Scholar] [CrossRef]
- Rivera, Y.; Berna, C.; Muñoz-Cobo, J.L.; Escrivá, A.; Córdova, Y. Experiments in free falling and downward cocurrent annular flows—Characterization of liquid films and interfacial waves. Nucl. Eng. Des. 2022, 392, 111769. [Google Scholar] [CrossRef]
- Cuadros, J.L.; Rivera, Y.; Berna, C.; Escrivá, A.; Muñoz-Cobo, J.L.; Monrós-Andreu, G.; Chiva, S. Characterization of the gas-liquid interfacial waves in vertical upward co-current annular flows. Nucl. Eng. Des. 2019, 346, 112–130. [Google Scholar] [CrossRef]
- Abdulkadir, M.; Mbalisigwe, U.P.; Zhao, D.; Hernandez-Perez, V.; Azzopardi, B.J.; Tahir, S. Characteristics of churn and annular flows in a large diameter vertical riser. Int. J. Multiph. Flow 2019, 113, 250–263. [Google Scholar] [CrossRef]
- Fossa, M. Design and performance of a conductance probe for measuring the liquid fraction in two-phase gas-liquid flows. Flow Meas. Instrum. 1998, 9, 103–109. [Google Scholar] [CrossRef]
- Devia, F.; Fossa, M. Design and optimisation of impedance probes for void fraction measurements. Flow Meas. Instrum. 2003, 14, 139–149. [Google Scholar] [CrossRef]
- Yang, Z.; Dang, Z.; Yang, X.; Ishii, M.; Shan, J. Downward two phase flow experiment and general flow regime transition criteria for various pipe sizes. Int. J. Heat Mass Transf. 2018, 125, 179–189. [Google Scholar] [CrossRef]
- Libert, N.; Morales, R.E.M.; da Silva, M.J. Capacitive measuring system for two-phase flow monitoring. Part 1: Hardware design and evaluation. Flow Meas. Instrum. 2016, 47, 90–99. [Google Scholar] [CrossRef]
- Jaworek, A.; Krupa, A.; Trela, M. Capacitance sensor for void fraction measurement in water/steam flows. Flow Meas. Instrum. 2004, 15, 317–324. [Google Scholar] [CrossRef]
- de Oliveira, P.M.; Strle, E.; Barbosa, J.R. Developing air-water flow downstream of a vertical 180° return bend. Int. J. Multiph. Flow 2014, 67, 32–41. [Google Scholar] [CrossRef]
- Huang, Z.; Xie, D.; Zhang, H.; Li, H. Gas–oil two-phase flow measurement using an electrical capacitance tomography system and a Venturi meter. Flow Meas. Instrum. 2005, 16, 177–182. [Google Scholar] [CrossRef]
- Zangl, H.; Fuchs, A.; Bretterklieber, T. Non-invasive measurements of fluids by means of capacitive sensors. e & i Elektrotechnik Und Inf. 2009, 126, 8–12. [Google Scholar]
- Pawloski, J.; Ching, C.; Shoukri, M. Measurement of void fraction and pressure drop of air-oil two-phase flow in horizontal pipes. J. Eng. Gas Turbines Power 2004, 126, 107–118. [Google Scholar] [CrossRef]
- Ahmed, H. Capacitance sensors for void-fraction measurements and flow-pattern identification in air–oil two-phase flow. IEEE Sens. J. 2006, 6, 1153–1163. [Google Scholar] [CrossRef]
- Elkow, K.J.; Rezkallah, K.S. Void fraction measurements in gas-liquid flows using capacitance sensors. Meas. Sci. Technol. 1996, 7, 1153. [Google Scholar] [CrossRef]
- Atkinson, C.; Huang, R. A theoretical model for capacitance measurement of liquid films in an annular flow. Math.-Ind. Case Stud. 2017, 7, 3. [Google Scholar] [CrossRef][Green Version]
- De Kerpel, K.; Ameel, B.; de Schampheleire, S.; T’Joen, C.; Canière, H.; de Paepe, M. Calibration of a capacitive void fraction sensor for small diameter tubes based on capacitive signal features. Appl. Therm. Eng. 2014, 63, 77–83. [Google Scholar] [CrossRef]
- De Kerpel, K.; Ameel, B.; T’Joen, C.; Canière, H.; de Paepe, M. Flow regime based calibration of a capacitive void fraction sensor for small diameter tubes. Int. J. Refrig. 2013, 36, 390–401. [Google Scholar] [CrossRef]
- Vieira, R.E.; Parsi, M.; Torres, C.F.; McLaury, B.S.; Shirazi, S.A.; Schleicher, E.; Hampel, U. Experimental characterization of vertical gas-liquid pipe flow for annular and liquid loading conditions using dual Wire-Mesh Sensor. Exp. Therm. Fluid Sci. 2015, 64, 81–93. [Google Scholar] [CrossRef]
- Vieira, R.E.; Parsi, M.; McLaury, B.S.; Shirazi, S.A.; Torres, C.F.; Schleicher, E.; Hampel, U. Experimental characterization of vertical downward two-phase annular flows using Wire-Mesh Sensor. Chem. Eng. Sci. 2015, 134, 324–339. [Google Scholar] [CrossRef]
- Johnson, I.D. Method and Apparatus for Measuring Water in Crude Oil. U.S. Patent 4644263A, 17 February 1987. Available online: https://patents.google.com/patent/US4644263A/en (accessed on 6 May 2020).
- Prasser, H.M.; Böttger, A.; Zschau, J. A new electrode-mesh tomograph for gas–liquid flows. Flow Meas. Instrum. 1998, 9, 111–119. [Google Scholar] [CrossRef]
- Almabrok, A.A.; Aliyu, A.M.; Lao, L.; Yeung, H. Gas/liquid flow behaviours in a downward section of large diameter vertical serpentine pipes. Int. J. Multiph. Flow 2016, 78, 25–43. [Google Scholar] [CrossRef]
- Banowski, M.; Beyer, M.; Szalinski, L.; Lucas, D.; Hampel, U. Comparative study of ultrafast X-ray tomography and wire-mesh sensors for vertical gas–liquid pipe flows. Flow Meas. Instrum. 2017, 53, 95–106. [Google Scholar] [CrossRef]
- Misawa, M.; Tiseanu, I.; Prasser, H.; Ichikawa, N.; Akai, M. Ultra-fast x-ray tomography for multi-phase flow interface dynamic studies. Kerntechnik 2003, 68, 85–90. [Google Scholar] [CrossRef]
- Aliyu, A.M.; Lao, L.; Almabrok, A.A.; Yeung, H. Interfacial shear in adiabatic downward gas/liquid co-current annular flow in pipes. Exp. Therm. Fluid Sci. 2016, 72, 75–87. [Google Scholar] [CrossRef]
- Aliyu, A.M.; Almabrok, A.A.; Baba, Y.D.; Archibong, A.E.; Lao, L.; Yeung, H.; Kim, K.C. Prediction of entrained droplet fraction in co-current annular gas–liquid flow in vertical pipes. Exp. Therm. Fluid Sci. 2017, 85, 287–304. [Google Scholar] [CrossRef]
- Tompkins, C.; Prasser, H.-M.; Corradini, M. Wire-mesh sensors: A review of methods and uncertainty in multiphase flows relative to other measurement techniques. Nucl. Eng. Des. 2018, 337, 205–220. [Google Scholar] [CrossRef]
- Velasco Peña, H.F.; Rodriguez, O.M.H. Applications of wire-mesh sensors in multiphase flows. Flow Meas. Instrum. 2015, 45, 255–273. [Google Scholar] [CrossRef]
- Lucas, D.; Beyer, M.; Szalinski, L.; Schütz, P. A new database on the evolution of air-water flows along a large vertical pipe. Int. J. Therm. Sci. 2010, 49, 664–674. [Google Scholar] [CrossRef]
- Da Silva, M.; Schleicher, E.; Hampel, U. Capacitance wire-mesh sensor for fast measurement of phase fraction distributions. Meas. Sci. Technol. 2007, 18, 2245. [Google Scholar] [CrossRef]
- Zboray, R.; Prasser, H.-M. Measuring liquid film thickness in annular two-phase flows by cold neutron imaging. Exp. Fluids 2013, 54, 1596. [Google Scholar] [CrossRef]
- Zboray, R.; Kickhofel, J.; Damsohn, M.; Prasser, H.-M. Cold-neutron tomography of annular flow and functional spacer performance in a model of a boiling water reactor fuel rod bundle. Nucl. Eng. Des. 2011, 241, 3201–3215. [Google Scholar] [CrossRef]
- Zboray, R.; Prasser, H.-M. Optimizing the performance of cold-neutron tomography for investigating annular flows and functional spacers in fuel rod bundles. Nucl. Eng. Des. 2013, 260, 188–203. [Google Scholar] [CrossRef]
- Stahl, P.; von Rohr, P.R. On the accuracy of void fraction measurements by single-beam gamma-densitometry for gas–liquid two-phase flows in pipes. Exp. Therm. Fluid Sci. 2004, 28, 533–544. [Google Scholar] [CrossRef]
- Trabold, T.A.; Kumar, R.; Vassallo, P.F. Experimental study of dispersed droplets in high- pressure annular flows. J. Heat Transf. 1999, 121, 924–933. [Google Scholar] [CrossRef]
- Omebere-Iyari, N.K.; Azzopardi, B.J.; Ladam, Y. Two-phase flow patterns in large diameter vertical pipes at high pressures. AIChE J. 2007, 53, 2493–2504. [Google Scholar] [CrossRef]
- Adineh, M.; Nematollahi, M.; Erfaninia, A. Experimental and numerical void fraction measurement for modeled two-phase flow inside a vertical pipe. Ann. Nucl. Energy 2015, 83, 188–192. [Google Scholar] [CrossRef]
- Zboray, R.; Guetg, M.; Kickhofel, J.; Barthel, F.; Sprewitz, U.; Hampel, U.; Prasser, H.-M. Investigating annular flows and the effect of functional spacers in an adiabatic double-subchannel model of a BWR fuel bundle by ultra-fast X-ray tomography. In Proceedings of the 14th International Topical Meeting on Nuclear Reactor Thermalhydraulics, NURETH-14, Toronto, ON, Canada, 25–30 September 2011. [Google Scholar]
- Fore, L.B.; Ibrahim, B.B.; Beus, S.G. Visual measurements of droplet size in gas-liquid annular flow. Int. J. Multiph. Flow 2002, 28, 1895–1910. [Google Scholar] [CrossRef][Green Version]
- Simmons, M.J.H.; Hanratty, T.J. Droplet size measurements in horizontal annular gas-liquid flow. Int. J. Multiph. Flow 2001, 27, 861–883. [Google Scholar] [CrossRef]
- Van’t Westende, J.M.C. Droplets in Annular-Dispersed Gas-Liquid Pipe-Flows. Doctoral’s Thesis, TU Delft, Delft, The Netherlands, 2008. [Google Scholar]
- Van’t Westende, J.M.C.; Kemp, H.K.; Belt, R.J.; Portela, L.M.; Mudde, R.F.; Oliemans, R.V.A. On the role of droplets in cocurrent annular and churn-annular pipe flow. Int. J. Multiph. Flow 2007, 33, 595–615. [Google Scholar] [CrossRef]
- Azzopardi, B.J. Drop sizes in annular two-phase flow. Exp. Fluids 1985, 3, 53–59. [Google Scholar] [CrossRef]
- Lopez De Bertodano, M.A.; Jan, C.S.; Beus, S.G. Annular flow entrainment rate experiment in a small vertical pipe. Nucl. Eng. Des. 1997, 178, 61–70. [Google Scholar] [CrossRef]
- Okawa, T.; Kotani, A.; Kataoka, I. Experiments for liquid phase mass transfer rate in annular regime for a small vertical tube. Int. J. Heat Mass Transf. 2005, 48, 585–598. [Google Scholar] [CrossRef]
- Sawant, P.; Ishii, M.; Mori, M. Prediction of amount of entrained droplets in vertical annular two-phase flow. Int. J. Heat Fluid Flow 2009, 30, 715–728. [Google Scholar] [CrossRef]
- Sarimeseli, A. Determination of drop sizes in annular gas/liquid flows in vertical and horizontal pipes. J. Dispers. Sci. Technol. 2009, 30, 694–697. [Google Scholar] [CrossRef]
- Azzopardi, B.J.; Teixeira, J.C.F. Detailed measurements of vertical annular two-phase flow-part I: Drop velocities and sizes. J. Fluids Eng. Trans. ASME 1994, 116, 792–795. [Google Scholar] [CrossRef]
- Azzopardi, B.J.; Zaidi, S.H. Determination of entrained fraction in vertical annular gas/liquid flow. J. Fluids Eng. Trans. ASME 2000, 122, 146–150. [Google Scholar] [CrossRef]
- Zaidi, S.H.; Altunbas, A.; Azzopardi, B.J. A comparative study of phase Doppler and laser diffraction techniques to investigate drop sizes in annular two-phase flow. Chem. Eng. J. 1998, 71, 135–143. [Google Scholar] [CrossRef]
- Hay, K.J.; Liu, Z.C.; Hanratty, T.J. Relation of deposition to drop size when the rate law is nonlinear. Int. J. Multiph. Flow 1996, 22, 829–848. [Google Scholar] [CrossRef]
- Fore, L.B.; Dukler, A.E. The distribution of drop size and velocity in gas-liquid annular flow. Int. J. Multiph. Flow 1995, 21, 137–149. [Google Scholar] [CrossRef]
- Dodge, L.G. Calibration of the malvern particle sizer. Appl. Opt.. 1984, 23, 2415–2419. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Liu, H.; Zhang, Z.; Sun, B.; Zhang, J.; Lou, W. Research on the effects of liquid viscosity on droplet size in vertical gas–liquid annular flows. Chem. Eng. Sci. 2020, 220, 115621. [Google Scholar] [CrossRef]
- Barbosa, J.R., Jr.; Hewitt, G.F.; König, G.; Richardson, S.M. Liquid entrainment, droplet concentration and pressure gradient at the onset of annular flow in a vertical pipe. Int. J. Multiph. Flow 2002, 28, 943–961. [Google Scholar] [CrossRef]
- Oliveira, J.L.G.; Passos, J.C.; Verschaeren, R.; Geld, C.v.d. Mass flow rate measurements in gas-liquid flows by means of a venturi or orifice plate coupled to a void fraction sensor. Exp. Therm. Fluid Sci. 2009, 33, 253–260. [Google Scholar] [CrossRef]
- Liu, W.; Lv, X.; Bai, B. Axial development of air–water annular flow with swirl in a vertical pipe. Int. J. Multiph. Flow 2020, 124, 103165. [Google Scholar] [CrossRef]
- Kim, H.Y.; Koyama, S.; Matsumoto, W. Flow pattern and flow characteristics for counter-current two-phase flow in a vertical round tube with wire-coil inserts. Int. J. Multiph. Flow 2001, 27, 2063–2081. [Google Scholar] [CrossRef]
- Kiran, R.; Ahmed, R.; Salehi, S. Experiments and CFD modelling for two phase flow in a vertical annulus. Chem. Eng. Res. Des. 2020, 153, 201–211. [Google Scholar] [CrossRef]
- Spedding, P.L. Holdup prediction in vertical upwards to downwards flow. Dev. Chem. Eng. Miner. Process. 1997, 5, 43–60. [Google Scholar] [CrossRef]
- Spedding, P.L.; Woods, G.S.; Raghunathan, R.S.; Watterson, J.K. Vertical two-phase flow. Part I: Flow regimes. Chem. Eng. Res. Des. 1998, 76, 612–619. [Google Scholar] [CrossRef]
- Spedding, P.L.; Woods, G.S.; Raghunathan, R.S.; Watterson, J.K. Vertical two-phase flow. Part III: Pressure drop. Chem. Eng. Res. Des. 1998, 76, 628–634. [Google Scholar] [CrossRef]
- Spedding, P.L.; Woods, G.S.; Raghunathan, R.S.; Watterson, J.K. Vertical Two-Phase Flow: Part II: Experimental Semi-Annular Flow and Hold-up. Chem. Eng. Res. Des. 1998, 76, 620–627. [Google Scholar] [CrossRef]
- Woods, G.S.; Spedding, P.L.; Watterson, J.K.; Raghunathan, R.S. Vertical two phase flow. Dev. Chem. Eng. Miner. Process. 1999, 7, 7–16. [Google Scholar] [CrossRef]
- Godbole, P.V.; Tang, C.C.; Ghajar, A.J. Comparison of Void Fraction Correlations for Different Flow Patterns in Upward Vertical Two-Phase Flow. Heat Transf. Eng. 2011, 32, 843–860. [Google Scholar] [CrossRef]
- Elgaddafi, R.; Ahmed, R.; Kiran, R.; Salehi, S.; Fajemidupe, O. Experimental and modeling studies of gas-liquid flow in vertical pipes at high superficial gas velocities. J. Nat. Gas Sci. Eng. 2022, 106, 104731. [Google Scholar] [CrossRef]
- Dong, Y.; Liao, R.; Luo, W.; Li, M. An Improved Pressure Drop Prediction Model Based on Okiszewski’s Model for Low Gas-liquid Ratio Two-Phase Upward Flow in Vertical Pipe. Int. J. Heat Technol. 2022, 40, 17–22. [Google Scholar] [CrossRef]
- Kumar, A.; Das, G.; Ray, S. Void fraction and pressure drop in gas-liquid downflow through narrow vertical conduits-experiments and analysis. Chem. Eng. Sci. 2017, 171, 117–130. [Google Scholar] [CrossRef]
- Hurlburt, E.; Hanratty, T. Measurement of drop size in horizontal annular flow with the immersion method. Exp. Fluids 2002, 32, 692–699. [Google Scholar] [CrossRef]
- Han, H.; Gabriel, K. Flow physics of upward cocurrent gas-liquid annular flow in a vertical small diameter tube. Microgravity Sci. Technol. 2006, 18, 27–38. [Google Scholar] [CrossRef]
- Jayanti, S.; Hewitt, G. Hydrodynamics and heat transfer in wavy annular gas-liquid flow: A computational fluid dynamics study. Int. J. Heat Mass Transf. 1997, 40, 2445–2460. [Google Scholar] [CrossRef]
- Han, H. A Study of Entrainment in Two-Phase upward Cocurrent Annular Flow in a Vertical Tube. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2005. [Google Scholar]
- Han, H.; Gabriel, K. A numerical study of entrainment mechanism in axisymmetric annular gas-liquid flow. J. Fluids Eng. Mar. 2007, 129, 293–301. [Google Scholar] [CrossRef]
- Xie, Z.; Hewitt, G.F.; Pavlidis, D.; Salinas, P.; Pain, C.C.; Matar, O.K. Numerical study of three-dimensional droplet impact on a flowing liquid film in annular two-phase flow. Chem. Eng. Sci. 2017, 166, 303–312. [Google Scholar] [CrossRef]
- Alipchenkov, V.; Nigmatulin, R.; Soloviev, S.; Stonik, O.; Zaichik, L.; Zeigarnik, Y. A three-fluid model of two-phase dispersed-annular flow. Int. J. Heat Mass Transf. 2004, 47, 5323–5338. [Google Scholar] [CrossRef]
- Liu, Y.; Li, W.Z. Numerical simulation of droplet size distribution in vertical upward annular flow. J. Fluids Eng. Trans. ASME 2010, 132, 121402. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, J.; Li, W.Z. A two-phase, two-component model for vertical upward gas-liquid annular flow. Int. J. Heat Fluid Flow 2011, 32, 796–804. [Google Scholar] [CrossRef]
- Saxena, A.; Prasser, H.M. A study of two-phase annular flow using unsteady numerical computations. Int. J. Multiph. Flow 2020, 126, 103037. [Google Scholar] [CrossRef]
- Kishore, B.N.; Jayanti, S. A multidimensional model for annular gas-liquid flow. Chem. Eng. Sci. 2004, 59, 3577–3589. [Google Scholar] [CrossRef]
- Hassani, M.; Motlagh, M.B.; Kouhikamali, R. Numerical investigation of upward air-water annular, slug and bubbly flow regimes. J. Comput. Appl. Res. Mech. Eng. 2020, 9, 331–341. [Google Scholar]
- Shaban, H.; Tavoularis, S. On the accuracy of gas flow rate measurements in gas–liquid pipe flows by cross-correlating dual wire-mesh sensor signals. Int. J. Multiph. Flow 2016, 78, 70–74. [Google Scholar] [CrossRef]
- Joseph, D.D.; Bannwart, A.C.; Liu, Y.J. Stability of annular flow and slugging. Int. J. Multiph. Flow 1996, 22, 1247–1254. [Google Scholar] [CrossRef][Green Version]
- Belt, R.J.; Van’t Westende, J.M.C.; Portela, L.M. Prediction of the interfacial shear-stress in vertical annular flow. Int. J. Multiph. Flow 2009, 35, 689–697. [Google Scholar] [CrossRef]
- Mudawwar, I.A.; El-Masri, M.A. Momentum and heat transfer across freely-falling turbulent liquid films. Int. J. Multiph. Flow 1986, 12, 771–790. [Google Scholar] [CrossRef]
- Vassallo, P. Near wall structure in vertical air-water annular flows. Int. J. Multiph. Flow 1999, 25, 459–476. [Google Scholar] [CrossRef]
- Hajiloo, M.; Chang, B.H.; Mills, A.F. Interfacial shear in downward two-phase annular co-current flow. Int. J. Multiph. Flow 2001, 27, 1095–1108. [Google Scholar] [CrossRef]
- Klyuev, N.I.; Solov’eva, E.A. Method for the annular gas-liquid mixture flow regime in a vertical cylindrical channel. Russ. Aeronaut. 2009, 52, 68–71. [Google Scholar] [CrossRef]
- Alves, M.V.C.; Waltrich, P.J.; Gessner, T.R.; Falcone, G.; Barbosa, J.R., Jr. Modeling transient churn-annular flows in a long vertical tube. Int. J. Multiph. Flow 2017, 89, 399–412. [Google Scholar] [CrossRef]
- Schubring, D.; Shedd, T.A. A model for pressure loss, film thickness, and entrained fraction for gas-liquid annular flow. Int. J. Heat Fluid Flow 2011, 32, 730–739. [Google Scholar] [CrossRef]
- Schubring, D.; Shedd, T.A. Critical friction factor modeling of horizontal annular base film thickness. Int. J. Multiph. Flow 2009, 35, 389–397. [Google Scholar] [CrossRef]
- Ishii, M.; Grolmes, M.A. Inception criteria for droplet entrainment in two-phase concurrent film flow. AIChE J. 1975, 21, 308–318. [Google Scholar] [CrossRef]
- Henstock, W.H.; Hanratty, T.J. The interfacial drag and the height of the wall layer in annular flows. AIChE J. 1976, 22, 990–1000. [Google Scholar] [CrossRef]
- Tatterson, D.F.; Dallman, J.C.; Hanratty, T.J. Drop sizes in annular gas-liquid flows. AIChE J. 1977, 23, 68–76. [Google Scholar] [CrossRef]
- Hori, K.; Nakasatomi, M.; Nishikawa, K.; Sekoguchi, N. Study of ripple region in cyclic two-phase flow: 3rd report, Effect of liquid viscosity on gas-liquid interface properties and friction coefficient. Trans. Jpn. Soc. Mech. Eng. 1978, 44, 3847–3856. [Google Scholar] [CrossRef]
- Hori, K.; Nakazatomi, M.; Nishikawa, K.; Sekoguchi, K. On Ripple of Annular Two-Phase Flow: 3. Effect of Liquid Viscosity on Characteristics of Wave and Interfacial Friction Factor. Bull. JSME 1979, 22, 952–959. [Google Scholar] [CrossRef]
- Ambrosini, W.; Andreussi, P.; Azzopardi, B.J. A physically based correlation for drop size in annular flow. Int. J. Multiph. Flow 1991, 17, 497–507. [Google Scholar] [CrossRef]
- Okawa, T.; Kitahara, T.; Yoshida, K.; Matsumoto, T.; Kataoka, I. New entrainment rate correlation in annular two-phase flow applicable to wide range of flow condition. Int. J. Heat Mass Transf. 2002, 45, 87–98. [Google Scholar] [CrossRef]
- MacGillivray, R.M. Gravity and Gas Density Effects on Annular Flow Average Film Thickness and Frictional Pressure Drop. Masters’s Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2004. [Google Scholar]
- Rahman, M.; Stevens, J.; Pardy, J.; Wheeler, D. An Improved Film Thickness Model for Annular Flow Pressure Gradient Estimation in Vertical Gas Wells. J. Pet. Environ. Biotechnol. 2017, 8, 1. [Google Scholar]
- Ju, P.; Liu, Y.; Yang, X.; Ishii, M. Wave characteristics of vertical upward adiabatic annular flow in pipes. Int. J. Heat Mass Transf. 2019, 145, 118701. [Google Scholar] [CrossRef]
- Ju, P.; Brooks, C.S.; Ishii, M.; Liu, Y.; Hibiki, T. Film thickness of vertical upward co-current adiabatic flow in pipes. Int. J. Heat Mass Transf. 2015, 89, 985–995. [Google Scholar] [CrossRef]
- Ghajar, A.J.; Bhagwat, S.M. Effect of void fraction and two-phase dynamic viscosity models on prediction of hydrostatic and frictional pressure drop in vertical upward gas-liquid two-phase flow. Heat Transf. Eng. 2013, 34, 1044–1059. [Google Scholar] [CrossRef]
- Tandon, T.N.; Varma, H.K.; Gupta, C.P. A void fraction model for annular two-phase flow. Int. J. Heat Mass Transf. 1985, 28, 191–198. [Google Scholar] [CrossRef]
- Cioncolini, A.; Thome, J.R. Void fraction prediction in annular two-phase flow. Int. J. Multiph. Flow 2012, 43, 72–84. [Google Scholar] [CrossRef]
- Kumar, P.; Das, A.K.; Mitra, S.K. Physical understanding of gas-liquid annular flow and its transition to dispersed droplets. Phys. Fluids 2016, 28, 072101. [Google Scholar] [CrossRef]
- Schadel, S.A.; Leman, G.W.; Binder, J.L.; Hanratty, T.J. Rates of atomization and deposition in vertical annular flow. Int. J. Multiph. Flow 1990, 16, 363–374. [Google Scholar] [CrossRef]
- McNeil, D.A.; Stuart, A.D. The effects of a highly viscous liquid phase on vertically upward two-phase flow in a pipe. Int. J. Multiph. Flow 2003, 29, 1523–1549. [Google Scholar] [CrossRef]
- Kocamustafaogullari, G.; Smits, S.R.; Razi, J. Maximum and mean droplet sizes in annular two-phase flow. Int. J. Heat Mass Transf. 1994, 37, 955–965. [Google Scholar] [CrossRef]
- Trabold, T.A.; Kumar, R. Vapor core turbulence in annular two-phase flow. Exp. Fluids 2000, 28, 187–194. [Google Scholar] [CrossRef]
- Kataoka, I.; Ishii, M.; Mishima, K. Generation and size distribution of droplet in annular two-phase flow. J. Fluids Eng. Trans. ASME 1983, 105, 230–240. [Google Scholar] [CrossRef]
- Azzopardi, B.J. Gas-Liquid Flows; Begell House: New York, NY, USA, 2006. [Google Scholar]
- Kolev, N.I.; Kolev, N. Multiphase Flow Dynamics; Springer: Berlin/Heidelberg, Germany, 2005; Volume 1. [Google Scholar]
- Kataoka, I.; Ishii, M.; Nakayama, A. Entrainment and desposition rates of droplets in annular two-phase flow. Int. J. Heat Mass Transf. 2000, 43, 1573–1589. [Google Scholar] [CrossRef]
- Lopez de Bertodano, M.A.; Assad, A.; Beus, S.G. Experiments for entrainment rate of droplets in the annular regime. Int. J. Multiph. Flow 2001, 27, 685–699. [Google Scholar] [CrossRef]
- Okawa, T.; Kataoka, I. Correlations for the mass transfer rate of droplets in vertical upward annular flow. Int. J. Heat Mass Transf. 2005, 48, 4766–4778. [Google Scholar] [CrossRef]
- Ryu, S.H.; Park, G.C. A droplet entrainment model based on the force balance of an interfacial wave in two-phase annular flow. Nucl. Eng. Des. 2011, 241, 3890–3897. [Google Scholar] [CrossRef]
- Liu, L.; Bai, B. Generalization of droplet entrainment rate correlation for annular flow considering disturbance wave properties. Chem. Eng. Sci. 2017, 164, 279–291. [Google Scholar] [CrossRef]
- Wang, G.; Sawant, P.; Ishii, M. A new entrainment rate model for annular two-phase flow. Int. J. Multiph. Flow 2020, 124, 103185. [Google Scholar] [CrossRef]
- Oliemans, R.V.A.; Pots, B.F.M.; Trompe, N. Modelling of annular dispersed two-phase flow in vertical pipes. Int. J. Multiph. Flow 1986, 12, 711–732. [Google Scholar] [CrossRef]
- Ishii, M.; Mishima, K. Droplet entrainment correlation in annular two-phase flow. Int. J. Heat Mass Transf. 1989, 32, 1835–1846. [Google Scholar] [CrossRef]
- Utsuno, H.; Kaminaga, F. Prediction of Liquid Film Dryout in Two-Phase Annular-Mist Flow in a Uniformly Heated Narrow Tube Development of Analytical Method under BWR Conditions. J. Nucl. Sci. Technol. 1998, 35, 643–653. [Google Scholar] [CrossRef][Green Version]
- Petalas, N.; Aziz, K. A Mechanistic Model for Multiphase Flow in Pipes. J. Can. Pet. Technol. 2000, 39, 000604. [Google Scholar] [CrossRef]
- Pan, L.; Hanratty, T.J. Correlation of entrainment for annular flow in vertical pipes. Int. J. Multiph. Flow 2002, 28, 363–384. [Google Scholar] [CrossRef]
- Sawant, P.; Ishii, M.; Mori, M. Droplet entrainment correlation in vertical upward co-current annular two-phase flow. Nucl. Eng. Des. 2008, 238, 1342–1352. [Google Scholar] [CrossRef]
- Cioncolini, A.; Thome, J.R. Prediction of the entrained liquid fraction in vertical annular gas-liquid two-phase flow. Int. J. Multiph. Flow 2010, 36, 293–302. [Google Scholar] [CrossRef]
- Cioncolini, A.; Thome, J.R. Entrained liquid fraction prediction in adiabatic and evaporating annular two-phase flow. Nucl. Eng. Des. 2012, 243, 200–213. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, H.; Liu, M. A probability model for fully developed annular flow in vertical pipes: Prediction of the droplet entrainment. Int. J. Heat Mass Transf. 2015, 84, 225–236. [Google Scholar] [CrossRef]






| Reference | Correlations of the Liquid Film Thickness |
|---|---|
| Ishii and Grolmes [217] (1975) | |
| Henstock and Hanratty [218] (1976) | |
| Tatterson et al. [219] (1977) | |
| Hori et al. [220,221] (1978) | |
| Ambrosini et al. [222] (1991) | |
| Fukano and Furukawa [94] (1998) | |
| Okawa et al. [223] (2002) | |
| MacGillivray [224] (2004) | |
| Hazuku et al. [68] (2008) | |
| Berna et al. [9] (2014) | |
| Pan et al. [39] (2015) | |
| Almabrok et al. [148] (2016) | |
| Rahman et al. [225] (2017) | |
| Ju et al. [226,227] (2019) | |
| Rivera et al. [125] (2021) | |
| Rivera et al. [127] (2022) | |
| Pan et al. [39] | |
| Ju et al. [226] | |
| Y. Rivera, et al. [125] |
| Reference | Correlations for the Void Fraction |
|---|---|
| Tandon et al. [229] (1985) | |
| Usui and Sato [93] (1989) | Free falling film, |
| Cioncolini and Thome [230] (2012) | |
| Kumar et al. [194] (2017) | Free falling film, |
| Reference | Prediction of the Droplet Size |
|---|---|
| Kocamustafaogullari et al. [234] (1994) | |
| Azzopardi [7] (1997) | |
| Fore et al. [165] (2002) | |
| Azzopardi [237] (2006) | |
| Berna et al. [8] (2015) | |
| Wang et al. [180] (2020) |
| Reference | Correlations of the Droplet Entrainment Rate |
|---|---|
| Bertodano et al. [170] (1997) | |
| Kataoka et al. [239] (2000) | |
| Bertodano et al. [240] (2001) | |
| Okawa and Kataoka [241] (2005) | |
| Ryu and Park [242] (2011) | |
| Liu and Bai [243] (2017) | |
| Wang et al. [244] (2020) |
| Reference | Correlations for the Entrainment Fraction |
|---|---|
| Oliemans et al. [245] (1986) | |
| Ishii and Mishima [246] (1989) | |
| Utsono and Kaminanga [247] (1998) | |
| Petalas and Aziz [248] (2000) | |
| Barbosa et al. [181] (2002) | |
| Pan and Hanratty [249] (2002) | |
| Sawant et al. [250] (2008) | |
| Sawant et al. [172] (2009) | |
| Cioncolini and Thome [251] (2010) | |
| Cioncolini and Thome [252] (2012) | |
| Berna et al. [8] (2015) | |
| Aliyu et al. [152] (2017) | |
| Zhang et al. [253] (2020) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, Y.; Stewart, C.; Kelly, D.; Campbell, D.; Gormley, M. Two-Phase Annular Flow in Vertical Pipes: A Critical Review of Current Research Techniques and Progress. Water 2022, 14, 3496. https://doi.org/10.3390/w14213496
Xue Y, Stewart C, Kelly D, Campbell D, Gormley M. Two-Phase Annular Flow in Vertical Pipes: A Critical Review of Current Research Techniques and Progress. Water. 2022; 14(21):3496. https://doi.org/10.3390/w14213496
Chicago/Turabian StyleXue, Yunpeng, Colin Stewart, David Kelly, David Campbell, and Michael Gormley. 2022. "Two-Phase Annular Flow in Vertical Pipes: A Critical Review of Current Research Techniques and Progress" Water 14, no. 21: 3496. https://doi.org/10.3390/w14213496
APA StyleXue, Y., Stewart, C., Kelly, D., Campbell, D., & Gormley, M. (2022). Two-Phase Annular Flow in Vertical Pipes: A Critical Review of Current Research Techniques and Progress. Water, 14(21), 3496. https://doi.org/10.3390/w14213496










