Abstract
This paper aims to design an integrated offshore structure capable of supporting a hybrid assembly of one wind plus two tidal turbines. The monopile has been found to be a suitable foundation type as the most inexpensive solution in water depths of less than 30 m. The Cook Strait in New Zealand is an ideal location for wind and tidal renewable energy sources due to its strong winds and tidal currents. Finite element analysis was performed to determine the displacement of the structure for different types of soils using OPTUM G3. After that, a macro-element model for soil was represented, considering the monopile as a Euler–Bernoulli beam model. The results enable the finding of optimum dimensions of monopiles with allowable tilt and deflection. Based on this, the diameter, thickness, and length of the monopile can be 6, 0.083, and 60 m, respectively. The maximum load occurs in extreme wind load scenarios when wind and waves move in same direction.
1. Introduction
1.1. Hybrid Generation from Offshore Renewable Sources
Deployed on floating bodies or along cables, offshore energy harvesters can convert wave, solar, tidal, ocean currents, and other renewable energy sources to stable electrical energy [1]. Creating hybrids with wind electricity generation would reduce the currently significant operations and maintenance (O&M) of wind turbines (WT), which is around 10–25% of the total cost of electricity, and a lower transmission cost [2,3]. By bringing together two marine renewable technologies with considerable synergies, the combined harnessing of offshore energies creates excellent potential for development. This is corroborated by some recent European Union (EU)-funded projects: MARINA, ORECCA, TROPOS, MERMAID, and H2OCEAN [4]. MARINA classifies combined wave–wind systems according to the technology, water depth (shallow, transition, or deep water), or location relative to the shoreline (shoreline, nearshore, offshore). ORECCA analyses the offshore renewable energies (ORE) combined resources in Europe. Looking particularly at Europe’s combined wave–wind resource, this can be divided into three main sea basins: the Mediterranean Sea, the North and Baltic Seas, and the Atlantic Ocean. TROPOS is aimed at developing a floating multi-purpose platform system for deep water [4]. The MERMAID project seeks to develop concepts for the next generation of offshore activities for multi-use ocean space. It proposes new design concepts for combining offshore activities, such as energy extraction, aquaculture, and platform-related transport at various ocean areas [5]. H2OCEAN is developing a wind–wave power open-sea platform for hydrogen generation with support for multiple energy users [6].
The main projects installed in the previous decade (2010–2019) were the 2.3 MW Hywind in Norway in 2009, the 2 MW Principle Power in Portugal in 2011, and the MOE project in Japan with capacities of 100-kW half-scale model in 2012, and 2 MW full scale in 2013 [7].
Da et al. (2009) propose a control scheme for a hybrid system. Adjusting the generator’s rotation speed can maximize the system’s output power under fluctuating wind or tidal currents [8]. Li et al. (2017) show the integration of floating wind turbines with a wave energy converter and tidal turbines increases power production by 22–45% [9]. Lande et al. (2019) modelled the co-location of a wind turbine with an array of tidal stream turbines in the MeyGen site located in Pentland Firth, UK. It will increase energy yield by around 11% and decrease the levelized cost by 10% [10]. Nichita et al. present the “accelerated simulation time” method and its experimental validation. Wind or tidal turbine characteristics are obtained using the simulation approach developed at the GREAH lab and are validated with an actual ocean turbine installed in the Circulating Water Channel at Inha University Ocean Engineering Laboratory, South Korea [11]. Phurailatpam et al. [12] present a DC microgrid for rural applications in India using wind turbines (WT) and photovoltaic panels (PV). Azaza et al. give some insight and techno-economic analysis of microgrid deployment in different Swedish regions using PV/WT/DG, a battery bank, and an energy management system to identify the optimal system size and configuration [13]. Thakur et al. designed, constructed, and tested a new physical simulator under different operating conditions in a real microgrid environment. The simulator replicates the behaviour of a designed wind turbine. The experiments have also shown that the designed wind turbine can work in harmony with PV power modules and battery storage in response to weather and load variations in an island microgrid environment [14]. Wang et al. analysed the stability of a microgrid system containing an offshore wind farm (OWF), an offshore tidal farm (OTF), and a seashore wave farm (SWF) fed to an onshore power grid through a high-voltage direct current (HVDC) link based on a voltage-source converter (VSC) [15]. Adetunji et al. proposed an optimized grid-connected microgrid for South Africa using photovoltaic panels (PV) and a supporting lead-acid battery for downtime [16]. Kitson et al. present a DC microgrid system, interfacing wind and solar using a power electronic interface with droop functions. A case study site in Nepal is simulated to demonstrate the system’s performance to variable generation and loads [17]. Oulis Rousis et al. designed an off-grid system in Greece relying on PV, diesel generators, and batteries for energy storage [18]. Phurailatpam et al. compared different scenarios of DC microgrids in the Indian context using wind and photovoltaic panels for India’s rural and urban power supply [19]. Faridnia et al. designed a grid-connected microgrid for a tidal farm near Darwin, in the north of Australia, including tidal power as the main supply, a pumped hydro system (PHS) with 1000 kWh capacity as the long-term storage system, and a micro-turbine (MT) to minimize the operating cost [20]. Colombo et al. added Photovoltaic (PV) to power-to-gas (P2G) to reduce emissions [21].
1.2. The Integration of Offshore Wind with Tidal Energy
Over the recent decades, offshore wind farms have attracted more investment [22]. It is estimated that onshore and offshore wind power will generate more than a third of the total electricity needed in the medium term, becoming the primary generation source by 2050 [23]. Compared with onshore wind energy resources, offshore wind fields have many advantages, such as persistent wind, faster-flowing speed, higher uniformity, and longer available time per year, flat sea surface, and low turbulence intensity, which promotes the vigorous development of the offshore wind power industry [24,25]. More importantly, installing wind turbines in the ocean can protect the environment [26] and save land resources [27]. The vast ocean area provides good conditions for developing large-scale wind farms and turbines [28]. The power generation by the identical turbines in the offshore area is 50–100% higher than in the onshore area [29]. However, the main issue for investors is capital cost which results in increasing the electricity cost for customers. The most expensive component of an offshore wind turbine is the foundation, accounting for 19% of the capital cost. In addition, foundation installation with 6% of the capital cost is the highest cost compared with other parts [30]. However, the cost of electricity using offshore wind is still high [31]. As another offshore energy source, installing tidal turbines has attracted less investment because tidal turbines are exposed to harsh currents. Their lifetime is low, and foundation design is complex in most cases, where the water depth is more than 30 metres [32]. However, tidal turbines can produce an enormous amount of electricity, more than four times per square meter of the rotor than wind turbines [33]. Integration of both wind and tidal turbines with the same foundation may be a way to reduce the cost of electricity [7] and enable predictable power generation from two different energy sources.
Although New Zealand is surrounded by water and has good potential for offshore energy, it has not yet been used for power generation. In recent years, several reports indicated the annual demand of electricity increases from current demand of 40 TWh to 70 TWh by 2050 [34]. Therefore, looking for new sources of harvesting power generation is essential.
This paper describes a preliminary design for an offshore structure capable of supporting a hybrid assembly of one wind plus two tidal turbines, as shown in Figure 1.

Figure 1.
Schematic of a hybrid system consisting of wind and tidal turbines.
The monopile has been found to be a suitable foundation type; it is one of the most inexpensive solutions for supporting the structures and is widely used in wind farm projects. Furthermore, the other reasons of choosing a monopile for integrating wind and tidal turbines are the ability to be driven into the seabed and connect directly to the tower, its simple structure, and being widely used in wind farm projects [35].
The design will be carried out using the foundation concepts of an offshore design [36]. The design procedure has three steps:
- (a)
- Site investigation;
- (b)
- Criteria for design;
- (c)
- Evaluation of the stability of design under combined loads.
Reducing the cost of electricity generation and integrating renewable energy sources are two essential factors in encouraging the development of novel ideas to tackle the lack of enough electricity and proposing alternatives for fossil fuels [16].
2. Environmental Parameters for Design
The MetOcean model identifies the Cook Strait between the North and South Island of New Zealand as the best area for offshore supplies, as shown in Figure 2 [37].

Figure 2.
National Depth-averaged Tidal Current Speeds for Mean Spring Flows (in m/s) [37].
The main geographical parameters of the optimized site in the Cook Strait are shown in Table 1.

Table 1.
The main geographical parameters of the site for foundation design.
The most important data from NIWA [38] ’s analysis is summarized in Table 2.

Table 2.
Wave data for Terawhiti.
The tidal information in the Cook Strait is tabulated in Table 3. The depth of the harbour mouth channel, where the turbines will be located, is an asset; it is neither too deep for access by divers if needed (31 m to a maximum 52 m) nor too shallow and therefore is not impacted by a lack of water at low tide. The sandbar surrounding the mouth protects the project from oceanic waves [40].

Table 3.
Tide data for Terawhiti [41,42].
Equivalent wind data will be sourced from the meteorological recording site closest to Terawhiti by NASA. These data are presented in Table 4 and Figure 3. These data are essential to estimate the wind stresses transmitted through the turbine’s support structure to its foundation.

Table 4.
The geological and geotechnical wind data of Terawhiti [36,43,44,45].

Figure 3.
Wind Speed Histogram for Terawhiti [42].
The Weibull two-parameter distribution function often describes wind speed variability. It is considered a standard approach for evaluating local wind load probabilities because it has been found to fit a wide collection of wind data [46]. The Weibull shape and scale parameters are denoted by s and K, respectively. s is dimensionless, and it indicates how peak the site under consideration is, whereas K has a unit of wind speed (m/s), and it shows how windy the site is [47].
To calculate Weibull parameters, the frequency percentage of Terawhiti results by Homer is used in the Weibull calculator [43], which results in s = 1.98 and K = 7.99 m/s.
The turbulence intensity varies with mean wind speed, which for Terawhiti is equal to 7.10 m/s, and quantifies how much the wind varies, typically within 10 min [36]. This value, I = 16%, may be obtained from the standard IEC 61400 [44].
Based on the DNV code, for heights above sea level (z) less than 60 metres, Lk is 5.67z, and for z above 60 m, Lk is 340.2 m [36]. As the height above sea level is 87m, the turbulence integral length scale is 340.2 m in this case.
3. Methods
All calculations in this section are based on the design method used by Bhattacharya [36]. The design criteria which will be checked for the possibility of a monopile design and design procedure, which are presented in Table 5 and Figure 4.

Table 5.
Main criteria for foundation design [36].

Figure 4.
Design Procedure of Offshore Wind and Tidal Turbines Monopiles.

Table 6.
General information of Wind turbine, Siemens SWT-3.6-107 Offshore 3.6 MW, for the hybrid system [35,36,48].

Table 7.
General information of tidal turbine, Atlantic Resources AR 2000, for the hybrid system [35,36].
IEC codes [49,50] as well as the DNV code [51] describe hundreds of load cases that need to be analysed to ensure the safe operation of turbines throughout their lifetime of 20–30 years. However, in terms of foundation design, not all these cases are significant or relevant. The main design requirements for foundation design are ULS (Ultimate Limit State), FLS (Fatigue Limit State), and SLS (Serviceability Limit State). Five load cases important for simplified foundation design are identified and described in Table 8.

Table 8.
Load Case Scenarios [36].
In Table 8, the Normal Turbulence Model (NTM) relates to the normal working conditions of the turbine. The Extreme Turbulence model (ETM) is for extreme turbulence conditions. The Extreme operating Gust (EOG) is the highest single occurrence wind load caused by a sudden change in the wind speed. ESS and EWH denote extreme sea state and extreme wave height, respectively. The significant wave height HS, used in ESS scenarios, is the average of the maximum one-third of all waves in the three hours, whereas the maximum wave height, Hm, used in EWH scenarios, is the maximum wave height for three hours [36].
4. Results
Initially, a finite element analysis was presented for different soils. Then, the results were used to determine wind and wave loads and then evaluated to see if the calculated dimensions of the monopile can result in an acceptable foundation design or not.
4.1. Finite Element Analysis
For the current application, an advanced analysis method represents a finite element, discrete element, or finite difference method. OPTUM G3 is used considering the different soils for foundation and how the type of soil affects the stability of the hybrid system. Optum CE develops fast, user-friendly software for the design of Geotech and Concrete structures. The software is developed with a focus on providing advanced FE analysis packages but at the same time making the tools accessible for engineering practitioners, including structural engineers, contractors, and building companies [48]. Table 9 shows the parameters used by OPTUM for simulations.

Table 9.
Geotechnical Parameters used by OPTUM software for simulations.
The unit weight of a soil mass is the ratio of the total weight of soil to the total volume of soil. The total mass of the structure after summarizing the weights of each element in Table 6 and Table 7 is 1780 tonnes. Applying this load to the foundation, using OPTUM G3 [48], as shown in Figure 5, confirms that the soil type of soft ormedium sand is more stable with less displacement and dissipation.
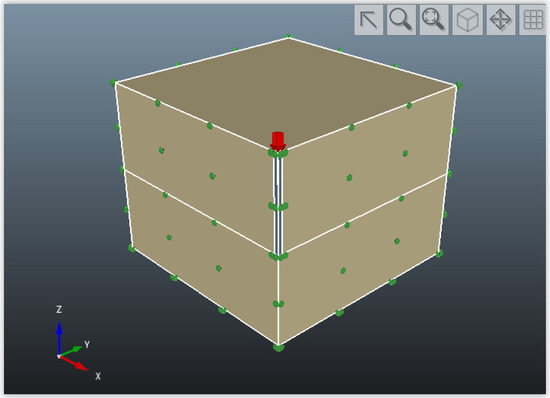
Figure 5.
Applying load to the structure using OPTUM.
After simulation by OPTUM, the results for different kinds of soils are represented in Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11.
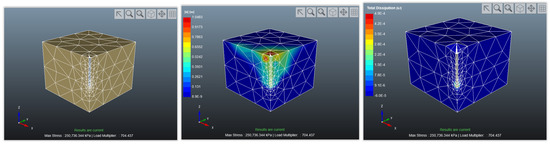
Figure 6.
The geometry after meshing (left), displacement (middle), and total dissipation energy (right) for Loose Sand.
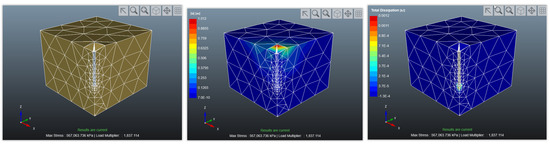
Figure 7.
The geometry after meshing (left), displacement (middle), and total dissipation energy (right) for Medium Sand.

Figure 8.
The geometry after meshing (left), displacement (middle), and total dissipation energy (right) for Dense Sand.
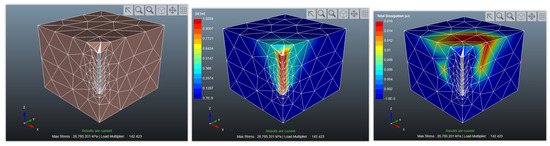
Figure 9.
The geometry after meshing (left), displacement (middle), and total dissipation energy (right) for Soft Clay.
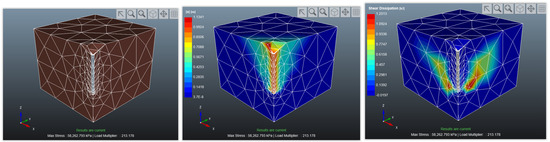
Figure 10.
The geometry after meshing (left), displacement (middle), and total dissipation energy (right) for Firm Clay.

Figure 11.
The geometry after meshing (left), displacement (middle), and total dissipation energy (right) for Stiff Clay.
The results are shown in Table 10.

Table 10.
OPTUM results for different types of seabed.
The results indicate that maximum displacement and dissipation will occur for Stiff-clay-MC soil and minimum displacement and dissipation are from Medium Sand-MC and Loose-Sand-MC, respectively.
4.2. Macro-Element Model
For estimating the natural frequency of an offshore foundation pile under load, a spring model based on the Euler–Bernoulli beam model (Figure 12) of a monopile foundation at the Terawhiti site is assumed with input parameters as follows:

Figure 12.
Mechanical Model of Foundation; KV (vertical stiffness), KL (lateral stiffness), KR (rocking stiffness), and KLR (cross-coupling) [54].
- Steel monopile, diameter 6 m, ensures rigid behavior, as recommended by Jose and Mathai [52].
- To validate Hooke’s stress-strain law, Poisson ratio 0.2, as recommended by Bowles [50] and OPTUM [48].
- The stiffness of 20 MPa is a typical value for the beam-on-elastic foundation sourced from Bowles [53] and OPTUM [48].
The initial stiffness of the foundation (i.e., KL, KR, and KLR) can be determined based on the pile dimensions and soil type. Once KL, KR, and KLR are known, one can predict the system’s natural frequency [54]. The results for this design are:
KL = 3848.25 MN/m, KLR = −133,488 MN and KR = 7,252,848 MNm/rad.
The simple cantilever beam formulas, as recommended by Arany [55], were used to estimate the natural frequency of the tower , which is 0.34 Hz and which is acceptable, as the condition is that the target frequency of the selected wind and tidal turbines, according to Table 5, is 0.24 Hz [36].
4.2.1. Wind Loads
Table 11 summarizes the main parameters of wind scenarios. The loads and moments will be used later in Section 4.2.3 to identify driving combined scenarios, either E1 or E5.

Table 11.
Load and overturning moment of wind scenarios (U-1)–(U-4) for Terawhiti.
The maximum wind load and moment were found for U3. As recommended by DNV 2014 [51] and IEC 2019 [50], the environmental load factor of γL = 1.35 multiplies on U3 moment load to result a total wind moment of 473.85 [MNm].
4.2.2. Wave Loads
The wave conditions recommended by Bhattacharya [36], as explained before in Table 2, are used for calculating critical wave loads acting on the substructure which is the summation of maximum inertia loads and maximum drag loads. The maximum inertia load occurs at the time instant t = 0 when the surface elevation η = 0 and the maximum of the drag load occurs when t = T/4 and η = H/2. Current loads due to the movement of water particles causing drag which are considered as a portion of wave loads according to above explanation.
The dynamic amplification of wave loading is calculated using the peak wave frequency and an assumed damping ratio as shown in Table 12. The total damping ratios for the along-wind (x) and cross-wind (y) directions are chosen conservatively as 3% and 1%, respectively, by Camp et al. (2004) [56].

Table 12.
Dynamic amplification factors and wave loads.
In calculating DAFs, as the difference in DAFx and DAFy for wave scenarios are negligible, a higher value is applied to loads.
4.2.3. Load Combinations for Ultimate Limit State (ULS)
Table 13 uses the calculated loads of Table 11 and Table 12 to find combined loads of different scenarios of Table 8. It can be seen that superior loads belong to E-3.

Table 13.
Calculated wind and wave loads.
Substituting the total overturning moment of 515.3 MNm from Table 13 and other values mentioned above in Equation (A5):
Substituting the above value ( in Equation (A3) in Appendix A, results in finding area moment of inertia (IP) and monopile diameter (DP) as depicted below:
Substituting DP in Equation (A2) results in the required thickness:
Lastly, the minimum length of the monopile for investigating this foundation design should be
Therefore, based on total load, the foundation dimensions should be:
The chosen values of DP and LP satisfy the above conditions. Therefore, the pile dimensions for the Terawhiti site to withstand total load are:
DP = 6 [m] tP = 0.083 [m] LP = 60 [m]
4.2.4. Long-Term Deflection & Rotation of the Pile Mudline Moment
From Table 13, the maximum load is 10.4 MN and the maximum moment is 515.3 MNm. Furthermore, from Section 4.2, KL = 3848.25 MN/m, KLR = −133488 MN, and KR = 7252848 MNm/rad. Using these values in Equations (A8) and (A9) results in
Based on the criteria design (Table 5), as and , the pile tip deflection and the rotation are acceptable.
5. Conclusions
This paper proposes a standard design for the foundation of a hybrid (wind+tidal) system for Terawhiti:
- The proposed tower is a hollow steel tube wall with a thickness of 0.027 m, 68 m high above the platform, tapering from 5 m at the base to 3 m at the top, and weighing 255 tonnes.
- The proposed transition piece is a steel tube with an internal diameter m to fit the top of the monopile, wall thickness of 0.083 m and extending 29 m below the platform level, and sheathing on top of the monopile. Weight: 300 tonnes.
- The proposed foundation is a monopile inserted into the seabed. It would be solid steel, 6 m in diameter, and 60 m long, weighing 700 tonnes. It would project above the seabed for 30 m (the upper 20 m would be inserted into the transition piece), and the lower 20 m would be placed in the seabed. The pile would be driven with a hydraulic hammer into the seabed.
- The acting loads are transferred to the foundation; they can be static depending on the total weight of the structure, which is calculated and analyzed with OPTUM G3 software, or dynamic (cyclic), which is investigated by combining wind and wave loads.
- The wind and water produce aerodynamic and hydrodynamic loads (thrust and drag) on the structure, which depend on the operational speed of turbines. However, to know the acceptability of foundation design, it is necessary to combine wind and wave loads in ULS design and calculate maximum loads and find the driven scenarios. Then, find the required dimensions of the pile and, based on the maximum load of the driven scenario, calculate deflection and check in ULS if the deflection is allowable or not.
- The combination of wind and wave loads indicates that the maximum load occurs for the E-3 scenario. Applying loads of this scenario results in acceptable deflection, tilt, and natural frequency for Terawhiti.
- Several iterations were done to reach the required pile dimensions after finding the maximum combined load for the driving scenario.
Author Contributions
Conceptualization, N.M.N., J.K. and L.B.; methodology, N.M.N., J.K. and L.B.; software, N.M.N.; validation, N.M.N., J.K. and L.B.; formal analysis, N.M.N.; investigation, N.M.N.; resources, N.M.N. and J.K.; data curation, N.M.N.; writing—original draft preparation, N.M.N. and J.K.; writing—review and editing, N.M.N. and J.K.; visualization, N.M.N.; supervision, J.K.; project administration, N.M.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
This appendix contains the equations used in Section 4; the DAFs are calculated as
where f ( is the excitation frequency, f0 is the Eigen frequency, and ξ is the damping ratio and wave periods from Table 12 and is 0.34 Hz.
The wall thickness of the monopile is estimated according to API 2A-WSD [57] as
This value is used for finding the area moment of inertia:
where IP, DP, and tP are the moment of inertia, diameter, and thickness of the monopile, respectively. The following criteria for maximum stress (see Table 5) needs to be allowable [36]:
where γM = 1.1 is the pile material safety factor and = 355 MPa is the pile yield stress (from Table 7). From Equation (A4), the required diameter is determined as:
The last dimension for a monopile design is length estimated by the formula given by Poulos and Davis [58]:
Stiffness values of Section 4.2 are used to find deformations in the foundation using:
where Fx = 10.4 MN and My = 515.3 MNm are highlighted in Table 13. Solving the matrix results in:
References
- Zhao, T.; Xu, M.; Xiao, X.; Ma, Y.; Li, Z.; Wang, Z.L. Recent progress in blue energy harvesting for powering distributed sensors in ocean. Nano Energy 2021, 88, 106199. [Google Scholar] [CrossRef]
- Sarma, N.; Tuohy, P.M.; Mohammed, A.; Djurovic, S. Rotor Electrical Fault Detection in DFIGs Using Wide-Band Controller Signals. IEEE Trans. Sustain. Energy 2020, 12, 623–633. [Google Scholar] [CrossRef]
- Karumalai, D. Offshore Integrated Renewable Power System. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Washington, DC, USA, 2020. [Google Scholar]
- Pérez-Collazo, C.; Greaves, D.; Iglesias, G. A review of combined wave and offshore wind energy. Renew. Sustain. Energy Rev. 2015, 42, 141–153. [Google Scholar] [CrossRef]
- Christensen, E.D.; Stuiver, M.; Guanche, R.; Møhlenberg, F.; Schouten, J.J.; Pedersen, O.S.; He, W.; Zanuttigh, B.; Koundouri, P. Go Offshore-Combining Food and Energy Production; Technical University of Denmark, Department of Mechanical Engineering: Lyngby, Denmark, 2015. [Google Scholar]
- H2OCEAN. Available online: http://www.vliz.be/projects/mermaidproject/project/related-projects/h2ocean.html (accessed on 7 September 2021).
- Chen, P.; Chen, J.; Hu, Z. Review of Experimental-Numerical Methodologies and Challenges for Floating Offshore Wind Turbines. J. Mar. Sci. Appl. 2020, 19, 339–361. [Google Scholar] [CrossRef]
- Da, Y.; Khaligh, A. Hybrid offshore wind and tidal turbine energy harvesting system with independently controlled rectifiers. In Proceedings of the 2009 35th Annual Conference of IEEE Industrial Electronics, Porto, Portugal, 3–5 November 2009. [Google Scholar]
- Li, L.; Gao, Y.; Yuan, Z.; Day, S.; Hu, Z. Dynamic response and power production of a floating integrated wind, wave and tidal energy system. Renew. Energy 2018, 116, 412–422. [Google Scholar] [CrossRef]
- Lande-Sudall, D.; Stallard, T.; Stansby, P. Co-located deployment of offshore wind turbines with tidal stream turbine arrays for improved cost of electricity generation. Renew. Sustain. Energy Rev. 2019, 104, 492–503. [Google Scholar] [CrossRef]
- Nichita, C.; Ashglaf, M.; Amara, Y.; Jo, C.H. Preliminary study of a concept of wind-tidal turbine coupling using functional similarities of real time emulation. Renew. Energy Power Qual. J. Tenerife 2019, 17, 371–376. [Google Scholar] [CrossRef]
- Phurailatpam, C.; Rajpurohit, B.; Wang, L. Optimization of DC microgrid for rural applications in India. In Proceedings of the 2016 IEEE Region 10 Conference (TENCON), Singapore, 22–25 November 2016. [Google Scholar]
- Azaza, M.; Wallin, F. Multi objective particle swarm optimization of hybrid micro-grid system: A case study in Sweden. Energy 2017, 123, 108–118. [Google Scholar] [CrossRef]
- Thakur, D.; Jiang, J. Design and Construction of a Wind Turbine Simulator for Integration to a Microgrid with Renewable Energy Sources. Electr. Power Components Syst. 2017, 45, 949–963. [Google Scholar] [CrossRef]
- Wang, L.; Lin, C.-Y.; Wu, H.-Y.; Prokhorov, A.V. Stability Analysis of a Microgrid System With a Hybrid Offshore Wind and Ocean Energy Farm Fed to a Power Grid Through an HVDC Link. IEEE Trans. Ind. Appl. 2017, 54, 2012–2022. [Google Scholar] [CrossRef]
- Adetunji, K.E.; Akinlabi, O.A.; Joseph, M.K. Developing a microgrid for tafelkop using homer. In Proceedings of the 2018 International Conference on Advances in Big Data, Computing and Data Communication Systems (icABCD), Durban, South Africa, 6–7 August 2018. [Google Scholar]
- Kitson, J.; Williamson, S.; Harper, P.; McMahon, C.; Rosenberg, G.; Tierney, M.; Bell, K.; Gautam, B. Modelling of an expandable, reconfigurable, renewable DC microgrid for off-grid communities. Energy 2018, 160, 142–153. [Google Scholar] [CrossRef]
- Rousis, A.O.; Tzelepis, D.; Konstantelos, I.; Booth, C.; Strbac, G. Design of a Hybrid AC/DC Microgrid Using HOMER Pro: Case Study on an Islanded Residential Application. Inventions 2018, 3, 55. [Google Scholar] [CrossRef]
- Phurailatpam, C.; Rajpurohit, B.S.; Wang, L. Planning and optimization of autonomous DC microgrids for rural and urban applications in India. Renew. Sustain. Energy Rev. 2018, 82, 194–204. [Google Scholar] [CrossRef]
- Faridnia, N.; Habibi, D.; Lachowicz, S.; Kavousifard, A. Optimal scheduling in a microgrid with a tidal generation. Energy 2018, 171, 435–443. [Google Scholar] [CrossRef]
- Colombo, P.; Saeedmanesh, A.; Santarelli, M.; Brouwer, J. Dynamic dispatch of solid oxide electrolysis system for high renewable energy penetration in a microgrid. Energy Convers. Manag. 2019, 204, 112322. [Google Scholar] [CrossRef]
- Green, R.; Vasilakos, N. The economics of offshore wind. Energy Policy 2011, 39, 496–502. [Google Scholar] [CrossRef]
- Sierra-Garcia, J.E.; Santos, M. Improving Wind Turbine Pitch Control by Effective Wind Neuro-Estimators. IEEE Access 2021, 9, 10413–10425. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, L.; Wang, M.; Shi, F.; Gong, Z. Comparative analysis of nonlinear dynamic response for offshore wind turbine structures under incoming wind speed. Ships Offshore Struct. 2020, 16, 326–333. [Google Scholar] [CrossRef]
- Kang, J.; Sun, L.; Soares, C.G. Fault Tree Analysis of floating offshore wind turbines. Renew. Energy 2019, 133, 1455–1467. [Google Scholar]
- Jeon, S.H.; Cho, Y.U.; Seo, M.W.; Cho, J.R.; Jeong, W.B. Dynamic response of floating substructure of spar-type offshore wind turbine with catenary mooring cables. Ocean Eng. 2013, 72, 356–364. [Google Scholar] [CrossRef]
- Hallowell, S.T.; Arwade, S.R.; Fontana, C.M.; DeGroot, D.J.; Aubeny, C.P.; Diaz, B.D.; Myers, A.T.; Landon, M.E. System reliability of floating offshore wind farms with multiline anchors. Ocean Eng. 2018, 160, 94–104. [Google Scholar] [CrossRef]
- Chen, Z.; Blaabjerg, F. Wind farm—A power source in future power systems. Renew. Sustain. Energy Rev. 2009, 13, 1288–1300. [Google Scholar] [CrossRef]
- Karlõševa, A.; Nõmmann, S.; Nõmmann, T.; Urbel-Piirsalu, E.; Budziński, W.; Czajkowski, M.; Hanley, N. Marine trade-offs: Comparing the benefits of off-shore wind farms and marine protected areas. Energy Econ. 2016, 55, 127–134. [Google Scholar] [CrossRef]
- Blanco, M.I. The economics of wind energy. Renew. Sustain. Energy Rev. 2009, 13, 1372–1382. [Google Scholar]
- Heptonstall, P.; Gross, R.; Greenacre, P.; Cockerill, T. The cost of offshore wind: Understanding the past and projecting the future. Energy Policy 2011, 41, 815–821. [Google Scholar] [CrossRef]
- Lande-Sudall, D.; Stallard, T.; Stansby, P. Co-located offshore wind and tidal stream turbines: Assessment of energy yield and loading. Renew. Energy 2018, 118, 627–643. [Google Scholar]
- Fraenkel, P. Marine Current Turbines: Exploiting Currents for Large-Scale Power Generation; IGG Publishing Ltd.: London, UK, 2007. [Google Scholar]
- Asian Productivity Organization. Ministry of Business, Innovation and Employment, Wind Generation Stack Update; Roaring40s Wind Power Ltd.: Wellington, New Zealand, 2020. [Google Scholar]
- Karimirad, M. Offshore Energy Structures: For Wind Power, Wave Energy and Hybrid Marine Platforms; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Bhattacharya, S. Design of Foundations for Offshore Wind Turbines; Wiley Online Library: Hoboken, NJ, USA, 2019. [Google Scholar]
- Huckerby, J.; Johnson, D.; Nobs Line, N.P. New Zealand’s wave and tidal energy resources and their timetable for development. In Proceedings of the International Conference on Ocean Energy (ICOE), Brest, France, 15–17 October 2008. [Google Scholar]
- NIWA Tide Forecaster. Available online: https://tides.niwa.co.nz/ (accessed on 10 June 2021).
- The KNMI/ERA-40 Wave Atlas. Available online: http://projects.knmi.nl/wave_atlas/atlas_book.html#c57a (accessed on 10 June 2021).
- Crest Energy. Available online: http://www.crest-energy.com/faq.htm (accessed on 2 July 2022).
- Linz Information about Tides around New Zealand. Available online: https://www.linz.govt.nz/sea/tides/introduction-tides/tides-around-new-zealand (accessed on 4 February 2021).
- Homer Pro. Available online: https://www.homerenergy.com/ (accessed on 2 March 2020).
- Weibull Calculator. Available online: https://wind-data.ch/tools/weibull.php (accessed on 10 December 2021).
- IEC 61400. Available online: https://en.wikipedia.org/wiki/IEC_61400 (accessed on 9 July 2020).
- RETScreen. Available online: https://www.nrcan.gc.ca/maps-tools-publications/tools/data-analysis-software-modelling/retscreen/7465 (accessed on 4 June 2020).
- Gupta, R.; Biswas, A. Wind data analysis of silchar (assam, india) by rayleighs and weibull methods. J. Mech. Eng. Res. 2010, 2, 10–24. [Google Scholar]
- Ayodele, T.R.; Jimoh, A.A.; Munda, J.; Agee, J.T. Statistical analysis of wind speed and wind power potential of Port Elizabeth using Weibull parameters. J. Energy South. Afr. 2012, 23, 30–38. [Google Scholar] [CrossRef]
- OPTUM CE. Available online: https://optumce.com/ (accessed on 10 March 2022).
- IEC 61400-1:2005; IEC Classification of Wind Turbines. IEC: Geneva, Switzerland, 2015.
- BS EN IEC 61400-3-1:2019; Wind Energy Generation Systems. Design Requirements for Fixed Offshore Wind Turbines. BSI Standards Limited: Geneva, Switzerland, 2019.
- Veritas, N. Environmental Conditions and Environmental Loads; Recommend Practice DNV-RP-C205; Det Norske Veritas: Dresden, Germany, 2014; Available online: https://home.hvl.no/ansatte/tct/FTP/V2022%20Hydrodynamikk/Litteratur/RP-C205.pdf (accessed on 3 November 2022).
- Jose, N.M.; Mathai, A. A Study on Lateral Deformation of Monopile of Offshore Wind Turbine due to Environmental Loads. Procedia Technol. 2016, 24, 287–294. [Google Scholar] [CrossRef]
- Bowles, L. Foundation Analysis and Design; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Bhattacharya, S.; Goda, K. Use of offshore wind farms to increase seismic resilience of Nuclear Power Plants. Soil Dyn. Earthq. Eng. 2016, 80, 65–68. [Google Scholar]
- Arany, L.; Bhattacharya, S.; Adhikari, S.; Hogan, S.; Macdonald, J. An analytical model to predict the natural frequency of offshore wind turbines on three-spring flexible foundations using two different beam models. Soil Dyn. Earthq. Eng. 2015, 74, 40–45. [Google Scholar] [CrossRef]
- Camp, T.R.; Morris, M.J.; Van Rooij, R.P.J.O.M.; Van Der Tempel, J.; Zaaijer, M.B.; Henderson, A.; Argyriadis, K.; Schwartz, S.; Just, H.; Grainger, W.; et al. Design Methods for Offshore Wind Turbines at Exposed Sites (Final Report of the OWTES Project EU JOULE III Project JOR3-CT98-0284); Garrad Hassan and Partners Ltd.: Bristol, UK, 2004. [Google Scholar]
- RP2A-WSD, A. Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms–Working Stress Design; American Petroleum Institute: Washington, DC, USA, 2000. [Google Scholar]
- Poulos, H.G.; Davis, E.H. Pile Foundation Analysis and Design; Wiley: New York, NY, USA, 1980; Volume 397. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).