Sensitivity Analysis and Determination of the Optimal Level of Water Use Efficiency for Winter Wheat and Barley under Different Irrigation Scenarios Using the AquaCrop Model in Arid and Semiarid Climatic Conditions (Case Study: Dehloran Plain, Iran)
Abstract
:1. Introduction
- (i)
- To evaluate the AquaCrop model for simulating the yield responses of winter wheat and barley at different irrigation levels by comparing the model results with those of field surveys.
- (ii)
- To calibrate the AquaCrop models for winter wheat and barley in a large agricultural area in Ilam Province in central Iran.
2. Materials and Methods
2.1. AquaCrop Model Structure
- The consideration of the effect of the harvest index (HI) for the calculation of the final biomass yield estimate.
- The consideration of the amount of evapotranspiration separately from soil evaporation (Es), transpiration (Ta), and ground crevices with the final performance calculation. Since there is little plant cover for plant growth in the first stage, the amount of evaporation from the soil surface is significant, and it is not necessary to consider when calculating the amount of water consumed by plants. In this model, the rate of evaporation from the soil surface is calculated using Ritchie’s equation (1972).
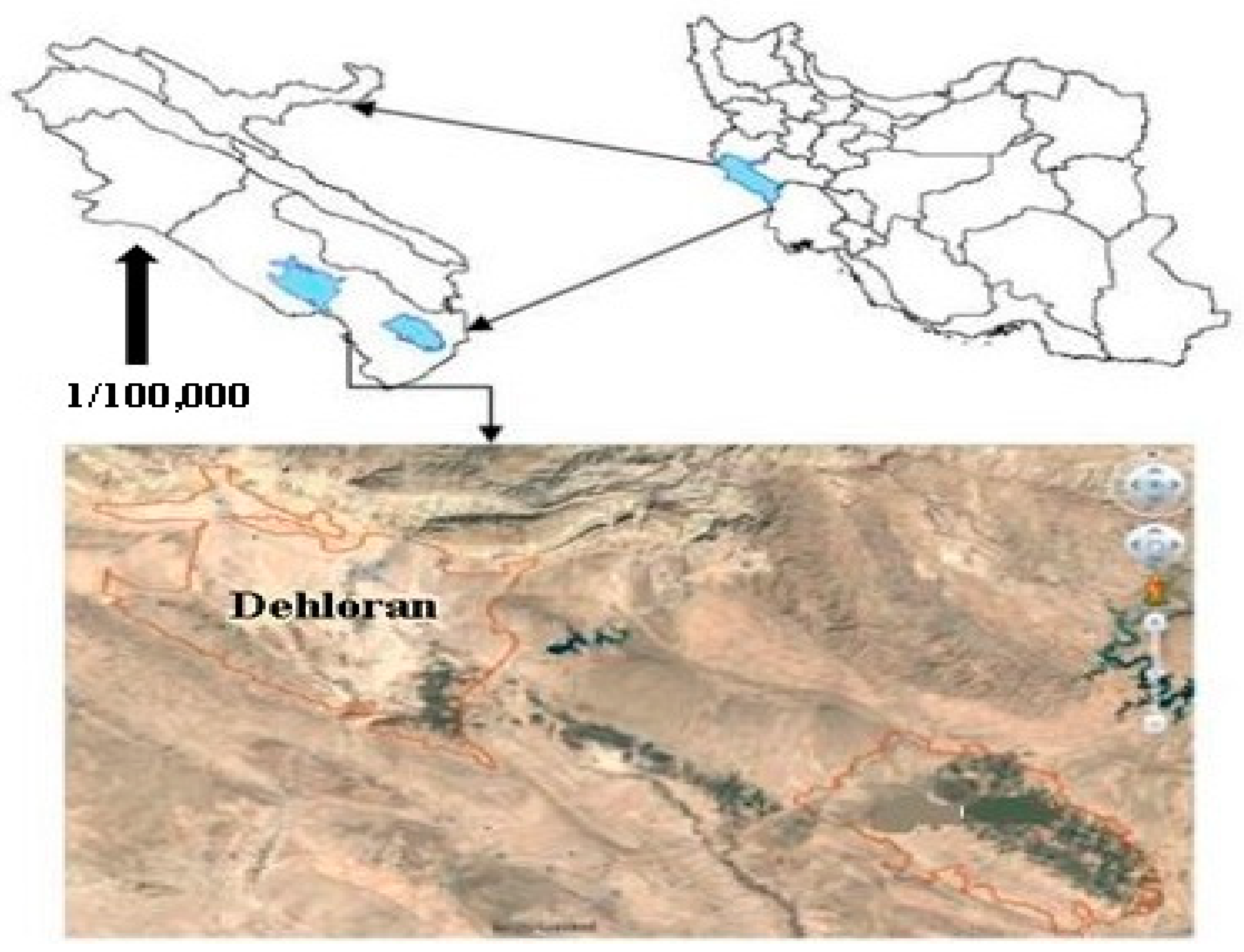
2.2. The study Area
2.3. Plant Data
2.4. Irrigation and Field Management
2.5. Meteorological Data
2.6. Soil Properties
2.7. Model Calibration
2.8. Model Validation and Performance Evaluation
2.9. Sensitivity Analysis of Input Data
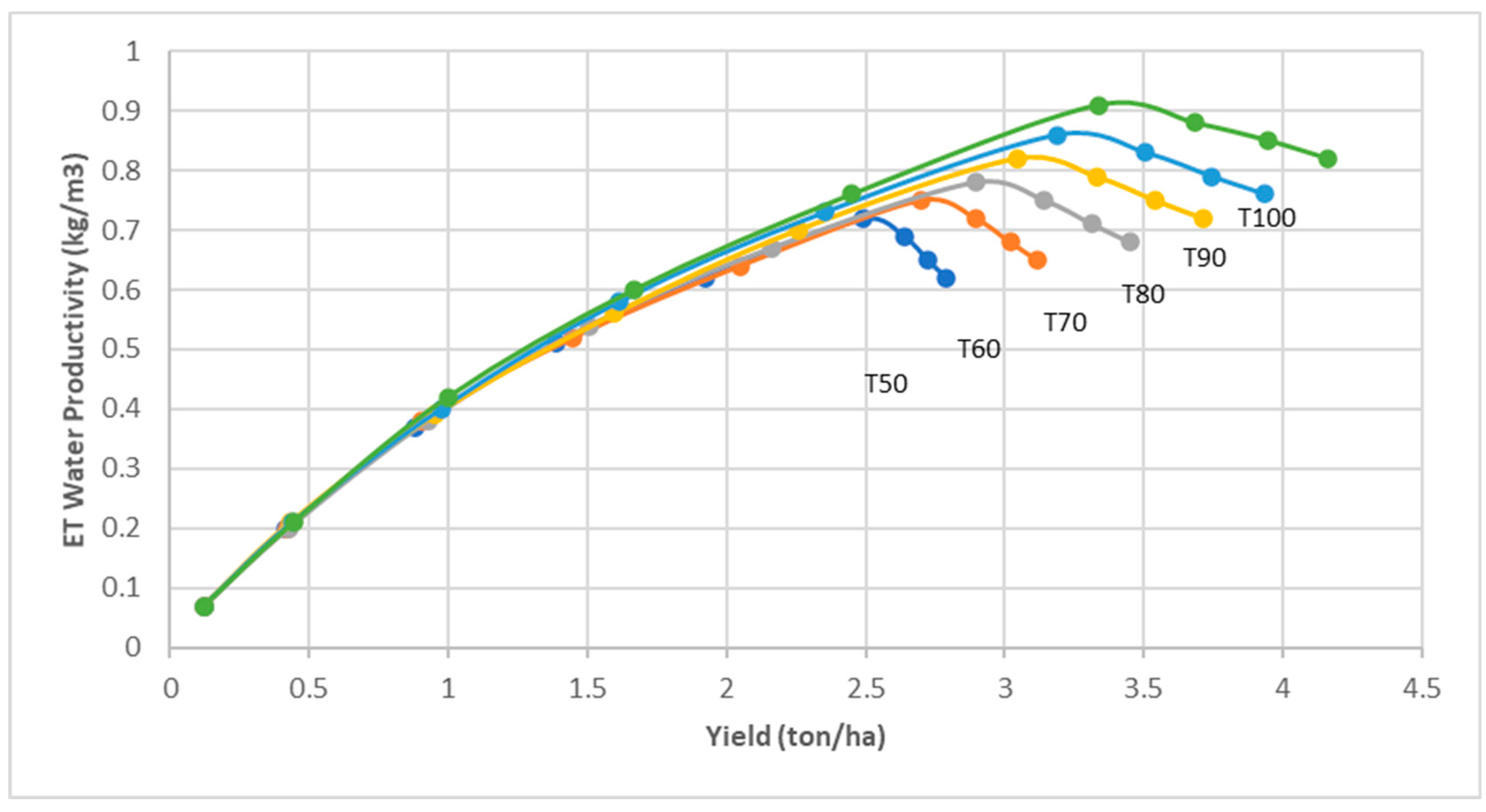
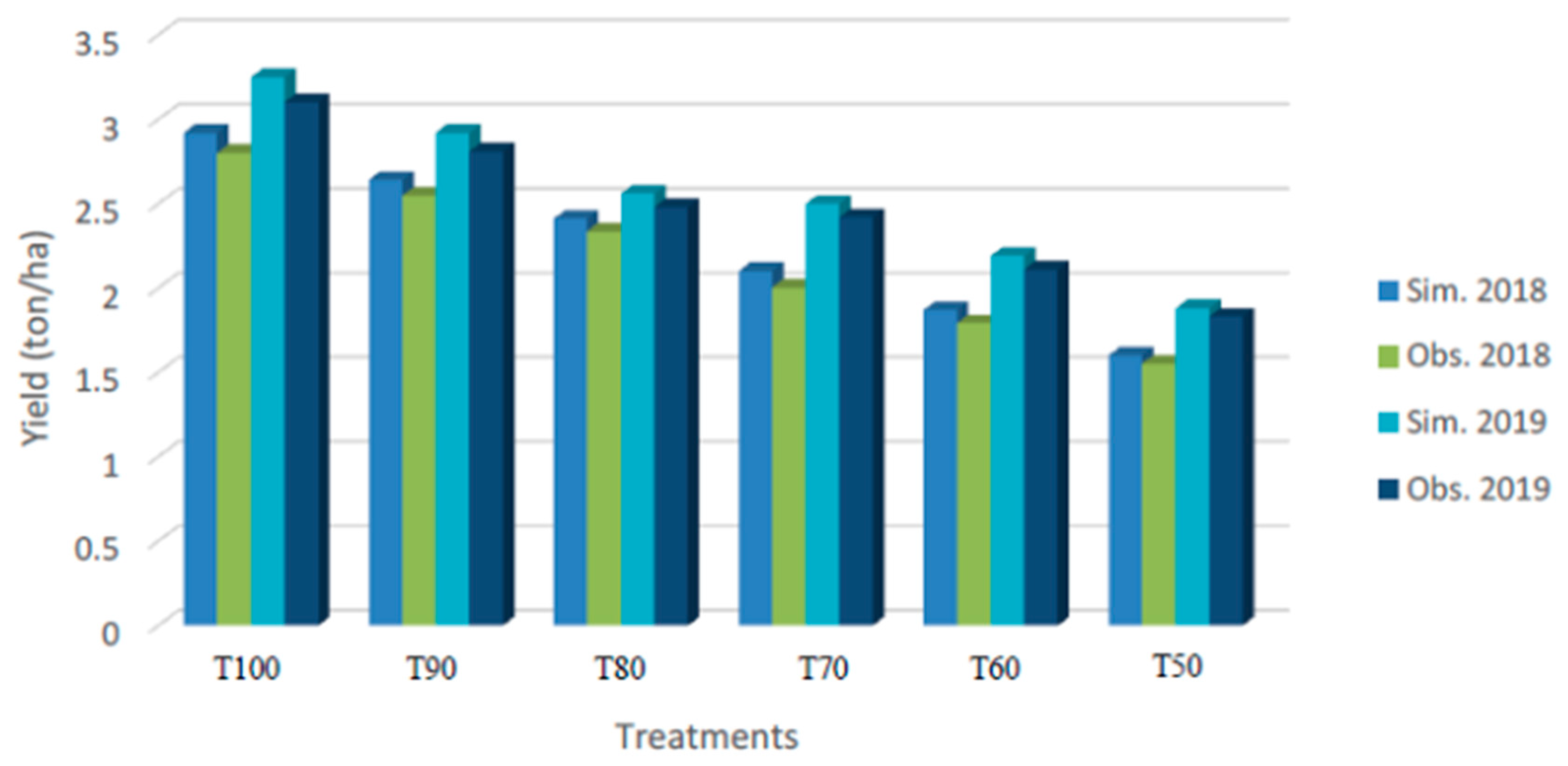
3. Results
3.1. Model Performance Evaluation
3.2. Model Validation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abedinpour, M. Agricultural Water Management with AquaCrop Model, 1st ed.; Isfahan University Jahad Publications: Isfahan, Iran, 2019; pp. 11–18, 81–86, 210–219. [Google Scholar]
- Saab, M.A.; Albrizio, R.; Nangia, V.; Karam, F.; Rouphael, Y. Developing scenarios to assess sunflower and soybean yield under different sowing dates and water regimes in the Bekaa valley (Lebanon): Simulations with Aquacrop. Int. J. Plant Prod. 2014, 8, 1735–6814. [Google Scholar] [CrossRef]
- Hamidreza, S.; Mohd, A.M.S.; Teang, S.L.; Sayed, F.M.; Arman, G.; Mohd, K.Y. Application of AquaCrop model in deficit irrigation management of Winter wheat in arid region. Afr. J. Agric. Res. 2011, 6, 2204–2215. [Google Scholar]
- Shirshahi, F.; Babazadeh, H.; Ebrahimipak, N.; Zeraatkish, Y. Calibration and evaluation of the performance of Aquacrop model in managing the amount and time of deficit Irrigation in wheat. Iran. J. Irrig. Sci. Eng. 2017, 41, 31–44. (In Persian) [Google Scholar]
- Sema, K.A.L.E.; Madenoğlu, S. Evaluating AquaCrop Model for Winter Wheat under Various Irrigation Conditions in Turkey. J. Agric. Sci. 2017, 24, 205–217. [Google Scholar]
- Ahmadi, S.H.; Mosallaeepour, E.; Kamgar-Haghighi, A.A.; Sepaskhah, A.R. Modeling Maize Yield and Soil Water Content with AquaCrop Under Full and Deficit Irrigation Managements. Water Resour. Manag. 2015, 29, 2837–2853. [Google Scholar] [CrossRef]
- Ramezani, M.; Babazadeh, H.; Sarai Tabrizi, M. Simulating Barley Yield under Different Irrigation Levels by using AquaCrop Model. Irrig. Sci. Eng. (JISE) 2019, 41, 161–172. [Google Scholar] [CrossRef]
- Goosheh, M.; Pazira, E.; Gholami, A.; Andarzian, B.; Panahpour, E. Improving Irrigation Scheduling of Wheat to Increase Water Productivity in Shallow Groundwater Conditions Using Aquacrop. Irrig. Drain. 2018, 67, 738–754. [Google Scholar] [CrossRef]
- Hellal, F.; Mansour, H.; Abdel-Hady, M.; El-Sayed, S.; Abdelly, C. Assessment water productivity of barley varieties under water stress by AquaCrop model. AIMS Agric. Food 2019, 4, 501–517. [Google Scholar] [CrossRef]
- Khoshravesh, M.; Mostafazadeh-Fard, B.; Heidarpour, M.; Kiani, A.-R. AquaCrop model simulation under different irrigation water and nitrogen strategies. Water Sci. Technol. 2013, 67, 232–238. [Google Scholar] [CrossRef] [PubMed]
- Masasi, B.; Taghvaeian, S.; Gowda, P.H.; Warren, J.; Marek, G. Simulating Soil Water Content, Evapotranspiration, and Yield of Variably Irrigated Grain Sorghum Using AquaCrop. JAWRA J. Am. Water Resour. Assoc. 2018, 55, 976–993. [Google Scholar] [CrossRef]
- Hoseinzadeh, S.; Astiaso Garcia, D. Techno-economic assessment of hybrid energy flexibility systems for islands’ decarbonization: A case study in Italy. Sustain. Energy Technol. Assess. 2022, 51. [Google Scholar] [CrossRef]
- Hoseinzadeh, S.; Ghasemi, M.H.; Heyns, S. Application of hybrid systems in solution of low power generation at hot seasons for micro hydro systems. Renew. Energy. 2020, 160, 323–332. [Google Scholar] [CrossRef]
- Mousavizadeh, S.; Honar, T.; Ahmadi, S. Assessment of the AquaCrop Model for simulating Canola under different irrigation managements in a semiarid area. Int. J. Plant Prod. 2016, 10, 425–445. [Google Scholar] [CrossRef]
- He, Q.; Li, S.; Hu, D.; Wang, Y.; Cong, X. Performance assessment of the AquaCrop model for film-mulched maize with full drip irrigation in Northwest China. Irrig. Sci. 2020, 39, 277–292. [Google Scholar] [CrossRef]
- Amiri, A.; Bahrani, S.; Irmak, N.; Mohammadiyan, R. Evaluation of irrigation scheduling and yield response for wheat cultivars using the AquaCrop model in an arid climate. Water Supply. 2021, 22, 602–614. [Google Scholar] [CrossRef]
- Kheir, A.M.S.; Alkharabsheh, H.M.; Seleiman, M.F.; Al-Saif, A.M.; Ammar, K.A.; Attia, A.; Zoghdan, M.G.; Shabana, M.M.A.; Aboelsoud, H.; Schillaci, C. Calibration and Validation of AQUACROP and APSIM Models to Optimize Wheat Yield and Water Saving in Arid Regions. Land 2021, 10, 1375. [Google Scholar] [CrossRef]
- Kheir, A.M.; Hoogenboom, G.; Ammar, K.A.; Ahmed, M.; Feike, T.; Elnashar, A.; Liu, B.; Ding, Z.; Asseng, S. Minimizing trade-offs between wheat yield and resource-use efficiency in the Nile Delta–A multi-model analysis. Field Crop. Res. 2022, 287. [Google Scholar] [CrossRef]
- Shen, X.; Wang, G.; Zeleke, K.T.; Si, Z.; Chen, J.; Gao, Y. Crop Water Production Functions for Winter Wheat with Drip Fertigation in the North China Plain. Agronomy 2020, 10, 876. [Google Scholar] [CrossRef]
- Soomro, K.B.; Alaghmand, S.; Shahid, M.R.; Andriyas, S.; Talei, A. Evaluation of Aquacrop Model in Simulating Bitter Ground Water Productivity under Saline Irrigation. Irrig. Drain. J. 2019, 69, 63–73. [Google Scholar] [CrossRef]
- Abedinpour, M.; Sarangi, A.; Rajput, T.; Singh, M.; Pathak, H.; Ahmad, T. Performance Evaluation of Aquacrop Model for Maize Crop in a Semi-Arid Environment. Agric. Water Manag. 2012, 110, 55–66. [Google Scholar] [CrossRef]
- Najarchi, M.; Kaveh, F.; Babazadeh, H.; Manshouri, M. Determination of the yield response factor for field crop deficit irrigation. Afr. J. Agric. Res. 2011, 6, 3700–3705. [Google Scholar] [CrossRef]










| Crop | Growth Period (Days) in Different Stages | Planting Date | Date of Harvest | ||||
|---|---|---|---|---|---|---|---|
| Vegetative Growth | Flowering | Seeding | Granulation | Senescence | |||
| Winter wheat | 30 | 60 | 70 | 20 | 180 | The second half of November | The second half of May |
| Barley | 20 | 60 | 70 | 20 | 170 | The second half of November | The third half of April |
| Crop | Maximum Depth of Root Development (cm) | Net Volume of Irrigation Water (m3) | Gross Volume of Irrigation Water (m3) | Net Need for Irrigation Cycle (mm) | Gross Need for Irrigation Cycle (mm) | Maximum Hydromodule (lit·s−1) | Number of Irrigations |
|---|---|---|---|---|---|---|---|
| Winter wheat | 120 | 3789 | 6888 | 63 | 115 | 1.15 | 6 |
| Barley | 100 | 3092 | 5622 | 62 | 113 | 1.04 | 5 |
| Month | ET (mm·day−1) | Sunny Hours | Wind Speed (Km·day−1) | Humidity (%) | Maximum Temperature (°C) | Minimum Temperature (°C) | Effective Rainfall (mm) | Rainfall (mm) |
|---|---|---|---|---|---|---|---|---|
| January | 1.93 | 6.3 | 164 | 59 | 18.1 | 8.8 | 33.5 | 41.9 |
| February | 3.01 | 7.2 | 181 | 48 | 22.7 | 12.1 | 24.2 | 30.3 |
| March | 4.66 | 7.7 | 225 | 42 | 28.4 | 16.6 | 28.3 | 35.4 |
| April | 5.98 | 8.2 | 181 | 32 | 35.4 | 22.9 | 18.3 | 22.9 |
| May | 10.01 | 10.7 | 302 | 22 | 42.7 | 29.1 | 0.1 | 0.1 |
| June | 10.83 | 11.3 | 294 | 20 | 45.6 | 31.7 | 0 | 0 |
| July | 10.28 | 10.9 | 259 | 20 | 46.6 | 32 | 0 | 0 |
| August | 10.28 | 10.7 | 251 | 21 | 43.4 | 28.7 | 1.1 | 1.4 |
| September | 7.05 | 9.2 | 216 | 26 | 37.4 | 24 | 2.5 | 3.1 |
| October | 4.21 | 7.1 | 181 | 43 | 28.1 | 16.9 | 22.7 | 28.4 |
| November | 2.3 | 6.3 | 147 | 58 | 20.4 | 10.8 | 39.5 | 49.4 |
| December | 1.69 | 6.2 | 147 | 63 | 17.4 | 8.3 | 39.5 | 49.4 |
| Soil | Value |
|---|---|
| Soil type | Lumi Sandy |
| Saturated hydraulic conductivity (mm·day−1) | 1200 |
| Saturated moisture (V %) | 41 |
| Crop capacity point (V %) | 22 |
| Permanent wilting point (V %) | 10 |
| Thickness of soil layer (m) | 2.5 |
| Soil penetration coefficient | 46 |
| Bulk density (gr·cm−3) | 1.4 |
| Crop Characteristics | Crop | Unit | ||
|---|---|---|---|---|
| Winter Wheat | Barley | |||
| Crop type | Root | Root | ||
| Planting method | Sowing | Sowing | ||
| Category of the plant in terms of carbon | C3 | C3 | ||
| Cropping period | 22 October | 22 October | ||
| Length of growing cycle | 180 | 170 | Days | |
| Canopy development | Canopy growth coefficient (CGC) | 18.40 | 11 | % inc. in CC relative to existi. CC per GDD |
| Canopy decline coeff. (CDC) at senescence | 8.70 | 9.40 | %; decrease in CC relative to CCx per GDD | |
| Canopy cover (CCo) | 6 | 6 | % at 90% emergence | |
| Maximum canopy cover | 93 | 93 | CCx (%) | |
| Shading surface during germination | 1.50 | 1.50 | cm2 | |
| Growing cycle | Germination | 30 | 20 | day |
| Flowering | 60 | 60 | day | |
| Granulation period | 90 | 70 | day | |
| Senescence | 110 | 90 | day | |
| Root deepening | Min. | 0.20 | 0.20 | m |
| Max. | 1.20 | 1.00 | m | |
| Time to reach maximum root depth | 70 | 70 | Day | |
| Temperature | Base temperature | 0 | 0 | °C |
| Cut-off temperature | 30 | 15 | °C | |
| Minimum degree of pollination | 5 | 5 | °C | |
| Maximum degree of pollination | 35 | 35 | °C | |
| Harvest Index | 50 | % | ||
| Soil water drainage deduction for vegetation development | P(upper) | 0.25 | 0.25 | At this amount, vegetative growth stops |
| P(lower) | 0.60 | 0.60 | At this amount, vegetative growth stops | |
| Upper threshold of stomatal conductance | P(upper) | 0.65 | 0.65 | Above this, stomata begin to close |
| Upper threshold of senescence stress | P(upper) | 0.65 | 0.65 | |
| Canopy growth factor | 5 | 3 | ||
| Stomatal control method factor | 2.50 | 3 | ||
| Transpiration | Transpiration coefficient at maximum coverage | 1.15 | 1 | |
| Effect of canopy on reducing evaporation at the end of growth | 50 | 50 | % | |
| Percentage decrease in Kc with age | 0.15 | 0.13 | % | |
| Irrigation method | Furrow irrigation | |||
| Available water | 70 | 70 | ||
| Number of irrigations | 6 | 5 | ||
| Salinity stress | Upper limit threshold of salinity stress | 15 | 15 | ds·m−1 |
| Salinity threshold decreases yield | 6 | 7 | ds·m−1 | |
| Treatment | Yield (ton/ha) | Pe | Biomass (ton/ha) | Pe | WP (kg·m−3) | Pe | |||
|---|---|---|---|---|---|---|---|---|---|
| Obs. | Sim. | (±%) | Obs. | Sim. | (±%) | Obs. | Sim. | (±%) | |
| T100 | 4.50 | 4.69 | 4.22 | 8.837 | 8.668 | 1.91 | 0.66 | 0.682 | 3.33 |
| T90 | 4.037 | 4.21 | 4.29 | 8.357 | 8.198 | 1.90 | 0.71 | 0.74 | 3.04 |
| T80 | 3.677 | 3.79 | 3.07 | 7.482 | 7.727 | 3.27 | 0.79 | 0.814 | 8.86 |
| T70 | 3.200 | 3.29 | 2.81 | 6.951 | 7.181 | 3.30 | 0.85 | 0.87 | 2.35 |
| T60 | 2.918 | 3.01 | 3.15 | 6.315 | 6.503 | 2.97 | 0.92 | 0.951 | 3.37 |
| T50 | 2.583 | 2.65 | 2.59 | 5.584 | 5.859 | 4.92 | 1.13 | 1.08 | 4.42 |
| Treatment | Yield (ton/ha) | Pe | Biomass (ton/ha) | Pe | WP (kg·m−3) | Pe | |||
|---|---|---|---|---|---|---|---|---|---|
| Obs. | Sim. | (±%) | Obs. | Sim. | (±%) | Obs. | Sim. | (±%) | |
| T100 | 2.80 | 2.92 | 4.29 | 11.71 | 11.34 | 3.16 | 0.71 | 0.74 | 4.23 |
| T90 | 2.548 | 2.64 | 3.61 | 10.84 | 10.599 | 2.22 | 0.76 | 0.79 | 3.95 |
| T80 | 2.335 | 2.41 | 3.21 | 9.721 | 9.857 | 1.40 | 0.84 | 0.82 | 2.38 |
| T70 | 2.002 | 2.1 | 4.90 | 8.863 | 9.112 | 2.81 | 0.87 | 0.90 | 3.45 |
| T60 | 1.79 | 1.87 | 4.47 | 7.947 | 8.183 | 2.97 | 1.02 | 1.06 | 3.92 |
| T50 | 1.55 | 1.6 | 3.23 | 6.882 | 7.195 | 4.55 | 1.06 | 1.10 | 3.77 |
| Treatment | Yield (ton/ha) | Pe | Biomass (ton/ha) | Pe | WP (kg·m−3) | Pe | |||
|---|---|---|---|---|---|---|---|---|---|
| Obs. | Sim. | (±%) | Obs. | Sim. | (±%) | Obs. | Sim. | (±%) | |
| T100 | 4.8 | 4.47 | 6.87 | 9.14 | 8.97 | 1.86 | 0.73 | 0.75 | 2.74 |
| T90 | 4.1 | 3.98 | 2.93 | 8.87 | 8.70 | 1.91 | 0.76 | 0.79 | 3.95 |
| T80 | 3.8 | 3.76 | 1.05 | 7.93 | 7.67 | 3.28 | 0.84 | 0.87 | 3.57 |
| T70 | 3.34 | 3.09 | 7.48 | 7.48 | 7.24 | 3.21 | 0.91 | 0.95 | 4.40 |
| T60 | 3.13 | 2.87 | 8.3 | 7.07 | 6.87 | 2.83 | 0.98 | 1.03 | 5.10 |
| T50 | 2.73 | 2.51 | 8.06 | 6.62 | 6.32 | 4.53 | 1.18 | 1.22 | 3.39 |
| Treatment | Yield (ton/ha) | Pe | Biomass (ton/ha) | Pe | WP (kg·m−3) | Pe | |||
|---|---|---|---|---|---|---|---|---|---|
| Obs. | Sim. | (±%) | Obs. | Sim. | (±%) | Obs. | Sim. | (±%) | |
| T100 | 3.1 | 3.25 | 4.84 | 12.3 | 12.00 | 2.44 | 0.74 | 0.778 | 5.14 |
| T90 | 2.81 | 2.92 | 3.91 | 11.46 | 11.28 | 1.57 | 0.79 | 0.82 | 3.8 |
| T80 | 2.48 | 2.56 | 3.23 | 10.47 | 10.37 | 0.95 | 0.87 | 0.91 | 4.6 |
| T70 | 2.42 | 2.50 | 3.31 | 9.86 | 9.65 | 2.13 | 0.91 | 0.962 | 5.71 |
| T60 | 2.11 | 2.19 | 3.79 | 8.77 | 8.57 | 2.28 | 1.1 | 1.152 | 4.73 |
| T50 | 1.83 | 1.88 | 2.73 | 7.62 | 7.36 | 3.41 | 1.17 | 1.22 | 4.27 |
| Absolute Value of the Critical Point of Winter Wheat: 3.43 Absolute Value of the Critical Point of Barley: 3.17 | Hypothesis H0: Yij = Yji H1: Yij ≠ Yji | |
|---|---|---|
| Significance Level: 0.05 | ||
| Irrigation scenarios | Absolute value of F statistic | Absolute value of F statistic |
| Winter Wheat | Barley | |
| 50% | 1.15 | 1.06 |
| 60% | 1.18 | 1.31 |
| 70% | 1.10 | 1.28 |
| 80% | 1.13 | 1.39 |
| 90% | 1.15 | 1.30 |
| 100% | 1.06 | 1.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khoshsirat, A.M.; Najarchi, M.; Jafarinia, R.; Mokhtari, S. Sensitivity Analysis and Determination of the Optimal Level of Water Use Efficiency for Winter Wheat and Barley under Different Irrigation Scenarios Using the AquaCrop Model in Arid and Semiarid Climatic Conditions (Case Study: Dehloran Plain, Iran). Water 2022, 14, 3455. https://doi.org/10.3390/w14213455
Khoshsirat AM, Najarchi M, Jafarinia R, Mokhtari S. Sensitivity Analysis and Determination of the Optimal Level of Water Use Efficiency for Winter Wheat and Barley under Different Irrigation Scenarios Using the AquaCrop Model in Arid and Semiarid Climatic Conditions (Case Study: Dehloran Plain, Iran). Water. 2022; 14(21):3455. https://doi.org/10.3390/w14213455
Chicago/Turabian StyleKhoshsirat, Amir Mahyar, Mohsen Najarchi, Reza Jafarinia, and Shahroo Mokhtari. 2022. "Sensitivity Analysis and Determination of the Optimal Level of Water Use Efficiency for Winter Wheat and Barley under Different Irrigation Scenarios Using the AquaCrop Model in Arid and Semiarid Climatic Conditions (Case Study: Dehloran Plain, Iran)" Water 14, no. 21: 3455. https://doi.org/10.3390/w14213455
APA StyleKhoshsirat, A. M., Najarchi, M., Jafarinia, R., & Mokhtari, S. (2022). Sensitivity Analysis and Determination of the Optimal Level of Water Use Efficiency for Winter Wheat and Barley under Different Irrigation Scenarios Using the AquaCrop Model in Arid and Semiarid Climatic Conditions (Case Study: Dehloran Plain, Iran). Water, 14(21), 3455. https://doi.org/10.3390/w14213455




